Steady-State Simulation of a Fixed-Bed Reactor for the Total Oxidation of Volatile Organic Components: Application of the Barkelew Criterion
Abstract
1. Introduction
2. Model Description
2.1. Reactor Model
| Parameter | Symbol | Units | Value |
|---|---|---|---|
| reactor configuration | |||
| number of tubes | Nt | - | 3000 |
| inner diameter | dt | m | 0.016 |
| wall thickness | dw | m | 0.002 |
| wall heat conductivity | λw | W m−1 K−1 | 48.9 + 0.0426 T [27] |
| tube length | Lt | m | 12.0 |
| bed porosity | εb | m3 m−3 | 0.49 |
| catalyst | |||
| equivalent particle diameter | dp | m | 2.33 × 10−3 |
| pore radius | rp | m | 6.34 × 10−9 |
| particle porosity | εp | m3 m−3 | 0.62 |
| tortuosity | τp | m m−1 | 2.0 [28] |
| density | kgcat mcat−3 | 3254 | |
| effective thermal conductivity | λe | J m−1 s−1 K−1 | 36.0 [27] |
| operating conditions | |||
| inlet temperature | T0 | K | 598 |
| reactor temperature | Tr | K | 648 |
| inlet total pressure | pt,0 | Pa | 2.10 × 10+5 |
| inlet total flow rate | Ft,0 | molt,0 s−1 | 26.6 |
| inlet mole fractions | 3.70 × 10−3 | ||
| 1.00 × 10−1 | |||
| 1.00 × 10−1 | |||
| heat of reaction | −ΔrH | J mol−1 | 1.98 × 10+6 |
| Parameter | Units | Value |
|---|---|---|
| Mass transfer | ||
| 0.14 | ||
| 1.91 | ||
| jD | - | 0.07 |
| Rep | - | 1.05 × 10+2 |
| Sc | - | 0.45 |
| lhs Equation (4) | - | 3.78 × 10−4 |
| - | 2.12 | |
| Heat transfer | ||
| α | 3.50 × 10+2 | |
| jH | - | 0.17 |
| Pr | - | 0.60 |
| lhs Equation (5) | - | 1.05 × 10−5 |
| - | 1.62 × 10−4 |
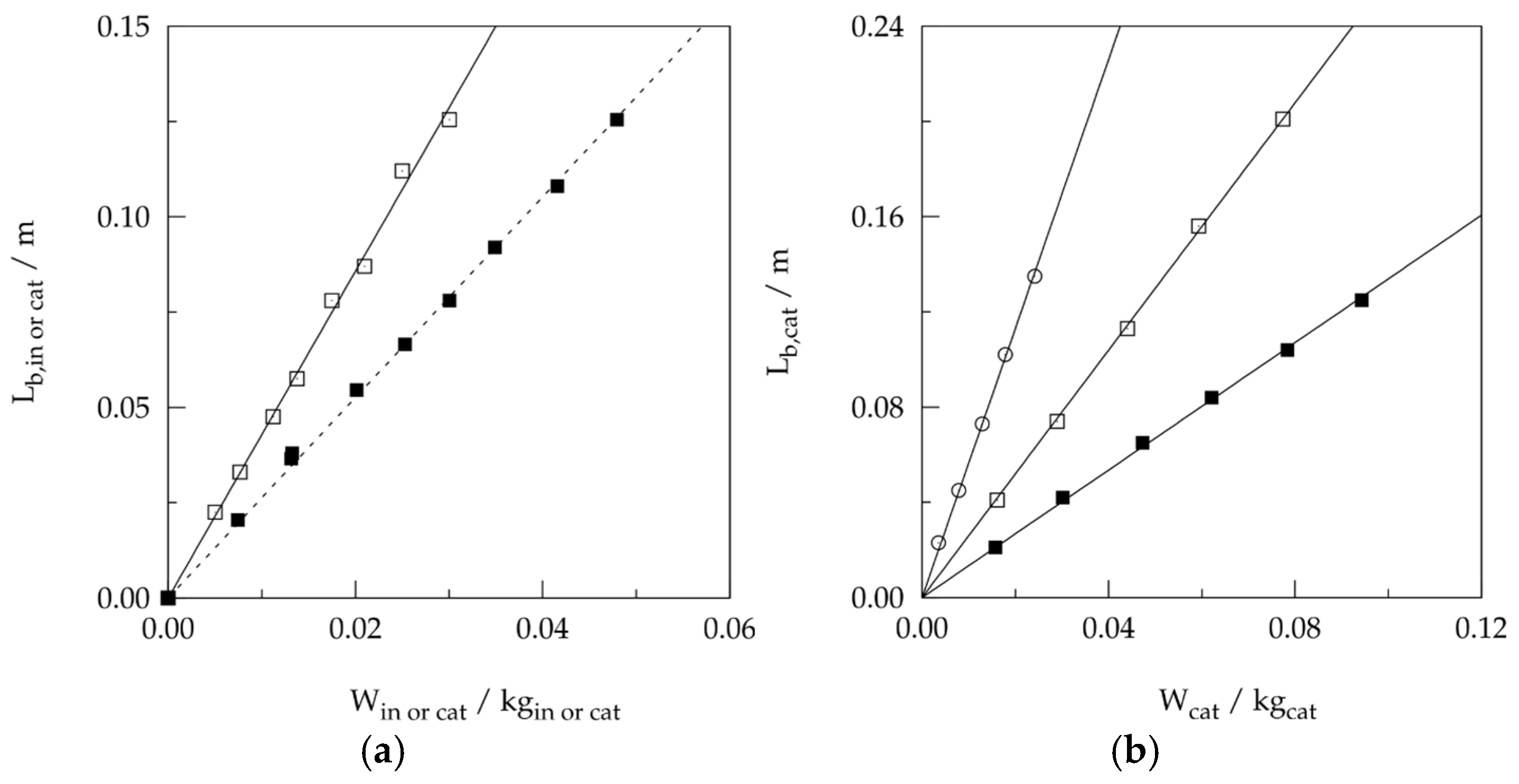
2.2. External Gradients
2.3. Kinetic Model
2.4. Solution Procedure
2.5. Reactor Duty in Total Oxidation Operation
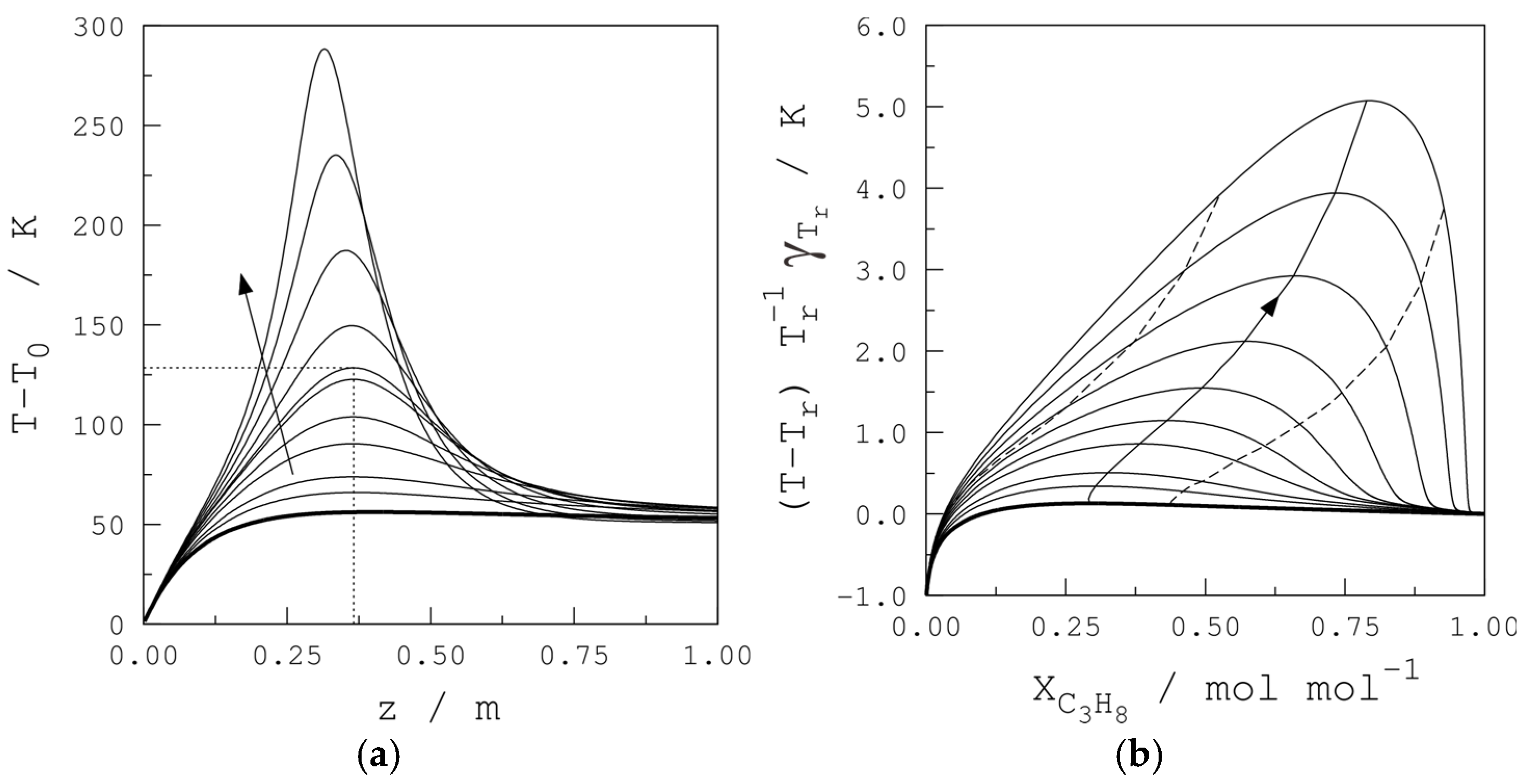
3. Safety and Runaway Criteria
4. Results and Discussion
4.1. Reactor Dimension and Operation Conditions
4.2. Base Case
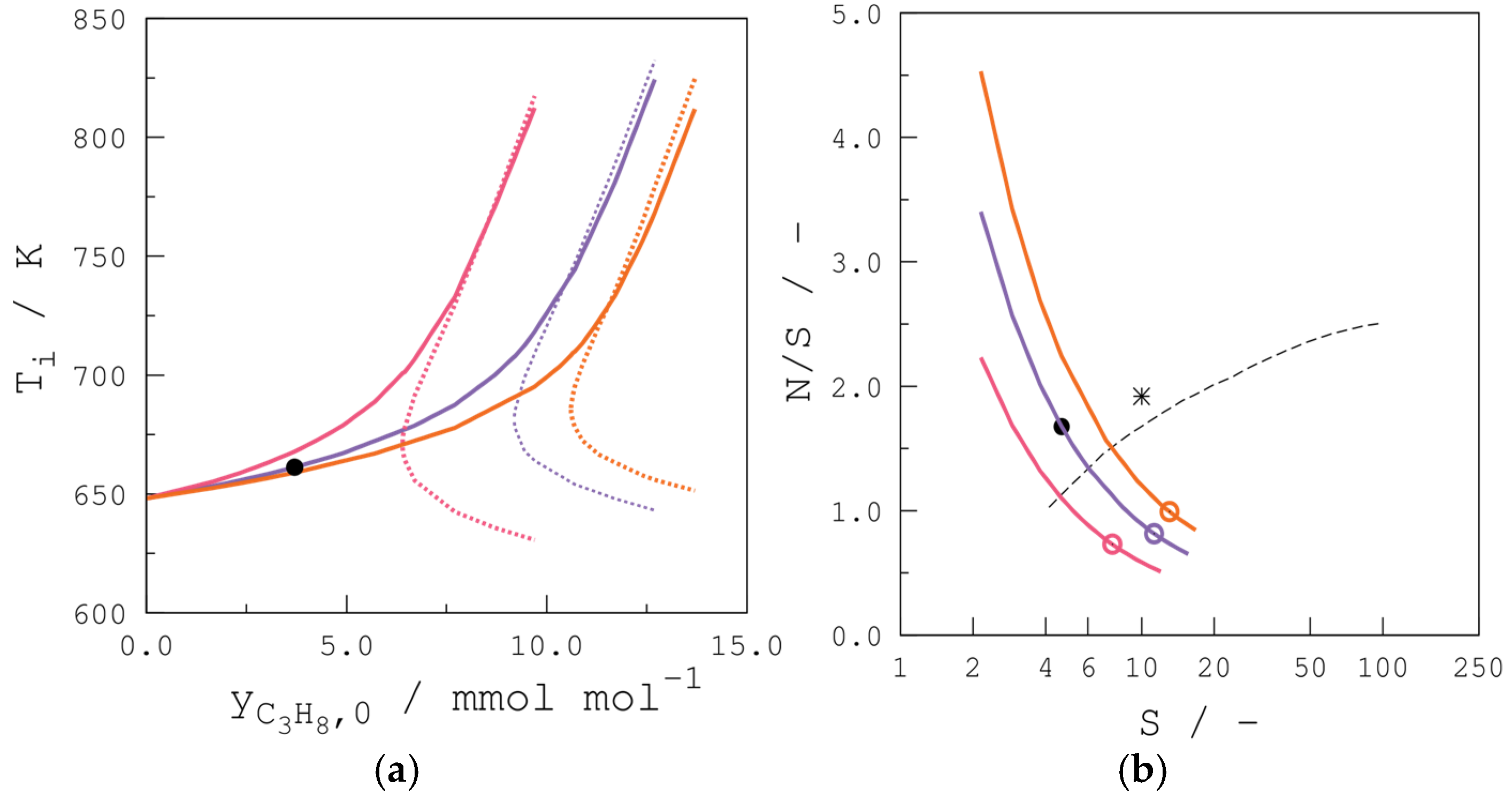
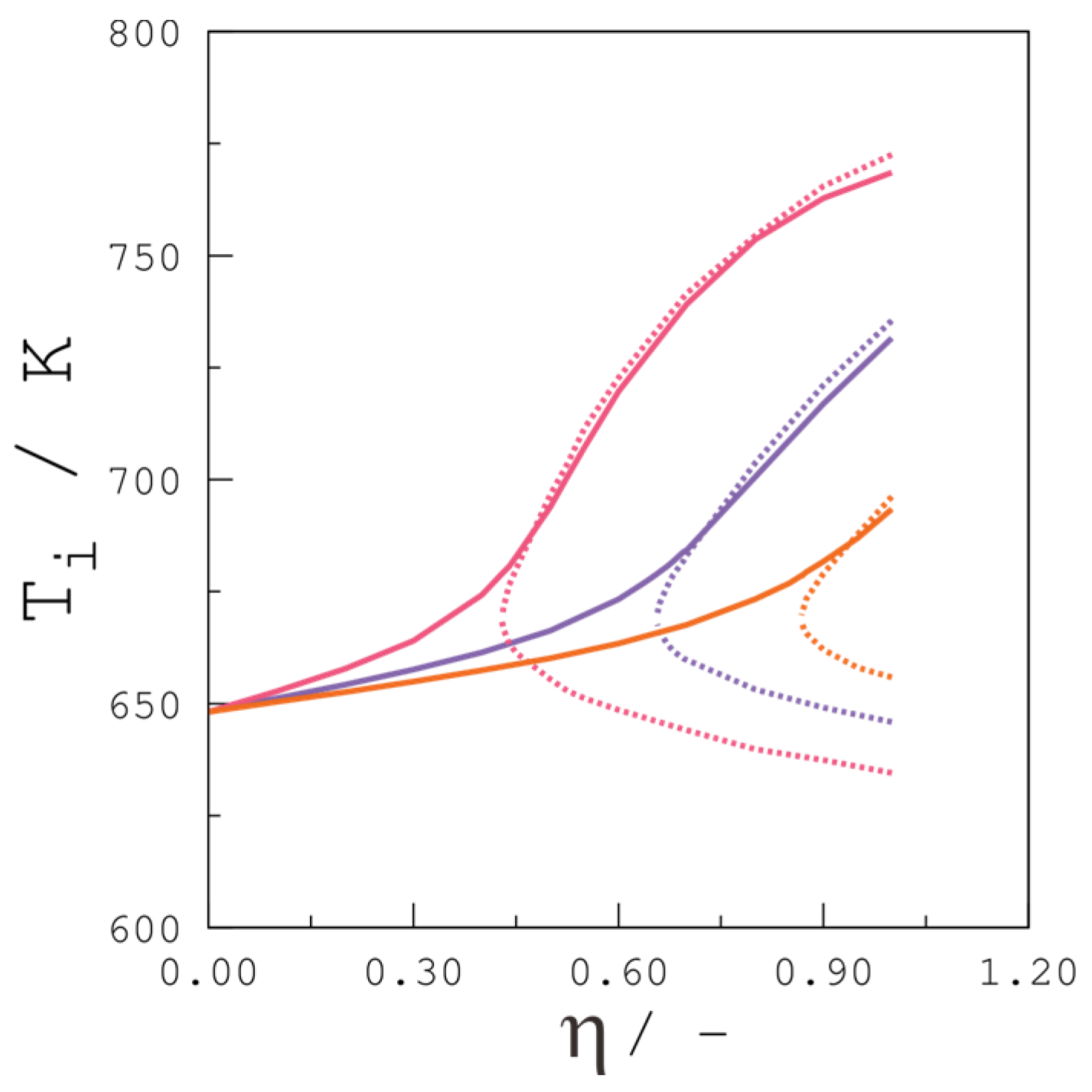
4.3. Variation of Inlet Conditions and Runaway Behavior
4.3.1. Total Inlet Pressure
4.3.2. Inlet Temperature
4.3.3. Propane Inlet Molar Fraction
4.3.4. Reactor Temperature
4.3.5. Water Inlet Pressure
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B
Appendix C. Symbols and Annotations
| Roman symbols | ||
| as | specific external surface | |
| cp,f | specific heat | J mol−1 K−1 |
| Ci | molar concentration of component i | mol m−3 |
| d | diameter | m |
| Di | diffusion coefficient for component i | m2 s−1 |
| EA | activation energy | kJ mol−1 |
| f | friction factor | - |
| Fi | molar flow rate of component i | mol s−1 |
| ΔHi | adsorption enthalpy for component i | kJ mol−1 |
| −ΔrH | reaction enthalpy | kJ mol−1 |
| k | reaction coefficient | dep. |
| mass transfer coefficient from gas to solid interface | ||
| k* | rate coefficient; see Equation (27) | |
| Kj | adsorption equilibrium coefficient for component j | kPa−1 |
| L | reactor length | m |
| N | defined by Equation (26) | - |
| Nt | number of tubes | - |
| p | pressure | kPa |
| ), based on particle diameter | - | |
| Pr | ) | - |
| Δp | pressure drop | kPa |
| r | specific reaction rate | |
| rp | mean pore radius | m |
| R | universal gas constant | kJ mol−1 K−1 |
| Rep | ), based on particle diameter | - |
| Rw,i | specific production rate of component i | |
| S | defined by Equation (25) | - |
| Sc | Schmidt number (= ) | - |
| ΔSi | adsorption entropy for component i | J mol−1 K−1 |
| T | temperature | K |
| u | velocity | m s−1 |
| U | overall heat transfer coefficient | J m−2 K−1 s−1 |
| X | fractional conversion | mol mol−1 |
| z | axial coordinate | m |
| Greek symbols | ||
| α | convective heat transfer coefficient | |
| γ | dimensionless activation energy | - |
| ε | porosity | m3 m−3 |
| η | effectiveness factor | - |
| θ | fraction of active sites | - |
| ϑ* | dimensionless temperature; see Equation (28) | - |
| λ | heat conductivity | J m−1 s−1 K−1 |
| ρ | density | kg m−3 |
| τ | tortuosity | m−2 m−2 |
| φ | generalized Thiele modulus | - |
| Ω | cross section of reactor | m2 |
| Subscripts | ||
| a | axial | |
| atm | atmospheric | |
| b | bed, bulk | |
| cat | catalyst | |
| diss | dissociation | |
| e | effective | |
| eq | equilibrium | |
| f | fluid | |
| h | heat transfer | |
| i | component i, interstitial, inflection point | |
| K | Knudsen | |
| m | molecular, mass transfer, mixture | |
| p | particle, pore | |
| r | reactor | |
| s | inside solid, superficial | |
| t | total, tube | |
| w | wall | |
| 0 | initial | |
| Superscripts | ||
| obs | observed | |
| s | condition at external surface | |
| * | critical, reference, surface species | |
| - | averaged | |
| Abbreviations and acronyms | ||
| LEL | lower explosion limit | |
| lhs | left hand side | |
| LH | Langmuir–Hinshelwood | |
| VOC | volatile organic component | |
References
- Theloke, J.; Friedrich, R. Compilation of a database on the composition of anthropogenic VOC emissions for atmospheric modeling in Europe. Atmos. Environ. 2007, 41, 4148–4160. [Google Scholar] [CrossRef]
- Tomasic, V. Application of the monoliths in DeNOx catalysis. Catal. Today 2007, 119, 106–113. [Google Scholar] [CrossRef]
- Froment, G.F.; Bischoff, K.B. Chemical Reactor Analysis, 2nd ed.; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Baptista, C.M.S.G.; Castro, J.A.A.M. A contribution to the study of runaway and parametric sensitivity in fixed bed catalytic reactors. Chem. Eng. Sci. 1996, 51, 3119–3124. [Google Scholar] [CrossRef]
- Velo, E.; Bosch, C.M.; Recasens, F. Thermal safety of batch reactors and storage tanks. Development and validation of runaway boundaries. Ind. Eng. Chem. Res. 1996, 25, 1288–1299. [Google Scholar] [CrossRef]
- Quina, M.M.J.; Ferreira, R.M.Q. Thermal runaway conditions of a partially diluted catalytic reactor. Ind. Eng. Chem. Res. 1999, 38, 4615–4623. [Google Scholar] [CrossRef]
- Zhang, J.; Tighe, C.J.; Hellgardt, K.; Unruh, D.; Bos, R. Generalized runaway diagrams for catalytic reactors with stacked catalyst activities. Chem. Eng. J. 2024, 502, 157960. [Google Scholar] [CrossRef]
- Calverley, E.M.; Witt, P.M.; Sweeney, J.D. Reactor runaway due to statistically driven axial activity variations in graded catalyst beds. Chem. Eng. Sci. 2012, 80, 393–401. [Google Scholar] [CrossRef]
- Kummer, A.; Varga, T. What do we know already about reactor runaway? A review. Process Saf. Environ. Prot. 2021, 147, 460–476. [Google Scholar] [CrossRef]
- Westerterp, K.R.; Molga, E.J. Safety and runaway prevention in batch and semibatch reactors—A review. Chem. Eng. Res. Des. 2006, 84, 543–552. [Google Scholar] [CrossRef]
- Yang, Y.N.; Jin, J.; Zhu, L.T.; Zhou, Y.N.; Luo, Z.H. Runaway criteria for predicting the thermal behavior of chemical reactors. Curr. Opin. Chem. Eng. 2023, 43, 100986. [Google Scholar] [CrossRef]
- Arpentier, P.; Cavani, F.; Trifirò, F. The Technology of Catalytic Oxidations; Technip: Paris, France, 2001. [Google Scholar]
- Morbidelli, M.; Varma, A. Parametric sensitivity and runaway in tubular reactors. AIChE J. 1982, 28, 705–713. [Google Scholar] [CrossRef]
- Young, L.C.; Finlayson, B.A. Axial dispersion in nonisothermal packed bed chemical reactors. Ind. Eng. Chem. Fundam. 1973, 12, 412–422. [Google Scholar] [CrossRef]
- Kulkarni, B.D.; Doriswamy, L.K. Estimation of effective transport properties in packed bed reactors. Catal. Rev. Sci. Eng. 1980, 22, 431–483. [Google Scholar] [CrossRef]
- Heynderickx, P.M.; Thybaut, J.W.; Poelman, H.; Poelman, D.; Marin, G.B. Kinetic modeling of the total oxidation of propane over anatase and vanadia sputter deposited catalysts. Appl. Catal. B Environ. 2009, 90, 295–306. [Google Scholar] [CrossRef]
- Heynderickx, P.M.; Thybaut, J.W.; Poelman, H.; Poelman, D.; Marin, G.B. Kinetic modeling of the total oxidation of propane over CuO-CeO2/γ-Al2O3. Appl. Catal. B Environ. 2010, 95, 26–38. [Google Scholar] [CrossRef]
- Donaubauer, P.J.; Schmalhorst, L.; Hunrichsen, O. 2D flow fields in fixed-bed reactor design: A robust methodology for continuum models. Chem. Eng. Sci. 2007, 208, 115137. [Google Scholar] [CrossRef]
- Kern, C.; Jess, A. On the role of radial dispersion in the behavior of a cooled fixed-bed reactor: Numerical investigation of Fischer–Tropsch synthesis with a cobalt-based catalyst. Chem. Eng. Technol. 2024, 47, e202400201. [Google Scholar] [CrossRef]
- de Smet, C.R.H.; de Croon, M.H.J.M.; Berger, R.J.; Marin, G.B.; Schouten, J.C. Design of adiabatic fixed-bed reactors for the partial oxidation of methane to synthesis gas. Application to production of methanol and hydrogen-for-fuel-cells. Chem. Eng. Sci. 2001, 56, 4849–4861. [Google Scholar] [CrossRef]
- De Groote, A.M.; Froment, G.F. Simulation of the catalytic partial oxidation of methane to synthesis gas. Appl. Catal. A Gen. 1996, 138, 245–264. [Google Scholar] [CrossRef]
- Lommerts, B.J.; Graaf, G.H.; Beenacker, A.C.M. Mathematical modeling of internal mass transport limitations in methanol synthesis. Chem. Eng. Sci. 2000, 55, 5589–5598. [Google Scholar] [CrossRef]
- Lee, J.K.; Ko, J.B.; Kim, D.H. Methanol steam reforming over Cu/ZnO/Al2O3 catalyst: Kinetics and effectiveness factor. Appl. Catal. A Gen. 2004, 278, 25–35. [Google Scholar] [CrossRef]
- Carrasco-Venegas, L.A.; nzález-Fernández, J.V.; Castañeda-Pérez, L.G.; Medina-Collana, J.T.; Palomino-Hernández, G.; Martínez-Hilario, D.G.; Trujillo-Pérez, S.A. Analysis of the effectiveness factor in a fixed-bed tubular reactor system: Catalytic dehydrogenation of cyclohexanol. Catalysts 2023, 13, 585. [Google Scholar] [CrossRef]
- Lee, S.B.; Cho, W.; Park, D.K.; Yoon, E.S. Analysis of the effectiveness factor in a fixed-bed tubular reactor system: Catalytic dehydrogenation of cyclohexanol. Korean J. Chem. Eng. 2006, 23, 522–530. [Google Scholar] [CrossRef]
- Kim, D.H.; Park, D.R.; Lee, J. Preferential CO oxidation over CuO-CeO2 in excess hydrogen: Effectiveness factors of catalyst particles and temperature window for CO removal. Int. J. Hydrog. Energy 2013, 38, 4429–4436. [Google Scholar] [CrossRef]
- Perry, R.H.; Green, D.W.; Maloney, J.O. Perry’s Chemical Engineers’ Handbook, 2nd ed.; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Zalc, J.M.; Reyes, S.C.; Iglesia, E. The effects of diffusion mechanism and void structure on transport rates and tortuosity factors in complex porous structures. Chem. Eng. Sci. 2004, 59, 2947–2960. [Google Scholar] [CrossRef]
- Berger, R.J.; Stitt, E.H.; Marin, G.B.; Kapteijn, F.; Moulijn, J.A. Eurokin. Chemical reaction kinetics in practice. Cattech 2001, 5, 30–60. [Google Scholar] [CrossRef]
- Welty, J.R.; Wicks, C.E.; Wilson, R.E.; Rorrer, G.L. Fundamentals of Momentum, Heat and Mass Transfer, 5th ed.; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Kunii, D.; Suzuki, M. Particle-to-fluid heat and mass transfer in packed beds of fine particles. Int. J. Heat Mass Transf. 1967, 10, 845–852. [Google Scholar] [CrossRef]
- Sengupta, A.; Thodos, G. Mass and heat transfer in the flow of fluids through fixed and fluidized beds of spherical particles. AIChE J. 1962, 8, 608–610. [Google Scholar] [CrossRef]
- Deacetis, J.; Thodos, G. Mass and heat transfer in flow of gases through spherical packings. Ind. Eng. Chem. 1960, 52, 1003–1006. [Google Scholar] [CrossRef]
- Barkelew, C.H. Stability of chemical reactors. Chem. Eng. Prop. Symp. Ser. 1959, 55, 37–46. [Google Scholar]
- Van Welsenaere, R.J.; Froment, G.F. Parametric sensitivity and runaway in fixed bed catalytic reactors. Chem. Eng. Sci. 1970, 25, 1503–1516. [Google Scholar] [CrossRef]
- Available online: https://people.sc.fsu.edu/~jburkardt/f77_src/rk4/rk4.f (accessed on 13 February 2025).
- Leva, M. Fluid flow through packed beds. Chem. Eng. 1949, 56, 115–120. [Google Scholar]
- Hicks, R.E. Pressure drop in packed beds of spheres. Ind. Eng. Chem. Fundam. 1970, 9, 500–502. [Google Scholar] [CrossRef]
- Fuller, E.N.; Schettler, P.D.; Giddings, J.C. New Method for Prediction of Binary Gas-Phase Diffusion Coefficients. Ind. Eng. Chem. Res. 1966, 58, 18–27. [Google Scholar] [CrossRef]
- Available online: https://people.sc.fsu.edu/~jburkardt/f77_src/toms446/toms446.html (accessed on 13 February 2025).
- Szeifert, F.; Chovan, T.; Nagy, L.; Abonyi, J.; Arva, P. Runaway of chemical reactions: Parametric sensitivity and stability. Hung. J. Ind. Chem. 2007, 35, 19–30. [Google Scholar] [CrossRef]
- Casson, V.; Lister, D.G.; Milazzo, M.F.; Maschio, G. Comparison of criteria for prediction of runaway reactions in the sulphuric acid catalyzed esterificationof acetic anhydride and methanol. J. Loss Prev. Process Ind. 2012, 25, 209–217. [Google Scholar] [CrossRef]
- Vianello, C.; Salzaon, E.; Brocanello, A.; Manzardo, A.; Maschio, G. Runaway reaction for the esterification of acetic anhydride with methanol catalyzed bysulfuric acid. Ind. Eng. Chem. Res. 2018, 57, 4195–4202. [Google Scholar] [CrossRef]
- Emig, G.; Hofman, H.; Hoffmann, U.; Fiand, U. Experimental studies on runaway of catalytic fixed-bed reactors (vinyl-acetate synthesis). Chem. Eng. Sci. 1980, 35, 249–257. [Google Scholar] [CrossRef]
- Moretti, E.C. Practical Solutions for Reducing Volatile Organic Compounds and Hazardous Air Pollutants; AIChE CWRT: New York, NY, USA, 2001; p. 150. [Google Scholar]
- Lin, H.; Gao, X.; Luo, Z.Y.; Cen, K.F.; Pei, M.X.; Huang, Z. Removal of NOx from wet flue gas by corona discharge. Fuel 2004, 83, 1251–1255. [Google Scholar] [CrossRef]
- Chen, J.-C.; Wey, M.-Y.; Yeh, C.-L.; Liang, Y.-S. Simultaneous treatment of organic compounds, CO, and NOx in the incineration flue gas by three-way catalyst. Appl. Catal. B Environ. 2004, 48, 25–35. [Google Scholar] [CrossRef]
- Heynderickx, P.M.; Thybaut, J.W.; Poelman, H.; Poelman, D.; Marin, G.B. The total oxidation of propane over supported Cu and Ce oxides: A comparison of single and binary metal oxides. J. Catal. 2010, 272, 109–120. [Google Scholar] [CrossRef]
- Available online: http://www.eurochlor.org/solventsemissionsdirective (accessed on 16 September 2009).
- Heynderickx, P.M. Steady-State Kinetic Modelling of the Total Oxidation of Propane over Metal Oxide Catalysts. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2009. Available online: https://biblio.ugent.be/publication/01J8PMN5S4RHQJG8BXWAFKAWN0 (accessed on 23 December 2009).



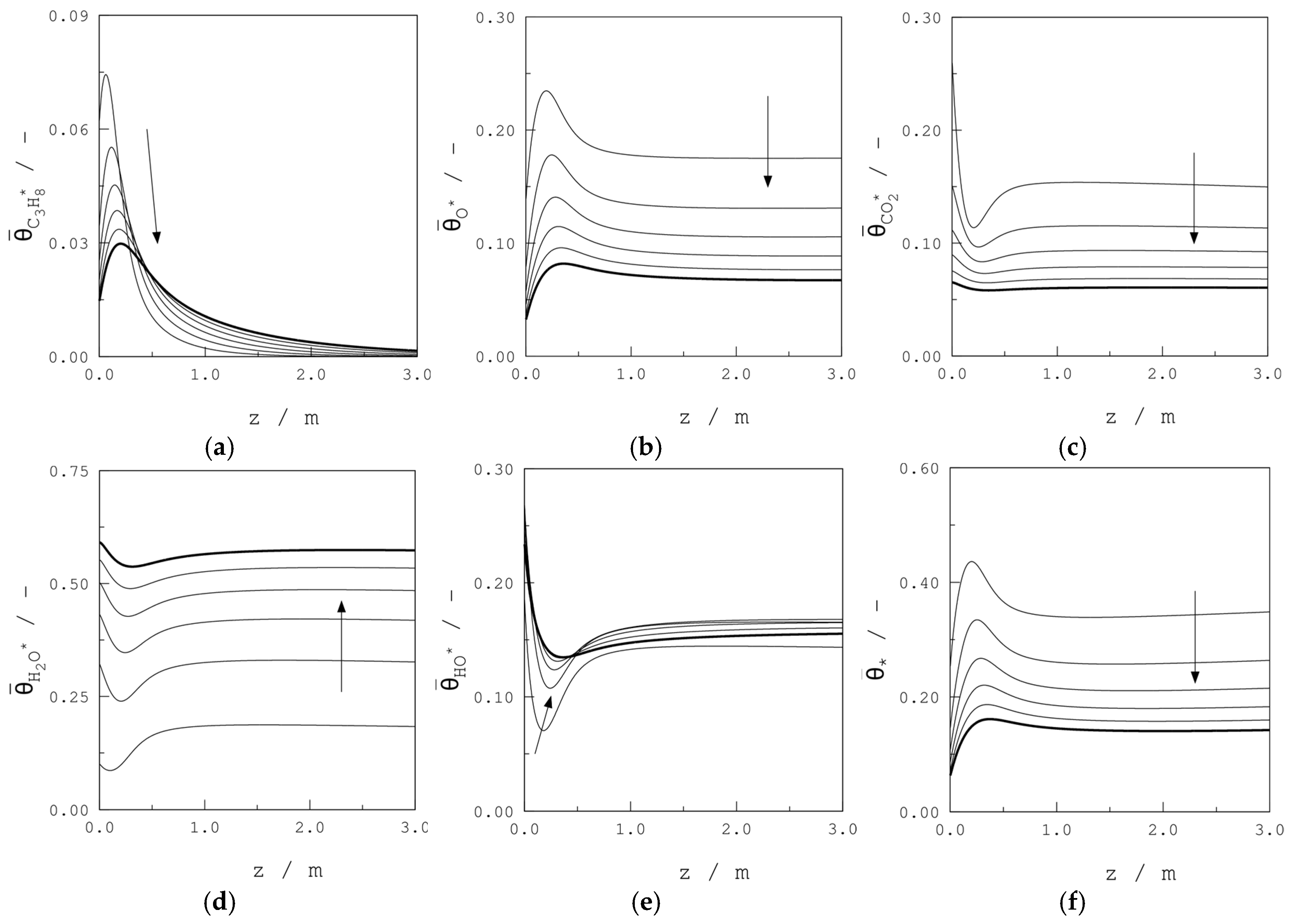
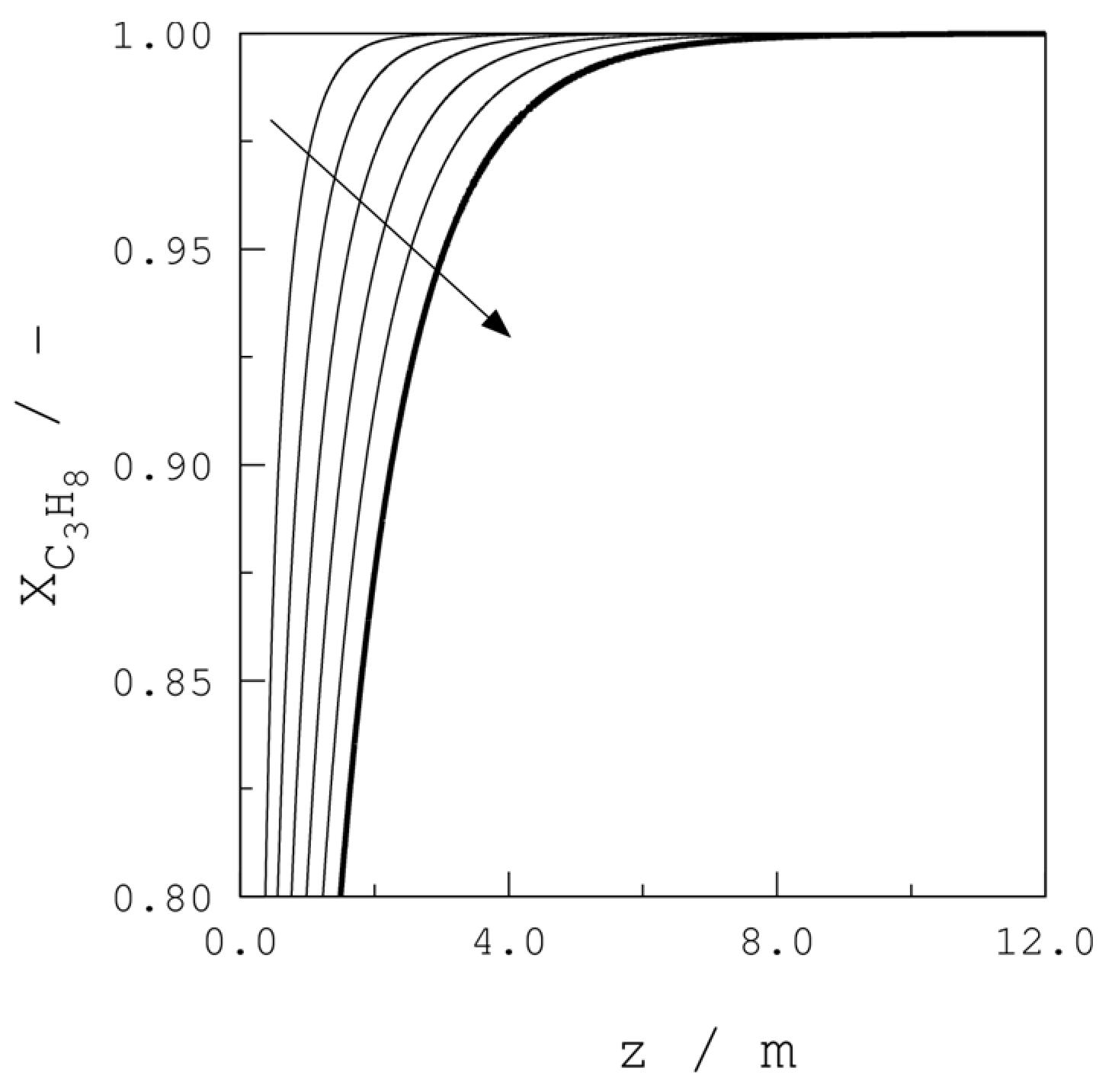
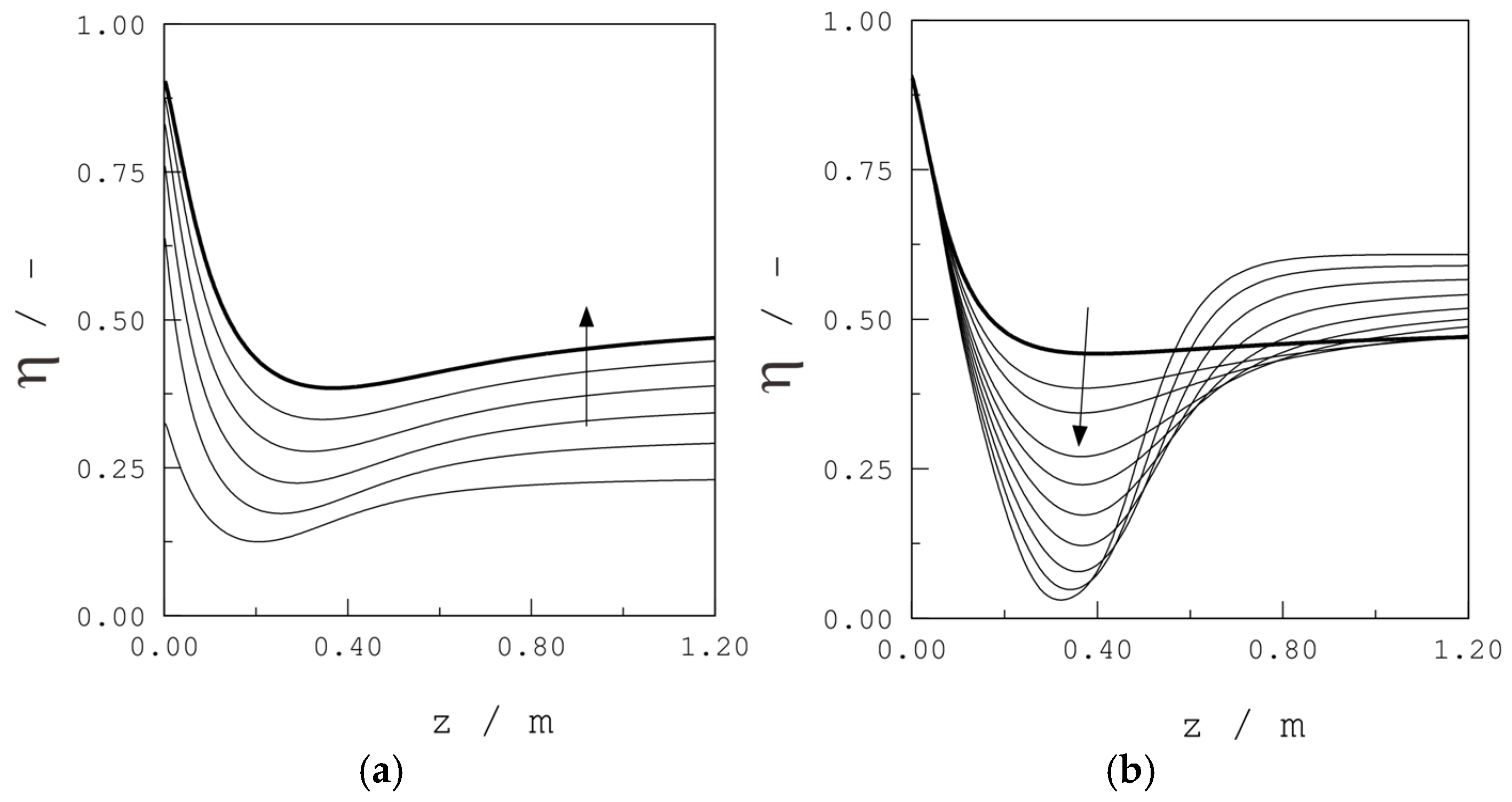
| Parameter | Units | Value |
|---|---|---|
| ks,0 | /mol kgcat−1 s−1 | (9.58 ± 1.11) 10+4 |
| E | /kJ mol−1 | 74.4 ± 4.6 |
| − | /J mol−1 K−1 | 97.7 ± 5.6 |
| − | /kJ mol−1 | 0.0 1 |
| −ΔS | /J mol−1 K−1 | 61.7 ± 0.4 |
| − | /kJ mol−1 | 0.0 1 |
| − | /J mol−1 K−1 | 154.2 ± 23.3 |
| − | /kJ mol−1 | 53.8 ± 20.0 |
| − | /J mol−1 K−1 | 173.3 ± 37.9 |
| − | /kJ mol−1 | 54.2 ± 23.7 |
| − | /J mol−1 K−1 | 156.5 ± 11.2 |
| − | /kJ mol−1 | 99.1 ± 10.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heynderickx, P.M.; Thybaut, J.W. Steady-State Simulation of a Fixed-Bed Reactor for the Total Oxidation of Volatile Organic Components: Application of the Barkelew Criterion. ChemEngineering 2025, 9, 46. https://doi.org/10.3390/chemengineering9030046
Heynderickx PM, Thybaut JW. Steady-State Simulation of a Fixed-Bed Reactor for the Total Oxidation of Volatile Organic Components: Application of the Barkelew Criterion. ChemEngineering. 2025; 9(3):46. https://doi.org/10.3390/chemengineering9030046
Chicago/Turabian StyleHeynderickx, Philippe M., and Joris W. Thybaut. 2025. "Steady-State Simulation of a Fixed-Bed Reactor for the Total Oxidation of Volatile Organic Components: Application of the Barkelew Criterion" ChemEngineering 9, no. 3: 46. https://doi.org/10.3390/chemengineering9030046
APA StyleHeynderickx, P. M., & Thybaut, J. W. (2025). Steady-State Simulation of a Fixed-Bed Reactor for the Total Oxidation of Volatile Organic Components: Application of the Barkelew Criterion. ChemEngineering, 9(3), 46. https://doi.org/10.3390/chemengineering9030046








