Experimental Investigation of Liquid Holdup in a Co-Current Gas–Liquid Upflow Moving Packed Bed Reactor with Porous Catalyst Using Gamma-Ray Densitometry
Abstract
1. Introduction
2. Materials and Methods
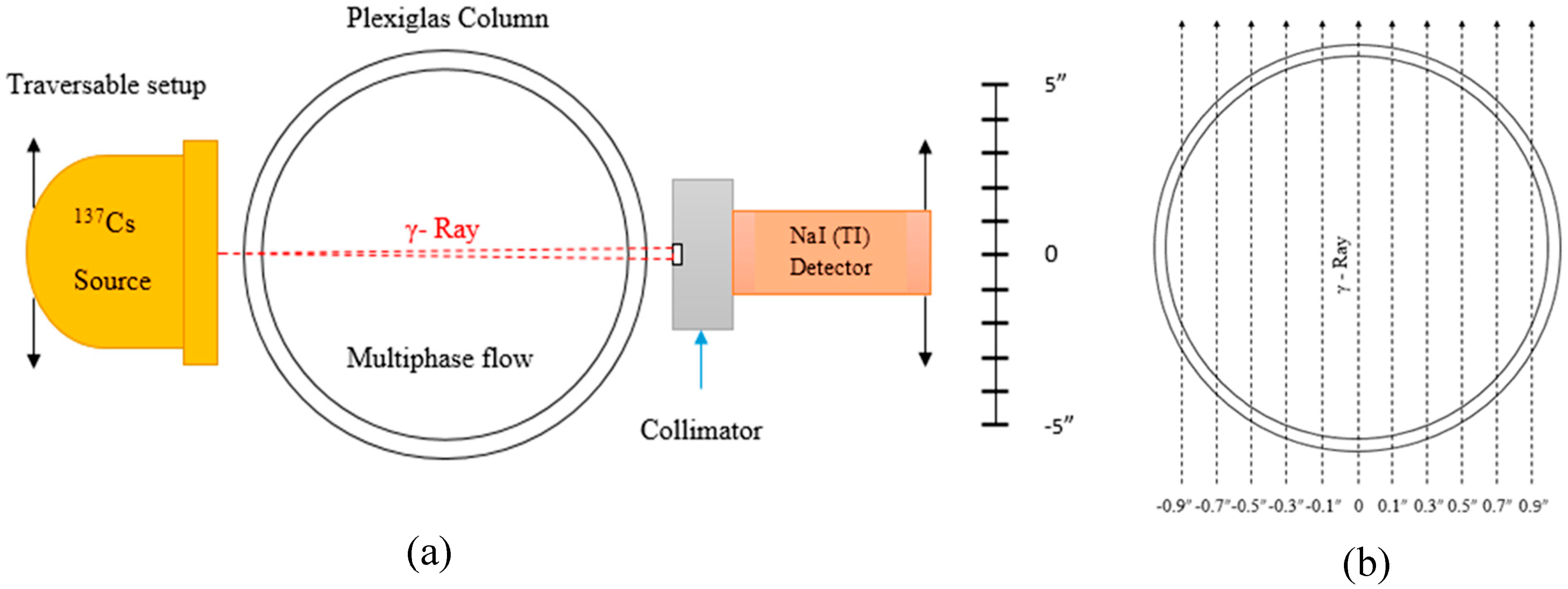
2.1. Experimental Setup
2.2. The Measurement Technique
2.3. The Principle of the Holdups’ Measurements and the New Methodology for Measuring External and Internal Liquid Holdups and Catalyst Porosity
- Gas–solid system:
- Liquid–solid system:
- Gas–liquid system:
- Gas phase:
- Solid phase:
- Liquid phase:
- I.
- Without column.
- II.
- The empty column for the wall attenuation.
- III.
- The column is filled only with water for the liquid attenuation.
- IV.
- The column is filled with packed bed for a dry catalyst representing the attenuation of the gas and solid phases.
- V.
- The packed column is filled with water first, then it is drained where the scan was for a wet catalyst attenuation (internal liquid holdup in the pores + static liquid holdup if any).
- VI.
- The packed bed is filled with water representing both liquid and solid attenuation.
- VII.
- Scanning the gas–liquid–solid flow under the desired operation at the same position where the holdups for all three phases can be obtained.
- I.
- Scanning without column (absorbing medium) (i.e., air only). In this scanning case, the GRD beam passes through the atmosphere from the source to the detector without any absorbing medium in between them. The obtained attenuation is due to air only () which represents the incident radiation () [31]. The gamma-ray source is placed on one side, and the scintillation detector is on the other side.
- II.
- Scanning the empty column for the wall attenuation of plexiglass (air inside only, baseline). In this scanning case, the GRD beam passes through the empty column, and the attenuation is due to the wall of the column and the gas (air) inside it. The obtained attenuation is due to wall column and air. The mass attenuation coefficient of the air () is negligible compared to the Plexiglas (), due to less interaction of air in comparison with Plexiglas. Hence:
- III.
- Scanning the column full of water for liquid attenuation (i.e., water inside only, liquid phase). In this scanning case, the same packed column is filled with water only in which the GRD beam passes through the column wall and the water. The obtained attenuation is due to the wall of the column and the liquid inside it:
- IV.
- Scanning the column packed with dry solid catalyst as (i.e., dry catalyst inside only, dry solid phase). In this scanning case, the same packed column was packed with dry solid particles only in which the GRD beam passes through the column wall, the dry catalyst, and the gas in voids of the bed. The obtained attenuation is due to the wall of the column, the dry solid catalyst, and the gas in voids between solid catalysts and in porosity, where the latter is negligible:
- V.
- Scanning the column packed with wet solid catalyst, (i.e., wet catalyst inside only—wet solid phase). The same packed bed, which has the dry solid catalyst particles, was filled with water for a sufficient time and then the column was left to drain for a number of hours to ensure that the external static liquid became negligible. The external static liquid holdup in this step is negligible as proper draining ensures that there is no liquid outside of the catalyst pores present in the measured line-averaged location. Additionally, the measurement is conducted using a line beam gamma-ray, penetrating only through catalyst particles or spherical particles within certain contact points. Consequently, it is logical to either disregard external static liquid holdup or to consider its impact minimal. Or it could be lumped within the measured internal static liquid holdup in case there is a need to account for it, which can be reasonably estimated by correlations reported in the literature. However, the work of Qi et al. [25], where cross-sectional measurements of liquid holdup were conducted, indicate that external static liquid holdup should not be overlooked and is combined with the internal liquid holdup within the pores of the catalysts. This approach suggests that aggregating internal liquid holdup with external static conditions at the contact points may correspond to the actual conditions within the catalyst bed [25]. Hence, in this measurement, the only liquid left is detained inside the catalyst’s pores due to the capillary force [16]. In this scanning case, the GRD beam passes through the column wall, the wet catalyst, and the void space of gas. The obtained attenuation is due to the wall of the column, the solid catalyst, the liquid inside the catalyst (porous), and the gas in voids between solid catalysts, where the latter is negligible:
- VI.
- Scanning the column packed with solid and liquid, (water—catalyst inside, liquid–solid phase). The same packed bed, which contains a wet solid catalyst inside, was filled with water, so the voids between the particles are currently filled with water. In this scanning case, the GRD beam passes through the column wall, the solid catalyst, and water. The obtained attenuation is due to the wall of the column, the solid catalyst, the liquid inside the catalyst (porous), and the liquid outside the catalyst in voids between solid catalysts:
- VIII.
- Scanning the column with the desired operation of gas and liquid phases, (air–water–catalyst, gas–liquid–solid). In this scanning case, the GRD beam passes through the column wall, catalyst, liquid, and gas as a three-phase liquid–solid–gas attenuation. The obtained attenuation is due to the wall of the column, the solid catalyst, the liquid inside the pore, the total liquid in the external void (dynamic + static), and the gas phase:
3. Results
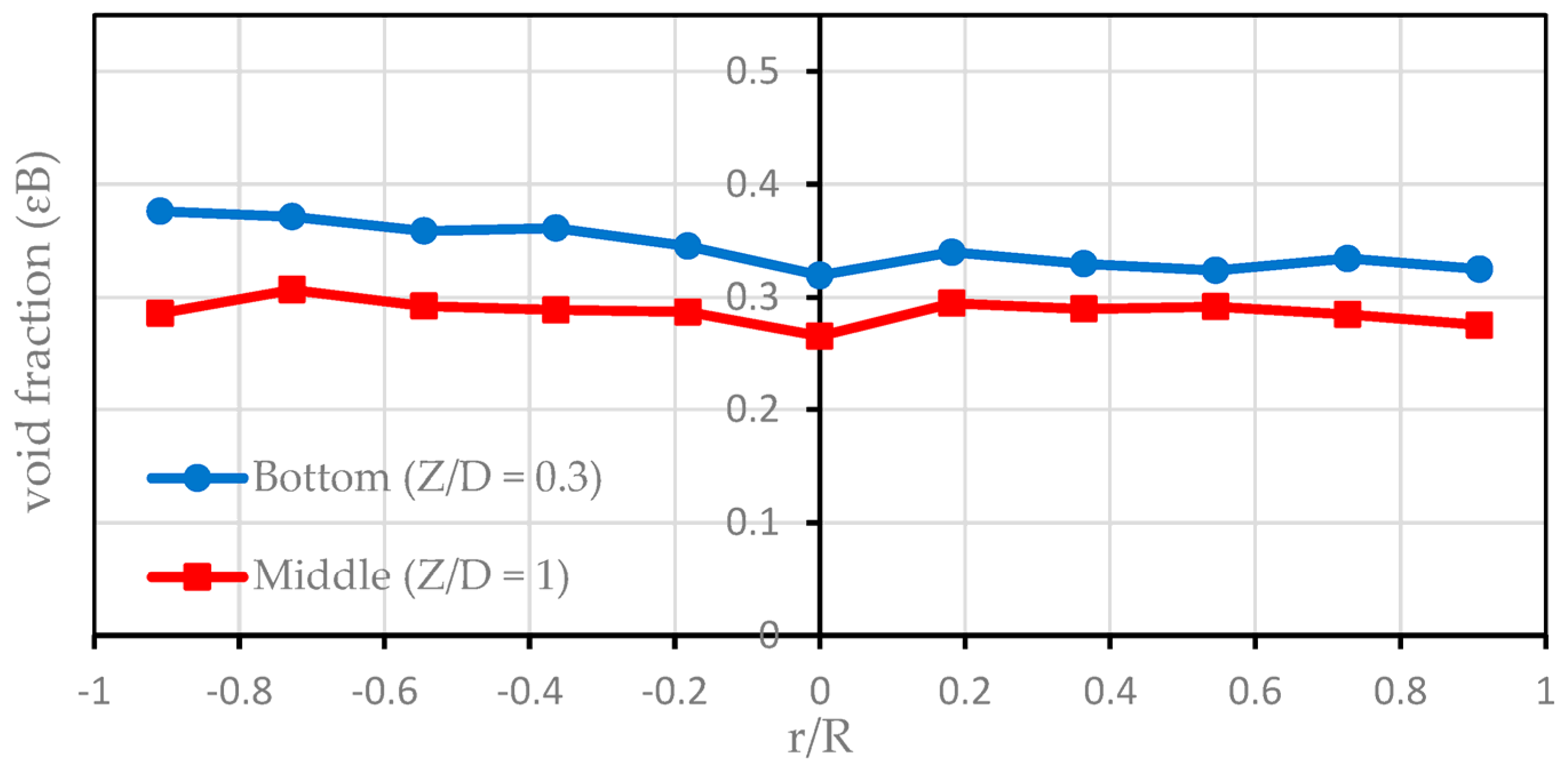
3.1. Diameter Profile of the Void Fraction with Wet Catalyst
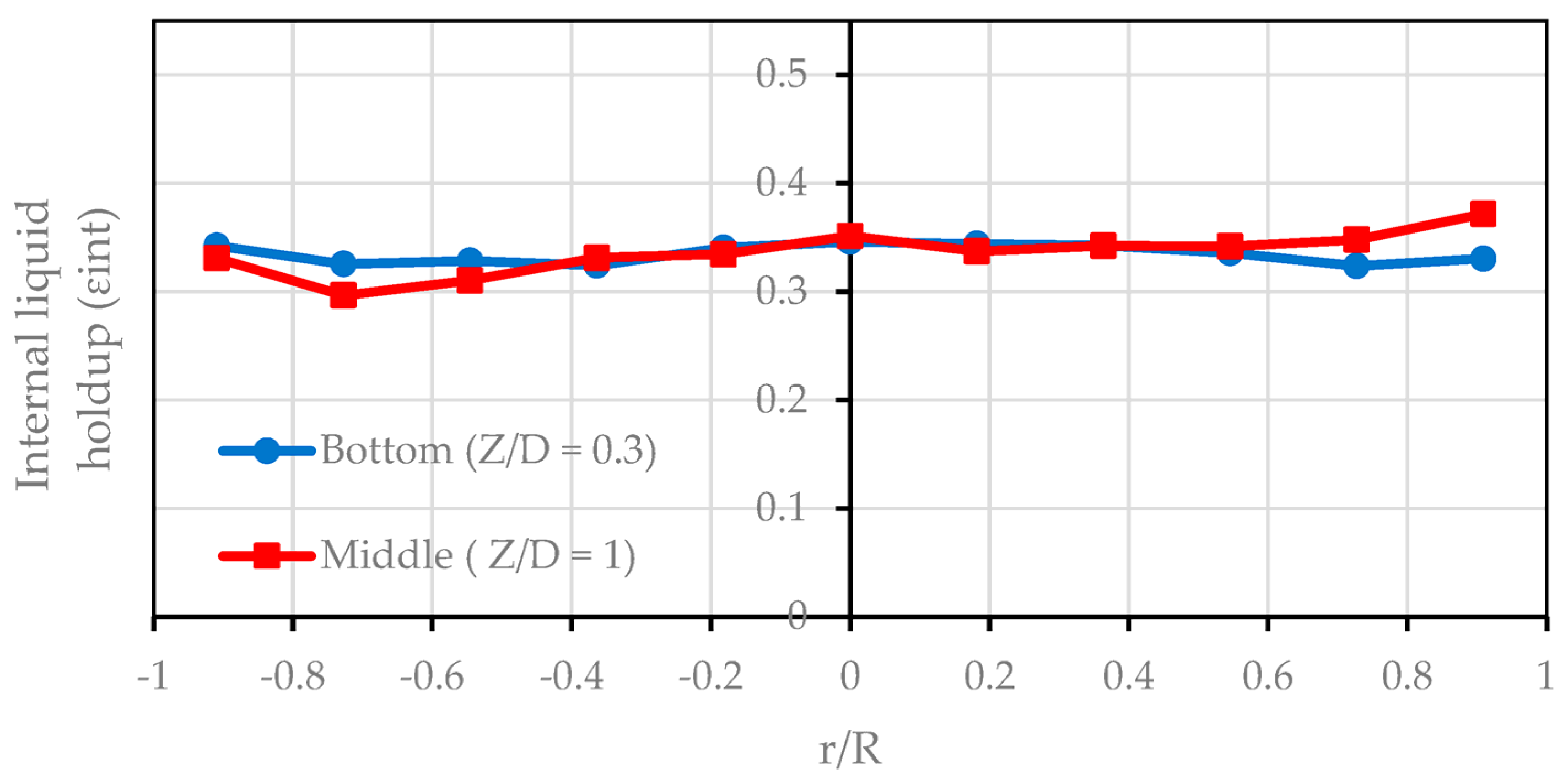
3.2. Diameter Profile of Line Average Internal Liquid Holdup
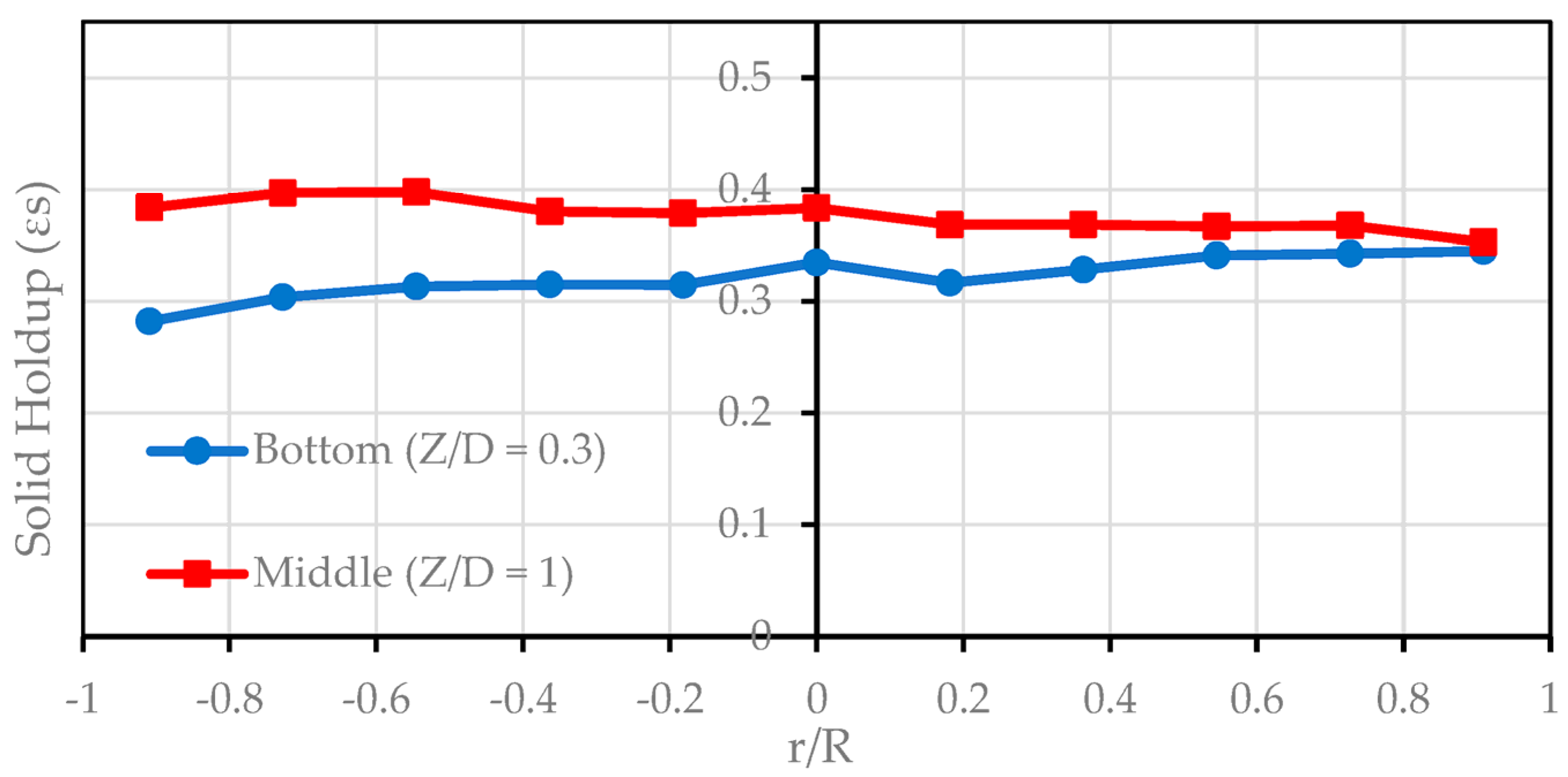
3.3. Radial Distribution of Solid Holdup ()
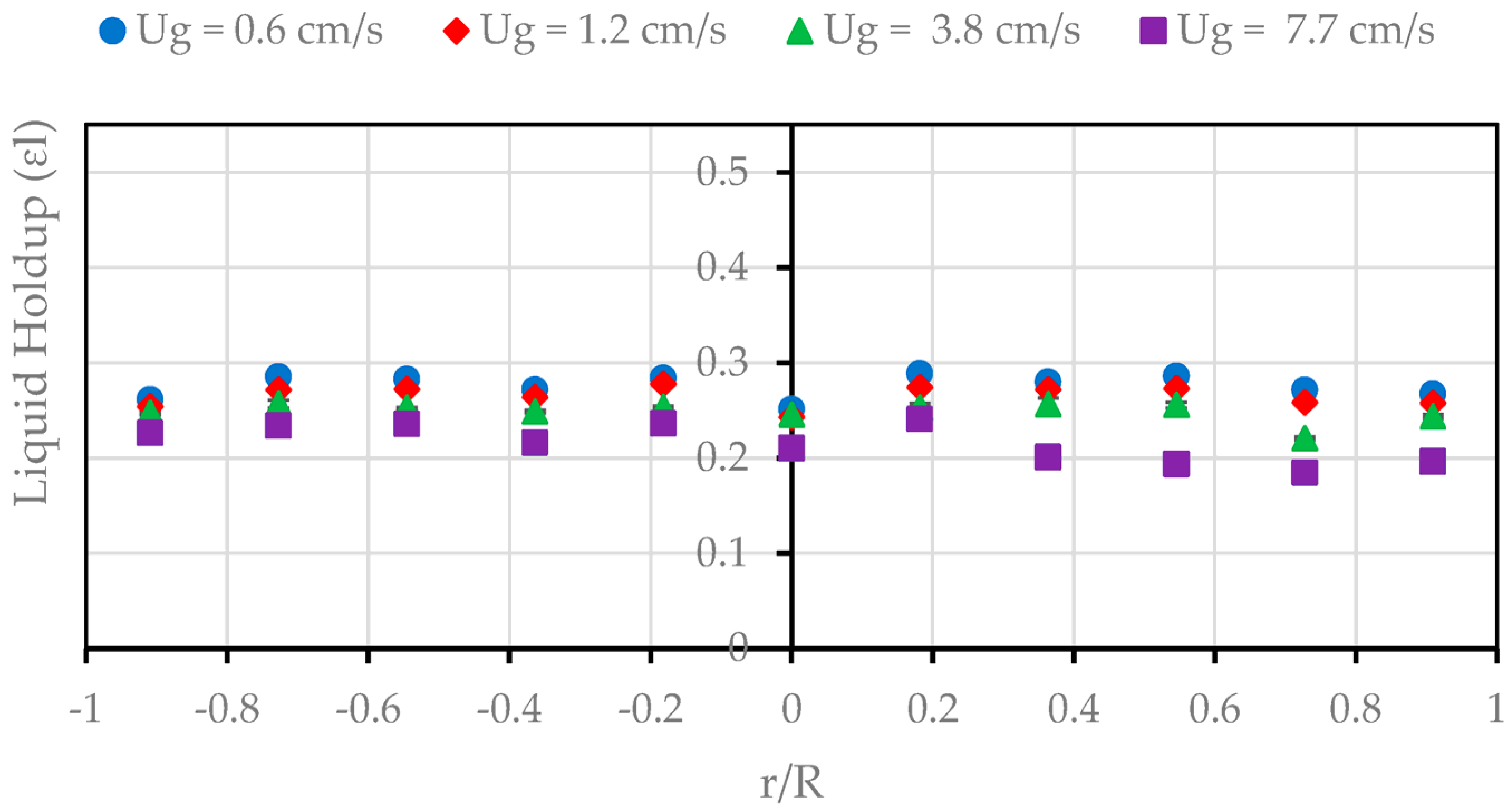
3.4. The Line Average Total External Liquid Holdup
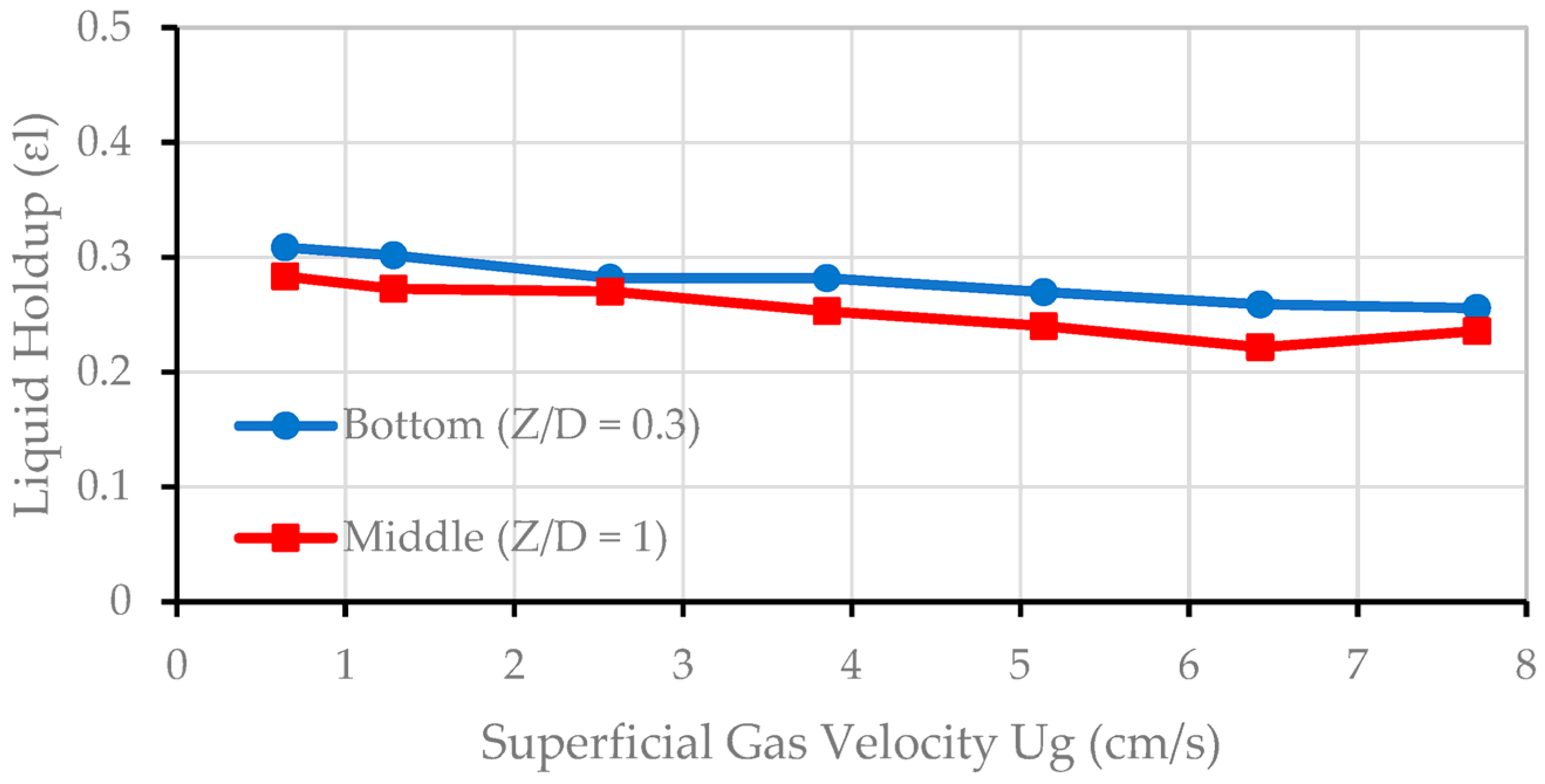
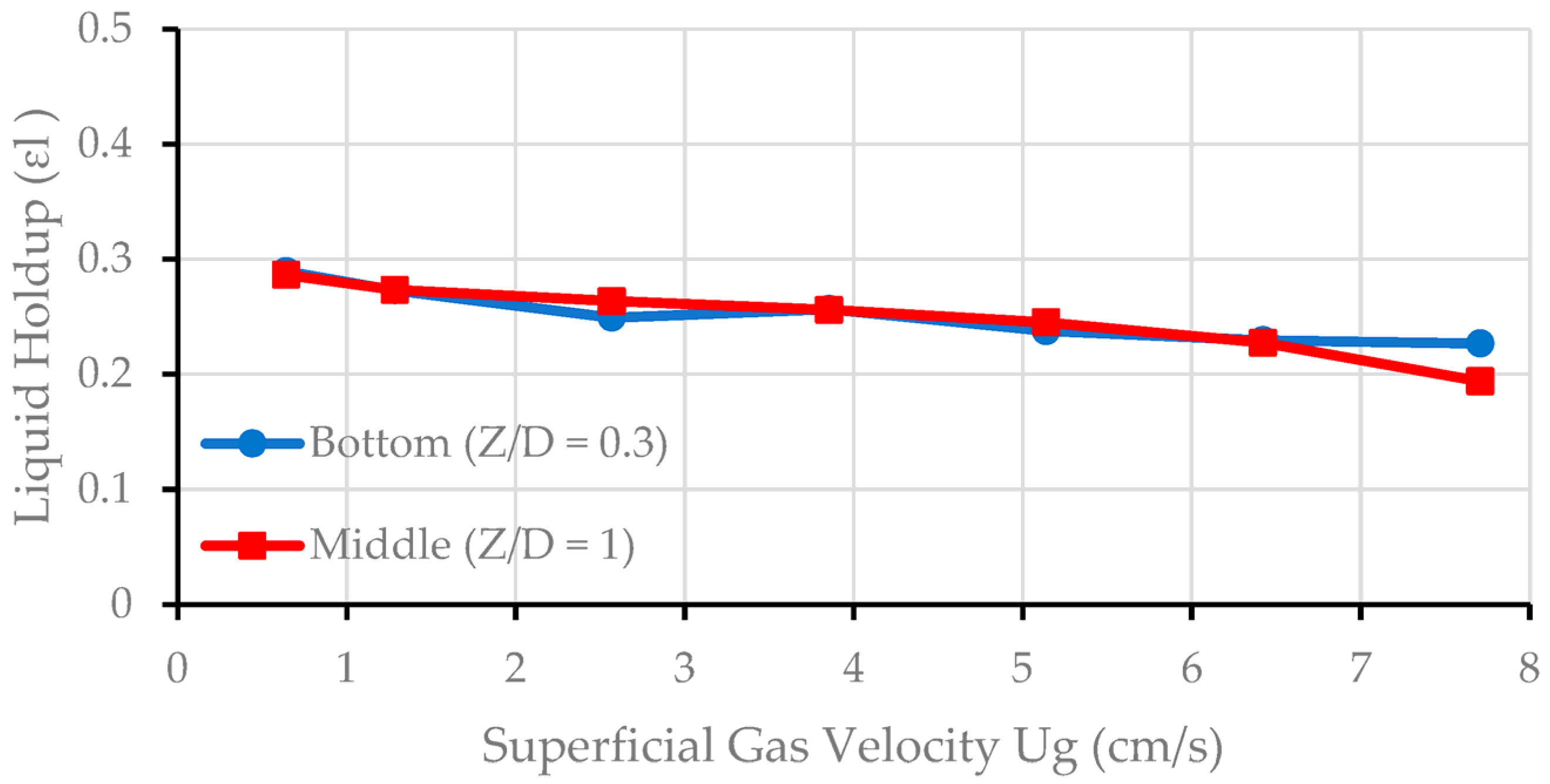
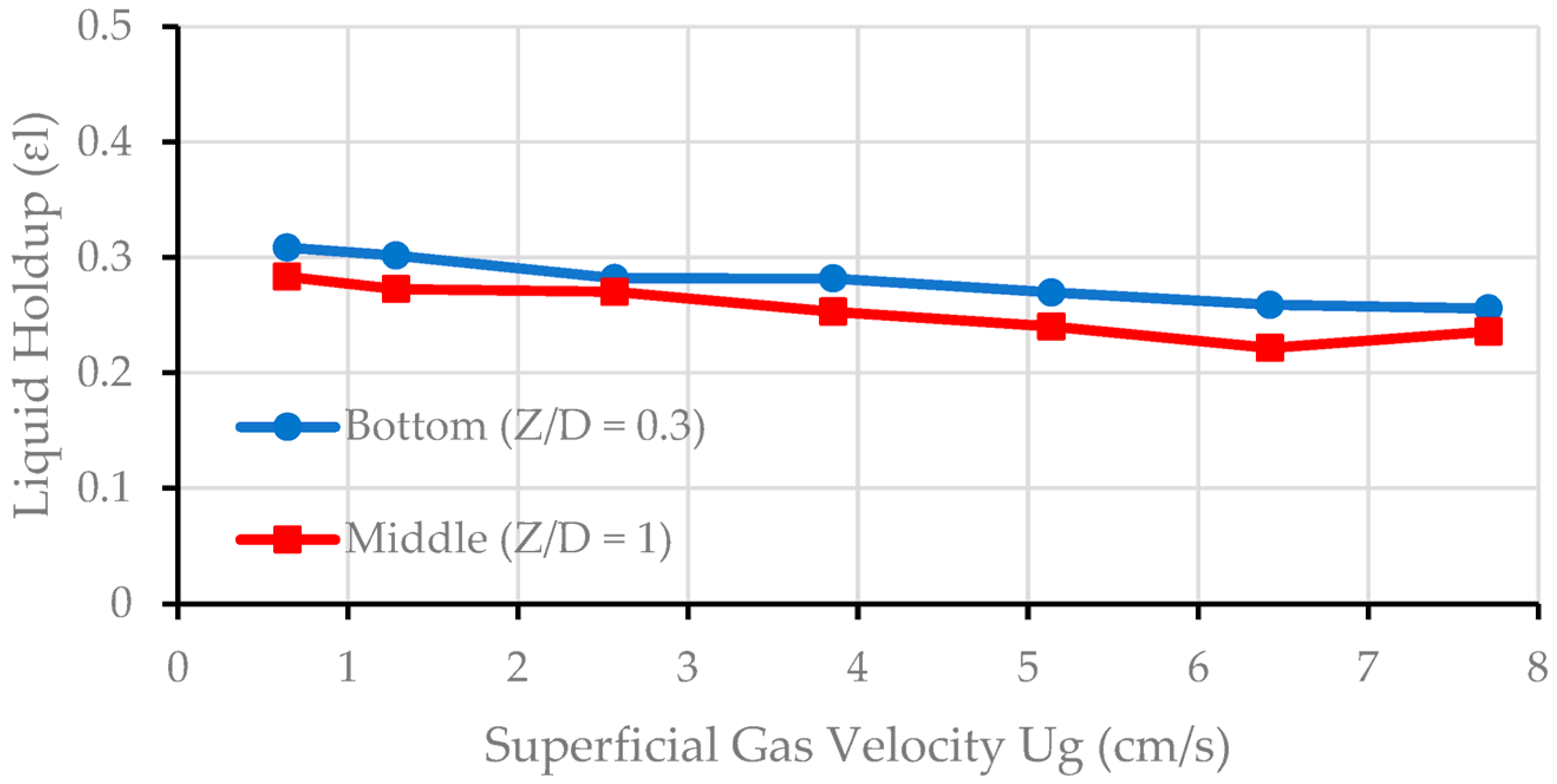
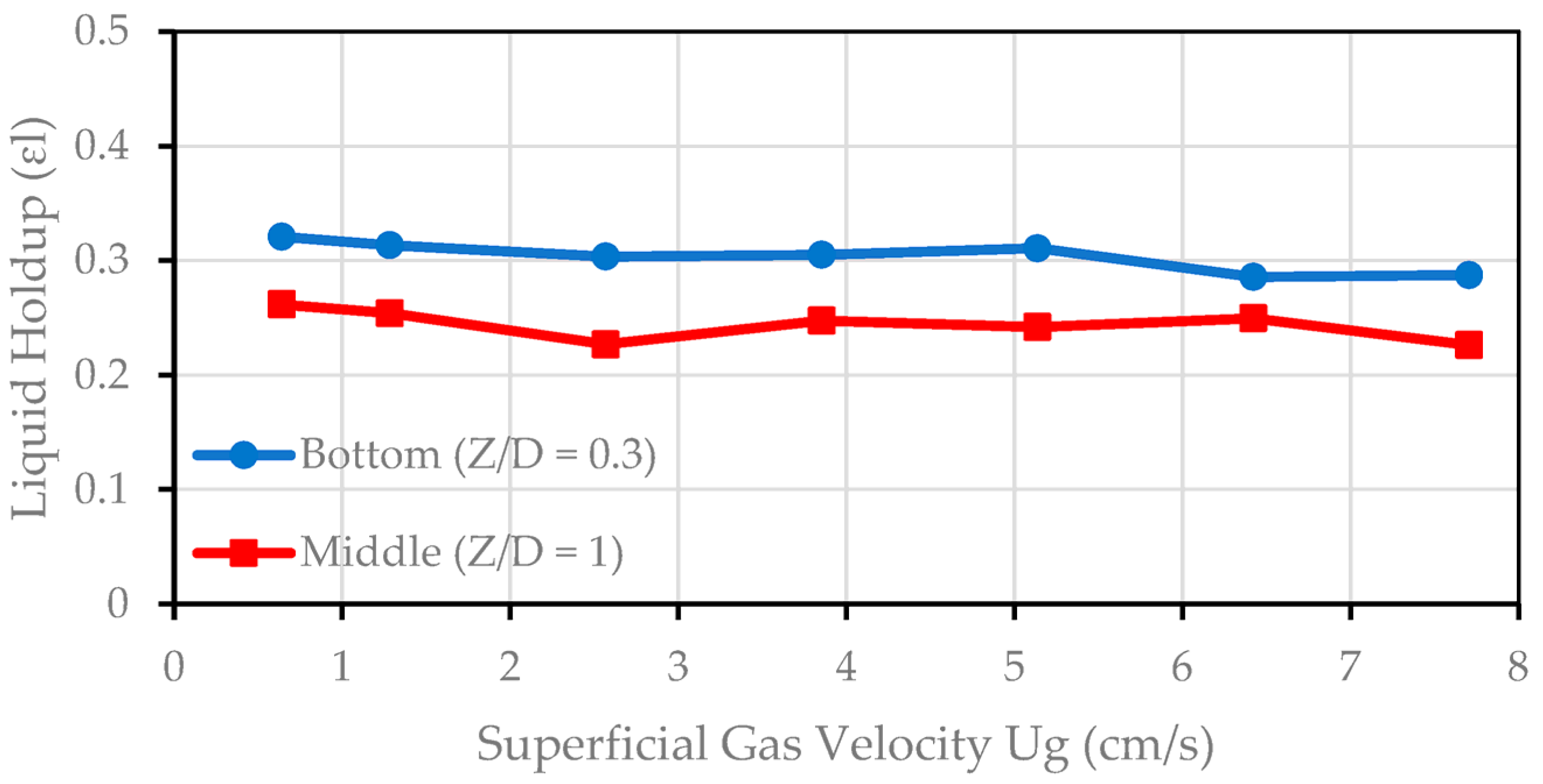
3.5. Effect of Superficial Velocity on the External Liquid Holdup
4. Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Y.; Gao, L.; Wen, L.; Zong, B. Recent advances in heavy oil hydroprocessing technologies. Recent Pat. Chem. Eng. 2009, 2, 22–36. [Google Scholar] [CrossRef]
- Bartholomew, C. Catalyst Deactivation in Hydrotreating of Residua: A Review; Marcel Dekker: New York, NY, USA, 1994. [Google Scholar]
- Ancheyta, J.; Alvarez-Majmutov, A.; Leyva, C. Hydrotreating of oil fractions. In Multiphase Catalytic Reactors: Theory, Design, Manufacturing, and Applications; Wiley Online Library: Hoboken, NJ, USA, 2016; pp. 295–329. [Google Scholar]
- Scheuerman, G.L.; Johnson, D.R.; Reynolds, B.E.; Bachtel, R.W.; Threlkel, R.S. Advances in Chevron RDS technology for heavy oil upgrading flexibility. Fuel Process. Technol. 1993, 35, 39–54. [Google Scholar] [CrossRef]
- Yin, F.; Afacan, A.; Nandakumar, K.; Chuang, K.T. Liquid holdup distribution in packed columns: Gamma ray tomography and CFD simulation. Chem. Eng. Process. Process Intensif. 2002, 41, 473–483. [Google Scholar] [CrossRef]
- Reynolds, B.E.; Lam, F.W.; Chabot, J.; Antezana, F.J.; Bachtel, R.; Gibson, K.R.; Threlkel, R.; Leung, P.C. Upflow Reactor System with Layered Catalyst Bed for Hydrotreating Heavy Feedstocks; U.S. Patent and Trademark Office: Washington, DC, USA, 2003. [Google Scholar]
- Delmon, B. New technical challenges and recent advances in hydrotreatment catalysis. A critical updating review. Catal. Lett. 1993, 22, 1–32. [Google Scholar] [CrossRef]
- Jasim, A.A.; Sultan, A.J.; Al-Dahhan, M.H. Influence of heat-exchanging tubes diameter on the gas holdup and bubble dynamics in a bubble column. Fuel 2019, 236, 1191–1203. [Google Scholar] [CrossRef]
- Iliuta, I.; Larachi, F. Catalytic Wet Oxidation in Three-Phase Moving-Bed Reactors: Modeling Framework and Simulations for On-Stream Replacement of a Deactivating Catalyst. Ind. Eng. Chem. Res. 2013, 52, 370–383. [Google Scholar] [CrossRef]
- Chander, A.; Kundu, A.; Bej, S.K.; Dalai, A.K.; Vohra, D.K. Hydrodynamic characteristics of cocurrent upflow and downflow of gas and liquid in a fixed bed reactor. Fuel 2001, 80, 1043–1053. [Google Scholar] [CrossRef]
- Al-Dahhan, M.H.; Duduković, M.P. Catalyst Bed Dilution for Improving Catalyst Wetting in Laboratory Trickle-Bed Reactors. AIChE J. 1996, 42, 2594–2606. [Google Scholar] [CrossRef]
- Urrutia, G.; Bonelli, P.; Cassanello, M.C.; Cukierman, A.L. On dynamic liquid holdup determination by the drainage method. Chem. Eng. Sci. 1996, 51, 3721–3726. [Google Scholar] [CrossRef]
- Kumar, R.K.; Rao, A.R.; Sankarshana, T.; Khan, A. Liquid Holdup in Concurrent Gas Liquid Upflow Through Packed Column with Random and Corrugated Structured Packing. In Proceedings of the World Congress on Engineering and Computer Science, San Francisco, CA, USA, 24–26 October 2012. [Google Scholar]
- Guo, J.; Al-Dahhan, M. Liquid holdup and pressure drop in the gas-liquid cocurrent downflow packed-bed reactor under elevated pressures. Chem. Eng. Sci. 2004, 59, 5387–5393. [Google Scholar] [CrossRef]
- Hamidipour, M.; Larachi, F. Characterizing the liquid dynamics in cocurrent gas–liquid flows in porous media using twin-plane electrical capacitance tomography. Chem. Eng. J. 2010, 165, 310–323. [Google Scholar] [CrossRef]
- Al-Dahhan, M.; Highfill, W. Liquid holdup measurement techniques in laboratory high pressure trickle bed reactors. Can. J. Chem. Eng. 1999, 77, 759–765. [Google Scholar] [CrossRef]
- Hubers, J.L.; Striegel, A.C.; Heindel, T.J.; Gray, J.N.; Jensen, T.C. X-ray computed tomography in large bubble columns. Chem. Eng. Sci. 2005, 60, 6124–6133. [Google Scholar] [CrossRef]
- Boyer, C.; Duquenne, A.-M.; Wild, G. Measuring techniques in gas–liquid and gas–liquid–solid reactors. Chem. Eng. Sci. 2002, 57, 3185–3215. [Google Scholar] [CrossRef]
- Shi, W.; Yin, G.; Wang, M.; Tao, L.; Wu, M.; Yang, Z.; Bai, J.; Xu, Z.; Zhu, Q. Progress of Electrical Resistance Tomography Application in Oil and Gas Reservoirs for Development Dynamic Monitoring. Processes 2023, 11, 2950. [Google Scholar] [CrossRef]
- Wang, Q.; Polansky, J.; Wang, M.; Wei, K.; Qiu, C.; Kenbar, A.; Millington, D. Capability of dual-modality electrical tomography for gas-oil-water three-phase pipeline flow visualisation. Flow Meas. Instrum. 2018, 62, 152–166. [Google Scholar] [CrossRef]
- Park, H.-S.; Chung, C.-H. Design and application of a single-beam gamma densitometer for void fraction measurement in a small diameter stainless steel pipe in a critical flow condition. Nucl. Eng. Technol. 2007, 39, 349–358. [Google Scholar] [CrossRef]
- Shollenberger, K.A.; Torczynski, J.R.; Adkins, D.R.; O’Hern, T.J.; Jackson, N.B. Gamma-densitometry tomography of gas holdup spatial distribution in industrial-scale bubble columns. Chem. Eng. Sci. 1997, 52, 2037–2048. [Google Scholar] [CrossRef]
- Alexander, V.; Albazzaz, H.; Al-Dahhan, M. Gas phase dispersion/mixing investigation in a representative geometry of gas-liquid upflow Moving Bed Hydrotreater Reactor (MBR) using developed gas tracer technique and method based on convolution/regression. Chem. Eng. Sci. 2019, 195, 671–682. [Google Scholar] [CrossRef]
- Toukan, A.; Alexander, V.; AlBazzaz, H.; Al-Dahhan, M.H. Identification of flow regime in a cocurrent gas–Liquid upflow moving packed bed reactor using gamma ray densitometry. Chem. Eng. Sci. 2017, 168, 380–390. [Google Scholar] [CrossRef]
- Qi, B.; Farid, O.; Uribe, S.; Al-Dahhan, M. Maldistribution and dynamic liquid holdup quantification of quadrilobe catalyst in a trickle bed reactor using gamma-ray computed tomography: Pseudo-3D modelling and empirical modelling using deep neural network. Chem. Eng. Res. Des. 2020, 164, 195–208. [Google Scholar] [CrossRef]
- Wild, G.; Larachi, F.; Laurent, A. The hydrodynamic characteristics of cocurrent downflow and cocurrent upflow gas-liquid-solid catalytic fixed bed reactors: The effect of pressure. Oil Gas Sci. Technol. 1991, 46, 467–490. [Google Scholar] [CrossRef]
- Alexander, V. Hydrodynamics Related Performance Evaluation of Upflow Moving Bed Hydrotreater Reactor (MBR) Using Developed Experimental Methods and CFD Simulation. Ph.D. Thesis, Missouri University of Science and Technology, Rolla, MO, USA, 2018. [Google Scholar]
- Al-Dahhan, M.; Kemoun, A.; Cartolano, A. Phase distribution in an upflow monolith reactor using computed tomography. AIChE J. 2006, 52, 745–753. [Google Scholar] [CrossRef]
- Rados, N.; Shaikh, A.; Al-Dahhan, M. Phase distribution in a high pressure slurry bubble column via a single source computed tomography. Can. J. Chem. Eng. 2005, 83, 104–112. [Google Scholar] [CrossRef]
- Efhaima, A.; Al-Dahhan, M.H. Local time-averaged gas holdup in fluidized bed reactor using gamma ray computed tomography technique (CT). Int. J. Ind. Chem. 2015, 6, 143–152. [Google Scholar] [CrossRef]
- Schlieper, G. Principles of gamma ray densitometry. Met. Powder Rep. 2000, 55, 20–23. [Google Scholar] [CrossRef]
- Bouteldja, H.; Hamidipour, M.; Larachi, F. Hydrodynamics of an inclined gas–liquid cocurrent upflow packed bed. Chem. Eng. Sci. 2013, 102, 397–404. [Google Scholar] [CrossRef]
- Jasim, A.A.; Sultan, A.J.; Al-Dahhan, M.H. Impact of heat exchanging internals configurations on the gas holdup and bubble properties in a bubble column. Int. J. Multiph. Flow 2019, 112, 63–82. [Google Scholar] [CrossRef]
- Saroha, A.K.; Khera, R. Hydrodynamic study of fixed beds with cocurrent upflow and downflow. Chem. Eng. Process. Process Intensif. 2006, 45, 455–460. [Google Scholar] [CrossRef]



| Column dimensions | |
| Bed height | 57 inches |
| Column diameter (inner) | 11 inches |
| Dimensionless axial measurement positions (Z/L) | Z/L = 0.38 (bottom), and Z/L = 1 (middle) |
| Dimensionless radial positions (r/R) | 0, +0.5, −0.5, +0.9, −0.9 |
| Experimental conditions | |
| Superficial gas velocity | Ug = 0.6, 1.2, 3.8, 7.7 cm/s |
| Superficial liquid velocity | Ul = 0.017 cm/s (constant) |
| Catalyst properties | |
| Geometry | Spherical, 3 mm in diameter |
| Bulk density | 570 kg/m3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toukan, A.; Jasim, A.; Alexander, V.; AlBazzaz, H.; Al-Dahhan, M. Experimental Investigation of Liquid Holdup in a Co-Current Gas–Liquid Upflow Moving Packed Bed Reactor with Porous Catalyst Using Gamma-Ray Densitometry. ChemEngineering 2024, 8, 54. https://doi.org/10.3390/chemengineering8030054
Toukan A, Jasim A, Alexander V, AlBazzaz H, Al-Dahhan M. Experimental Investigation of Liquid Holdup in a Co-Current Gas–Liquid Upflow Moving Packed Bed Reactor with Porous Catalyst Using Gamma-Ray Densitometry. ChemEngineering. 2024; 8(3):54. https://doi.org/10.3390/chemengineering8030054
Chicago/Turabian StyleToukan, Ali, Ahmed Jasim, Vineet Alexander, Hamza AlBazzaz, and Muthanna Al-Dahhan. 2024. "Experimental Investigation of Liquid Holdup in a Co-Current Gas–Liquid Upflow Moving Packed Bed Reactor with Porous Catalyst Using Gamma-Ray Densitometry" ChemEngineering 8, no. 3: 54. https://doi.org/10.3390/chemengineering8030054
APA StyleToukan, A., Jasim, A., Alexander, V., AlBazzaz, H., & Al-Dahhan, M. (2024). Experimental Investigation of Liquid Holdup in a Co-Current Gas–Liquid Upflow Moving Packed Bed Reactor with Porous Catalyst Using Gamma-Ray Densitometry. ChemEngineering, 8(3), 54. https://doi.org/10.3390/chemengineering8030054






