Improved Fault Detection in Chemical Engineering Processes via Non-Parametric Kolmogorov–Smirnov-Based Monitoring Strategy
Abstract
:1. Introduction
- A novel fault detection strategy, termed PCA–KS, is developed by merging the Kolmogorov–Smirnov (KS) test with Principal Component Analysis (PCA). PCA serves a dual purpose in dimensionality reduction and residual generation. Under normal operating conditions, residuals cluster around zero, reflecting the influence of measurement noise and uncertainties. However, when faults are present, residuals deviate considerably from zero. The Kolmogorov–Smirnov test is subsequently employed to evaluate these residuals for fault detection. Notably, this semi-supervised approach does not require prior knowledge of the system, enhancing its practicality and adaptability across various industrial and engineering applications.
- The proposed PCA–KS approach is validated using both a simulated Plug-Flow Reactor (PFR) process and the Tennessee Eastman (TE) process. The evaluation involves various types of faults, including sustained bias faults, intermittent faults, and drift faults. Additionally, the performance of PCA–KS is compared with established techniques, such as PCA-T2, PCA-SPE, and PCA-CUSUM, ensuring a fair and accurate assessment. To quantitatively evaluate the performance of the investigated methods, five statistical evaluation metrics are employed. The results demonstrate the promising capability of the PCA–KS approach, characterized by a high detection rate and reduced false alarms.
2. Methodology
2.1. Fault Detection Based on PCA
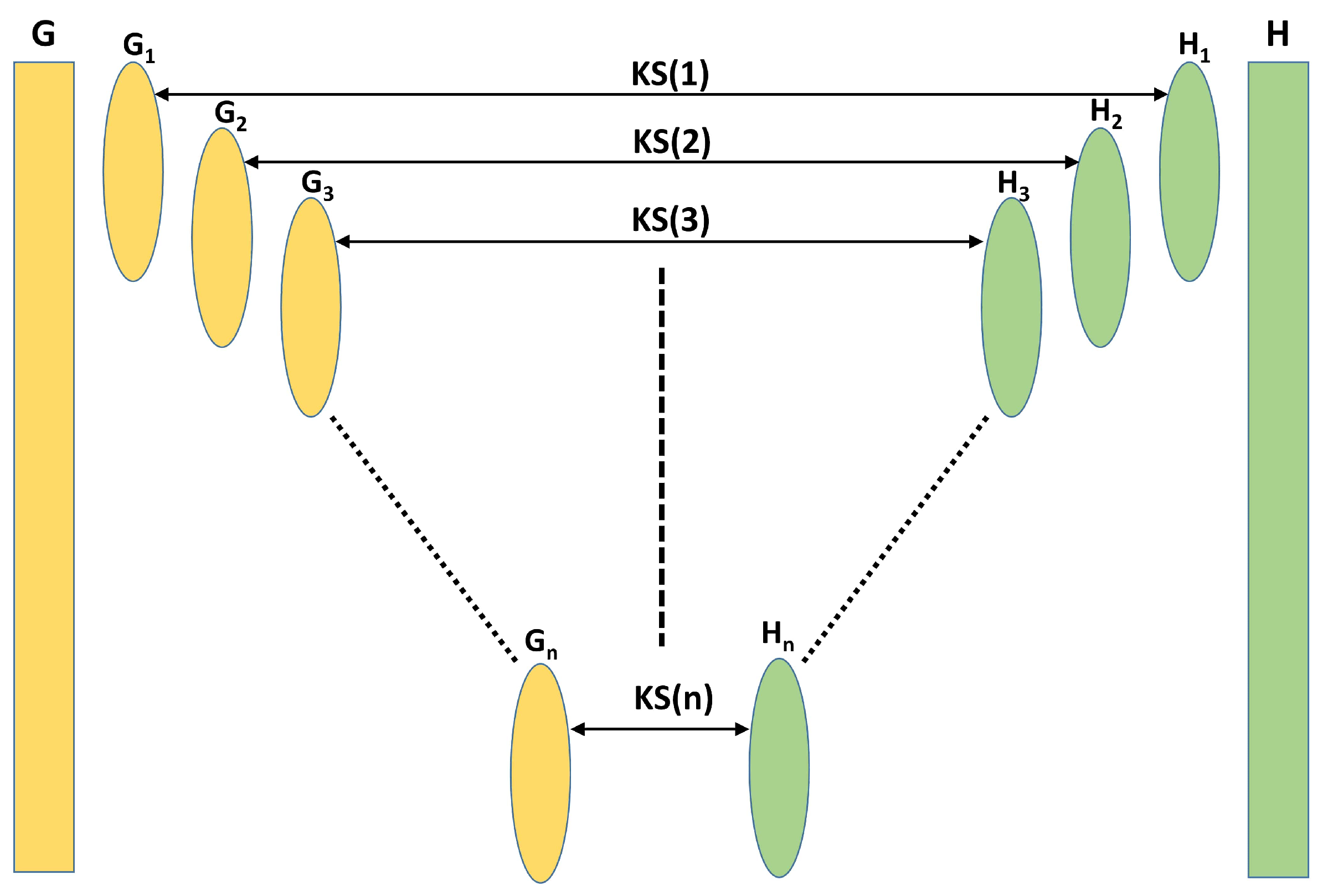
2.2. Kolmogorov–Smirnov-Based Fault Indicator
- Data Collection: Gather data from the system or process that you want to monitor and detect faults in.
- Data Preprocessing: Prepare the collected data for analysis. This step may involve data cleaning, normalization, and transformation to ensure that it is suitable for the KS-based fault detection approach.
- Select Reference Data: Choose a dataset or set of observations representing normal or fault-free operation. This reference dataset will serve as a baseline for comparison.
- Calculate Empirical CDFs: Compute the Empirical Cumulative Distribution Functions (ECDFs) for both the reference data and the incoming data stream. These ECDFs represent the distribution of the data in both cases.
- Apply the KS Test: Use the Kolmogorov–Smirnov (KS) test to compare the two ECDFs. The KS test will quantify the maximum difference (KS statistic) between the two distributions.
- Threshold Setting: Define a threshold value or critical value for the KS statistic. This threshold will determine when a fault is detected. If the KS statistic exceeds this threshold, it indicates a significant difference between the two distributions.
- Monitoring in a Moving Window: Implement a moving window approach to continuously monitor the incoming data stream. The window moves over time, and at each step the KS statistic is computed for the data within the window.
- Fault Detection: Compare the computed KS statistic with the predefined threshold in the moving window. If the KS statistic exceeds the threshold, it suggests a fault or anomaly in the data.
2.3. The PCA–KS-Based Fault Detection Strategy
| Algorithm 1: PCA–KS-based Fault Detection Strategy |
Offline Stage:
Online Stage:
|
- Recall (Sensitivity): Recall, often referred to as sensitivity, measures the ability of an FD strategy to correctly identify true positive cases [54].Recall provides insights into the strategy’s ability to detect actual faults when they occur, minimizing the chances of missing any real issues.
- Precision: Precision evaluates the precision and accuracy of an FD strategy in correctly detecting true positive cases [54].Precision is valuable for assessing the strategy’s reliability in avoiding false alarms, ensuring that when it signals a fault, it is highly likely to be a real issue.
- F1-Score: The F1-score is a harmonic mean of precision and recall. It balances these two metrics, making it a useful overall performance indicator. The F1-score is calculated as follows [54]:The F1-score takes both false alarms and missed faults into account, providing a holistic view of the strategy’s performance. It helps in achieving a balance between precision and recall, ensuring that the FD strategy is effective in both detecting true faults and avoiding false alarms.
3. Results and Discussion
3.1. Plug Flow Reactor
3.1.1. Modeling and Data Description
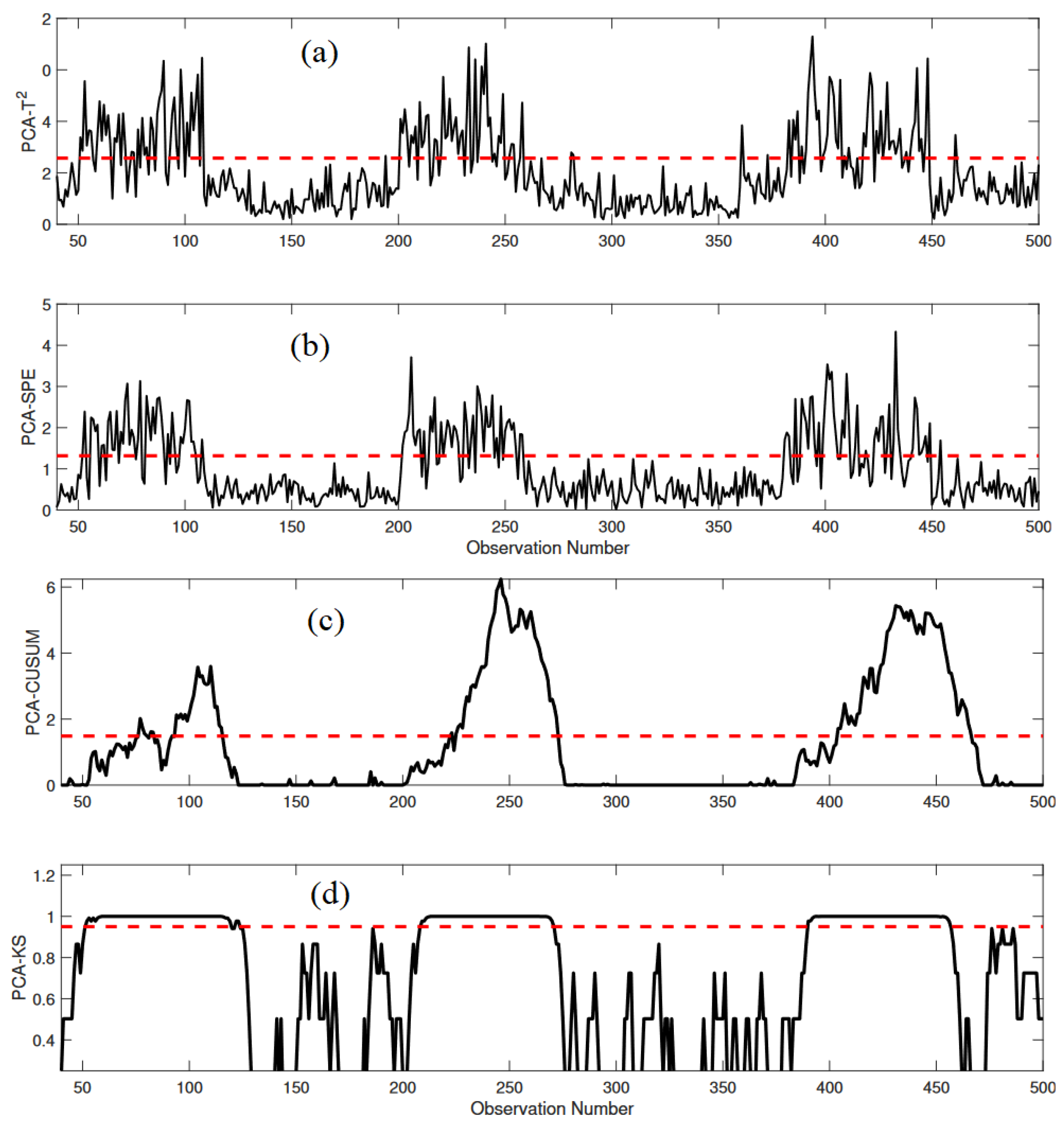
3.1.2. Different Fault Scenarios
- Bias Fault: A bias fault is a sudden and significant deviation in a variable’s behavior from its normal range. It can be mathematically expressed aswhere is the variable’s normal range and b represents the bias introduced at time, t. Bias faults are characterized by a pronounced and persistent shift in sensor readings.
- Drift Fault: Sensor drift is characterized by a gradual and exponential change in sensor readings over time. This phenomenon is attributed to the aging of the sensing element and can be mathematically defined aswhere M denotes the slope of the drift and represents the time at which the fault begins. Drift faults are a consistent departure from normal behavior, growing progressively.
- Intermittent Fault: Intermittent sensor faults are marked by irregular intervals of appearance and disappearance. These faults are characterized by short instances of variation in sensor readings, typically in the form of small variations in the bias term, followed by a return to normal behavior.
3.1.3. Monitoring Results
3.2. Tennessee Eastman Process
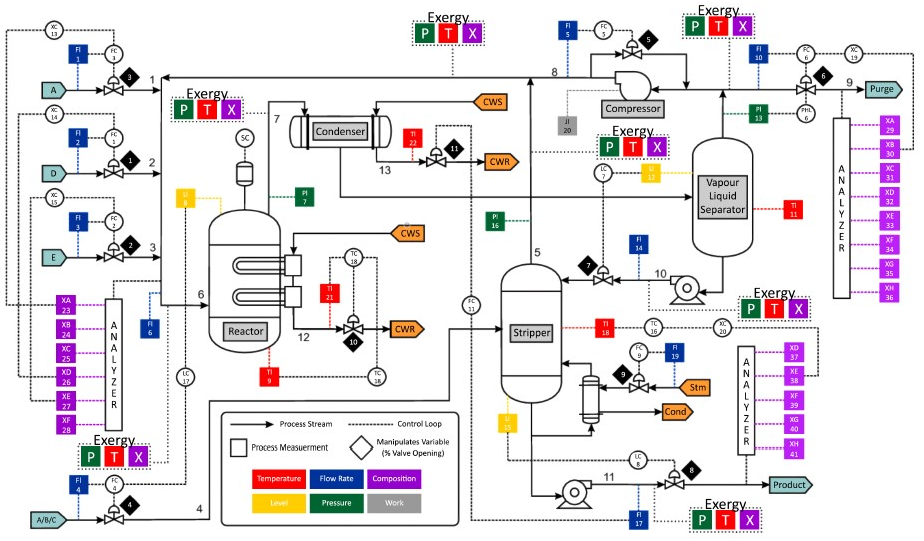
3.2.1. Overview of TE Benchmark Process
3.2.2. Monitoring Results
4. Conclusions
5. Future Work: Exploring New Frontiers
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khan, F.I.; Abbasi, S. Major accidents in process industries and an analysis of causes and consequences. J. Loss Prev. Process Ind. 1999, 12, 361–378. [Google Scholar] [CrossRef]
- Fuente, M.J.D.L.; Sainz-Palmero, G.I.; Galende-Hern¡ndez, M. Dynamic Decentralized Monitoring for Large-Scale Industrial Processes Using Multiblock Canonical Variate Analysis Based Regression. IEEE Access 2023, 11, 26611–26623. [Google Scholar] [CrossRef]
- Kini, K.R.; Madakyaru, M. Performance Evaluation of Independent Component Analysis-Based Fault Detection Using Measurements Corrupted with Noise. J. Control Autom. Electr. Syst. 2021, 32, 642–655. [Google Scholar] [CrossRef]
- Shao, L.; Kang, R.; Yi, W.; Zhang, H. An Enhanced Unsupervised Extreme Learning Machine Based Method for the Nonlinear Fault Detection. IEEE Access 2021, 9, 48884–48898. [Google Scholar] [CrossRef]
- Dhara, V.R.; Dhara, R. The Union Carbide disaster in Bhopal: A review of health effects. Arch. Environ. Health Int. J. 2002, 57, 391–404. [Google Scholar] [CrossRef] [PubMed]
- Bowonder, B. The bhopal accident. Technol. Forecast. Soc. Chang. 1987, 32, 169–182. [Google Scholar] [CrossRef]
- Cullen, L.W. The public inquiry into the Piper Alpha disaster. Drill. Contract. 1993, 49. [Google Scholar]
- Venkatasubramanian, V.; Rengaswamy, R.; Yin, K.; Kavuri, S.N. A review of process fault detection and diagnosis: Part I: Quantitative model-based methods. Comput. Chem. Eng. 2003, 27, 293–311. [Google Scholar] [CrossRef]
- Lou, Z.; Wang, Y.; Lu, S.; Sun, P. Process Monitoring Using a Novel Robust PCA Scheme. Ind. Eng. Chem. Res. 2021, 60, 4397–4404. [Google Scholar] [CrossRef]
- Harrou, F.; Sun, Y.; Madakyaru, M.; Bouyedou, B. An improved multivariate chart using partial least squares with continuous ranked probability score. IEEE Sens. J. 2018, 18, 6715–6726. [Google Scholar] [CrossRef]
- Harrou, F.; Madakyaru, M.; Sun, Y. Improved nonlinear fault detection strategy based on the Hellingerdistance metric: Plug flow reactor monitoring. Energy Build. 2017, 143, 149–161. [Google Scholar] [CrossRef]
- Alauddin, M.; Khan, F.; Imtiaz, S.; Ahmed, S. A Bibliometric Review and Analysis of Data-Driven Fault Detection and Diagnosis Methods for Process Systems. Ind. Eng. Chem. Res. 2018, 57, 10719–10735. [Google Scholar] [CrossRef]
- Clark, R.N.; Fosth, D.C.; Walton, V.M. Detecting instrument malfunctions in control systems. IEEE Trans. Aerosp. Electron. Syst. 1975, AES-11, 465–473. [Google Scholar] [CrossRef]
- Patton, R.J.; Chen, J. A review of parity space approaches to fault diagnosis. IFAC Proc. Vol. 1991, 24, 65–81. [Google Scholar] [CrossRef]
- Benothman, K.; Maquin, D.; Ragot, J.; Benrejeb, M. Diagnosis of uncertain linear systems: An interval approach. Int. J. Sci. Tech. Autom. Control Comput. Eng. 2007, 1, 136–154. [Google Scholar]
- Yin, S.; Ding, S.X.; Xie, X.; Luo, H. A review on basic data-driven approaches for industrial process monitoring. IEEE Trans. Ind. Electron. 2014, 61, 6418–6428. [Google Scholar] [CrossRef]
- Venkatasubramanian, V.; Rengaswamy, R.; Kavuri, S.N.; Yin, K. A review of process fault detection and diagnosis part 3: Process history based methods. Comput. Chem. Eng. 2003, 27, 327–346. [Google Scholar] [CrossRef]
- Md Nor, N.; Che Hassan, C.R.; Hussain, M.A. A review of data-driven fault detection and diagnosis methods: Applications in chemical process systems. Rev. Chem. Eng. 2020, 36, 513–553. [Google Scholar] [CrossRef]
- Harrou, F.; Dairi, A.; Sun, Y.; Kadri, F. Detecting abnormal ozone measurements with a deep learning-based strategy. IEEE Sens. J. 2018, 18, 7222–7232. [Google Scholar] [CrossRef]
- Montgomery, D.C. Introduction to Statistical Quality Control; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Hawkins, D.M.; Olwell, D.H. Cumulative Sum Charts and Charting for Quality Improvement; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Dao, P.B. A CUSUM-Based Approach for Condition Monitoring and Fault Diagnosis of Wind Turbines. Energies 2021, 14, 3236. [Google Scholar] [CrossRef]
- Lucas, J.M.; Saccucci, M.S. Exponentially weighted moving average control schemes: Properties and enhancements. Technometrics 1990, 32, 1–12. [Google Scholar] [CrossRef]
- Kresta, J.V.; Macgregor, J.F.; Marlin, T.E. Multivariate statistical monitoring of process operating performance. Can. J. Chem. Eng. 1991, 69, 35–47. [Google Scholar] [CrossRef]
- Ge, Z.; Song, Z. Multivariate Statistical Process Control: Process Monitoring Methods and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Nawaz, M.; Maulud, A.S.; Zabiri, H.; Suleman, H.; Tufa, L.D. Multiscale Framework for Real-Time Process Monitoring of Nonlinear Chemical Process Systems. Ind. Eng. Chem. Res. 2020, 59, 18595–18606. [Google Scholar] [CrossRef]
- Li, J.; Yan, X. Process monitoring using principal component analysis and stacked autoencoder for linear and nonlinear coexisting industrial processes. J. Taiwan Inst. Chem. Eng. 2020, 112, 322–329. [Google Scholar] [CrossRef]
- Sarita, K.; Devarapalli, R.; Kumar, S.; Malik, H.; Garcia Marquez, F.P.; Rai, P. Principal component analysis technique for early fault detection. J. Intell. Fuzzy Syst. 2022, 42, 861–872. [Google Scholar] [CrossRef]
- Li, W.; Yue, H.H.; Cervantes, S.V.; Qin, S.J. Recursive PCA for adaptive process monitoring. J. Process Control 2000, 10, 471–486. [Google Scholar] [CrossRef]
- Chai, Y.; Tao, S.; Mao, W.; Zhang, K.; Zhu, Z. Online incipient fault diagnosis based on Kullback Leibler divergence and recursive principle component analysis. Can. J. Chem. Eng. 2018, 96, 426–433. [Google Scholar] [CrossRef]
- Ku, W.; Storer, R.H.; Georgakis, C. Disturbance Detection and Isolation by Dynamic Principal Component Analysis. Chemom. Intell. Lab. Syst. 1995, 30, 179–196. [Google Scholar] [CrossRef]
- Bakshi, B.R. Multiscale analysis and modeling using wavelets. J. Chemom. 1999, 13, 415–434. [Google Scholar] [CrossRef]
- Cheng, T.; Dairi, A.; Harrou, F.; Sun, Y.; Leiknes, T. Monitoring influent conditions of wastewater treatment plants by nonlinear data-based techniques. IEEE Access 2019, 7, 108827–108837. [Google Scholar] [CrossRef]
- Ahsan, M.; Mashuri, M.; Kuswanto, H.; Prastyo, D.D. Intrusion detection system using multivariate control chart Hotelling’s T2 based on PCA. Int. J. Adv. Sci. Eng. Inf. Technol. 2018, 8, 1905–1911. [Google Scholar] [CrossRef]
- Nahm, F.S. Nonparametric statistical tests for the continuous data: The basic concept and the practical use. Korean J. Anesthesiol. 2016, 69, 8–14. [Google Scholar] [CrossRef] [PubMed]
- Harrou, F.; Nounou, M.N.; Nounou, H.N.; Madakyaru, M. Statistical fault detection using PCA-based GLR hypothesis testing. J. Loss Prev. Process Ind. 2013, 26, 129–139. [Google Scholar] [CrossRef]
- Harmouche, J.; Delpha, C.; Diallo, D. Incipient fault detection and diagnosis based on Kullback-Leibler divergence using principal component analysis: Part II. Signal Process. 2015, 109, 334–344. [Google Scholar] [CrossRef]
- Zhang, X.; Delpha, C.; Diallo, D. Performance evaluation of Jensen–Shannon divergence-based incipient fault diagnosis: Theoretical proofs and validations. Struct. Health Monit. 2022, 22, 1628–1646. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, B.; Lu, N. A Newly Robust Fault Detection and Diagnosis Method for High-Speed Trains. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2198–2208. [Google Scholar] [CrossRef]
- Altukife, F. Nonparametric control chart based on sum of ranks. Pak. J.-Stat. 2003, 19, 291–300. [Google Scholar]
- Das, N. A non-parametric control chart for controlling variability based on squared rank test. J. Ind. Syst. Eng. 2008, 2, 114–125. [Google Scholar]
- Diana, G.; Tommasi, C. Cross-validation methods in principal component analysis: A comparison. Stat. Methods Appl. 2002, 11, 71–82. [Google Scholar] [CrossRef]
- Joe Qin, S. Statistical process monitoring: Basics and beyond. J. Chemom. A J. Chemom. Soc. 2003, 17, 480–502. [Google Scholar] [CrossRef]
- Harrou, F.; Sun, Y.; Madakyaru, M. Kullback-leibler distance-based enhanced detection of incipient anomalies. J. Loss Prev. Process Ind. 2016, 44, 73–87. [Google Scholar] [CrossRef]
- Pratt, J.W.; Gibbons, J.D. Kolmogorov-Smirnov Two-Sample Tests. In Concepts of Nonparametric Theory; Springer Series in Statistics; Springer: New York, NY, USA, 1981. [Google Scholar]
- Guo, P.; Fu, J.; Yang, X. Condition Monitoring and Fault Diagnosis of Wind Turbines Gearbox Bearing Temperature Based on Kolmogorov-Smirnov Test and Convolutional Neural Network Model. Energies 2018, 11, 2248. [Google Scholar] [CrossRef]
- Test, K.S. The Concise Encyclopedia of Statistics; Springer: New York, NY, USA, 2008. [Google Scholar]
- Khoshnevisan, D. Empirical Processes, and the Kolmogorov-Smirnov Statistic Math 6070; University of Utah: Salt Lake City, UT, USA, 2006. [Google Scholar]
- Stephens, M.A. Introduction to Kolmogorov (1933) On the Empirical Determination of a Distribution; Springer: New York, NY, USA, 1992. [Google Scholar]
- Kar, C.; Mohanty, A. Application of KS test in ball bearing fault diagnosis. J. Sound Vib. 2004, 269, 439–454. [Google Scholar] [CrossRef]
- Athreya, K.B.; Roy, V. General Glivenko—Cantelli theorems. Stat 2016, 5, 306–311. [Google Scholar] [CrossRef]
- Singh, R.S. On the Glivenko-Cantelli Theorem for Weighted Empiricals Based on Independent Random Variables. Ann. Probab. 1975, 3, 371–374. [Google Scholar] [CrossRef]
- Bolbolamiri, N.; Sanai, M.S.; Mirabadi, A. Time-Domain Stator Current Condition Monitoring: Analyzing Point Failures Detection by Kolmogorov-Smirnov (K-S) Test. Int. J. Electr. Comput. Energ. Electron. Commun. Eng. 2012, 6, 587–592. [Google Scholar]
- Powers, D.M. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. arXiv 2020, arXiv:2010.16061. [Google Scholar]
- Downs, J.; Vogel, E. A plant-wide industrial process control problem. Comput. Chem. Eng. 1993, 17, 245–255. [Google Scholar] [CrossRef]
- Yin, S.; Ding, S.X.; Haghani, A.; Hao, H.; Zhang, P. A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process. J. Process Control 2012, 22, 1567–1581. [Google Scholar] [CrossRef]
- Hu, M.; Hu, X.; Deng, Z.; Tu, B. Fault Diagnosis of Tennessee Eastman Process with XGB-AVSSA-KELM Algorithm. Energies 2022, 15, 3198. [Google Scholar] [CrossRef]









| Process Variable | Description | Value/Unit |
|---|---|---|
| Flow rate of reactant | 1 m/min | |
| u | Flow rate of heating fluid in jacket | 0.5 m/min |
| Concentrations of reactant A | 4 mol/L | |
| Concentrations of reactant B | 0 mol/L | |
| Temperature of fluid in reactor | 320 K | |
| Temperature of fluid in jacket | 375 K | |
| Enthalpy of dynamic reaction in Equation (25) | 0.5480 kcal/kmol | |
| Enthalpy of dynamic reaction in Equation (25) | 0.9860 kcal/kmol | |
| Density of fluid in the reactor | 0.09 kg/L | |
| Density of fluid in the jacket | 0.10 kg/L | |
| Heat capacity of fluid in the reactor | 0.231 kcal/(kg K) | |
| Heat capacity of fluid in the jacket | 0.80 kcal/(kg K) | |
| Volume of the reactor | 10 lt | |
| Volume of the jacket | 8 lt | |
| Heat transfer coefficient of the reactor | 0.20 kcal/(min K) | |
| R | Gas constant | 1.987 kcal/(min K) |
| Arrhenius constant | min | |
| Arrhenius constant | min | |
| Activation enegy of reaction in Equation (25) | 20,000 kcal/kmol | |
| Activation enegy of reaction in Equation (25) | 50,000 kcal/kmol |
| Fault Number | Description | Variable | Type of Fault |
|---|---|---|---|
| F1 | Large step (3.5% of total variation) | Temperature T5 | Bias |
| F2 | Medium step (2% of total variation) | Temperature T5 | Bias |
| F3 | Small step (0.9% of total variation) | Temperature T5 | Bias |
| F4 | Multiple step (2% of total variation) | Temperature T6 | Intermittent |
| F5 | Ramp (Slope of 0.002) | Product concentration | Drift |
| Fault | Index | PCA- | PCA-SPE | PCA-CUSUM | PAC-KS |
|---|---|---|---|---|---|
| F1 | FDR | 99.00 | 99.00 | 99.00 | 100.00 |
| FAR | 1.00 | 0.80 | 0.00 | 0.00 | |
| Precision | 99.33 | 99.49 | 100.00 | 100.00 | |
| Recall | 99.00 | 99.00 | 99.00 | 100.00 | |
| F1-score | 99.10 | 99.20 | 99.50 | 100.00 | |
| F2 | FDR | 98.26 | 92.75 | 95.75 | 100.00 |
| FAR | 1.75 | 3.15 | 0.00 | 0.00 | |
| Precision | 98.80 | 97.70 | 100.00 | 100.00 | |
| Recall | 98.26 | 92.75 | 95.75 | 100.00 | |
| F1-score | 98.50 | 95.20 | 97.80 | 100.00 | |
| F3 | FDR | 44.00 | 63.25 | 77.45 | 98.87 |
| FAR | 3.50 | 1.21 | 0.00 | 0.00 | |
| Precision | 95.00 | 98.80 | 100.00 | 100.00 | |
| Recall | 44.00 | 63.25 | 77.45 | 98.87 | |
| F1-score | 60.10 | 77.11 | 87.29 | 99.43 | |
| F4 | FDR | 72.89 | 73.33 | 87.23 | 98.34 |
| FAR | 2.19 | 1.13 | 5.43 | 1.26 | |
| Precision | 95.10 | 92.50 | 90.65 | 98.00 | |
| Recall | 72.89 | 73.33 | 87.23 | 98.34 | |
| F1-score | 82.52 | 79.80 | 89.34 | 98.16 | |
| F5 | FDR | 64.67 | 77.87 | 41.67 | 94.34 |
| FAR | 5.75 | 4.00 | 0.00 | 0.00 | |
| Precision | 94.40 | 96.68 | 100.00 | 100.00 | |
| Recall | 64.67 | 77.87 | 41.67 | 94.34 | |
| F1-score | 76.79 | 86.00 | 58.82 | 97.08 |
| No. | Fault | D-Stat Value |
|---|---|---|
| 1 | No fault | 0.2875 |
| 2 | Fault F1 | 0.9900 |
| 3 | Fault F2 | 0.9074 |
| 4 | Fault F3 | 0.8198 |
| 5 | Fault F4 | 0.8588 |
| 6 | Fault F5 | 0.9425 |
| Fault | Index | PCA- | PCA-SPE | PCA-CUSUM | PCA–KS |
|---|---|---|---|---|---|
| IDV1 | FDR | 97.95 | 99.10 | 94.33 | 99.65 |
| FAR | 1.63 | 3.77 | 0.00 | 5.00 | |
| Precision | 99.10 | 97.95 | 100.00 | 98.02 | |
| Recall | 97.95 | 99.10 | 94.33 | 99.65 | |
| F1-score | 98.48 | 98.40 | 97.08 | 98.70 | |
| IDV2 | FDR | 94.59 | 98.52 | 75.00 | 98.81 |
| FAR | 1.75 | 1.75 | 0.00 | 9.75 | |
| Precision | 99.13 | 99.16 | 100.00 | 95.89 | |
| Recall | 94.59 | 98.52 | 75.00 | 98.81 | |
| F1-score | 96.67 | 98.68 | 85.71 | 97.77 | |
| IDV4 | ADR | 72.43 | 97.25 | 98.00 | 98.41 |
| FAR | 1.26 | 1.89 | 0.00 | 1.20 | |
| Precision | 99.23 | 99.01 | 100.00 | 99.46 | |
| Recall | 72.43 | 97.25 | 98.00 | 98.41 | |
| F1-score | 83.57 | 98.25 | 98.98 | 98.87 | |
| IDV5 | ADR | 62.16 | 62.67 | 93.67 | 97.94 |
| FAR | 1.18 | 1.87 | 0.00 | 1.50 | |
| Precision | 99.12 | 98.80 | 100.00 | 99.25 | |
| Recall | 62.16 | 62.67 | 93.67 | 97.94 | |
| F1-score | 76.50 | 76.90 | 96.71 | 98.68 | |
| IDV6 | ADR | 98.53 | 98.63 | 68.33 | 99.50 |
| FAR | 0.63 | 0.78 | 0.00 | 7.25 | |
| Precision | 99.70 | 99.71 | 100.00 | 97.12 | |
| Recall | 98.53 | 98.63 | 68.33 | 99.50 | |
| F1-score | 99.22 | 99.67 | 81.18 | 97.93 | |
| IDV7 | FDR | 99.35 | 99.51 | 99.51 | 100.00 |
| FAR | 1.89 | 3.71 | 0.00 | 15.63 | |
| Precision | 99.33 | 98.38 | 100.00 | 94.15 | |
| Recall | 99.35 | 99.51 | 99.51 | 100.00 | |
| F1-score | 99.34 | 98.90 | 99.74 | 97.00 | |
| IDV8 | FDR | 92.43 | 92.96 | 92.00 | 97.94 |
| FAR | 0.63 | 1.89 | 0.00 | 6.88 | |
| Precision | 99.76 | 99.07 | 100.00 | 97.09 | |
| Recall | 92.43 | 92.96 | 92.00 | 97.94 | |
| F1-score | 95.83 | 95.92 | 95.83 | 97.66 | |
| IDV10 | ADR | 33.14 | 59.82 | 84.00 | 95.59 |
| FAR | 1.89 | 4.50 | 0.00 | 10.62 | |
| Precision | 97.97 | 96.85 | 100.00 | 95.02 | |
| Recall | 33.14 | 59.82 | 84.00 | 95.59 | |
| F1-score | 49.57 | 73.95 | 90.81 | 95.61 | |
| IDV11 | ADR | 63.17 | 73.61 | 55.00 | 92.35 |
| FAR | 0.63 | 5.03 | 0.00 | 2.50 | |
| Precision | 99.66 | 92.50 | 100.00 | 98.74 | |
| Recall | 63.17 | 73.61 | 55.00 | 92.35 | |
| F1-score | 77.32 | 83.67 | 70.96 | 95.44 | |
| IDV12 | ADR | 93.67 | 90.91 | 79.50 | 99.51 |
| FAR | 1.89 | 3.14 | 0.00 | 14.37 | |
| Precision | 99.17 | 98.43 | 100.00 | 93.59 | |
| Recall | 93.67 | 94.52 | 79.50 | 99.01 | |
| F1-score | 96.38 | 86.00 | 88.57 | 96.29 | |
| IDV13 | ADR | 87.68 | 90.62 | 86.67 | 89.35 |
| FAR | 0.00 | 0.00 | 0.00 | 0.00 | |
| Precision | 100.00 | 100.00 | 100.00 | 100.00 | |
| Recall | 87.68 | 90.62 | 86.67 | 89.35 | |
| F1-score | 93.43 | 95.07 | 93.00 | 94.24 | |
| IDV14 | ADR | 98.21 | 94.43 | 68.50 | 98.24 |
| FAR | 1.89 | 1.26 | 0.00 | 1.23 | |
| Precision | 99.20 | 99.40 | 100.00 | 99.45 | |
| Recall | 98.21 | 94.43 | 68.50 | 98.24 | |
| F1-score | 98.37 | 96.85 | 81.30 | 98.79 |
| No. | Fault | D-Stat Value |
|---|---|---|
| 1 | No fault | 0.2250 |
| 2 | IDV(1) | 0.9894 |
| 3 | IDV(2) | 0.9393 |
| 4 | IDV(4) | 0.9994 |
| 5 | IDV(5) | 0.9825 |
| 6 | IDV(6) | 0.9950 |
| 7 | IDV(7) | 0.8282 |
| 8 | IDV(8) | 0.9195 |
| 9 | IDV(10) | 0.8183 |
| 10 | IDV(11) | 0.8028 |
| 11 | IDV(12) | 0.8995 |
| 12 | IDV(13) | 0.9060 |
| 13 | IDV(14) | 0.9027 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kini, K.R.; Madakyaru, M.; Harrou, F.; Menon, M.K.; Sun, Y. Improved Fault Detection in Chemical Engineering Processes via Non-Parametric Kolmogorov–Smirnov-Based Monitoring Strategy. ChemEngineering 2024, 8, 1. https://doi.org/10.3390/chemengineering8010001
Kini KR, Madakyaru M, Harrou F, Menon MK, Sun Y. Improved Fault Detection in Chemical Engineering Processes via Non-Parametric Kolmogorov–Smirnov-Based Monitoring Strategy. ChemEngineering. 2024; 8(1):1. https://doi.org/10.3390/chemengineering8010001
Chicago/Turabian StyleKini, K. Ramakrishna, Muddu Madakyaru, Fouzi Harrou, Mukund Kumar Menon, and Ying Sun. 2024. "Improved Fault Detection in Chemical Engineering Processes via Non-Parametric Kolmogorov–Smirnov-Based Monitoring Strategy" ChemEngineering 8, no. 1: 1. https://doi.org/10.3390/chemengineering8010001
APA StyleKini, K. R., Madakyaru, M., Harrou, F., Menon, M. K., & Sun, Y. (2024). Improved Fault Detection in Chemical Engineering Processes via Non-Parametric Kolmogorov–Smirnov-Based Monitoring Strategy. ChemEngineering, 8(1), 1. https://doi.org/10.3390/chemengineering8010001





