Temperature Distribution and Thermal Criticality of Kinetics Exothermic Reactant in Concentric Cylinders Subject to Various Boundary Conditions
Abstract
1. Introduction
2. The Basic Model Equations
3. Methods of Solutions
3.1. Semi-Analytical Method
3.2. Results Presentation and Comparison
3.3. Concentric Cylinder Heat Propagation of Reactive Specie
4. Parameter-Dependent Thermal Criticality Bifurcation Solutions
4.1. Implementation of a Weighted Residual Analytical Solution
4.2. Ignition Slice and Thermal Runaway
5. Conclusions
- The species reaction temperature distribution is a monotonically enhancing function of the radius with variations in thermal diffusion parameters.
- Analytical values show that produces a concave function of with variations in the terms and .
- The and reduces as the concentric cylinder gap is increased.
- Certain parameter changes significantly influenced the heat distribution and thermal explosion under various boundary conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Makinde, O.D.; Maserumule, R.L. Thermal criticality and entropy analysis for a variable viscosity couette flow. Phys. Scr. 2008, 78, 015402. [Google Scholar] [CrossRef]
- Salawu, S.O.; Disu, A.B. Branch-chain criticality and explosion for a generalized thermal Oldroyd 6-constant Couette reactive fluid flow. S. Afr. J. Chem. Eng. 2020, 34, 90–96. [Google Scholar] [CrossRef]
- Ajadi, S.O.; Gol’dshtein, V. Critical behaviour in a three-step reaction kinetics model. Combust. Theory Model. 2009, 13, 1–16. [Google Scholar] [CrossRef]
- Boddington, T.; Gray, P.; Wake, G.C. Theory of thermal explosion with simultaneous parallel reactions I. Foundations and the one-dimensional case. Proc. R. Soc. Lond. A 1984, 393, 85–100. [Google Scholar]
- Boddington, T.; Feng, C.G.; Gray, P. Thermal explosion, criticality and Disapperance of criticality in systems with distributed temperature I. Arbitrary Biot number and general reactionrate laws. Proc. R. Soc. Lond. A 1983, 390, 247–264. [Google Scholar]
- Graham-Eagle, J.G.; Wake, G.C. The theory of thermal explosion with simultaneous parallel reactions III. Disappearance of critical behaviour with the exothermic and endothermic reactions. Proc. R. Soc. Lond. A 1986, 407, 183–198. [Google Scholar]
- Okoya, S.S.; Ajadi, S.O. Critical parameters for thermal condition equations. Mech. Res. Commun. 1999, 26, 363–370. [Google Scholar] [CrossRef]
- Okoya, S.S. Thermal stability for a reactive viscous flow in a slab. Mech. Res. Commun. 2006, 33, 728–733. [Google Scholar] [CrossRef]
- Varatharajan, B.; Williams, F.A. Chemical-kinetics description of high temperature ignition and detonation of acetylene-oxygen-diluent systems. Combust. Flame 2001, 124, 624–645. [Google Scholar] [CrossRef]
- Okoya, S.S. Ignition times for a branched-chain thermal explosion chemistry with heat loss. Toxicol. Environ. Chem. 2009, 91, 905–910. [Google Scholar] [CrossRef]
- Salawu, S.O.; Okoya, S.S. On criticality for a branched-chain thermal reactive-diffusion in a cylinder. Combust. Sci. Technol. 2020, 192, 1–16. [Google Scholar] [CrossRef]
- Okoya, S.S. Disappearance of criticality in a branched-chain thermal explosion with heat loss. Combust. Flame 2006, 144, 410–414. [Google Scholar] [CrossRef]
- Semenov, N.N. Some Problems in Chemical Kinetics and Reactivity. Part 2; Pergamon Press: London, UK, 1959. [Google Scholar]
- Zeldovich, Y.B.; Barenblatt, G.I.; Librovich, V.B.; Makhviladze, G.M. The Mathematical Theory of Combustion and Explosions; Consultants Bureau: New York, NY, USA, 1985. [Google Scholar]
- Salawu, S.O.; Kareem, R.A.; Shamshuddin, M.D.; Khan, S.U. Double exothermic reaction of viscous dissipative Oldroyd 8-constant fluid and thermal ignition in a channel. Chem. Phys. Lett. 2020, 760, 138011. [Google Scholar] [CrossRef]
- Aleksandrov, E.N.; Kuznetsov, N.M.; Kozlov, S.N. Initiation of chain and thermal explosions by the reactor surface. criterion for the participation of branching chains in a thermal explosion. Combust. Explos. Shock Waves 2007, 43, 530–537. [Google Scholar] [CrossRef]
- Stolin, A.M.; Bostandzhiyan, S.A.; Plotnikova, N.V. Conditions for occurence of hydrodynamic thermal explosion in flows of power-law fluid. Heat Transf. Sov. Res. 1978, 10, 86–93. [Google Scholar]
- Okoya, S.S. Criticality effects on non-Newtonian fluids with viscous heating and thermal conductivity in cylindrical enclosure. J. Niger. Math. Soc. 2007, 26, 1–10. [Google Scholar]
- Kumar, M.M.J.; Satyamurty, V.V. Limiting Nusselt numbers for laminar forced convection in asymmetrically heated annuli with viscous dissipation. Int. Commun. Heat Mass Transf. 2011, 38, 923–927. [Google Scholar] [CrossRef]
- Tasnim, S.H.; Mahmud, S. Mixed convection and entropy generation in a vertical annular space. Exergy Int. J. 2002, 2, 373–379. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary Layer Theory; Springer: New York, NY, USA, 2000; pp. 1–10. [Google Scholar]
- Machover, E.; Mastorakos, E. Numerical investigation of the stochastic behavior of light-round in annular non-premixed combustors. Combust. Sci. Tech. 2017, 189, 1467–1485. [Google Scholar] [CrossRef]
- Shonhiwa, T.; Zaturski, M.B. Disappearance of criticality in thermal explosion for reactive viscous flows. Combut. Flame 1987, 67, 175–177. [Google Scholar] [CrossRef]
- Okoya, S.S. Computational study of thermal influence in axial annular flow of a reactive third grade fluid with non-linear viscosity. Alex. Engin. J. 2019, 58, 401–411. [Google Scholar] [CrossRef]
- Yaseen, M.; Rawat, S.K.; Kumar, M. Falkner–Skan problem for a stretching or shrinking wedge with nanoparticle aggregation. J. Heat Transf. 2022, 144, 102501. [Google Scholar] [CrossRef]
- Das, S.; Chakraborty, S.; Jana, R.N.; Makinde, O.D. Mixed convective couette flow of reactive nanofluids between concentric vertical cylindrical pipes. J. Nanofluids 2015, 4, 485–493. [Google Scholar] [CrossRef]
- Frank-Kamenetskii, D.A. Diffusion and Heat Transfer in Chemical Kinetics; Plenum Press: New York, NY, USA, 1969. [Google Scholar]
- Ajadi, S.O. Approximate analytic solution for critical parameters in thermal explosion problem. Appl. Math. Comput. 2011, 218, 2005–2010. [Google Scholar] [CrossRef]
- Kurose, R.; Makino, H. Large eddy simulation of a solid-fuel jet flame. Combust. Flame 2003, 135, 1–16. [Google Scholar] [CrossRef]
- Jha, B.K.; Samalia, A.K.; Ajibade, A.O. Transient free-convective flow of reactive viscous fluid in a vertical channel. Int. Commun. Heat Mass Transf. 2011, 38, 633–639. [Google Scholar] [CrossRef]
- Li, J.; Zhong, B. Experimental investigation on heat loss and combustion in methane/ oxygen micro-tube combustor. Appl. Therm. Eng. 2008, 28, 707–716. [Google Scholar] [CrossRef]
- Salawu, S.O.; Disu, A.B.; Dada, M.S. On criticality for a generalized Couette flow of a branch-chain thermal reactive third-grade fluid with Reynolds viscosity model. Sci. World J. 2020, 2020, 7915954. [Google Scholar]
- Oderinu, R.A.; Aregbesola, Y.A.S. Using Laguerre’s quadrature in the weighted residual method for problems with semi infinite domain. Int. J. Pure Appl. Math. 2012, 75, 95–107. [Google Scholar]
- Salawu, S.O.; Oderinu, R.A.; Ohaegbue, A.D. Current density and thermodynamic analysis of energy optimization for double exothermic reaction of magneto-Oldroyd 8-constant material. J. King Saud Univ. Sci. 2021, 33, 101374. [Google Scholar] [CrossRef]

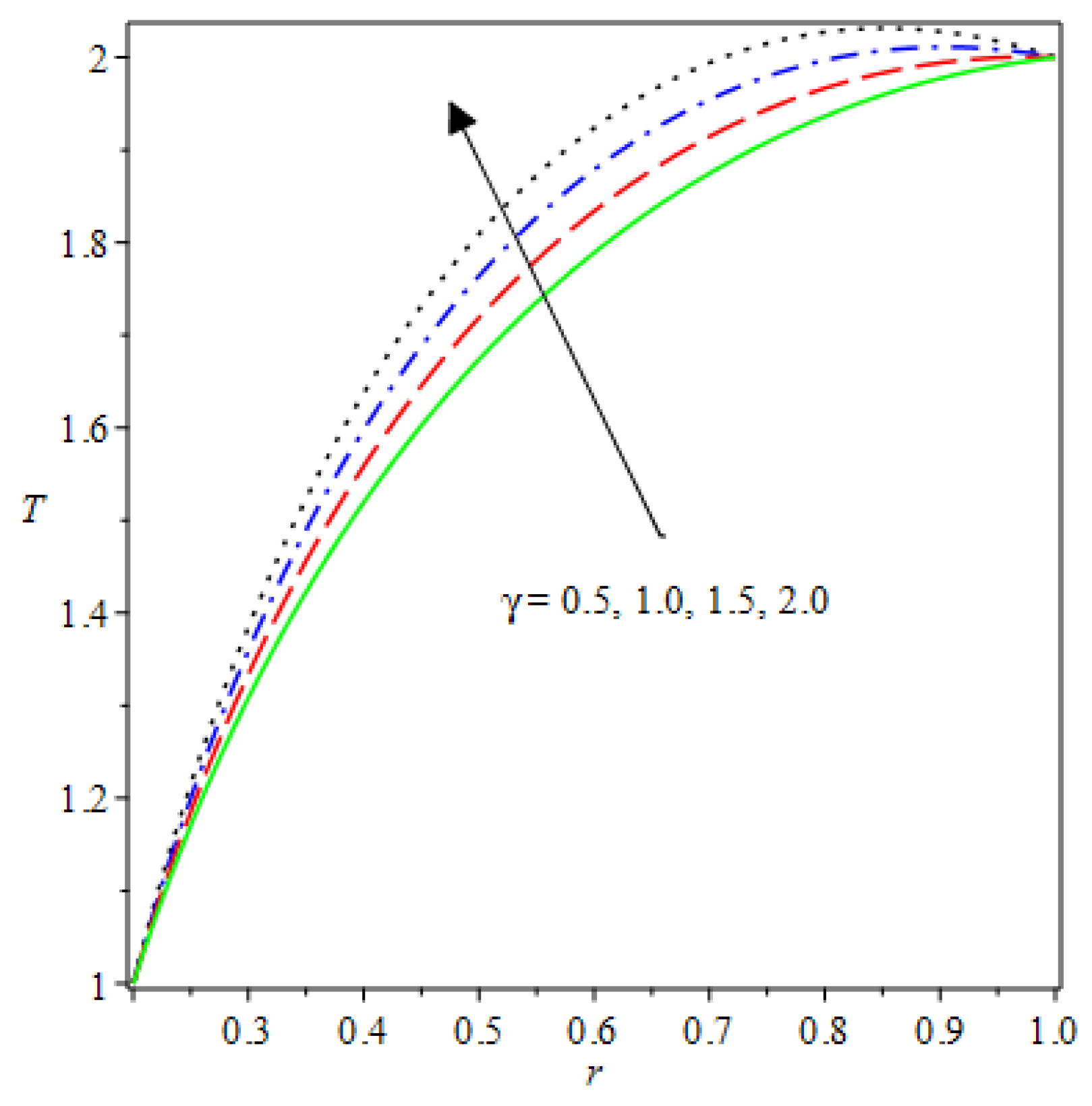
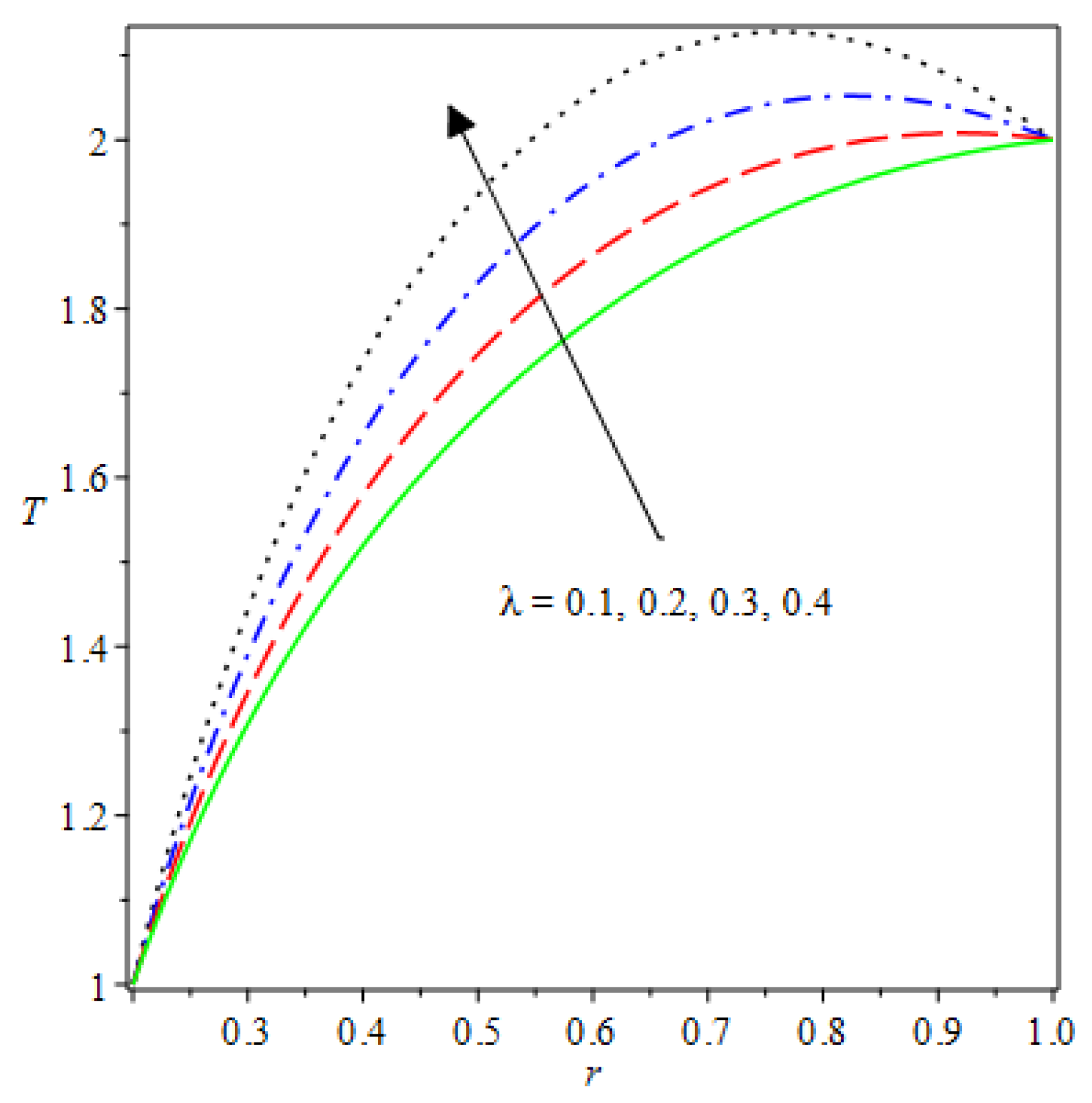

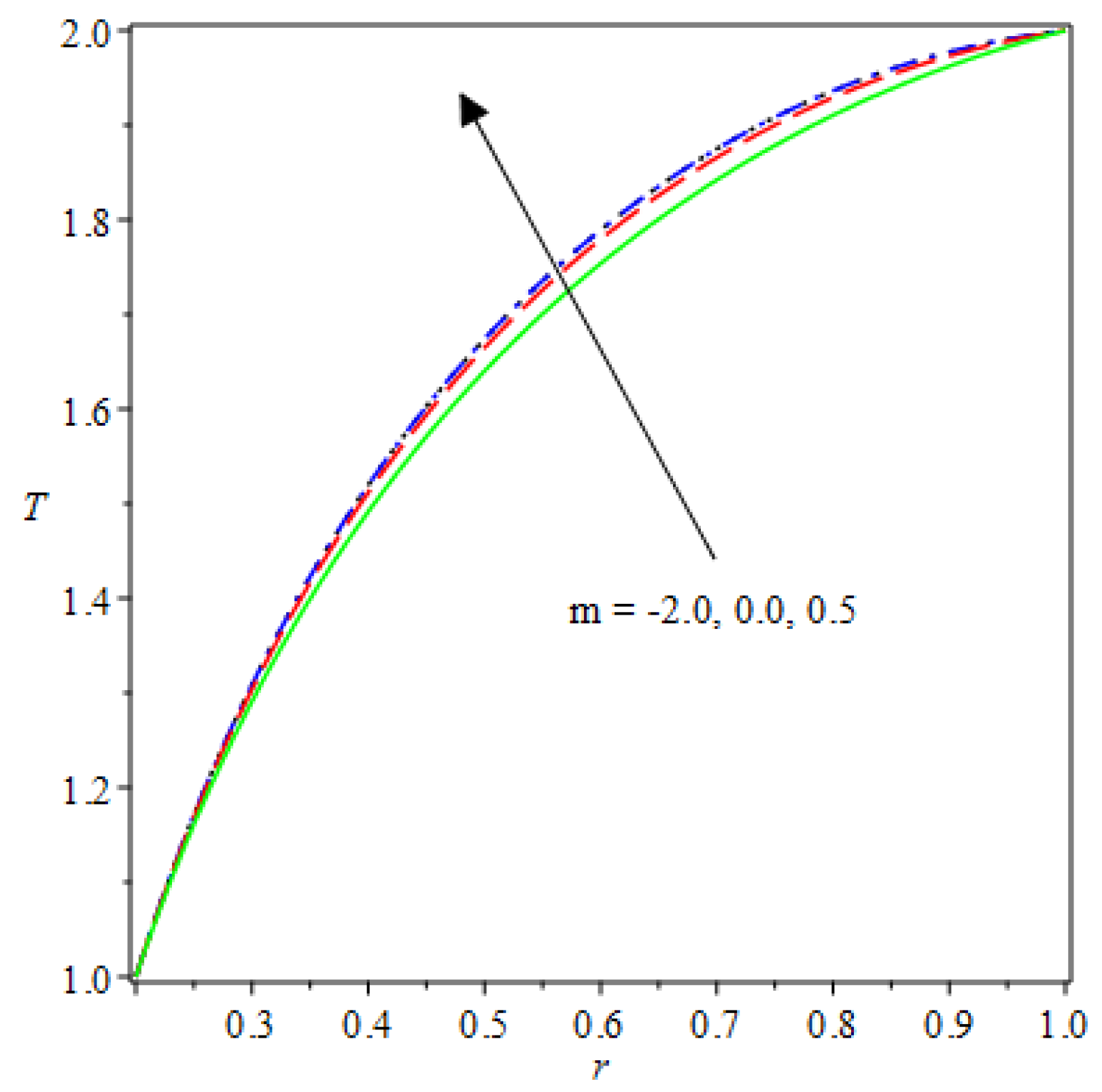
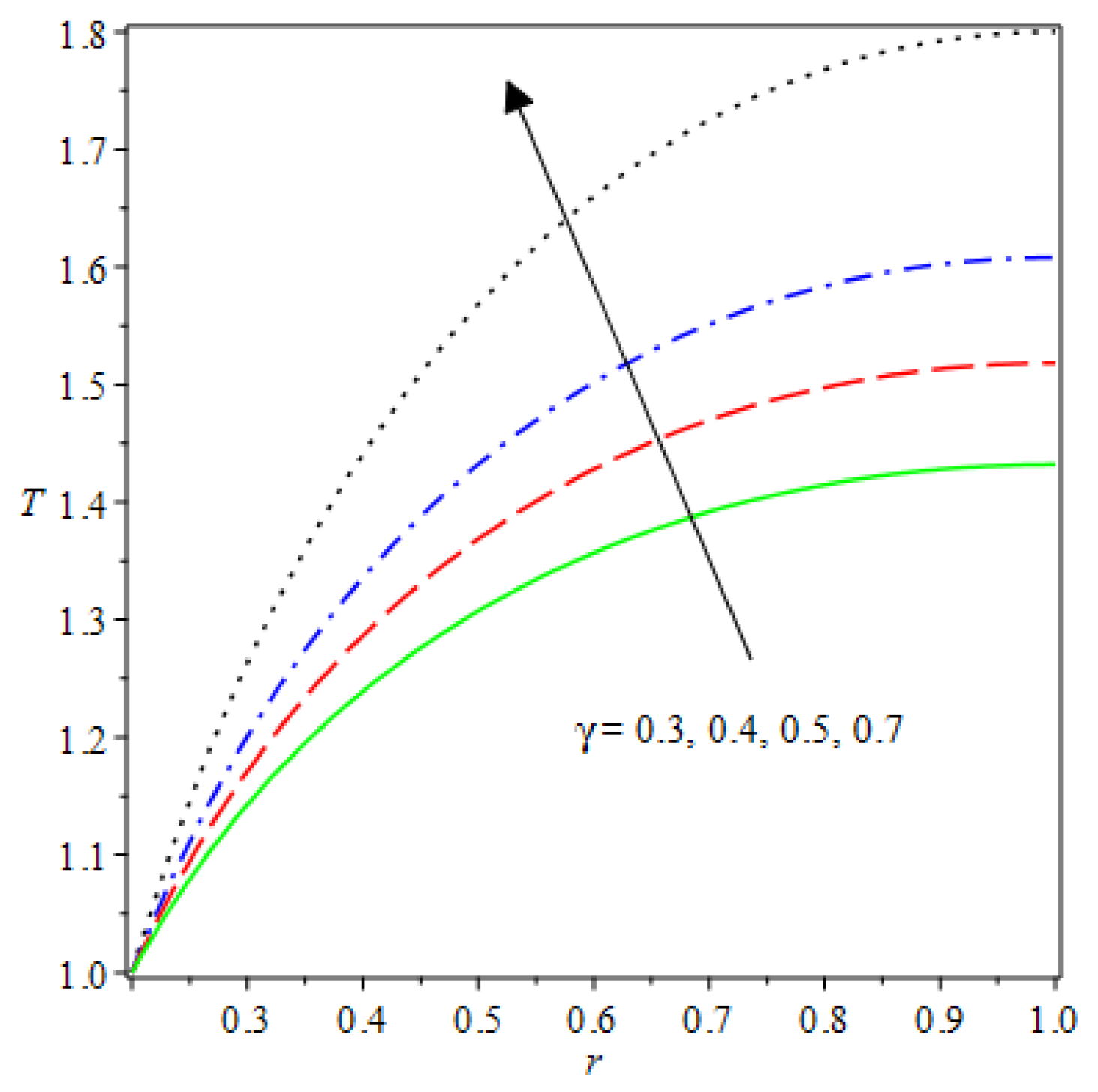

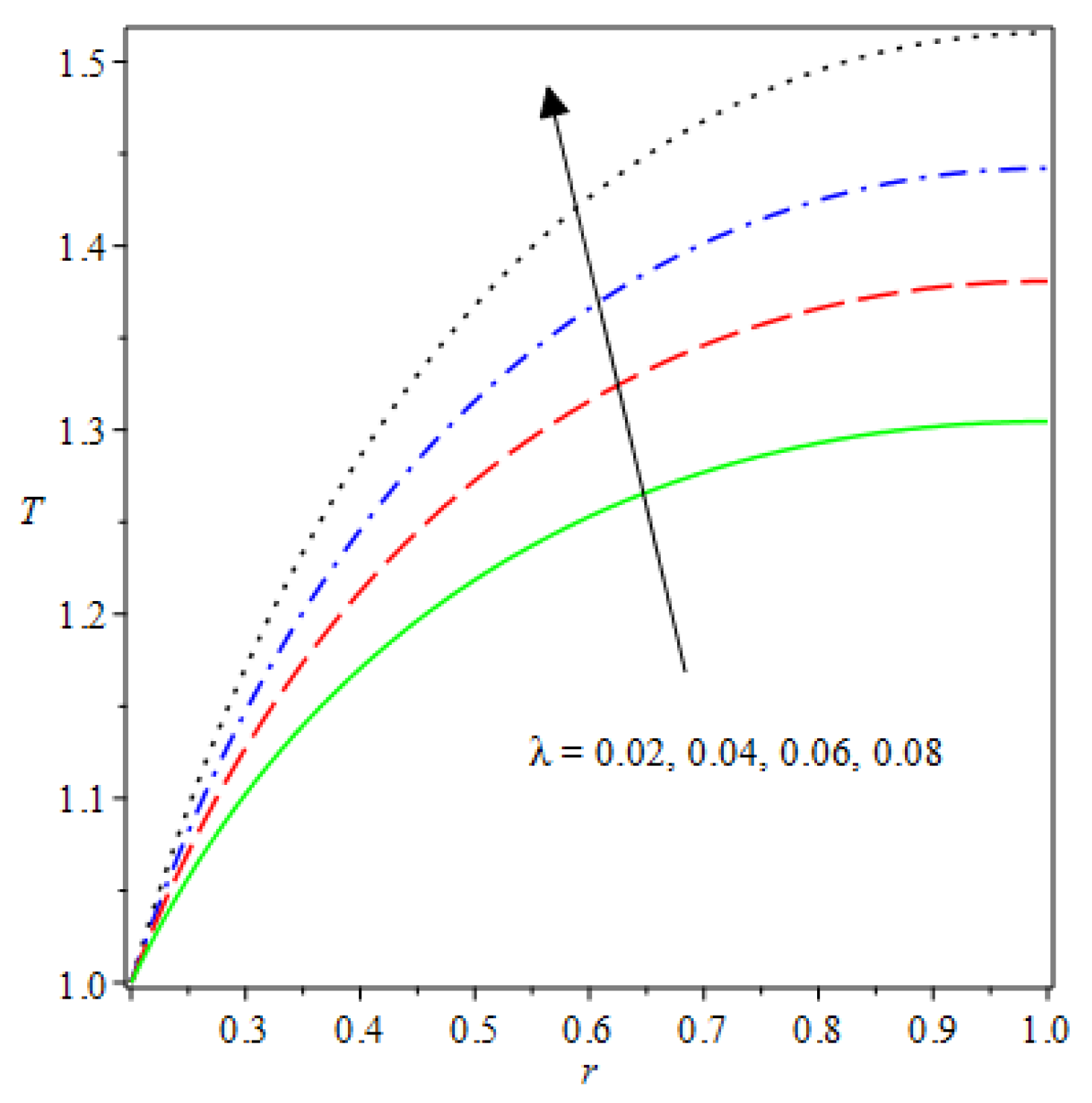
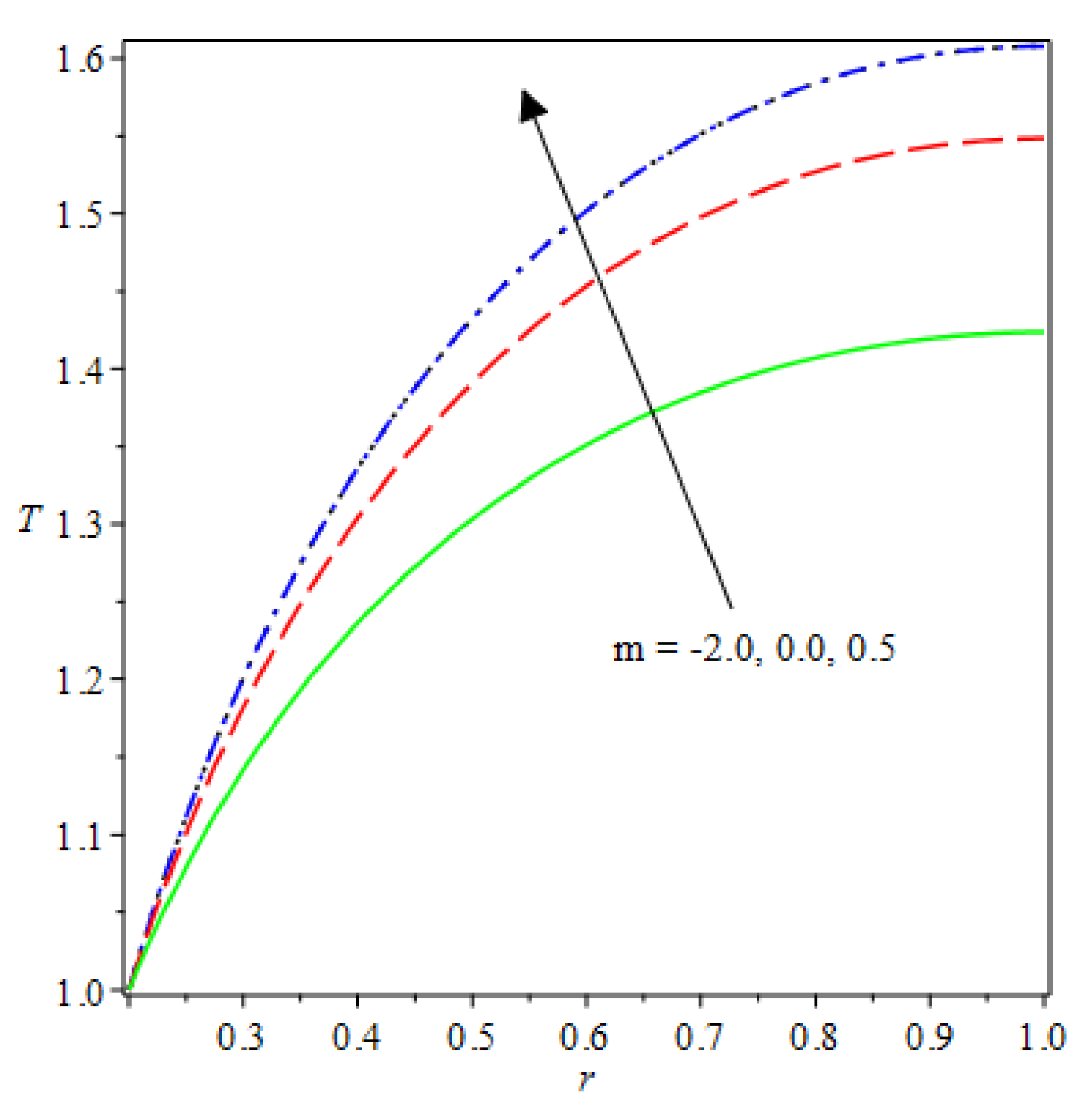
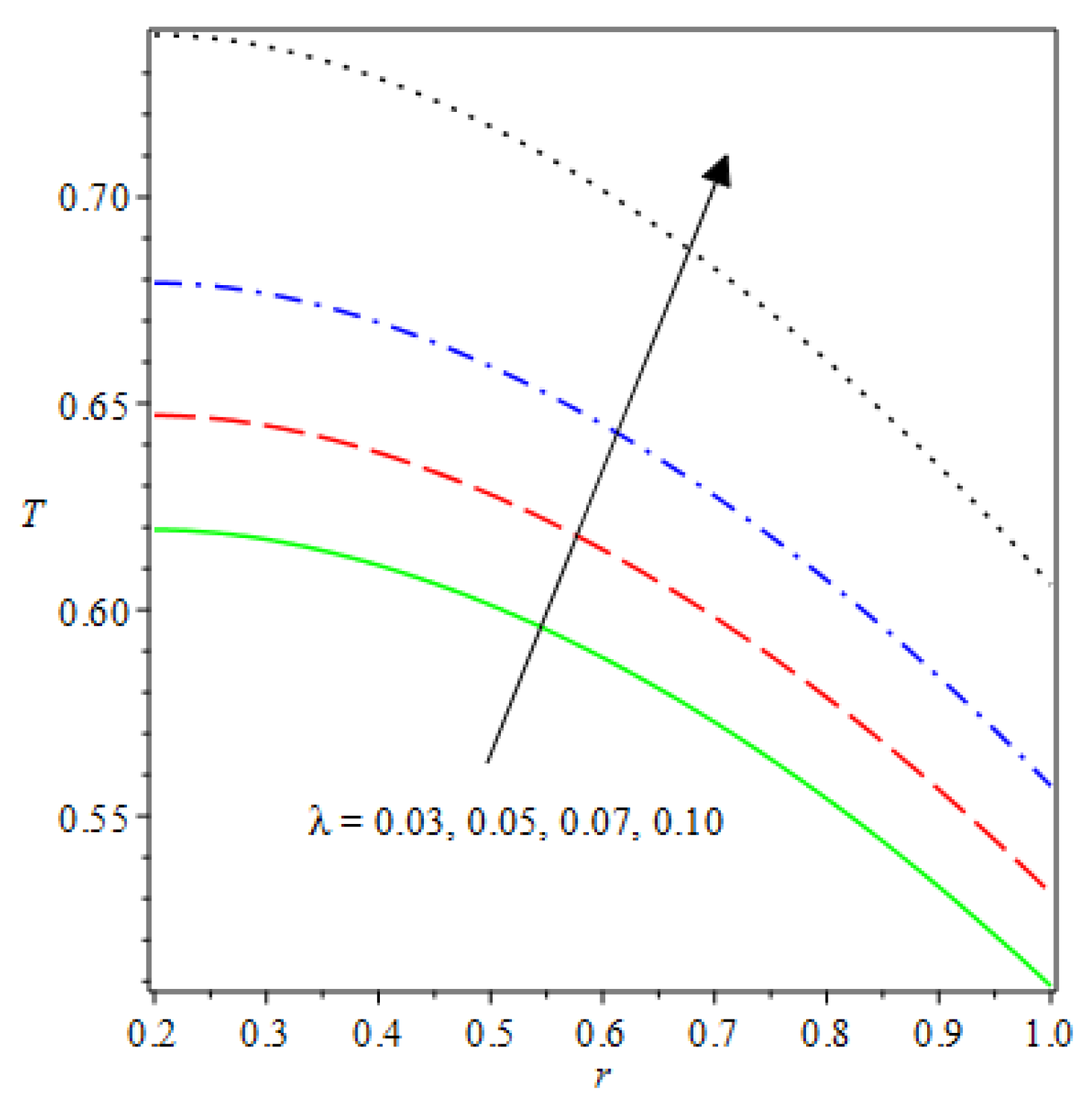
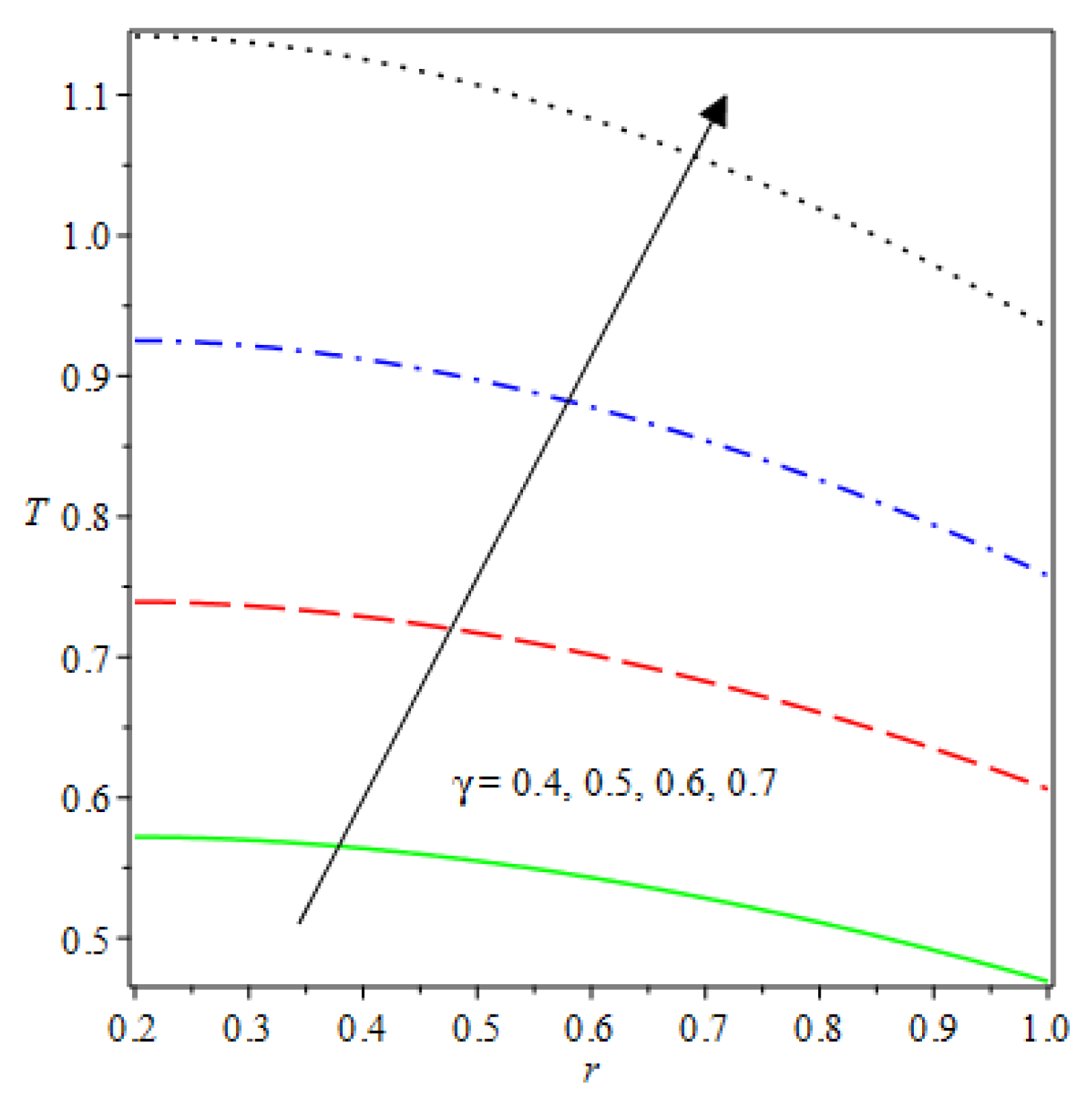
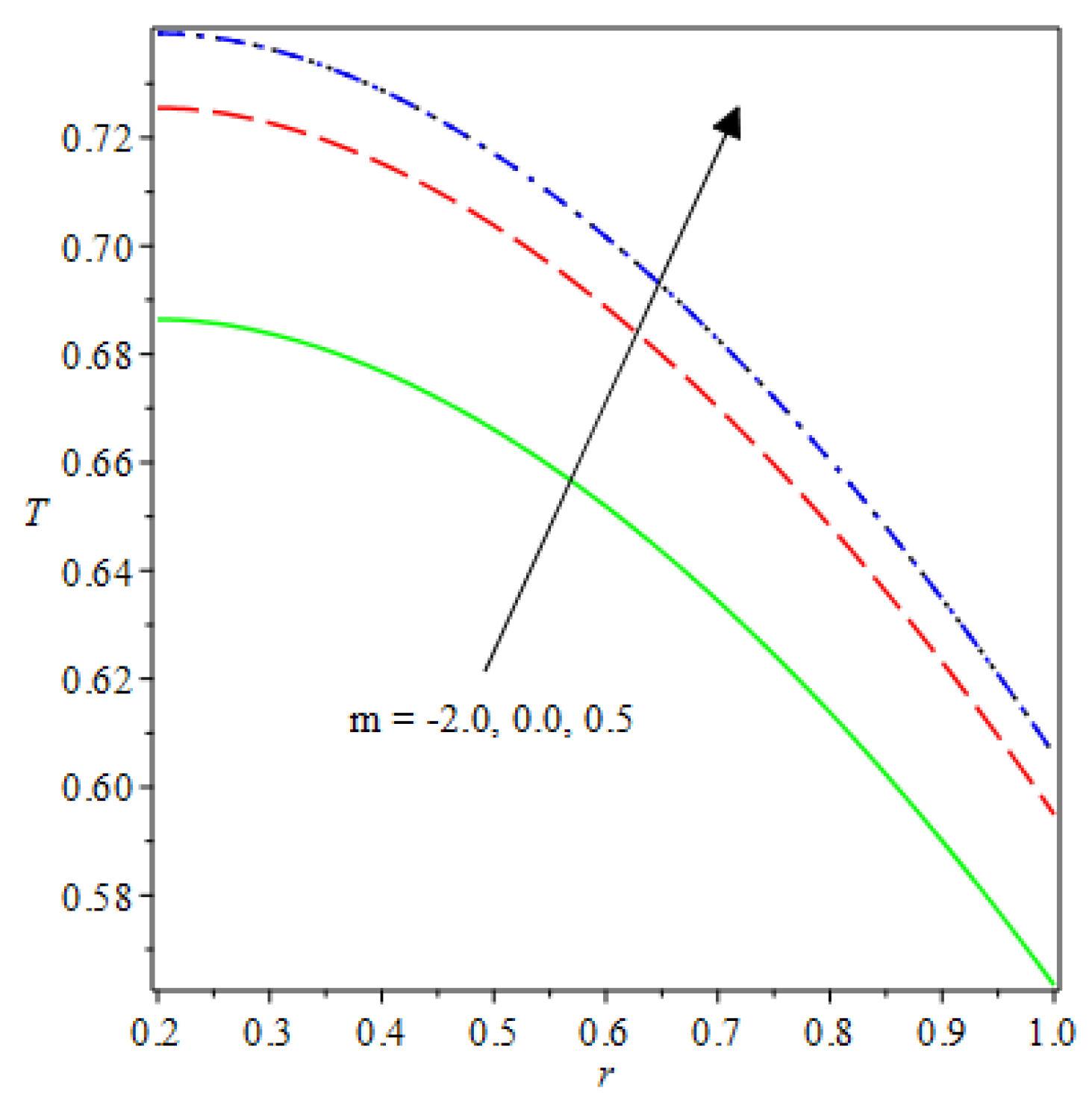
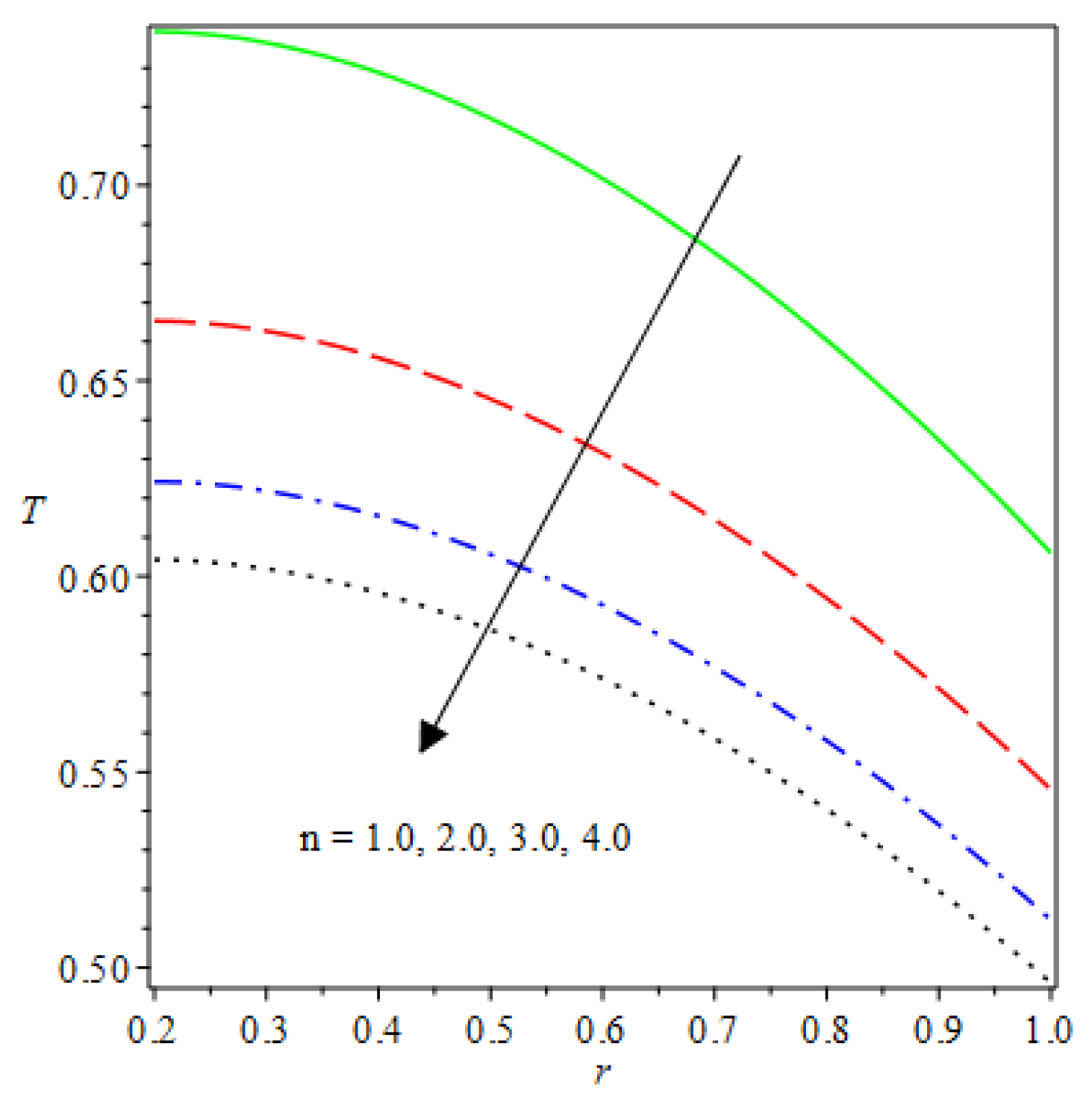
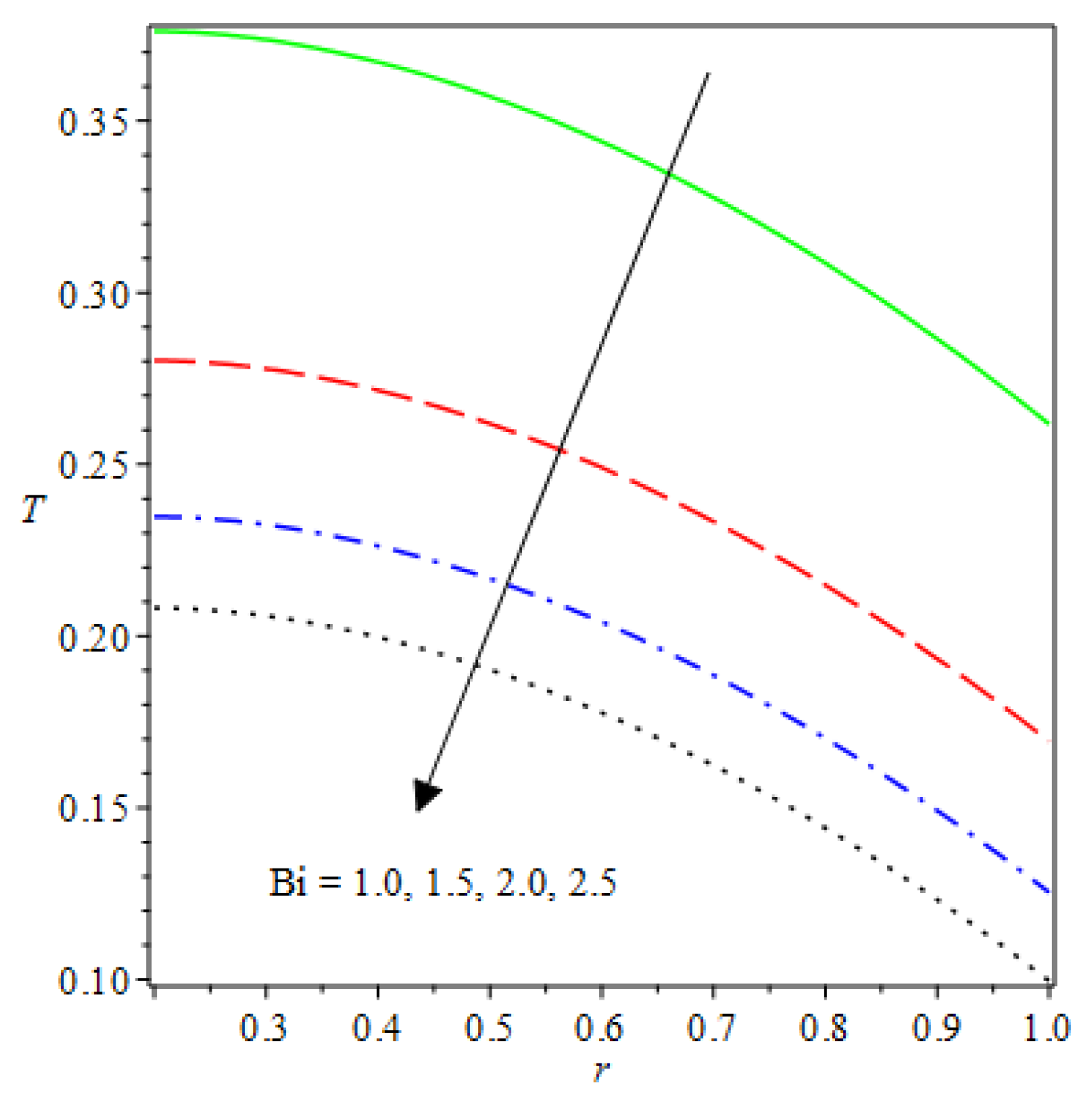
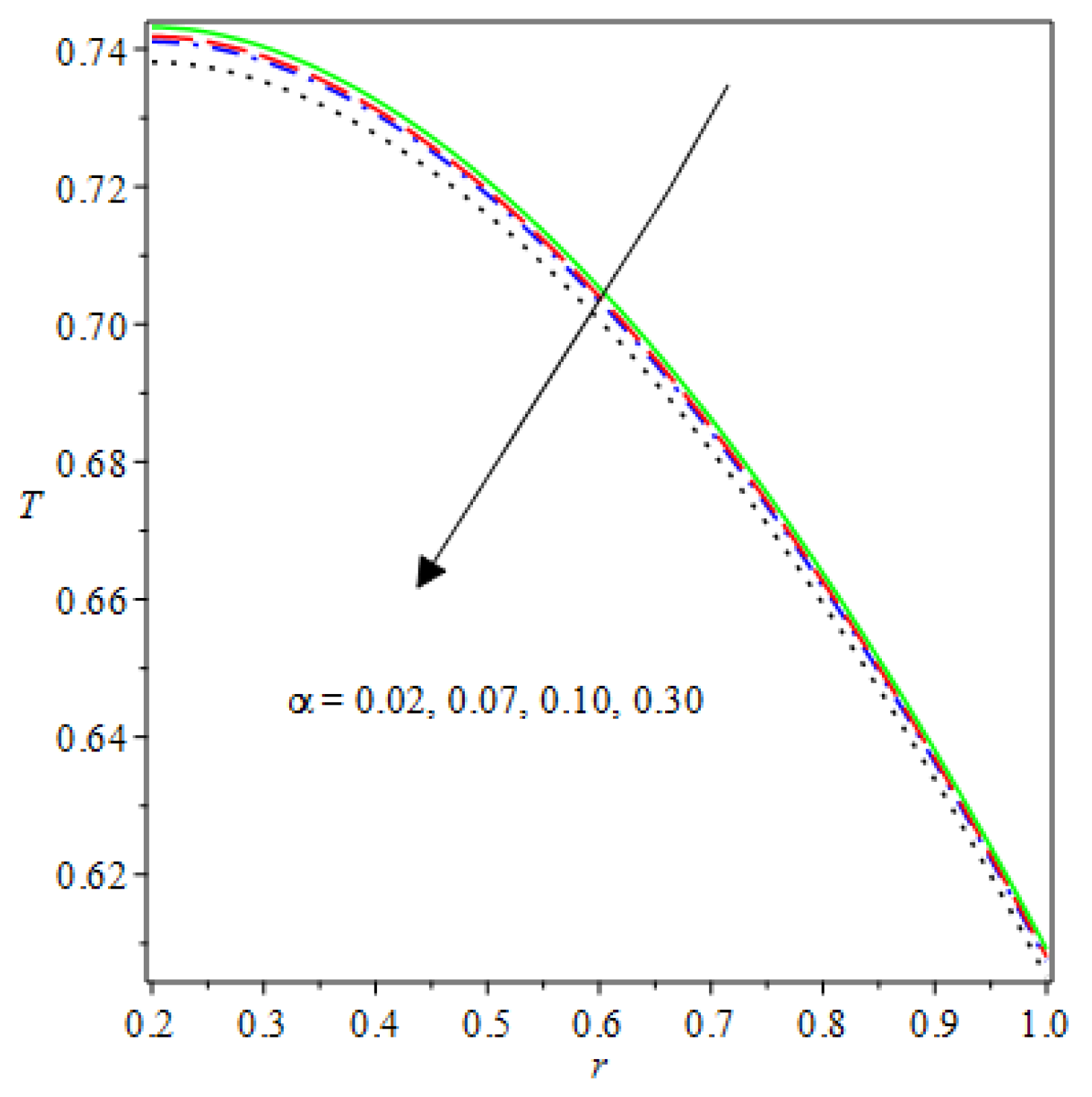
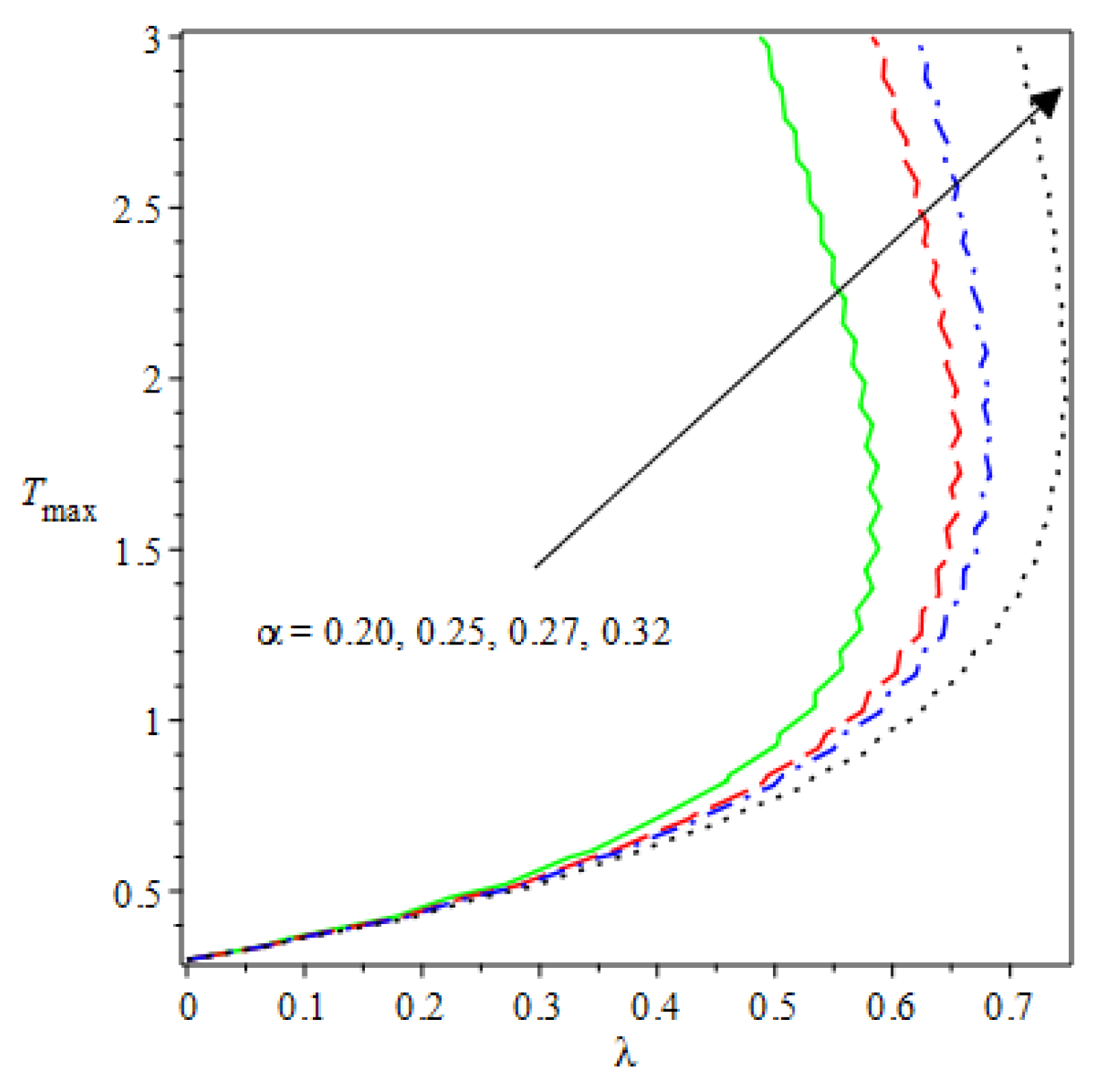

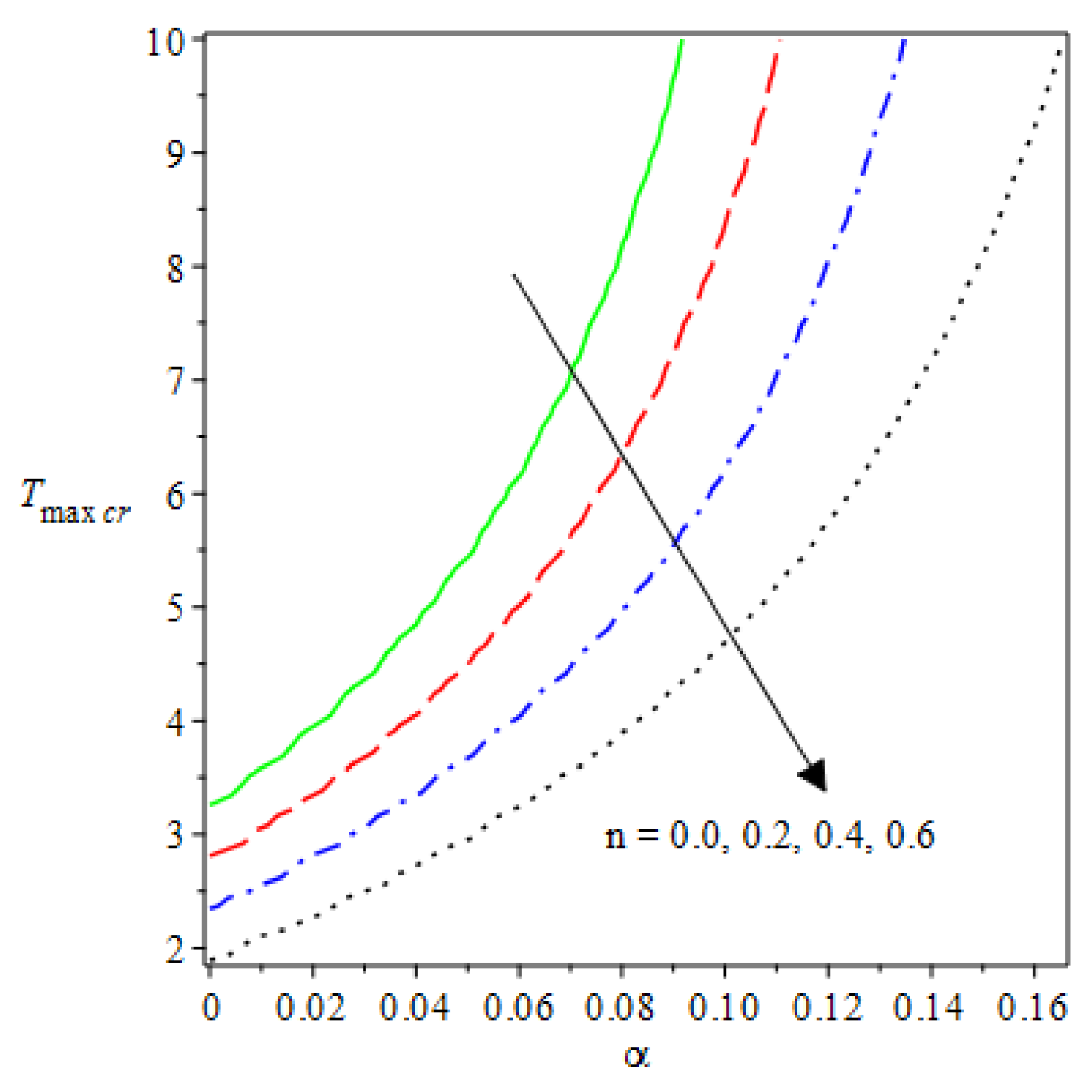
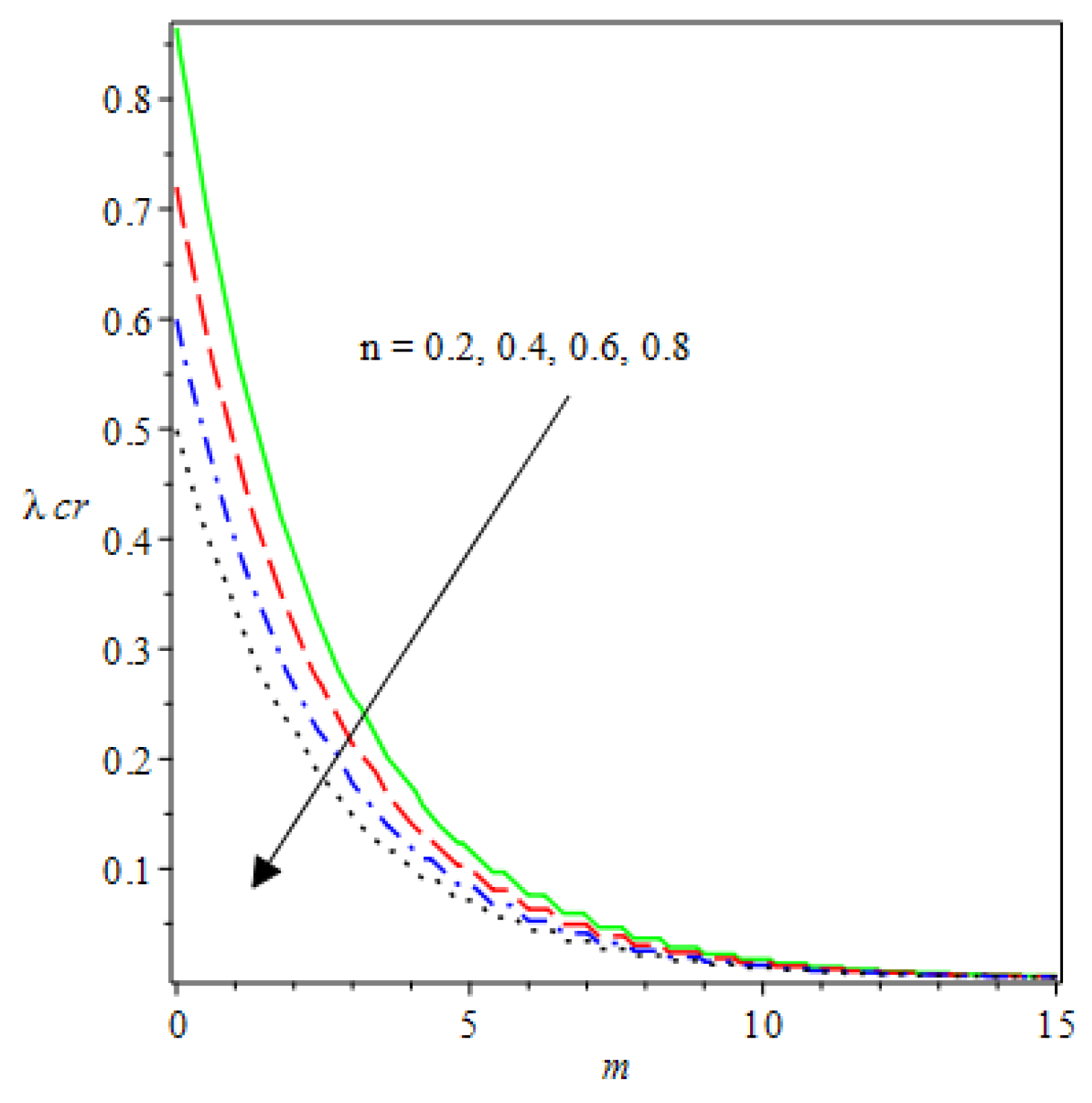
| m | n | Asymmetric Conditions | Mixed Type 2 Conditions | |||
|---|---|---|---|---|---|---|
| 0.5 | 0.1 | 0.2 | 0.5 | 1.0 | 0.142605760 | 0.826773598 |
| 0.7 | 0.068713729 | 0.939952662 | ||||
| 0.07 | 0.236601339 | 0.629676051 | ||||
| 0.15 | 0.020551671 | 1.220893443 | ||||
| 0.1 | 0.092234542 | 0.995247778 | ||||
| 0.3 | 0.173033013 | 0.743315791 | ||||
| −2.0 | 0.312229943 | 0.460637107 | ||||
| 0.0 | 0.189263346 | 0.714959625 | ||||
| 0.3 | 0.253515080 | 0.561043255 | ||||
| 0.7 | 0.196972165 | 0.687664032 |
| h | PWRM Outcomes | R-K Numerical Outcomes | Absolute Error |
|---|---|---|---|
| 0.2 | 1.000000000 | 1.000000000 | 0 |
| 0.3 | 1.200701962 | 1.200703920 | |
| 0.4 | 1.335717301 | 1.335744481 | |
| 0.5 | 1.432171360 | 1.432174785 | |
| 0.6 | 1.501899779 | 1.501899963 | |
| 0.7 | 1.551207219 | 1.551203670 | |
| 0.8 | 1.583825778 | 1.583822025 | |
| 0.9 | 1.602183557 | 1.602186780 | |
| 1.0 | 1.608005656 | 1.608005997 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salawu, S.O.; Okoya, S.S. Temperature Distribution and Thermal Criticality of Kinetics Exothermic Reactant in Concentric Cylinders Subject to Various Boundary Conditions. ChemEngineering 2023, 7, 19. https://doi.org/10.3390/chemengineering7020019
Salawu SO, Okoya SS. Temperature Distribution and Thermal Criticality of Kinetics Exothermic Reactant in Concentric Cylinders Subject to Various Boundary Conditions. ChemEngineering. 2023; 7(2):19. https://doi.org/10.3390/chemengineering7020019
Chicago/Turabian StyleSalawu, Sulyman Olakunle, and Samuel Segun Okoya. 2023. "Temperature Distribution and Thermal Criticality of Kinetics Exothermic Reactant in Concentric Cylinders Subject to Various Boundary Conditions" ChemEngineering 7, no. 2: 19. https://doi.org/10.3390/chemengineering7020019
APA StyleSalawu, S. O., & Okoya, S. S. (2023). Temperature Distribution and Thermal Criticality of Kinetics Exothermic Reactant in Concentric Cylinders Subject to Various Boundary Conditions. ChemEngineering, 7(2), 19. https://doi.org/10.3390/chemengineering7020019






