Sensitivity Analysis and Cost Estimation of a CO2 Capture Plant in Aspen HYSYS
Abstract
:1. Introduction
1.1. Literature Review
1.2. Scope of the Study
2. Materials and Methods
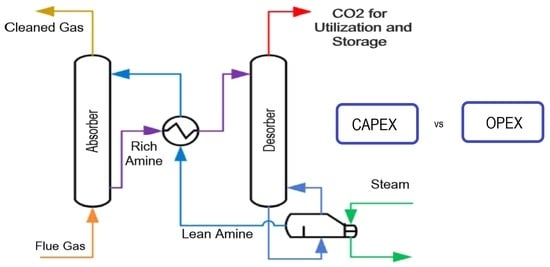
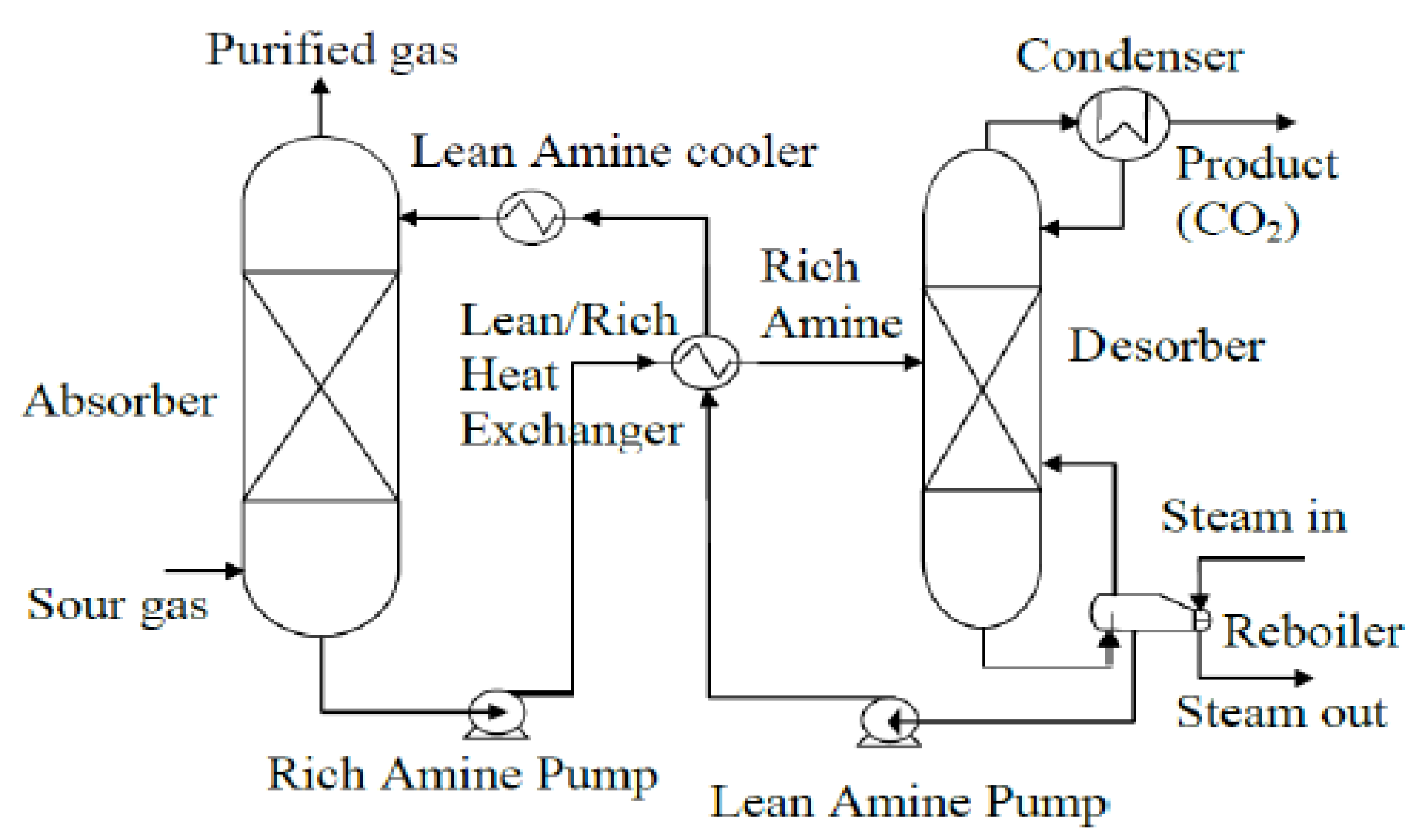
2.1. Process Description and Available Parameters
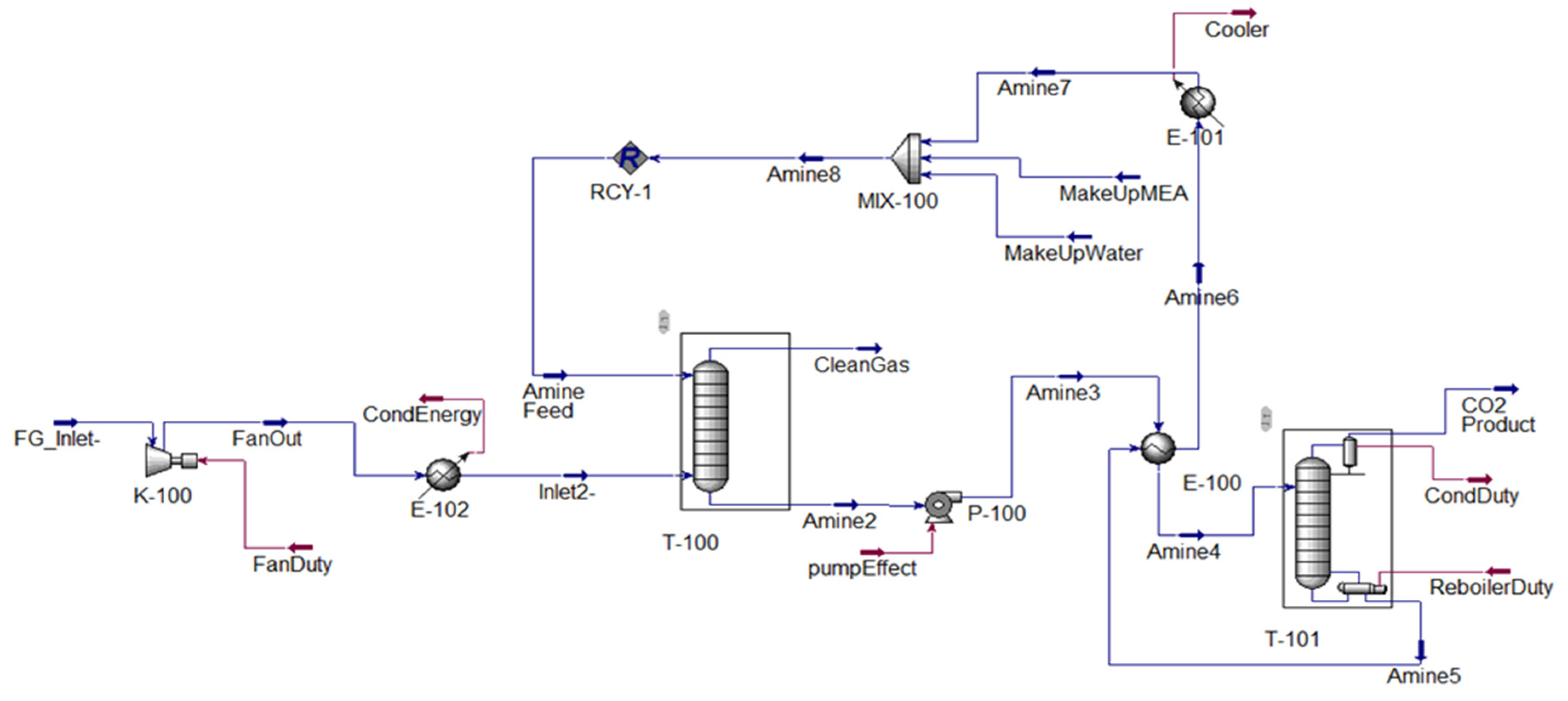
2.2. Specifications and Simulation
3. Dimensioning and Cost Estimation
3.1. Scope of Analysis
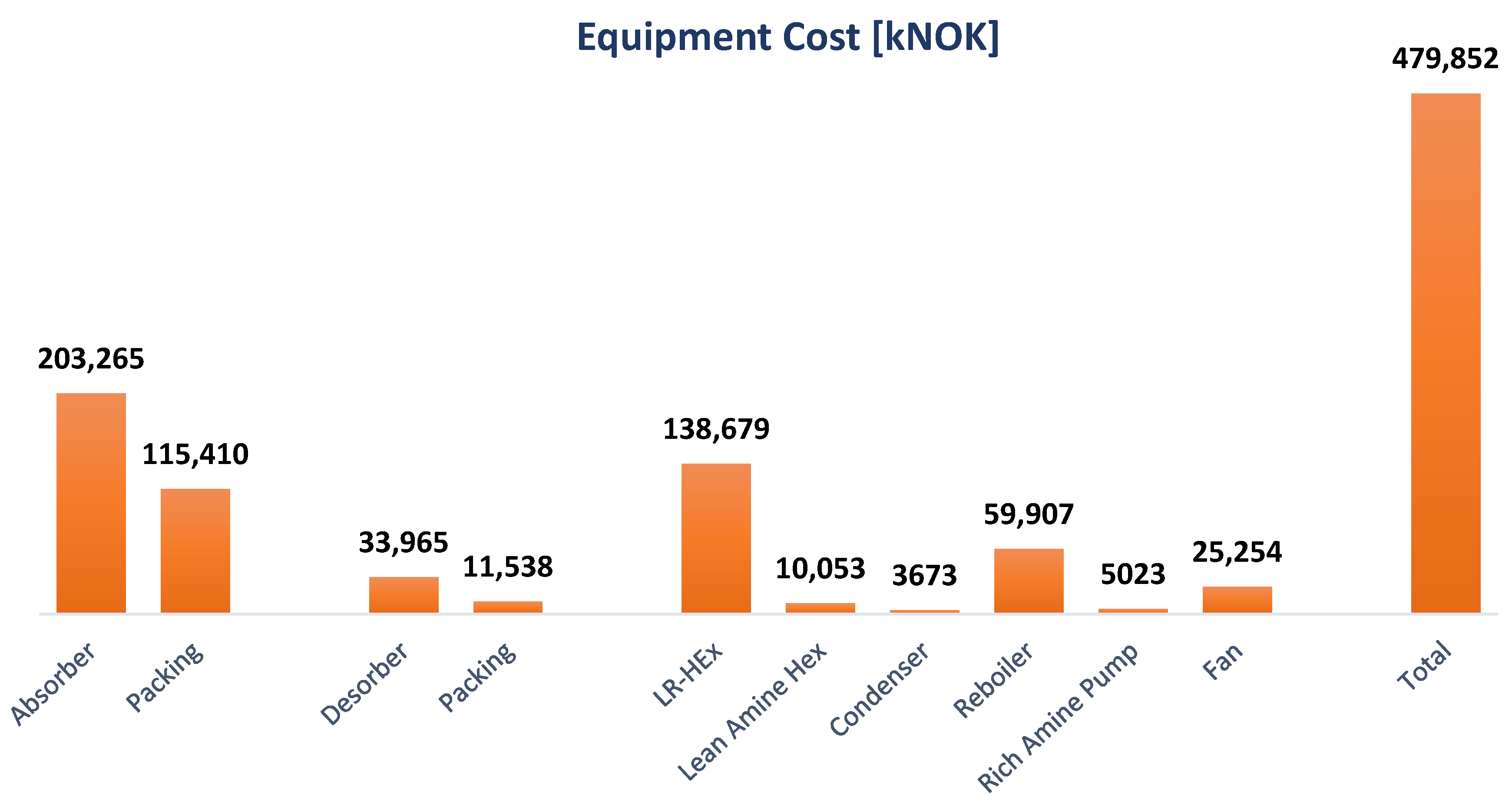
3.2. Dimensioning of Equipment
3.3. Capital Cost Estimation
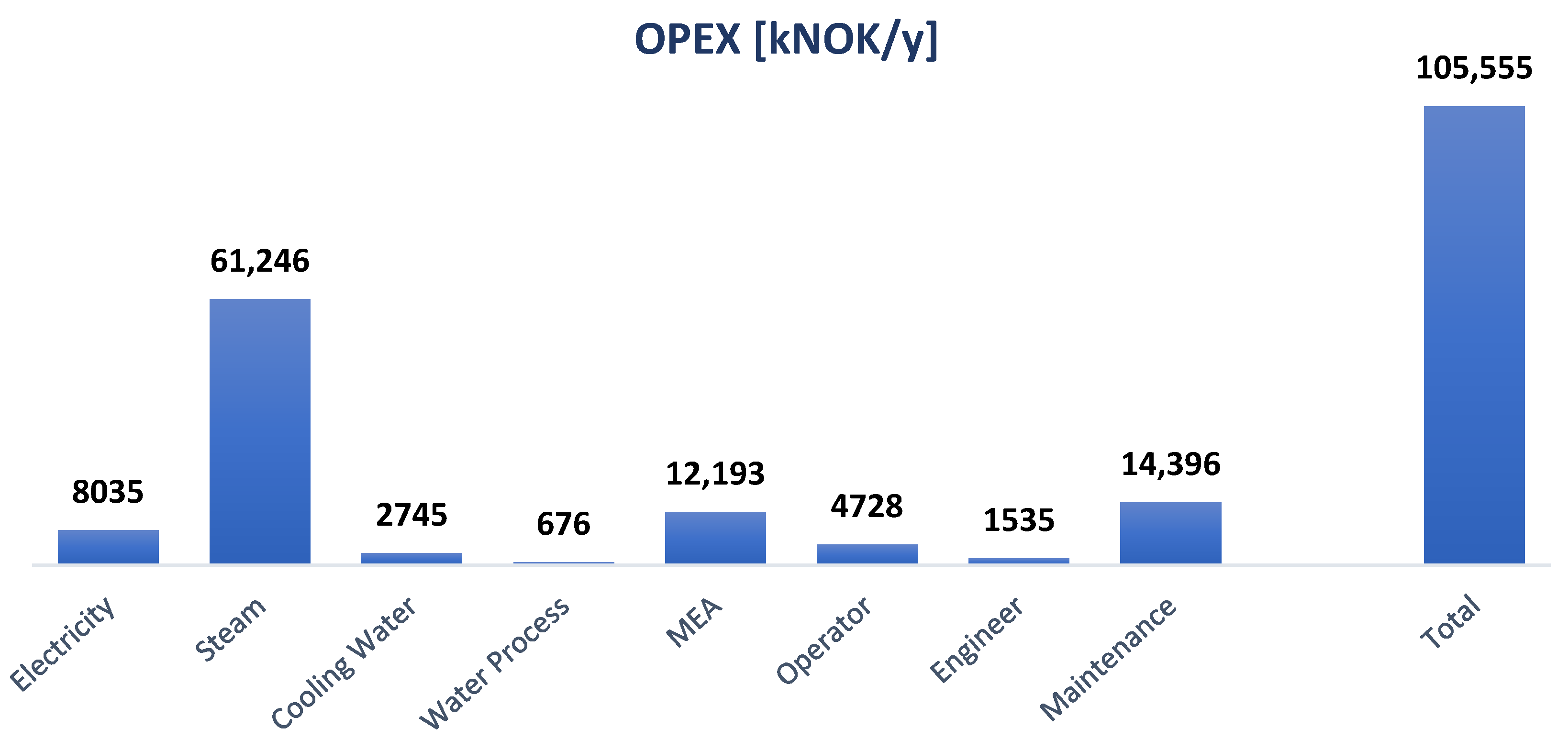
3.4. Operating Cost Estimation
4. Methods for Optimization
4.1. Absorber Packing Height
4.2. Removal Efficiency
4.3. The Lean/Rich Heat Exchanger Minimum Temperature Approach
4.4. Approach to Size Factor’s Exponent Derivation
5. Results and Discussion
5.1. Base Case Evaluation
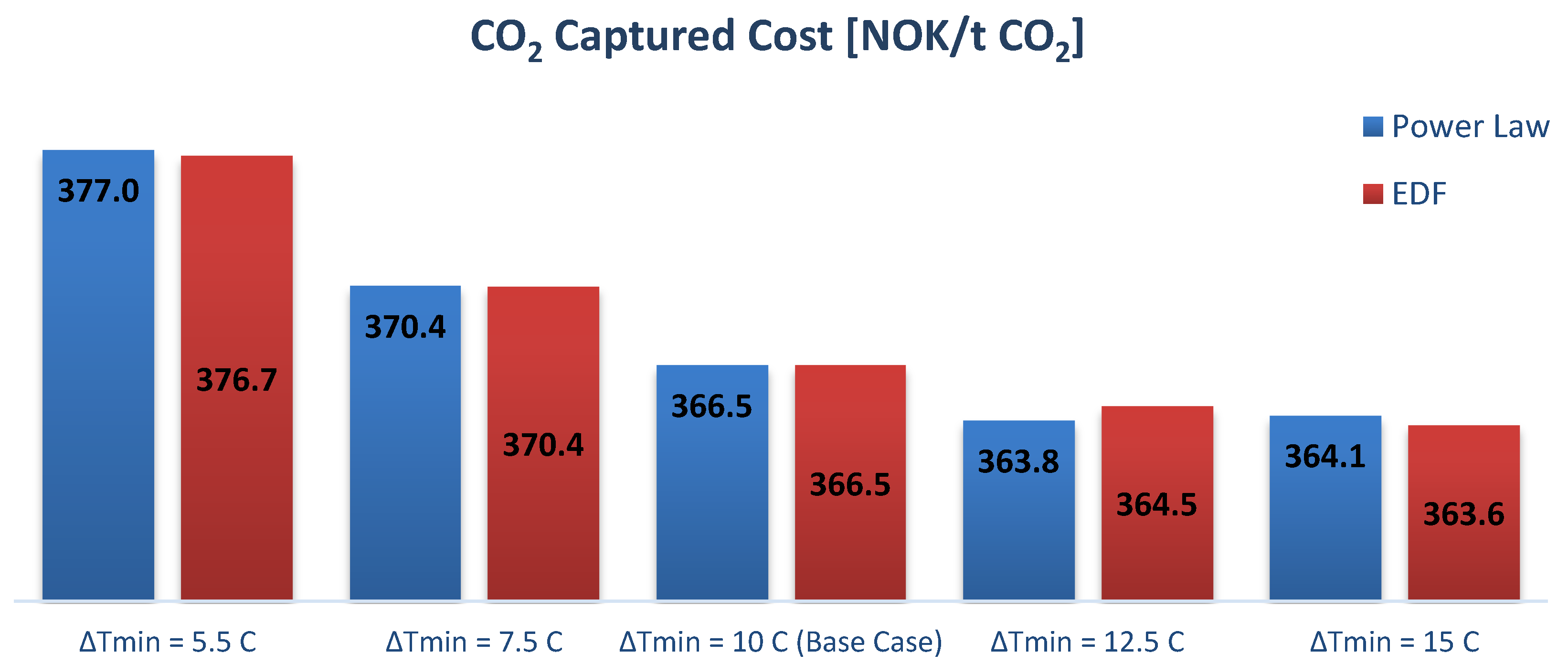
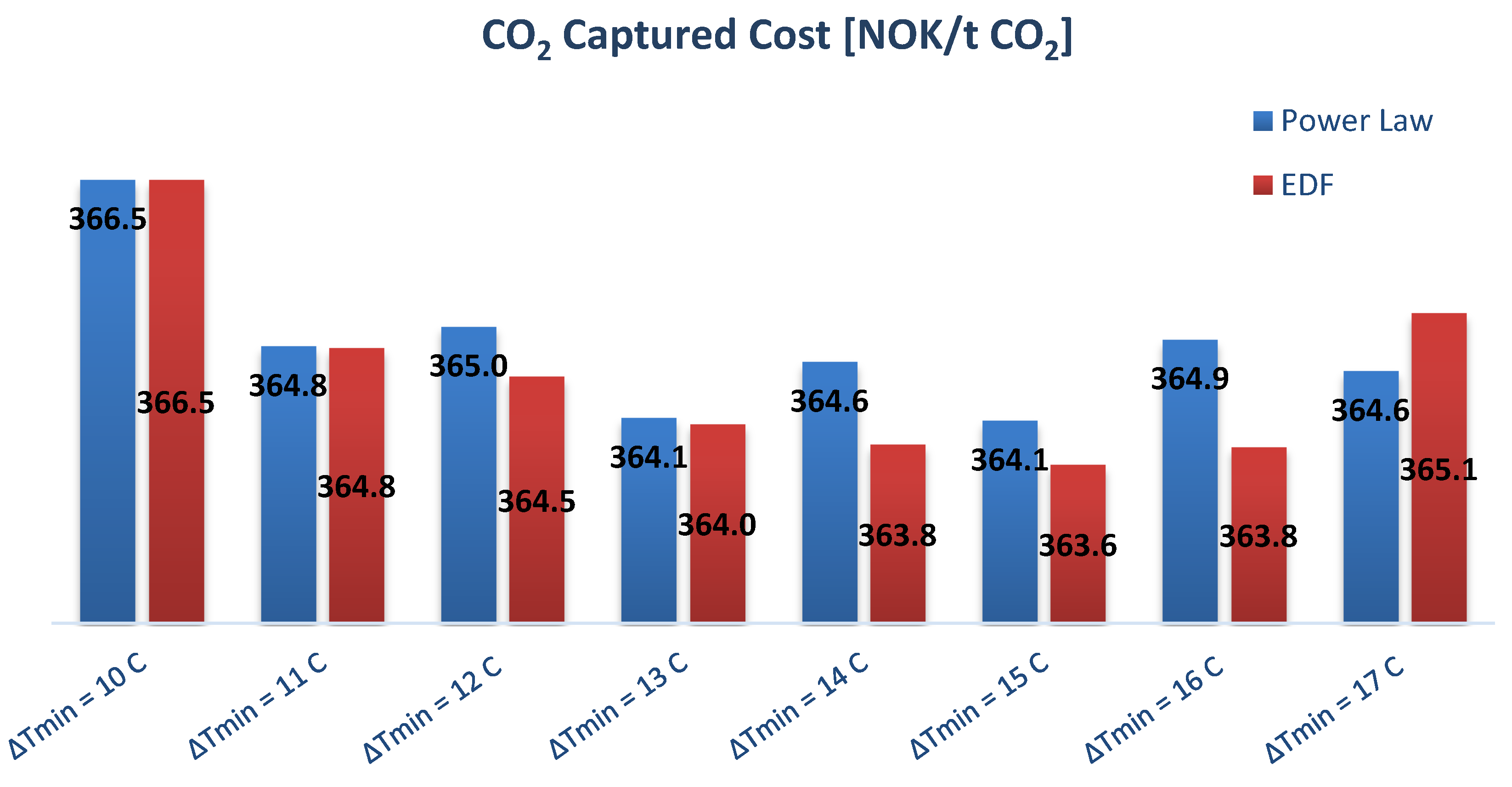
5.2. Minimum Temperature Approach (ΔTmin) in Lean/Rich Heat Exchanger
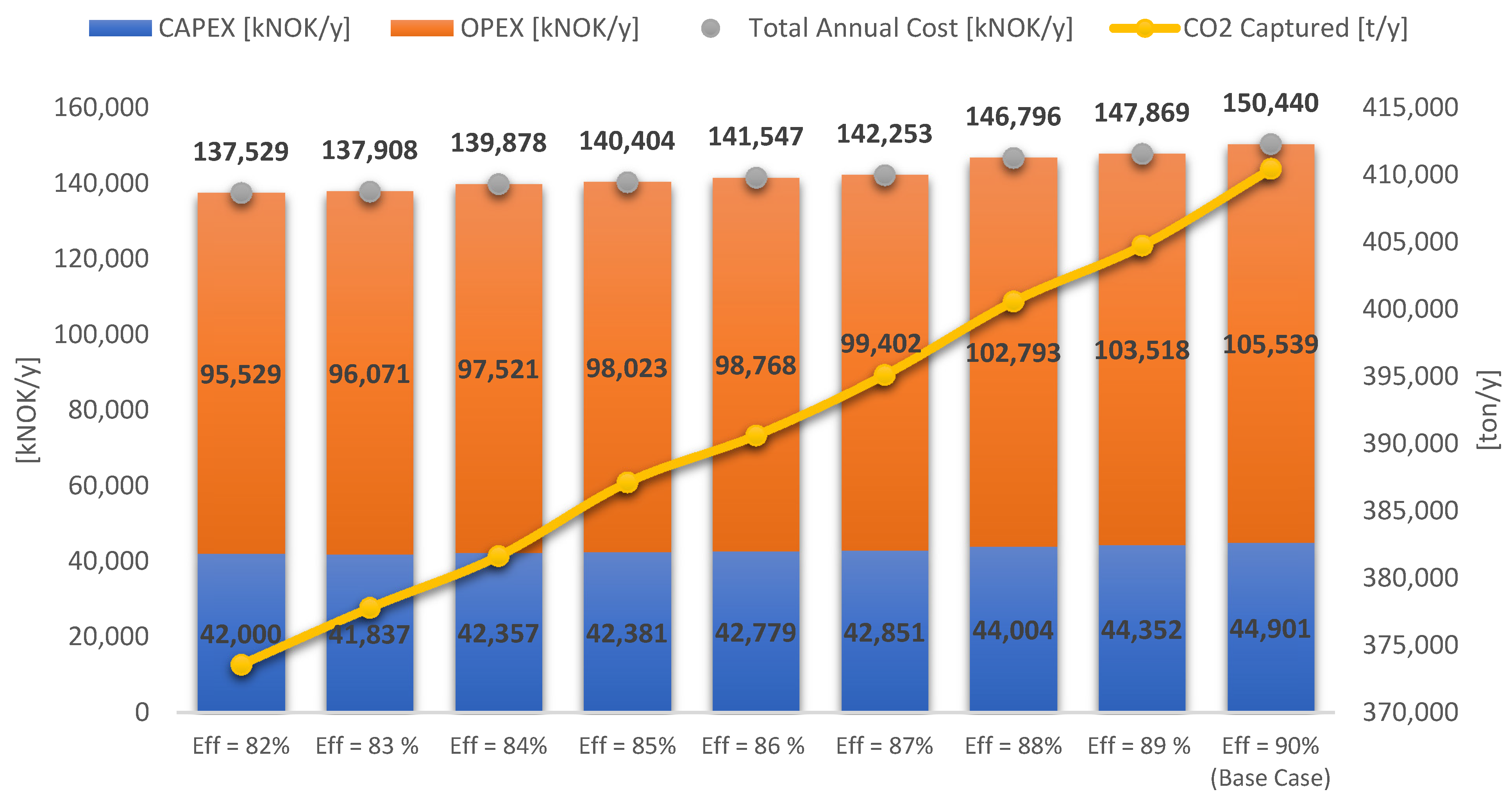
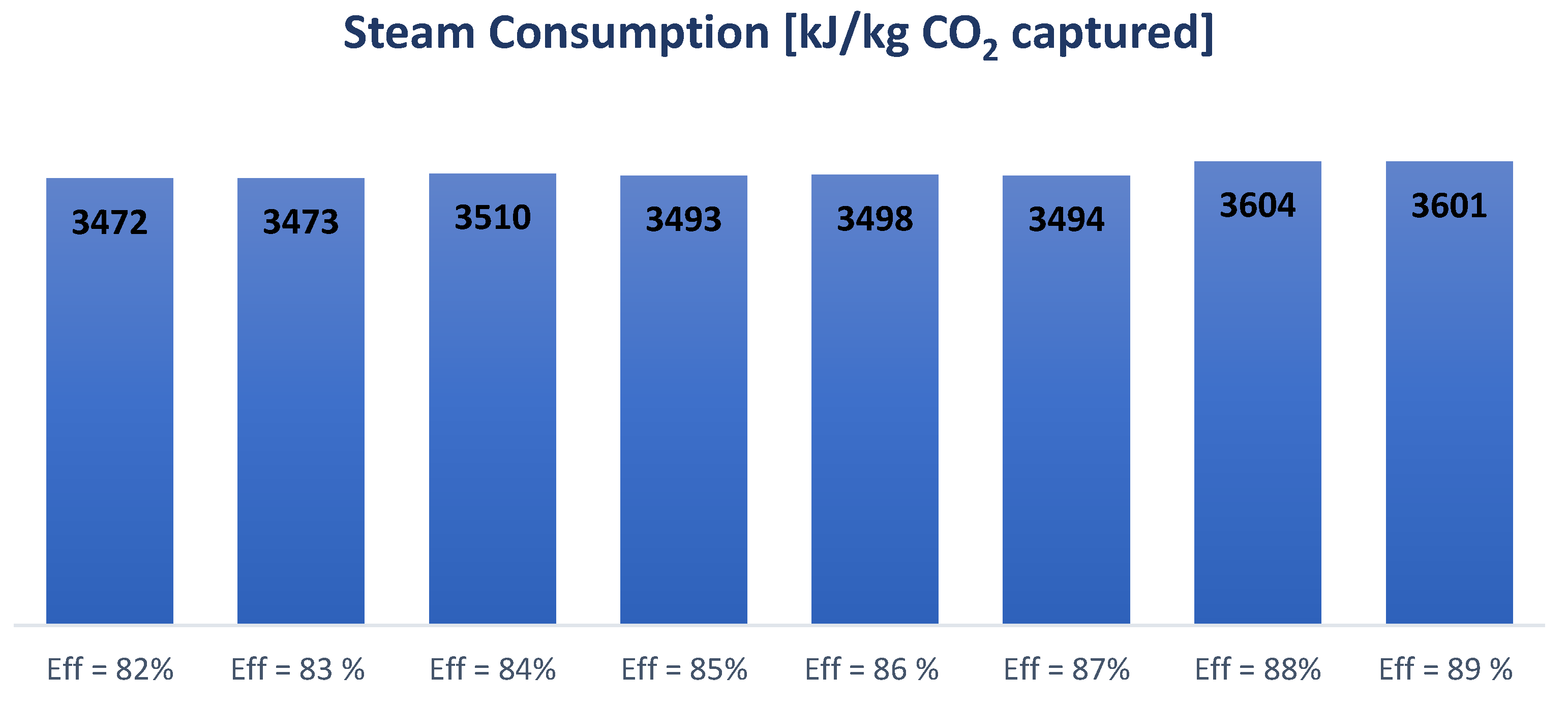
5.3. CO2 Removal Efficiency
5.4. Absorber Packing Height
5.5. Size factor’s Exponent Derivation
5.6. Comparison with Earlier Reports
5.6.1. Absorber Stages
5.6.2. Minimum Temperature Approach in the Lean/Rich Heat Exchanger
5.6.3. Total Efficiency
5.6.4. Reboiler Duty
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Causes of Climate Change. Available online: https://ec.europa.eu/clima/climate-change/causes-climate-change_en (accessed on 26 October 2021).
- IEA—International Energy Agency, IEA. Available online: https://www.iea.org (accessed on 26 October 2021).
- Aromada, S.A.; Øi, L. Simulation of improved absorption configurations for CO2 capture. In Proceedings of the 56th Conference on Simulation and Modelling (SIMS 56), Linköping, Sweden, 7–9 October 2015; Linköping University Electronic Press: Linköping, Sweden, 2015. [Google Scholar]
- Jinadasa, M.H.W.N.; Jens, K.-J.; Halstensen, M. Process Analytical Technology for CO2 Capture. In Carbon Dioxide Chemistry, Capture and Oil Recovery; Karamé, I., Shaya, J., Srour, H., Eds.; InTech: London, UK, 2018. [Google Scholar] [CrossRef] [Green Version]
- Patel, H.A.; Byun, J.; Yavuz, C.T. Carbon Dioxide Capture Adsorbents: Chemistry and Methods. ChemSusChem 2017, 10, 1303–1317. [Google Scholar] [CrossRef] [PubMed]
- Kallevik, O.B. Cost Estimation of CO2 Removal in HYSYS. Master’s Thesis, Høgskolen i Telemark, Porsgrunn, Norway, 2010. [Google Scholar]
- Øi, L.E. Removal of CO2 from Exhaust Gas. Ph.D. Thesis, Telemark University College, Porsgrunn, Norway, 2012. [Google Scholar]
- Rubin, E.S.; Short, C.; Booras, G.; Davison, J.; Ekstrom, C.; Matuszewski, M.; McCoy, S. A proposed methodology for CO2 capture and storage cost estimates. Int. J. Greenh. Gas Control 2013, 17, 488–503. [Google Scholar] [CrossRef]
- Van der Spek, M.; Roussanaly, S.; Rubin, E.S. Best practices and recent advances in CCS cost engineering and economic analysis. Int. J. Greenh. Gas Control 2019, 83, 91–104. [Google Scholar] [CrossRef]
- Luo, X. Process Modelling, Simulation and OPTIMISATION of Natural Gas Combined Cycle Power Plant Integrated with Carbon Capture, Compression and Transport. Ph.D. Thesis, School of Engineering, The University of Hull, Hull, UK, 2016. [Google Scholar]
- Øi, L.E.; Bråthen, T.; Berg, C.; Brekne, S.K.; Flatin, M.; Johnsen, R.; Moen, I.G.; Thomassen, E. Optimization of configurations for amine based CO2 absorption using Aspen HYSYS. Energy Procedia 2014, 51, 224–233. [Google Scholar] [CrossRef] [Green Version]
- Roussanaly, S.; Lindqvist, K.; Anantharaman, R.; Jakobsen, J. A Systematic Method for Membrane CO2 Capture Modeling and Analysis. Energy Procedia 2014, 63, 217–224. [Google Scholar] [CrossRef] [Green Version]
- Øi, L.E.; Eldrup, N.; Aromada, S.; Haukås, A.; HelvigIda Hæstad, J.; Lande, A.M. Process Simulation, Cost Estimation and Optimization of CO2 Capture using Aspen HYSYS. In Proceedings of the 61st International Conference of Scandinavian Simulation, Virtual Conference, Oulu, Finland, 22–24 September 2020. [Google Scholar]
- Ali, H.; Eldrup, N.H.; Normann, F.; Skagestad, R.; Øi, L.E. Cost Estimation of CO2 Absorption Plants for CO2 Mitigation–Method and Assumptions. Int. J. Greenh. Gas Control 2019, 88, 10–23. [Google Scholar] [CrossRef]
- Aromada, S.A.; Eldrup, N.H.; Øi, L.E. Capital cost estimation of CO2 capture plant using Enhanced Detailed Factor (EDF) method: Installation factors and plant construction characteristic factors. Int. J. Greenh. Gas Control 2021, 110, 103394. [Google Scholar] [CrossRef]
- FEED-Study-Report-DG3_redacted_version_03-2.pdf. Available online: https://ccsnorway.com/wp-content/uploads/sites/6/2020/07/FEED-Study-Report-DG3_redacted_version_03-2.pdf (accessed on 26 October 2021).
- Fagerheim, S. Process Simulation of CO2 Absorption at TCM Mongstad. Master’s Thesis, University of South-Eastern Norway, Porsgrunn, Norway, 2019. [Google Scholar]
- Iliuta, I.; Larachi, F. Modeling and simulations of NOx and SO2 seawater scrubbing in packed-bed columns for marine applications. Catalysts 2019, 9, 489. [Google Scholar] [CrossRef] [Green Version]
- Ali, H. Techno-Economic Analysis of CO2 Capture Concepts. Ph.D. Thesis, University of South-Eastern Norway, Porsgrunn, Norway, 2019. [Google Scholar]
- ClearTax, Cost Inflation Index FY 2021-22—Overview, Calculation, Benefits & Examples. Available online: https://cleartax.in/s/cost-inflation-index (accessed on 28 October 2021).
- Exchange Rates. Available online: https://www.norges-bank.no/en/topics/Statistics/exchange_rates/ (accessed on 28 October 2021).
- Baumann, C. Cost-to-Capacity Method: Applications and Considerations. M&TS J. 2014, 30, 49–56. [Google Scholar]
- Smith, R. Chemical Process Design and Integration; John Wiley & Sons Ltd.: Chichester, UK, 2005; pp. 17–19. [Google Scholar]
- “What Is R-Squared?”, Investopedia. Available online: https://www.investopedia.com/terms/r/r-squared.asp (accessed on 6 November 2021).
- Amrollahi, Z.; Ystad, P.A.M.; Ertesvåg, I.S.; Bolland, O. Optimized process configurations of post-combustion CO2 capture for. natural-gas-fired power plant–Power plant efficiency analysis. Int. J. Greenh. Gas Control 2012, 8, 1–11. [Google Scholar] [CrossRef]
- Sipöcz, N.; Tobiesen, A.; Assadi, M. Integrated modelling and simulation of a 400 MW NGCC power plant with CO2 capture. Energy Procedia 2011, 4, 1941–1948. [Google Scholar] [CrossRef] [Green Version]
- Nwaoha, C.; Beaulieu, M.; Tontiwachwuthikul, P.; Gibson, M.D. Techno-economic analysis of CO2 capture from a 1.2 million MTPA cement plant using AMP-PZ-MEA blend. Int. J. Greenh. Gas Control 2018, 78, 400–412. [Google Scholar] [CrossRef]
- Husebye, J.; Brunsvold, A.L.; Roussanaly, S.; Zhang, X. Techno Economic Evaluation of Amine based CO2 Capture: Impact of CO2 Concentration and Steam Supply. Energy Procedia 2012, 23, 381–390. [Google Scholar] [CrossRef] [Green Version]




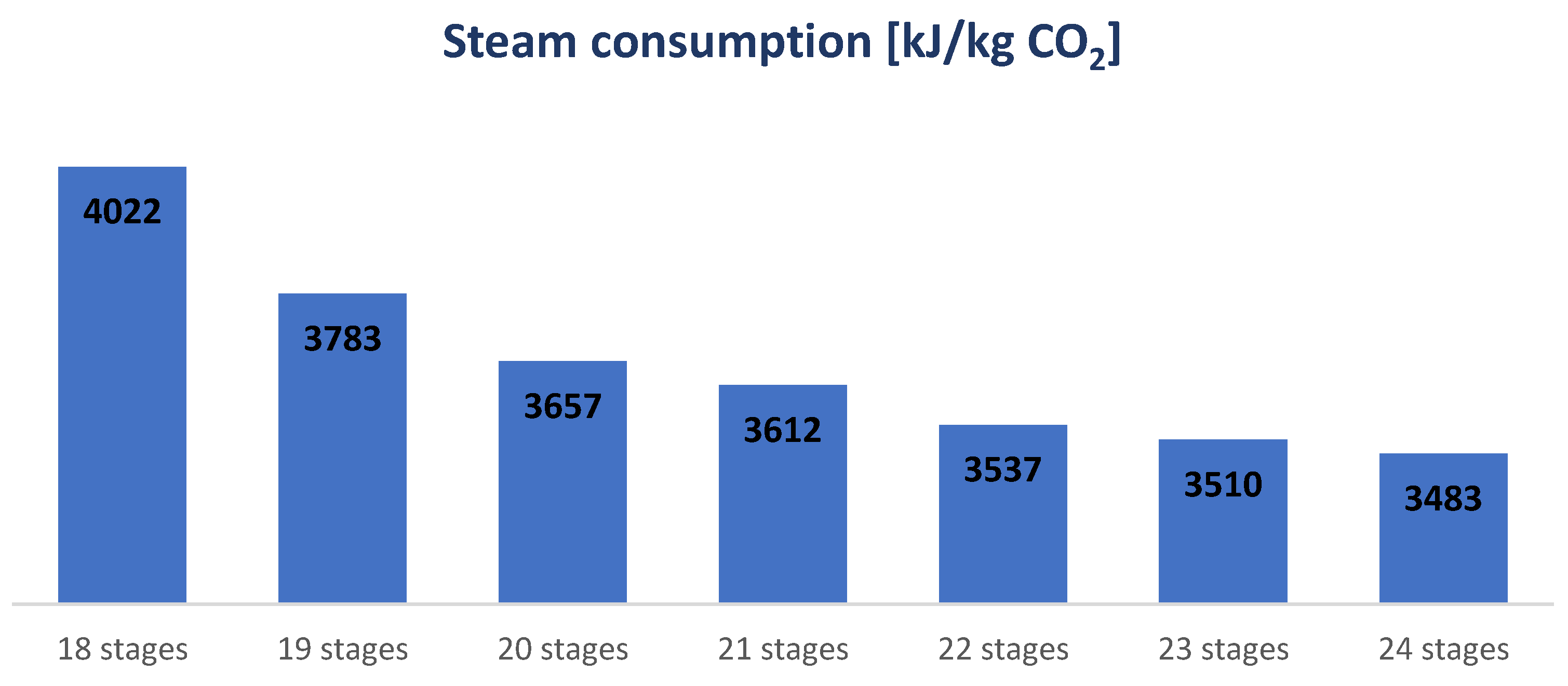
| Items | Specifications (Unit) | Value |
|---|---|---|
| Inlet Flue Gas | Temperature (°C) | 60 |
| Pressure (kPa) | 101 | |
| Molar flow rate (kmol/h) | 17,110 | |
| O2 content (mole%) | 9 | |
| CO2 content (mole%) | 7.5 | |
| H2O content (mole%) | 6.7 | |
| N2 content (mole%) | 76.8 | |
| Flue gas to absorber | Temperature (°C) | 40 |
| Pressure (kPa) | 111 | |
| Lean MEA | Temperature (°C) | 45 |
| Pressure (kPa) | 101 | |
| Molar flow rate (kmol/h) | 42,110 | |
| MEA content (W%) | 29.48 | |
| CO2 content (W%) | 5.58 | |
| Absorber | Number of stages | 20 |
| Murphree efficiency (%) | 15 | |
| Rich amine pump pressure (kPa) | 200 | |
| Rich amine temp. out of Lean/Rich HEx (°C) | 102.9 | |
| Desorber | Number of stages in stripper | 8 |
| Murphree efficiency (%) | 50 | |
| Reflux ratio in the desorber | 0.3 | |
| Reboiler temperature (°C) | 120 | |
| Pressure (kPa) | 200 |
| Year | Cost-Inflation Index |
|---|---|
| 2019 | 289 |
| 2020 | 301 |
| 2021 | 317 |
| Item | Symbol | Unit | Value |
|---|---|---|---|
| Operating lifetime | n | (Years) | 25 1 |
| Operating hours p | - | (h/year) | 8000 |
| Discount rate | r | (%) | 8 |
| Exchange rate | - | (NOK/EUR) | 9.8 |
| Electricity cost | - | (EUR/kWh) | 0.06 |
| Steam cost | - | (EUR/kWh) | 0.015 |
| Cooling water cost | - | (EUR/m3) | 0.022 |
| Water process cost | - | (EUR/m3) | 0.203 |
| MEA cost | - | (EUR/m3) | 1516 |
| Maintenance cost | - | (EUR/year) | 3% of CAPEX |
| Operator cost | - | (EUR/year) | 80,414 (×6 operators) |
| Engineer cost | - | (EUR/year) | 156,650 (1 engineer) |
| Equipment | Material | Capacity Unit | Size | Cost (kEUR) | Data Points | Exponent Factor | R2 |
|---|---|---|---|---|---|---|---|
| Lean HEx | SS316 | m2 | 322.7 | 177.3 | 9 | 0.71 | 0.960 |
| Lean/rich HEx | SS316 | m2 | 8258.1 | 3311.6 | 9 | 1.07 | 0.992 |
| Condenser | SS316 | m2 | 66.9 | 48.6 | 9 | 0.7 | 0.985 |
| Reboiler | SS316 | m2 | 3050.4 | 1430.2 | 9 | 0.86 | 0.981 |
| Pump | SS316 | kW | 26.4 | 60.9 | 9 | 0.75 | 0.989 |
| Fan | CS | kW | 1020.3 | 528.7 | 9 | 0.23 | 0.937 |
| Equipment | Material | Capacity Unit | Size | Cost (kEUR) | Data Points | Exponent Factor | R2 |
|---|---|---|---|---|---|---|---|
| Lean HEx | SS316 | m2 | 251.2 | 150.8 | 20 | 0.77 | 0.972 |
| Lean/rich HEx | SS316 | m2 | 5890.3 | 2344.1 | 20 | 1.00 | 0.999 |
| Condenser | SS316 | m2 | 78.1 | 57.8 | 20 | 0.67 | 0.943 |
| Reboiler | SS316 | m2 | 3056.7 | 1396.3 | 20 | 0.98 | 0.997 |
| Pump | SS316 | kW | 25.8 | 60.2 | 20 | 1.02 | 0.999 |
| Study | CO2 Capture Rate (%) | CO2 Concentration (mol%) | ΔTmin (°C) | Absorber Packing Height (m) | Reboiler Duty (kJ/kg) |
|---|---|---|---|---|---|
| This work (Base Case) | 90 | 7.5 | 10 | 20 | 3654 |
| Ali et al. [14] | 90 | 22–28 | 10 | 15 | 3970 |
| Aromada et al. [3] | 85 | 3.73 | 10 | 20 | 3600 |
| Øi et al. [13] | 90 | 17.8 | 10 | 12 | 3500 |
| Amrollahi et al. [25] | 90 | 3.8 | 8.5 | 13 | 3740 |
| Sipöcz et al. [26] | 90 | 4.2 | 10 | 26.9 * | 3930 |
| Nwaoha et al. [27] | 90 | 11.5 | 10 | 22 (36 Stages) | 3860 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shirdel, S.; Valand, S.; Fazli, F.; Winther-Sørensen, B.; Aromada, S.A.; Karunarathne, S.; Øi, L.E. Sensitivity Analysis and Cost Estimation of a CO2 Capture Plant in Aspen HYSYS. ChemEngineering 2022, 6, 28. https://doi.org/10.3390/chemengineering6020028
Shirdel S, Valand S, Fazli F, Winther-Sørensen B, Aromada SA, Karunarathne S, Øi LE. Sensitivity Analysis and Cost Estimation of a CO2 Capture Plant in Aspen HYSYS. ChemEngineering. 2022; 6(2):28. https://doi.org/10.3390/chemengineering6020028
Chicago/Turabian StyleShirdel, Shirvan, Stian Valand, Fatemeh Fazli, Bernhard Winther-Sørensen, Solomon Aforkoghene Aromada, Sumudu Karunarathne, and Lars Erik Øi. 2022. "Sensitivity Analysis and Cost Estimation of a CO2 Capture Plant in Aspen HYSYS" ChemEngineering 6, no. 2: 28. https://doi.org/10.3390/chemengineering6020028
APA StyleShirdel, S., Valand, S., Fazli, F., Winther-Sørensen, B., Aromada, S. A., Karunarathne, S., & Øi, L. E. (2022). Sensitivity Analysis and Cost Estimation of a CO2 Capture Plant in Aspen HYSYS. ChemEngineering, 6(2), 28. https://doi.org/10.3390/chemengineering6020028