Predicted Mutual Solubilities in Water + C₅-C₁₂ Hydrocarbon Systems. Results at 298 K

Abstract

Mutual solubilities of water with n-alkanes, cycloalkanes, iso-alkanes (branched alkanes), alkenes, alkynes, alkadienes, and alkylbenzenes were calculated at 298 K for 153 systems not yet measured. Recommended data for 64 systems reported in the literature were compared with the predicted values. The solubility of the hydrocarbons in water was calculated with a thermodynamically based equation, which depends on specific properties of the hydrocarbon. The concentration in the second coexisting liquid phase (water in hydrocarbon) was calculated using liquid-liquid equilibrium with an equation of state, which takes into account the self-association of water and co-association of water with π-bonds of the hydrocarbons.

1. Introduction

An example of liquid-liquid equilibrium, LLE, in a hydrocarbon + water system is shown in Figure 1.

Figure 1 is typical for systems investigated in this paper. The two liquids and vapor exist up to the three-phase critical temperature, T_3c. At T_3c, hydrocarbon-rich phase disappears, but water saturated with the hydrocarbon and the vapor still exists. The solubilities in the coexisting phases are strongly asymmetric. The solubility of the hydrocarbon in the water-rich phase is very low. It exhibits a minimum at room temperature, which is shown in Figure 2. The water in hydrocarbon solubility is rapidly increasing, as a monotonic function of temperature. Unlike the benzene + water system, shown in Figure 1, many other systems are represented only by a few and often scattered experimental points.

Since these systems are of significant importance for chemical and related industry and environment protection, much effort has been made to develop suitable correlation and prediction methods. Among the correlation methods, the work of Tsonopoulos [1,2] results in suitable correlation equations. However, this excellent method has two disadvantages. First, both branches are correlated independently by different equations that are not thermodynamically interrelated. The second disadvantage is that these equations cannot be extended for systems for which no experimental data exist. Various attempts have been made to develop predictive methods. Among others, group contribution methods and equations of state incorporated with an association term were tested. The UNIFAC and the ASOG methods are the best-known group-contribution methods. We have calculated LLE in the representative group of selected water + hydrocarbon systems with below mentioned versions of the UNIFAC method and the ASOG method [3]. The original UNIFAC method and its modifications (Dortmund and Lyngby) are mostly intended to represent primarily VLE data and are not suitable for the quantitative prediction of LLE in hydrocarbon + water systems. Magnussen et al. [4] developed the UNIFAC-LLE method. This version was examined by Gupte and Danner [5] but reported results for hydrocarbon + water systems are rather ambiguous (the number of systems examined is small, and the precision of the reported deviations is insufficient for interpretation). According to our calculations, this method is also not suitable for the quantitative prediction of LLE in hydrocarbon + water systems. Hooper et al. [6] developed the modified UNIFAC method aimed at the prediction of liquid-liquid equilibria for water-organic liquid systems over a wide temperature range. This modified UNIFAC successfully represents the hydrocarbon-rich phase but cannot correctly predict the minimum solubility of hydrocarbons in water. Voutsas and Tassios [7] examined and modified this version of the UNIFAC method. They introduced the Flory–Huggins combinatorial contribution with adjusted r and q structural parameters for water and developed new interaction parameters for the H2O-CH2 and H2O-ACH groups. This is probably the best attempt. However, while this is the first time this method predicted the minima fairly well, it still does not reproduce all the features of aqueous solutions of hydrocarbons. The main disadvantage is the inability to model alkene, alkyne, and alkylbenzene groups. The method was originally tested only for five systems with relatively low hydrocarbons, from n-pentane to n-octane, cyclohexane, and benzene. When we performed calculations for higher hydrocarbons, increased positive deviations in both solubilities were observed. We proposed [3] new and improved interaction parameters for water with the main groups CH2 and ACH.

In 2015, Kang et al. [8,9] published a comprehensive, newly modified UNIFAC parameter matrix, based on the same formulations as those used for the modified UNIFAC (Dortmund). In most cases, the authors used the same main- and subgroups and van der Waals properties as in modified UNIFAC (Dortmund). Parameters were fitted using critically evaluated phase equilibrium data stored in the NIST databank (including selected data for LLE). Critical evaluation of selected data was performed with the use of algorithms developed at NIST. Unfortunately, for the interaction parameters of the H2O group with the main-groups CH2, ACH, and ACCH2, the values are the same as previously in the modified UNIFAC (Dortmund) [10]. New interaction parameters have been proposed only for the interaction between the main-groups C=C and H2O.

Among the equations of state, the CPA [11,12,13], SAFT [12,14,15,16] APACT [14], PHCT [14], and Peng–Robinson [14,17] equations were applied to these systems. According to authors of these papers, these highly complex equations are not able to satisfactorily represent the experimental data and are not superior to the simple cubic Peng–Robinson equation with the simple van der Waals-type mixing rules. Since in all above equations of state some adjustable parameters must be fitted to experimental data, none of these equations can be considered as purely predictive as UNIFAC. Results of application are far from a satisfactory representation of data, particularly concerning the solubility of hydrocarbons in water. Vega et al. [15] obtained the solubility minima of n-alkanes in water using Soft-SAFT. However, these predicted minima did not quantitatively agree with recommended values, the representation of the other data points was not satisfactory, and these predictions cannot be regarded as qualitative. An exception is the successful application of the PC-SAFT to binary mixtures of n-alkanes and water as reported by Haarmann et al. [18].

A brief overview of the different methods (e.g., different versions of the SAFT equation) can be found in the works of Gupte and Danner [5], Vega et al. [15], Oracz and Góral [3], Safamirzaei and Modarress [19], Oliveira et al. [13], or Haarmann et al. [18] cited above.

Other noteworthy methods are: the COSMO-RS method used by Klamt [20], the use of artificial neural networks by Safamirzaei and Modarress [19] (as an example of using ANNs for these problems), or the use of molecular dynamics methods by Morgado et al. [21].

The conclusion is that the reported predictive methods are of very limited value. Some of them fairly well predict the solubility of water in hydrocarbons, but they are usually unsatisfactory for predicting the solubility of hydrocarbons in water.

In our work, we analyzed all available binary solubility data for systems of water with n-alkanes, cycloalkanes, iso-alkanes (branched alkanes), alkenes, alkynes, alkadienes and alkylbenzenes. The resulting method of the LLE prediction was described in papers [22,23,24,25]. In this method, the calculation of such solubilities as those shown in Figure 1 consists of two steps:

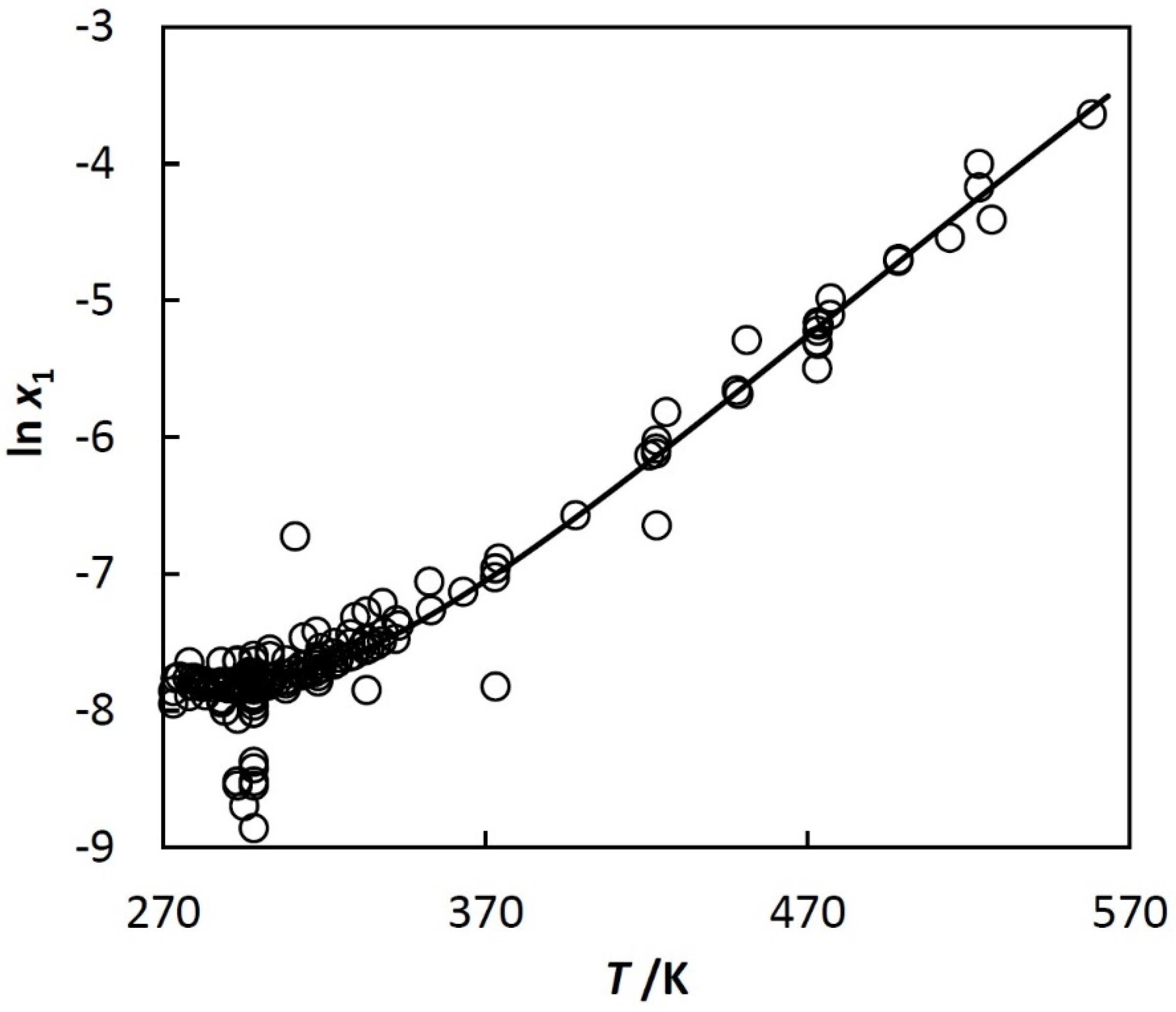
• Solubilities of hydrocarbons in water are approximated with a thermodynamically based equation described in the next section. The two coefficients of this equation are linearly dependent on the excluded volume of the hydrocarbon molecule, which enables prediction.
• Solubilities of water in hydrocarbons are calculated using liquid–liquid equilibrium calculations. The input data for these calculations are concentrations in the second liquid phase predicted by the previously mentioned smoothing equation.

In these two steps, an extensive body of experimental data is described with a few adjustable parameters, providing a framework for the comparison of experimental data and supporting the recognition of systematic error. During the adjustment of the parameters to a large number of experimental points, the experimental errors partially compensate each other, which makes the calculated solubilities more reliable than individual experimental points. Error analysis is given in papers [22,23,24,25]. The method approximates numerical experimental values with analytical equations, allowing for temperature interpolation and extrapolation, which is important for engineering practice. It is also possible to make extrapolations to other systems not investigated experimentally.

The calculated solubilities were used as the reference values for the evaluation of experimental data in volume 81 of the IUPAC Solubility Data Series [26,27,28,29,30,31,32,33,34,35,36,37]. Based on all available literature data, the experimental recommended data for the mutual solubility of water with hydrocarbons for 64 systems were proposed. In this paper, this set of recommended data is appended with mutual solubilities at 298.15 K for 153 systems, which were not investigated experimentally. The prediction can also be applied at other temperatures and for other hydrocarbons using programs and databases described in this paper. We believe that our work reduces the necessity for further measurements in this field. (However, some independent measurements would be useful for testing our predictions).

2. Solubility of Hydrocarbons in Water

To show more detail, the left part of Figure 1 is plotted in Figure 2 using other coordinates. The shape of the curve shown in Figure 2 is typical for n-alkanes, cycloalkanes, iso-alkanes (branched alkanes), alkenes, alkynes, alkadienes, and alkylbenzenes, but their solubilities are quite different. The reference data in [25] and [23] show that, for example, the mole fraction of benzene in water at 298.15 K is 4·10⁻⁴, whereas for decane it decreases to 3·10⁻⁹.

The mole fraction of the hydrocarbon in water, x_h, at temperature T along the three-phase equilibrium line is described by a thermodynamic equation:

$${\left[\partial ln x_{\mathrm{h}}/\partial \left(1/T\right)\right]}_P\cong -{\Delta }_{\mathrm{sln}}{h}_{\mathrm{h}}/R,$$

(1)

where Δ_slnh_h is the partial molar enthalpy of solution of the hydrocarbon. The calorimetric measurements suggest that Δ_slnh_h is a linearly increasing function of temperature going through zero at a temperature T_min. In this case, Δ_slnh_h can be approximated with the equation:

$${\Delta }_{\mathrm{sln}}{h}_{\mathrm{h}}/R=C_{\mathrm{h}}·\left(T-T_{\min }\right).$$

(2)

Integration of Equation (1) with Δ_slnh_h as expressed with Equation (2) yields Equation (3)

$$ln x_{\mathrm{h}}=ln x_{\mathrm{h},\min }+C_{\mathrm{h}}·f\left(T/T_{\min }\right),$$

(3)

where x_h,min is the minimum value of x_h at T = T_min. The function f(T/T_min) results from the integration of Equation (2):

$$f\left(T/T_{\min }\right)=T_{\min }/T-ln\left(T_{\min }/T\right)-1.$$

(4)

For alkylbenzenes, instead of Equation (2), a logarithmic function was assumed, which leads to Equation (5):

$$g\left(T/T_{\min }\right)=\left(T_{\min }/T\right)ln\left(T_{\min }/T\right)-\left(T_{\min }/T\right)+1.$$

(5)

Equation (3) was used for approximation of experimental solubility data of the hydrocarbons. An example is shown in Figure 2, where the approximating curve is calculated with Equations (3) and (5). At the beginning of the investigation, ln x_h,min, T_min, and C_h in Equation (3) were treated as adjustable parameters. After the analysis of experimental data, it was found (see papers [22,23,24,25]) that T_min is constant for a given class of hydrocarbons, whereas ln x_h,min and C_h depend linearly on the excluded volume, b_h, of the hydrocarbon. The excluded volume is used in equations of state of van der Waals type. Here, the Redlich–Kwong Equation of state (RK EoS) is used, where b is calculated with:

$$b=0.08664·\frac{R·T_c}{P_c}.$$

(6)

In the above equation T_c is the critical temperature and P_c is the critical pressure of the corresponding substance.

An example of the mentioned linear dependence is shown in Figure 3 (Others are given in papers [22,23,24,25].)

The linear dependences introduced into Equation (3) give a general formula for n–alkanes, branched alkanes, and cycloalkanes as well as unsaturated hydrocarbons:

$$ln x_{\mathrm{h}}=c_1+c_2{b}_{\mathrm{h}}+c_{\pi }{L}_{\mathrm{h}}+c_3{b}_{\mathrm{h}}f\left(T/T_{\min }\right),$$

(7)

where L_h is the number of π–bonds in the hydrocarbon, e.g., L_h = 1 for alkenes, L_h = 2 for alkadienes and alkynes, and L_h = 4 for alkadiynes. If L_h = 0, then Equation (7) describes the solubility of n–alkanes, iso-alkanes, and cycloalkanes.

The analogous linear relations for ln x_h,min and C_h, which hold for alkylbenzenes, introduced into Equation (3) give:

$$ln x_{\mathrm{h}}=\left(c_4+c_5{b}_{\mathrm{h}}\right)+\left(c_6+c_7{b}_{\mathrm{h}}\right)·g\left(T/T_{\min }\right),$$

(8)

The coefficients c_π and c₁–c₇ in Equations (7) and (8) as well as the corresponding values of T_min were obtained from simultaneous regression of all experimental solubility data reported in literature for given class of hydrocarbons. Prior to regression, the plots of the solubility data were inspected in order to remove evidently outlying experimental points. After the regression, the most outlying point was removed and the remaining points were regressed once more, yielding new a estimation of the standard deviation. This procedure was repeated until the deviation of the most outlying point in the remaining data set did not exceed three times the estimated standard deviation.

The following values of the parameters in Equation (7) were obtained: c₁ = −4.08, c₂/mol·cm⁻³ = −0.073, c₃/mol·cm⁻³ = 0.376, c_π = 1.10, or c_π = 0.79 for conjugated π-bonds; T_min/K = 298 (cycloalkanes); T_min/K = 306 (other hydrocarbons).

The values of the coefficients in Equation (8) are as follows c₄ = −2.605; c₅/mol·cm⁻³ = −0.063; c₆ = 7.98; c₇/mol·cm⁻³ = 0.267; T_min/K = 290.

Equations (7) and (8) with the obtained coefficients c₁–c₇ are valid at least up to T_3c. Error analysis is given in papers [22,23,24,25]. It shows that standard deviation of the calculated x_h depends on T and b_h but in all cases it is below 10% of the calculated x_h. Equations (7) and (8) approximate together almost 1000 experimental points for 64 systems using a relatively small number of adjustable parameters. The analysis of the deviations shows that they are randomly distributed and can be ascribed mainly to error of the experimental data. No trends were observed. In such a situation, the experimental random errors compensate each other during the regression, which makes the resulting Equations (7) and (8) more accurate than individual experimental points. Linear dependences such as that shown in Figure 3 were very useful for disclosing systematic errors of hydrocarbon solubility data.

There were no cases when measurements from different laboratories agreed with each other but not did not agree with the calculated values. As a rule, discrepancies occurred in systems represented by a few experimental points measured by one laboratory. Based on tests described in papers [22,23,24,25], we conclude that the observed discrepancies between experimental and calculated values result mainly from errors in the experimental data.

Additionally, the accuracy of the prediction also depends on the accuracy of the excluded volume, b, used as the input data in the Equations (7) or (8). The influence of b can be easily estimated from these equations. To estimate this, we calculated values of b from experimental T_c and P_c for n-alkanes from pentane to hexadecane. These values of b were plotted vs. the number of carbon atoms. From this plot, we estimated the standard deviation of b for this series is below 1 cm³·mol⁻¹. This corresponds to a standard deviation of x_h at room temperature equal to about 7% whereas the estimated standard deviation of the experimental mole fractions is about 30%. However, for some hydrocarbons, error in b can be much greater, so values of b calculated from experimental or predicted critical parameters must be selected with care before using them in the Equations (7) or (8).

The above parameters, and estimates of accuracy, are for mixtures with of n-alkanes, cycloalkanes, iso-alkanes, alkenes, alkadienes, alkynes, and alkylbenzenes having the number of carbon atoms between five and eleven. This limit is particularly important for alkanes. For heavier alkanes, the observed linearity shown in Figure 3 changes rapidly.

3. Solubility of Water in Hydrocarbons

Component concentrations in two coexisting liquid phases are related to each other by thermodynamic constraints of phase equilibrium. Hence, the solubility in one phase can be calculated using the concentration of the second liquid phase as the input data. To make such calculations, Economou and Tsonopoulos [14] applied equations of state SAFT and APACT for water + alkane systems. They started from the experimental solubility of water in hydrocarbons and tried to calculate the solubility curve of the alkanes in analogy to that shown in Figure 2. In conclusion, the authors wrote: “We have tested several models of hydrogen bonding for water as well as different mixing rules and found that none of these theories provide a quantitative estimate of the n-alkane solubility in water nor do they predict the n-alkane solubility minimum”.

In this work, the solubility of water in hydrocarbons was calculated by a method developed by Góral [38]. The method of correlation is called EoSC (Equation of State + Chemical term). In this method, a pure liquid is described by the cubic equation of state (EoS) with properly adjusted “effective” parameters. This approach is widely used in methods, which extends cubic EoS to associating mixtures using complicated mixing rules for the parameters in EoS. In the EoSC, the classical mixing rules are not modified. Instead, the chemical potential of the component derived from the cubic EoS is appended with a chemical term, which accounts for hydrogen bonding. It is defined as an excess function resulting from a change of the association of the pure substance when it is transferred to a mixture. Application of the EoSC for water systems is described in papers [22,23,24,25]. The input information for the LLE correlation is the solubility of a hydrocarbon in water, x_h, calculated with Equation (7) or Equation (8). The output is the solubility of water, x_w, in the hydrocarbon as a function of temperature. It is calculated from the constraints of chemical potentials at equilibrium:

$${\mu }_{\mathrm{h}}^{\left(1\right)}\left(x_{\mathrm{h}},\Theta \right)={\mu }_{\mathrm{h}}^{\left(2\right)}\left(x_{\mathrm{w}},\Theta \right),$$

(9a)

$${\mu }_{\mathrm{w}}^{\left(1\right)}\left(x_{\mathrm{h}},\Theta \right)={\mu }_{\mathrm{w}}^{\left(2\right)}\left(x_{\mathrm{w}},\Theta \right),$$

(9b)

where ${\mu }_{\mathrm{h}}^{\left(1\right)}$, ${\mu }_{\mathrm{h}}^{\left(2\right)}$, ${\mu }_{\mathrm{w}}^{\left(1\right)},$ and ${\mu }_{\mathrm{w}}^{\left(2\right)}$ are the chemical potentials of hydrocarbon and water in the first and the second phase, respectively. Equations (9a) and(9b) contain one adjustable binary parameter, Θ, in the physical part of the EoSC. Otherwise, the chemical potentials are based on a model of association. Once the parameters of the model are fixed, Equations (9a) and (9b) at given temperature and under the saturated vapor pressure contain three variables, x_h, x_w, and, where the hydrocarbon solubility, x_h, is known from the smoothing equations (Equations (7) or (8)) described in the previous section. Thus, two unknown quantities, Θ and x_w-mole fractions of water in the hydrocarbon, can be found by solving Equations (9a) and (9b). Such treatment ensures internal thermodynamic consistency between both branches of the solubility curve. Additional comments are presented in Appendix A.

The standard deviation of the calculated mole fraction of water in hydrocarbon does not exceed 5% at room temperatures and increases to about 10% at elevated temperatures, say sixty degrees below T_3c.

4. Calculated Solubility Values

The calculated values for 217 systems at 298 K are listed below in

Table 1. Calculated mutual solubilities in hydrocarbon + water systems at 298.00 K, x_h–mole fraction of hydrocarbon in water, x_w–mole fraction of water in the hydrocarbon. Whenever possible the recommended experimental data taken from [23,24,25] and/or [26,27,28,29,30,31,32,33,34,35,36,37] are reported in the second row. Aqueous solubilities for six hydrocarbons at 298.15 K measured by Dohányosová et al. [39] are included for comparison. For five of them, there was no prior experimental data. It should be noted that these data were not critically evaluated.

Formula	Name	CAS RN	xh	xw
C5H6	1,3-Cyclopentadiene	542-92-7	1.50·10−4 1.80·10−4 [24]	1.93·10−3
C5H8	Cyclopentene	142-29-0	1.89·10−4 1.62·10−4 [24]	1.33·10−3
C5H8	2-Methyl-1,3-butadiene	78-79-5	1.38·10−4 1.70·10−4 [24]	1.98·10−3
C5H8	3-Methyl-1,2-butadiene	598-25-4	3.63·10−4	3.44·10−3
C5H8	3-Methyl-1-butyne	598-23-2	4.69·10−4	3.47·10−3
C5H8	1,2-Pentadiene	591-95-7	2.42·10−4	3.39·10−3
C5H8	cis-1,3-Pentadiene	1574-41-0	1.07·10−4	1.95·10−3
C5H8	trans-1,3-Pentadiene	2004-70-8	1.02·10−4	1.97·10−3
C5H8	1,4-Pentadiene	591-93-5	2.54·10−4	3.50·10−3
C5H8	2,3-Pentadiene	591-96-8	2.92·10−4	3.41·10−3
C5H8	1-Pentyne	627-19-0	3.58·10−4 4.15·10−4 [24]	3.43·10−3
C5H8	2-Pentyne	627-21-4	2.60·10−4	3.40·10−3
C5H10	Cyclopentane	287-92-3	4.31·10−5 4.22·10−5 [23]	3.86·10−4
C5H10	2-Methyl-1-butene	563-46-2	7.42·10−5	1.55·10−3
C5H10	2-Methyl-2-butene	513-35-9	7.31·10−5 8.30·10−5 [24]	1.50·10−3
C5H10	3-Methyl-1-butene	563-45-1	6.23·10−5	1.68·10−3
C5H10	1-Pentene	109-67-1	4.90·10−5 3.80·10−5 [24]	1.63·10−3
C5H10	cis-2-Pentene	627-20-3	5.38·10−5	1.55·10−3
C5H10	trans-2-Pentene	646-04-8	5.67·10−5	1.55·10−3
C5H12	2-Methylbutane	78-78-4	1.33·10−5 1.24·10−5 [23]	6.61·10−4
C5H12	Pentane	109-66-0	1.12·10−5 1.19·10−5 [23]	6.26·10−4 4.81·10−4 [23]
C6H6	Benzene	71-43-2	4.09·10−4 4.11·10−4 [25]	2.94·10−3 3.09·10−3 [25]
C6H8	1,4-Cyclohexadiene	628-41-1	2.19·10−4 1.57·10−4 [24]	3.43·10−3
C6H10	Cyclohexene	110-83-8	5.35·10−5 4.67·10−5	1.34·10−3 1.69·10−3
C6H10	1,5-Hexadiene	592-42-7	6.46·10−5	3.34·10−3
C6H10	1-Hexyne	693-02-7	8.58·10−5 7.89·10−5 [24]	3.32·10−3
C6H12	Cyclohexane	110-82-7	1.33·10−5 1.25·10−5 [23]	4.00·10−4 3.75·10−4 [23]
C6H12	2,3-Dimethyl-1-butene	563-78-0	2.98·10−5	1.51·10−3
C6H12	2,3-Dimethyl-2-butene	563-79-1	1.34·10−5	1.49·10−3
C6H12	3,3-Dimethyl-1-butene	558-37-2	2.75·10−5	1.62·10−3
C6H12	2-Ethyl-1-butene	760-21-4	2.42·10−5	1.48·10−3
C6H12	1-Hexene	592-41-6	1.12·10−5 1.18·10−5 [24]	1.57·10−3 1.89·10−3 [24]
C6H12	cis-2-Hexene	7688-21-3	1.47·10−5	1.51·10−3
C6H12	trans-2-Hexene	4050-45-7	9.37·10−6	1.56·10−3
C6H12	cis-3-Hexene	7642-09-3	1.57·10−5	1.51·10−3
C6H12	trans-3-Hexene	13269-52-8	9.51·10−6	1.56·10−3
C6H12	Methylcyclopentane	96-37-7	1.03·10−5 0.96·10−5 [23]	4.52·10−4
C6H12	2-Methyl-1-pentene	763-29-1	2.12·10−5 1.70·10−5 [24]	1.51·10−3
C6H12	2-Methyl-2-pentene	625-27-4	1.87·10−5	1.49·10−3
C6H12	3-Methyl-1-pentene	760-20-3	2.56·10−5	1.53·10−3
C6H12	cis-3-Methyl-2-pentene	922-62-3	1.87·10−5	1.49·10−3
C6H12	trans-3-Methyl-2-pentene	616-12-6	1.11·10−5	1.53·10−3
C6H12	4-Methyl-1-pentene	691-37-2	2.13·10−5	1.56·10−3
C6H12	cis-4-Methyl-2-pentene	691-38-3	2.00·10−5	1.55·10−3
C6H12	trans-4-Methyl-2-pentene	674-76-0	1.18·10−5	1.59·10−3
C6H14	2,2-Dimethylbutane	75-83-2	4.08·10−6 3.85·10−6 [23]	6.70·10−4
C6H14	2,3-Dimethylbutane	79-29-8	3.85·10−6 3.99·10−6 [23]	6.25·10−4
C6H14	Hexane	110-54-3	2.43·10−6 2.50·10−6 [23]	6.09·10−4 5.10·10−4 [23]
C6H14	2-Methylpentane	107-83-5	2.88·10−6 2.88·10−6 [23]	6.41·10−4
C6H14	3-Methylpentane	96-14-0	3.48·10−6 3.74·10−6 [23]	6.04·10−4 4.5·10−4 [23]
C7H8	1,3,5-Cycloheptatriene	544-25-2	1.13·10−4 1.21·10−4 [24]	3.37·10−3
C7H8	Methylbenzene	108-88-3	1.09·10−4 1.12·10−4 [25]	2.81·10−3 2.80·10−3 [25]
C7H12	1-Heptyne	628-71-7	1.98·10−5 1.76·10−5 [24]	3.21·10−3
C7H12	1-Methylcyclohexene	591-49-1	1.23·10−5 0.97·10−5 [24]	1.37·10−3
C7H14	Cycloheptane	291-64-5	4.30·10−6 5.50·10−6 [24]	3.88·10−4
C7H14	1,1-Dimethylcyclopentane	1638-26-2	3.58·10−6	4.90·10−4
C7H14	cis-1,2-Dimethylcyclopentane	1192-18-3	2.71·10−6	4.73·10−4
C7H14	trans-1,2-Dimethylcyclopentane	822-50-4	3.25·10−6	4.84·10−4
C7H14	cis-1,3-Dimethylcyclopentane	2532-58-3	3.38·10−6	4.85·10−4
C7H14	trans-1,3-Dimethylcyclopentane	1759-58-6	3.25·10−6	4.85·10−4
C7H14	Ethylcyclopentane	1640-89-7	2.50·10−6	4.65·10−4
C7H14	1-Heptene	592-76-7	2.43·10−6	1.54·10−3 1.70·10−3 [24]
C7H14	2-Heptene	592-77-8	3.63·10−6 2.70·10−6 [24]	1.51·10−3
C7H14	Methylcyclohexane	108-87-2	2.90·10−6 2.90·10−6 [23]	4.66·10−4
C7H14	2,3,3-Trimethyl-1-butene	594-56-9	3.16·10−6	1.62·10−3
C7H16	3-Ethylpentane	617-78-7	9.24·10−7	5.82·10−4
C7H16	2,2-Dimethylpentane	590-35-2	8.84·10−7 7.90·10−7 [23]	6.60·10−4
C7H16	2,3-Dimethylpentane	565-59-3	1.05·10−6 0.94·10−6 [23]	5.90·10−4
C7H16	2,4-Dimethylpentane	108-08-7	8.04·10−7 7.92·10−7 [23]	6.58·10−4
C7H16	3,3-Dimethylpentane	562-49-2	1.21·10−6 1.06·10−6 [23]	5.99·10−4
C7H16	Heptane	142-82-5	5.31·10−7 5.30·10−7 [23]	6.00·10−4 6.70·10−4 [23]
C7H16	2-Methylhexane	591-76-4	6.32·10−7 4.57·10−7 [23]	6.23·10−4
C7H16	3-Methylhexane	589-34-4	7.69·10−7 8.89·10−7 [23]	6.02·10−4
C7H16	2,2,3-Trimethylbutane	464-06-2	1.33·10−6	7.51·10−4
C8H10	1,2-Dimethylbenzene	95-47-6	3.55·10−5 3.61·10−5 [25]	2.62·10−3 2.60·10−3 [25]
C8H10	1,3-Dimethylbenzene	108-38-3	2.74·10−5 2.70·10−5 [25]	2.68·10−3 2.60·10−3 [25]
C8H10	1,4-Dimethylbenzene	106-42-3	2.63·10−5 2.66·10−5 [25]	2.68·10−3 2.70·10−3 [25]
C8H10	Ethylbenzene	100-41-4	3.19·10−5 3.18·10−5 [25]	2.67·10−3 2.60·10−3 [25]
C8H14	1,7-Octadiene	3710-30-3	2.92·10−6	3.11·10−3
C8H14	1-Octyne	629-05-0	4.36·10−6 4.40·10−6 [24]	3.12·10−3
C8H16	Cyclooctane	292-64-8	1.22·10−6 1.27·10−6 [23] 0.93·10−6 [39]	3.97·10−4
C8H16	1,1-Dimethylcyclohexane	590-66-9	1.02·10−6	4.83·10−4
C8H16	cis-1,2-Dimethylcyclohexane	2207-01-4	7.89·10−7 9.60·10−7 [23] 9.57·10−7 [39]	4.69·10−4
C8H16	trans-1,2-Dimethylcyclohexane	6876-23-9	9.27·10−7 7.59·10−7 [39]	4.78·10−4
C8H16	cis-1,3-Dimethylcyclohexane	638-04-0	1.00·10−6	4.80·10−4
C8H16	trans-1,3-Dimethylcyclohexane	2207-03-6	9.01·10−7	4.76·10−4
C8H16	cis-1,4-Dimethylcyclohexane	624-29-3	9.01·10−7	4.76·10−4
C8H16	trans-1,4-Dimethylcyclohexane	2207-04-7	1.02·10−6	4.83·10−4
C8H16	Ethylcyclohexane	1678-91-7	7.72·10−7 6.26·10−7 [39]	4.63·10−4
C8H16	1-Ethyl-1-methylcyclopentane	16747-50-5	5.3410−7	5.27·10−4
C8H16	1-Octene	111-66-0	4.72·10−7 4.00·10−7 [24]	1.52·10−3
C8H16	trans-2-Octene	13389-42-9	8.59·10−7	1.47·10−3
C8H16	Propylcyclopentane	2040-96-2	5.24·10−7	4.87·10−4
C8H16	1,1,2-Trimethylcyclopentane	4259-00-1	5.42·10−7	5.54·10−4
C8H16	1,1,3-Trimethylcyclopentane	4516-69-2	4.28·10−7	6.06·10−4
C8H18	2,2-Dimethylhexane	590-73-8	1.88·10−7 2.01·10−7 [39]	6.49·10−4
C8H18	2,3-Dimethylhexane	584-94-1	2.21·10−7	5.98·10−4
C8H18	2,4-Dimethylhexane	589-43-5	2.00·10−7	6.32·10−4
C8H18	3,3-Dimethylhexane	563-16-6	2.47·10−7	6.11·10−4
C8H18	2,5-Dimethylhexane	592-13-2	1.56·10−7 1.79·10−7 [39]	6.51·10−4
C8H18	3-Ethylhexane	619-99-8	1.94·10−7	5.94·10−4
C8H18	3-Ethyl-2-methylpentane	609-26-7	2.75·10−7	5.86·10−4
C8H18	3-Ethyl-3-methylpentane	1067-08-9	3.56·10−7	5.63·10−4
C8H18	2-Methylheptane	592-27-8	1.22·10−7	6.28·10−4
C8H18	3-Methylheptane	589-81-1	1.55·10−7 1.25·10−7 [23]	6.07·10−4
C8H18	4-Methylheptane	589-53-7	1.54·10−7	6.12·10−4
C8H18	Octane	111-65-9	1.03·10−7 1.04·10−7 [23]	6.04·10−4 5.01·10−4 [23]
C8H18	2,2,3,3-Tetramethylbutane	594-82-1	5.23·10−7	5.21·10−4
C8H18	2,2,3-Trimethylpentane	564-02-3	3.33·10−7	6.00·10−4
C8H18	2,2,4-Trimethylpentane	540-84-1	2.53·10−7 3.23·10−7 [23]	6.69·10−4 5.07·10−4 [23]
C8H18	2,3,3-Trimethylpentane	560-21-4	3.91·10−7	5.71·10−4
C9H12	1-Ethyl-2-methylbenzene	611-14-3	1.00·10−5 1.12·10−5 [25]	2.53·10−3
C9H12	1-Ethyl-3-methylbenzene	620-14-4	7.81·10−6	2.57·10−3
C9H12	1-Ethyl-4-methylbenzene	622-96-8	6.63·10−6	2.56·10−3
C9H12	(1-Methylethyl)benzene	98-82-8	1.00·10−5 1.09·10−5 [25]	2.60·10−3
C9H12	Propylbenzene	103-65-1	8.85·10−6 8.23·10−6 [25]	2.57·10−3
C9H16	1-Nonyne	3452-09-3	0.92·10−6 1.00·10−6 [24]	3.08·10−3
C9H18	Butylcyclopentane	2040-95-1	9.86·10−8	5.08·10−4
C9H18	(1-Methylethyl)cyclohexane	696-29-7	1.18·10−7	5.26·10−4
C9H18	1-Nonene	124-11-8	7.98·10−8	1.51·10−3
C9H18	Propylcyclohexane	1678-92-8	9.03·10−8	5.19·10−4
C9H20	3,3-Diethylpentane	1067-20-5	1.54·10−7	5.22·10−4
C9H20	2,2-Dimethylheptane	1071-26-7	4.20·10−8	6.38·10−4
C9H20	2,3-Dimethylheptane	3074-71-3	4.08·10−8	6.11·10−4
C9H20	2,4-Dimethylheptane	2213-23-2	5.10·10−8	6.22·10−4
C9H20	2,5-Dimethylheptane	2216-30-0	4.69·10−8	6.17·10−4
C9H20	2,6-Dimethylheptane	1072-05-5	3.63·10−8	6.36·10−4
C9H20	3,3-Dimethylheptane	4032-86-4	6.66·10−8	5.97·10−4
C9H20	3,4-Dimethylheptane	922-28-1	5.35·10−8	5.96·10−4
C9H20	3,5-Dimethylheptane	926-82-9	6.14·10−8	6.02·10−4
C9H20	4,4-Dimethylheptane	1068-19-5	7.00·10−8	6.04·10−4
C9H20	3-Ethyl-2,2-dimethylpentane	16747-32-3	1.00·10−7	5.88·10−4
C9H20	3-Ethyl-2,3-dimethylpentane	16747-33-4	1.37·10−7	5.32·10−4
C9H20	3-Ethyl-2-methylhexane	16789-46-1	5.79·10−8	5.99·10−4
C9H20	3-Ethyl-3-methylhexane	3074-76-8	1.02·10−7	5.60·10−4
C9H20	3-Ethyl-4-methylhexane	3074-77-9	7.31·10−8	5.77·10−4
C9H20	3-Ethyl-2,4-dimethylpentane	1068-87-7	6.60·10−8	6.00·10−4
C9H20	4-Ethylheptane	2216-32-2	4.86·10−8	5.94·10−4
C9H20	3-Ethylheptane	15869-80-4	4.59·10−8	5.92·10−4
C9H20	2-Methyloctane	3221-61-2	2.72·10−8	6.18·10−4
C9H20	4-Methyloctane	2216-34-4	3.53·10−8	6.07·10−4
C9H20	Nonane	111-84-2	1.91·10−8 1.71·10−8 [23]	6.08·10−4 5.60·10−4 [23]
C9H20	2,2,3,3-Tetramethylpentane	7154-79-2	1.49·10−7	5.49·10−4
C9H20	2,2,3,4-Tetramethylpentane	1186-53-4	7.70·10−8	6.16·10−4
C9H20	2,2,4,4-Tetramethylpentane	1070-87-7	9.23·10−8	6.45·10−4
C9H20	2,3,3,4-Tetramethylpentane	16747-38-9	1.11·10−7	5.62·10−4
C9H20	2,2,3-Trimethylhexane	16747-25-4	7.53·10−8	6.14·10−4
C9H20	2,2,4-Trimethylhexane	16747-26-5	7.21·10−8	6.34·10−4
C9H20	2,2,5-Trimethylhexane	3522-94-9	5.67·10−8	6.60·10−4 5.34·10−4 [23]
C9H20	2,3,3-Trimethylhexane	16747-28-7	8.91·10−8	5.83·10−4
C9H20	2,3,4-Trimethylhexane	921-47-1	6.05·10−8	5.99·10−4
C9H20	2,3,5-Trimethylhexane	1069-53-0	5.58·10−8	6.29·10−4
C9H20	2,4,4-Trimethylhexane	16747-30-1	8.22·10−8	6.12·10−4
C9H20	3,3,4-Trimethylhexane	16747-31-2	1.08·10−7	5.62·10−4
C10H14	Butylbenzene	104-51-8	2.35·10−6 2.40·10−6 [25]	2.46·10−3
C10H14	sec-Butylbenzene	135-98-8	2.84·10−6 2.36·10−6 [25]	2.51·10−3
C10H14	tert-Butylbenzene	98-06-6	2.19·10−6	2.53·10−3
C10H14	1,2-Diethylbenzene	135-01-3	2.19·10−6	2.47·10−3
C10H14	1,3-Diethylbenzene	141-93-5	2.32·10−6	2.48·10−3
C10H14	1,4-Diethylbenzene	105-05-5	1.75·10−6	2.47·10−3
C10H14	1-Ethyl-2,3-dimethylbenzene	933-98-2	1.73·10−6	2.40·10−3
C10H14	1-Ethyl-2,4-dimethylbenzene	874-41-9	1.97·10−6	2.44·10−3
C10H14	1-Ethyl-3,5-dimethylbenzene	934-74-7	2.19·10−6	2.47·10−3
C10H14	2-Ethyl-1,3-dimethylbenzene	2870-04-4	1.89·10−6	2.43·10−3
C10H14	2-Ethyl-1,4-dimethylbenzene	1758-88-9	2.03·10−6	2.45·10−3
C10H14	4-Ethyl-1,2-dimethylbenzene	934-80-5	1.91·10−6	2.43·10−3
C10H14	Isobutylbenzene	538-93-2	4.78·10−6	2.51·10−3
C10H14	1-Methyl-2- (1-methylethyl)benzene	527-84-4	2.38·10−6	2.49·10−3
C10H14	1-Methyl-3- (1-methylethyl)benzene	535-77-3	2.55·10−6	2.51·10−3
C10H14	1-Methyl-4- (1-methylethyl)benzene	99-87-6	2.03·10−6	2.50·10−3 2.68·10−3 [25]
C10H14	1-Methyl-2-propylbenzene	1074-17-5	2.12·10−6	2.46·10−3
C10H14	1-Methyl-3-propylbenzene	1074-43-7	2.28·10−6	2.48·10−3
C10H14	1-Methyl-4-propylbenzene	1074-55-1	2.19·10−6	2.47·10−3
C10H14	1,2,3,4-Tetramethylbenzene	488-23-3	1.34·10−6	2.34·10−3
C10H14	1,2,3,5-Tetramethylbenzene	527-53-7	1.59·10−6	2.38·10−3
C10H14	1,2,4,5-Tetramethylbenzene	95-93-2	2.26·10−6	2.40·10−3
C10H16	d-Limonene	5989-27-5	7.64·10−7	3.07·10−3
C10H20	1-Butylcyclohexane	1678-93-9	1.53·10−8	5.40·10−4
C10H20	1-Decene	872-05-9	1.27·10−8	1.50·10−3
C10H20	Pentylcyclopentane	3741-00-2	1.68·10−8 1.50·10−8 [23]	5.29·10−4
C10H22	2,4-Dimethyl-3- (1-methylethyl)pentane	13475-79-1	1.47·10−8	6.23·10−4
C10H22	2,3-Dimethyloctane	7146-60-3	7.58·10−9	6.16·10−4
C10H22	2,4-Dimethyloctane	4032-94-4	1.01·10−8	6.27·10−4
C10H22	2,5-Dimethyloctane	15869-89-3	9.23·10−9	5.87·10−4
C10H22	2,6-Dimethyloctane	2051-30-1	8.65·10−9	6.20·10−4
C10H22	3,3-Dimethyloctane	4110-44-5	1.21·10−8	6.07·10−4
C10H22	3,5-Dimethyloctane	15869-93-9	1.18·10−8	6.10·10−4
C10H22	4,5-Dimethyloctane	15869-96-2	1.08·10−8	6.07·10−4
C10H22	4-Ethyl-2,2-dimethylhexane	52896-99-8	8.34·10−8	5.31·10−4
C10H22	3-Ethyl-2,2,4-trimethylpentane	52897-18-4	2.28·10−8	6.03·10−4
C10H22	3-Ethyl-2,3,4-trimethylpentane	52897-19-5	3.35·10−8	5.45·10−4
C10H22	2-Methylnonane	871-83-0	3.82·10−9	6.52·10−4
C10H22	3-Methylnonane	5911-04-6	6.37·10−9	6.08·10−4
C10H22	4-Methylnonane	17301-94-9	6.90·10−9	6.10·10−4
C10H22	5-Methylnonane	15869-85-9	7.00·10−9	6.12·10−4
C10H22	2,2,3,3,4-Pentamethylpentane	16747-44-7	3.23·10−8	5.63·10−4
C10H22	2,2,3,4,4-Pentamethylpentane	16747-45-8	2.18·10−8	5.93·10−4
C10H22	4-Propylheptane	3178-29-8	1.20·10−8	6.09·10−4
C10H22	2,2,3,3-Tetramethylhexane	13475-81-5	3.72·10−8	5.60·10−4
C10H22	2,2,3,5-Tetramethylhexane	52897-09-3	2.09·10−8	6.27·10−4
C10H22	2,2,5,5-Tetramethylhexane	1071-81-4	1.50·10−8	6.88·10−4
C10H22	2,3,3,4-Tetramethylhexane	52897-10-6	2.99·10−8	5.62·10−4
C10H22	2,3,3,5-Tetramethylhexane	52897-11-7	4.23·10−8	5.75·10−4
C10H22	2,3,4,4-Tetramethylhexane	52897-12-8	2.35·10−8	5.83·10−4
C10H22	2,3,4,5-Tetramethylhexane	52897-15-1	1.52·10−8	6.17·10−4
C10H22	3,3,4,4-Tetramethylhexane	5171-84-6	4.90·10−8	5.56·10−4
C10H22	2,2,4-Trimethylheptane	14720-74-2	1.47·10−8	6.43·10−4
C10H22	2,2,6-Trimethylheptane	1190-83-6	1.10·10−8	6.55·10−4
C10H22	2,4,6-Trimethylheptane	2613-61-8	1.39·10−8	6.44·10−4
C10H22	2,5,5-Trimethylheptane	1189-99-7	9.65·10−9	6.50·10−4
C10H22	3,3,5-Trimethylheptane	7154-80-5	1.73·10−8	6.11·10−4
C10H22	Decane	124-18-5	3.33·10−9 2.50·10−9 [23]	6.15·10−4 5.70·10−4 [23]
C11H16	Pentylbenzene	538-68-1	5.20·10−7 4.68·10−7 [25]	2.38·10−3
C11H22	1-Undecene	821-95-4	1.94·10−9	1.50·10−3
C11H24	Undecane	1120-21-4	4.79·10−10 5.07·10−10 [23]	6.29·10−4 6.0·10−4 [23]
C12H18	1,4-Diisopropylbenzene	100-18-5	1.81·10−7	2.40·10−3
C12H18	Hexylbenzene	1077-16-3	0.98·10−7 1.01·10−7 [25]	2.31·10−3

. In the same table, the experimental values are given for 64 systems. This set of recommended data was selected from all available data reported in the literature. For 153 other systems, only the predicted solubilities given in Table 1 are available. In this paper, prediction is limited to these hydrocarbons, for which critical parameters have been measured. The prediction of the mutual solubility in other hydrocarbon + water systems is also possible, but one has to estimate values of the critical constants using one of the methods published in literature.

The estimated standard deviation of x_h or x_w resulting from accuracy of the method is estimated to within 5% of the calculated mole fraction.