Dynamically Operated Fischer–Tropsch Synthesis in PtL—Part 2: Coping with Real PV Profiles
Abstract
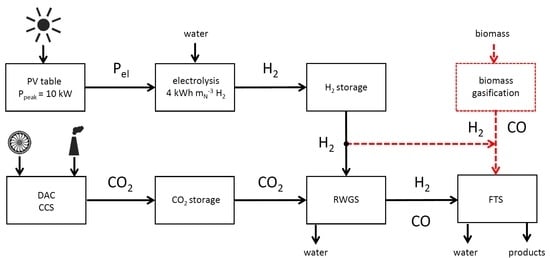
1. Introduction
2. Materials and Methods
2.1. Experimental Setup and Process Analysis
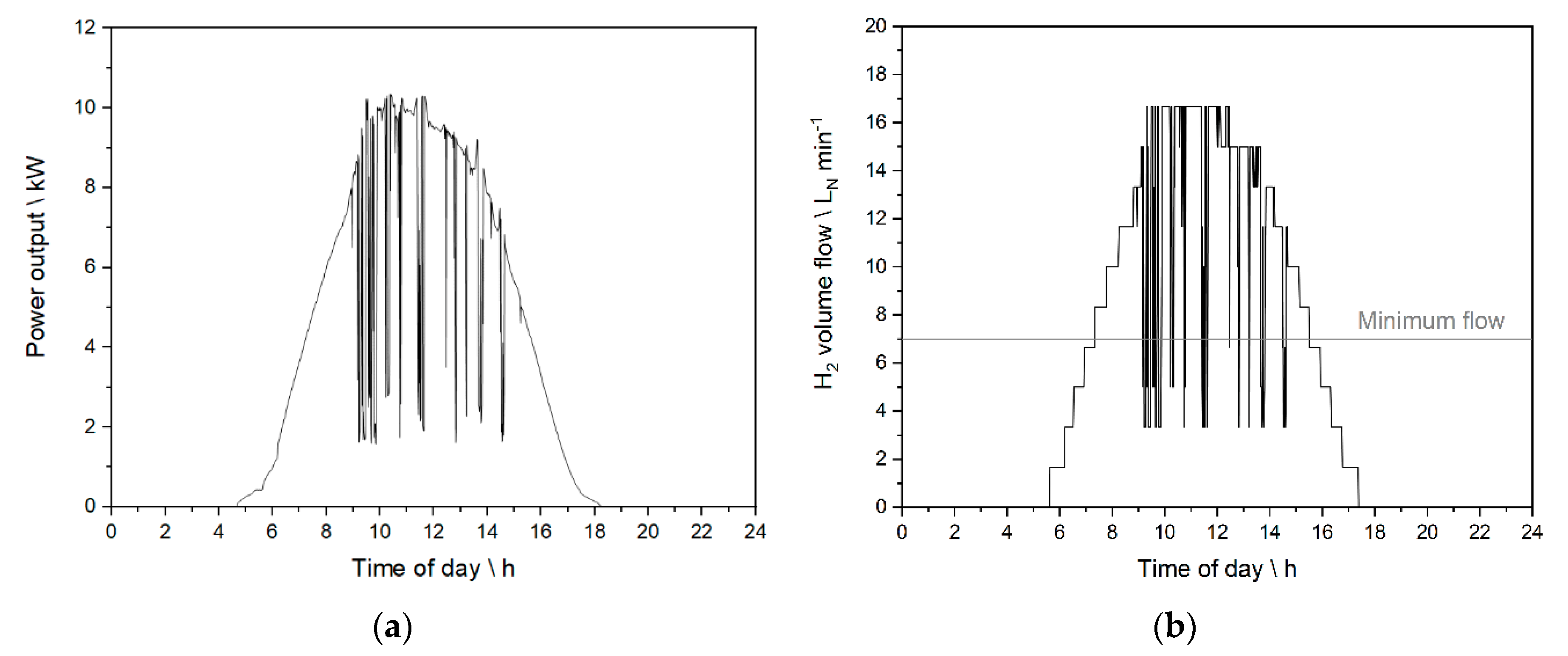
2.2. Real Photovoltaic Profiles and Discretization of the Feed
2.3. Experimental Base Cases
2.4. Calculation of Conversion Levels during Quick Process Changes
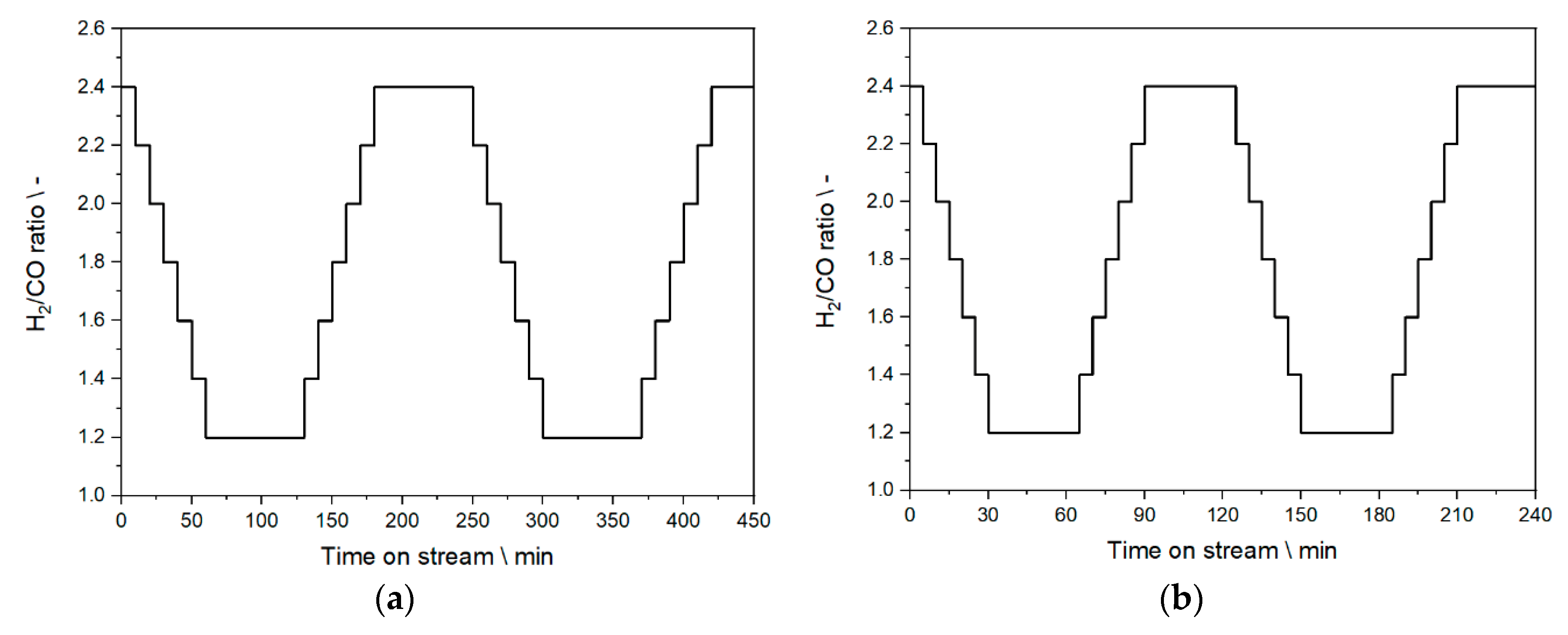
2.5. Step Change Experiments—Experimental Design
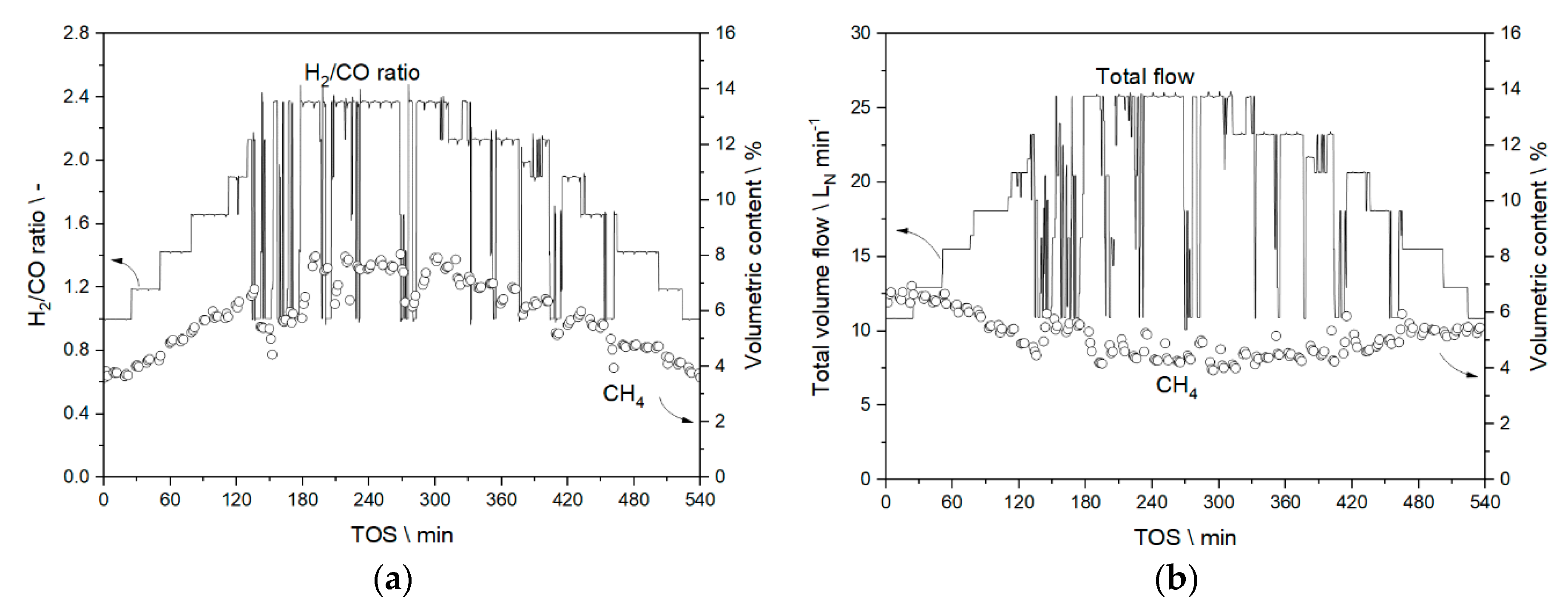
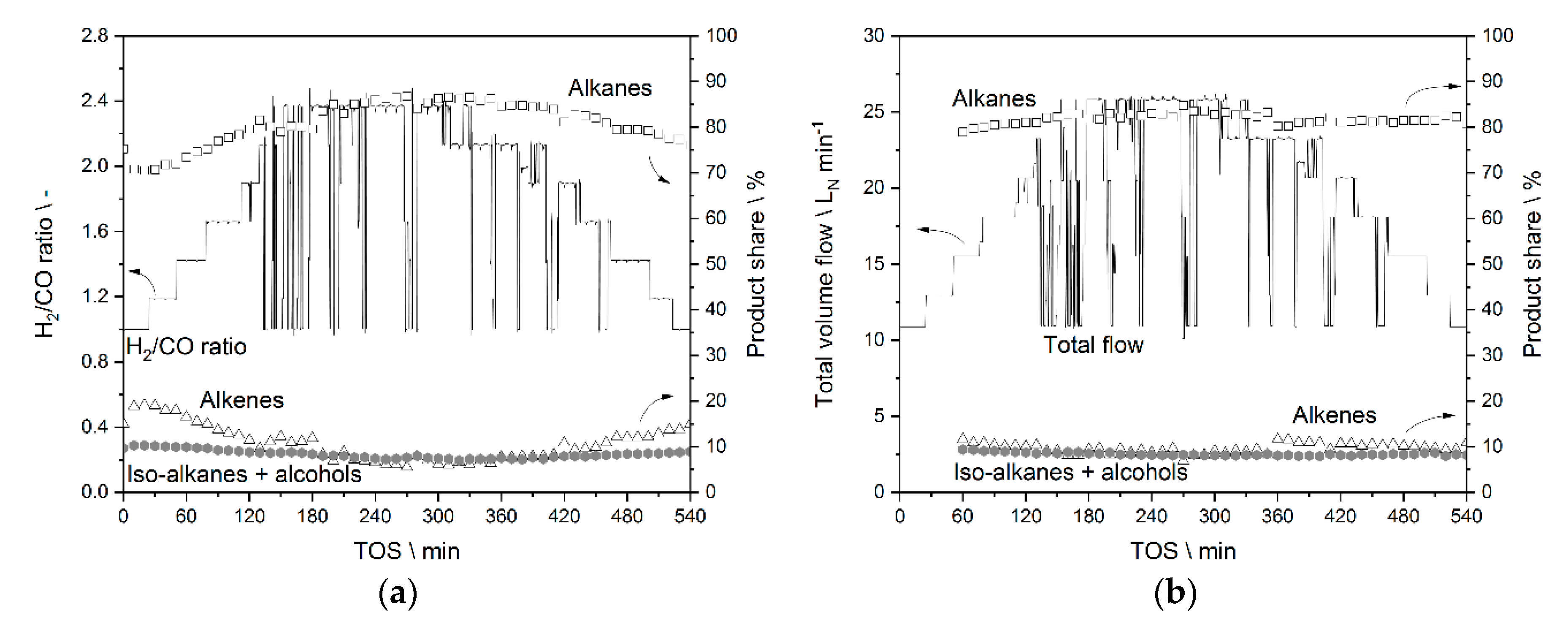
2.6. Experiments Based on the PV Profile
3. Results and Discussion
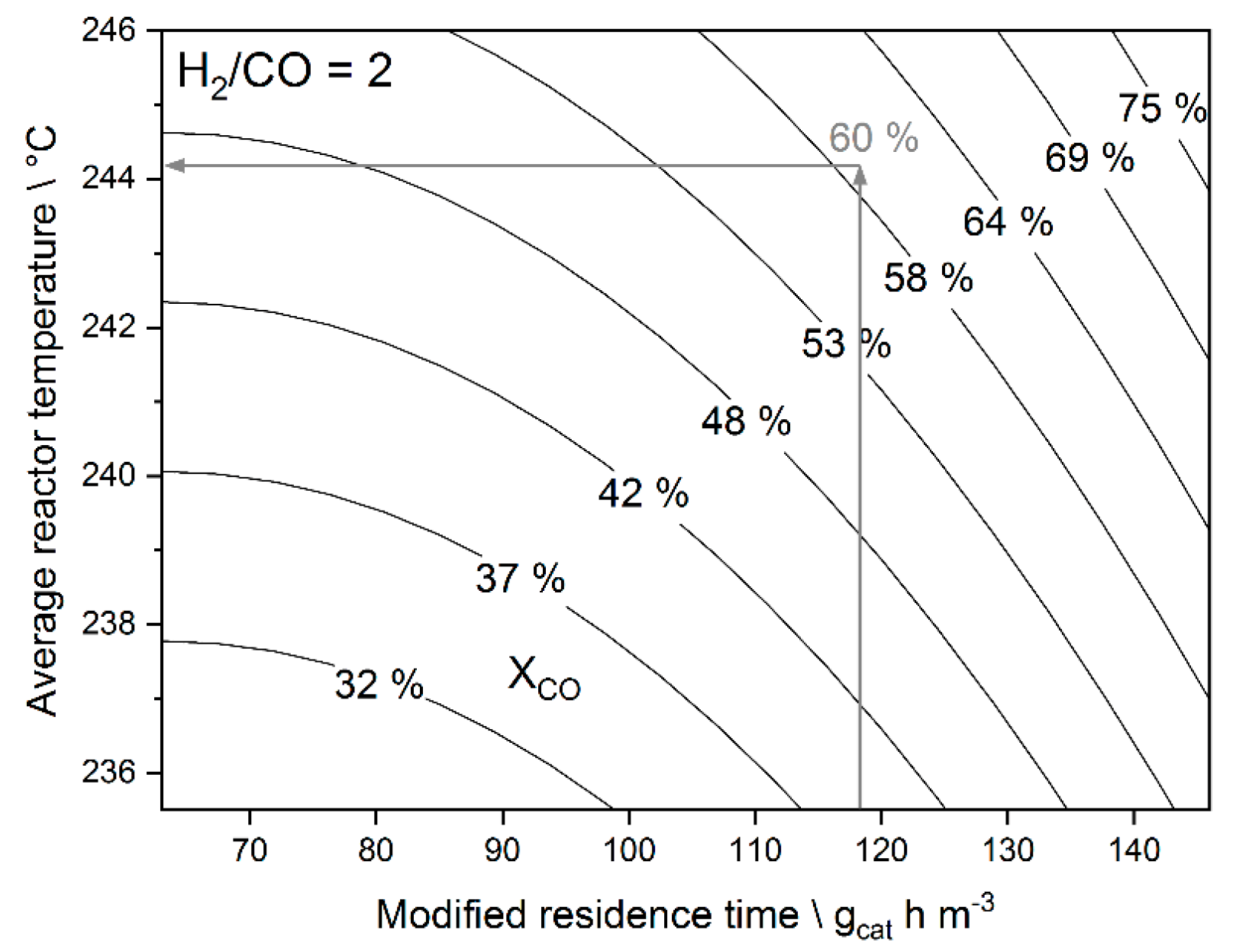
3.1. Linear Regression Model
3.2. Step Change Experiments—Results
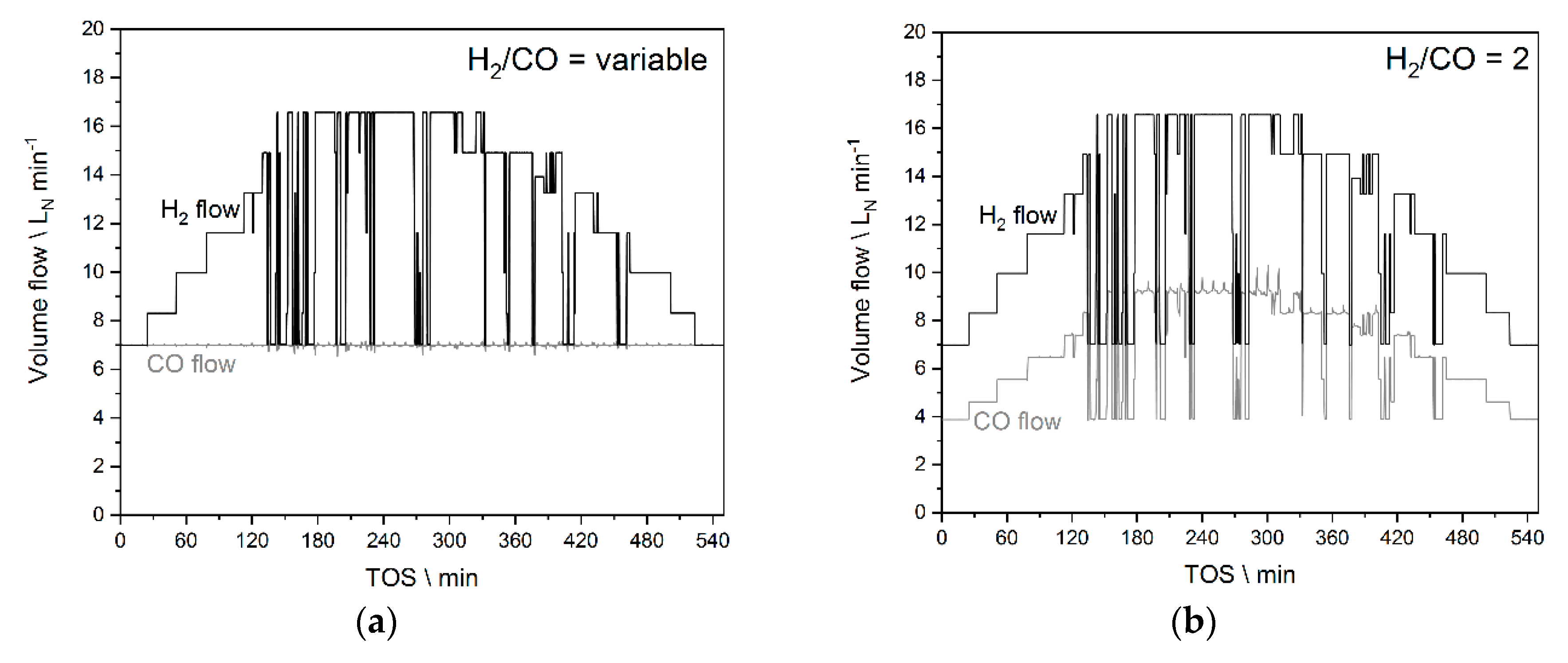
3.3. Experiments Based on the PV Profile—Results
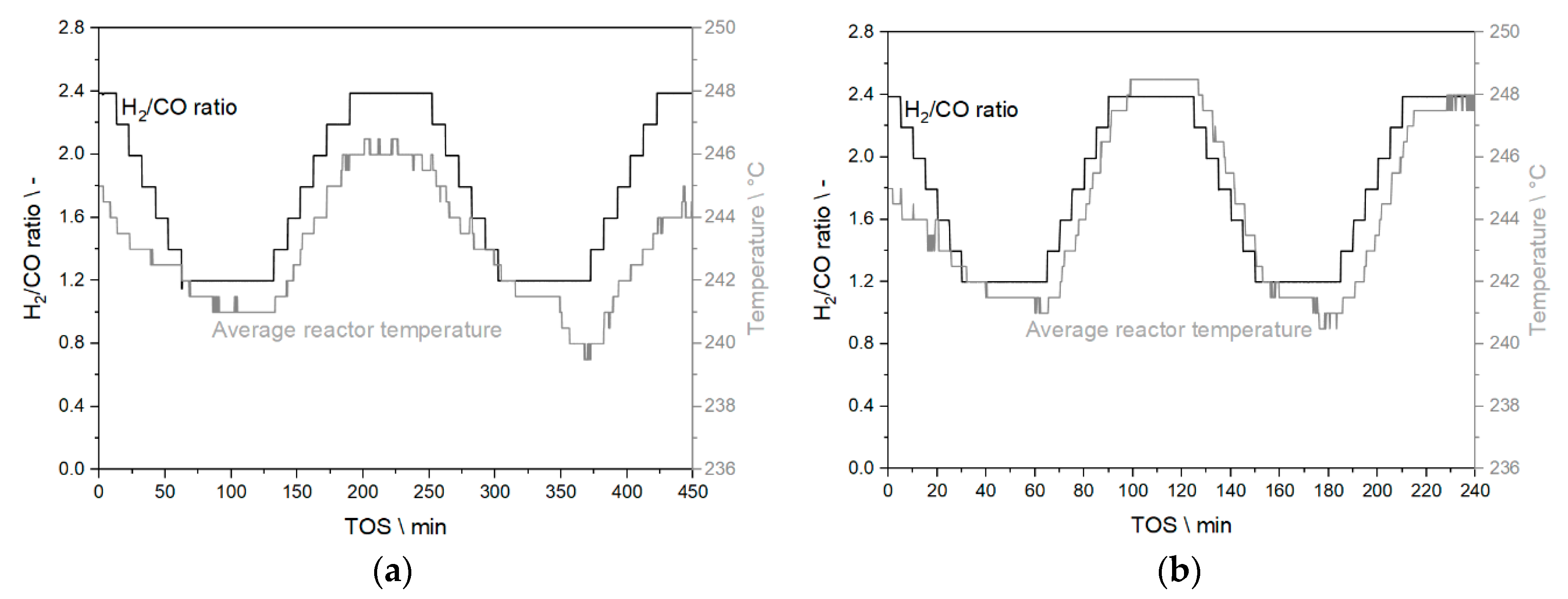
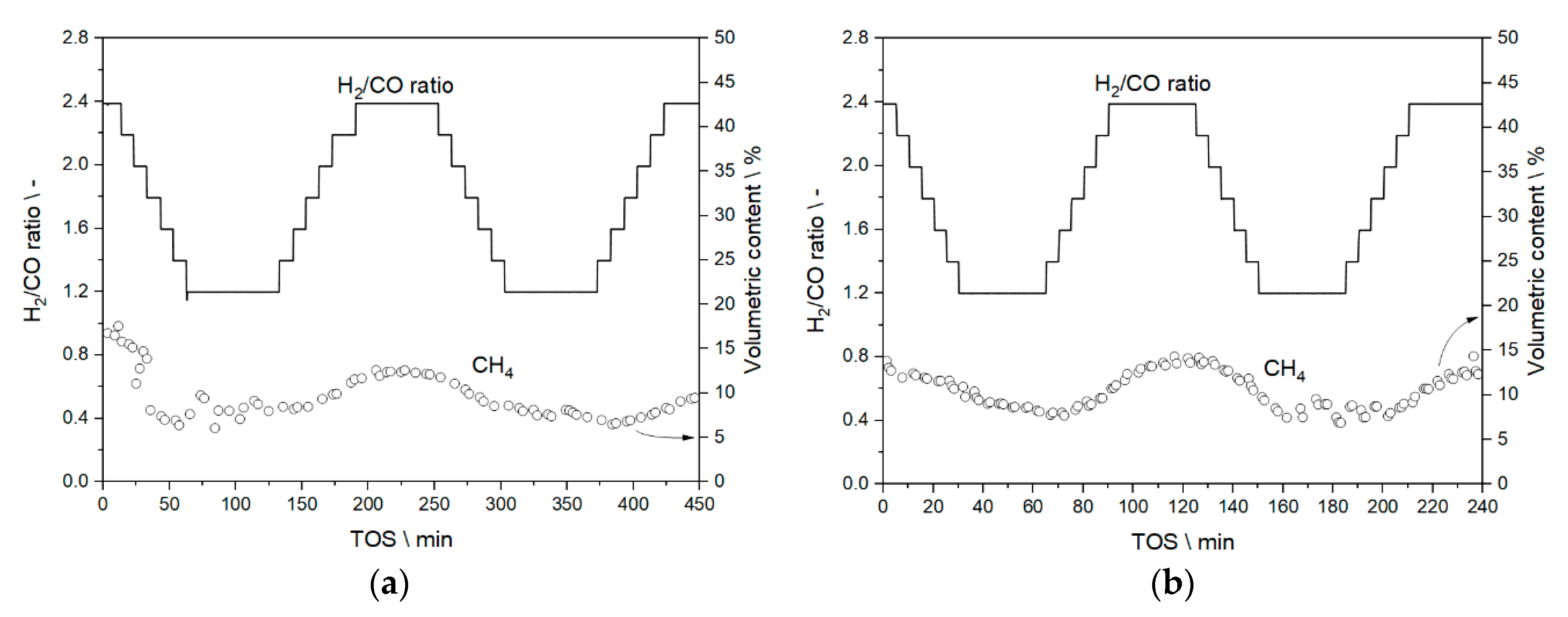
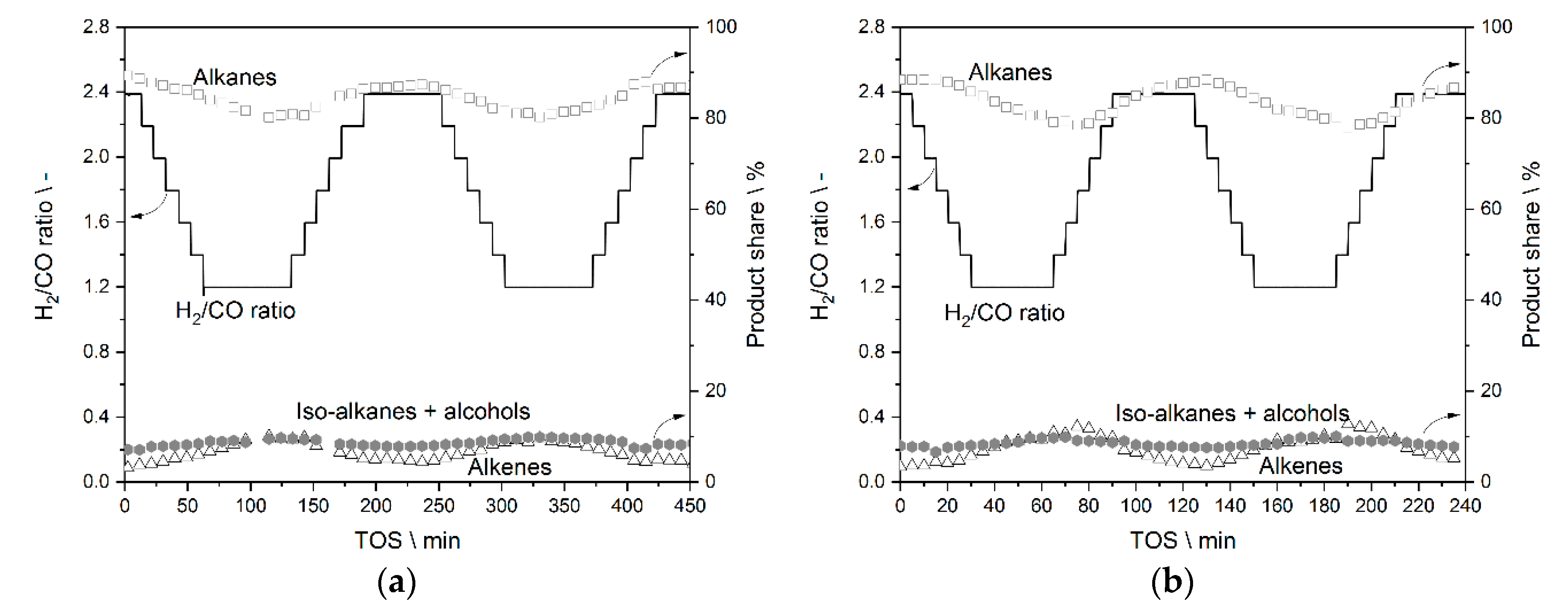
3.3.1. Results from Experiments without Temperature Manipulation
3.3.2. Results from Temperature Adaptation to Reach Targeted Conversion Levels
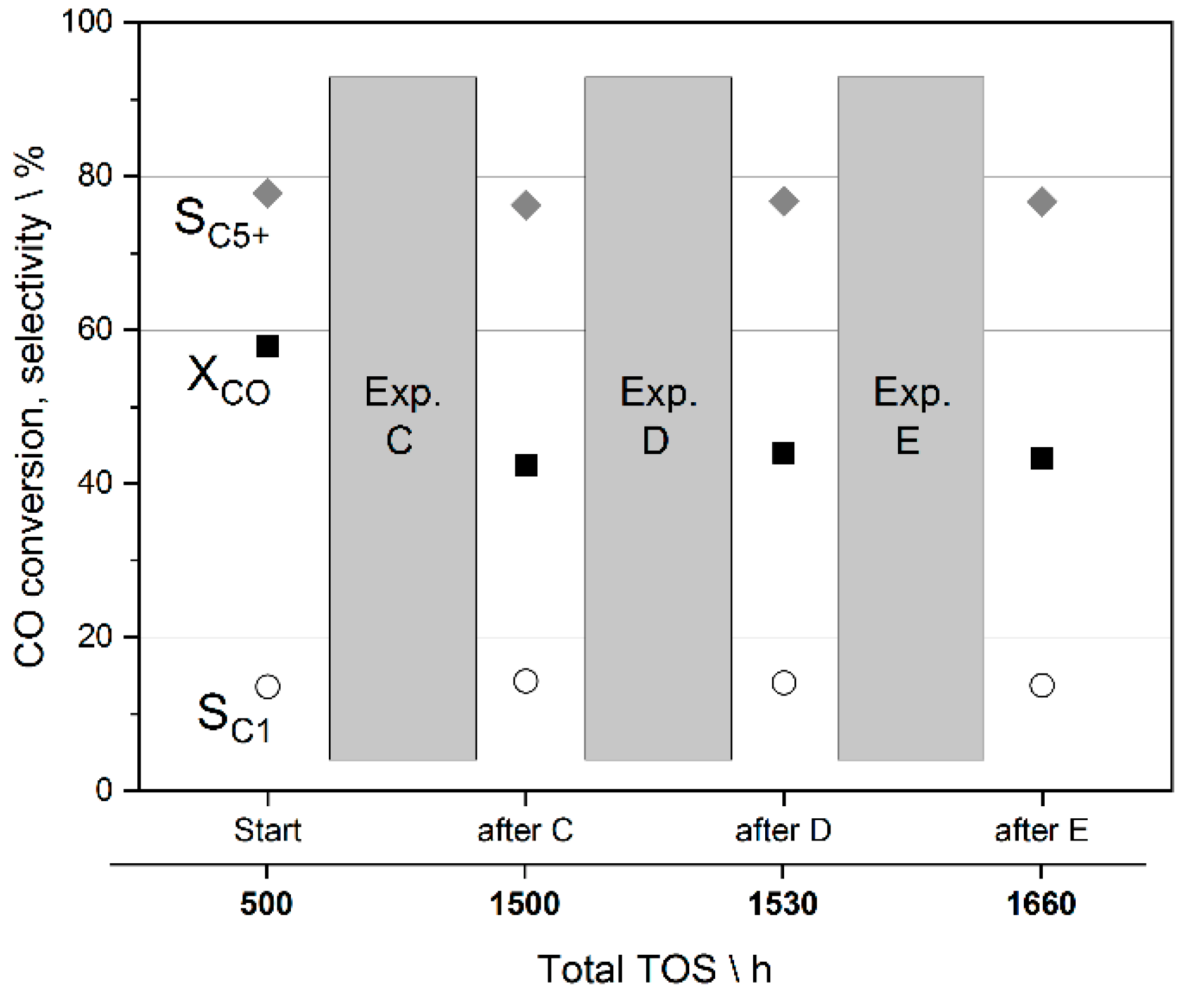
3.4. Preliminary Analysis of Effects on Catalyst Stability during the Studies
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- UN Climate Change. Historic Paris Agreement on Climate Change: 195 Nations Set Path to Keep Temperature Rise Well Below 2 Degrees Celsius. Available online: http://newsroom.unfccc.int/unfccc-newsroom/finale-cop21/ (accessed on 3 April 2018).
- BMU. Hendricks startet Dialog zum Klimaschutzplan 2050. Available online: https://www.bmu.de/pressemitteilung/hendricks-startet-dialog-zum-klimaschutzplan-2050/?tx_ttnews%5BbackPid%5D=3915 (accessed on 12 February 2020).
- Le Quéré, C.; Andrew, R.M.; Friedlingstein, P.; Sitch, S.; Hauck, J.; Pongratz, J.; Pickers, P.A.; Korsbakken, J.I.; Peters, G.P.; Canadell, J.G.; et al. Global Carbon Budget 2018. Earth. Syst. Sci. Data 2018, 10, 2141–2194. [Google Scholar] [CrossRef]
- Dittmeyer, R.; Boeltken, T.; Piermartini, P.; Selinsek, M.; Loewert, M.; Dallmann, F.; Kreuder, H.; Cholewa, M.; Wunsch, A.; Belimov, M.; et al. Micro and micro membrane reactors for advanced applications in chemical energy conversion. Curr. Opin. Chem. Eng. 2017, 17, 108–125. [Google Scholar] [CrossRef]
- Maitlis, P.M.; de Klerk, A. (Eds.) Greener Fischer–Tropsch Processes for Fuels and Feedstocks; Wiley-VCH: Weinheim, Germany, 2013; ISBN 3527329455. [Google Scholar]
- Verein Deutscher Ingenieure (VDI). VDI-Statusreport Regenerative Energien. Available online: https://www.vdi.de/ueber-uns/presse/publikationen/details/vdi-statusreport-regenerative-energien (accessed on 11 April 2020).
- SAPEA—Science Advice for Policy by European Academies. Novel Carbon Capture and Utilisation Technologies. Available online: https://www.sapea.info/wp-content/uploads/CCU-report-web-version.pdf (accessed on 11 April 2020).
- International Energy Agency (IEA). World Energy Outlook 2016. Available online: https://webstore.iea.org/world-energy-outlook-2016 (accessed on 11 April 2020).
- Vaillancourt, K.; Bahn, O.; Roy, P.O.; Patreau, V. Is there a future for new hydrocarbon projects in a decarbonizing energy system? A case study for Quebec (Canada). Appl. Energy 2018, 218, 114–130. [Google Scholar] [CrossRef]
- Ridjan, I.; Mathiesen, B.V.; Connolly, D. Terminology used for renewable liquid and gaseous fuels based on the conversion of electricity: A review. J. Clean. Prod. 2016, 112, 3709–3720. [Google Scholar] [CrossRef]
- Li, W.; Wang, H.; Jiang, X.; Zhu, J.; Liu, Z.; Guo, X.; Song, C. A short review of recent advances in CO2 hydrogenation to hydrocarbons over heterogeneous catalysts. RSC Adv. 2018, 8, 7651–7669. [Google Scholar] [CrossRef]
- Reuß, M.; Grube, T.; Robinius, M.; Preuster, P.; Wasserscheid, P.; Stolten, D. Seasonal storage and alternative carriers: A flexible hydrogen supply chain model. Appl. Energy 2017, 200, 290–302. [Google Scholar] [CrossRef]
- Kotzur, L.; Markewitz, P.; Robinius, M.; Stolten, D. Time series aggregation for energy system design: Modeling seasonal storage. Appl. Energy 2018, 213, 123–135. [Google Scholar] [CrossRef]
- Schmidt, P.; Batteiger, V.; Roth, A.; Weindorf, W.; Raksha, T. Power-to-Liquids as Renewable Fuel Option for Aviation: A Review. Chem. Ing. Tech. 2018, 127–140. [Google Scholar] [CrossRef]
- De Klerk, A. Fischer–Tropsch Refining, 1st ed.; Wiley-VCH: Weinheim, Germany, 2011; ISBN 3527326057. [Google Scholar]
- Piermartini, P.; Boeltken, T.; Selinsek, M.; Pfeifer, P. Influence of channel geometry on Fischer–Tropsch synthesis in microstructured reactors. Chem. Eng. J. 2017, 313, 328–335. [Google Scholar] [CrossRef]
- Myrstad, R.; Eri, S.; Pfeifer, P.; Rytter, E.; Holmen, A. Fischer–Tropsch synthesis in a microstructured reactor. Catal. Today 2009, 147, 301–304. [Google Scholar] [CrossRef]
- Loewert, M.; Hoffmann, J.; Piermartini, P.; Selinsek, M.; Dittmeyer, R.; Pfeifer, P. Microstructured Fischer–Tropsch reactor scale-up and opportunities for decentralized application. Chem. Eng. Technol. 2019, 2202–2214. [Google Scholar] [CrossRef]
- Kalz, K.F.; Kraehnert, R.; Dvoyashkin, M.; Dittmeyer, R.; Gläser, R.; Krewer, U.; Reuter, K.; Grunwaldt, J.D. Future Challenges in Heterogeneous Catalysis: Understanding Catalysts under Dynamic Reaction Conditions. ChemCatChem 2017, 9, 17–29. [Google Scholar] [CrossRef]
- Silveston, P.; Hudgins, R.R.; Renken, A. Periodic operation of catalytic reactors-introduction and overview. Catal. Today 1995, 25, 91–112. [Google Scholar] [CrossRef]
- Güttel, R. Study of Unsteady-State Operation of Methanation by Modeling and Simulation. Chem. Eng. Technol. 2013, 83. [Google Scholar] [CrossRef]
- Iglesias González, M. Gaseous Hydrocarbon Synfuels from H2/CO2 based on Renewable Electricity Kinetics, Selectivity and Fundamentals of Fixed-Bed Reactor Design for Flexible Operation. Ph.D. Thesis, Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany, 2016. [Google Scholar]
- Iglesias González, M.; Schaub, G. Fischer–Tropsch synthesis with H2/CO2-catalyst behavior under transient conditions. Chem. Ing. Tech. 2015, 87, 848–854. [Google Scholar] [CrossRef]
- Eilers, H.; González, M.I.; Schaub, G. Lab-scale experimental studies of Fischer–Tropsch kinetics in a three-phase slurry reactor under transient reaction conditions. Catal. Today 2015. [Google Scholar] [CrossRef]
- Mutz, B.; Carvalho, H.W.P.; Mangold, S.; Kleist, W.; Grunwaldt, J.-D. Methanation of CO2: Structural response of a Ni-based catalyst under fluctuating reaction conditions unraveled by operando spectroscopy. J. Catal. 2015, 327, 48–53. [Google Scholar] [CrossRef]
- Kreitz, B.; Wehinger, G.D.; Turek, T. Dynamic simulation of the CO2 methanation in a micro-structured fixed-bed reactor. Chem. Eng. Sci. 2019, 195, 541–552. [Google Scholar] [CrossRef]
- Kreitz, B.; Friedland, J.; Güttel, R.; Wehinger, G.D.; Turek, T. Dynamic Methanation of CO2—Effect of Concentration Forcing. Chem. Ing. Tech. 2019, 91, 576–582. [Google Scholar] [CrossRef]
- Fache, A.; Marias, F.; Guerré, V.; Palmade, S. Optimization of fixed-bed methanation reactors: Safe and efficient operation under transient and steady-state conditions. Chem. Eng. Sci. 2018, 192, 1124–1137. [Google Scholar] [CrossRef]
- Tauer, G.; Kern, C.; Jess, A. Transient Effects during Dynamic Operation of a Wall-Cooled Fixed-Bed Reactor for CO2 Methanation. Chem. Eng. Technol. 2019, 42, 2401–2409. [Google Scholar] [CrossRef]
- Theurich, S.; Rönsch, S.; Güttel, R. Transient Flow Rate Ramps for Methanation of Carbon Dioxide in an Adiabatic Fixed-Bed Recycle Reactor. Energy Technol. 2020, 8, 1901116. [Google Scholar] [CrossRef]
- Bremer, J.; Sundmacher, K. Operation range extension via hot-spot control for catalytic CO2 methanation reactors. React. Chem. Eng. 2019, 4, 1019–1037. [Google Scholar] [CrossRef]
- Fache, A.; Marias, F.; Guerré, V.; Palmade, S. Intermittent Operation of Fixed-Bed Methanation Reactors: A Simple Relation Between Start-Up Time and Idle State Duration. Waste Biomass Valoriz. 2020, 11, 447–463. [Google Scholar] [CrossRef]
- Fache, A.; Marias, F.; Chaudret, B. Catalytic reactors for highly exothermic reactions: Steady-state stability enhancement by magnetic induction. Chem. Eng. J. 2020, 390, 124531. [Google Scholar] [CrossRef]
- Fache, A.; Marias, F. Dynamic operation of fixed-bed methanation reactors: Yield control by catalyst dilution profile and magnetic induction. Renew. Energy 2020, 151, 865–886. [Google Scholar] [CrossRef]
- Bremer, J.; Rätze, K.H.G.; Sundmacher, K. CO2 methanation: Optimal start-up control of a fixed-bed reactor for power-to-gas applications. AIChE J. 2017, 63, 23–31. [Google Scholar] [CrossRef]
- Theurich, S. Unsteady-state operation of a fixed-bed recycle reactor for the methanation of carbon dioxide. Ph.D. Thesis, Ulm university, Ulm, Germany, 2019. [Google Scholar]
- Adesina, A.A.; Silveston, P.L.; Hudgins, R.R. A Comparison of Forced Feed Cycling of the Fischer–Tropsch Synthesis over Iron and Cobalt Catalysts. In Catalysis on the Energy Scene; Elsevier: Amsterdam, Netherlands, 1984; pp. 191–196. ISBN 9780444424020. [Google Scholar]
- Loewert, M.; Pfeifer, P. Dynamically Operated Fischer–Tropsch Synthesis in PtL-Part 1: System Response on Intermittent Feed. ChemEngineering 2020, 4, 21. [Google Scholar] [CrossRef]
- Sun, C.; Zhan, T.; Pfeifer, P.; Dittmeyer, R. Influence of Fischer–Tropsch synthesis (FTS) and hydrocracking (HC) conditions on the product distribution of an integrated FTS-HC process. Chem. Eng. J. 2017, 310, 272–281. [Google Scholar] [CrossRef]
- Sun, C.; Pfeifer, P.; Dittmeyer, R. One-stage syngas-to-fuel in a micro-structured reactor: Investigation of integration pattern and operating conditions on the selectivity and productivity of liquid fuels. Chem. Eng. J. 2017, 326, 37–46. [Google Scholar] [CrossRef]
- Tremel, A. Electricity-Based Fuels; Springer International Publishing: Cham, Switzerland, 2018; ISBN 9783319724591. [Google Scholar]
- SIEMENS. SILYZER 300-Die Nächste Dimension der PEM-Elektrolyse. Available online: https://assets.new.siemens.com/siemens/assets/api/uuid:abae9c1e48d6d239c06d88e565a25040ed2078dc/version:1524040818/ct-ree-18-047-db-silyzer-300-db-de-en-rz.pdf (accessed on 29 March 2020).
- Monaco, F.; Lanzini, A.; Santarelli, M. Making synthetic fuels for the road transportation sector via solid oxide electrolysis and catalytic upgrade using recovered carbon dioxide and residual biomass. J. Clean. Prod. 2018, 170, 160–173. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Stiller, C. Grundlagen der Mess-und Regelungstechnik; Shaker: Aachen, Germany, 2006; ISBN 3-8322-5582-6. [Google Scholar]
- Mueller, J.P.; Massaron, L. Machine Learning for Dummies; John Wiley & Sons, Inc.: New York, NY, USA, 2016; ISBN 978-1-119-24551-3. [Google Scholar]
- Todic, B.; Ma, W.; Jacobs, G.; Davis, B.H.; Bukur, D.B. Effect of process conditions on the product distribution of Fischer–Tropsch synthesis over a Re-promoted cobalt-alumina catalyst using a stirred tank slurry reactor. J. Catal. 2014, 311, 325–338. [Google Scholar] [CrossRef]
- Van der Laan, G.P.; Beenackers, A.A.C.M. Kinetics and Selectivity of the Fischer–Tropsch Synthesis: A Literature Review. Catal. Rev. 1999, 41, 255–318. [Google Scholar] [CrossRef]
- Yates, I.C.; Satterfield, C.N. Hydrocarbon selectivity from cobalt Fischer–Tropsch catalysts. Energy Fuels 1992, 6, 308–314. [Google Scholar] [CrossRef]
- Dry, M.E. Practical and theoretical aspects of the catalytic Fischer–Tropsch process. Appl. Catal. A-Gen. 1996, 138, 319–344. [Google Scholar] [CrossRef]
- VDI-Gesellschaft Verfahrenstechnik und Chemieingenieurwesen. VDI Heat Atlas, 2nd ed.; Springer: Heidelberg/Neckar, Germany, 2010; ISBN 9783540799993. [Google Scholar]
- Rønning, M.; Tsakoumis, N.E.; Voronov, A.; Johnsen, R.E.; Norby, P.; van Beek, W.; Borg, Ø.; Rytter, E.; Holmen, A. Combined XRD and XANES studies of a Re-promoted Co/γ-Al2O3 catalyst at Fischer–Tropsch synthesis conditions. Catal. Today 2010, 155, 289–295. [Google Scholar] [CrossRef]
- Grunwaldt, J.-D.; Clausen, B.S. Combining XRD and EXAFS with on-Line Catalytic Studies for in situ Characterization of Catalysts. Top. Catal. 2002, 18, 37–43. [Google Scholar] [CrossRef]
- Rochet, A.; Moizan, V.; Pichon, C.; Diehl, F.; Berliet, A.; Briois, V. In situ and operando structural characterisation of a Fischer–Tropsch supported cobalt catalyst. Catal. Today 2011, 171, 186–191. [Google Scholar] [CrossRef]
- Loewert, M.; Serrer, M.-A.; Carambia, T.; Stehle, M.; Zimina, A.; Kalz, K.F.; Lichtenberg, H.; Saraci, E.; Pfeifer, P.; Grunwaldt, J.-D. Bridging the gap between industry and synchrotron: An operando study at 30 bar over 300 h during Fischer–Tropsch synthesis. React. Chem. Eng. 2020. [Google Scholar] [CrossRef]




| Temperature °C | Syngas ratio - | τmod gcat h m−3 | |
|---|---|---|---|
| Min. value | 235.5 | 1.49 | 65.17 |
| Max. value | 246 | 2.20 | 158.02 |
| Data | τmod gcat h m−3 | H2/CO - | T °C | τnorm - | H2/COnorm - | Tnorm - | XCO % |
|---|---|---|---|---|---|---|---|
| 1 | 93.91 | 1.98 | 245 | 0.3073 | 0.6855 | 0.9048 | 65.25 |
| 2 | 81.81 | 1.98 | 245 | 0.1779 | 0.6935 | 0.9048 | 55.72 |
| 3 | 72.74 | 2.11 | 244.5 | 0.0809 | 0.8757 | 0.8571 | 49.05 |
| 4 | 65.17 | 2.00 | 244.5 | 0.0000 | 0.7190 | 0.8571 | 41.58 |
| 5 | 65.27 | 2.00 | 235.5 | 0.0010 | 0.7214 | 0.0000 | 27.51 |
| 6 | 72.62 | 1.99 | 235.5 | 0.0797 | 0.7102 | 0.0000 | 27.61 |
| 7 | 81.74 | 1.99 | 235.5 | 0.1772 | 0.6993 | 0.0000 | 30.90 |
| 8 | 93.69 | 1.98 | 235.5 | 0.3050 | 0.6867 | 0.0000 | 36.06 |
| 9 | 158.02 | 1.94 | 235.5 | 0.9928 | 0.6295 | 0.0000 | 43.38 |
| 10 | 158.69 | 1.93 | 240 | 1.0000 | 0.6247 | 0.4286 | 57.79 |
| 11 | 141.32 | 1.49 | 244.5 | 0.8143 | 0.0000 | 0.8571 | 60.14 |
| 12 | 130.71 | 1.73 | 246 | 0.7008 | 0.3367 | 1.0000 | 62.14 |
| 13 | 121.26 | 1.96 | 244.5 | 0.5997 | 0.6593 | 0.8571 | 67.37 |
| 14 | 113.44 | 2.18 | 244.5 | 0.5161 | 0.9761 | 0.8571 | 71.34 |
| 15 | 94.22 | 2.19 | 241.5 | 0.3106 | 0.9875 | 0.5714 | 57.91 |
| 16 | 93.80 | 2.20 | 241 | 0.3061 | 0.9980 | 0.5238 | 42.37 |
| 17 | 94.69 | 2.20 | 240.5 | 0.3157 | 1.0000 | 0.4762 | 44.03 |
| 18 | 95.10 | 2.20 | 239 | 0.3200 | 0.9993 | 0.3333 | 43.29 |
| 19 | 107.33 | 1.96 | 238 | 0.4508 | 0.6658 | 0.2381 | 40.53 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loewert, M.; Riedinger, M.; Pfeifer, P. Dynamically Operated Fischer–Tropsch Synthesis in PtL—Part 2: Coping with Real PV Profiles. ChemEngineering 2020, 4, 27. https://doi.org/10.3390/chemengineering4020027
Loewert M, Riedinger M, Pfeifer P. Dynamically Operated Fischer–Tropsch Synthesis in PtL—Part 2: Coping with Real PV Profiles. ChemEngineering. 2020; 4(2):27. https://doi.org/10.3390/chemengineering4020027
Chicago/Turabian StyleLoewert, Marcel, Michael Riedinger, and Peter Pfeifer. 2020. "Dynamically Operated Fischer–Tropsch Synthesis in PtL—Part 2: Coping with Real PV Profiles" ChemEngineering 4, no. 2: 27. https://doi.org/10.3390/chemengineering4020027
APA StyleLoewert, M., Riedinger, M., & Pfeifer, P. (2020). Dynamically Operated Fischer–Tropsch Synthesis in PtL—Part 2: Coping with Real PV Profiles. ChemEngineering, 4(2), 27. https://doi.org/10.3390/chemengineering4020027