Drying-Induced Strain-Stress and Deformation of Thin Ceramic Plate
Abstract
1. Introduction
2. Experiments
2.1. Sample Preparation
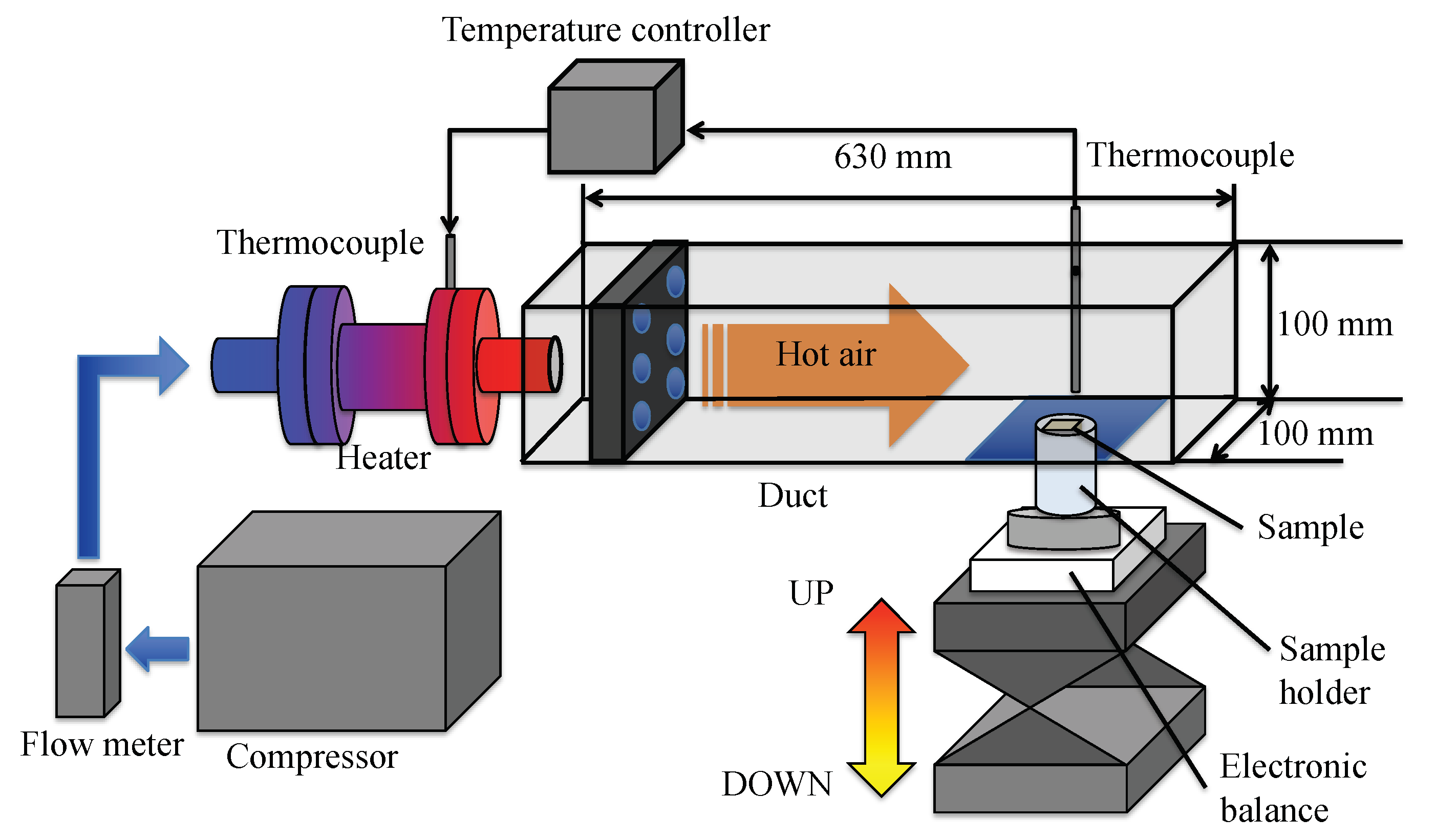
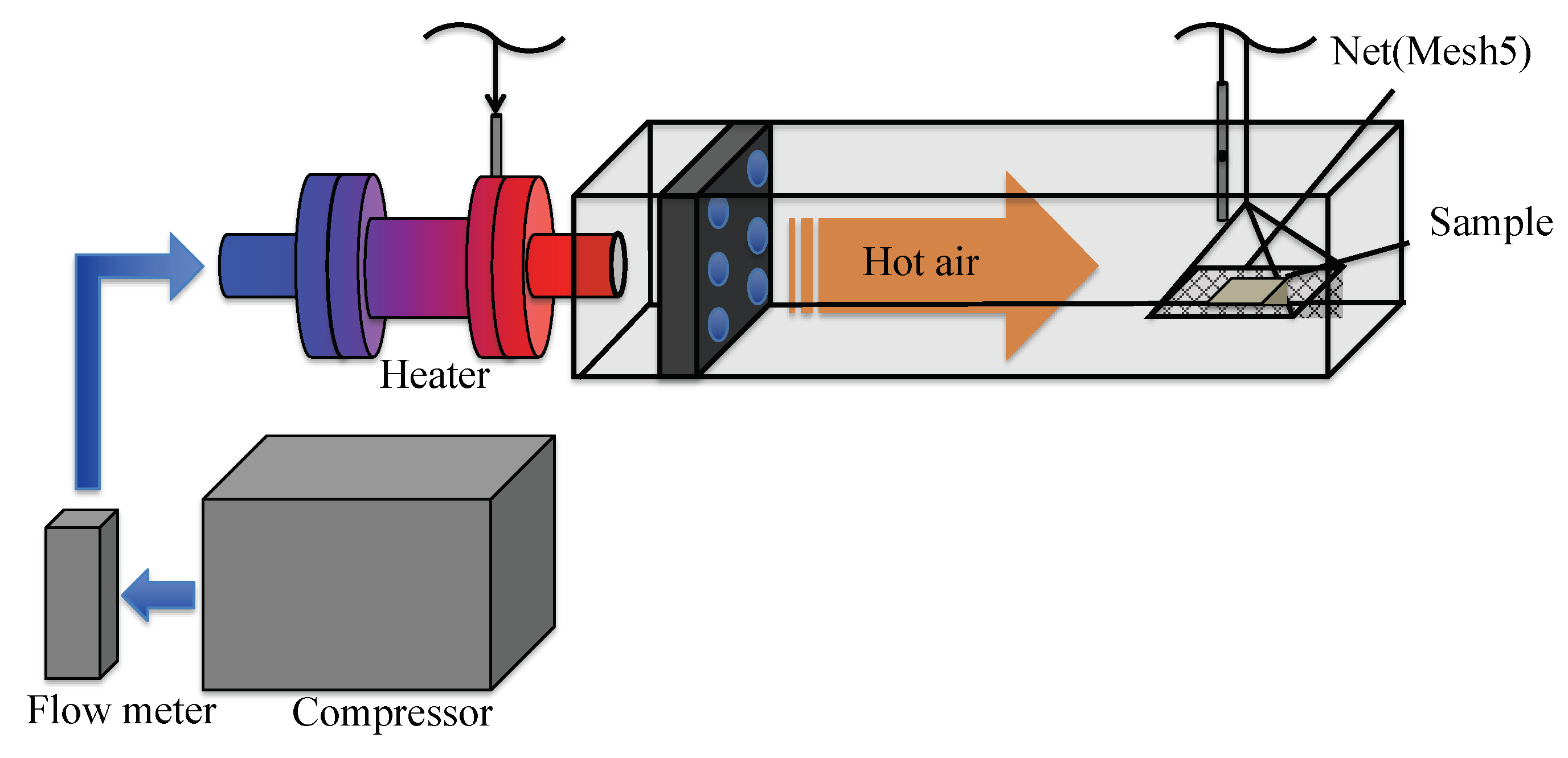
2.2. Drying Experiments
3. Modeling
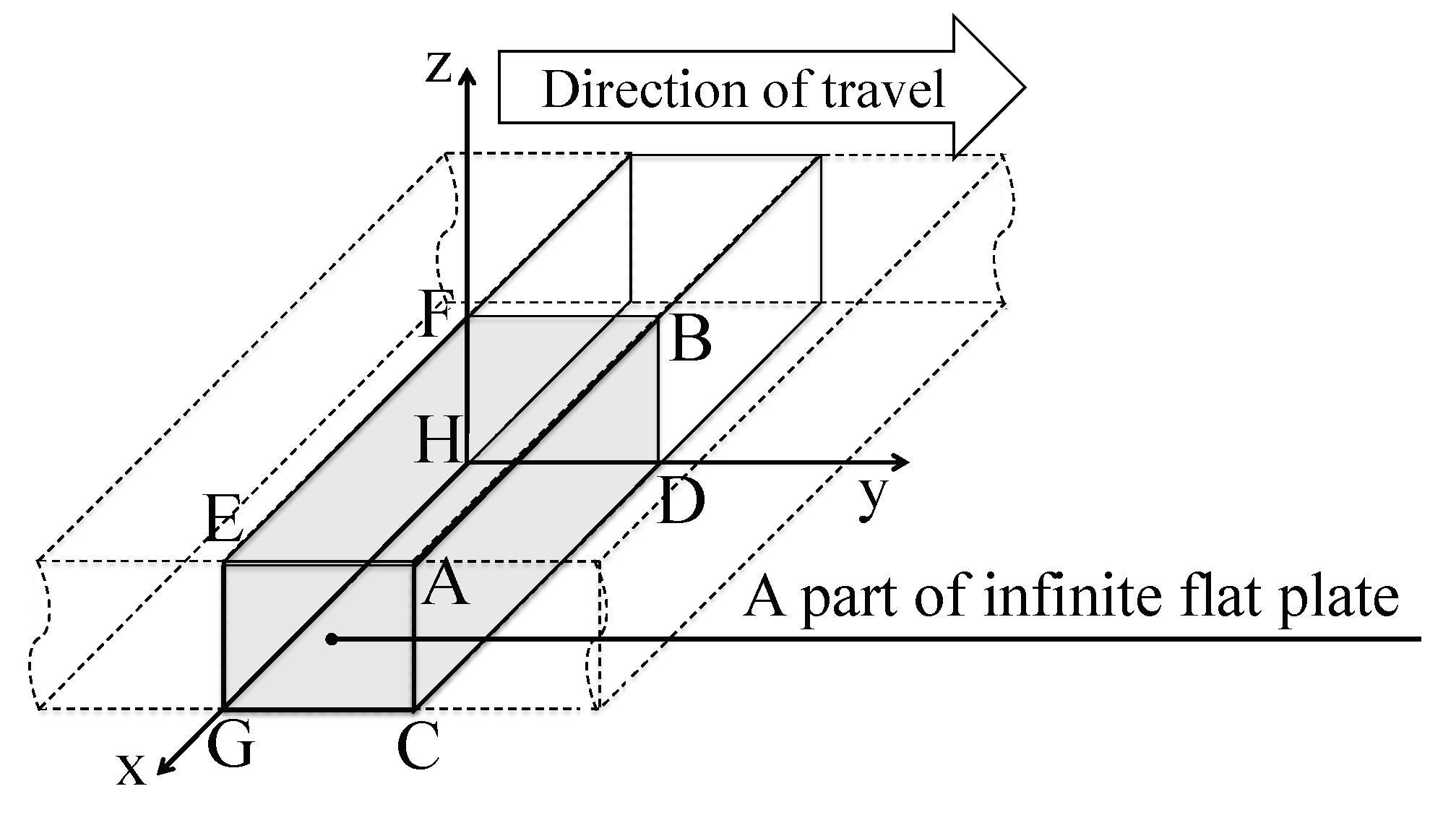
3.1. Heat and Moisture Transfer
3.2. Strain-Stress Analysis
3.3. Physical Properties and Parameters for Simulation
4. Results and Discussion
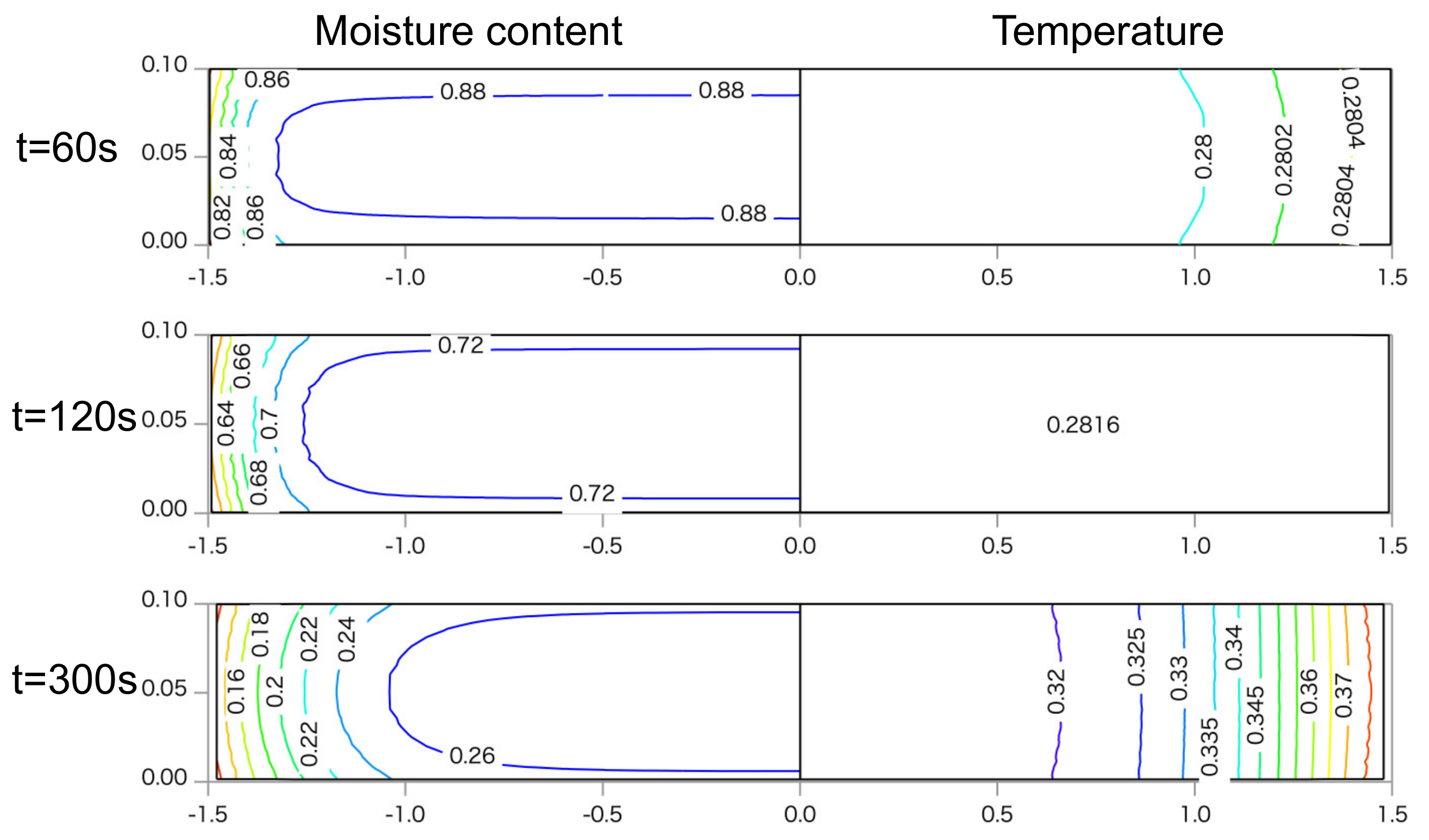
4.1. Transient Moisture Content and Temperature
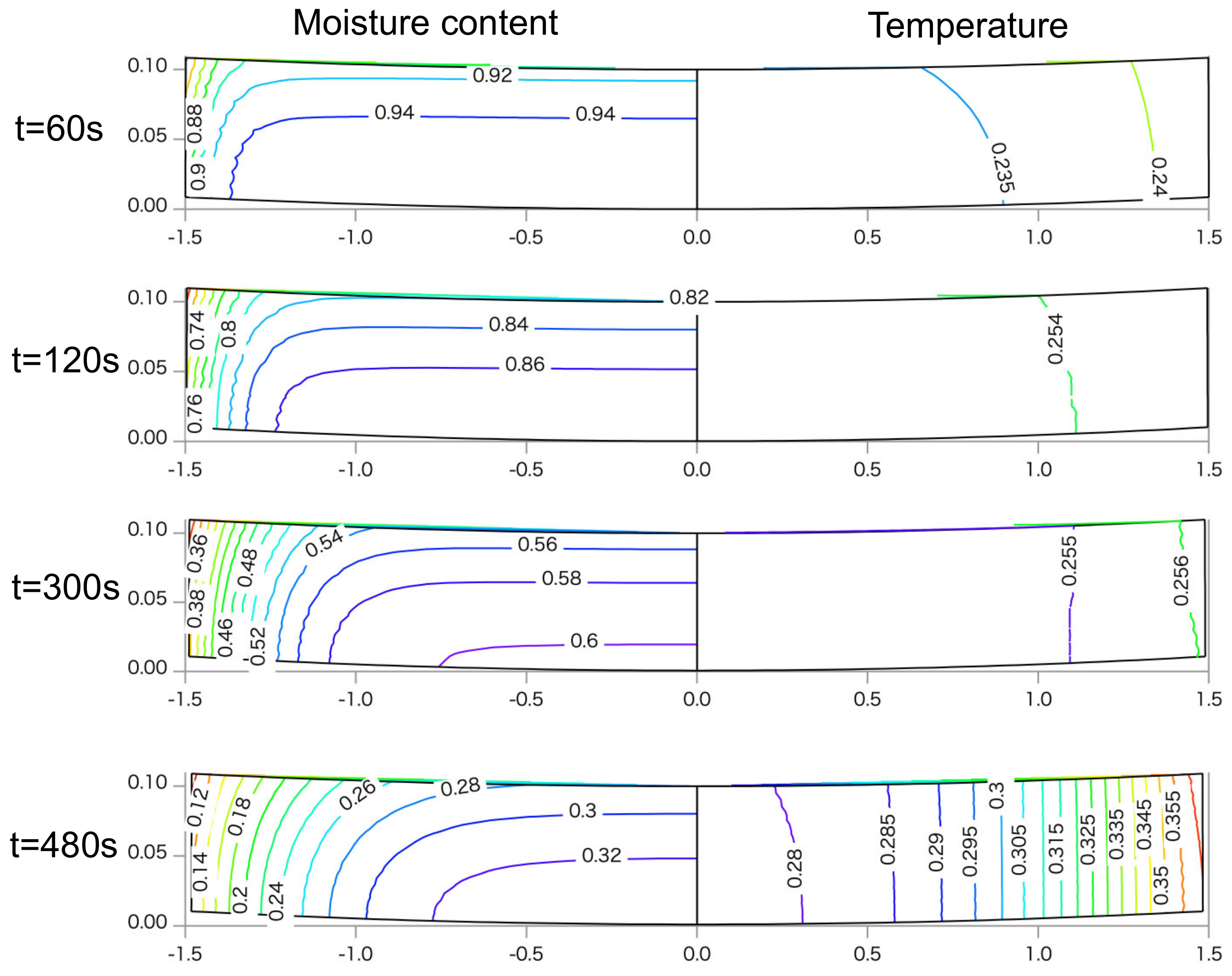
4.2. Profiles of Moisture Content and Temperature
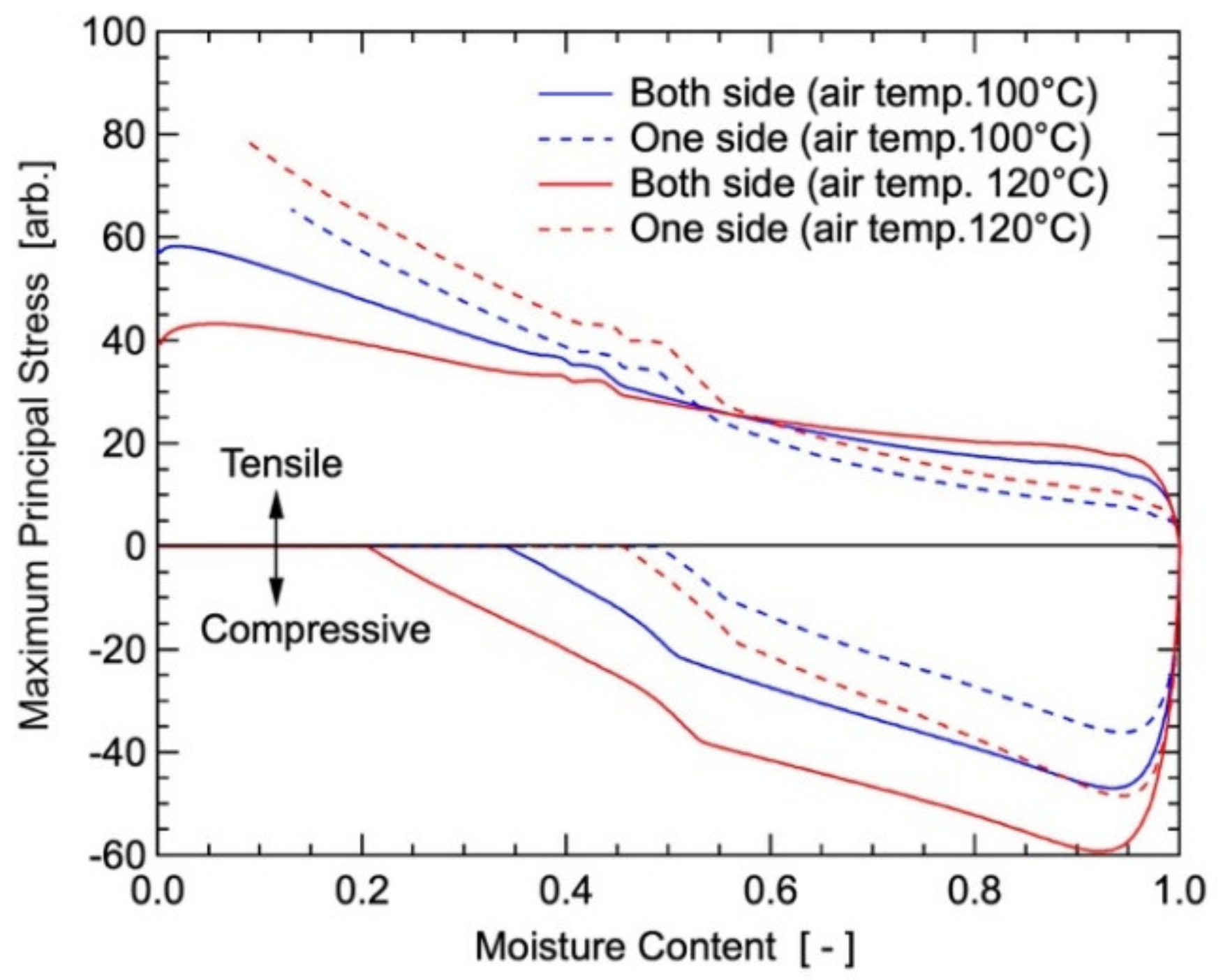
4.3. Drying-Induced Stress Formation
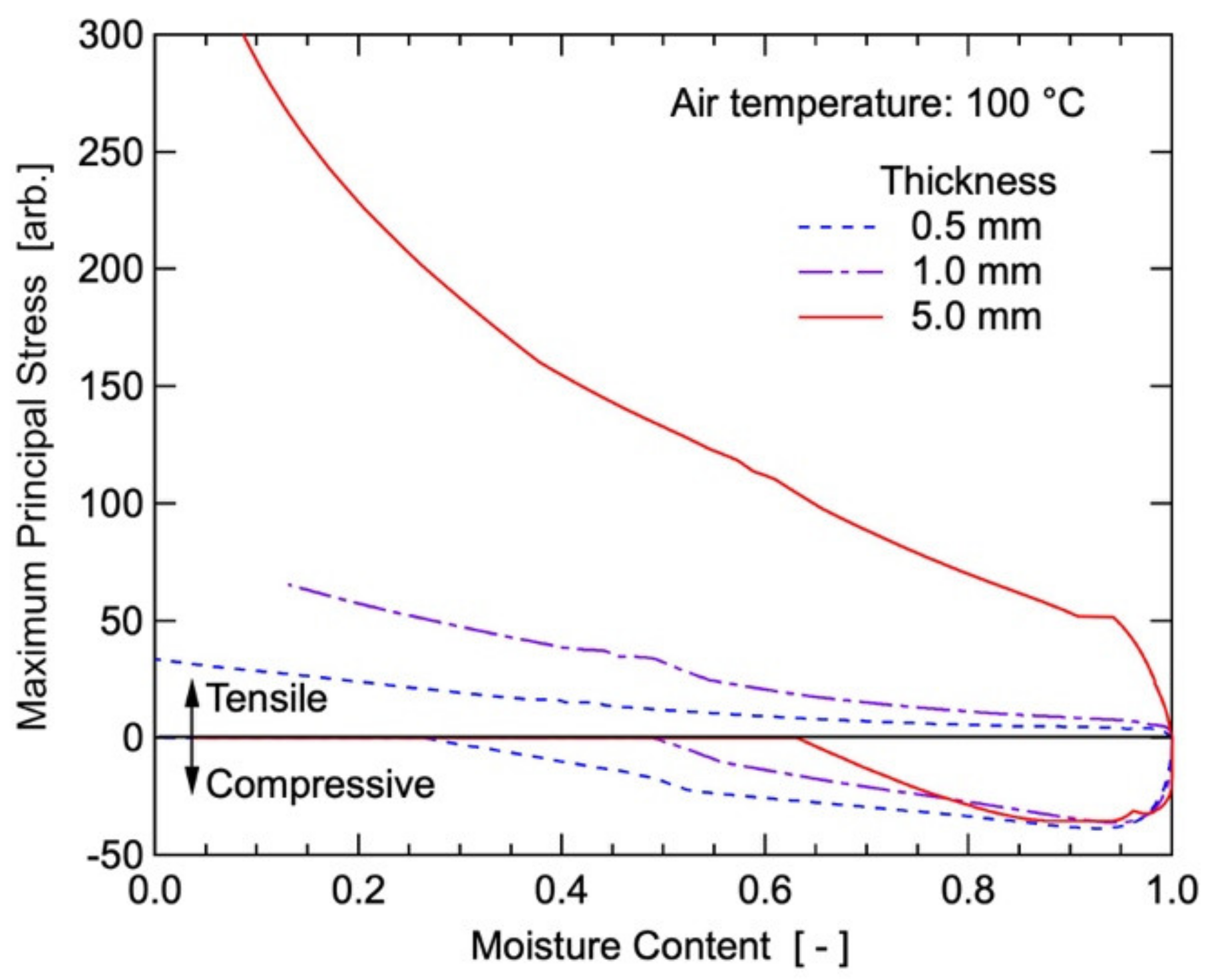
4.4. Effect of Plate Thickness on Drying-Induced Stress
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Bi | Biot number defined by Equation (8) |
| Bir | Biot number relating to radiative heat transfer defined by Equation (8) |
| c | specific heat of wet clay |
| cpa | specific heat of wet air |
| Dw | moisture diffusivity in sample |
| E(t) | relaxation modulus equivalent to Young’s modulus |
| Fi | i element of body force vector |
| G(t) | shear modulus |
| G1, G2 | moduli defined by Equations (16) and (17) |
| Gijkl | tensor correlating between stress and strain defined by Equation (15) |
| h | heat transfer coefficient |
| Ha | absolute humidity of hot air |
| He | saturated absolute humidity at surface temperature of wet sample |
| J* | moisture flux vector |
| K(t) | bulk modulus |
| k | mass transfer coefficient of moisture |
| La | latent heat of water |
| Le | Lewis number defined by Equation (8) |
| l0 | representative length |
| Nh | heat transfer parameter defined by Equation (8) |
| Nm | mass transfer parameter defined by Equation (8) |
| n | outward normal unit vector |
| q* | heat flux vector |
| Sv | volume shrinkage |
| T | temperature |
| t | time |
| Ui | i element of displacement vector |
| V | volume of sample |
| W | moisture content of dry solid base |
| Wc | critical moisture content |
| x, y, z | coordinate |
| α | thermal diffusivity of sample |
| δij | Kronecker’s delta |
| εij | ij element of strain tensor |
| ε*ij | ij element of strain tensor relating to stress generation |
| εsij | ij element of strain tensor caused by free shrinkage |
| θ | dimensionless time |
| ν | Poisson’s ratio |
| η | correction factor of drying rate defined by Equation (10) |
| λ | thermal conductivity of sample |
| ρ | density of wet clay |
| ρd | dry density excluding water in wet clay |
| σij | ij element of stress tensor |
| σr | Stefan-Boltzmann constant |
| τ | dummy value for integration |
| ϕ | blackness |
| superscripts | |
| * | dimensionless parameters |
| 0 | initial condition |
| a | hot air |
| i, j, k, l | x, y or z coordinate |
| s | surface of sample |
References
- Gong, Z.X.; Mujumdar, A.S.; Itaya, Y.; Mori, S.; Hasatani, M. Drying of Clay and Nonclay Media: Heat and Mass Transfer and Quality Aspects. Dry. Technol. 1998, 16, 1119–1152. [Google Scholar] [CrossRef]
- Itaya, Y.; Taniguchi, S.; Hasatani, M. A Numerical Study of Transient Deformation and Stress Behavior of a Clay Slab during Drying. Dry. Technol. 1997, 15, 1–21. [Google Scholar] [CrossRef]
- Itaya, Y.; Mori, S.; Hasatani, M. Effect of Intermittent Heating on Drying-Induced Strain-Stress of Molded Clay. Dry. Technol. 1999, 17, 1261–1271. [Google Scholar] [CrossRef]
- Itaya, Y.; Okouchi, K.; Mori, S. Effect of heating modes on internal strain-stress formation during drying of molded ceramics. Dry. Technol. 2001, 19, 1491–1504. [Google Scholar] [CrossRef]
- Kowalski, S.J.; Rybicki, A. Qualitative aspect of convective and microwave drying of saturated porous materials. Dry. Technol. 2004, 22, 1173–1189. [Google Scholar] [CrossRef]
- Kowalski, S.J.; Rajewska, K.; Rybicki, A. Mechanical effects in saturated capillary-porous materials during convective and microwave drying. Dry. Technol. 2004, 22, 2291–2308. [Google Scholar] [CrossRef]
- Scherer, G.W. Theory of Drying. J. Am. Ceram. Soc. 1990, 73, 3–14. [Google Scholar] [CrossRef]
- Shishido, I.; Maruyama, T.; Funaki, M.; Ohtani, S. On the Drying Mechanism of Shrinkage Material. Kagaku Kogaku Ronbunshu 1987, 13, 78–85. [Google Scholar] [CrossRef][Green Version]
- Shishido, I.; Muramatsu, T.; Ohtani, S. Local Moisture Content and Stress Distributions within Clay during Drying Shrinkage. Kagaku Kogaku Ronbunshu 1988, 14, 87–94. [Google Scholar] [CrossRef][Green Version]
- Kowalski, S.J.; Rybicki, A. Thermo-hydro-mechanical Aspect of Drying. In Handbook of Industrial Drying, 4th ed.; CRC Press: Boca Raton, FL, USA, 2014; pp. 1239–1260. [Google Scholar]
- Zhang, J.; Gao, Y.; Wang, Z. Evaluation of Shrinkage Induced Cracking Performance of Low Shrinkage Engineered Cementitious Composite by Ring Tests. Compos. Part B Eng. 2013, 52, 21–29. [Google Scholar] [CrossRef]
- Heydari, M.; Khalili, K.; Ahmadi-Brooghani, S.Y. More Comprehensive 3D Modeling of Clay-Like Material Drying. AIChE J. 2018, 64, 1469–1478. [Google Scholar] [CrossRef]
- Holmes, D.M.; Vasant Kumar, R.; Clegg, W.J. Cracking during Lateral Drying of Alumina Suspension. J. Am. Ceram. Soc. 2006, 89, 1908–1913. [Google Scholar] [CrossRef]
- Holmes, D.M.; Tegeler, F.; Clegg, W.J. Stresses and Strains in Colloidal Films during Lateral Drying. J. Eur. Ceram. Soc. 2008, 28, 1381–1387. [Google Scholar] [CrossRef]
- Lampenscherf, S.; Pompe, W. Mechanical Behavior of Granular Ceramic Film during Drying. Z. Met. Mater. Res. Adv. Tech. 1998, 89, 96–105. [Google Scholar]
- Singh, K.B.; Tirumkudulu, M.S. Cracking in Drying Colloidal Films. Phys. Rev. Lett. 2007, 98, 218302. [Google Scholar] [CrossRef] [PubMed]
- Raisul Islam, M.; Ho, J.C.; Mujumdar, A.S. Simulation of liquid diffusion-controlled drying of shrinking thin slabs subjected to multiple heat sources. Dry. Technol. 2003, 21, 413–438. [Google Scholar] [CrossRef]





| Terms | Run 1 | Run 2 | Run 3 | Run 4 | Run 5 |
|---|---|---|---|---|---|
| Drying mode | One side drying | Both sides drying | |||
| Hot air temperature [°C] | 100 | 100 | 120 | 100 | 120 |
| Sample thickness [mm] | 1.0 | 0.5 | 1.0 | 1.0 | 1.0 |
| Sample width [mm] | 10.0 | 10.0 | 10.0 | 10.0 | 10.0 |
| Sample length [mm] | 30.0 | 30.0 | 30.0 | 30.0 | 30.0 |
| Initial sample weight [g] | 0.622 | 0.295 | 0.673 | 0.640 | 0.667 |
| Initial sample temperature [°C] | 10.0 | 13.2 | 7.4 | 6.6 | 7.2 |
| Sample moisture content [kg-water/kg-dry solid] | 0.359 | 0.316 | 0.417 | 0.420 | 0.381 |
| Air flow rate at atmospheric temperature [L/min] | 50 | 50 | 50 | 50 | 50 |
| Air humidity [kg-moisture/kg-dry air] | 1.8 × 10−3 | 5.9 × 10−3 | 1.8 × 10−3 | 1.8 × 10−3 | 1.8 × 10−3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Itaya, Y.; Hanai, H.; Kobayashi, N.; Nakagawa, T. Drying-Induced Strain-Stress and Deformation of Thin Ceramic Plate. ChemEngineering 2020, 4, 9. https://doi.org/10.3390/chemengineering4010009
Itaya Y, Hanai H, Kobayashi N, Nakagawa T. Drying-Induced Strain-Stress and Deformation of Thin Ceramic Plate. ChemEngineering. 2020; 4(1):9. https://doi.org/10.3390/chemengineering4010009
Chicago/Turabian StyleItaya, Yoshinori, Hiroya Hanai, Nobusuke Kobayashi, and Tsuguhiko Nakagawa. 2020. "Drying-Induced Strain-Stress and Deformation of Thin Ceramic Plate" ChemEngineering 4, no. 1: 9. https://doi.org/10.3390/chemengineering4010009
APA StyleItaya, Y., Hanai, H., Kobayashi, N., & Nakagawa, T. (2020). Drying-Induced Strain-Stress and Deformation of Thin Ceramic Plate. ChemEngineering, 4(1), 9. https://doi.org/10.3390/chemengineering4010009





