Heterogeneous Phases Reaction Equilibrium in an Oxy-Thermal Carbide Furnace
Abstract
:1. Introduction
2. Basic Thermodynamic Behavior of the Chemical Reaction System
2.1. pVT Behavior of the Gas Phase
2.2. Thermodynamic Equilibrium of the Reaction System
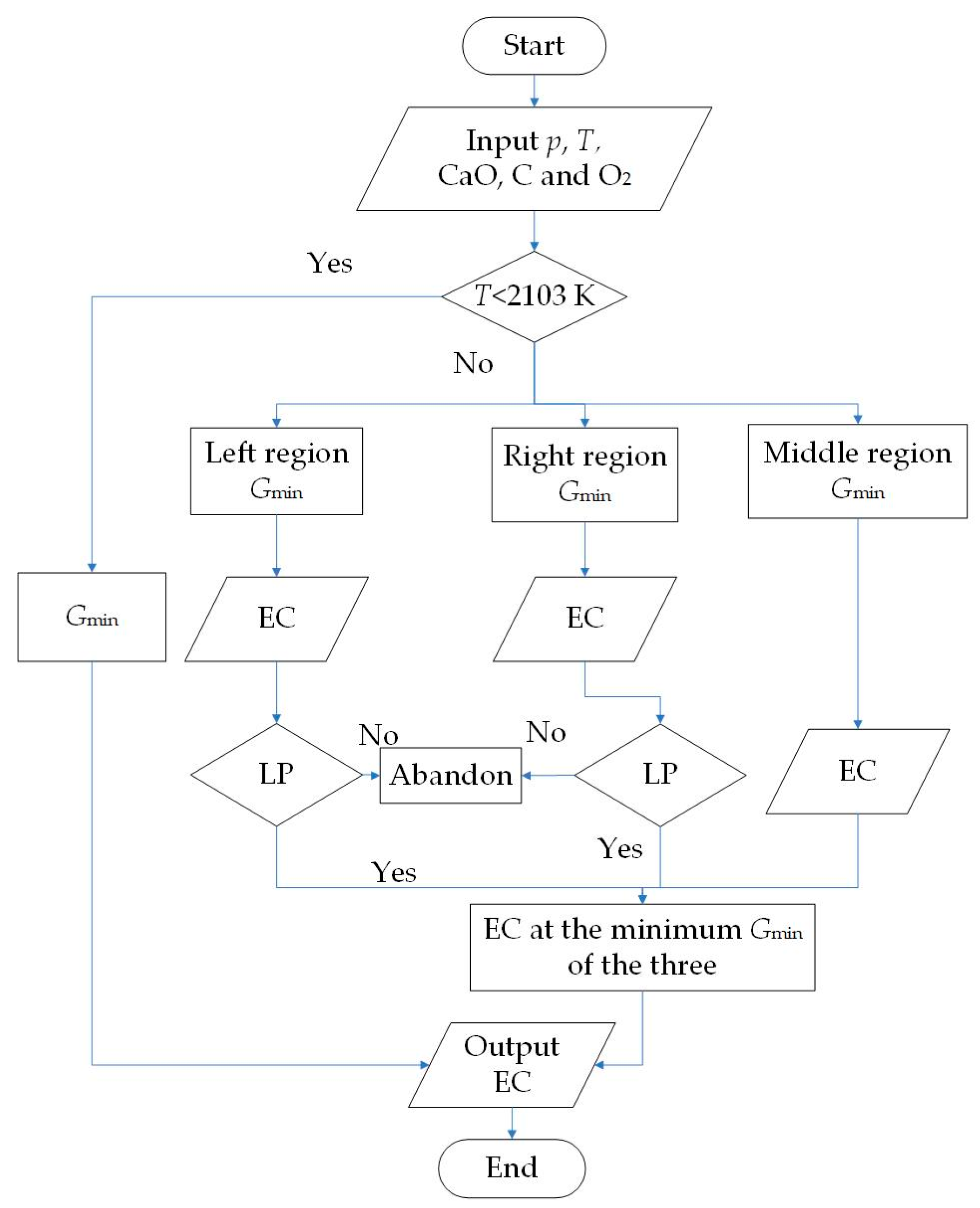
3. Equilibrium Composition in the Oxy-Thermal Carbide Furnace
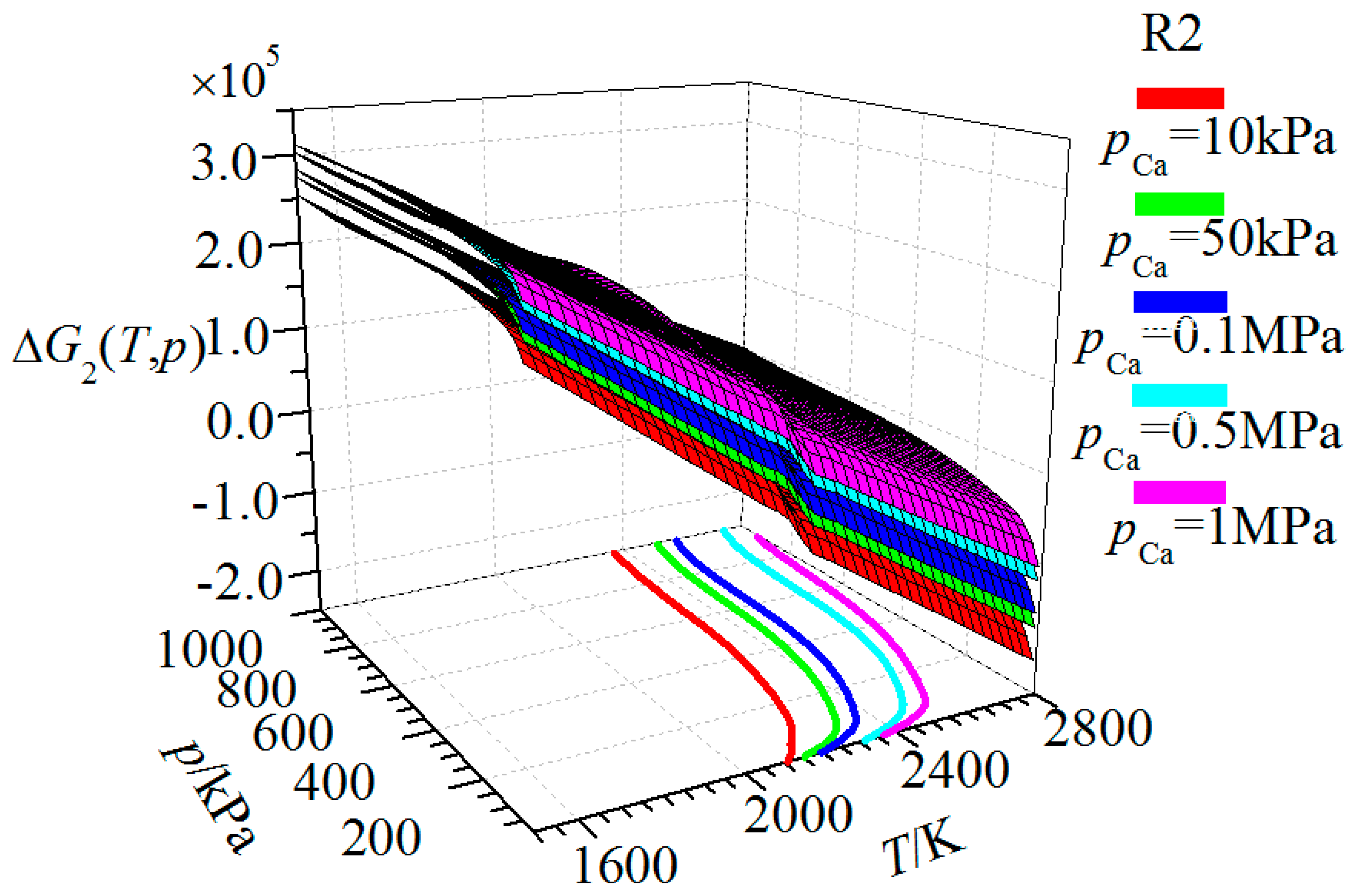
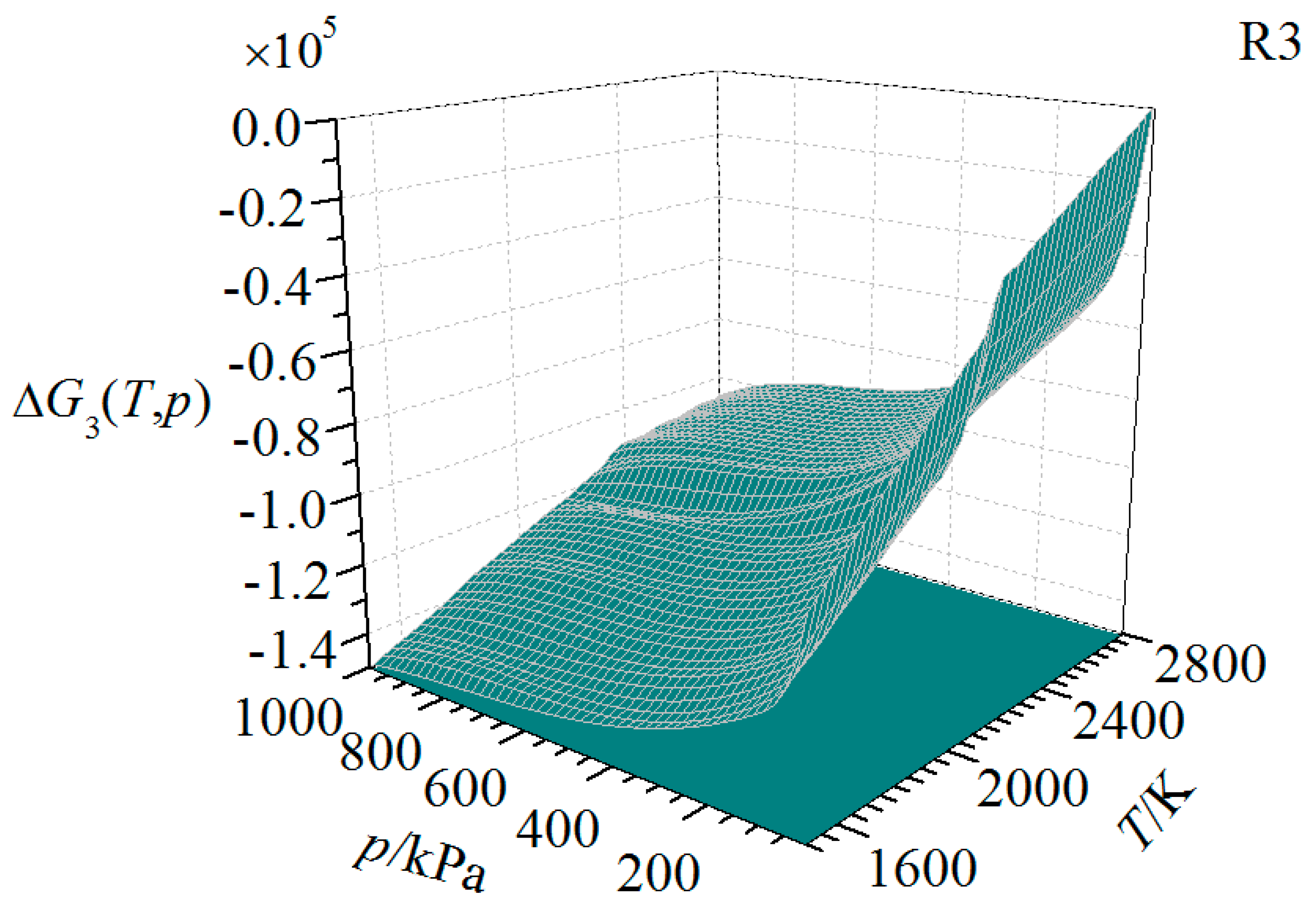
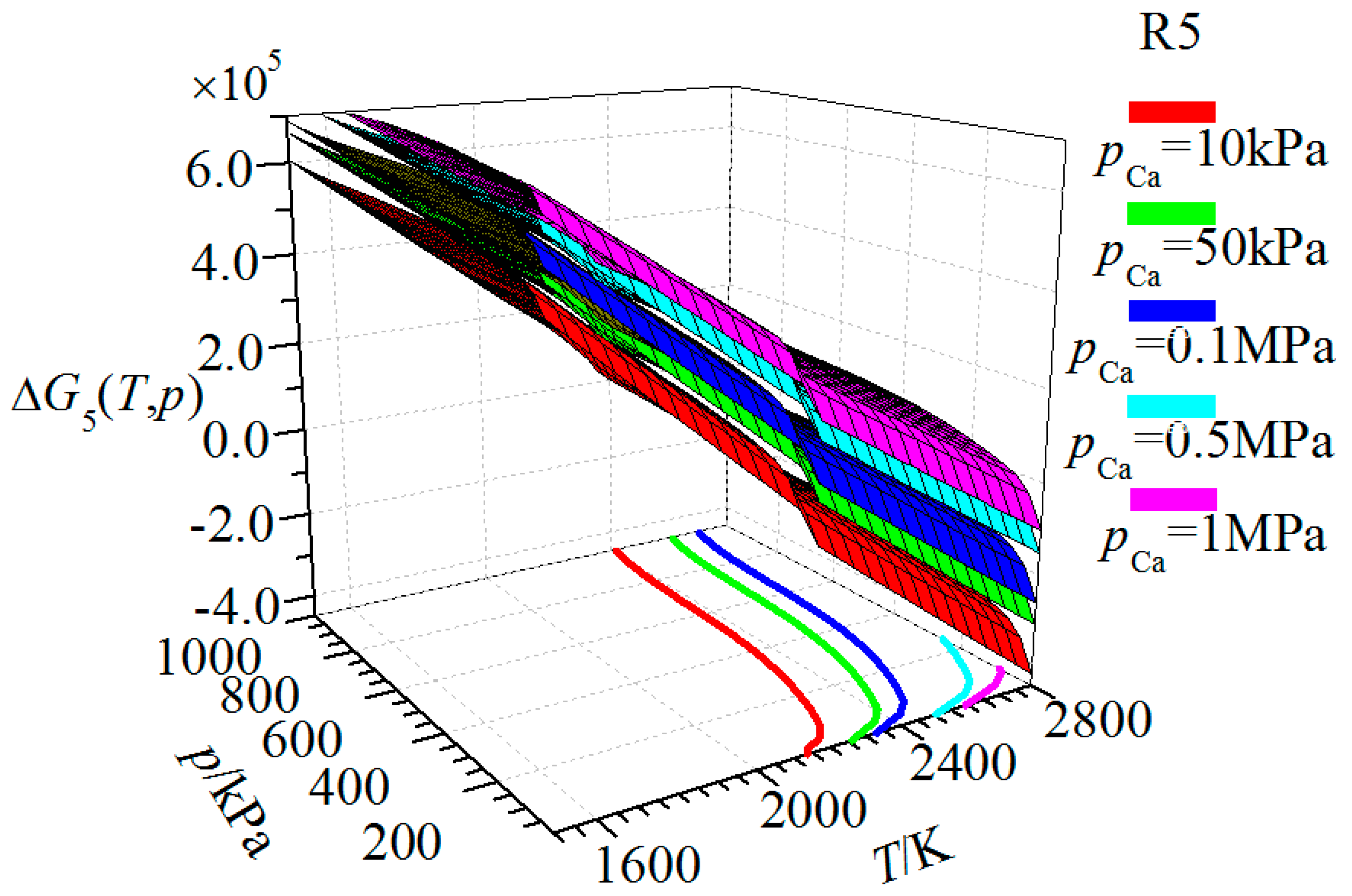
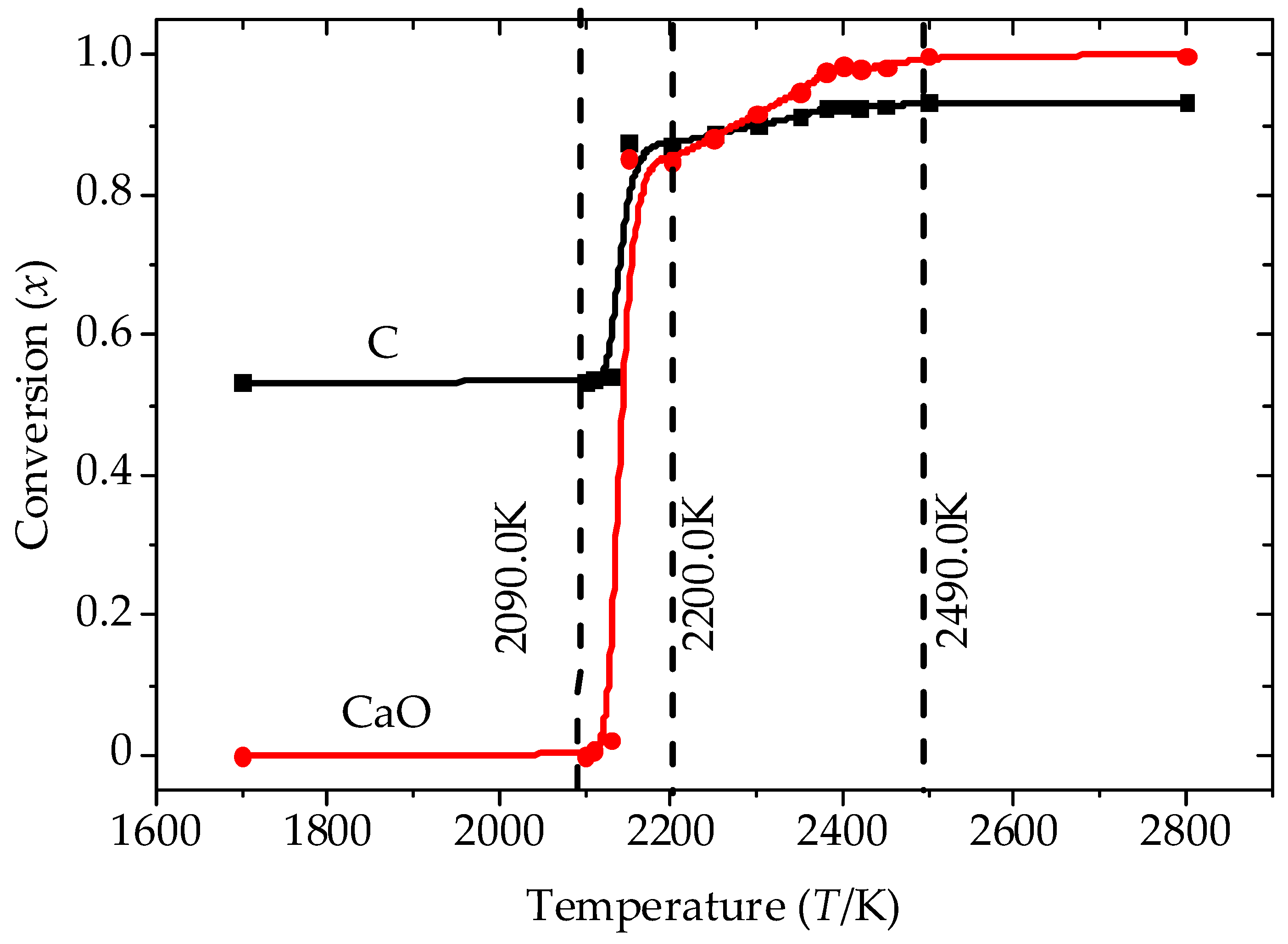
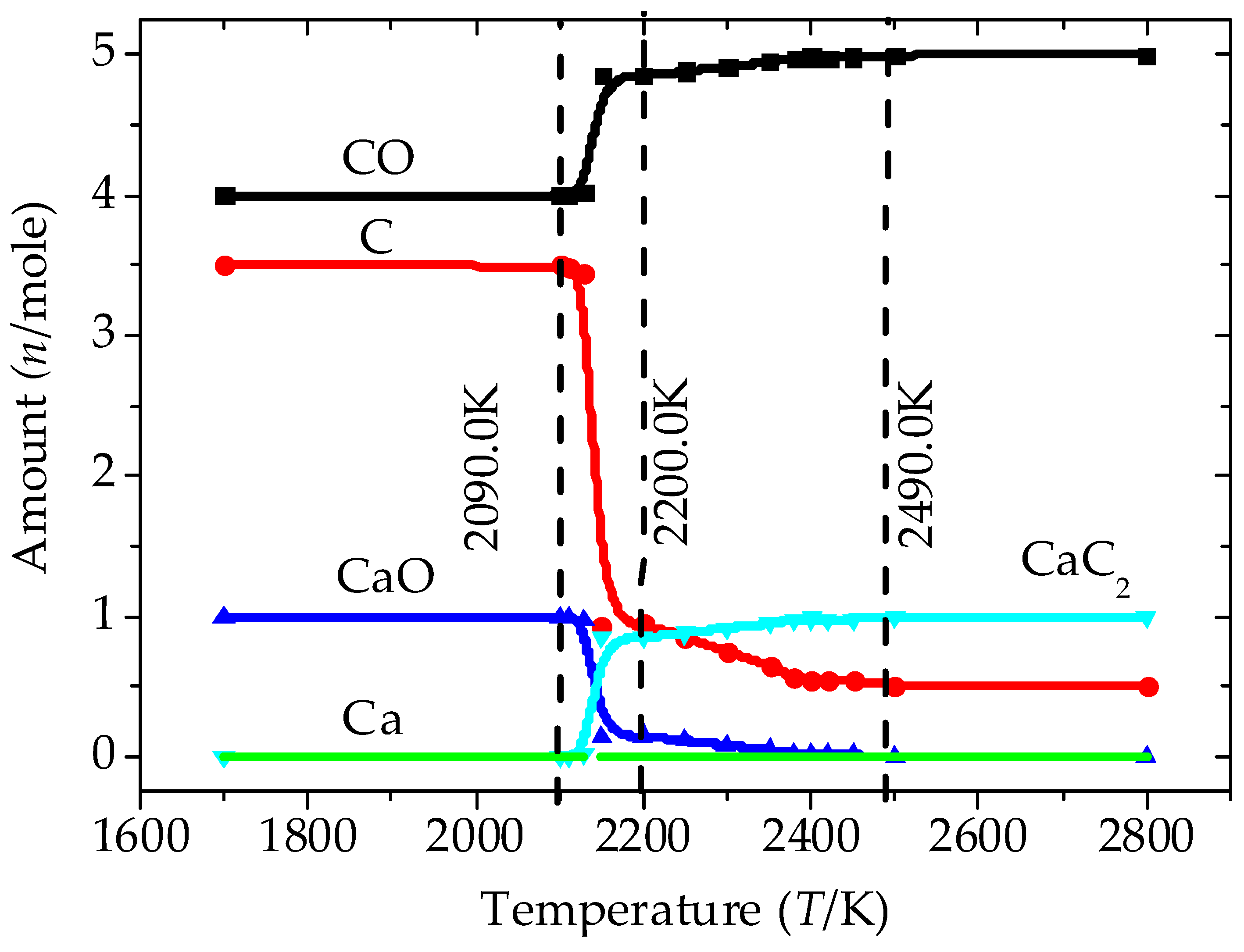
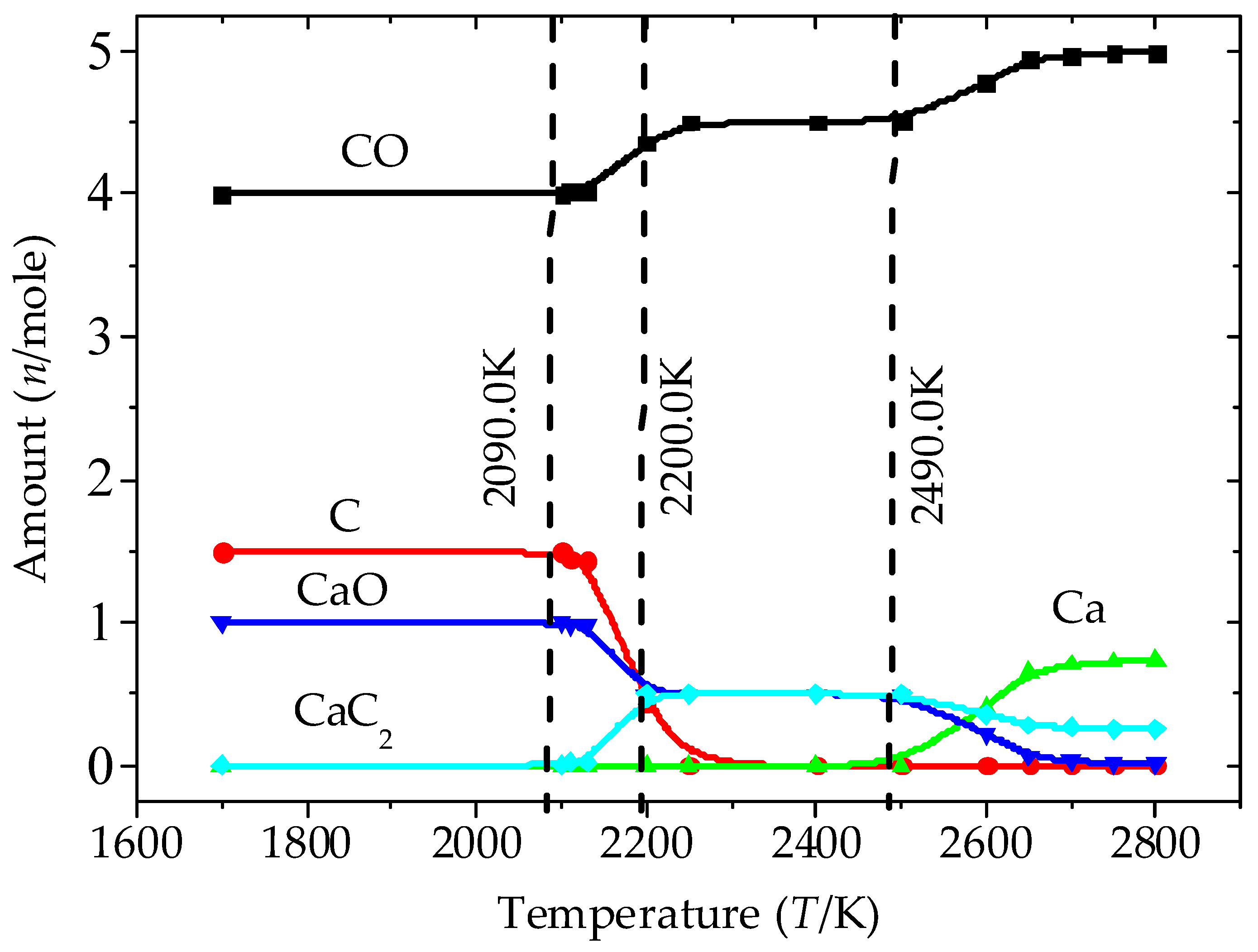
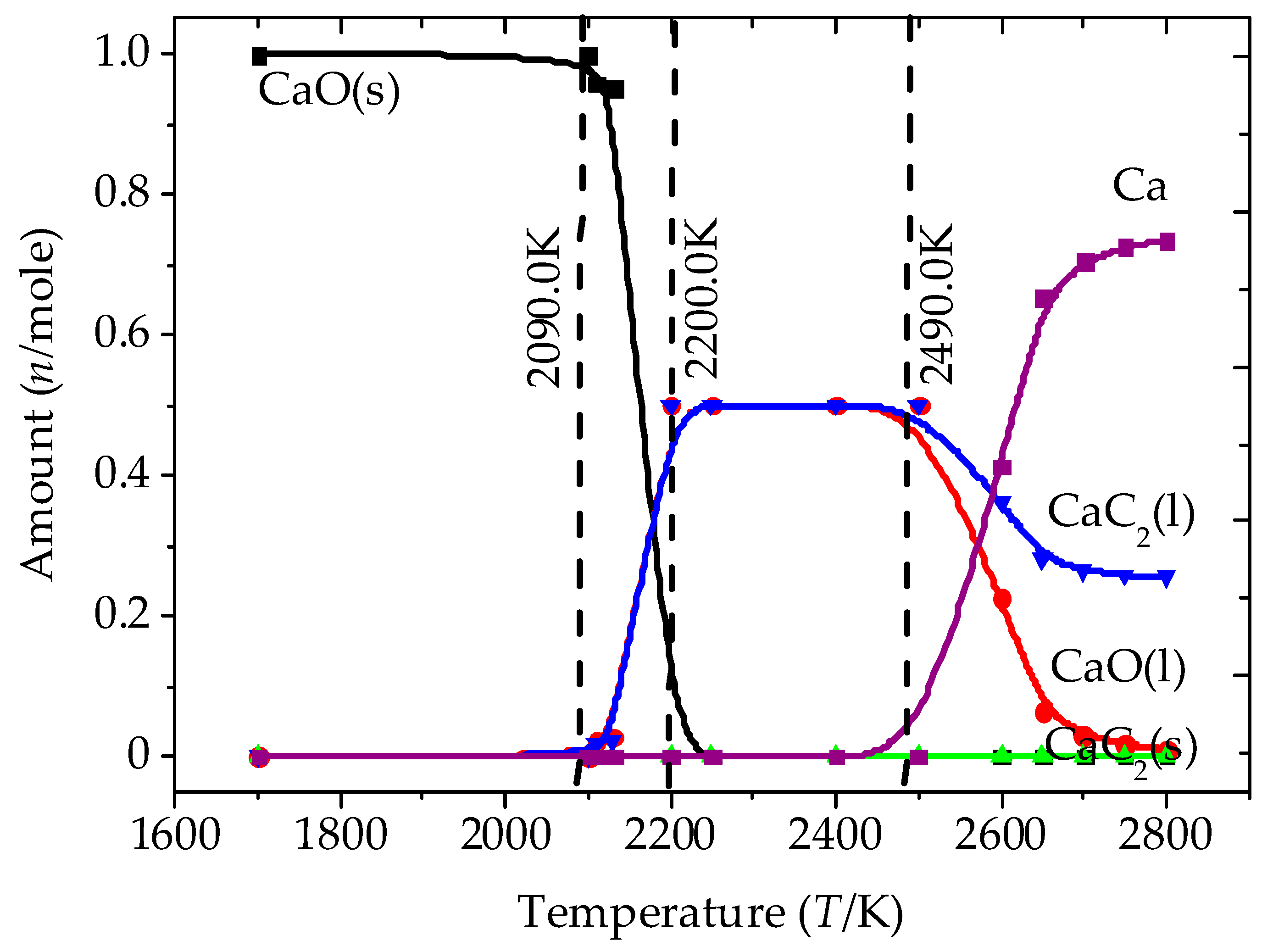
3.1. Analysis of the Equilibrium Composition under Conditions of Excess C
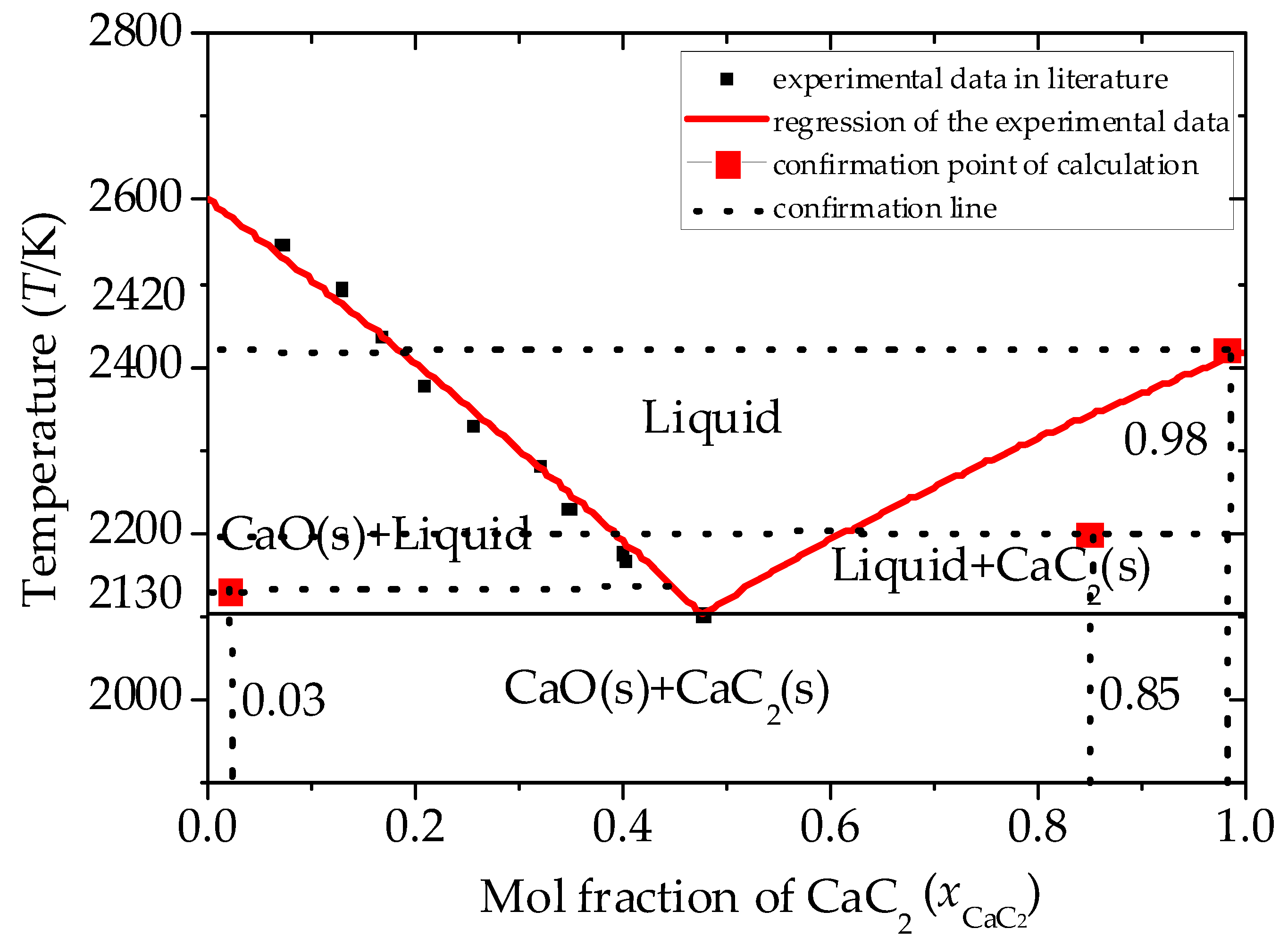
3.2. Analysis of the Equilibrium Composition at a Condition of Limited C
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Szmant, H. Organic Building Blocks of the Chemical Industry; John Wiley & Sons. Inc.: Hoboken, NJ, USA, 1989; pp. 255–256. [Google Scholar]
- Sun, W. Reviews of the calcium carbide industry in 2012 and prospect in 2013. Econ. Anal. China’s Pet. Chem. Ind. 2013, 4, 29–31. [Google Scholar]
- Erasmus, L. The application of plasma-arc technology for the production of calcium carbide. In Proceedings of the Electric Furnace Conference Proceedings, Toronto, ON, Canada, 12–15 November 1991; pp. 293–298. [Google Scholar]
- Guo, J.; Zheng, D.X. Thermodynamic analysis of low-rank-coal-based oxygen-thermal acetylene manufacturing process system. Ind. Eng. Chem. Res. 2012, 51, 13414–13422. [Google Scholar] [CrossRef]
- Mi, Y.; Zheng, D.X.; Guo, J.; Chen, X.H.; Jin, P. Assessment of energy use and carbon footprint for low-rank coal-based oxygen-thermal and electro-thermal calcium carbide. Fuel Process. Technol. 2014, 119, 305–315. [Google Scholar] [CrossRef]
- Tagawa, H.; Sugawara, H. The kinetics of the formation of calcium carbide in a solid-solid reaction. J. Ceram. Chem. Jpn. 1962, 35, 1276–1279. [Google Scholar] [CrossRef]
- Muller, M. Structure, properties and reactions of CaO in burnt lime. Part 3. Composite reactions of CaO and C in solid and liquid state. Scand. J. Metall. 1990, 19, 210–217. [Google Scholar]
- EI-Nass, M.; Munz, R. Production of calcium carbide in a plasma-jet fluid bed reactor. In Proceedings of the ISPC-12, Minneapolis, MN, USA, 21–25 August 1995; pp. 613–618. [Google Scholar]
- EI-Nass, M.; Munz, R.; Ajersch, F. Solid-phase synthesis of calcium carbide in a plasma reactor. Plasma Chem. Plasma Process. 1998, 18, 409–427. [Google Scholar] [CrossRef]
- Rai, H.; Gregory, N. The time dependence of effusion cell steady-state pressure of carbon monoxide and calcium vapors generated by the interaction of calcium oxide and graphite. J. Phys. Chem. 1970, 74, 529–534. [Google Scholar] [CrossRef]
- Brookes, C.; Gall, E.; Hudgins, R. A model for the formation of calcium carbide in solid pellets. Can. J. Chem. Eng. 1975, 53, 527–533. [Google Scholar] [CrossRef]
- Wiik, K.; Raaness, O.; Olsen, S. Formation of calcium from calcium vapor and carbon. Scand. J. Metall. 1983, 13, 1347–1354. [Google Scholar]
- Kim, S.; Raymond, F.; Baddour, B. CaC2 Production from CaO and coal or hydrocarbons in a rotating-arc reactor. Ind. Eng. Chem. Process Des. Dev. 1979, 18, 323–328. [Google Scholar] [CrossRef]
- Wang, J.; Kayoko, M.; Takayuki, T. High-temperature interactions between coal char and mixtures of calcium oxide, quartz and kaolinite. Energy Fuels 2001, 15, 1145–1152. [Google Scholar] [CrossRef]
- Thoburn, W.; Pidgeon, L. Differential thermal analysis of calcium carbide formation. Can. Metall. Q. 1965, 4, 205–217. [Google Scholar] [CrossRef]
- Li, G.D.; Liu, Q.Y.; Liu, Z.Y. Production of calcium carbide from fine biochars. Angew. Chem. Int. Ed. 2010, 49, 8480–8483. [Google Scholar] [CrossRef] [PubMed]
- Muftah, H. Synthesis of Calcium Carbide in a Plasma Spout Fluid Bed. Ph.D. Thesis, McGill University, Montréal, QC, Canada, 1996. [Google Scholar]
- Guo, J.; Zheng, D.X.; Chen, X.H.; Mi, Y.; Liu, Z.Y. Chemical reaction equilibrium behaviors of an oxy-thermal carbide furnace reaction system. Ind. Eng. Chem. Res. 2013, 52, 17773–17780. [Google Scholar] [CrossRef]
- Stals, J.; Peters, C.; Diepen, G. Measurements and calculation of the three-phase equilibrium (solid compound + liquid + gas) in the binary (sulfur dioxide + p-toluidine) where the compound in liquid and gas is dissociated into its components. J. Chem. Thermodyn. 1979, 11, 1107–1112. [Google Scholar] [CrossRef]
- Ruff, O.; Foerster, E. Calcium carbide, its formation and decomposition. Z. Anorg. Allg. Chem. 1923, 131, 321–347. [Google Scholar] [CrossRef]
- Flusin, G.; Aall, C. Sur l’étude du système CaC2-CaO. Compt. Rend. 1935, 201, 451–453. [Google Scholar]
- Li, G.D.; Liu, Q.Y.; Liu, Z.Y. Kinetic behaviors of CaC2 production from coke and CaO. Ind. Eng. Chem. Res. 2013, 53, 527–535. [Google Scholar] [CrossRef]
- Kameyama, N. Electrochemistry: Theory and Applications, Vol. III-2; Maruzen: Tokyo, Japan, 1956; pp. 134–141. [Google Scholar]
- Juza, R.; Schuster, H. The phase diagram of the calcium oxide-calcium carbide system. Z. Anorg. Allg. Chem. 1961, 311, 62–75. [Google Scholar] [CrossRef]
- Ji, L.M.; Liu, Q.Y.; Liu, Z.Y. Thermodynamic analysis of calcium carbide production. Ind. Eng. Chem. Res. 2014, 53, 2537–2543. [Google Scholar] [CrossRef]
- Li, G.D.; Liu, Q.Y.; Liu, Z.Y. CaC2 production from pulverized coke and CaO at low temperature – influence of minerals in coal-derived coke. Ind. Eng. Chem. Res. 2011, 51, 10748–10754. [Google Scholar] [CrossRef]
- Smith, J.M.; Van Ness, H.C.; Abbott, M.M. Introduction to Chemical Engineering Thermodynamics, 6th ed.; McGraw-Hill Co. Inc.: New York, NY, USA, 2001; pp. 390–476. [Google Scholar]
- Peng, D.Y.; Robinson, D.B. A new two-constant equation of state. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Aspen Plus. Aspen Plus IGCC Mode; Aspen Technology: Bedford, MA, USA, 2008. [Google Scholar]
- Binnewies, M.; Milke, E. Thermodynamical Data of Elements and Compounds; Wiley-Vch Verlag GmbH: Weinheim, Germany, 2002. [Google Scholar]
- Barin, I. Thermochemical Data of Pure Substances, 3rd ed.; Wiley-Vch Verlag GmbH: Weinheim, Germany, 1995; pp. 422–441. [Google Scholar]
- Healy, G. The Calculation of an internal energy balance in the smelting of Calcium Carbide. J. S. Afr. Inst. Min. Metall. 1995, 9, 225–232. [Google Scholar]
- Lindberg, D.; Chartrand, P. Thermodynamic evaluation and optimization of the (Ca + C + O + S) system. J. Chem. Thermodyn. 2009, 41, 1111–1124. [Google Scholar] [CrossRef]
- Vonka, P.; Leitner, J. Calculation of chemical equilibrium in complex system: System restrictions. Collect. Czech. Chem. Commun. 2000, 65, 1443–1452. [Google Scholar] [CrossRef]
- Aljarrha, M.; Medraj, M. Thermsodynamic assessment of the phase equilibria in the Al-Ca-Sr system using the modified quasichemical model. J. Chem. Thermodyn. 2008, 40, 724–734. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are available from the authors. |
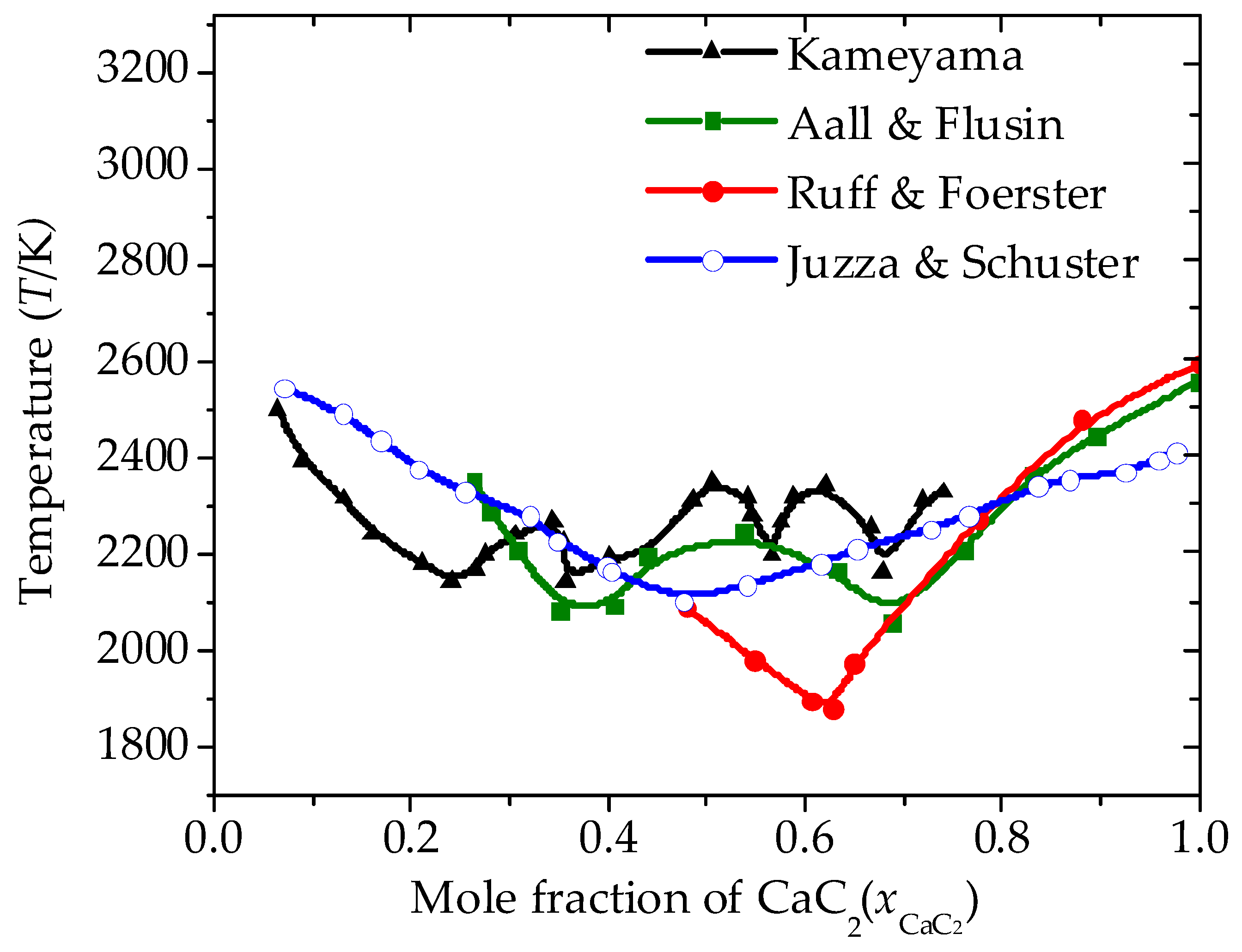
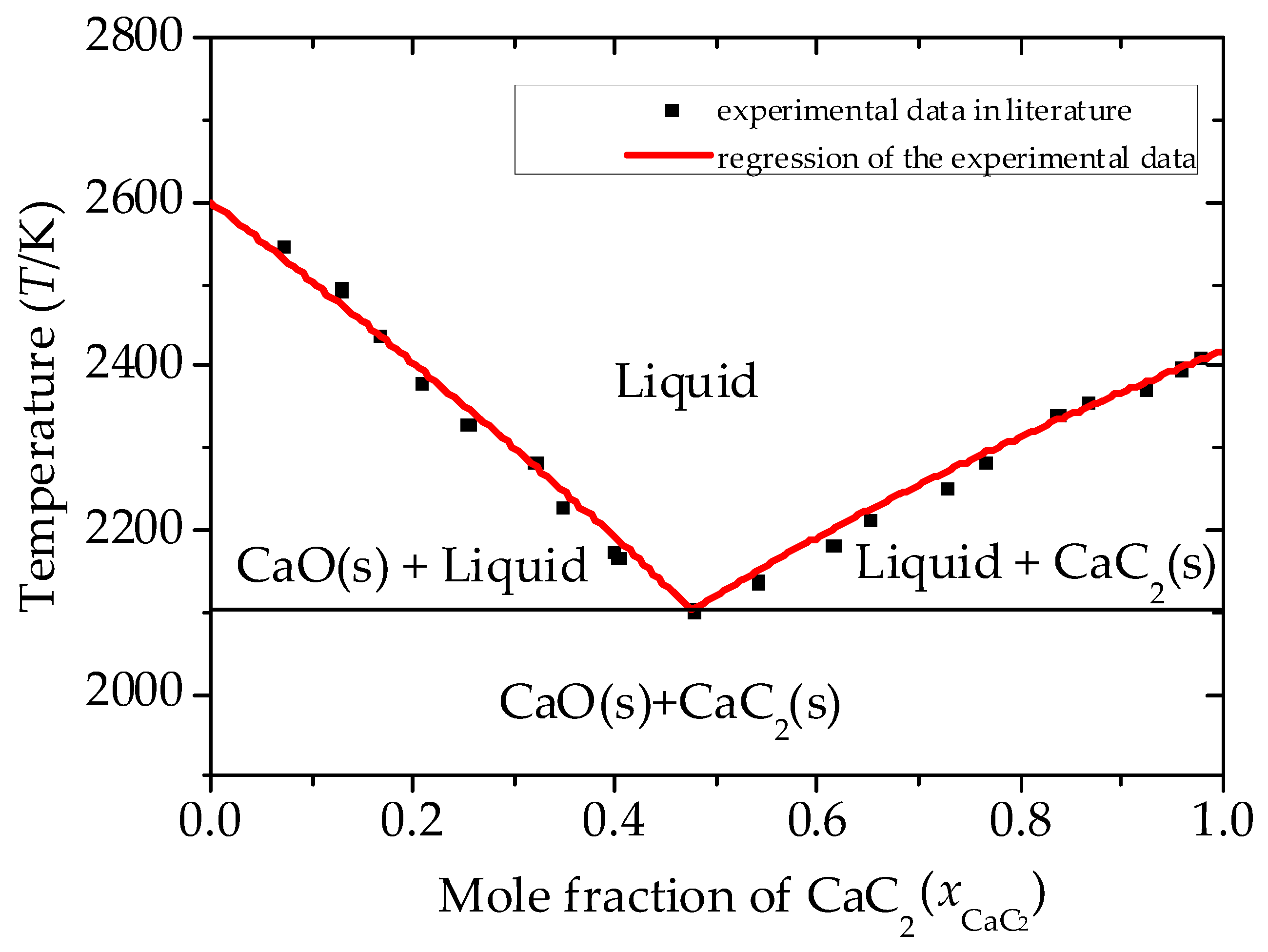
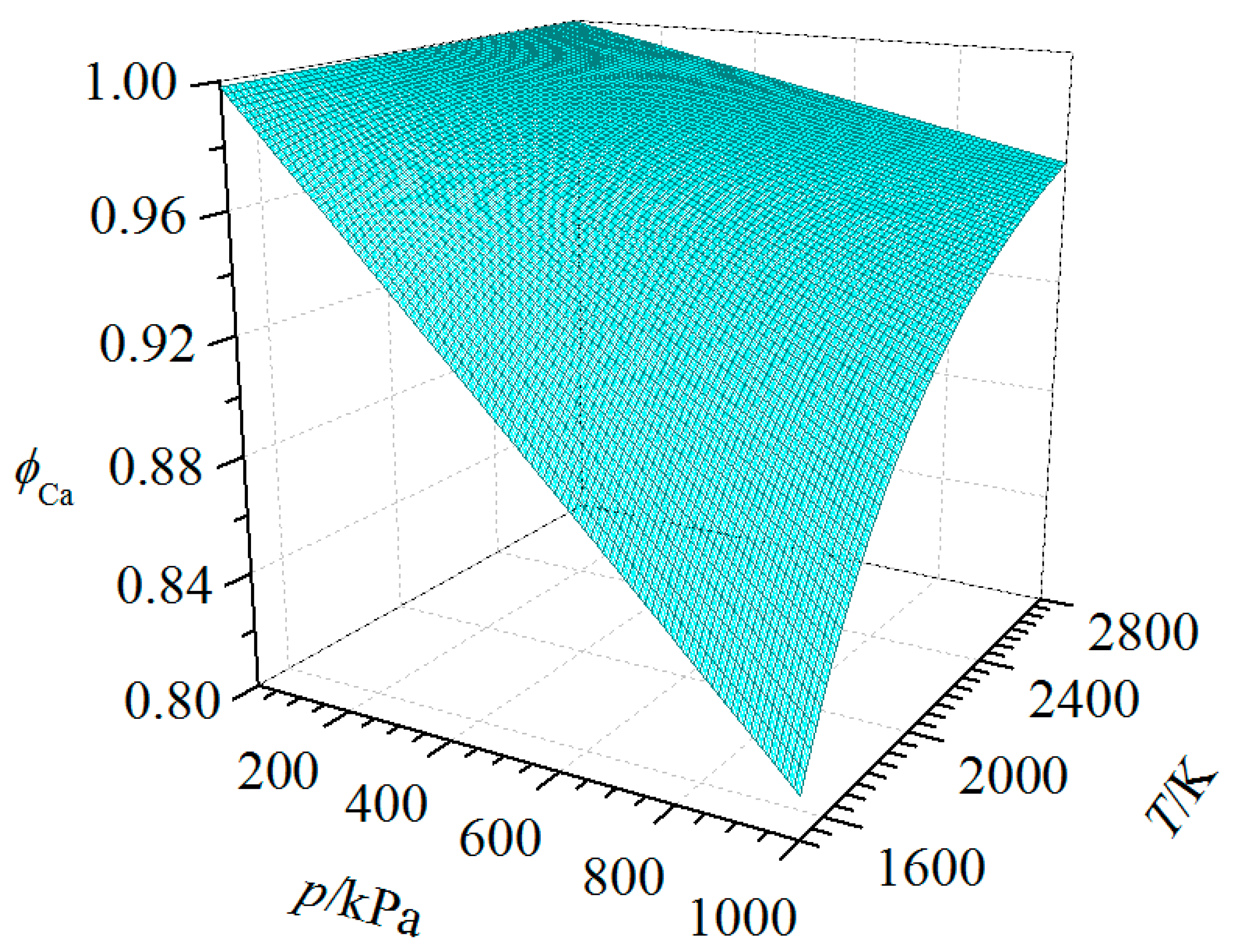
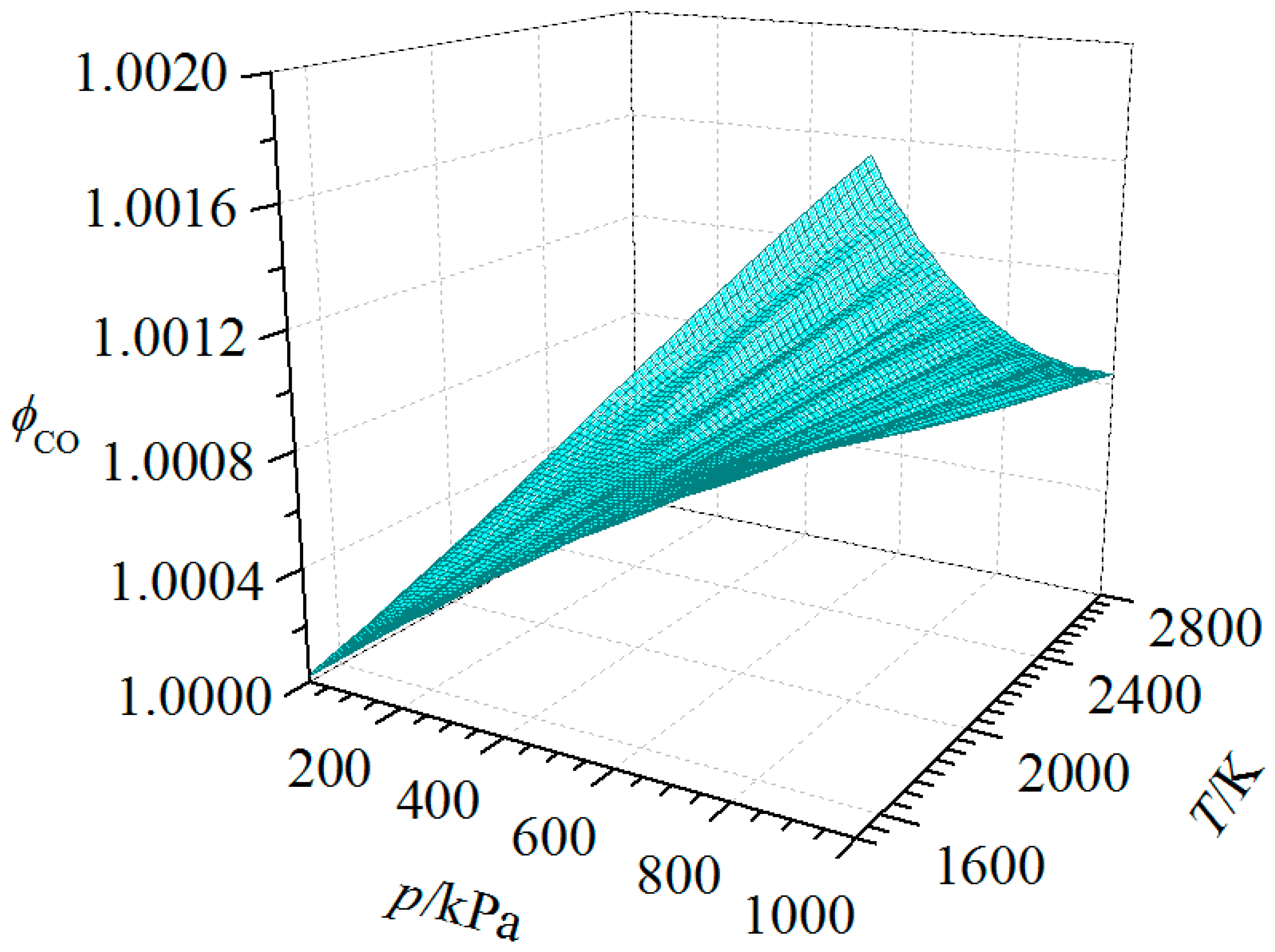





| Substance | T | |||
|---|---|---|---|---|
| K | J·mol−1 | J·mol−1·K−1 | J·mol−1·K−1 | |
| C (graphite) | 298.15–1100 | 0 | 5.74 | 0.084 + 0.038911 × T − 146,400 × T−2 − 0.000017364 × T2 |
| 1100–4073 | 24.435 + 0.000418 × T − 3,163,100 × T−2 | |||
| O2 (g) | 298.15–3000 | 0 | 205.04 | 29.957 + 0.00418 × T − 167,400 × T−2 |
| CO (g) | 298.15–2800 | −110,541 | 197.527 | 28.409 + 0.0041 × T − 46,000 × T−2 |
| Ca (g) | 298.15–2800 | −178,146 | 154.674 | 20.832 |
| CaO (s) | 298.15–2845 | −635,090 | 37.75 | 58.7912 − 1,147,146 × T−2 − 133.904 × T−0.5 + 102,978,787.9 × T−3 |
| CaO (l) | 298.15–2845 | −555,594 | 65.69 | 58.7912 − 1,147,146 × T−2 − 133.904 × T−0.5 + 102,978,787.9 × T−3 |
| CaC2 (s) | 298.15–1275 | −53,030.3 | 79.1553 | 64.4336 + 0.008368 × T |
| 1275–3000 | 75.1028 | |||
| CaC2 (l) | 298.15–3000 | 3802.2 | 96.825 | 75.1028 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, W.; Chen, X.; Wang, Q.; Gao, M.; Zheng, D.; Mai, Y.; Hu, W. Heterogeneous Phases Reaction Equilibrium in an Oxy-Thermal Carbide Furnace. ChemEngineering 2020, 4, 2. https://doi.org/10.3390/chemengineering4010002
Xiong W, Chen X, Wang Q, Gao M, Zheng D, Mai Y, Hu W. Heterogeneous Phases Reaction Equilibrium in an Oxy-Thermal Carbide Furnace. ChemEngineering. 2020; 4(1):2. https://doi.org/10.3390/chemengineering4010002
Chicago/Turabian StyleXiong, Wenjie, Xiaohui Chen, Quanyong Wang, Min Gao, Danxing Zheng, Yuliang Mai, and Wei Hu. 2020. "Heterogeneous Phases Reaction Equilibrium in an Oxy-Thermal Carbide Furnace" ChemEngineering 4, no. 1: 2. https://doi.org/10.3390/chemengineering4010002
APA StyleXiong, W., Chen, X., Wang, Q., Gao, M., Zheng, D., Mai, Y., & Hu, W. (2020). Heterogeneous Phases Reaction Equilibrium in an Oxy-Thermal Carbide Furnace. ChemEngineering, 4(1), 2. https://doi.org/10.3390/chemengineering4010002




