Drying Technology Assisted by Nonthermal Pulsed Filamentary Microplasma Treatment: Theory and Practice
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation
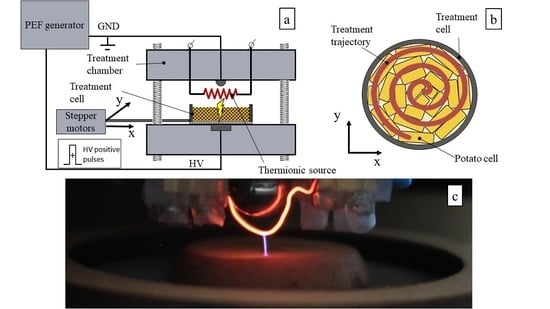
2.2. Nonthermal Pulsed Filamentary Microplasma Treatment Assisted by TE
2.3. Drying
2.4. Statistical Analysis
3. Theory
3.1. Problem Definition
3.2. Boundary Conditions
3.3. Finite Element Formulation
4. Results and Discussion
4.1. Solution Method of a Coupled System of the Differential Equations
- Heat conductivity coefficient = 0.6 j/m·K·s, which can be defined from the literature [22];
- Heat capacity J/kg·K [24];
- Air capacity = 0.8 × 10−3 kg/kg·K [22];
- Thermogradient coefficient δ for food products can be defined in the range of δ = 0.01–0.02 °M /K [15];
- Dry body density = 210 kg/m3 [25];
- Latent heat λ is a thermodynamic constant and has a value of λ = 2258 kJ/kg for water evaporation during drying [26];
- The m-basic moisture content is depending on relative humidity according to tables [25].
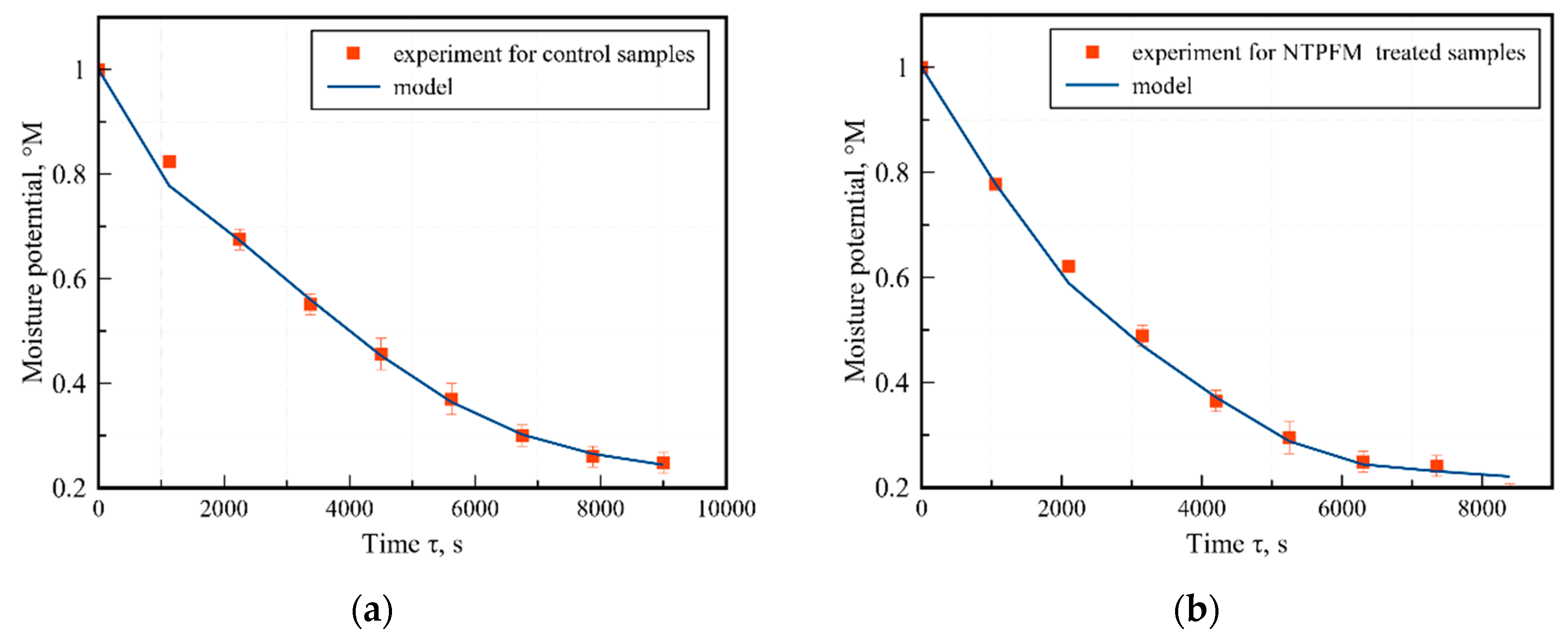
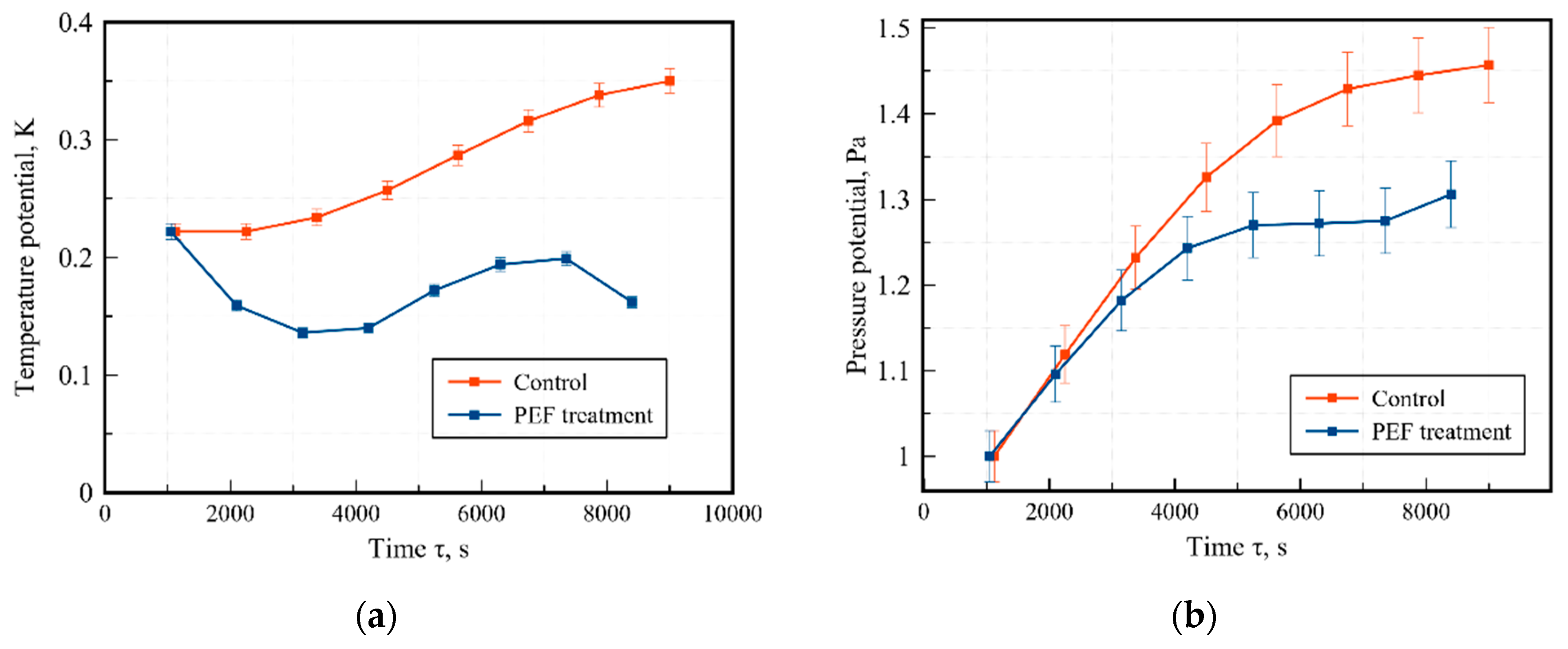
4.2. Experimental Results
4.3. Results of Numerical Modelling
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Traffano-Schiffo, M.V.; Tylewicz, U.; Castro-Giraldez, M.; Fito, P.J.; Ragni, L.; Dalla Rosa, M. Effect of pulsed electric fields pre-treatment on mass transport during the osmotic dehydration of organic kiwifruit. Innov. Food Sci. Emerg. Technol. 2016, 38, 243–251. [Google Scholar] [CrossRef]
- Smith, K.C.; Weaver, J.C. Electrodiffusion of molecules in aqueous media: A robust, discretized description for electroporation and other transport phenomena. IEEE Trans. Biomed. Eng. 2012, 59, 1514–1522. [Google Scholar] [CrossRef] [PubMed]
- Granot, Y.; Rubinsky, B. Mass transfer model for drug delivery in tissue cells with reversible electroporation. Int. J. Heat Mass Transf. 2008, 51, 5610–5616. [Google Scholar] [CrossRef] [PubMed]
- Shorstkii, I.A. Evaluation of the effect of a pulsed electric discharge on the process of substance transfer in plant material at the initial moment of time. Universities proceedings. Food Technol. 2019, 2, 73–77. [Google Scholar]
- Shorstkii, I.A.; Khudykov, D.A. Pulsed electric field pre-treatment efficiency analysis in processes of biomaterials drying. Vestnik VGUIT [Proc. VSUET] 2018, 80, 49–54. [Google Scholar] [CrossRef]
- Wiktor, A.; Śledź, M.; Małgorzata, N.; Chudoba, T.; Witrowa-Rajchert, D. Pulsed Electric Field Pretreatment for Osmotic Dehydration of Apple Tissue: Experimental and Mathematical Modeling Studies. Dry. Technol. Int. J. 2014, 32, 408–417. [Google Scholar] [CrossRef]
- Mahnič-Kalamiza, S.; Vorobiev, E. Dual-porosity model of liquid extraction by pressing from biological tissue modified by electroporation. J. Food Eng. 2014, 137, 76–87. [Google Scholar] [CrossRef]
- Parniakov, O.; Bals, O.; Lebovka, N.; Vorobiev, E. Pulsed electric field assisted vacuum freeze-drying of apple tissue. Innov. Food Sci. Emerg. Technol. 2016, 35, 52–57. [Google Scholar] [CrossRef]
- Won, Y.C.; Min, S.C.; Lee, D.U. Accelerated Drying and Improved Color Properties of Red Pepper by Pretreatment of Pulsed Electric Fields. Dry. Technol. Int. J. 2015, 33, 926–932. [Google Scholar] [CrossRef]
- Pavlin, M.; Miklavcic, D. Theoretical and experimental analysis of conductivity, ion 1285 diffusion and molecular transport during cell electroporation—Relation between short-lived and long-lived pores. Bioelectrochemistry 2008, 74, 38–46. [Google Scholar] [CrossRef] [PubMed]
- Bouzrara, H.; Vorobiev, E. Solid-liquid expression of cellular materials enhanced by pulsed electric field. Chem. Eng. Process. 2003, 42, 249–257. [Google Scholar] [CrossRef]
- Lebovka, N.I.; Shynkaryk, N.V.; Vorobiev, E. Pulsed electric field enhanced drying of potato tissue. J. Food Eng. 2007, 78, 606–613. [Google Scholar] [CrossRef]
- Liu, C.; Grimi, N.; Lebovka, N.; Vorobiev, E. Convective air, microwave, and combined drying of potato pre-treated by pulsed electric fields. Dry. Technol. 2018, 1–10. [Google Scholar] [CrossRef]
- Zhang, X.L.; Zhong, C.S.; Mujumdar, A.S.; Yang, X.H.; Deng, L.Z.; Wang, J.; Xiao, H.W. Cold plasma pretreatment enhances drying kinetics and quality attributes of chili pepper (Capsicum annuum L.). J. Food Eng. 2019, 241, 51–57. [Google Scholar] [CrossRef]
- Li, S.; Chen, S.; Han, F.; Xv, Y.; Sun, H.; Ma, Z.; Chen, J.; Wu, W. Development and Optimization of Cold Plasma Pretreatment for Drying on Corn Kernels. J. Food Sci. 2019, 84, 2181–2189. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.I.H.; Wellard, R.M.; Nagy, S.A.; Joardder, M.U.H.; Karim, M.A. Experimental investigation of bound and free water transport process during drying of hygroscopic food material. Int. J. Therm. Sci. 2017, 117, 266–273. [Google Scholar] [CrossRef]
- Kudra, T.; Martynenko, A. Electrohydrodynamic drying: Theory and experimental validation. Dry. Technol. 2019. [Google Scholar] [CrossRef]
- Lykov, A.V. Drying Theory; Energiya: Moscow, Russia, 1968. [Google Scholar]
- Kamangar, T.; Farsam, H. Composition of pistachio kernels of various Iranian origins. J. Food Sci. 1997, 42, 135–136. [Google Scholar] [CrossRef]
- Shorstkii, I.; Mirshekarloo, M.S.; Koshevoi, E. Application of Pulsed Electric Field for Oil Extraction from Sunflower Seeds: Electrical Parameter Effects on Oil Yield. J. Food Process Eng. 2017, 40, e12281. [Google Scholar] [CrossRef]
- Lykov, A.V.; Mihailov, Y.A. Heat and Mass Transfer Theory; Energiya: Moscow, Russia, 1963. [Google Scholar]
- Ginzburg, A.S. Thermophysical Characteristics of Foodstuffs and Food Materials; Food Industry: Moscow, Russia, 1975. [Google Scholar]
- Wu, Y. Effect of Pressure on Heat and Mass Transfer in Starch-based Food Systems. Ph.D. Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 1997. [Google Scholar]
- Tsukada, T.; Sakai, N.; Hayakawa, K. Computerised model for strain-stress analysis of food undergoing simultaneous heat and mass transfer. J. Food Sci. 1991, 56, 1438–1445. [Google Scholar] [CrossRef]
- Nikitina, L.M. Thermodynamic Parameters and Mass Transfer Coefficients in Moist Materials; Energiya: Moscow, Russia, 1968. [Google Scholar]
- Barron, R.F.; Nellis, G.F. Cryogenic Heat Transfer, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]


| = 0.6 J/m·K·s | δ = 0.02 °M/K |
| = 0.03 kg/ m·K·s | = 0.1 |
| = 9 × 10−4 kg·m·K/s | = 210 kg/m3 |
| J/kg·K | = 2.25 × 106 J/kg |
| cm = 0.02 kg/kg·°M | = 0.8 × 10−3 kg/kg·K |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shorstkii, I.; Koshevoi, E. Drying Technology Assisted by Nonthermal Pulsed Filamentary Microplasma Treatment: Theory and Practice. ChemEngineering 2019, 3, 91. https://doi.org/10.3390/chemengineering3040091
Shorstkii I, Koshevoi E. Drying Technology Assisted by Nonthermal Pulsed Filamentary Microplasma Treatment: Theory and Practice. ChemEngineering. 2019; 3(4):91. https://doi.org/10.3390/chemengineering3040091
Chicago/Turabian StyleShorstkii, Ivan, and Evgeny Koshevoi. 2019. "Drying Technology Assisted by Nonthermal Pulsed Filamentary Microplasma Treatment: Theory and Practice" ChemEngineering 3, no. 4: 91. https://doi.org/10.3390/chemengineering3040091
APA StyleShorstkii, I., & Koshevoi, E. (2019). Drying Technology Assisted by Nonthermal Pulsed Filamentary Microplasma Treatment: Theory and Practice. ChemEngineering, 3(4), 91. https://doi.org/10.3390/chemengineering3040091