An Engineering Toolbox for the Evaluation of Metallic Flow Field Plates
Abstract
1. Introduction
2. Materials and Methods
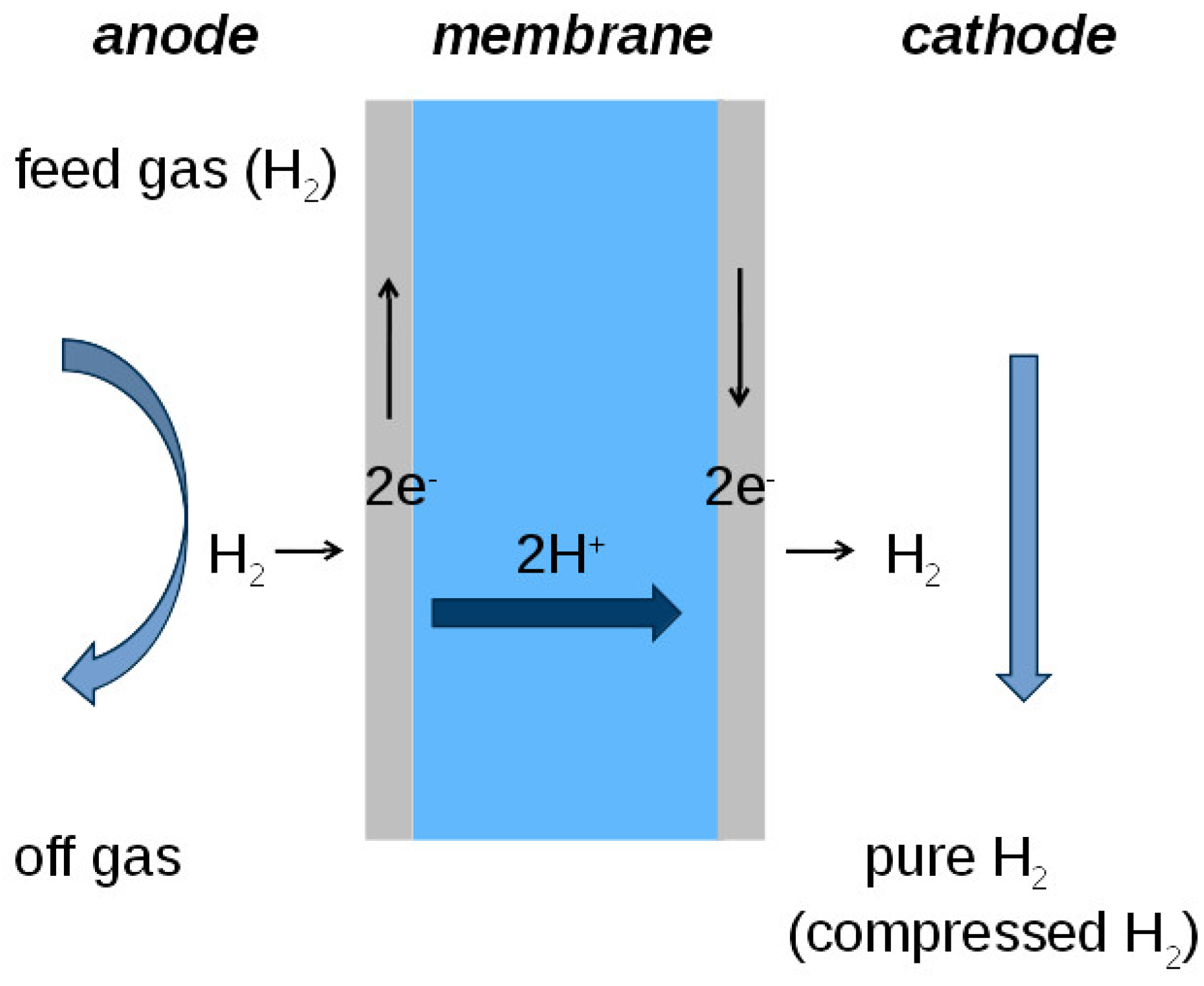
2.1. The Principle of Electrochemical Hydrogen Purification and Compression
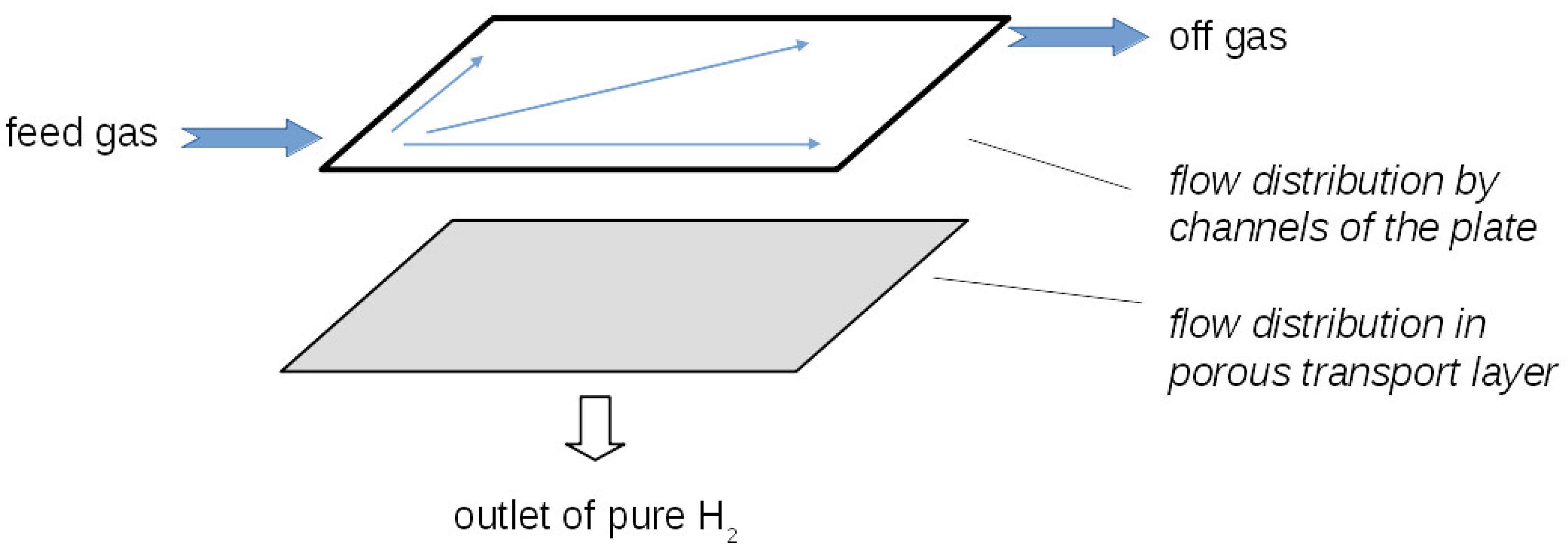
2.2. Computational Model for the Anode Flow Field Plate
2.3. Simplified Mixture Model
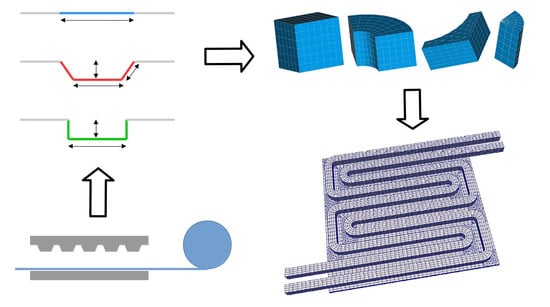
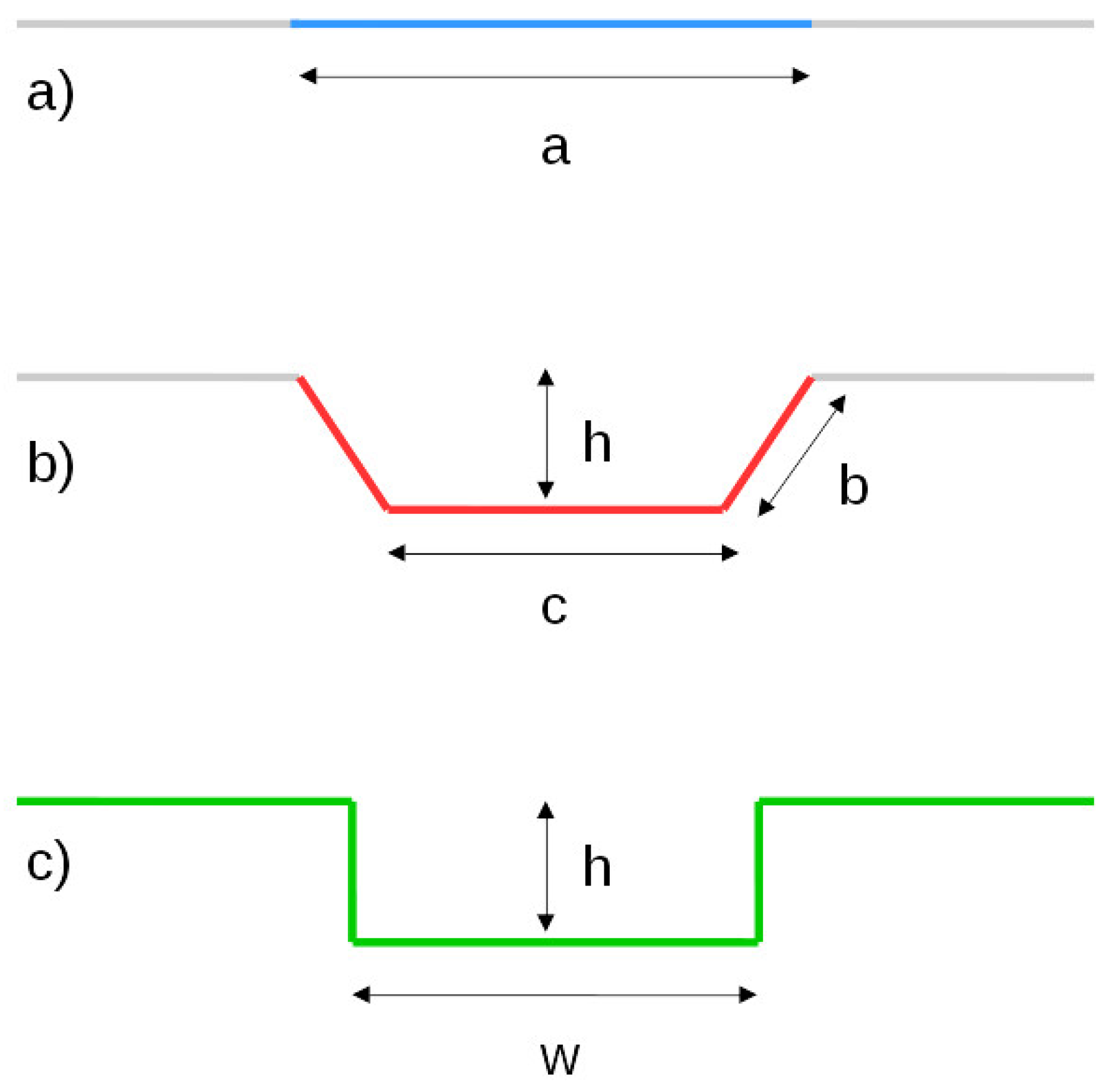
2.4. Equivalent Channel Geometry
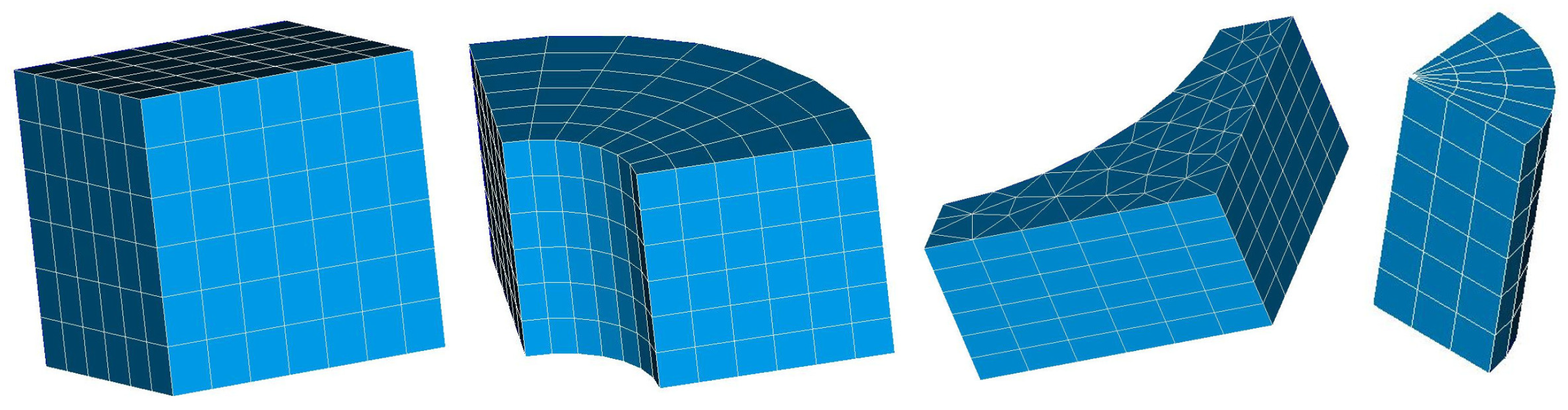
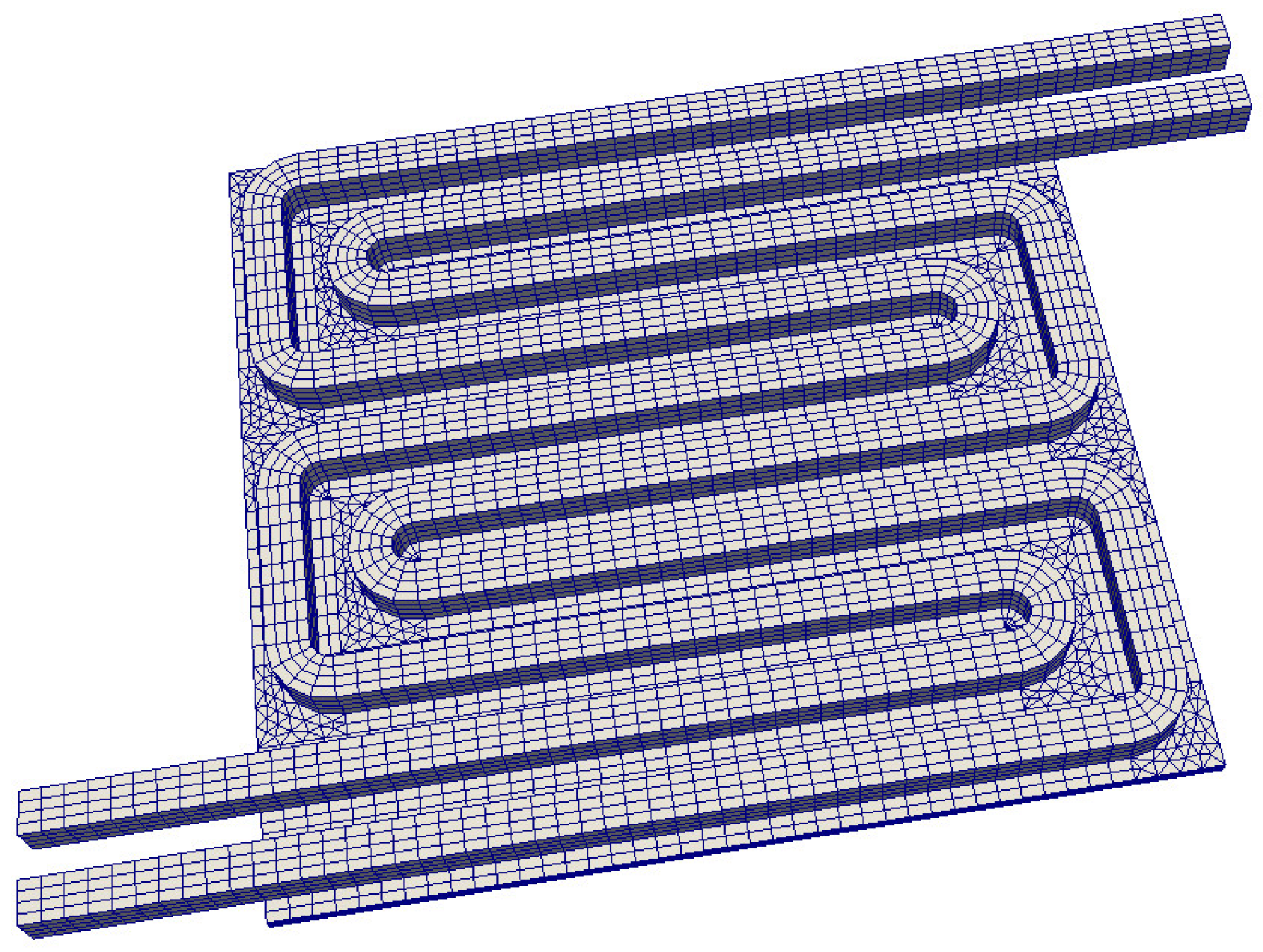
2.5. Automated Mesh Generation
- Total width of the flow field
- Number of parallel channels
- Channel width
- Channel height
- Channel/rib ratio (this defines the width of the ribs)
- Total number of 180 bends (U-turns)
- Mesh resolution of channel cross section
- Mesh resolution in the main flow direction
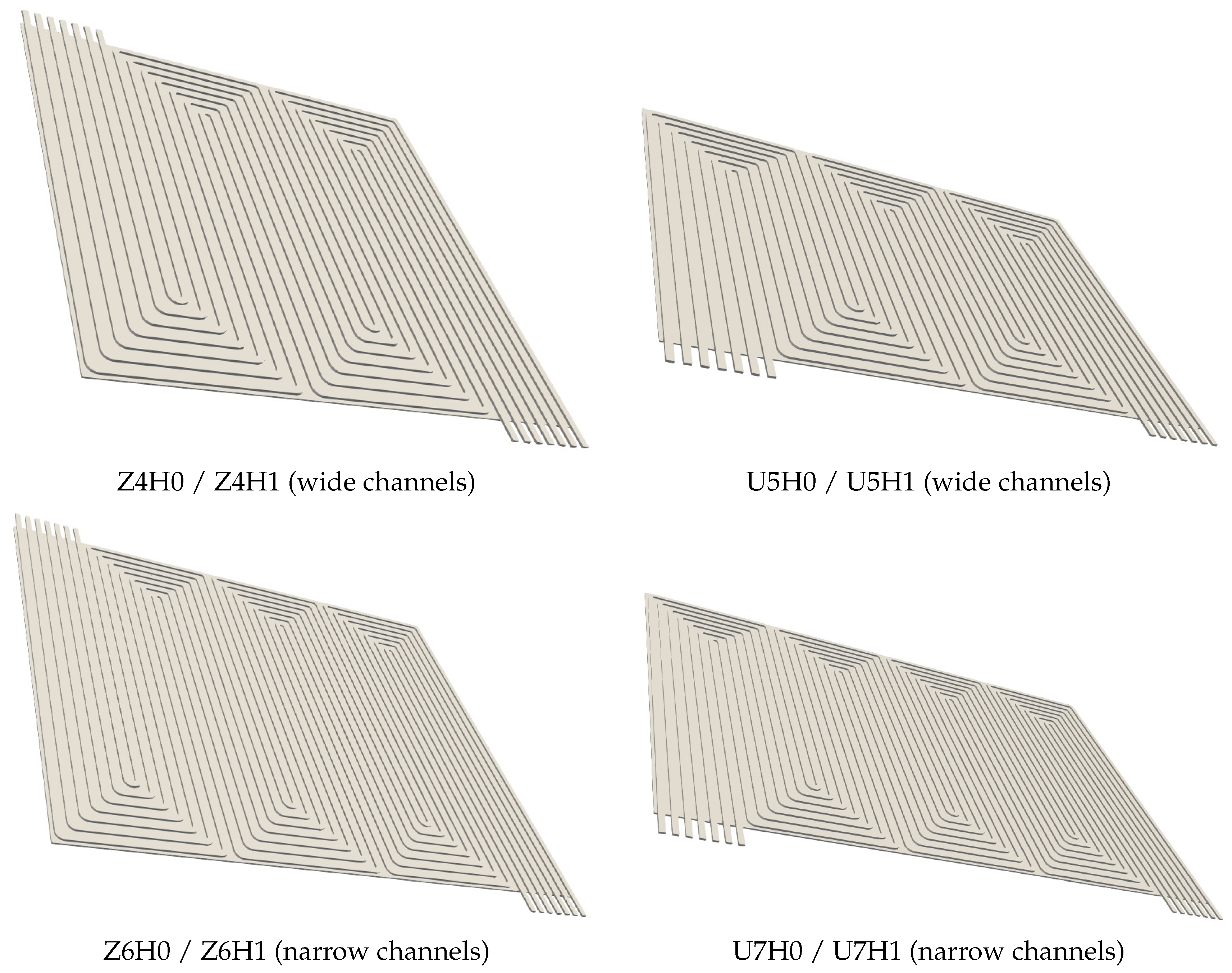
- Two general designs (“Z” and “U”) with seven parallel channels and a cell area of 100 cm
- Two different channel widths
- Two different channel heights (intrusion of porous media)
- Two different gas compositions
- Two different current densities for hydrogen extraction
- Three different levels of hydrogen extraction (80%, 95% and 99% for robustness tests)
3. Results and Discussion
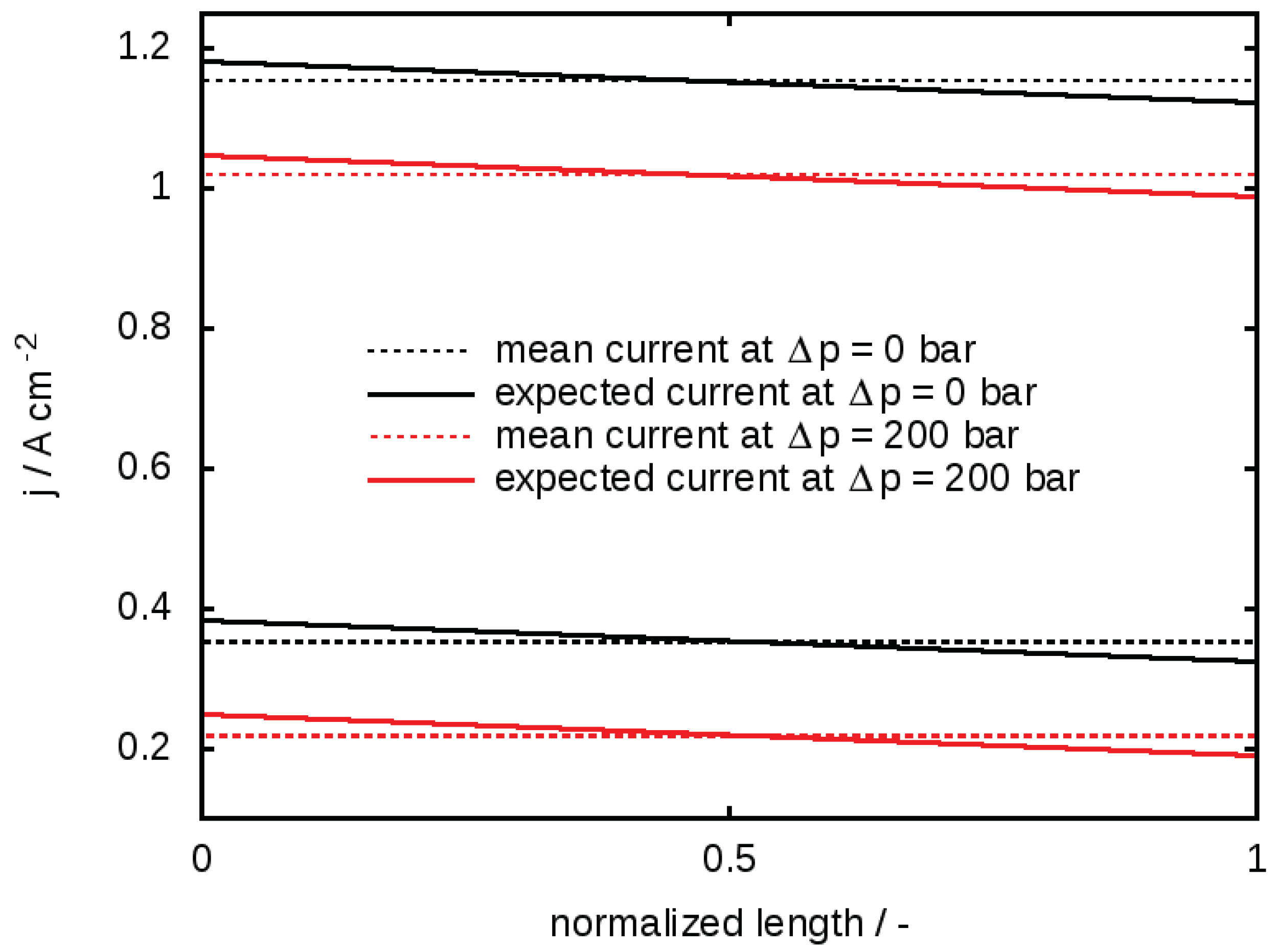
3.1. The Serpentine Effect
3.2. Sensitivity Analysis
3.2.1. Mesh Dependence
3.2.2. Variation of Permeability
3.3. Selected Simulation Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sreedhar, I.; Kamani, K.M.; Kamani, B.M.; Reddy, B.M.; Venugopal, A. A Bird’s Eye view on process and engineering aspects of hydrogen storage. Renew. Sustain. Energy Rev. 2018, 91, 838–860. [Google Scholar] [CrossRef]
- Abdalla, A.M.; Hossain, S.; Nisfindy, O.B.; Azad, A.T.; Dawood, M.; Azad, A.K. Hydrogen production, storage, transportation and key challenges with applications: A review. Energy Convers. Manag. 2018, 165, 602–657. [Google Scholar] [CrossRef]
- MEMPHYS—Membrane Based Purification of Hydrogen System. 2017. Available online: http://www.memphys.eu/ (accessed on 30 July 2019).
- Fuel Cells and Hydrogen Joint Undertaking: Project MEMPHYS. 2017. Available online: https://www.fch.europa.eu/project/membrane-based-purification-hydrogen-system (accessed on 30 July 2019).
- Abdulla, A.; Laney, K.; Padilla, M.; Sundaresan, S.; Benziger, J. Efficiency of hydrogen recovery from reformate with a polymer electrolyte hydrogen pump. AIChE J. 2011, 57, 1767–1779. [Google Scholar] [CrossRef]
- Schorer, L.; Schmitz, S.; Weber, A. Membrane based purification of hydrogen system (MEMPHYS). Int. J. Hydrog. Energy 2019, 44, 12708–12714. [Google Scholar] [CrossRef]
- Rochlitz, L.; Steinberger, M.; Oechsner, R.; Weber, A.; Schmitz, S.; Schillinger, K.; Wolff, M.; Bayler, A. Second use or recycling of hydrogen waste gas from the semiconductor industry—Economic analysis and technical demonstration of possible pathways. Int. J. Hydrog. Energy 2019, 44, 17168. [Google Scholar] [CrossRef]
- Lee, H.K.; Choi, H.Y.; Choi, K.H.; Park, J.H.; Lee, T.H. Hydrogen separation using electrochemical method. J. Power Sources 2004, 132, 92–98. [Google Scholar] [CrossRef]
- Onda, K.; Ichihara, K.; Nagahama, M.; Minamoto, Y.; Araki, T. Separation and compression characteristics of hydrogen by use of proton exchange membrane. J. Power Sources 2007, 164, 91. [Google Scholar] [CrossRef]
- Bouwman, P. Fundamentals of Electrochemical Hydrogen Compression. In PEM Electrolysis for Hydrogen Production—Principles and Applications; Bessarabov, D., Wang, H., Li, H., Zhao, N., Eds.; CRC Press: Boca Raton, FL, USA, 2015; p. 269. [Google Scholar] [CrossRef]
- Bouwman, P.J. Advances In Electrochemical Hydrogen Compression And Purification. ECS Trans. 2016, 75, 503–510. [Google Scholar] [CrossRef]
- Matsuura, T.; Kato, M.; Hori, M. Study on metallic bipolar plate for proton exchange membrane fuel cell. J. Power Sources 2006, 161, 74–78. [Google Scholar] [CrossRef]
- Peng, L.; Lai, X.; Liu, D.; Hu, P.; Ni, J. Flow channel shape optimum design for hydroformed metal bipolar plate in PEM fuel cell. J. Power Sources 2008, 178, 223–230. [Google Scholar] [CrossRef]
- Jung, S.P.; Lee, C.; Chen, C.C.; Chang, W.S.; Yang, C.C. Development of novel proton exchange membrane fuel cells using stamped metallic bipolar plates. J. Power Sources 2015, 283, 429–442. [Google Scholar] [CrossRef]
- Janßen, H.; Edelmann, A.; Mildebrath, T.; Müller, P.; Lehnert, W.; Stolten, D. Design and experimental validation of an HT-PEFC stack with metallic BPP. Int. J. Hydrog. Energy 2018, 43, 18488–18497. [Google Scholar] [CrossRef]
- Tawfik, H.; Hung, Y.; Mahajan, D. Metal bipolar plates for PEM fuel cell—A review. J. Power Sources 2007, 163, 755–767. [Google Scholar] [CrossRef]
- Karimi, S.; Fraser, N.; Roberts, B.; Foulkes, F.R. A Review of Metallic Bipolar Plates for Proton Exchange Membrane Fuel Cells: Materials and Fabrication Methods. Adv. Mater. Sci. Eng. 2012, 2012, 828070. [Google Scholar] [CrossRef]
- Peng, L.; Yi, P.; Lai, X. Design and manufacturing of stainless steel bipolar plates for proton exhcange membrane fuel cells. Int. J. Hydrog. Energy 2014, 39, 21127–21153. [Google Scholar] [CrossRef]
- Taherian, R. A review of composite and metallic bipolar plates in proton exchange membrane fuel cell: Materials, fabrication, and material selection. J. Power Sources 2014, 265, 370–390. [Google Scholar] [CrossRef]
- Mahabunphachai, S.; Cora, Ö.S.; Koç, M. Effect of manufacturing processes on formability and surface topography of proton exchange membrane fuel cell metallic bipolar plates. J. Power Sources 2010, 195, 5269–5277. [Google Scholar] [CrossRef]
- Xu, Z.; Peng, L.; Yi, P.; Lai, X. An investigation on the formability of sheet metals in the micro/meso scale hydroforming process. Int. J. Mech. Sci. 2019, 150, 265–276. [Google Scholar] [CrossRef]
- Khatir, F.A.; Elyasi, M.; Ghadikolaee, T.H.; Hosseinzadeh, M. Evaluation of effective parameters on stamping of metallic bipolar plates. Proced. Eng. 2017, 183, 322–329. [Google Scholar] [CrossRef]
- Chen, T.C.; Lin, J.C.; Lee, R.M. Analysis of deep drawing process for stainless steel micro-channel array. Materials 2017, 10, 423. [Google Scholar] [CrossRef]
- Hu, Q.; Zhang, D.; Fu, H. Effect of flow-field dimensions on the formability of Fe-Ni-Cr alloys as bipolar plate for PEM (proton exchange membrane) fuel cell. Energy 2015, 83, 156–163. [Google Scholar] [CrossRef]
- Xu, Y.; Peng, L.; Yi, P.; Lai, X. Analysis of the flow distribution for thin stamped bipolar plates with tapered channel shape. Int. J. Hydrog. Energy 2016, 41, 5084–5095. [Google Scholar] [CrossRef]
- Imbrioscia, G.M.; Fasoli, H.J. Simulation and study of proposed modifications over straight-parallel flow field design. Int. J. Hydrog. Energy 2014, 39, 8861–8867. [Google Scholar] [CrossRef]
- Hu, P.; Peng, L.; Zhang, W.; Lai, X. Optimization design of slotted-interdigitated channel for stamped thin metal bipolar plate in proton exchange membrane fuel cell. J. Power Sources 2009, 187, 407–414. [Google Scholar] [CrossRef]
- Iranzo, A.; Rosa, F.; Pino, J. A simulation tool for geometrical analysis and Optimization of fuel cell bipolar plates: Development, validation and results. Energies 2009, 2, 582–594. [Google Scholar] [CrossRef]
- OpenFOAM—The open source CFD toolbox/ESI Group. 2019. Available online: https://www.openfoam.com/ (accessed on 30 July 2019).
- OpenFOAM—The OpenFOAM Foundation. 2019. Available online: https://openfoam.org/ (accessed on 30 July 2019).
- Kocha, S.S.; Yang, J.D.; Yi, J.S. Characterization of Gas Crossover and Its Implications in PEM Fuel Cells. AIChE J. 2006, 52, 1916–1925. [Google Scholar] [CrossRef]
- Ibeh, B.; Gardner, C.; Ternan, M. Separation of hydrogen from a hydrogen/methane mixture using a PEM fuel cell. Int. J. Hydrog. Energy 2007, 32, 908–914. [Google Scholar] [CrossRef]
- Gardner, C.L.; Ternan, M. Electrochemical separation of hydrogen from reformate using PEM fuel cell technology. J. Power Sources 2007, 171, 835–841. [Google Scholar] [CrossRef]
- Barbir, F.; Görgün, H. Electrochemical hydrogen pump for recirculation of hydrogen in a fuel cell stack. J. Appl. Electrochem. 2007, 37, 359–365. [Google Scholar] [CrossRef]
- Rohland, B.; Eberle, K.; Ströbel, R.; Scolta, J.; Garche, J. Electrochemical hydrogen compressor. Electrochim. Acta 1998, 43, 3841–3846. [Google Scholar] [CrossRef]
- Ströbel, R.; Oszcipok, M.; Fasil, M.; Rohland, B.; Jörissen, L.; Garche, J. The compression of hydrogen in an electrochemical cell based on a PE fuel cell design. J. Power Sources 2002, 105, 208–215. [Google Scholar] [CrossRef]
- Grigoriev, S.A.; Shtatniy, I.G.; Millet, P.; Porembsky, V.I.; Fateev, V.N. Description and characterization of an electrochemical hydrogen compressor/concentrator based on solid polymer electrolyte technology. Int. J. Hydrog. Energy 2011, 36, 4148–4155. [Google Scholar] [CrossRef]
- Janssen, G.J.M.; Overvelde, M.L.J. Water transport in the proton-exchange-membrane fuel cell: Measurements of the effective drag coeffcient. J. Power Sources 2001, 101, 117–125. [Google Scholar] [CrossRef]
- Yan, Q.; Toghiani, H.; Wu, J. Investigation of water transport through membrane in a PEM fuel cell by water balance experiments. J. Power Sources 2006, 158, 316–325. [Google Scholar] [CrossRef]
- Weber, A.; Borup, R.L.; Darling, R.M.; Das, P.K.; Dursch, T.J.; Gu, W.; Harvey, D.; Kusoglu, A.; Litster, S.; Mench, M.M.; et al. A Critical Review of Modeling Transport Phenomena in Polymer-Electrolyte Fuel Cells. J. Electrochem. Soc. 2014, 161, F1254–F1299. [Google Scholar] [CrossRef]
- Reimer, U.; Ehlert, J.; Janßen, H.; Lehnert, W. Water distribution in high temperature polymer electrolyte fuel cells. Int. J. Hydrog. Energy 2016, 41, 1837–1845. [Google Scholar] [CrossRef]
- Thomassen, M.; Sheridan, E.; Kvello, J. Electrochemical hydrogen separation and compression using polybenzimidazole (PBI) fuel cell technology. J. Nat. Gas Sci. Eng. 2010, 2, 229–234. [Google Scholar] [CrossRef]
- Li, Q.; Aili, D.; Hjuler, H.A.; Jensen, J.O. (Eds.) High Temperature Polymer Electrolyte Membrane Fuel Cells; Springer: Cham, Switzerland; Heidelberg, Germany; New York, NY, USA; Dordrecht, The Netherlands; London, UK, 2016. [Google Scholar] [CrossRef]
- Nordio, M.; Rizzi, F.; Manzolini, G.; Mulder, M.; Raymakers, L.; Van Sint Annalanda, M.; Gallucci, F. Experimental and modelling study of an electrochemical hydrogen compressor. Chem. Eng. J. 2019, 369, 432–442. [Google Scholar] [CrossRef]
- NIST Chemistry WebBook. 2019. Available online: https://webbook.nist.gov/chemistry/fluid/ (accessed on 30 July 2019).
- Casati, C.; Longhi, P.; Zanderighi, L.; Bianchi, F. Some fundamental aspects in electrochemical hydrogen purification/compression. J. Power Sources 2008, 180, 103–113. [Google Scholar] [CrossRef]
- El-kharouf, A.; Mason, T.J.; Brett, D.J.L.; Pollet, B.G. Ex-situ characterisation of gas diffusion layers for proton exchange membrane fuel cells. J. Power Sources 2012, 218, 393–404. [Google Scholar] [CrossRef]
- Froning, D.; Brinkmann, J.; Reimer, U.; Schmidt, V.; Lehnert, W.; Stolten, D. 3D analysis, modeling and simulation of transport processes in compressed fibrous microstructures, using the Lattice Boltzmann method. Electrochim. Acta 2013, 110, 325–334. [Google Scholar] [CrossRef]
- Kim, A.R.; Jung, H.M.; Um, S. An engineering approach to optimal metallic bipolar plate designs reflecting gas diffusion layer compression effects. Energy 2014, 66, 50–55. [Google Scholar] [CrossRef]
- Zhang, X.M.; Zhang, X.X. Impact of Compression on Effective Thermal Conductivity and Diffusion Coefficient of Woven Gas Diffusion Layers in Polymer Electrolyte Fuel Cells. Fuel Cells 2014, 14, 303–311. [Google Scholar] [CrossRef]
- Froning, D.; Junliang, Y.; Gaiselmann, G.; Reimer, U.; Manke, I.; Schmidt, V.; Lehnert, W. Impact of compression on gas transport in non-woven gas diffusion layers of high temperature polymer electrolyte fuel cells. J. Power Sources 2016, 318, 26–34. [Google Scholar] [CrossRef]
- SALOME—The Open Source Integration Platform for Numerical Simulation. 2019. Available online: https://salome-platform.org/ (accessed on 30 July 2019).
- Pharoah, J.G. On the permeability of gas diffusion media used in PEM fuel cells. J. Power Sources 2005, 144, 77–82. [Google Scholar] [CrossRef]
- Shimpalee, S.; Van Zee, J.W. Numerical studies on rib & channel dimension of flow-field on PEMFC performance. Int. J. Hydrog. Energy 2007, 32, 842–856. [Google Scholar] [CrossRef]
- Baek, S.M.; Jeon, D.H.; Kim, C.J. Pressure drop and flow distribution characteristics of single and parallel serpentine flow fields for polymer electrolyte membrane fuel cells. J. Mech. Sci. Technol. 2012, 26, 2995–3006. [Google Scholar] [CrossRef]
- Suresh, P.V.; Jayanti, S. Peclet number analysis of cross-flow in porous gas diffusion layer of polymer electrolyte membrane fuel cell (PEMFC). Environ. Sci. Pollut. Res. 2016, 23, 20120–20130. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Q.; Shen, S.; Yan, X.; Zhu, F.; Cheng, X.; Zhang, J. The respective effect of under-rib convection and pressure drop of flow fields on the performance of PEM fuel cells. Sci. Rep. 2017, 7, 43447. [Google Scholar] [CrossRef]
- Zhang, S.; Reimer, U.; Beale, S.B.; Lehnert, W.; Stolten, D. Modeling polymer electrolyte fuel cells: A high precision analysis. Appl. Energy 2019, 233–234, 1094–1103. [Google Scholar] [CrossRef]
- Dicks, A.L. The role of carbon in fuel cells. J. Power Sources 2006, 156, 128–141. [Google Scholar] [CrossRef]
- Hartnig, C.; Jörissen, L.; Kerres, J.; Lehnert, W.; Scholta, J. Polymer electrolyte membrane fuel cells. In Materials for Fuel Cells; Gasik, M., Ed.; CRC Press: Boca Raton, FL, USA; Boston, MA, USA; London, UK; New York, NY, USA, 2008; pp. 101–184. [Google Scholar] [CrossRef]
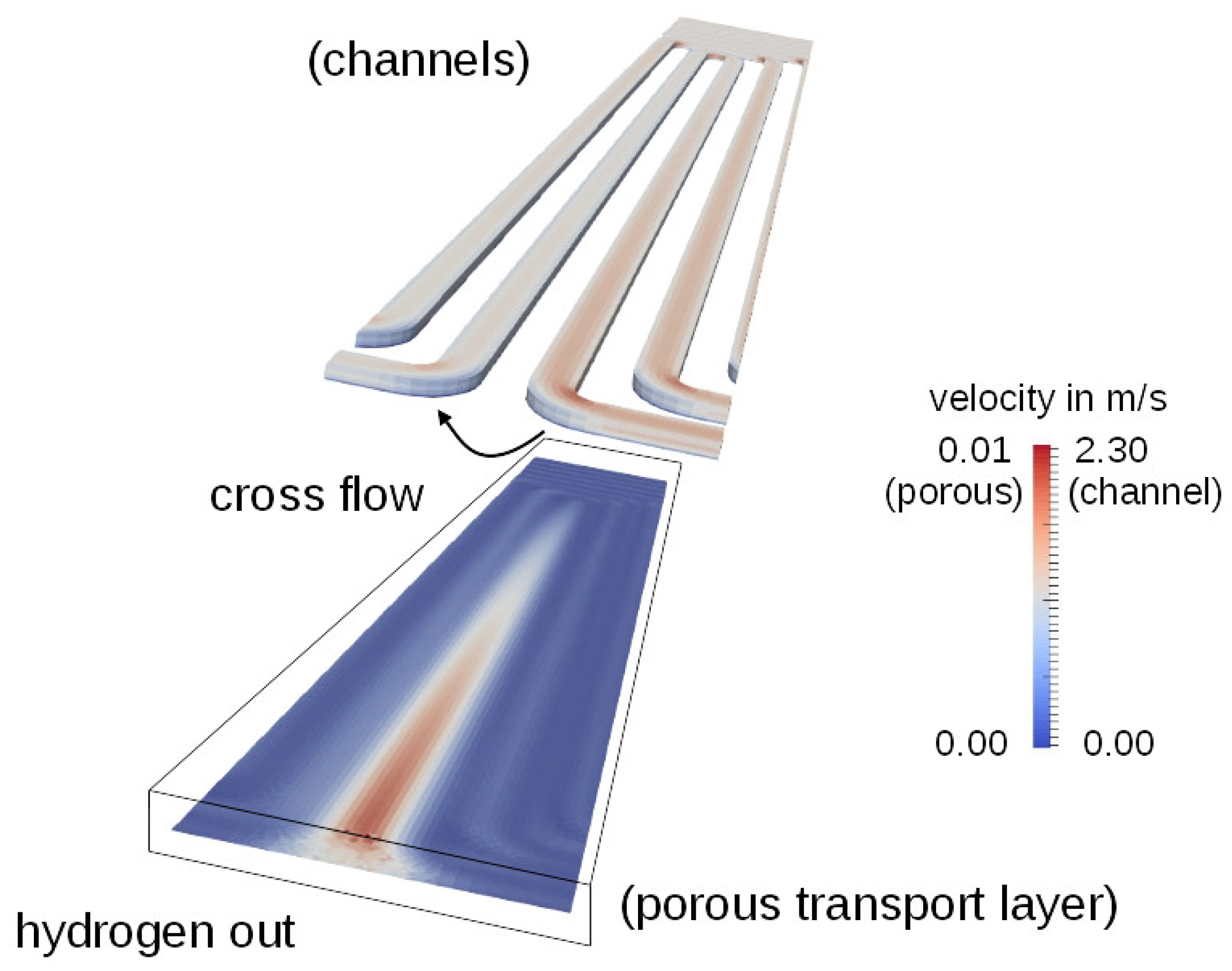
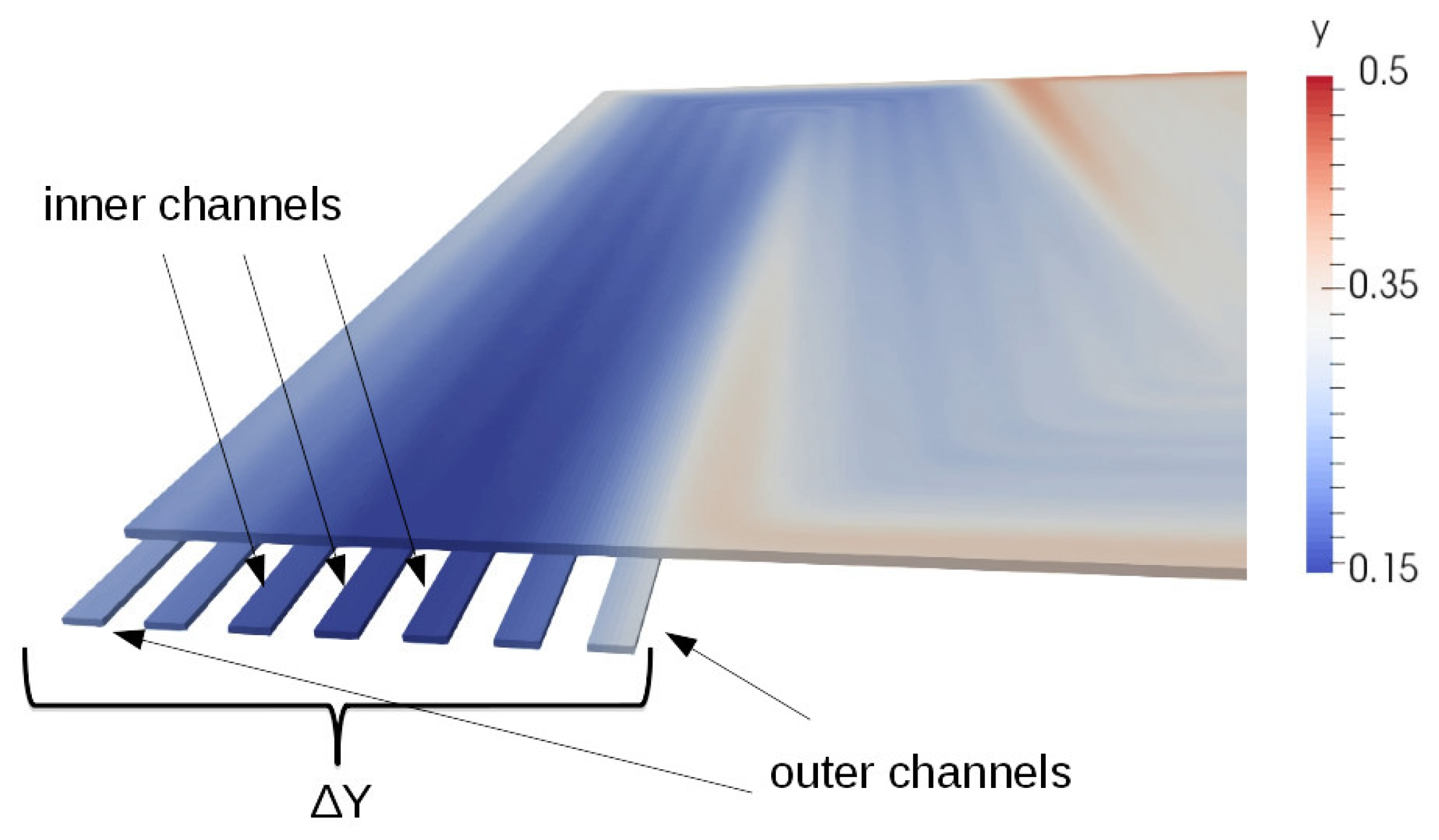
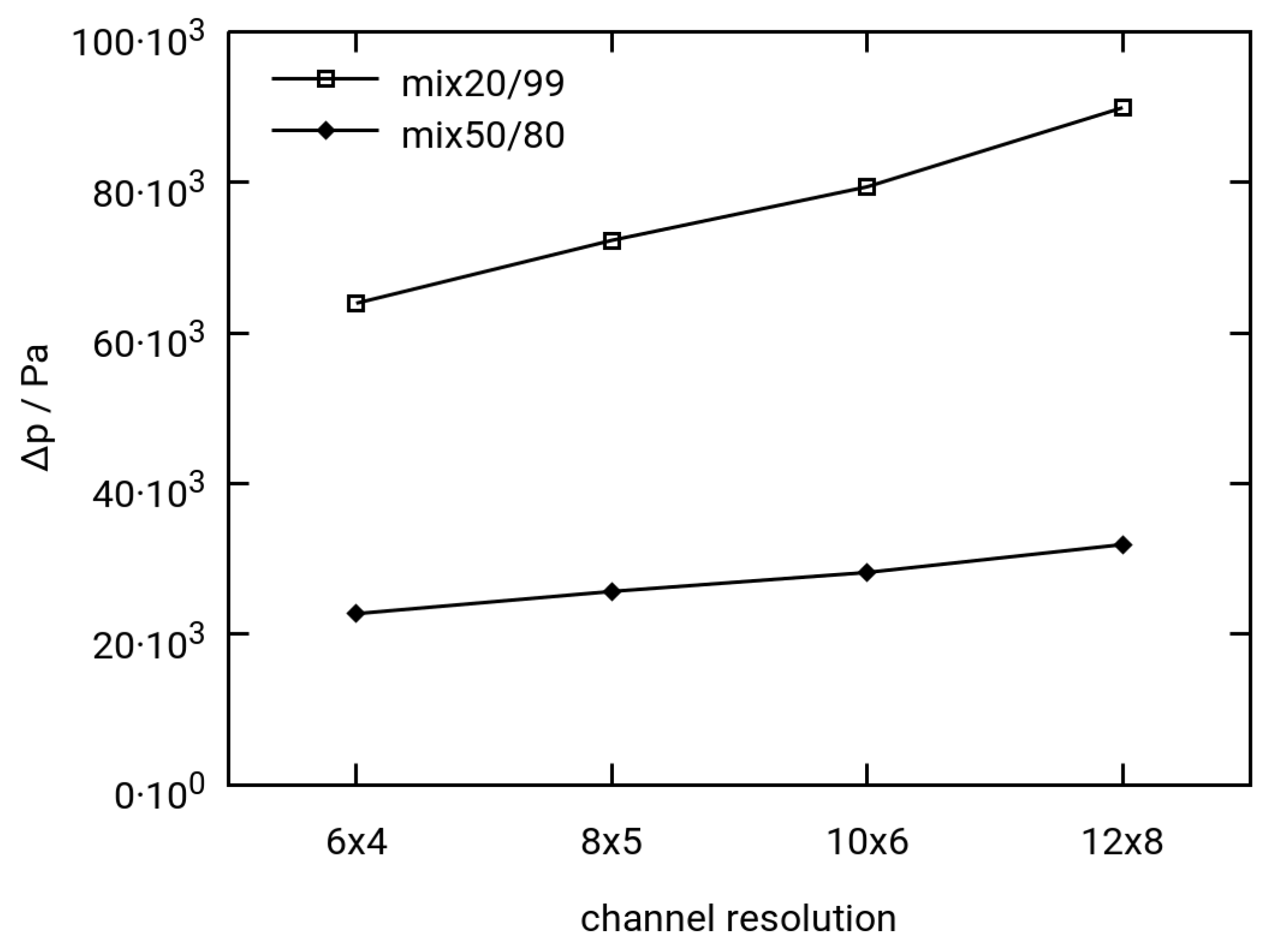
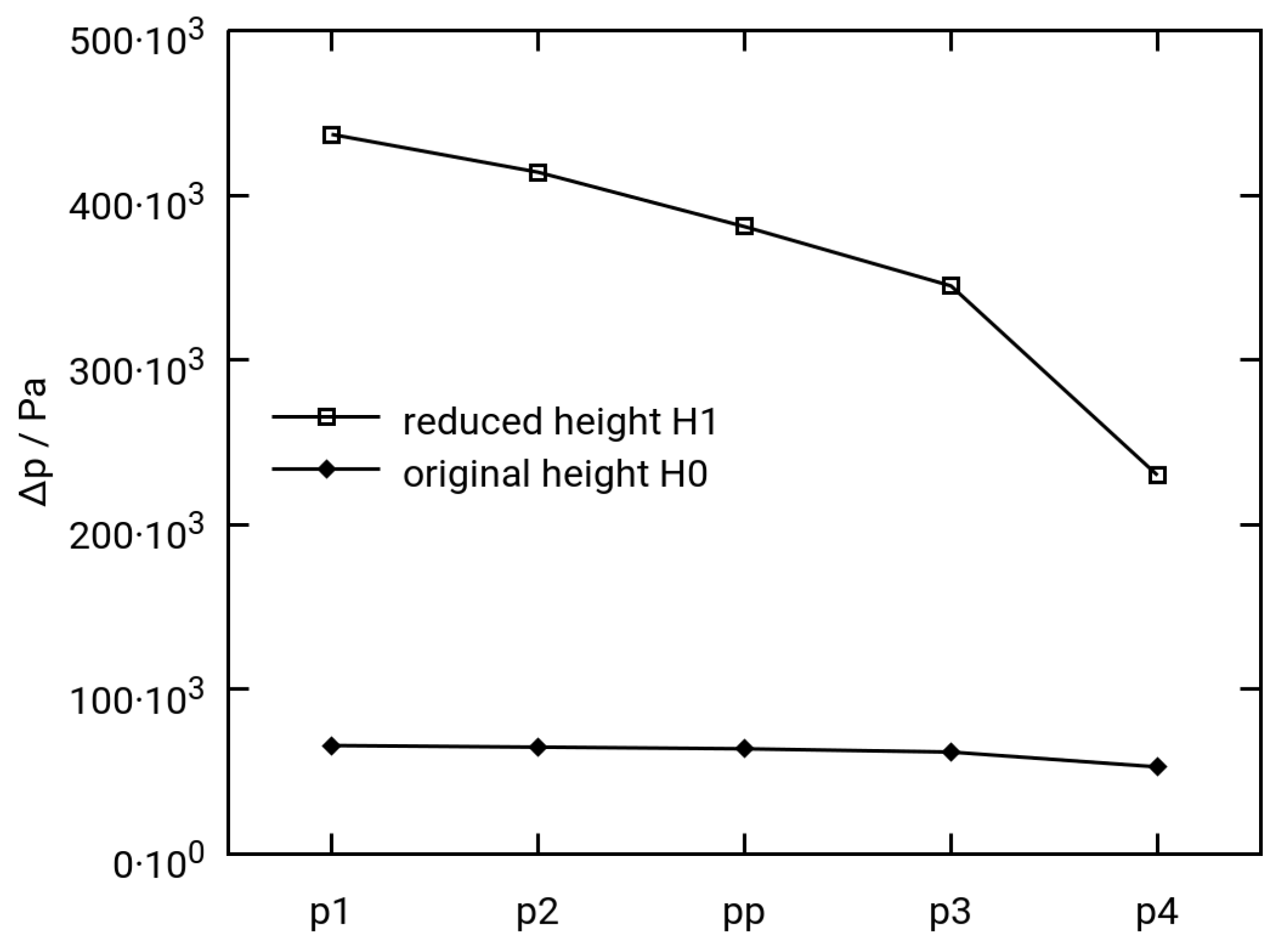
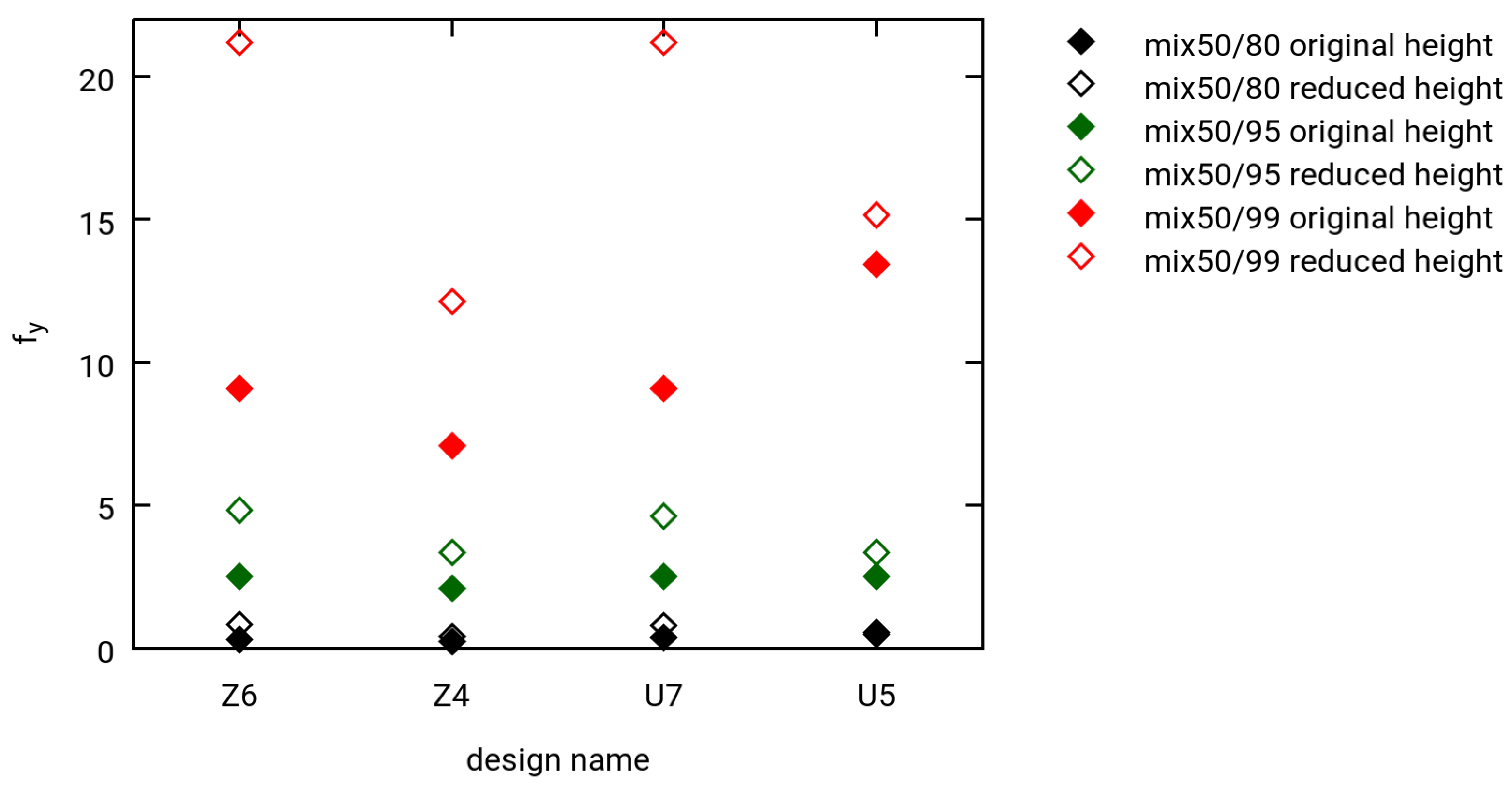
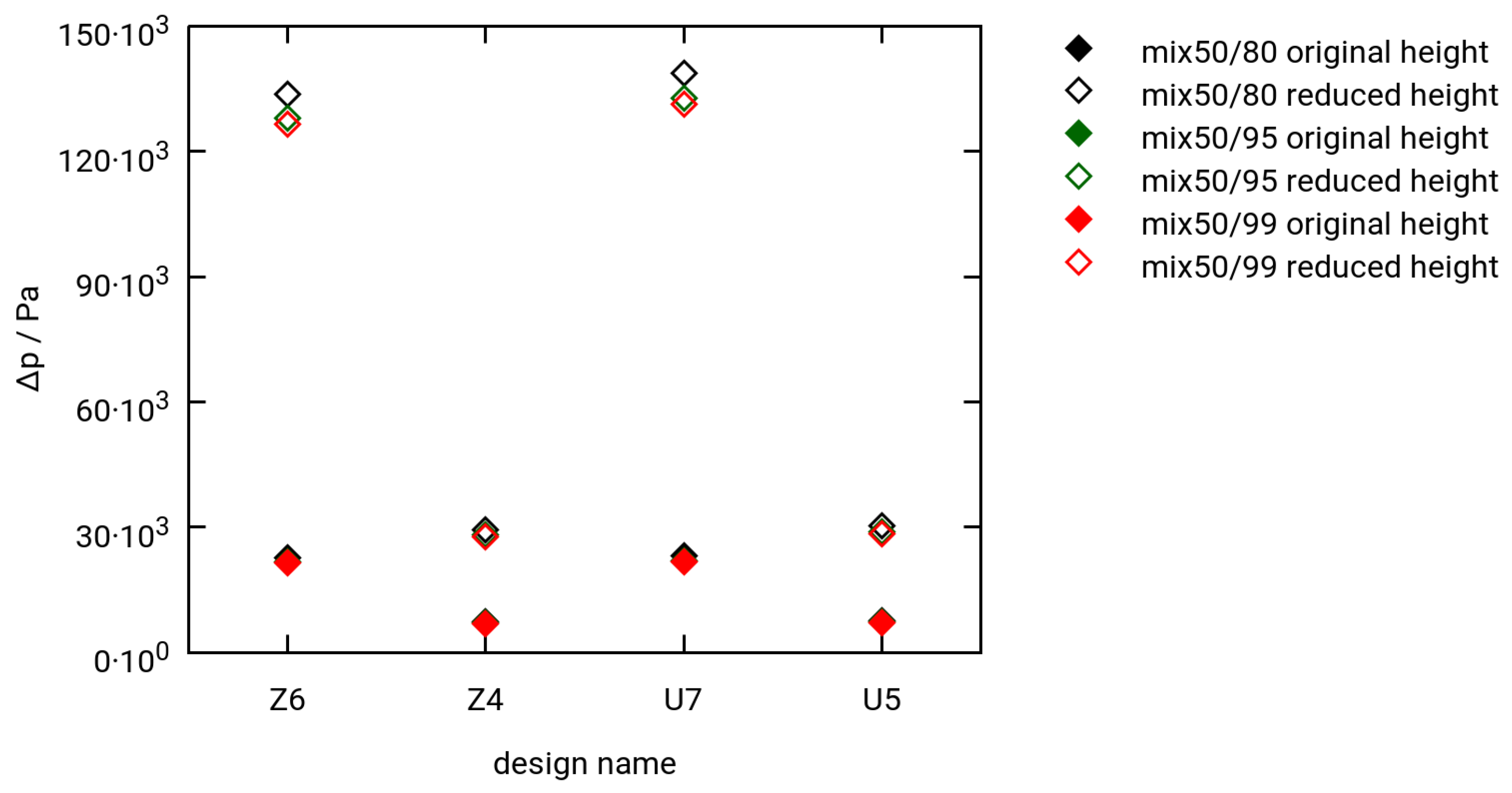
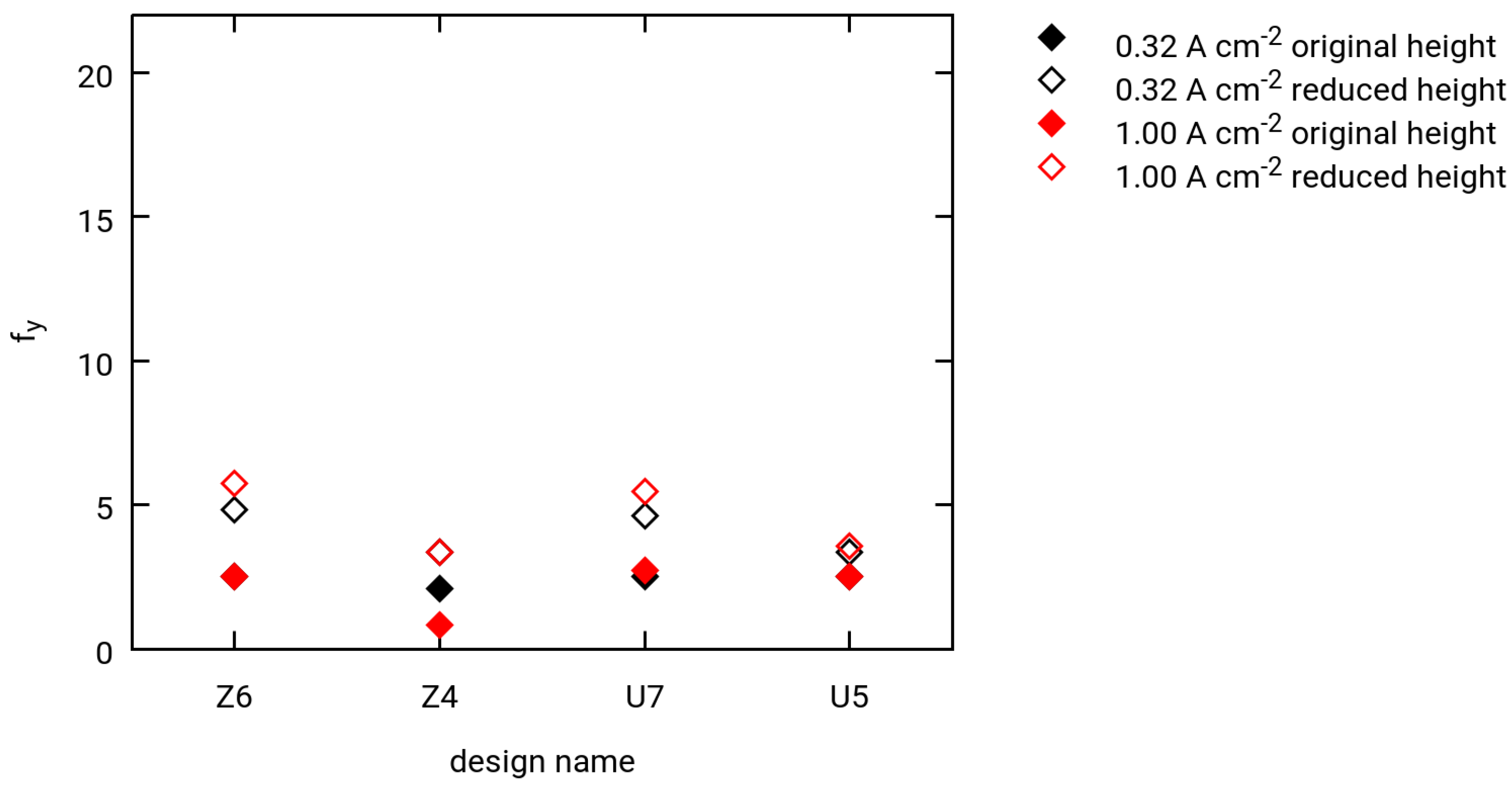
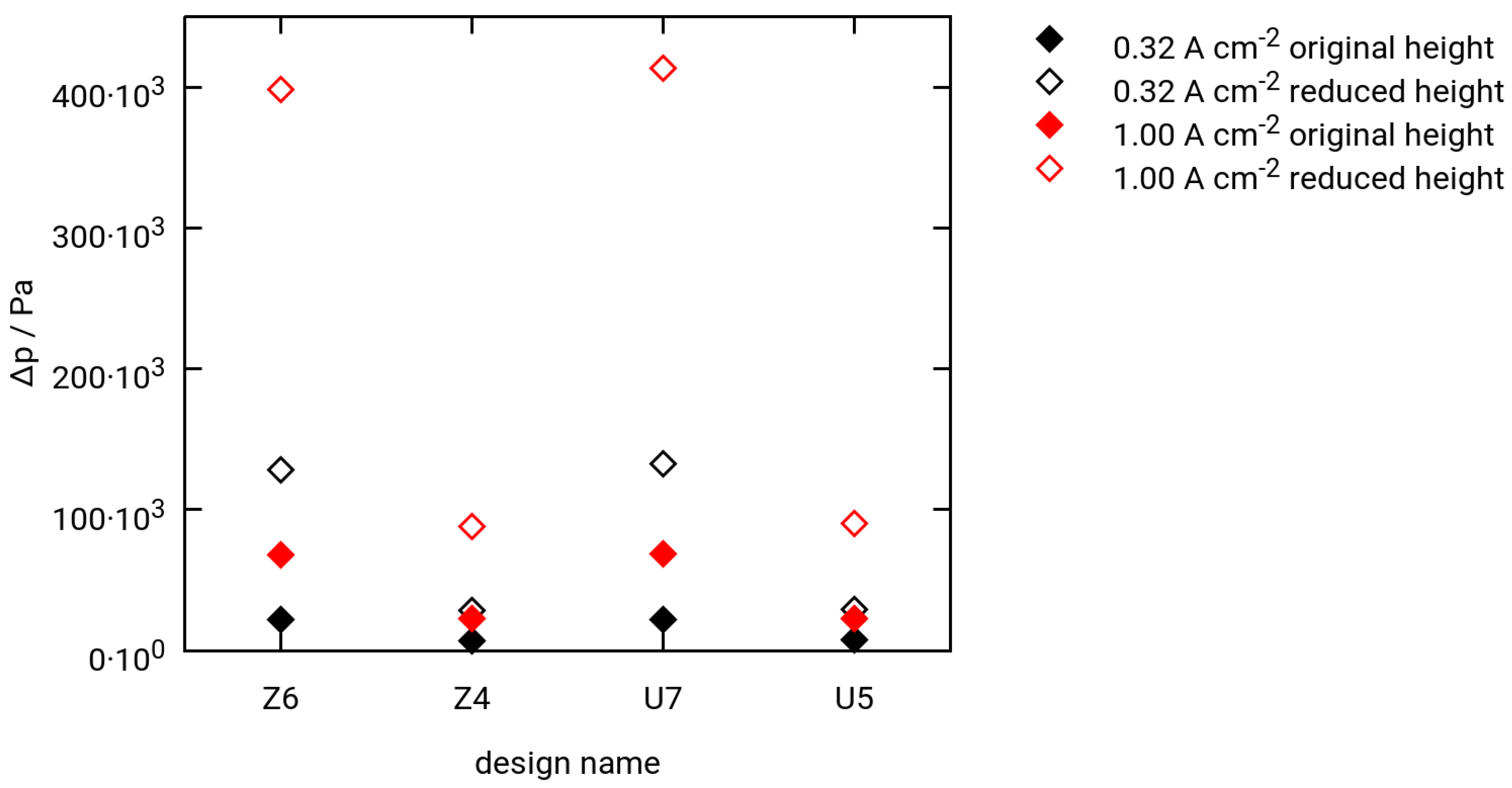
| Parameter | Value | Comment |
|---|---|---|
| Feed gas pressure | 1 bar | Pa, i.e., not pressurized |
| H outlet pressure | 200 bar | Pa |
| Feed gas composition | gas mix containing 50% H | |
| H recovery | 95% | or better |
| Operating temperature | 295 K | from test cell |
| Ohmic resistance | 0.5 cm | fitted |
| Parameter | Value | Reference |
|---|---|---|
| Density | 82.622 g m | ideal gas law |
| Dynamic viscosity | Pa s | [45] |
| Kinematic viscosity | m s | calculated |
| Effective diffusion coefficient | m s | [46] |
| Parameter | Value |
|---|---|
| in-plane permeability (x) | m |
| in-plane permeability (y) | m |
| through-plane permeability (z) | m |
| overall thickness | m |
| a/mm | 0.80 | 1.00 | 1.20 | 1.40 | 1.60 | 1.80 | 2.00 |
| b/mm | 0.50 | 0.60 | 0.75 | 0.88 | 1.00 | 1.13 | 1.25 |
| /mm | 0.27 | 0.35 | 0.41 | 0.47 | 0.54 | 0.61 | 0.68 |
| (max)/mm | 0.18 | 0.28 | 0.40 | 0.54 | 0.71 | 0.89 | 1.10 |
| h/mm | 0.25 | 0.25 | 0.35 | 0.40 | 0.45 | 0.50 | 0.55 |
| /mm | 0.16 | 0.20 | 0.34 | 0.46 | 0.59 | 0.73 | 0.89 |
| /mm | 0.35 | 0.36 | 0.49 | 0.56 | 0.64 | 0.71 | 0.78 |
| “Z” Configuration | “U” Configuration | |||
|---|---|---|---|---|
| channel width/mm | 1.14 | 1.46 | 1.14 | 1.46 |
| U turns | 6 | 4 | 7 | 5 |
| resulting overall length/mm | 111.72 | 102.20 | 127.70 | 123.48 |
| flow field width/mm | 89.50 | 97.80 | 78.30 | 81.00 |
| channel height /mm | 0.40 | 0.50 | 0.40 | 0.50 |
| channel height /mm | 0.20 | 0.30 | 0.20 | 0.30 |
| model name in results | Z6H0/Z6H1 | Z4H0/Z4H1 | U7H0/U7H1 | U5H0/U5H1 |
| Channel Resolution/Cells | Total Mesh Size/Cells | Comp. Time/h |
|---|---|---|
| 6 × 4 | 876,720 | 0.9 |
| 8 × 5 | 1,987,440 | 4.2 |
| 10 × 6 | 3,656,604 | 6.9 |
| 12 × 8 | 6,979,504 | 9.2 |
| Variant | in-plane/m | through-plane/m |
|---|---|---|
| p1 | ||
| p2 | ||
| pp | ||
| p3 | ||
| p4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reimer, U.; Froning, D.; Nelissen, G.; Raymakers, L.F.J.M.; Zhang, S.; Beale, S.B.; Lehnert, W. An Engineering Toolbox for the Evaluation of Metallic Flow Field Plates. ChemEngineering 2019, 3, 85. https://doi.org/10.3390/chemengineering3040085
Reimer U, Froning D, Nelissen G, Raymakers LFJM, Zhang S, Beale SB, Lehnert W. An Engineering Toolbox for the Evaluation of Metallic Flow Field Plates. ChemEngineering. 2019; 3(4):85. https://doi.org/10.3390/chemengineering3040085
Chicago/Turabian StyleReimer, Uwe, Dieter Froning, Gert Nelissen, Leonard F. J. M. Raymakers, Shidong Zhang, Steven B. Beale, and Werner Lehnert. 2019. "An Engineering Toolbox for the Evaluation of Metallic Flow Field Plates" ChemEngineering 3, no. 4: 85. https://doi.org/10.3390/chemengineering3040085
APA StyleReimer, U., Froning, D., Nelissen, G., Raymakers, L. F. J. M., Zhang, S., Beale, S. B., & Lehnert, W. (2019). An Engineering Toolbox for the Evaluation of Metallic Flow Field Plates. ChemEngineering, 3(4), 85. https://doi.org/10.3390/chemengineering3040085