Selection of Optimum Separation Sequence for Multicomponent Distillation

Abstract

This paper considers the process of multicomponent distillation. It is shown that energy consumption (per mole of mixture being separated) depends monotonously on efficiency if the capacity is constant and separation is reversible. Authors suggest the technique for selection of distillation sequence for which the total energy consumption in the cascade of columns reaches its minimum. This sequence is determined by values of thermal coefficients. Coefficients themselves depend on temperatures in the reboiler and condenser. This paper offers the algorithm for the calculation of these coefficients.

1. Introduction

The analysis of multicomponent distillation is not a novel field of science and is covered in many sources (for example References [1,2,3,4]), yet it contains many unsolved or partially solved problems. One of the most important problems of multicomponent distillation is the estimation of minimum energy consumption for the process and separation and calculation of separation sequence corresponding to this consumption.

Molar fractions and boiling points for each component are assumed to be known, so the composition of ingoing and outgoing streams are given. At a first glance, the energy consumption depends only on compositions, if one will not consider the irreversibility factors. It would be true for processes consuming mechanical or electrical energy, such as membrane separation or centrifugation. But for processes consuming the heat energy, such as distillation or simple evaporation, it is not true. The energy consumption in this case depends on temperatures of streams and these temperatures are determined by the choice of separation sequence.

For choosing the optimal separation sequence many authors suggest ad hoc heuristics without any justification. An example of such a heuristic is “at the first stage the lightest component must be separated” or “at the first stage the component with the maximum molar (mass, volumetric) fraction must be separated”. Our current paper tries to present rigorous methods for choosing the optimal separation sequence.

At first we will consider the unit fractionating column under some assumptions and will find the relationship between the energy consumption, capacity and separation order. Then we will write the inequality determining the choice of the separation order such that on every stage the energy consumption is minimum if the process is reversible. We will show that the efficiency of the column depends on its reversible efficiency monotonously, so the optimum separation order for the cascade of columns must not differ from the one obtained for a “reversible cascade.”

2. Limiting Capabilities of a Multicomponent Fractional Distillation Columns

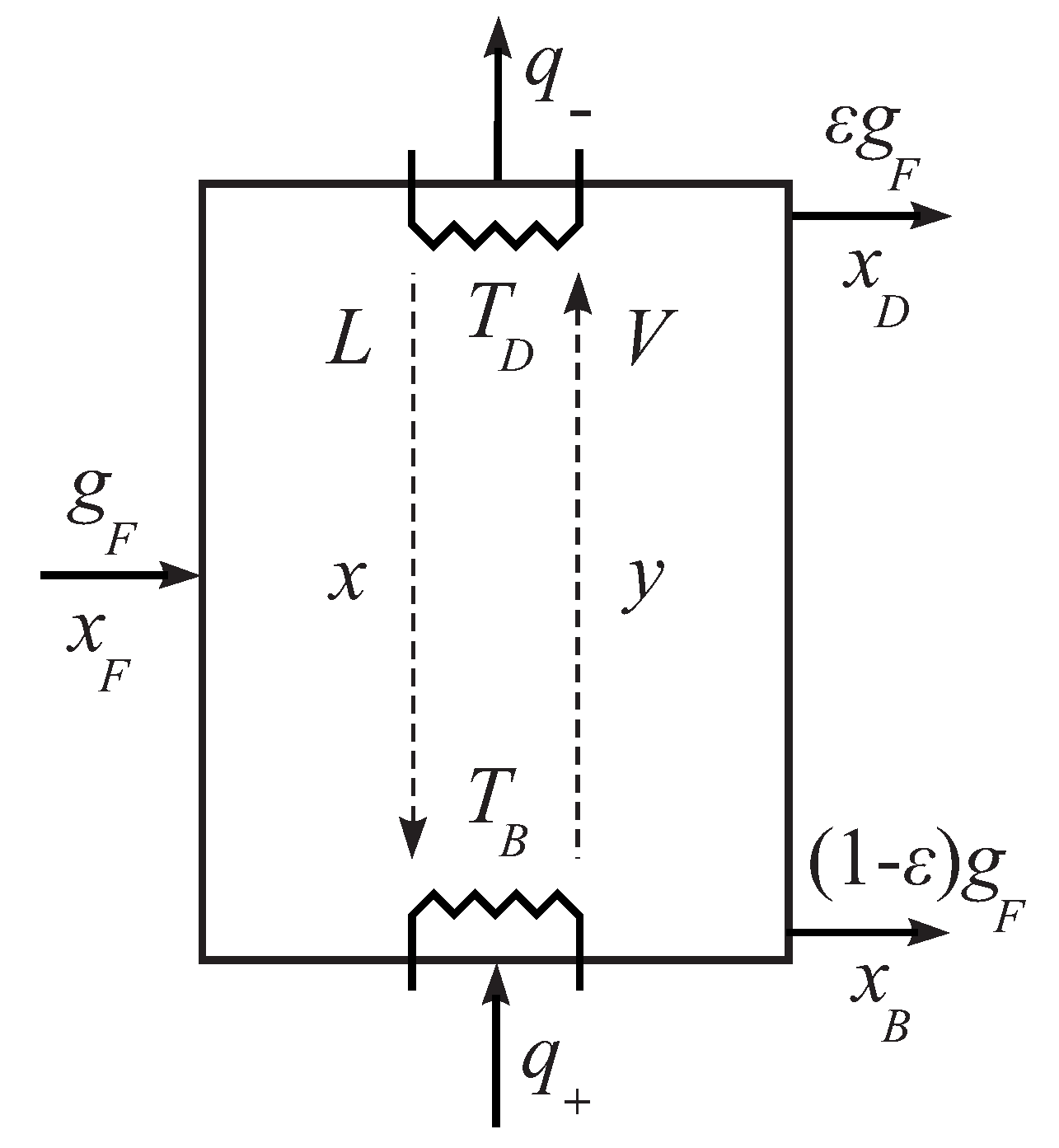
We will consider a model of a simple distillation column where one stream of the heat energy enters the reboiler and another one leaves the condenser.

There are main assumptions made in this paper are as follows:

• Mass transfer on a plate or in a packing section is equimolar and the fluid stream changes abruptly at the feed point.
• At every plate or packing section the pressure and the temperature of the fluid and the vapor streams are equal (they differ from one plate to another).
• Diffusion effects between consequent plate are negligible.
• The enthalpy of outgoing streams is being transferred to the incoming ones and the irreversibility of this process is negligible.
• The stream of the mixture being separated comes to the column at the plate where the temperature of the liquid stream is equal to the one of the feed and the entropy generation due to the mixing of streams with different compositions is negligible (It is not quite clear whether this last assumption is always acceptable. This question is the subject of the current research).

The process of separation of multicomponent mixture into two fractions in a distillation column is characterized by the following parameters:

• Molar fractions of components in the feed stream $x_{Fi}$, boiling points $T_i^0$ and molar latent heats of vaporization $r_i$, $i=1,\dots ,n$ (at standard conditions). It is assumed the from $i<j$ follows that $T_i^0<T_j^0$.
• The composition of products: the distillate $x_{Di}$ and the bottom product $x_{Bi}$.
• Parameters of a column: pressure $\overline{P}$, temperature in reboiler $T_B$, temperature in condenser $T_D$ (Figure 1). These values depend on a chosen separation order.

If compositions of outgoing and incoming streams are fixed, these streams are proportional to each other. This means that any of the liquid streams can be taken as the objective one. We will take the feed stream $g_F$ as the objective stream. In this case the efficiency of the column is the ratio of the feed stream and the stream of a heat $q_{+}$ supplied to the reboiler of a column.

Thermodynamic Balance Equations for Binary Distillation and Relationship Between Energy Consumption and Capacity of Column

At first we need to write down the balance equations for matter, energy and entropy [5,6], assuming that the heat of mixing is negligible:

$$g_F{x}_{Fi}-g_F\epsilon x_{Di}-g_F(1-\epsilon )x_{Bi}=0,i=1,2,....$$

(1)

$$q_{+}-q_{-}+g_F\sum _i{h}_{Fi}-g_{{}_F}\epsilon \sum _i{h}_{Di}-g_{{}_F}(1-\epsilon )\sum _i{h}_{Bi}=0,$$

(2)

$$g_{{}_F}\epsilon \sum _i{s}_{Di}+g_F(1-\epsilon )\sum _i{s}_{Bi}+\frac{q_{-}}{T_D}-g_{{}_F}\sum _i{s}_{Fi}-\frac{q_{+}}{T_B}=\sigma \ge {\sigma }_{min}.$$

(3)

Here $\sigma >0$ is the entropy generation in a column, $h_i$—molar enthalpy, $s_i$—molar entropy of the i-th component.

The fraction of upper product is

$$\epsilon =\frac{x_{Fi}-x_{Bi}}{x_{Di}-x_{Bi}},i=1,2,....$$

(4)

streams of the feed and products have temperatures $T_F$, $T_D$ and $T_B$ correspondingly.

We will assume that a column is adiabatic, so $q_{+}=q_{-}=q$.

From (2) and (3) one can obtain:

$$\begin{array}{c}q=g_{{}_F}\frac{T_B}{T_B-T_D}[\sum _i(s_{Fi}{T}_D-h_{Fi})-\epsilon \sum _i(s_{Di}{T}_D-h_{Di})-\hfill \\ -(1-\epsilon )\sum _i(s_{Bi}{T}_D-h_{Bi})]+\sigma +\frac{T_B{T}_D}{T_B-T_D}=q^0+\sigma \frac{T_B{T}_D}{T_B-T_D}.\hfill \end{array}$$

(5)

The first addend in the right hand side of (5), denoted as $q^0$, is the energy consumption for a reversible process (when heat and mass transfer is infinitely slow, that is, the column is infinitely large). This value depends only on properties of incoming and outgoing streams and it is proportional to $g_F$. The second addend corresponds to the irreversible losses of energy.

Taking into account that the difference $(h_i-T_D{s}_i)$ for every component is equal to its chemical potential $\mu$ at $T=T_D$, we obtain the relationship between the heat stream and the capacity of the column:

$$\begin{array}{c}q=g_{{}_F}\frac{T_B}{T_B-T_D}\left[\epsilon \sum _i{\mu }_i(T_D,x_{DI})+(1-\epsilon )\sum _i{\mu }_i(T_D,x_{Bi})-\sum _i{\mu }_i(T_D,x_{Fi})\right]+\hfill \\ +\sigma \frac{T_B{T}_D}{T_B-T_D}.\hfill \end{array}$$

(6)

Chemical potential is calculated as

$${\mu }_i(T,P,x_i)={\mu }_{i0}(P,T)+RTln{x}_i,i=1,2,.....$$

(7)

Because the chemical potential at every plate of the column corresponds to equal temperature and pressure, their difference does not contain the value ${\mu }_{i0}(P,T)$. This difference depends only on the composition of fluid streams so, the right hand side of (6) can be written as:

$$q=g_{{}_F}\frac{T_B}{T_B-T_D}\left[W_F-\epsilon W_D-(1-\epsilon )W_B\right]+\frac{\sigma T_D{T}_B}{T_B-T_D}=\frac{p_0}{{\eta }_{{}_c}}+\frac{\sigma T_D}{{\eta }_{{}_c}}.$$

(8)

Here

$$W_{ji}=-R{T}_D\left[x_{i}ln{x}_i+(1-x_i)ln(1-x_i)\right](j=F,D,B)$$

(9)

is the work of a reversible separation of one mole of the j-th stream into pure components and the expression in square brackets in (8) is the work of a reversible separation of one mole of the feed stream with the corresponding molar fraction $x_{{}_F}$ into two streams with molar fractions $x_{{}_B}$ and $x_{{}_D}$ at the temperature $T_D$. We will be denoting this value as $A_G$. The value

$${\eta }_{{}_c}=(1-T_D/T_B)$$

(10)

is analogous to the Carnot efficiency.

Assuming that the entropy generation in (8) is zero, we obtain the lower (reversible) estimate for the energy consumption of the fractional distillation: $q^0=\frac{g_F{W}_G}{{\eta }_{{}_c}}$. A reversible fractionating column can be idealized as a heat engine with the hot source having the temperature $T_B$ and the cold sink having the temperature $T_D$. This engine produces the power of separation $p^0=g_F{W}_G$.

3. Optimal Separation Sequence for Multicomponent Fractional Distillation

Cascade of Two Binary Distillation Columns

We consider the system of two reversible fractionating columns, separating the feed stream into three fractions, the composition of which is given. The value of the reversible separation power $p^0=g_F{W}_G$ is also given. It does not depend on a separation sequence but the efficiency and fraction of power per column $\gamma$ depend on this sequence. The problem is to choose the optimal sequence from two possible ones, so the total energy consumption will be minimal. Because the energy consumption is proportional to the capacity, we assume that $g_F=1$. We denote the efficiency of the first column as ${\eta }_1$ and the efficiency of the second one as ${\eta }_2$. The separation sequence, when the most volatile component (MVC) is being separated at the first stage, is called the direct one and the sequence, when the least volatile component is being separated at the first stage, is called the indirect one.

We assume that the first column of the direct sequence produces the fraction ${\gamma }_1$ of the total power and the second column produces the fraction $(1-{\gamma }_1)$ of this power. For the indirect sequence these values are denoted as ${\gamma }_2$ and $(1-{\gamma }_2)$.

The direct sequence is preferable if

$$\frac{{\gamma }_1}{{\eta }_{1,23}}+\frac{1-{\gamma }_1}{{\eta }_{2,3}}<\frac{{\gamma }_2}{{\eta }_{12,3}}+\frac{1-{\gamma }_2}{{\eta }_{1,2}}.$$

(11)

The left hand side (lhs) of (11) is proportional to the energy consumption per mole for the direct sequence and the proportionality coefficient is $\frac{1}{W_G}$. The right hand side (rhs) of this inequality is proportional to the energy consumption per mole for the indirect sequence. The comma between indices corresponds to the composition of a mixture being separated. So ${\eta }_{1,2},{\eta }_{2,3}$ are efficiencies of a separation of the mixture of the first and second or the second and third components correspondingly at the second stage.

If the inequality (11) has the opposite sign, the indirect sequence will be preferable. Efficiencies in this inequality are determined by the ration of boiling points of components. For the first stage of the direct sequence it is the ratio of $T_1$ to $T_{23}$, the boiling point of the mixture of the second and the third component. For the second stage of the direct sequence it is the ratio of $T_2$ and $T_3$. The left hand side and right hand side of (11) determine the thermodynamic difficulty of a separation. We will denote them as $C_{1,23}$ for the direct sequence and as $C_{12,3}$ for the indirect one.

The inequality (11) allows one to compare values of reversible energy consumption for any chosen separation sequences and states that the optimal sequence is the one for which the difficulty C is the lowest (the reversible efficiency in this case is maximal). The following necessary condition of optimality is true: If the separation sequence corresponds to the minimal energy consumption, then for every two-column cascade in the whole system its partial sequence must be chosen in the way that minimizes the value of C.

For three-component mixture with the vector of molar fractions $x_1,x_2,x_3$ the condition (11) can be rewritten as:

$$\begin{array}{c}[x_{1}ln{x}_1+(1-x_1)ln(1-x_1)]\frac{T_{23}-T_1}{T_{23}}+\hfill \\ +[x_{2}ln{x}_2+x_{3}ln{x}_3-(1-x_1)ln(1-x_1)]\frac{T_3-T_2}{T_3}>\hfill \\ >[x_{3}ln{x}_3+(1-x_3)ln(1-x_3)]\frac{T_3-T_{12}}{T_3}+\hfill \\ +[x_{2}ln{x}_2+x_{1}ln{x}_1-(1-x_3)ln(1-x_3)]\frac{T_2-T_1}{T_2}.\hfill \end{array}$$

(12)

Here $T_{12}$ and $T_{23}$ are bubble points of mixtures of corresponding components. The following chain of inequalities is true:

$$T_1<T_{12}<T_2<T_{23}<T_3.$$

(13)

In the specific case when the ratio of boiling points depends only on compositions of fractions adjacent to the point where separation is made ${\eta }_{12}\approx {\eta }_1,{\eta }_{23}\approx {\eta }_2$ and condition (11) is especially simple:

$$({\gamma }_1+{\gamma }_2-1)\left(\frac{1}{{\eta }_1}-\frac{1}{{\eta }_2}\right)<0.$$

(14)

In this case the following Rule is true: If the first column of the cascade has the highest capacity, the separation sequence must be chosen in the way in which the efficiency of one stage is greater than the one of next stages.

Because boiling points of fractions are going closer when the number of stage increases, the efficiency decreases from the first stage to the last one.

In the most of cases, the sign of the first factor in left hand side of (14) is positive, because the feed stream for the first column is greater than feed streams of succeeding columns.

We will show that for a three-component mixture the function

$$F={\gamma }_1+{\gamma }_2-1$$

(15)

is positive when molar fractions of components are non-zero.

The sign of F (15) is equal to the sign of

$$F_0=(1-x_1-x_3)ln(1-x_1-x_3)-x_{1}ln{x}_1-x_{3}ln{x}_3.$$

(16)

Derivatives of this function

$$\frac{\partial F_0}{\partial x_1}=ln\frac{1-x_1}{1-x_1-x_3},\frac{\partial F_0}{\partial x_3}=ln\frac{1-x_3}{1-x_1-x_3}$$

(17)

are positive for non-zero molar fractions of components and become zero when $x_1=0$ or $x_3=0$. The function $F_0$ reaches its minimum on coordinate axes and its minimal value is zero.

So, for every two-column cascade, the rule of the decrease of the efficiency is true, when temperatures in a reboiler and a condenser are determined only by compositions of fractions adjacent to the point at which the separation is made.

Cascade of Three Binary Distillation Columns

For a cascade consisting of three distillation columns we must choose one sequence of three possible variants: 1(234); (12)(34); (123)(4). The difficulty of the separation can be computed for every sequence:

$$\begin{array}{c}{C}_{1\left(234\right)}=C_{1,234}+(1-x_1)min[C_{2,34};C_{23,4}],\hfill \\ C_{\left(12\right)\left(34\right)}=C_{12,34}+(x_1+x_2)C_{1,2}+(x_3+x_4)C_{3,4},\hfill \\ C_{\left(123\right)4}=C_{123,4}+(1-x_4)min[C_{1,23};C_{12,3}].\hfill \end{array}$$

(18)

The optimum sequence corresponds to the minimum of (18).

4. Parametrization of the Column Capacity as the Function of the Energy Consumption

Take a closer look on the total entropy generation as a function of the capacity of the column. This allows one to use the Equation (8) and obtain the relationship between the capacity and the energy consumption.

We assume that the heat transfer in the reboiler and condenser is governed by the linear law:

$$q={\beta }_B(T_{+}-T_B)={\beta }_D(T_D-T_{-}),$$

(19)

where $T_{+}$ and $T_{-}$ are temperatures of heating vapor and cooling fluid correspondingly and ${\beta }_B$, ${\beta }_D$ are coefficients of heat transfer in the reboiler and the condenser. Kinetics of heat transfer at every plate or each packing section are described by

$$g_i(y,y^0)=k\frac{\left[{\mu }_i(T,y_i^0)-{\mu }_i(T,y_i)\right]}{T}.$$

(20)

Here $y_i$ is the vapor molar fraction of the i-th component, corresponding to the operating line, $y_i^0$ is its equilibrium vapor fraction, ${\mu }_i$ are chemical potentials, k is the effective coefficient of a mass transfer, T is the temperature on a plate.

Reference [6] gives the expression for the entropy generation as a function of the energy consumption:

$${\sigma }_{min}=q^2\left(\left[\frac{1}{{\beta }_B{T}_B{T}_{+}}+\frac{1}{{\beta }_D{T}_D{T}_{-}}\right]+\left[2\sum _i\frac{(x_{Di}-x_{Bi})}{k{r}_i^2}\right]\right).$$

(21)

After substituting this expression into (8) one can obtain the expression for the boundary of the reachable set of a column:

$$g\le bq-a{q}^2,$$

(22)

where b and a are characteristic coefficients that are functions of column properties:

$$a=\left[\frac{1}{{\beta }_{{}_B}{T}_B{T}_{+}}+\frac{1}{{\beta }_{{}_D}{T}_D{T}_{-}}+2\sum _i\frac{(x_{Di}-x_{Bi})}{k{r}_i^2}\right]\frac{T_D}{W_G},$$

(23)

$$b=\frac{T_B-T_D}{T_B{W}_G}=\frac{{\eta }_c}{W_G}.$$

(24)

The coefficient b is the reversible efficiency of a column. It is equal to the ratio of its thermal (Carnot-like) efficiency and reversible work of separation. The coefficient a determines the irreversibility of transfer processes within a column. The possibility of such parametrization allows one to reveal the relationship between the efficiency of a reversible column and the efficiency of an irreversible one.

The efficiency of a column is a function of characteristic coefficients:

$$\eta =\frac{g}{q}=b-aq.$$

(25)

It follows from (25) that the efficiency reaches its maximum $b={\eta }_{rev}$ in a reversible process, when values of $g_F$ and q vanish. The operating region of the boundary of the reachable set corresponds to such values of q for which the capacity of a column does not decrease. This region is bounded by the value $q^{*}=\frac{b}{2a}$.

Introducing the relative heat stream $q_0=\frac{q}{q^{*}}$ and substituting it into (25) instead of q one can obtain

$$\eta =b(1-0,5q_0).$$

(26)

It means that within the operating region ($0<q_0\le 1$) the efficiency of an irreversible column depends monotonously on the efficiency of a reversible column. For the operating mode with the maximal capacity the former is equal to the half of the latter. This fact allows us to state that recommendations about the choice of a separation sequence made for reversible columns are true for irreversible ones. If every column in the cascade is working at its maximal capacity, the energy consumption will be approximately two times larger than its reversible estimate.

It is worth to note that the reversible efficiency b depends only on temperatures in the reboiler and the condenser and the composition of the feed flux but the irreversibility coefficient a depends also on the latent enthalpy of vaporization of MVC and kinetic coefficients of heat and mass transfer.

The right hand side of (22) can be good approximation to the relationship between the capacity of the column and its energy consumption. Characteristic coefficients can be determined experimentally and recomputed using (23), (24) if some process’ parameters change. If $q_1,g_1$ and $q_2>q_1,g_2>g_1$ are measured values of the energy consumption and the capacity of a column within its operating region, then characteristic coefficient can be calculated using:

$$a=\frac{g_1{q}_2-g_2{q}_1}{q_2^2{q}_1-q_1^2{q}_2},b=\frac{g_1{q}_2^2-g_2{q}_1^2}{q_1{q}_2^2-q_2{q}_1^2}.$$

(27)

Complete Separation

Now we analyse the case of the complete separation when there are no components that are present in both upper and lower products. In this case:

$$\epsilon =\sum _{i=1}^{\nu }{x}_{Fi},1-\epsilon =\sum _{i=\nu +1}^n{x}_{Fi}.$$

(28)

Taking into account that $x_{Di}=x_{Fi}/\epsilon$ and $x_{Bi}=x_{Fi}/(1-\epsilon )$, we rewrite the expression for the molar work of the separation as

$$W_G=-R{T}_D(\epsilon ln\epsilon +(1-\epsilon )ln(1-\epsilon )),$$

(29)

so the value of the energy consumption per mole of the mixture being separated is equal

$$q_m=\frac{1}{b}=-\frac{1}{{\eta }_c}R{T}_D(\epsilon ln\epsilon +(1-\epsilon )ln(1-\epsilon )).$$

(30)

5. Computation of the Thermal Efficiency

To compute the value of the thermal efficiency, one must use some procedure to compute temperatures in the reboiler and the consender. Here we present one possibility to do this.

The temperature in the condenser is usually taken as $T_D=323$ K, so the cooling liquid is the water at the temperature 300 K. To adjust this temperature the pressure within the column must be changed for every mixture.

The composition of the vapor stream $y_D$ and the liquid one $x_D$ within the condenser are related to each other through the value of vapor-liquid equilibrium ratio $K_{iD}$. These values depend on properties of the i-th component, the temperature $T_D$ and the pressure $\overline{P}$:

$$y_{Di}=x_{Di}{K}_{iD}(T_D,\overline{P}).$$

(31)

Because the molar fraction of every component in the vapor phase at the equilibrium is equal to the ratio of its partial pressure $P_{iD}$ to the total pressure $\overline{P}$, we can write

$$K_{iD}(T_D,\overline{P})=\frac{P_i^0\left(T_D\right)}{\overline{P}}.$$

(32)

Here, the partial pressure $P_{iD}\left(T_D\right)$ is defined as the product of the pressure of the vapor of a pure component $P_{iD}^0\left(T_D\right)$ and its molar fraction in the liquid phase.

We consider the VLE in the upper part of a column. The composition of the stream coming out of the condenser is determined by the composition of the vapor y in one. The composition of the liquid stream within the condenser is determined by y, the pressure $\overline{P}$ and the temperature $T_D$

$$x_D=\frac{y_D}{K_D(T_D,\overline{P})}.$$

(33)

Because ${\sum }_i{x}_{Di}=1$, one can write, using (32), (33):

$$\overline{P}=\frac{1}{\sum _{i=1}^n\frac{x_{Di}}{P_i^0\left(T_D\right)}}.$$

(34)

The same way, one can find the value of the temperature within the reboiler $T_B$, using the value of $\overline{P}$ and compositions of corresponding streams:

$$\overline{P}=\sum _{i=1}^n{x}_{Bi}{P}_i^0\left(T_B\right).$$

(35)

The Equation (35) is highly non-linear and can be solved only numerically but since its right hand side is monotonous with respect to $T_B$, it has only one real root.

In the case, when components are ideal liquids, one can use the Antoine equation [7] to calculate vapor pressures of components:

$$P_i^0\left(T\right)={10}^{\left(A_i-\frac{B_i}{T+C_i}\right)},$$

(36)

where $A_i$, $B_i$ and $C_i$ are empirical coefficients widely presented in various sources. If components are not ideal liquids, one must use more complex equations for this task [4].

The algorithm of computation of the thermal efficiency is following:

• The temperature in the condenser $T_D$, compositions of the feed and product streams $x_F$, $x_D$, $x_B$ and Antoine equation coefficients $A_i$, $B_i$, $C_i$ are given for every component.
• The total pressure is computed using the VLE Equation (34). Necessary values of the vapor pressure for every component are computed using the Antoine Equation (36).
• The VLE equation for the reboiler (35) is solved numerically to find $T_B$.
• Values of $T_D$ and $T_B$ are substituted into (10)

Example 1. Two-Component Mixture

We consider the separation of the mixture mentioned in Reference [4], using the data from Reference [8], summarized in the

Table 1. Data for Example 1.

Component	${\mathit{x}}_{\mathit{F}}$	${\mathit{x}}_{\mathit{D}}$	${\mathit{x}}_{\mathit{B}}$	A	B	C	r, kJ/mole
Benzene	0.4	0.95	0.1	4.01814	1203.835	−53.226	33.9
Toluene	0.6	0.05	0.9	4.07827	1343.943	−53.773	37

. We will find the value of $K_T$, using the above-mentioned algorithm.

1. The temperature in the condenser in given $T_D=323$ K. Properties of the feed and product streams are given in the Table 1.

2. Partial pressures of pure components are computed using (36).

$$P_1^0\left(T_D\right)={10}^{\left(4.01814-\frac{1203.835}{323+53.226}\right)}=6.58\mathrm{bar}.$$

$$P_2^0\left(T\right)={10}^{\left(4.07827-\frac{1343.943}{323+53.773}\right)}=3.25\mathrm{bar}.$$

The total pressure is computed using (34)

$$\begin{array}{c}\overline{P}=\frac{1}{\frac{0.95}{6.58}+\frac{0.05}{3.25}}=6.26\mathrm{bar}.\hfill \end{array}$$

3. The VLE equation for the reboiler is (35):

$$\begin{array}{c}6.26=0.1·{10}^{\left(4.01814-\frac{1203.835}{T_B+53.226}\right)}+0.9·{10}^{\left(4.07827-\frac{1343.943}{T_B+53.773}\right)}.\hfill \end{array}$$

Solving it for $T_B$ we obtain $T_B=351\mathrm{K}$.

4. The value of the thermal efficiency is equal to (10):

$${\eta }_c=\frac{351-323}{351}=0.08.$$

Example 2. Multi-Component Mixture

We consider the process of the separation of the mixture mentioned in Reference [4]. The data are taken from Reference [8] and summarized in the

Table 2. Data for Example 2.

Component	${\mathit{x}}_{\mathit{F}}$	${\mathit{x}}_{\mathit{D}}$	${\mathit{x}}_{\mathit{B}}$	A	B	C	r	${\mathit{T}}_0$, K
Methane	0.26	0.435	0	3.9895	443.028	−0.49	8.5	111.65
Ethane	0.09	0.15	0	4.50706	791.3	−6.422	9.76	184
Propane	0.25	0.41	0.01	4.53678	1149.36	24.906	16.25	231
n-Butane	0.17	0.005	0.417	4.35576	1175.581	−2.071	22.4	272
n-Pentane	0.11	0	0.274	3.9892	1070.617	−40.454	26.5	309
n-Hexane	0.12	0	0.299	3.45604	1044.038	−53.893	31	341

. We will find the value of $K_T$, using the above-mentioned algorithm.

1. The temperature in the condenser in given $T_D=323$ K. Properties of the feed and product streams are given in the Table 2.

2. The total pressure is computed using (34):

$$\overline{P}=36.35\mathrm{bar}.$$

3. Solution of the VLE equation for the reboiler is:

$$T_B=425\mathrm{K}.$$

4. The thermal efficiency is

$${\eta }_c=\frac{425-323}{425}=0.24.$$

6. Results

The paper shows using thermodynamic balance equations that for the fractional distillation of ideal mixtures the estimate of its capacity as a function of the energy consumption has a form of concave upward parabola. This function is characterized by only two parameters: one is the reversible efficiency and another is the irreversibility coefficient. These parameters determine the maximum capacity of a column and its efficiency in such operating mode. We have shown that the efficiency of an irreversible column increase monotonously as a function of the efficiency of a reversible one. The efficiency corresponding to the operating mode with maximum capacity is equal to the half of the reversible efficiency. This fact allows one to use exceptionally simple rule for selection of optimum separation sequence for multicomponent distillation: “If the first column of the cascade has the highest capacity, the separation sequence must be chosen in the way in which the efficiency of one stage is greater than the one of next stages.”