Insights from Mathematical Modelling into Energy Requirement and Process Design of Continuous and Batch Stirred Tank Aerobic Bioreactors

Abstract

Bioreaction kinetics, oxygen transfer and energy modelling were applied to stirred tank aerobic bioreactors. This was done to investigate how key input design variables influence bioreactor size, feed and wasted substrate, and electrical energy requirements for aeration and cooling, and to compare batch and continuous modes of operation. Oxygen concentration in the liquid is a key input design variable, but its selection is challenging as it can result in design trade-offs. Reducing its value caused a decrease in electrical energy requirement, however this tended to increase the working volume of the bioreactor. The minimum or near-to-minimum total energy requirement for oxygen transfer occurred when operating at the onset of flooding throughout the bioreaction time. For typical K_S values, continuous mode of operation required a much smaller bioreactor volume, due to higher operating cell concentration, and this is a major advantage of continuous over batch.

1. Introduction

Stirred tank bioreactors may be operated in batch or continuous mode to achieve a required productivity or specified mass of product in a specified time. Selection of key input design variables can be challenging. These include oxygen and substrate concentrations in the bioreactor liquid, air flowrate, agitator power input, and operating temperatures for the cooling. These selections will influence key process design outputs, such as bioreactor sizing, energy requirement and environmental impact. Bioreactor sizing is determined by the bioreactor volume, which will impact cost and physical footprint. The major energy requirements for aerobic bioreactors are energy required for oxygen transfer and bioreactor cooling, which have significant associated energy costs. Environmental impact is associated with emissions from energy supply, in particular its carbon footprint, and with substrate required and wasted substrate through raw materials being extracted from nature and waste being discharged to nature. Consequently, there are usually many design objectives, such as minimising the energy needed and size of the bioreactor, and impacts on the natural environment, some of which may conflict with each other, making it challenging to select values for design input variables.

Supply of air for oxygen transfer is a major energy requirement in industrial scale aerobic bioreactors [1]. Oxygen concentration in the bioreactor liquid is an important design variable as it can influence both the bioreaction kinetics and energy requirement for oxygen transfer, which in turn can influence the cooling requirement. Agitator mechanical power input and air flowrate are the two main determinants of the oxygen transfer rate under direct operational control, whose specification has a major influence on energy requirement. Manipulation and control of the agitator power and/or air flowrate throughout the bioreaction provides an opportunity for energy saving by providing an oxygen transfer rate (OTR) that satisfies the oxygen uptake rate (OUR) in a more energy efficient way [2,3,4,5]. Evaluation of the relationship between the volumetric mass transfer coefficient (k_La) and agitator power and air flowrate is crucial in the design, operation and scale-up of bioreactors [1,6,7,8,9,10,11,12]. Oxygen transfer rate in a bioreactor is strongly influenced by the oxygen concentration in the broth, the broth’s physical chemical properties, agitator selection, and hydrodynamic conditions [1,13,14,15,16,17,18].

Even though there is much work presented on oxygen transfer and bioreaction dynamics in the literature, there is little presented on the application of mathematical modelling to analysing energy requirements in bioreactors and how this may interact with other key process design output variables, such as the size of the bioreactor. Alves and Vasconcelos [19] showed energy savings of 10 to 20% could be achieved by applying a mathematical optimisation procedure to aerobic bioreactions. Kreyenschulte et al. [20] developed a computation tool to assess the energy demand at large-scale based on small-scale data. They examined the impact of a number of constraints and showed that the minimum energy consumption for oxygen transfer was achieved by operating close to the onset of flooding for bioreactor volumes of 20 m³ and larger using conventional agitators. Fitzpatrick et al. [2] carried out a mathematical simulation study for a batch system, which showed that the minimum or near-minimum total energy requirement for oxygen transfer occurred when operating at the onset of impeller flooding throughout the bioreaction, by continuously varying both impeller power and air flowrate over the bioreaction time. Operating at the onset of flooding may not be practical to implement in practice. However, the minimum energy can be approached by dividing the bioreaction time into a small number of time segments with appropriately chosen constant agitator powers and varying the air flowrate within each segment. This is potentially much more practical to implement.

The objectives of this study are: (1) to apply mathematical modelling to investigate the influence of key input design variables on bioreactor working volume, energy requirement and feed/wasted substrate, and how this may result in design trade-offs between conflicting design objectives in aerobic stirred tank bioreactors; and (2) to compare batch and continuous modes of operation.

2. Mathematical Modelling

The stirred tank bioreactor modelled has a six bladed Rushton turbine impeller used with a standard design configuration. A height to tank diameter ratio of 1 and the impeller diameter to tank diameter ratio of 0.35 was used in this study. The product production rate (P_R) for both the continuous and batch bioreactors is given a value of 100 kg h⁻¹. Details of the mathematical models are provided in the following sections and the calculations for the continuous mode were implemented using Microsoft Excel (Microsoft, Seattle, WA, USA) and those for batch mode were mainly implemented using Matlab (MathWorks, Natick, MA, USA).

2.1. Bioreaction Kinetics

Cell growth is modelled using a first order kinetic model represented by Equation (1):

$$r_x=\mu X$$

(1)

where r_x is the cell growth rate, X is the cell concentration and µ is the specific growth rate, which is modelled using the Monod model (Equation (2)):

$$\mu =\left(\frac{{\mu }_{\max }S}{K_S+S}\right)\left(\frac{C_{OL}}{K_O+C_{OL}}\right)$$

(2)

where S and C_OL are the sugar and oxygen concentrations, respectively, µ_max, K_S and K_O are constants.

The rate of change of product concentration (r_p) and sugar concentration (r_s) due to microbial metabolism were modelled using the following Equations (3) and (4):

$$r_p=\mathsf{\alpha }{r}_x+\beta X$$

(3)

$$r_s=-\left(\frac{1}{Y_{XS}}{r}_x+\frac{1}{Y_{PS}}{r}_p+m_{S}X\right)$$

(4)

Suitable values for the constants in the bioreaction model equations are presented in

Table 1. Values for constants in bioreaction kinetic model.

μmax (h−1)	KS (g·L−1)	KO (g·L−1)	α	β (h−1)	YXS	YPS	mS (h−1)
0.25	0.005	0.000363	2.9220	0.1314	0.55	1	0.025

, and these were selected from considering published works in the literature. Values for µ_max and K_S can vary significantly where some reported values for µ_max varied from 0.09–4.2 h⁻¹ [21,22,23,24]. K_S values are typically in the mg·L⁻¹ range, with reported values typically varying from 0.07 to 200 mg·L⁻¹ [21,25,26], although Znad et al. [22] reported a value of 130,900 mg·L⁻¹. K_O can have significant variation but typically it is in the range of 0.1 to 1 mg·L⁻¹ [22,26,27]. The values of Y_XS, Y_PS and m_S were obtained from van’t Riet and Tramper [21]. The values of α and β were obtained from Znad et al. [22].

For the continuous bioreactor the steady-state sugar and product mass balance equations are provided in Equations (5) and (6):

$$r_s=-D_R\left(S_0-S_f\right)$$

(5)

$$r_p=D_R\left(P_f-P_0\right)$$

(6)

where D_R is the dilution rate, S_f and P_f are the steady-state sugar and product concentrations, respectively in the CSTB, and P₀ is the concentration of any product in the feed.

Sugar and product concentrations in the feed were S₀ = 150 g·L⁻¹ and P₀ = 0 g·L⁻¹, respectively. For the batch bioreactor, the initial cell concentration was X₀ = 0.25 g·L⁻¹, and the bioreaction was completed when sugar concentration was reduced to 0.1 g·L⁻¹. For the CSTB, the kinetic modelling was applied to evaluate µ, P_f and the steady-state cell concentration (X_f) for given values of S_f. For batch, it was applied to evaluate the evolution of substrate, product and cell concentration over time, and in particular the final product concentration and bioreaction time when the bioreaction was completed.

2.2. Bioreactor Working Volume and Substrate Utilisation

Considering the values evaluated in Section 2.1, the following modelling equations were applied to evaluate the working volume of the bioreactor and the amounts of feed and wasted sugar. These were applied to the CSTB and batch operation for a specified product production rate (P_R = 100 kg·h⁻¹). The feed flowrate requirement for the CSTB was also evaluated.

2.2.1. Continuous Bioreactor

The feed volumetric flowrate (F) required to satisfy the product production rate (P_R) by the continuous stirred tank bioreactor (CSTB) is obtained from Equation (7):

$$P_R=F P_f$$

(7)

where F is the feed volumetric flowrate.

For a CSTB operating at steady-state, Equation (8) applies:

$$\mu =D_R= \frac{F}{V_L}$$

(8)

where D_R is the dilution rate and V_L is the working volume of the CSTB. Equation (8) is used to calculate V_L.

The mass flowrate of sugar substrate entering the CSTB (F_S0) is given in Equation (9):

$$F_{S0}=F S_0$$

(9)

The mass flowrate of wasted sugar leaving the CSTB (F_SW) is given in Equation (10):

$$F_{SW}=F S_f$$

(10)

2.2.2. Batch Bioreactor

The working volume of the batch bioreactor is evaluated from Equation (11):

$$P_R=\frac{V_L P_b}{\left(t_b+t_d\right)}$$

(11)

where P_b is the product concentration at the bioreaction time (t_b) when the bioreaction is completed and the sugar concentration (S_b) is 0.1 g·L⁻¹. The average downtime between batches (t_d) is given a value of 8 h.

The mass per unit time of feed substrate (M_SI) and wasted substrate (M_SW) is given in Equations (12) and (13), respectively:

$$M_{SI}=\frac{V_L{S}_0}{\left(t_b+t_d\right)}$$

(12)

$$M_{SW}=\frac{V_L{S}_b}{\left(t_b+t_d\right)}$$

(13)

2.3. Oxygen Transfer and Detrmination of Agitator Power Requirement

The OUR was modelled using Equation (14):

$$OUR=\delta \frac{dX}{dt}+\varphi X$$

(14)

where $\delta$ is the yield of oxygen consumed for cell growth and $\varphi$ is the oxygen consumption coefficient for maintenance. The values of δ and $\varphi$ can vary significantly depending on the bioreaction. The following values were selected: δ = 0.64 and $\varphi$ = 0.032 h⁻¹ based on a range of values provided in an OUR review article by Garcia-Ochoa et al. [28].

The mass transfer Equation (15) was used to calculate the k_La value required to supply the oxygen transfer rate (OTR) to satisfy the OUR at steady-state:

$$OTR=k_{L}a\left(C_{OL}^{*}-C_{OL}\right)$$

(15)

where:

$$C_{OL}^{*}=\frac{C_{OG}}{M}$$

(16)

C_OG is the oxygen concentration in the air bubbles and M is the Henry’s law equilibrium constant (=35). C_OG varies from the concentration of oxygen in the ambient air (C_OGI = 280 mg·L⁻¹) to the concentration of oxygen in the air leaving the bioreactor (C_OGO). Thus Equation (17) was used to evaluate an average equilibrium concentration of oxygen in the liquid:

$$C_{OL}^{*}=\frac{\frac{\left(C_{OGI}+C_{OGO}\right)}{2}}{M}$$

(17)

A mass balance on the bioreactor was used to evaluate another expression for OTR (Equation (18)):

$$OTR=\frac{F_G}{V_L}\left(C_{OGI}-C_{OGO}\right)$$

(18)

where F_G is air volumetric flowrate and V_L is the working volume of the bioreactor.

The correlation relationship between k_La and agitator mechanical power input in the gassed bioreactor (Pag) and air superficial velocity (v_s) is given by Equation (19). This equation was used to calculate Pag in the mathematical simulations:

$$k_{L}a=K{\left(\frac{Pag}{V_L}\right)}^{n_1}{\left(v_s\right)}^{n_2}$$

(19)

The values of the constants were K = 0.026, n₁ = 0.4 and n₂ = 0.5 and these were obtained from van’t Riet [29]. Equation (19) is an important correlation and the values of the constants in this equation should be experimentally evaluated in the application of this modelling approach to a real bioreaction. Furthermore, the size of the bioreactor volume may influence the values of constants in Equation (19). Even though the bioreactor volume changes in this study, a simplifying assumption is made that the values of the constants do not vary in Equation (19). However, in the application of the mathematical approach to a real bioreactor, some work should also be undertaken to investigate how scale-up influences these constants.

The air superficial velocity (v_s) is defined in Equation (20):

$$v_s=\frac{F_G}{A_T}$$

(20)

where A_T is the cross-sectional area of the bioreactor. The parameter vvm is used in this study, because the air flowrate is commonly expressed in terms of vvm in the bioprocess industry [15], and this is defined in Equation (21):

$$vvm=\frac{F_G}{V_L}$$

(21)

where the units are expressed as minutes⁻¹.

The above equations were typically solved in the following order. Firstly, OUR was evaluated from Equation (14). Then for a given value of vvm, F_G and v_s were evaluated from Equations (21) and (20), respectively. C_OL is given a constant value, thus OTR = OUR. C_OGO was calculated from Equation (18), after which $C_{OL}^{*}$ was calculated from Equation (17). Then, k_La was calculated from Equation (15) and Pag was calculated from Equation (19).

2.4. Flooding and Phase Equilibrium Constraints

The air flowrate is limited by impeller flooding and this depends on the mechanical power input (Pag). The air flowrate (F_GF) at the onset of flooding, for a fixed value of Pag, was evaluated by solving Equations (22)–(24). Equation (22) was obtained from Bakker et al. [18]:

$$N_A=30\left(N_{Fr}\right){\left(\frac{D}{T}\right)}^{3.5}$$

(22)

where:

$$N_A=\left(\frac{F_{GF}}{N{D}^3}\right) and N_{Fr}=\left(\frac{N^{2}D}{g}\right)$$

D and T are impeller and tank diameters, respectively. Equation (23) is the power number equation:

$$Pag=N_{PG}\rho N^3{D}^5$$

(23)

where the density (ρ) = 1 kg·L⁻¹, N is the impeller rotational speed and N_PG is the impeller power number. N_PG varies with the air flow rate, and Equation (24) was applied to take this into account. This equation was obtained from Bakker et al. [18] along with values for the constants:

$$\frac{N_{PG}}{N_P}=1-\left(b-a \mu \right)N_{Fr}^{d}tanh\left(c N_A\right)$$

(24)

where N_P is the ungassed power number (=6), μ is the liquid viscosity (5 mPa·s), a = 0.72, b = 0.72, c = 24, d = 0.25 [flat-bladed turbine impeller].

The oxygen concentration in the air leaving the bioreactor (C_OGO) was limited by the equilibrium constraint (25):

$$C_{OGO}\ge M\left(C_{OL}\right)$$

(25)

2.5. Aeration System Power Requirement

The agitator mechanical power input requirement was estimated from Equation (19). The compressor mechanical power requirement for a specific air flowrate was estimated from Equation (26):

$$P_C=\frac{\gamma }{\gamma -1}{F}_G{P}_{atm}\left({\left(\frac{P_i}{P_{atm}}\right)}^{\frac{\gamma -1}{\gamma }}-1\right)\left(\frac{1}{{\eta }_C}\right)$$

(26)

where P_atm is atmospheric pressure and Pi is the atmospheric pressure plus the static pressure acting on the bottom of the bioreactor due to weight of liquid, γ = 1.4. η_C is the isentropic efficiency of the compressor (assumed to be constant at 0.7). The sum of the agitator and compressor electrical power requirements (P_tot) was given by Equation (27):

$$P_{tot}=\left(\frac{Pag+P_C}{{\eta }_m}\right)$$

(27)

where η_m is the electric motor efficiency (assumed to be constant at 0.9 for both the agitator and compressor). For the batch bioreactor, the power will vary over time, thus the average power requirement over the batch cycle time is evaluated. The average electrical power requirement was defined as the batch electrical energy requirement divided by the batch cycle time. This is useful for comparison with CSTB power requirement.

2.6. Refrigeration Power Requirement for Cooling

The temperature in an industrial scale bioreactor is typically controlled by cooling to remove net heat production. This is typically achieved by passing cooling water through the jacket of the bioreactor and/or through an internal cooling coil or external heat exchanger. A water cooling system, such as a vapour compression refrigeration system, is typically used to remove the heat from the cooling water when it leaves the bioreactor so that the cooling water is continuously reused, and the cooling system requires energy [20].

It is assumed that the main sources of heat are microbial metabolic energy and heat dissipated by mechanical agitation. Consequently, the rate of total heat production (H_T) is given in Equation (28):

$$H_T=H_M+Pag$$

(28)

where H_M is the rate of microbial metabolic energy production, which is estimated from Equation (29):

$$H_M=Y_{HO}·OUR·V_L$$

(29)

where Y_HO = 14.7 kJ·g⁻¹ of oxygen [21].

Water is used as the coolant to remove heat from the bioreactor. It is assumed that the cooling water enters the bioreactor heat transfer system at 20 °C and exits at 25 °C, and a vapor compression refrigeration cycle is used to cool the water back down to 20 °C. The refrigeration system is assumed to be operated at refrigerant evaporation temperature (T_E) of 15 °C and a condensation temperature (T_C) of 35 °C. The refrigeration electrical power requirement (P_ref) was estimated using the co-efficient of performance (COP) in Equation (30):

$$P_{ref}=\frac{H_T}{{\eta }_{m}COP}$$

(30)

COP was estimated as 8.6 in Equations (31) and (32) using the COP of a Carnot refrigerator:

$$CO{P}_{Carnot}=\frac{T_E}{T_C-T_E}$$

(31)

$$COP={\eta }_{r}CO{P}_{Carnot}$$

(32)

where η_r is the refrigeration efficiency which is typically around 0.6.

3. Results and Discussion

3.1. Bioreaction Kinetics

Bioreaction kinetics will be highly influenced by the specific cell growth rate and how this is influenced by the sugar and oxygen concentrations in the bioreaction liquid. Figure 1a illustrates the influence of oxygen concentration on specific growth rate, which shows that it slowly decreases in value as the oxygen concentration is reduced within the range of 8 mg·L⁻¹ down to about 2 mg·L⁻¹. There is a more precipitous decrease at lower oxygen concentrations because the value of K_O is 0.363 mg·L⁻¹. On the other hand, the sugar concentration during bioreaction varies from 150 g·L⁻¹ down to 0.1 g·L⁻¹ and this does not have a major influence on specific growth rate, as illustrated in Figure 1a.

The effect of the steady-state sugar concentration (S_f) on the CSTB bioreaction kinetics (at a steady-state oxygen concentration of 2 mg·L⁻¹) is illustrated in Figure 1b. As S_f decreases, product concentration increases as more sugar is converted, and cell concentration increases as the average residence time increases. The batch bioreaction kinetics (at C_OL = 2 mg·L⁻¹) is illustrated in Figure 1c. The batch bioreaction progresses slowly up to about 10 h after which there are significant changes in concentrations and the bioreaction time is about 23 h. The evolution of OUR is also presented in Figure 1c, where the OUR reaches a maximum of 4.7 g·L⁻¹·h⁻¹ towards the end of the bioreaction.

3.2. Bioreactor Volume and Feed/Wasted Sugar Substrate

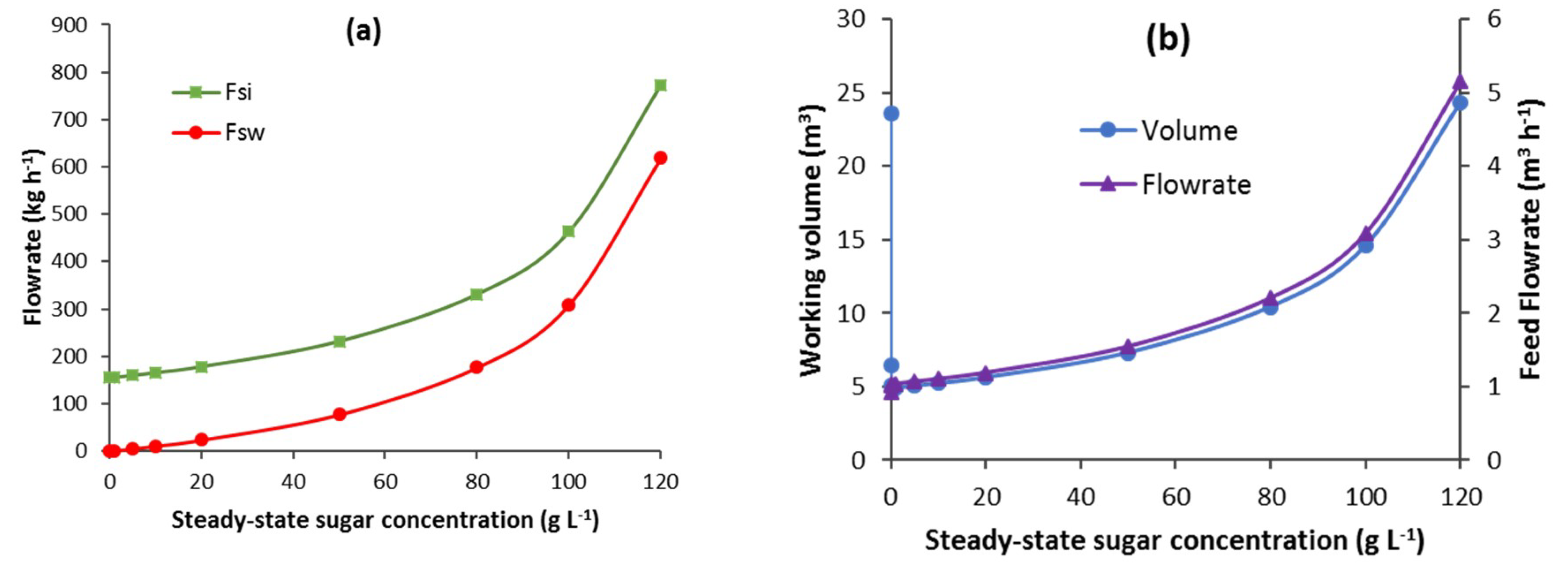
3.2.1. CSTB

The specification of S_f is very important in the process design of a CSTB to produce a specified rate of product leaving the bioreactor, as it impacts on the size of the bioreactor, the amount of feed sugar required and wasted sugar leaving the bioreactor. Figure 2a shows that operating at higher values of S_f results in both a larger feed sugar requirement and more unused or wasted sugar leaving the bioreactor. This is because more wasted sugar requires more feed sugar to meet the product production specification.

In Figure 2b, increasing S_f results in higher feed flowrate, which is to be expected as more feed sugar is required because less of the feed substrate is being metabolised when operating at higher values of S_f. The bioreactor working volume is a key design variable. Re-arranging Equation (8) gives Equation (33) which is used to evaluate the working volume (V_L):

$$V_L=\frac{F}{D_R} =\frac{F}{\mu }$$

(33)

From this equation, it can be seen that increasing F results in larger working volumes, thus larger working volumes are required when operating at higher values of S_f, as illustrated in Figure 2b. Furthermore, there is a trade-off between F and μ, as can be seen from Equation (33), because they both decrease as S_f decreases and thus trade-off against each other in the determination of V_L, which produces the minimum. However, for this bioreaction, the minimum V_L of about 4.9 m³ occurs at a low value of S_f at around 1 g·L⁻¹ and V_L is only slightly larger at 5.1 m³ at a very low S_f value of 0.1 g·L⁻¹. Consequently, for this bioreaction, it is desirable to operate at low steady-state sugar concentration (e.g., 0.1–1 g·L⁻¹) because this reduces bioreactor working volume, feed sugar requirement and wasted sugar leaving the bioreactor.

C_OL has a significant impact on the specific growth rate at lower values of around 1 mg·L⁻¹ and less, as illustrated in Figure 1a. Consequently, simulations were run to investigate the effect of C_OL on the feed and wasted sugar and on the bioreactor working volume. Figure 3a shows the effect of C_OL on the amount of wasted sugar, where it is shown that there were only very small differences. Similar trends were obtained for the feed sugar requirement and feed volumetric flowrate. Overall, C_OL has very little impact on these variables.

Figure 3b shows the impact of C_OL on the working volume of bioreactor, which shows a major impact, especially at low concentrations, e.g., at less than 0.5 mg·L⁻¹. The specific growth rate is reduced by lowering C_OL, which results in a larger bioreactor working volume, considering Equation (33), as the feed flowrate is not much affected. Consequently, the influence of C_OL on the specific growth rate is directly impacting on the bioreactor working volume.

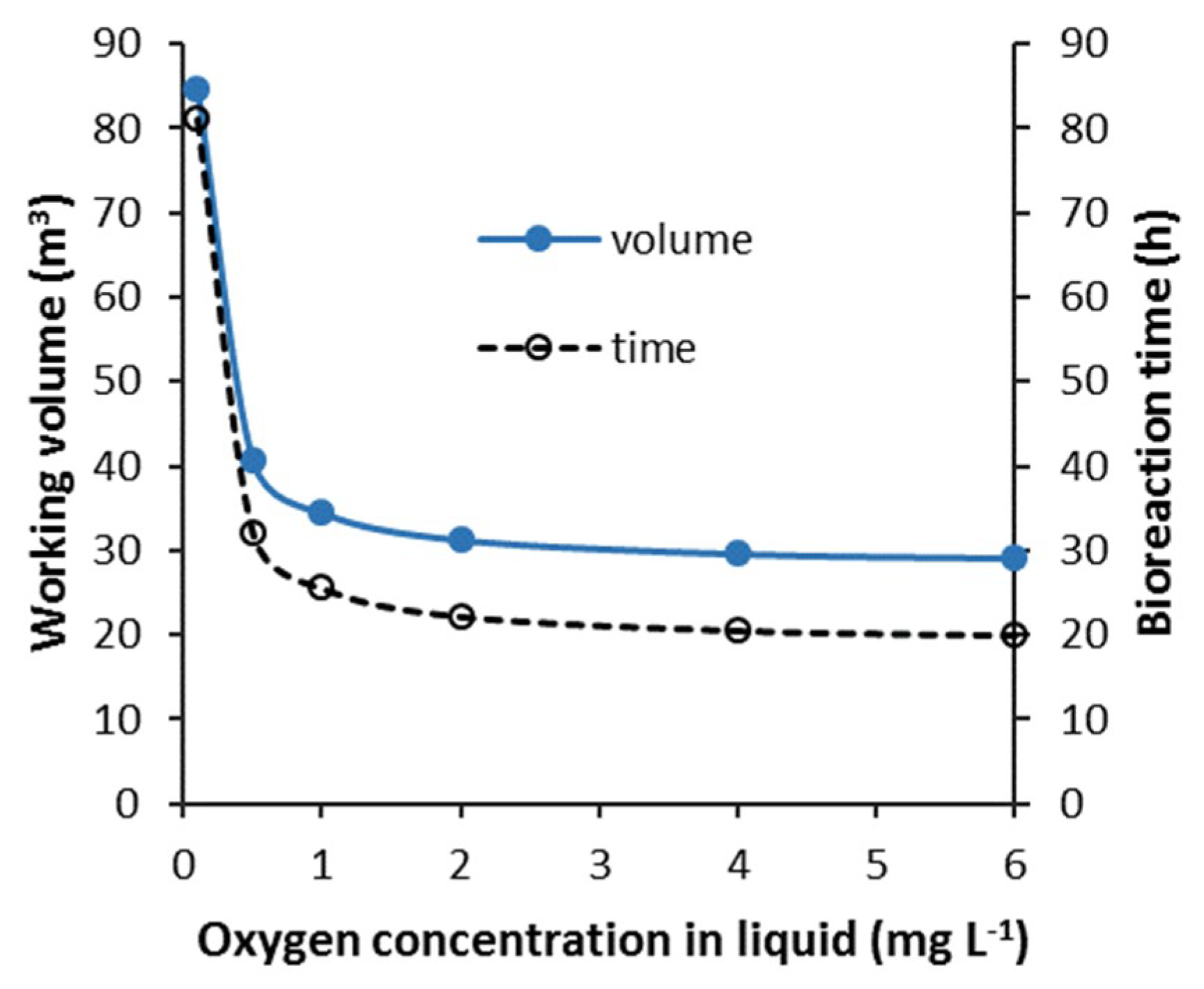
3.2.2. Batch

The batch bioreactor is different from the CSTB insofar as there is no requirement to select a steady-state sugar concentration, as the sugar concentration varies from the feed concentration of 150 g·L⁻¹ to a final concentration of 0.1 g·L⁻¹. The low final concentration ensures that there is little wasted sugar (M_SW = 0.1 kg·h⁻¹) which consequently reduces the feed sugar requirement (M_SI = 155 kg·h⁻¹). Comparing this to the CSTB operated at S_f = 1 g·L⁻¹ (and at the same C_OL of 2 mg·L⁻¹) shows that wasted and feed sugar is slightly greater for the CSTB at M_SW = 1 kg·h⁻¹ and M_SI = 155.7 kg·h⁻¹ (C_OL = 2 mg·L⁻¹). However, the working volume of the batch bioreactor is much greater (batch V_L = 31 m³ and CSTB V_L = 5 m³). This is mainly due to the differences in cell concentration and in-part due to the down-time between batches. For the CSTB, the steady-state cell concentration is about 27 g·L⁻¹ while cell concentration increases slowly during the batch bioreaction from a low value of 0.25 up to around 27 g·L⁻¹. Consequently, this lower bioreactor working volume is a major advantage for the CSTB, especially when it is operated at lower values of S_f, as can be seen from Figure 2b.

Like the CSTB, C_OL influences the bioreaction kinetics, which in turn influences the bioreaction time and the working volume of the batch bioreactor to produce a given amount of product. This is illustrated in Figure 4 and shows that the C_OL only starts to significantly influence V_L when it is reduced below around 1 mg·L⁻¹, which is to be expected considering that K_O is 0.363 mg·L⁻¹.

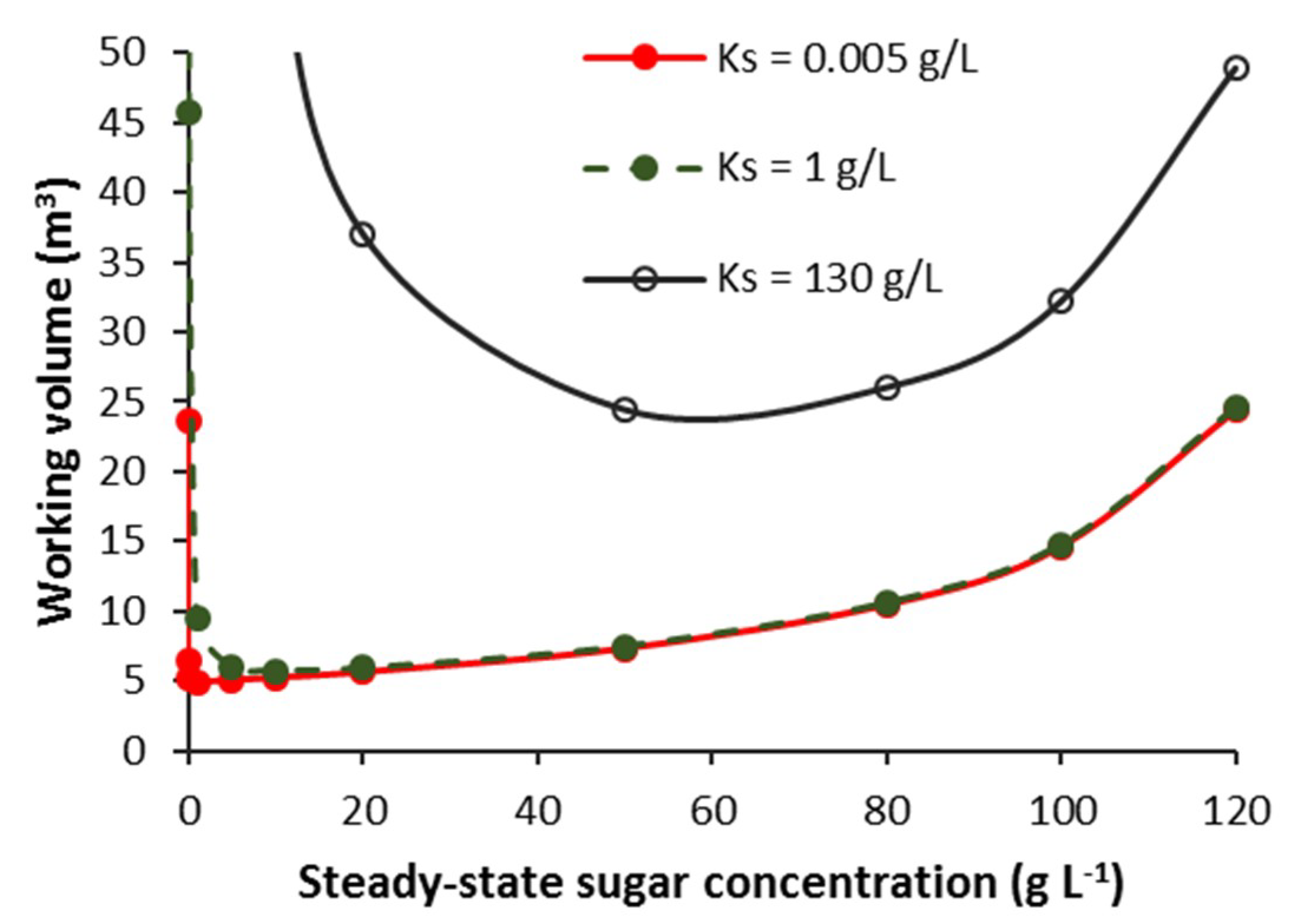
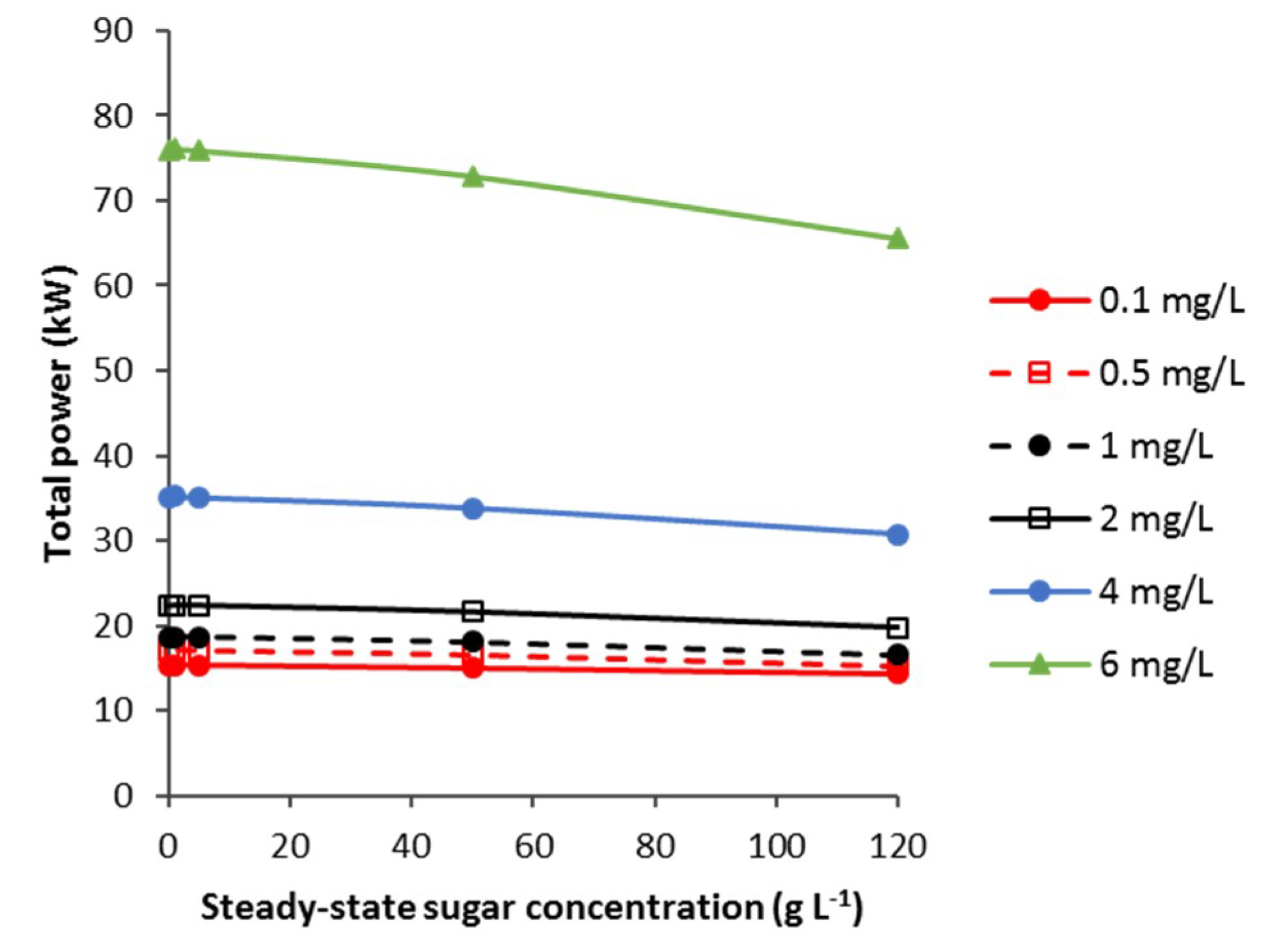
3.2.3. Effect of K_S and Sugar Concentration

Batch operation has a potential advantage over the CSTB insofar as the sugar concentration during batch varies from a high value in the feed down to a low value at the end, while the CSTB has to operate at a single constant steady-state value of S_f. On one hand, a CSTB operated at S_f values higher than the final batch concentration leads to higher feed sugar requirement and wasted sugar. On the other hand, operating at lower S_f values near to the final batch value may slow the bioreaction kinetics and increase V_L of the CSTB in comparison to the batch bioreactor, however this depends on K_S. In this work, K_S is given a value of 0.005 g·L⁻¹ and Figure 2a shows that S_f can be operated at low values before V_L minimises. Consequently, the CSTB can be operated at a low S_f value providing the benefits of both lower V_L and lower feed/wasted sugar. In practice, a wide range of K_S values have been reported typically varying from 0.00007 to 0.2 g·L⁻¹ (as highlighted in Section 2.1), although Znad et al. [22] reported an extremely high value of 130 g·L⁻¹ for a fungal bioreaction. Simulations were performed at three K_S values of 0.005, 1 and the extreme value of 130 g·L⁻¹ to investigate the effect of K_S and S_f on the bioreactor working volume. These results are presented in Figure 5 and it can be seen that for typical K_S values, the CSTB can be operated at low S_f values where V_L is maintained at or close to its minimum. This results in a V_L lower than that of batch mainly because of the higher cell concentration in the CSTB and also partly because it has no downtime between batches. This has also the benefit of greatly reducing the wasted sugar and the consequential feed sugar requirement.

The extreme value of K_S (= 130 g·L⁻¹) shows that the minimum V_L occurs at a S_f value of about 50 g·L⁻¹, and thus the selection of S_f represents a trade-off between reducing V_L and reducing feed/wasted sugar, as highlighted by Fitzpatrick et al. [30]. This is an extreme case, but may occur in some bioreactions, such as pelleted fungal bioreactions, possibly due to sugar mass transfer resistance.

3.3. Electrical Power Requirement for Oxygen Transfer

The oxygen concentration in the bioreactor liquid (C_OL) influences cell growth and the oxygen mass transfer driver, which in turn influence the OTR and the electrical power requirement. Thus, the initial part of the analysis on power requirement is conducted at a constant C_OL value of 2 mg·L⁻¹, and the effect of varying C_OL is presented later.

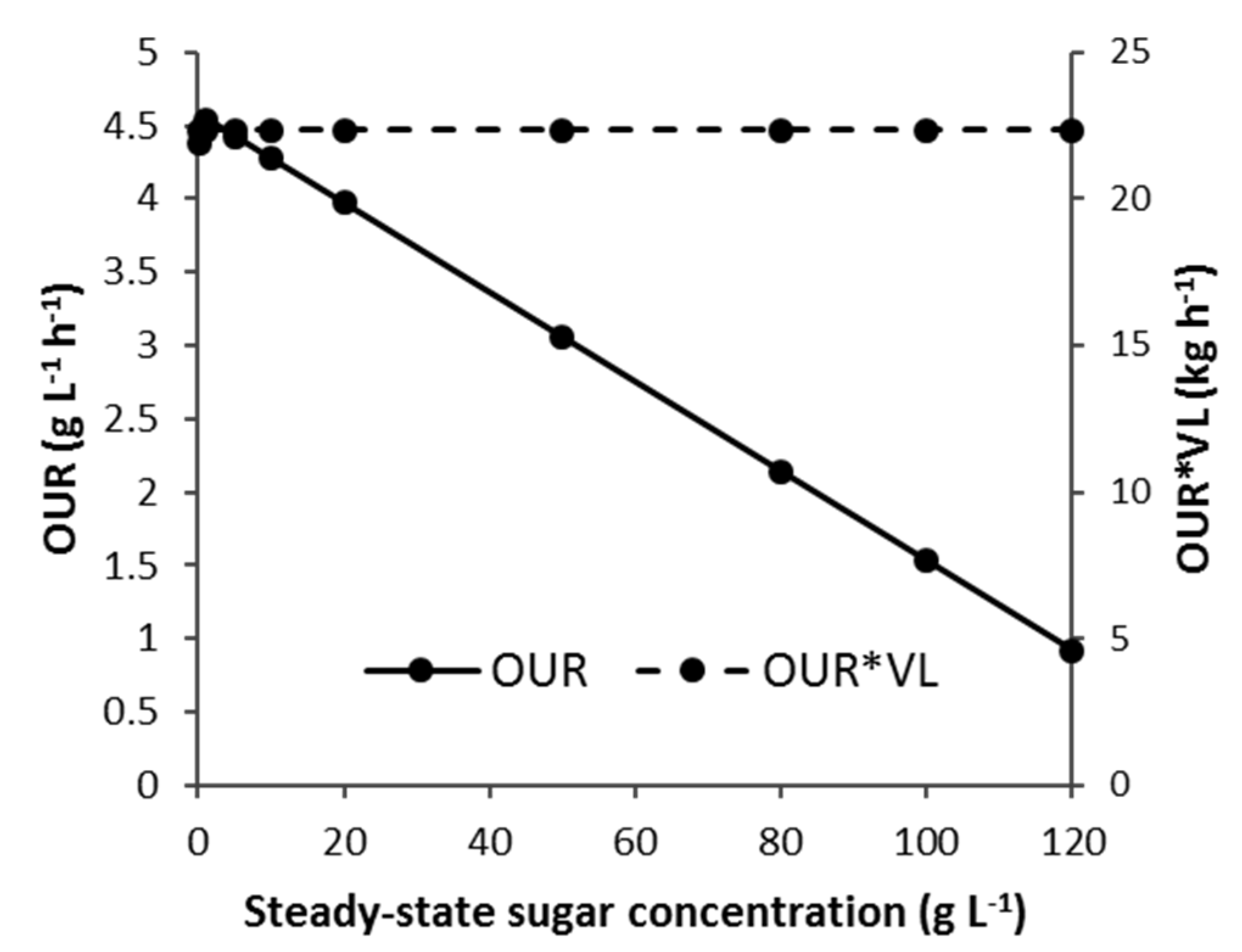
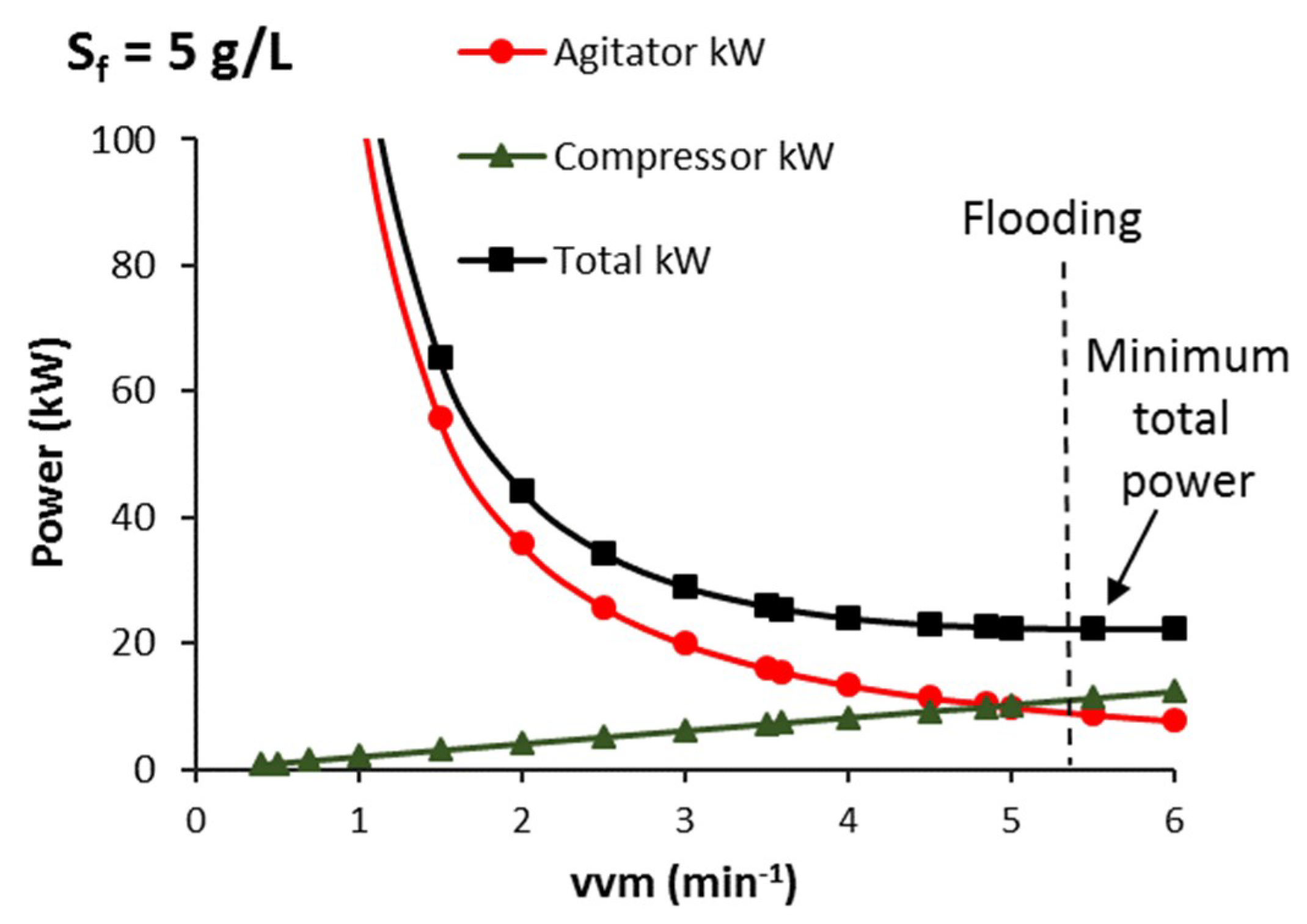
3.3.1. CSTB—Effect of vvm, Agitator Mechanical Power and Steady-State Sugar Substrate Concentration

The oxygen transfer system must be able to supply an OTR equal to the OUR, in order to maintain C_OL at a constant value of 2 mg·L⁻¹. This is achieved by a combination of air flow and mechanical agitation, subject to the constraints of agitator flooding and phase equilibrium outlined in Section 2.4. The OTR and the power requirements of the compressor and agitator will depend on the OUR, which in turn is influenced by S_f, as illustrated in Figure 6. The OUR increases as S_f decreases, because more of the feed substrate is being utilized resulting in higher cell concentrations, which results in higher OUR according to Equation (14). However, Figure 6 also shows that the total OUR in the bioreactor volume remains fairly constant, and this is because the bioreactor volume decreases as S_f decreases, as illustrated in Figure 2b, which counteracts the effect of the increasing OUR.

Simulations were performed to evaluate the effect of vvm on the compressor, agitator and total power requirements at different values of S_f. Data for S_f = 5 g·L⁻¹ are presented in Figure 7. This shows there can be a major variation in total electric power requirement (i.e., compressor + agitator power), to supply the same OTR, depending on the selection of vvm. Consequently, care needs to be taken in selecting vvm, so as to avoid excessive total power requirement, and this can result in major savings in aeration system energy requirement.

To supply the OTR required to meet the OUR, Figure 7 shows that the compressor power increases linearly with vvm while agitator power decreases in an exponential fashion, which results in a trade-off. Consequently, there exists a value of vvm where the total power is minimised. In the simulations performed in this study, this minimum tended to be located at a value of vvm that was beyond the flooding constraint, as illustrated in Figure 7, and was thus constrained to the onset of flooding. For those whose minimum was located before flooding, the total minimum power was within 5% of that at flooding.

Furthermore, the constants used in the k_La correlation Equation (19), the values of OUR and bioreactor working volume will all influence the minimum total power requirement and whether or not it is constrained by flooding. Fitzpatrick et al. [2] examined this by performing simulations for a typical range of values for OUR and bioreactor working volume and for five different sets of constants in the k_La correlation equation (which were originally presented by Benz (2013). These simulations were applied to a system with similar bioreaction kinetics as in this work. This analysis showed that the minimum total power requirement tended to be constrained by flooding for many of the scenarios, and was close to the value at flooding for those scenarios where the minimum occurred before the onset of flooding. Consequently, the modelling showed that the minimum or near-minimum total power requirement occurred when operating at the onset of impeller flooding.

3.3.2. CSTB—Agitator and Compressor Power Requirement that Minimises Total Electrical Power for Aeration

From the above section, there are design values of vvm (and corresponding air compressor power) and agitator power that will minimise total electrical power requirement to supply the OTR for an OUR at a given S_f. These were evaluated as a function of S_f for C_OL = 2 mg·L⁻¹, and these data are presented in Figure 8. These data show that the minimum total power does not majorly change and there is a gradual reduction from 22.5 kW (at S_f = 1 mg·L⁻¹) to 19.5 kW (at S_f = 120 g·L⁻¹).

It should be recognized that the constants used in the k_La correlation Equation (19) will have an impact on the calculated total power requirement for oxygen transfer. Fitzpatrick et al. [30] examined this by investigating the effect of five different sets of constants in the k_La correlation equation (which were originally presented by Benz (2013) and regarded as providing a somewhat typical variation). This was applied to a system with similar bioreaction kinetics as in this work. The analysis showed that the correlation requiring the highest power had a power requirement of just over double that of the lowest power requirement correlation. The correlation applied in this work is close to that displaying the highest power requirement.

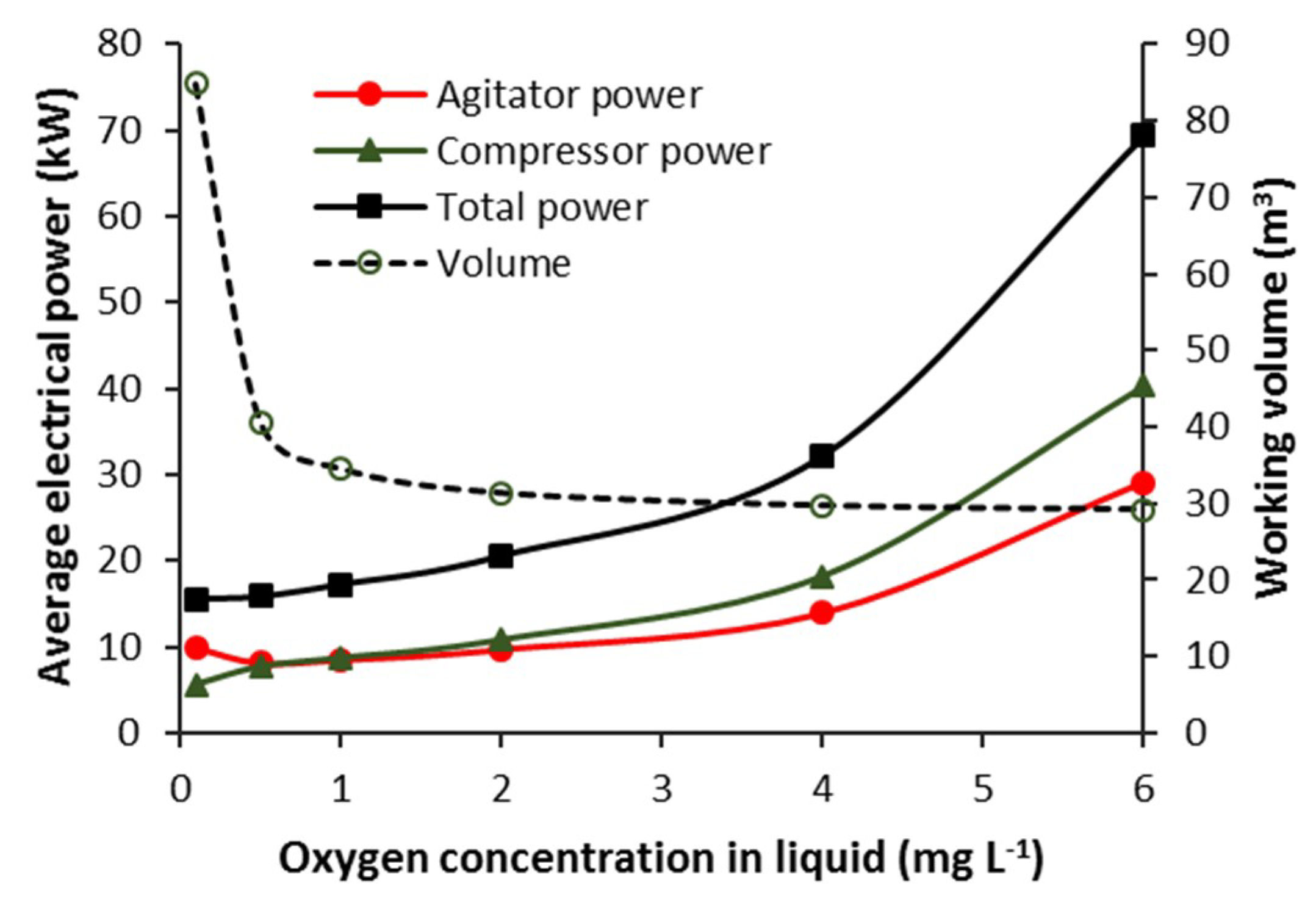
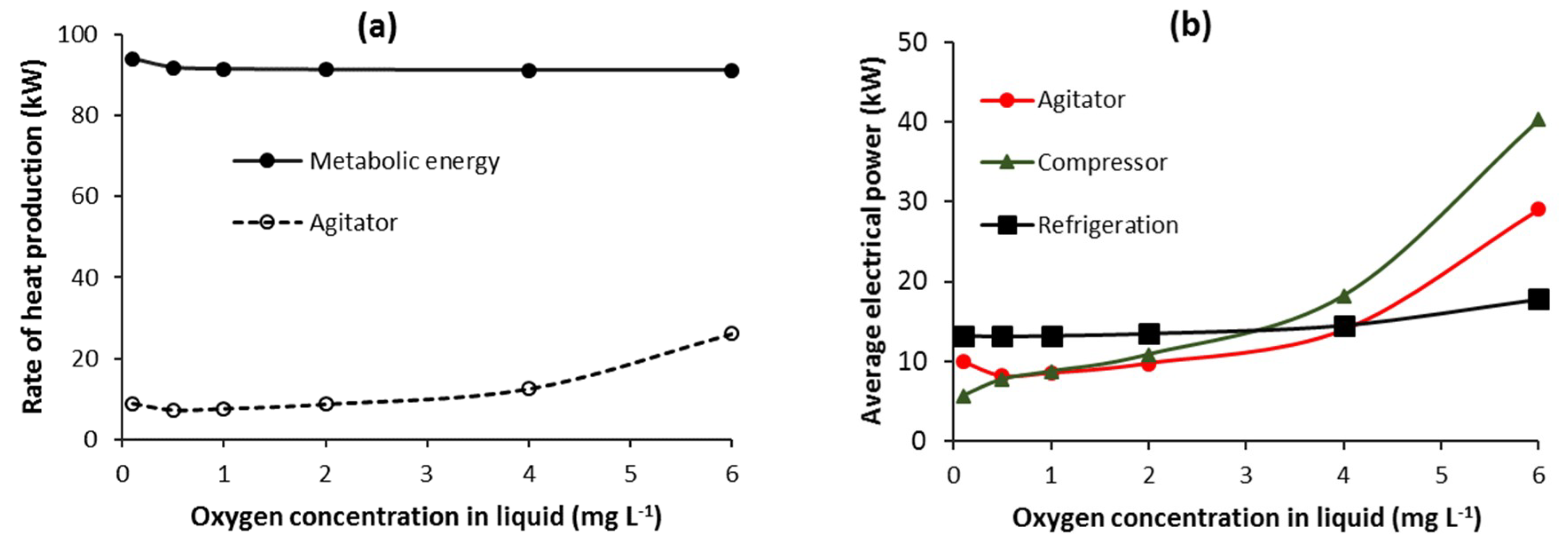
3.3.3. CSTB—Effect of Steady-State Oxygen Concentration (C_OL)

C_OL will influence bioreaction kinetics, which in-turn can influence the working volume of the bioreactor, feed flowrate to the bioreactor, amount of feed sugar required and wasted or unutilized sugar leaving the bioreactor, as discussed earlier. It will also influence the electrical power requirement for the aeration system, because lowering C_OL will increase the oxygen mass transfer driving force which will reduce the k_La required to supply a required OTR. Consequently, this section investigates the influence of C_OL on these aspects.

Steady-state oxygen concentration can have a major impact on the minimum total electrical power requirement, as illustrated in Figure 9. Reducing C_OL has a beneficial effect of reducing the total power requirement. This is because of an increase in the oxygen mass transfer driver which results in a lower k_La required to the deliver the OTR to satisfy the OUR requirement. However on the other hand, Section 3.2 shows that reducing C_OL can increase the working volume of the bioreactor. This results in a trade-off between aeration system power requirement and bioreactor working volume, and this is illustrated in Figure 10.

3.3.4. Batch—Agitator and Compressor Power Requirement

In batch mode, the OUR varies throughout the bioreaction, as illustrated in Figure 1c. The batch bioreactor can be operated using many different combinations of Pag and vvm to provide the OTR required to satisfy the OUR throughout the bioreaction subject to constraints of impeller flooding, phase equilibrium and oxygen starvation (not allowing C_OL to be less than a value that causes the microbes to die due to oxygen starvation). For example, a batch bioreactor may be operated at constant values of Pag and vvm; it may be operated such that C_OL is controlled at a constant value by maintaining Pag constant and varying vvm throughout the bioreaction.

The analysis above on the CSTB shows that there exists an optimum combination of Pag and vvm for a specific value of OUR that minimises total power requirement for oxygen transfer, subject to constraints. This idea can be extended to a batch bioreactor controlled at a fixed C_OL, where it can be applied over the whole of the bioreaction time to evaluate the combinations of vvm and Pag that minimise the total electrical power requirement at each time increment throughout the bioreaction. Consequently, continuously controlling the bioreactor at these optimal combinations of Pag and vvm throughout the entire bioreaction provides the minimum total energy requirement for oxygen transfer for the bioreactor.

Simulations were performed to estimate the minimum total energy at constant values of C_OL varying from 0.1 to 6 mg·L⁻¹. From this the corresponding average electrical powers were calculated and these are presented in Figure 11. This shows that reducing C_OL leads to lower total electrical power/energy requirement for oxygen transfer, which is due to the higher mass transfer driver. Like the CSTB, there is an inherent process design trade-off whereby lower C_OL which leads to lower electrical power requirement on one hand but leads to larger bioreaction times and larger bioreactor working volumes on the other hand, and this is also illustrated in Figure 11.

3.4. Refrigeration Electrical Power Requirement for Cooling

In addition to the electrical power requirement for oxygen transfer, the power requirement for the refrigeration system may also be significant. This section compares these power requirements and how they are influenced by C_OL. In Section 2.6, it was assumed that the main sources of bioreactor heat production were metabolic and agitation.

Simulations were performed for both batch and CSTB, and the results for the batch are presented in Figure 12. The average rate of metabolic heat production and agitator heat dissipation are presented in Figure 12a. This shows that the metabolic heat is dominant especially at lower values of C_OL. Figure 12b shows that the refrigeration power requirement is significant. There is little variation up to about C_OL = 2 mg·L⁻¹, where the refrigeration power requirement is around 13.3 kW, after which it gradually increases up to 17.8 kW at C_OL = 6 mg·L⁻¹, due to the increased agitator heat dissipation shown in Figure 12a.

Figure 12b compares the refrigeration, agitator and air compressor power requirements and how they are influenced by C_OL. At C_OL = 2 mg·L⁻¹, the refrigeration, agitator and air compressor power requirements represent about 40%, 28% and 32%, respectively of their combined total. It should be kept in mind that the agitator and air compressor powers presented in Figure 12b represent values that minimised the power requirement for oxygen transfer and that the COP of the refrigeration system was estimated as 8.6, as these factors will influence the comparison. Overall, the electrical power requirements (both for oxygen transfer and refrigeration) were very similar for both batch and CSTB.

3.5. Process Design Optimisation/Trade-Offs and Comparison of Batch and CSTB

From a process design perspective, the selection of the operating oxygen concentration in the bioreaction liquid and the steady-state sugar concentration in the CSTB are very important. However there may be no values for these variables that are totally desirable because there are conflicts between the desired objectives of minimising the following:

• Working volume of the bioreactor
• Amount of feed sugar required
• Amount of wasted or unutilised sugar leaving the bioreactor
• Electric energy requirement for oxygen transfer and cooling
• Greenhouse gas emissions associated with electric energy supply
• Cost

In batch mode of operation the initial sugar concentration was constrained by the concentration in the feed and the final concentration was reduced to a specified low value which resulted in low wasted sugar and consequently lowered the feed sugar requirement. For the CSTB, a steady-state sugar concentration (S_f) needs to be selected. Here, there is a potential trade-off between lower S_f values leading to lower feed and wasted substrate (and associated environmental impact) on one hand and the potential for higher bioreactor volumes on the other hand due to bioreactor volume displaying a minimum value as illustrated in Figure 2b. However the effect on bioreactor volume and the position of this minimum is greatly influenced by the value of K_S, as illustrated in Figure 5. The result of these simulations showed that for typical values of K_S, S_f could be chosen as a low value, such as 1 g·L⁻¹, and thus have the dual benefit of approaching both minimum volume and minimum feed/wasted substrate. In terms of comparing bioreactor volume requirement for batch and CSTB, the simulations showed that the CSTB required a much smaller volume, especially when operated at lower values of S_f, and this is a major advantage of CSTB over batch.

The specification of C_OL is crucial. Decreasing C_OL causes a decrease in electrical energy requirement (and associated greenhouse gas emissions), however this tends to increase the working volume of the bioreactor for both batch and CSTB. This is especially true when values of C_OL decrease below 1 mg·L⁻¹, where there tended to be an exponential increase in the working volume. Consequently, there is no value of C_OL that satisfies all the desired objectives and thus a compromise must be sought to zone in on a value that is considered satisfactory. Output from the simulations may help in the determination of such satisfactory values. For, example, selecting a C_OL value in the range of 0.5 to 2 mg·L⁻¹ (Figure 10) appears to represent a good compromise between the working volume of the bioreactor and the electrical power requirement. A more structured optimisation approach could be applied to evaluate a value of C_OL that minimises the economic cost subject to constraints (such as limits on greenhouse gas emissions).

4. Conclusions

Mathematical modelling can be usefully applied in the process design and optimisation of a CSTB and batch bioreactor. For a steady state value of OUR in a CSTB, the oxygen transfer and energy equations were applied to evaluate a vvm/Pag combination that produced the minimum total power requirement for oxygen transfer, subject to the phase equilibrium and flooding constraints. This analysis was then extended to the batch bioreactor where it was applied to the whole of the OUR – time profile during batch bioreaction. This was applied to evaluate the combinations of vvm/Pag that minimised total energy requirement for the bioreaction at constant C_OL. It was shown that the minimum or near-to-minimum total energy requirement occurred when operating at the onset of flooding throughout the bioreaction.

Oxygen concentration (C_OL) and CSTB steady-state sugar concentration (S_f) are two important input process design variables that can impact on important design output variables, such as the working volume of the bioreactor, energy requirements and impacts on the environmental. Decreasing C_OL has the beneficial effect of reducing the aeration system energy requirement and associated carbon footprint, however at the same time, it can slow down the bioreaction leading to the need for a larger sized bioreactor and associated cost. This shows that varying C_OL and S_f may be beneficial for some design output variables but may be detrimental to the values of others. Consequently, compromises and trade-offs are required to determine superior process designs. Mathematical modelling can assist in more precisely zoning in quantitatively on the selection of values for key input design variables, such as C_OL and S_f. This can be coupled with economic and environmental optimisation that can help produce a best compromise between conflicting design output variables. The mathematical modelling can also highlight design sensitivities to changes in input variable values which can cause undesirable adverse changes in key design variables. Finally it is important that the model equations and values of constants in the equations are appropriate and representative.