On the Impact of the Dynamics of Heat Transfer of the Thermal Machine Working Fluid and Heat Sources on the Shape of the Boundary of the Set of Realizable Regimes
Abstract
:1. Introduction
- Find the dynamic laws of heat transfer with sources for which the efficiency of the machine in the maximum power mode does not depend on the dynamic coefficients
- Determine the laws of dynamics in which the cycle corresponding to the maximum efficiency at a given heat consumption consists of two and three isotherms.
- If the optimal cycle consists of three isotherms, then sources two of them are realized?
2. Averaged Optimization and Convex Hulls of a Function
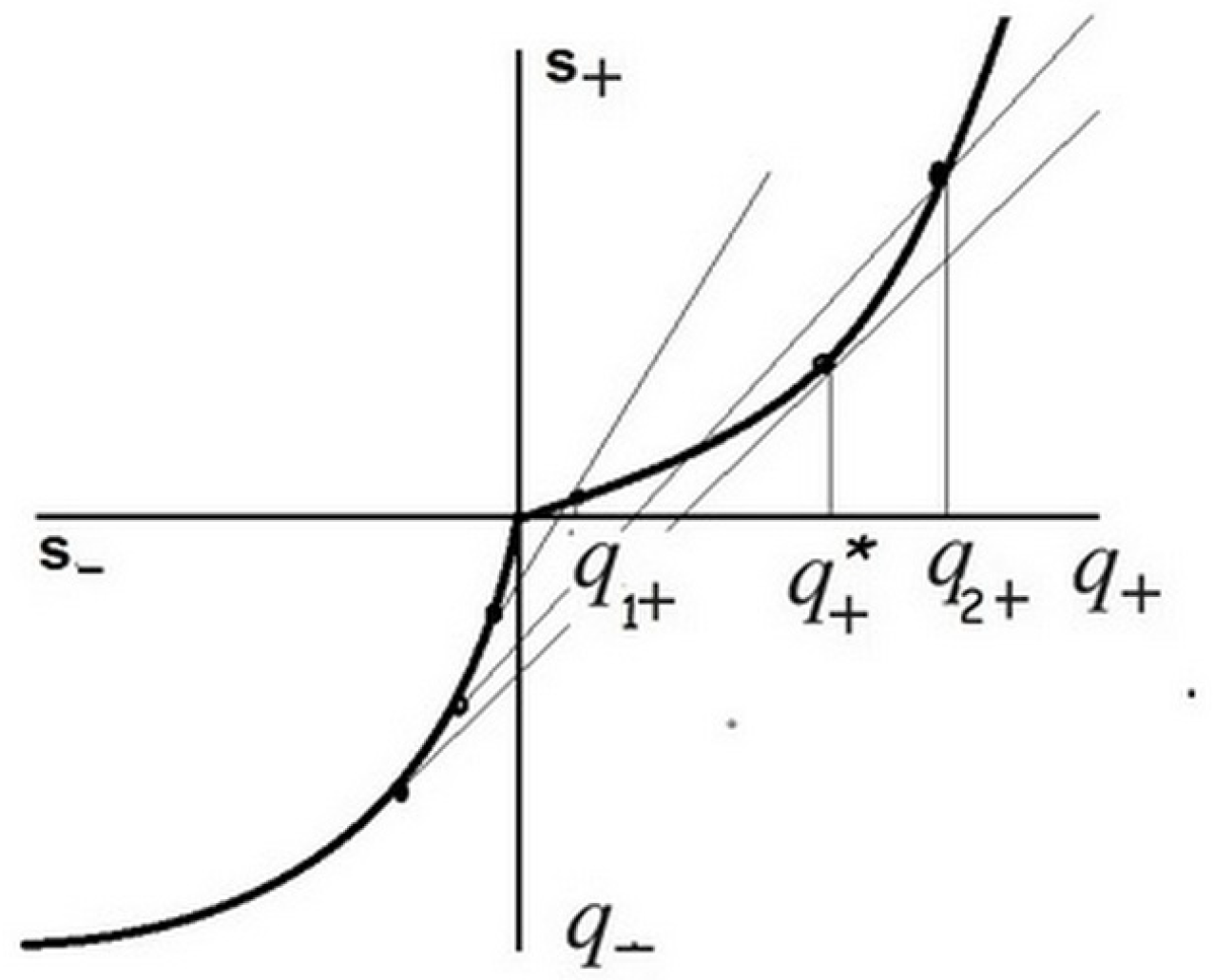
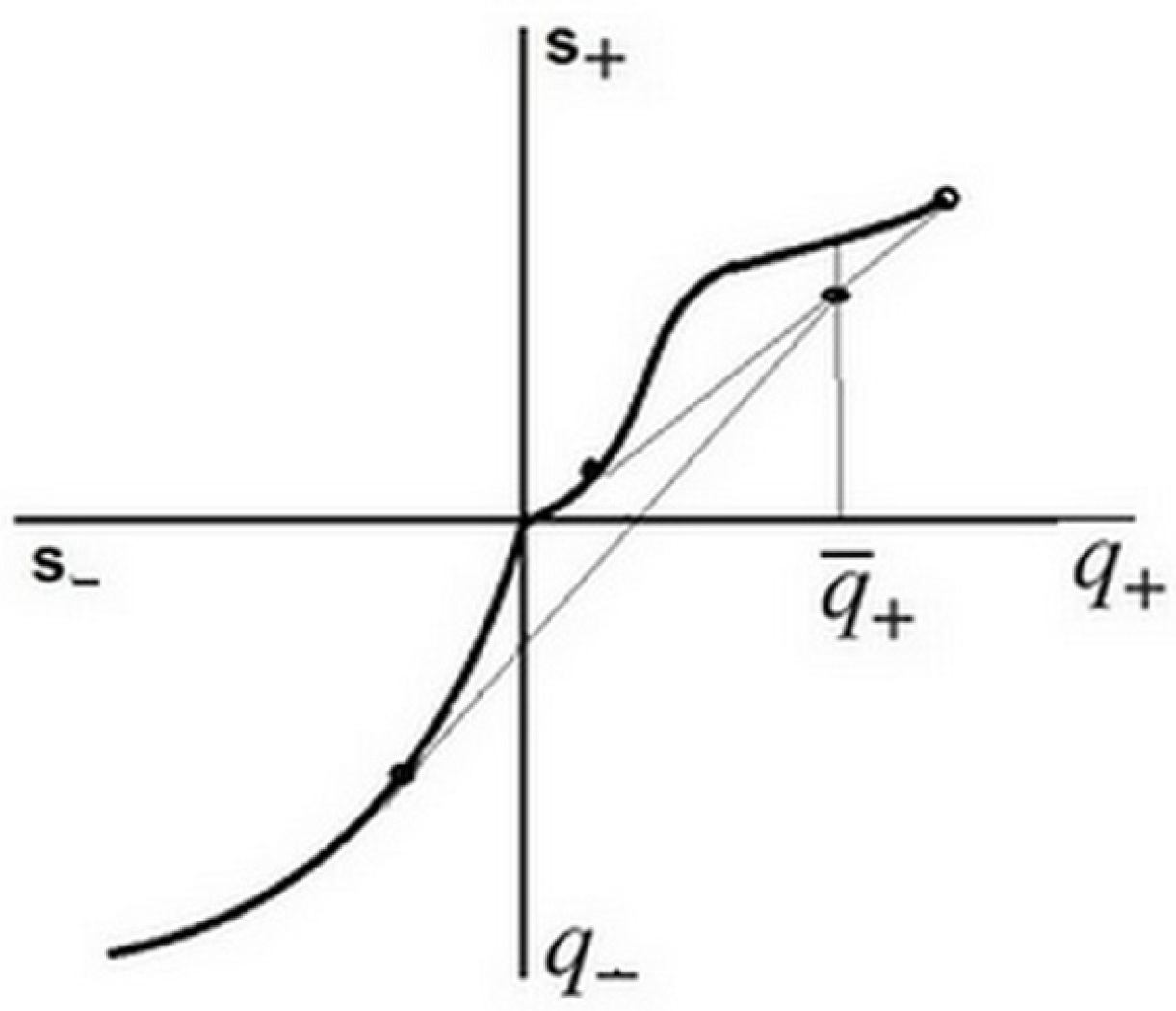
2.1. Convex Hulls of a Function
2.2. Averaged Problem of Conditional Optimization
3. “Natural” Dynamic Functions and Optimal Cycles Structure
- are continuous and differentiable with respect to their arguments everywhere except for . and hold true (these are the monotonicity conditions). The same applies to the signs of the derivatives on .
- The sign of the heat flux coincides with the sign of the temperature difference (the second law of thermodynamics). at holds true.
- The dynamic dependence can be written in the form , where the heat transfer coefficient is proportional to the contact surface of the working fluid with the source. For example, the dependency of type does not match this requirement. This type of dynamic was investigated in [7]. The optimal cycle consisted of three isotherms and three adiabats in this work.
Statement of the Problem and Solutions Structure Corresponding to the Boundary of Realizability Region
- The optimal solution of this problem can take no more than three (base) values of the vector ; i.e., no more than three isothermal sections with adiabatic transitions from one isotherm to another, where is the base solution index.
- The duration of each isothermal section is a certain part of the cycle time, and the adiabatic transitions occurs instantaneously.
4. Graphic Interpretation of the Solution
5. The Optimal Solution
The Relation between the Power and the Entropy Production in the System
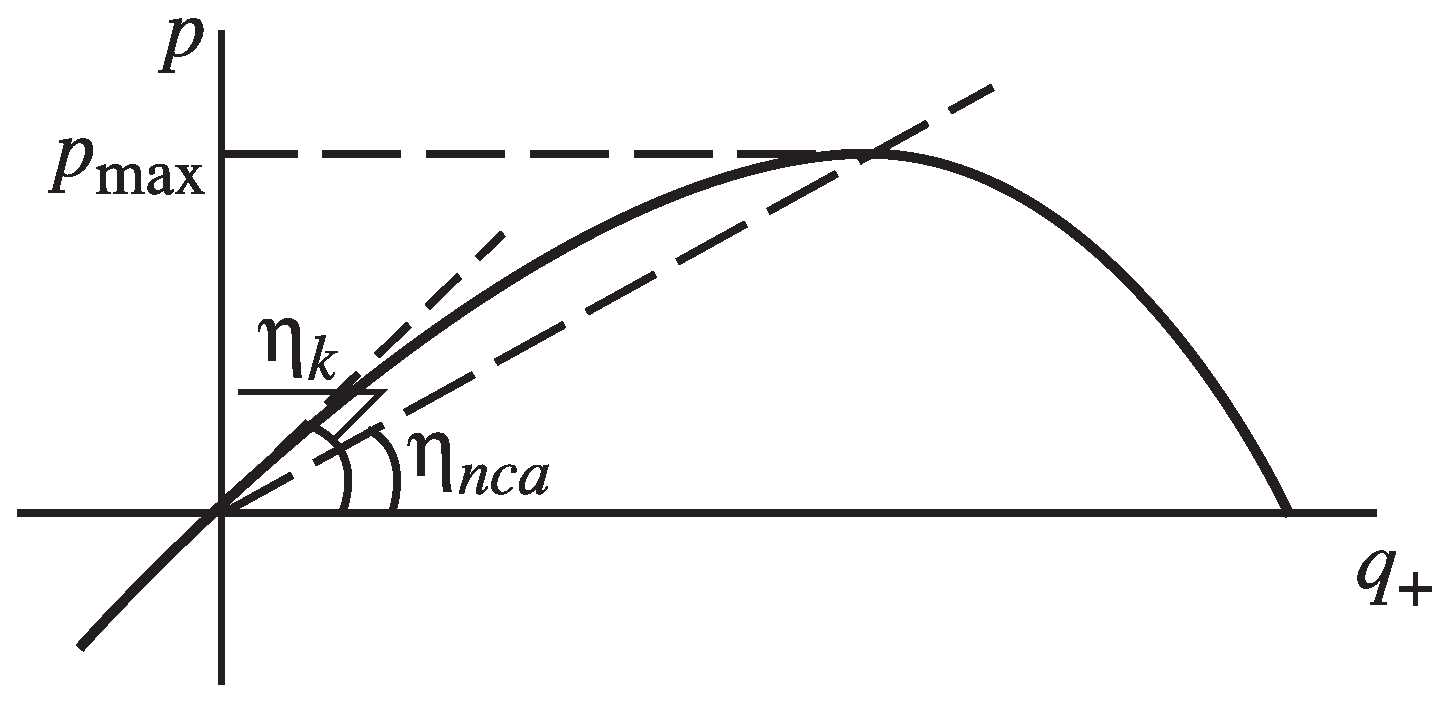
6. The Realizability Region Boundary
6.1. Characteristic Points of the Boundary
- The origin of coordinates where and p tend to zero. The energy and conversion efficiency for any heat exchange law at this point is .
- The point at which the power of the machine is maximal. This point is denoted by . The corresponding energy conversion efficiency and heat flux will be denoted by and .
- The point at which the irreversibility of the processes is so great that the power of the machine turns out to be zero. The value of the heat flux corresponding to this point is denoted by .
6.2. Boundary Construction
6.3. Conditions of Independence Efficiency of the Machine in the Mode of Maximum Power from Coefficients of Heat Exchange with Sources
6.4. Novikov Case
7. The Boundary of the Realizability Region for Two Types of Heat Transfer Dynamics
7.1. Newtonian Heat Transfer Laws
7.2. The Linear Phenomenological Law
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. The Problem on Conditional Maximum of Function and the Averaged Statement of This Problem
- —
- Write the function in the next form (Lagrange function)
- —
- Search for its unconditional maximum on the set allocated only by the restrictions on the components of the vector x. This maximum will depend on the Lagrange indefinite multiplier.
- —
- Solve the equation for
References
- Rodionov, V.G. Energy: Problems of the Present and Possibilities of the Future; ENAS: Moscow, Russia, 2010; ISBN 978-5-4248-0002-3. (In Russian) [Google Scholar]
- Novikov, I.I. The efficiency of atomic power stations. At. Energy 1957, 3, 409–412. [Google Scholar] [CrossRef]
- Curzon, F.L.; Ahlborn, B. Efficiency of Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Rozonoer, L.I.; Tsirlin, A.M. Optimal Control of Thermodynamic Processes I. Autom. Remote Control 1983, 44, 55–62. [Google Scholar]
- Rozonoer, L.I.; Tsirlin, A.M. Optimal Control of Thermodynamic Processes II. Autom. Remote Control 1983, 44, 209–220. [Google Scholar]
- Rozonoer, L.I.; Tsirlin, A.M. Optimal Control of Thermodynamic Processes III. Autom. Remote Control 1983, 44, 314–326. [Google Scholar]
- Orlov, V.N. Analytical solutions in optimal control of cyclic heat engine with a nonuniform working fluid. Phys. Rev. A 1990, 42, 4317. [Google Scholar] [CrossRef]
- Tsirlin, A.M. The Methods of Averaged Optimization and Their Applications; Fizmatlit: Moscow, Russia, 1997. (In Russian) [Google Scholar]
- Tsirlin, A.M. Problems and methods of averaged optimization. Proc. Steklov Inst. Math. 2008, 261, 270. [Google Scholar] [CrossRef]
- Andresen, B.; Berry, R.S.; Ondrechen, M.J.; Salamon, P. Thermodynamics for processes in finite time. Acc. Chem. Res. 1984, 17, 266–271. [Google Scholar] [CrossRef]
- Chen, L.G.; Wu, C.; Sun, F.R. Finite time thermodynamic optimization or entropy generation minimization of energy systems. J. Non-Equilib. Thermodyn. 1999, 24, 327–359. [Google Scholar] [CrossRef]
- Hoffman, K.H.; Burzler, J.M.; Fischer, A.; Schaller, M.; Schubert, S. Optimal process paths for endoreversible systems. J. Non-Equilib. Thermodyn. 2003, 28, 233–268. [Google Scholar] [CrossRef]
- Chen, L.G. Finite-Time Thermodynamic Analysis of Irreversible Processes and Cycles; High Education Press: Beijing, China, 2005. (In Chinese) [Google Scholar]
- Sieniutycz, S.; Jezowski, J. Energy Optimization in Process Systems; Elsevier: Oxford, UK, 2009. [Google Scholar]
- Hoffmann, K.H.; Andresen, B.; Salamon, P. Finite-time thermodynamics tools to analyze dissipative processes. In Advances in Chemical Physics; Dinner, A.R., Ed.; Wiley: Hoboken, NJ, USA, 2014; Volume 157, pp. 57–67. ISBN 978-1-1189-5959-6. [Google Scholar]
- Ahmadi, M.H.; Ahmadi, M.A.; Pourfayaz, F. Thermodynamic analysis and evolutionary algorithm based on multi-objective optimization performance of actual power generating thermal cycles. Appl. Therm. Eng. 2016, 99, 996–1005. [Google Scholar] [CrossRef]
- Chen, L.G.; Xia, S.J.; Sun, F.R. Optimal paths for minimizing entropy generation during heat transfer processes with a generalized heat transfer law. J. Appl. Phys. 2009, 105, 044907. [Google Scholar] [CrossRef]
- Wang, Y.; Tu, Z.C. Efficiency at maximum power output of linear irreversible Carnot-like heat engines. Phys. Rev. 2012, 85, 011127. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Ayala, J.; Arias-Hernandez, L.A.; Angulo-Brown, F. Connection between maximum-work and maximum-power thermal cycles. Phys. Rev. 2013, 88, 052142. [Google Scholar] [CrossRef] [PubMed]
- Caratheodory, C.F. Vorlesungen über Reelle Funktionen; Vieweg + Teubner Verlag: Wiesbaden, Germany, 1927. [Google Scholar]
- Berry, R.S.; Kasakov, V.A.; Sieniutycz, S.; Szwast, Z.; Tsirlin, A.M. Thermodynamic Optimization of Finite Time Processes; Wiley: Chichester, UK, 1999. [Google Scholar]
- Boshnyakovich, F. Technical Thermodynamics; Holt, Rinehart and Winston: New York, NY, USA, 1965. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaeva, M.A.; Tsirlin, A.M.; Didina, O.V. On the Impact of the Dynamics of Heat Transfer of the Thermal Machine Working Fluid and Heat Sources on the Shape of the Boundary of the Set of Realizable Regimes. ChemEngineering 2019, 3, 36. https://doi.org/10.3390/chemengineering3020036
Zaeva MA, Tsirlin AM, Didina OV. On the Impact of the Dynamics of Heat Transfer of the Thermal Machine Working Fluid and Heat Sources on the Shape of the Boundary of the Set of Realizable Regimes. ChemEngineering. 2019; 3(2):36. https://doi.org/10.3390/chemengineering3020036
Chicago/Turabian StyleZaeva, Margarita A., Anatoly M. Tsirlin, and Olga V. Didina. 2019. "On the Impact of the Dynamics of Heat Transfer of the Thermal Machine Working Fluid and Heat Sources on the Shape of the Boundary of the Set of Realizable Regimes" ChemEngineering 3, no. 2: 36. https://doi.org/10.3390/chemengineering3020036
APA StyleZaeva, M. A., Tsirlin, A. M., & Didina, O. V. (2019). On the Impact of the Dynamics of Heat Transfer of the Thermal Machine Working Fluid and Heat Sources on the Shape of the Boundary of the Set of Realizable Regimes. ChemEngineering, 3(2), 36. https://doi.org/10.3390/chemengineering3020036





