Dry Reforming of Methane in a Pd-Ag Membrane Reactor: Thermodynamic and Experimental Analysis
Abstract
:1. Introduction
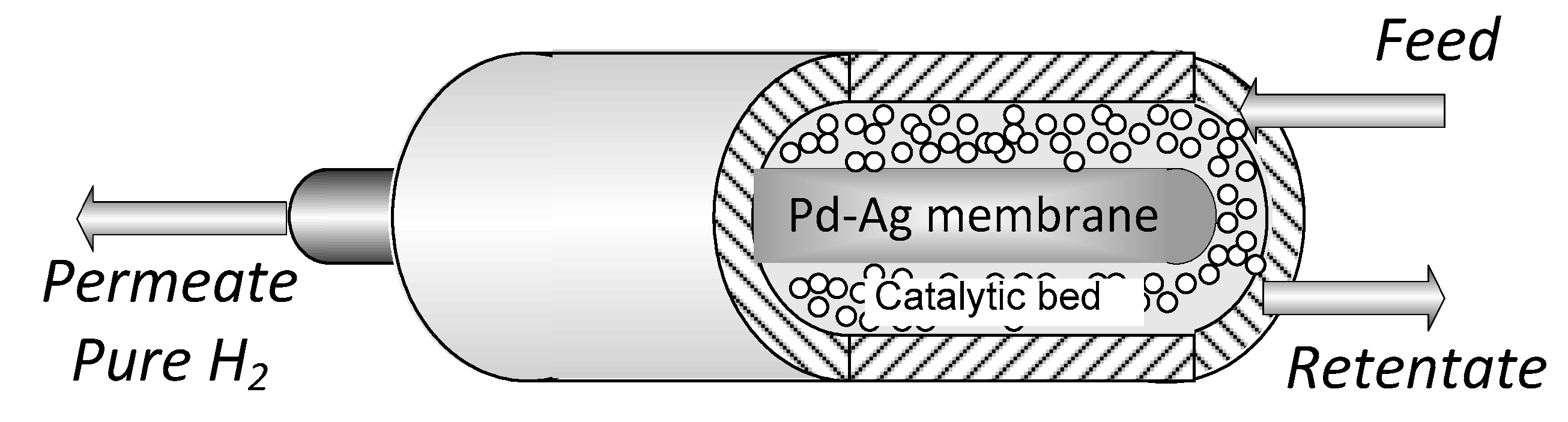
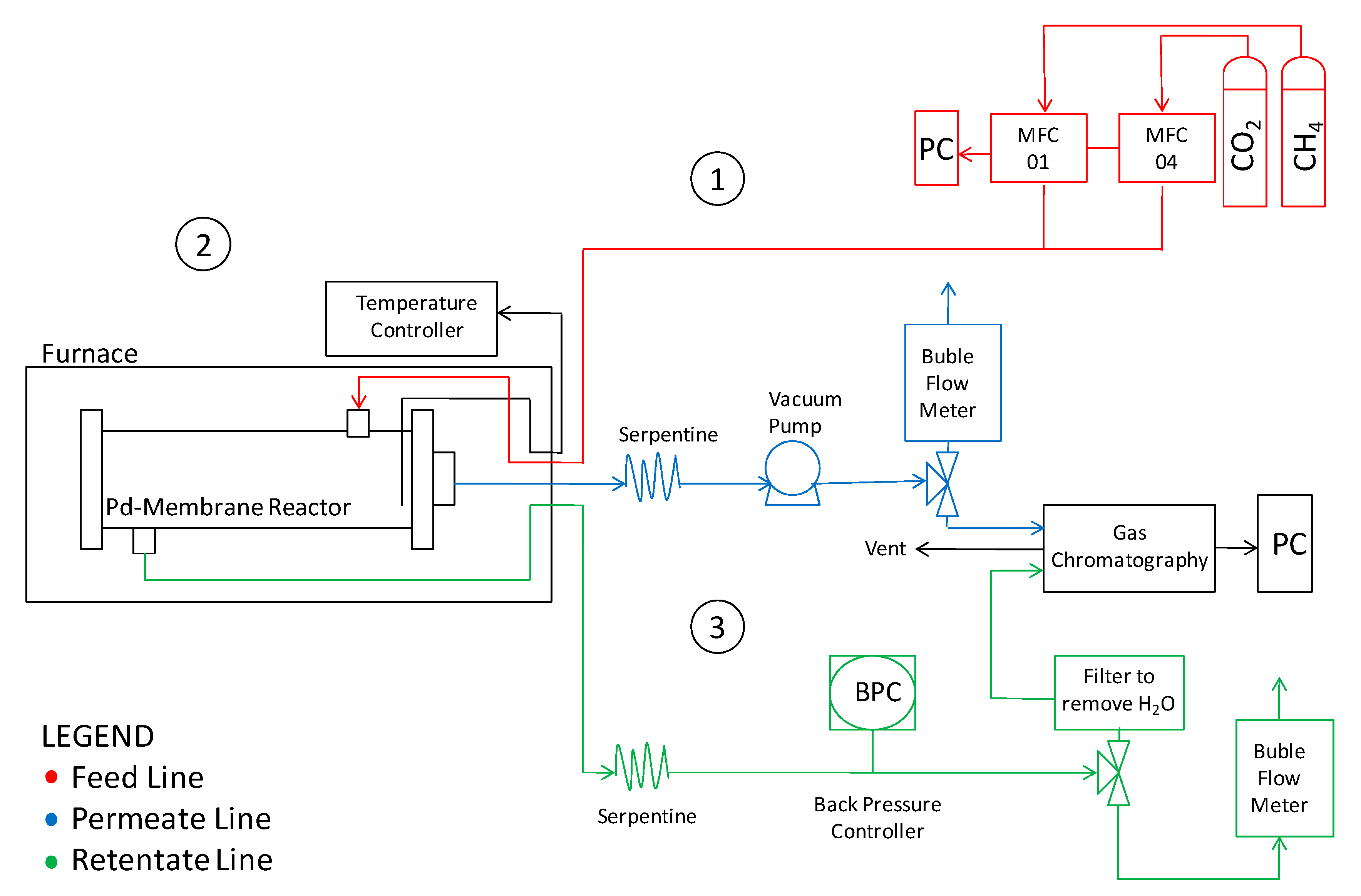
2. Materials and Methods
3. Results and Discussion
3.1. Thermodynamic Analysis
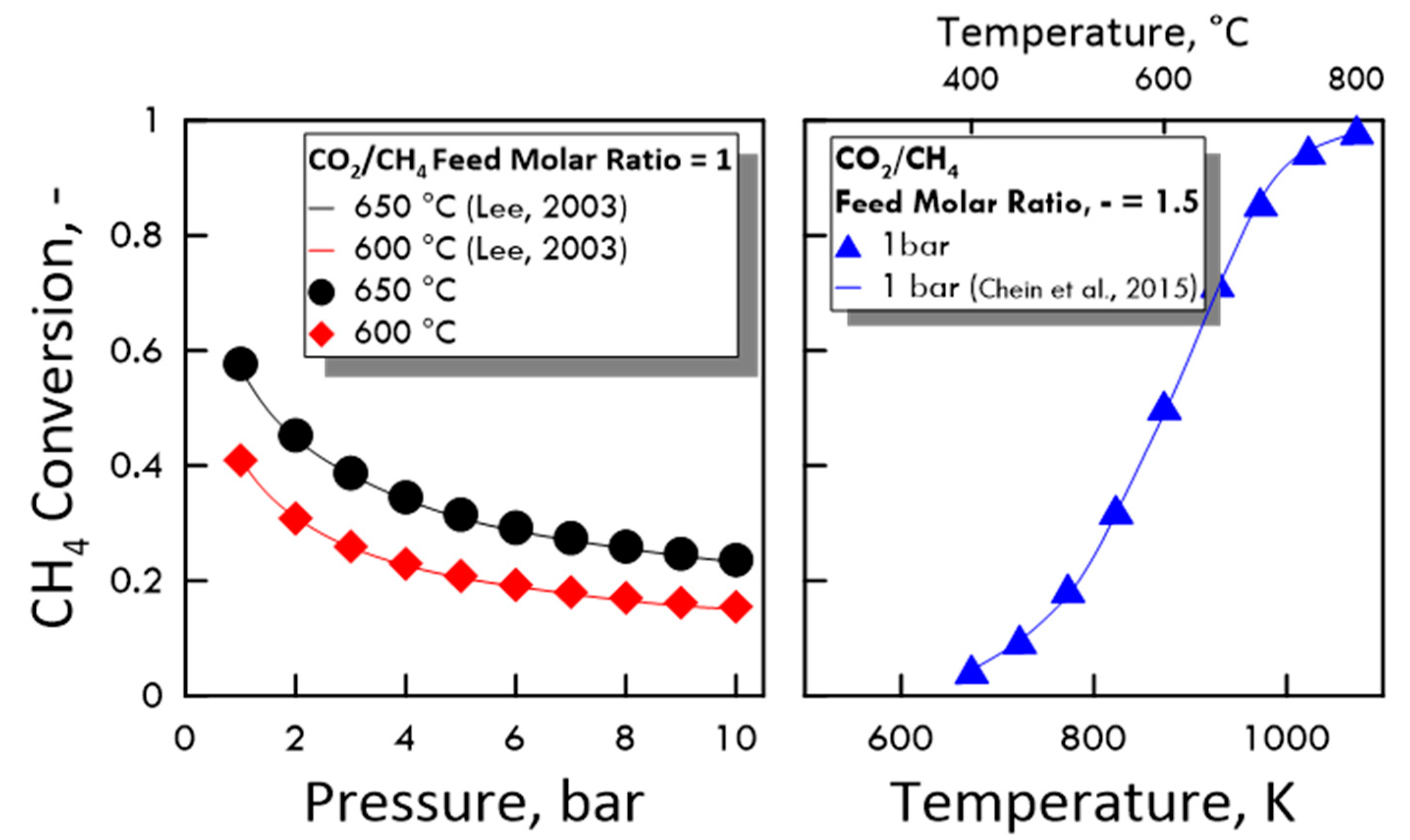
3.1.1. Calculation Validation
3.1.2. Equilibrium Calculation: DRM and RWGS
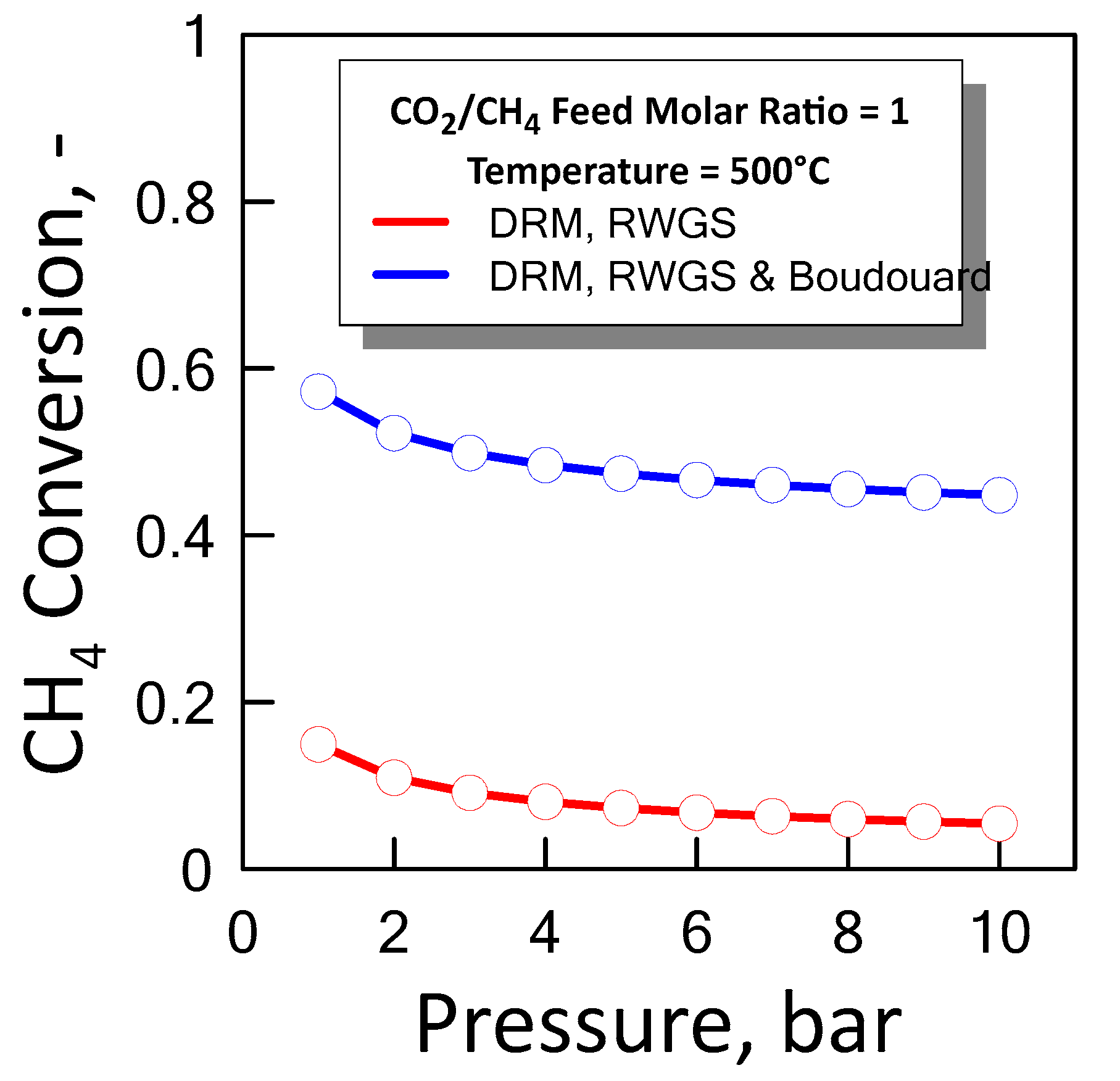
3.1.3. Equilibrium Calculation: DRM, Reverse WGS and Boudouard Reactions
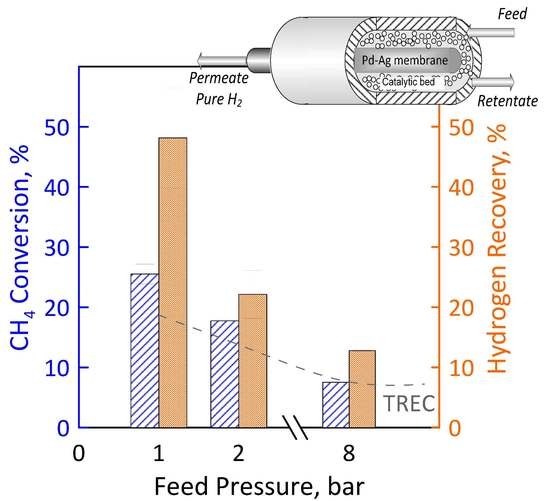
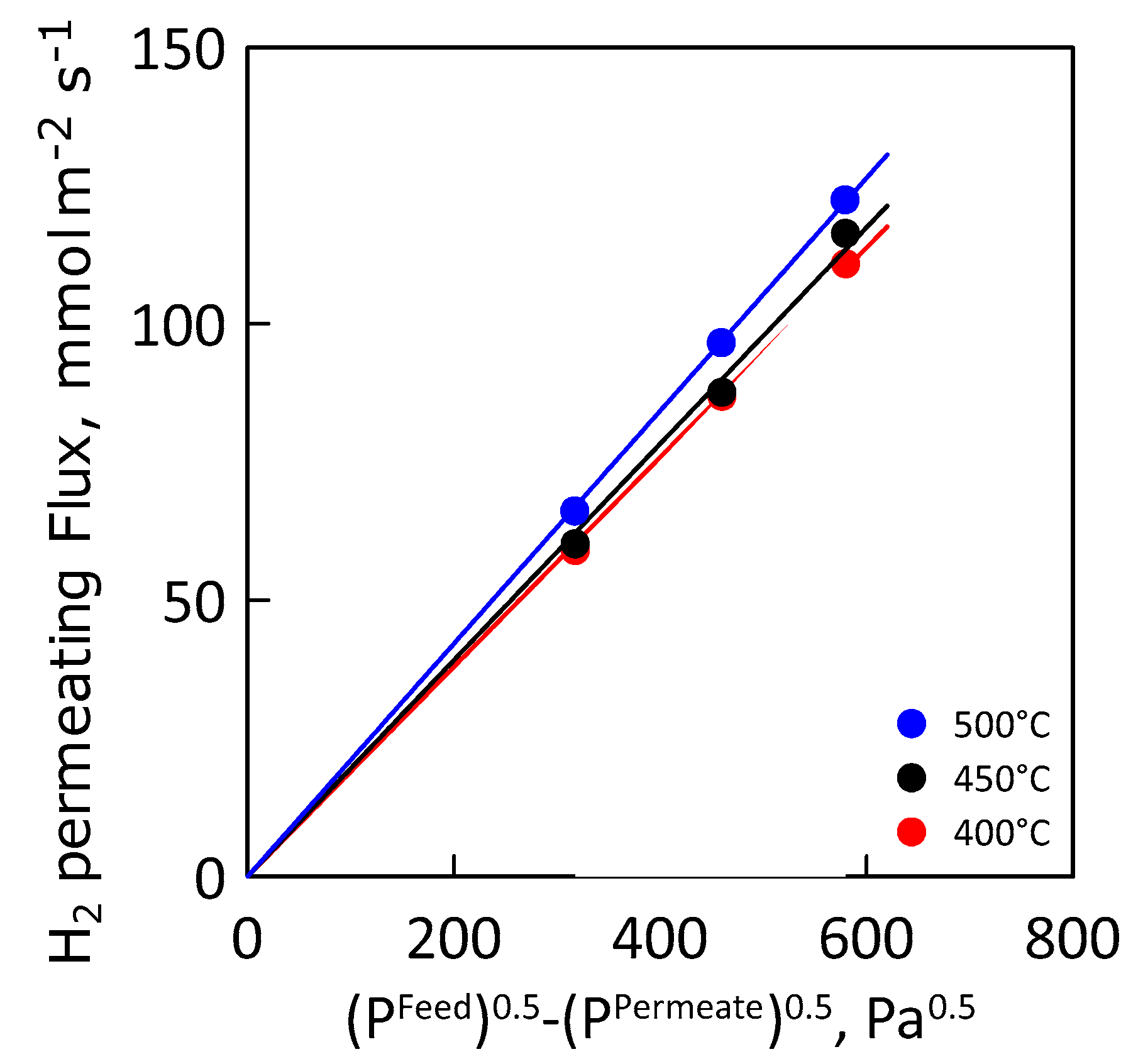
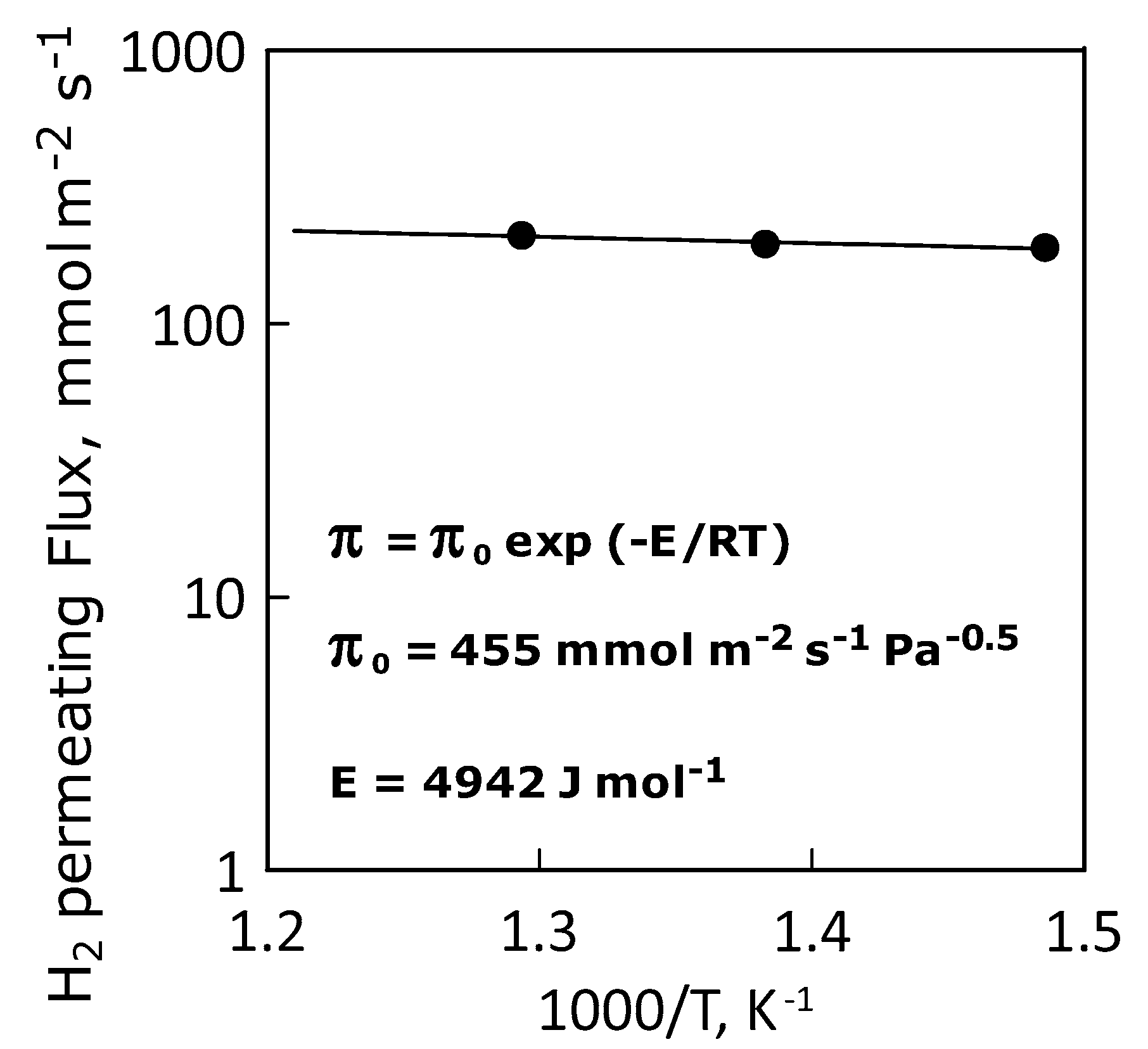
3.2. Permeation Measurements
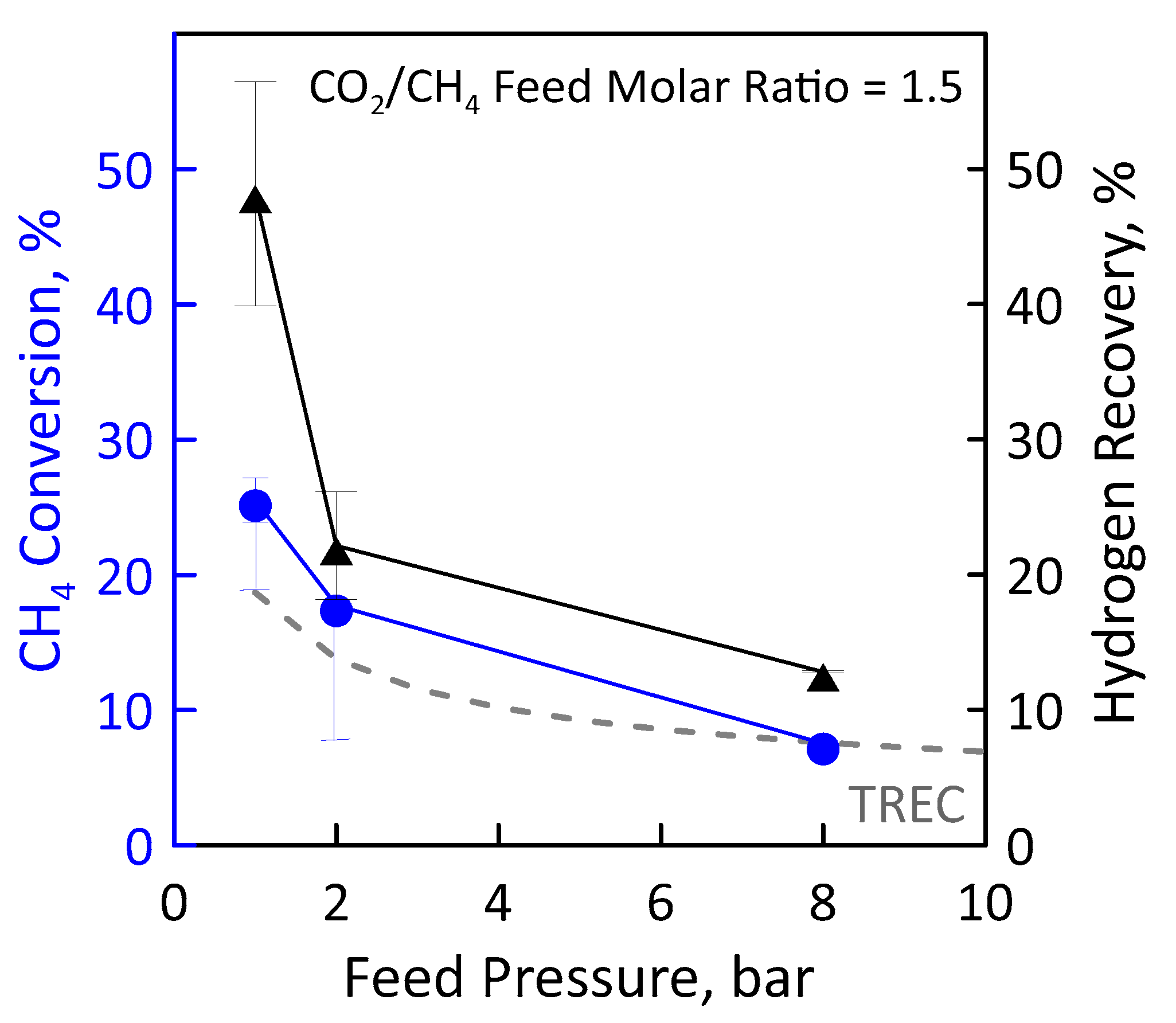
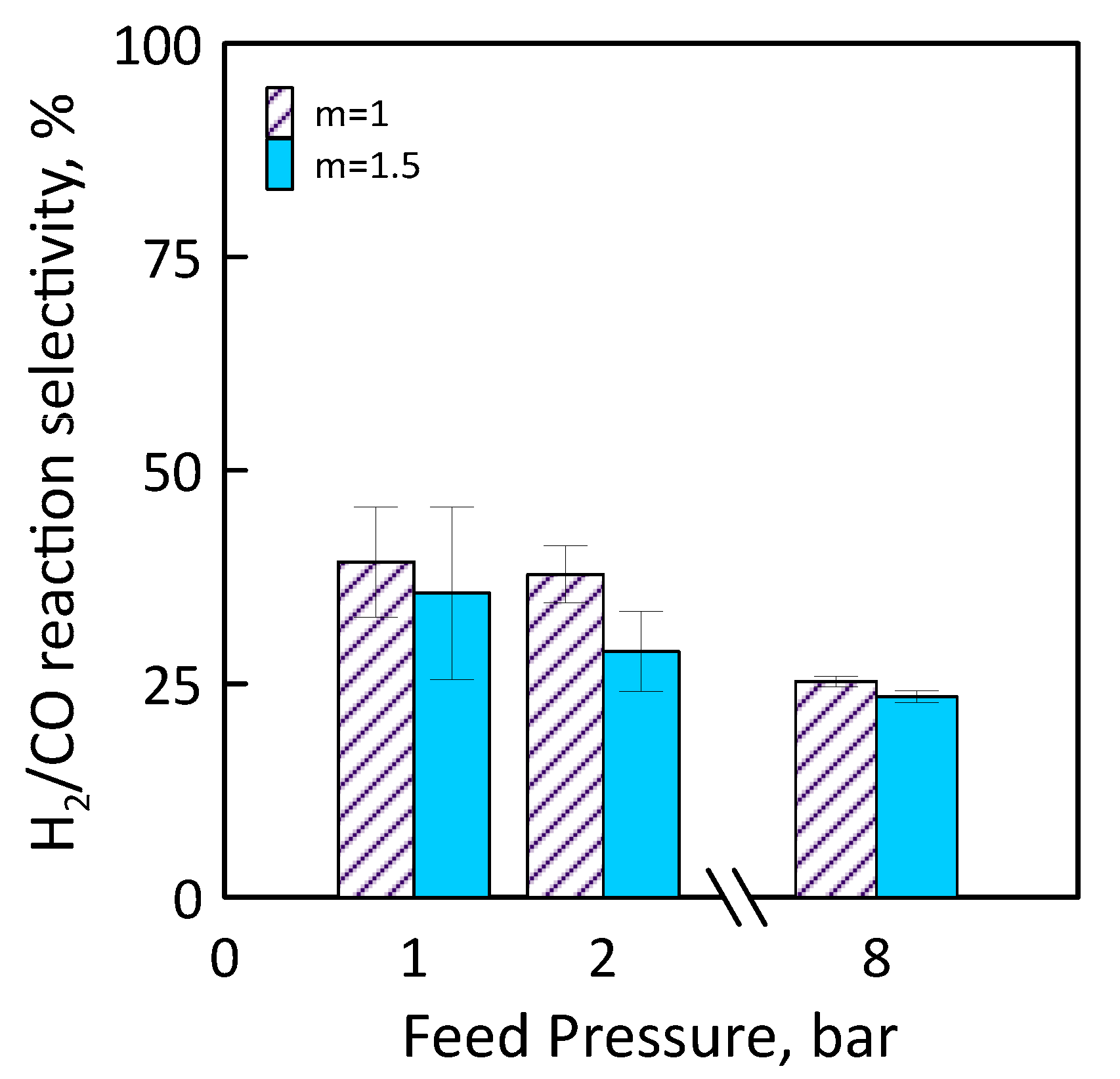
3.3. Reaction Measurements
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Calculation Approach for Thermodynamic Equilibrium
Appendix A.2. Equilibrium Calculation: Numerical Procedure
References
- Henriques, I.; Sadorsky, P. Investor implications of divesting from fossil fuels. Glob. Financ. J. 2017, in press. [Google Scholar] [CrossRef]
- Hanley, E.S.; Deane, J.P.; Gallachóir, B.P.Ó. The role of hydrogen in low carbon energy futures—A review of existing perspectives. Renew. Sustain. Energy Rev. 2017, 82, 3027–3045. [Google Scholar] [CrossRef]
- Hydrogen: Fuel for Our Future? Available online: http://www.worldwatch.org/node/4516 (accessed on 9 October 2018).
- Wadhwani, S.; Wadhwani, A.K.; Agarwal, R.B. Clean Coal Technologies—Recent Advances. In Proceedings of the First International Conference on Clean Coal Technologies for Our Future, Chia Laguna, Sardinia, Italy, 21–23 October 2002. [Google Scholar]
- Muradov, N. Low to near-zero CO2 production of hydrogen from fossil fuels: Status and perspectives. Int. J. Hydrogen Energy 2017, 42, 14058–14088. [Google Scholar] [CrossRef]
- Vivas, F.J.; de las Heras, A.; Segura, F.; Andújar, J.M. A review of energy management strategies for renewable hybrid energy systems with hydrogen backup. Renew. Sustain. Energy Rev. 2018, 82, 126–155. [Google Scholar] [CrossRef]
- Akhtera, P.; Farkhondehfal, M.A.; Hernández, S.; Hussain, M.; Fina, A.; Saracco, G.; Khan, A.U.; Russo, N. Environmental issues regarding CO2 and recent strategies for alternative fuels through photocatalytic reduction with titania-based materials. J. Environ. Chem. Eng. 2016, 4, 3934–3953. [Google Scholar] [CrossRef]
- Pomilla, F.R.; Brunetti, A.; Marcì, G.; García-López, E.I.; Fontananova, E.; Palmisano, L.; Barbieri, G. CO2 to liquid fuels: Photocatalytic conversion in a continuous membrane reactor. ACS Sustain. Chem. Eng. 2018, 6, 8743. [Google Scholar] [CrossRef]
- Sellaro, M.; Bellardita, M.; Brunetti, A.; Fontananova, E.; Palmisano, L.; Drioli, E.; Barbieri, G. CO2 conversion in a photocatalytic continuous membrane reactor. RSC Adv. 2016, 6, 67418–67427. [Google Scholar] [CrossRef]
- Kohen, A.; Cannio, R.; Bartolucci, S.; Klinman, J.P. Enzyme dynamics and hydrogen tunneling in a thermophilic alcohol dehydrogenase. Nature 1999, 399, 496–499. [Google Scholar] [CrossRef] [PubMed]
- Marpani, F.; Pinelo, M.; Meyer, A.S. Enzymatic conversion of CO2 to CH3OH via reverse dehydrogenase cascade biocatalysis: Quantitative comparison of efficiencies of immobilized enzyme systems. Biochem. Eng. J. 2017, 127, 217–228. [Google Scholar] [CrossRef]
- Nocera, D.G. The artificial leaf. Acc. Chem. Res. 2012, 45, 767–776. [Google Scholar] [CrossRef] [PubMed]
- Bensaid, S.; Centi, G.; Garrone, E.; Perathoner, S.; Saracco, G. Towards artificial leaves for solar hydrogen and fuels from carbon dioxide. ChemSusChem 2012, 5, 500–521. [Google Scholar] [CrossRef] [PubMed]
- Chabi, S.; Papadantonakis, K.M.; Lewis, N.S.; Freund, M.S. Membranes for artificial photosynthesis. Energy Environ. Sci. 2017, 10, 1320–1338. [Google Scholar] [CrossRef]
- Guczi, L.; Stefler, G.; Geszti, O.; Sajó, I.; Pászti, Z.; Tompos, A.; Schay, Z. Methane dry reforming with CO2: A study on surface carbon species. Appl. Catal. A Gen. 2010, 375, 236–241. [Google Scholar] [CrossRef]
- Bucharkina, T.V.; Gavrilova, N.N.; Kryzhanovskiy, A.S.; Skudin, V.V.; Shulmin, D.A. Dry reforming of methane in contactor and distributor membrane reactors. Pet. Chem. 2015, 55, 932–939. [Google Scholar] [CrossRef]
- Usman, M.; Wan Daud, W.M.A.; Abbas, H.F. Dry reforming of methane: Influence of process parameters—A review. Renew. Sustain. Energy Rev. 2015, 45, 710–744. [Google Scholar] [CrossRef]
- Kim, S.; Ryi, S.K.; Lim, H. Techno-economic analysis (TEA) for CO2 reforming of methane in a membrane reactor for simultaneous CO2 utilization and ultra-pure H2 production. Int. J. Hydrogen Energy 2018, 43, 5881–5893. [Google Scholar] [CrossRef]
- Roy, P.S.; Song, J.; Kim, K.; Park, C.S.; Raju, A.S.K. CO2 conversion to syngas through the steam-biogas reforming process. J. CO2 Util. 2018, 25, 275–282. [Google Scholar] [CrossRef]
- Oyama, S.T.; Hacarlioglu, P.; Gu, Y.; Lee, D. Dry reforming of methane has no future for hydrogen production: Comparison with steam reforming at high pressure in standard and membrane reactors. Int. J. Hydrogen Energy 2012, 37, 10444–10450. [Google Scholar] [CrossRef]
- Drioli, E.; Barbieri, G.; Brunetti, A. Membrane Engineering for the Treatment of Gases, 2nd ed.; Royal Society of Chemistry: Cambridge, UK, 2017; ISBN 978-1-78262-875-0. [Google Scholar]
- Wang, S.; Lu, G.; Millar, G.J. Carbon dioxide reforming of methane to produce synthesis gas over metal-supported catalysts: State of the art. Energy Fuel 1996, 10, 896–904. [Google Scholar] [CrossRef]
- Bosko, M.L.; Munera, J.F.; Lombardo, E.A.; Cornaglia, L.M. Dry reforming of methane in membrane reactors using Pd and Pd–Ag composite membranes on a NaA zeolite modified porous stainless steel support. J. Membr. Sci. 2010, 364, 17–26. [Google Scholar] [CrossRef]
- Gallucci, F.; Tosti, S.; Basile, A. Pd-Ag tubular membrane reactors for methane dry reforming: A reactive method for CO2 consumption and H2 production. J. Membr. Sci. 2008, 317, 96–105. [Google Scholar] [CrossRef]
- Garcıa-Garcıa, F.R.; Soria, M.A.; Mateos-Pedrero, C.; Guerrero-Ruiz, A.; Rodrıguez-Ramos, I.; Li, K. Dry reforming of methane using Pd-based membrane reactors fabricated from different substrates. J. Membr. Sci. 2013, 435, 218–225. [Google Scholar] [CrossRef]
- Silva, F.A.; Hori, C.E.; da Silva, A.M.; Mattos, L.V.; Munera, J.; Cornaglia, L. Hydrogen production through CO2 reforming of CH4 over Pt/CeZrO2/Al2O3 catalysts using a Pd-Ag membrane reactor. Catal. Today 2012, 193, 64–73. [Google Scholar] [CrossRef]
- Fedotov, A.S.; Antonov, D.O.; Uvarov, V.I.; Tsodikov, M.V. Original hybrid membrane-catalytic reactor for the Co-Production of syngas and ultrapure hydrogen in the processes of dry and steam reforming of methane, ethanol and DME. Int. J. Hydrogen Energy 2018, 43, 7046–7054. [Google Scholar] [CrossRef]
- Sumrunronnasak, S.; Tantayanon, S.; Kiatgamolchai, S.; Sukonket, T. Improved hydrogen production from dry reforming reaction using a catalytic packed-bed membrane reactor with Ni-based catalyst and dense PdAgCu alloy membrane. Int. J. Hydrogen Energy 2016, 41, 2621–2630. [Google Scholar] [CrossRef]
- Alique, D.; Martinez-Diaz, D.; Sanz, R.; Calles, J.A. Review of supported Pd-based membranes preparation by electroless plating for ultra-pure hydrogen production. Membranes 2018, 8, 5. [Google Scholar] [CrossRef] [PubMed]
- Safariamin, M.; Tidahy, L.H.; Abi-Aad, E.; Siffert, S.; Aboukais, A. Dry reforming of methane in the presence of ruthenium-based catalysts. C. R. Chim. 2009, 12, 748–753. [Google Scholar] [CrossRef]
- Jeon, J.; Nam, S.; Ko, C.H. Rapid evaluation of coke resistance in catalysts for methane reforming using low steam-to-carbon ratio. Catal. Today 2018, 309, 140–146. [Google Scholar] [CrossRef]
- Simakov, D.S.A.; Leshkov, Y.R. Highly efficient methane reforming over a low-loading Ru/γ-Al2O3 catalyst in a Pd-Ag membrane reactor. AIChE J. 2018, 64, 3101–3108. [Google Scholar] [CrossRef]
- Lee, D. Catalytic Reforming of CH4 with CO2 in a Membrane Reactor: A Study on Effect of Pressure. Doctoral Dissertations, VirginiaTech, Blacksburg, VA, USA, 2003; pp. 66–91. [Google Scholar]
- Chein, R.Y.; Chen, Y.C.; Yu, C.T.; Chung, J.N. Thermodynamic analysis of dry reforming of CH4 with CO2 at high pressures. J. Nat. Gas Sci. Eng. 2015, 26, 617–629. [Google Scholar] [CrossRef]
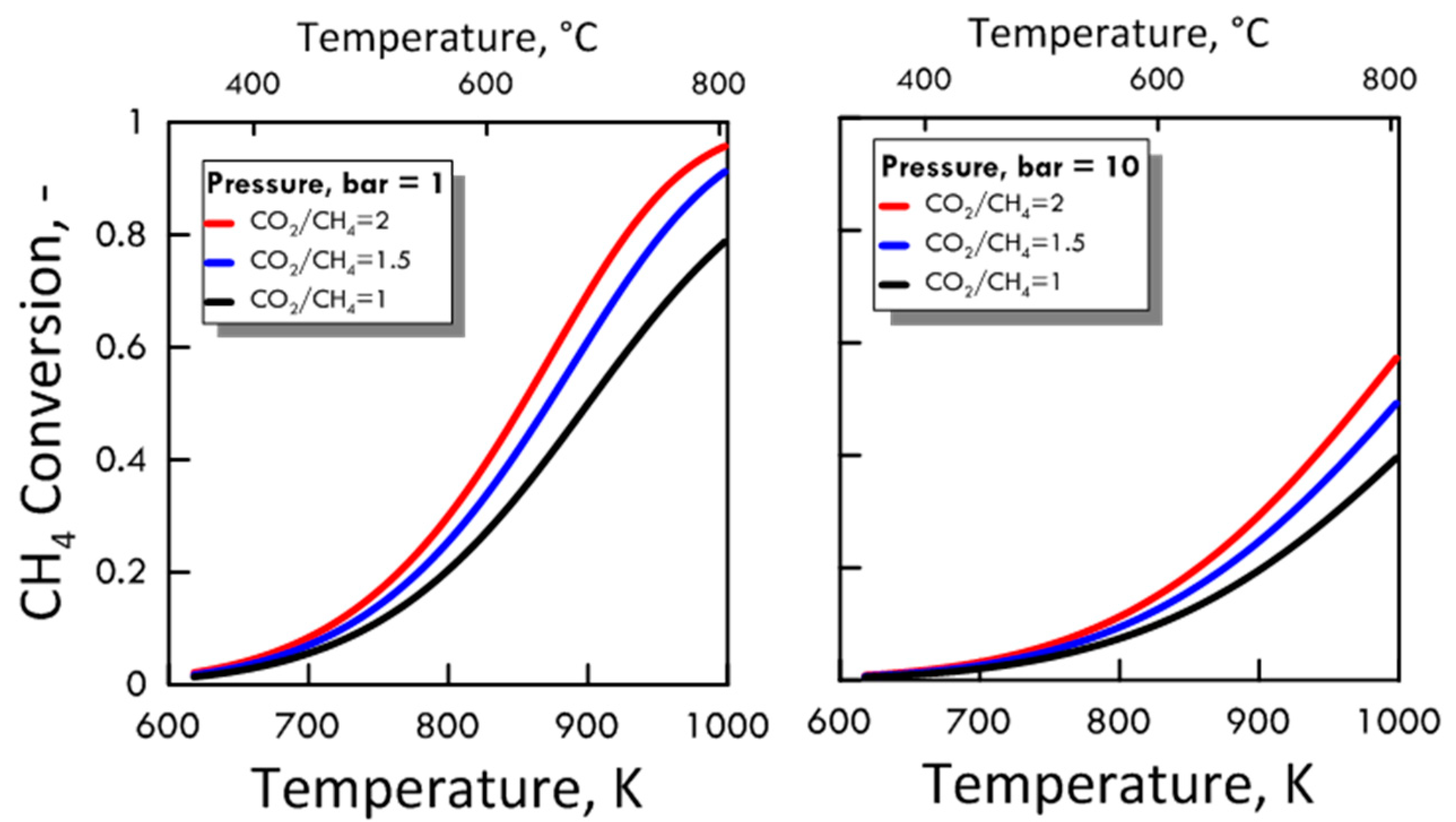
 ), reverse WGS (
), reverse WGS (  ) and Boudouard (
) and Boudouard (  ) reactions.
) reactions.
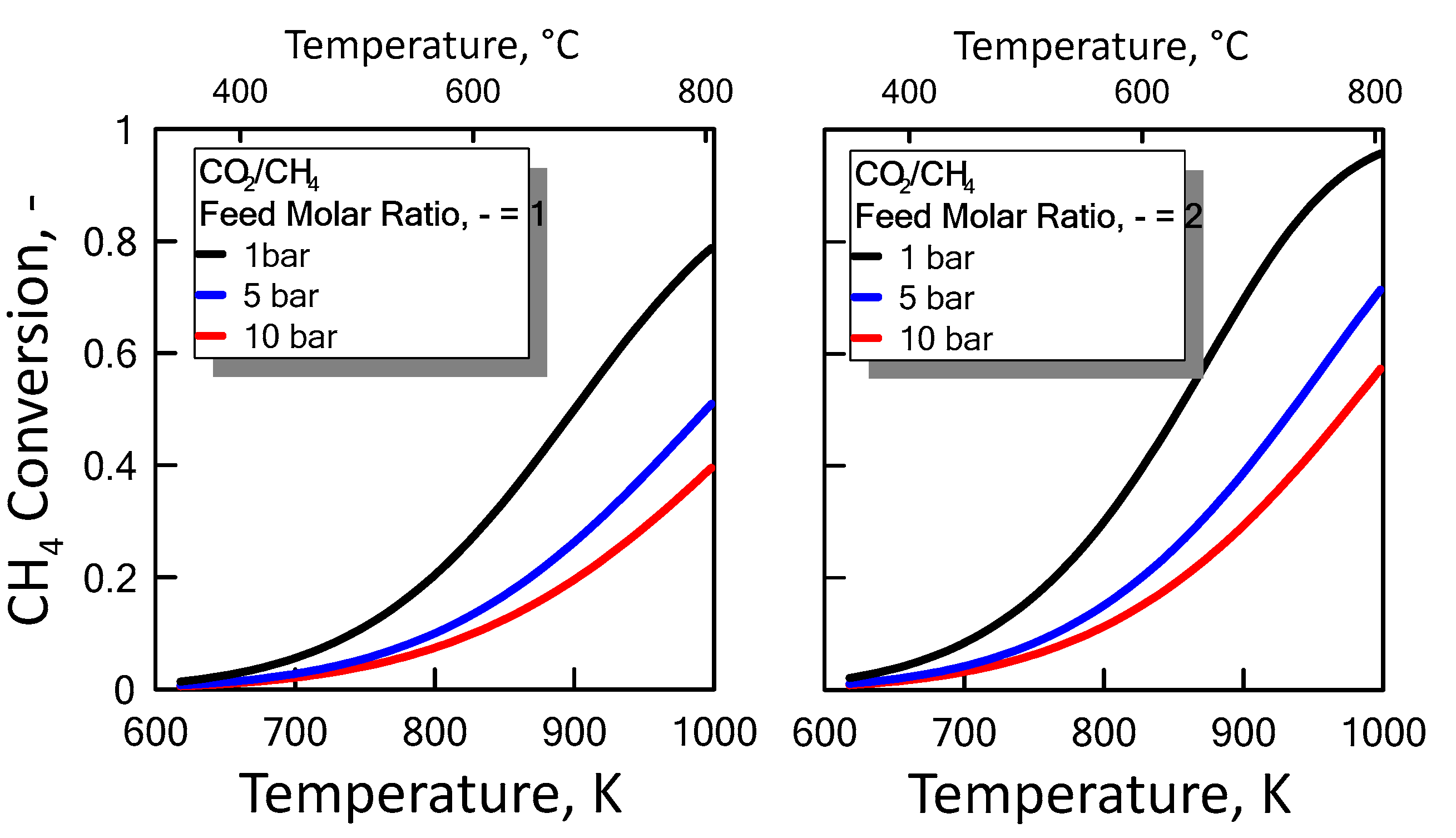
 ), reverse WGS (
), reverse WGS (  ) and Boudouard (
) and Boudouard (  ) reactions.
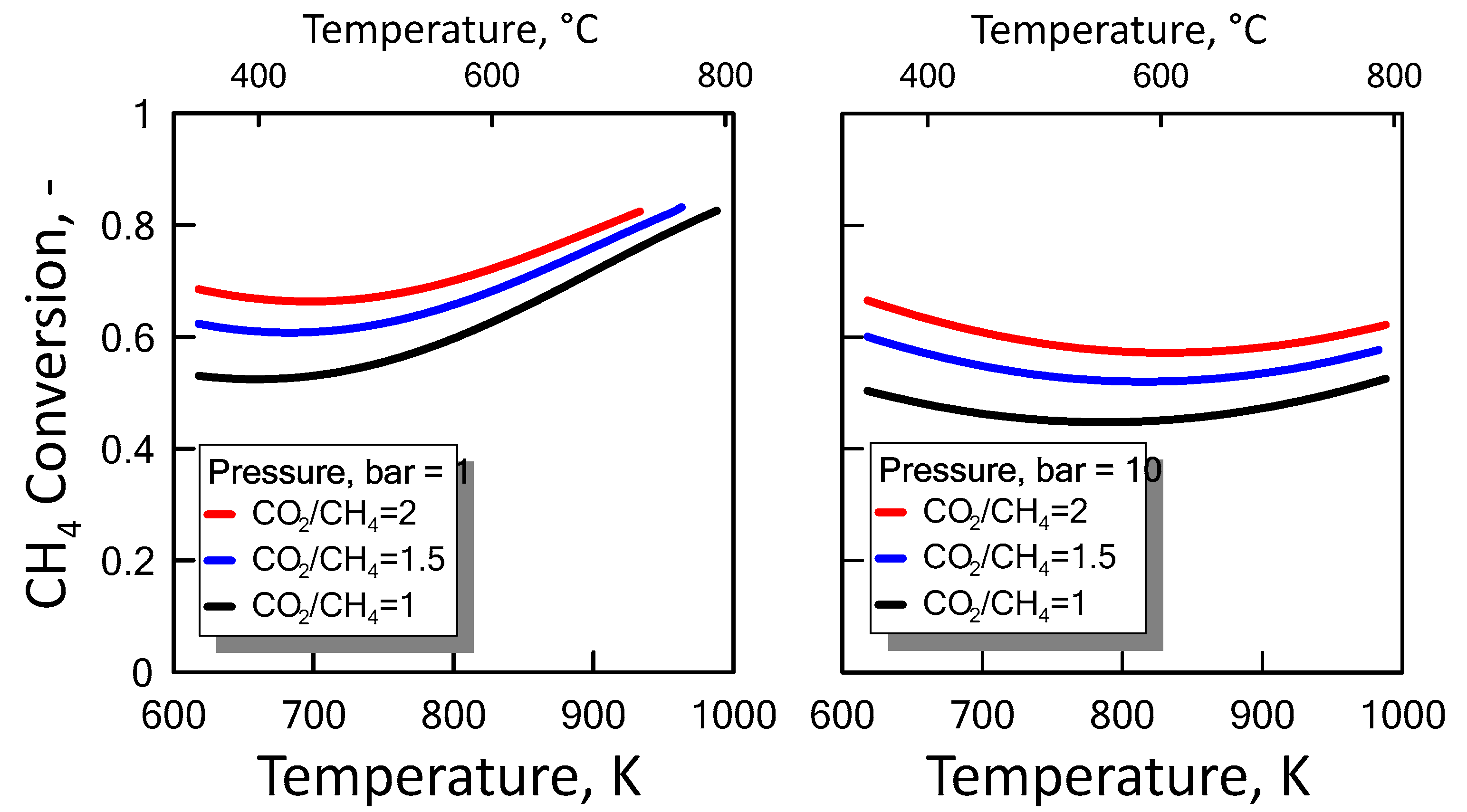
) reactions.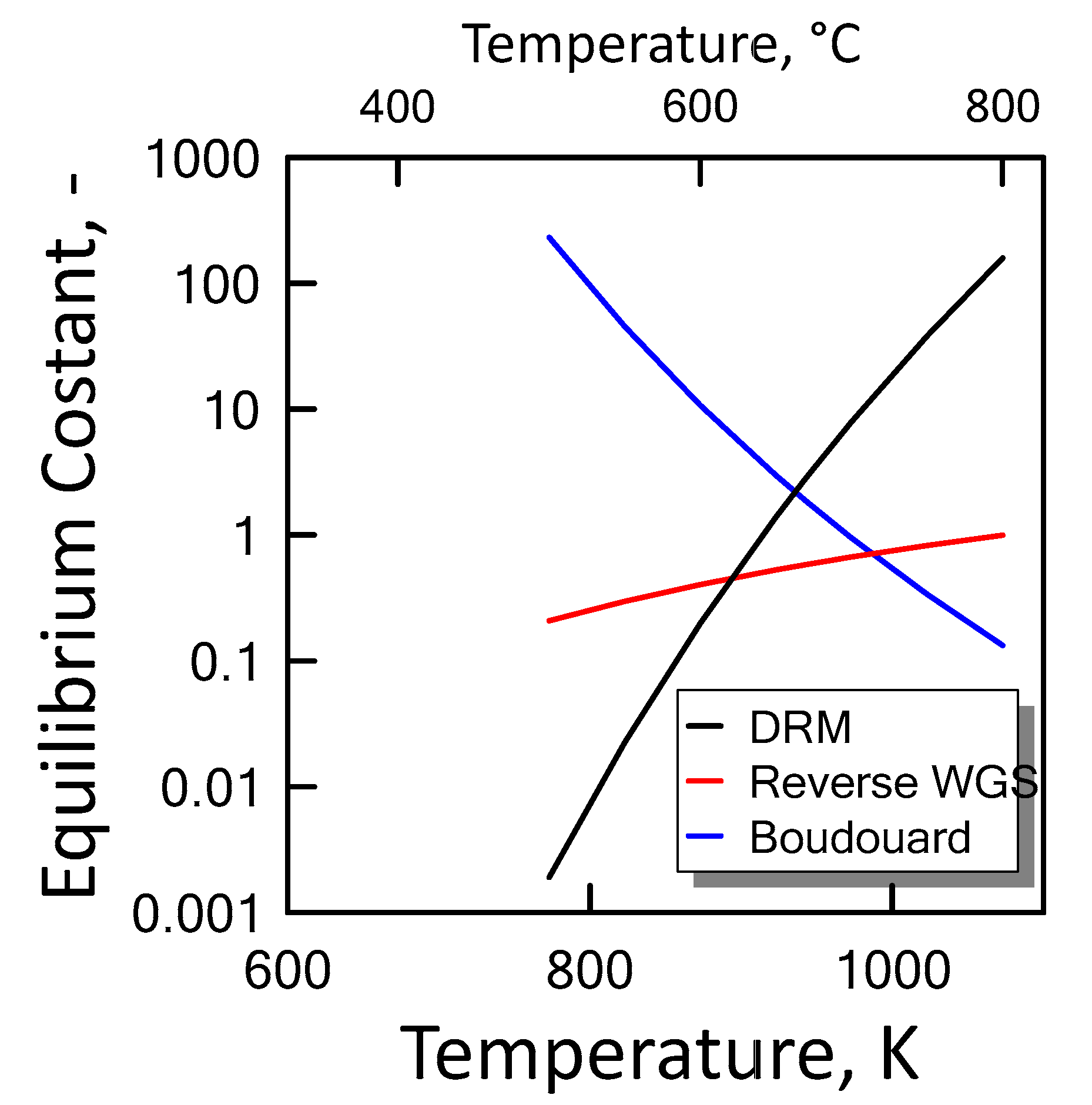


| Membrane | Pd-Ag Commercial (Goodfellow) Self-Supported |
|---|---|
| Thickness | 100 micrometers |
| Superficial Area | 3 cm2 |
| Outer Diameter | 1 mm |
| Length | 93 mm |
| Catalyst Weight | 8.5 g |
| Temperature, °C | Permeation | 400, 450, 500 |
| Reaction | 500 | |
| Pressure, bar | Feed | 1–8 |
| Permeate | 0.02; 1 | |
| CO2/CH4 Feed Molar Ratio | 1, 1.5 | |
| GHSV, h−1 | 100 | |
| Equilibrium Constant Keq | ||||
|---|---|---|---|---|
| DRM | RWGS | |||
| Lee (2003) [33] | MATLAB code | Lee (2003) [33] | MATLAB code | |
| 600 °C | 0.19 | 0.20 | 0.37 | 0.40 |
| 650 °C | 1.31 | 1.38 | 0.48 | 0.53 |
| Apparent Activation Energy, E | J·mol−1 | 4942 |
| Permeance Pre-Exponential Factor | mol·m−2·s−1·Pa−0.5 | 455 |
| Hydrogen Permeance, mol·m−2·s−1·Pa−0.5 | 400 °C | 190 |
| 450 °C | 196 | |
| 500 °C | 211 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caravella, A.; Brunetti, A.; Grandinetti, M.; Barbieri, G. Dry Reforming of Methane in a Pd-Ag Membrane Reactor: Thermodynamic and Experimental Analysis. ChemEngineering 2018, 2, 48. https://doi.org/10.3390/chemengineering2040048
Caravella A, Brunetti A, Grandinetti M, Barbieri G. Dry Reforming of Methane in a Pd-Ag Membrane Reactor: Thermodynamic and Experimental Analysis. ChemEngineering. 2018; 2(4):48. https://doi.org/10.3390/chemengineering2040048
Chicago/Turabian StyleCaravella, Alessio, Adele Brunetti, Monia Grandinetti, and Giuseppe Barbieri. 2018. "Dry Reforming of Methane in a Pd-Ag Membrane Reactor: Thermodynamic and Experimental Analysis" ChemEngineering 2, no. 4: 48. https://doi.org/10.3390/chemengineering2040048
APA StyleCaravella, A., Brunetti, A., Grandinetti, M., & Barbieri, G. (2018). Dry Reforming of Methane in a Pd-Ag Membrane Reactor: Thermodynamic and Experimental Analysis. ChemEngineering, 2(4), 48. https://doi.org/10.3390/chemengineering2040048