Performance of Helical Ribbon and Screw Impellers for Mixing Viscous Fluids in Cylindrical Reactors
Abstract
1. Introduction
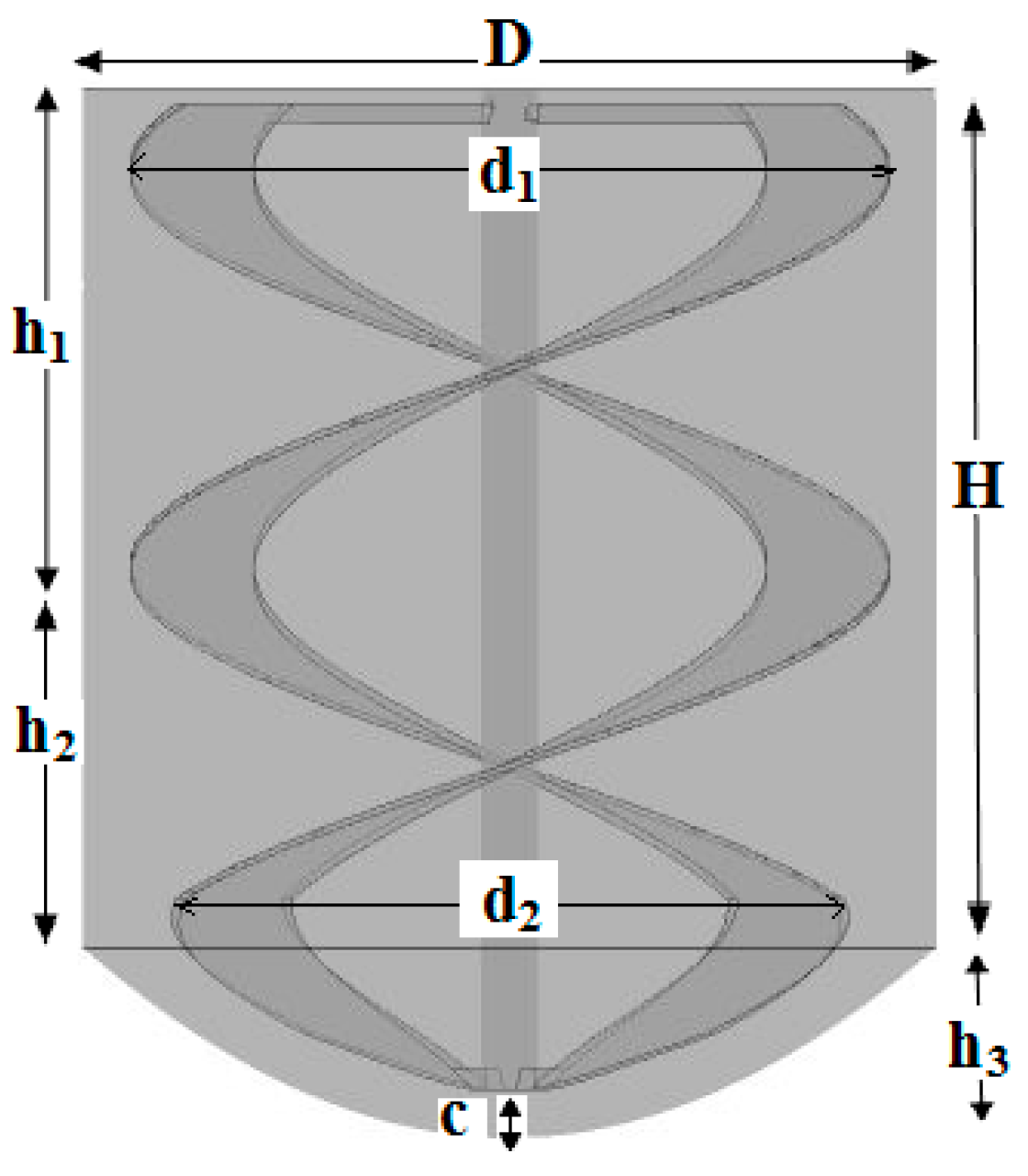
2. Geometry of the Mixing System
3. Materials and Methods
3.1. Variable Definition
3.2. Numerical Simulation
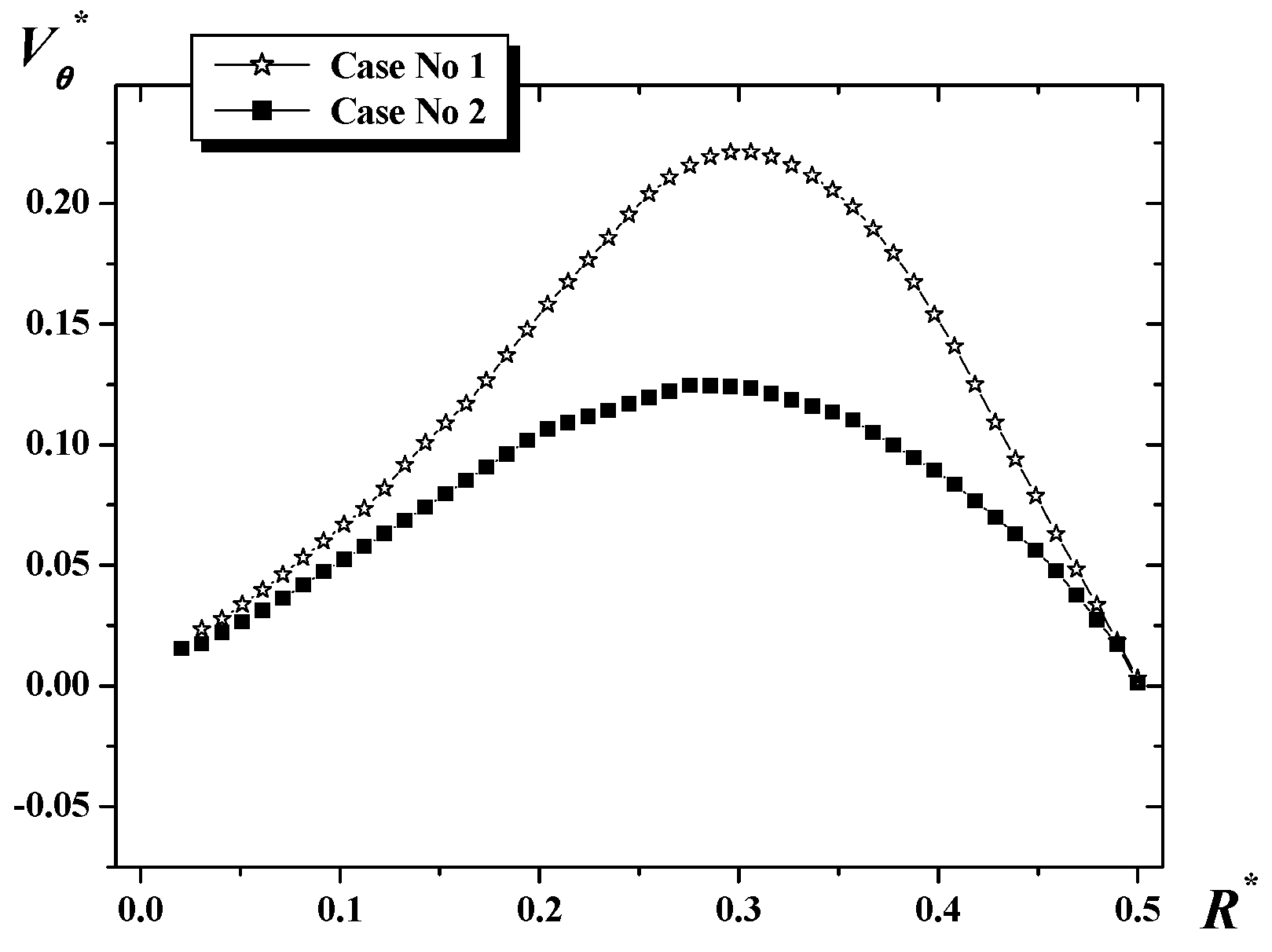
4. Validation of the Predicted Results
5. Results and Discussion
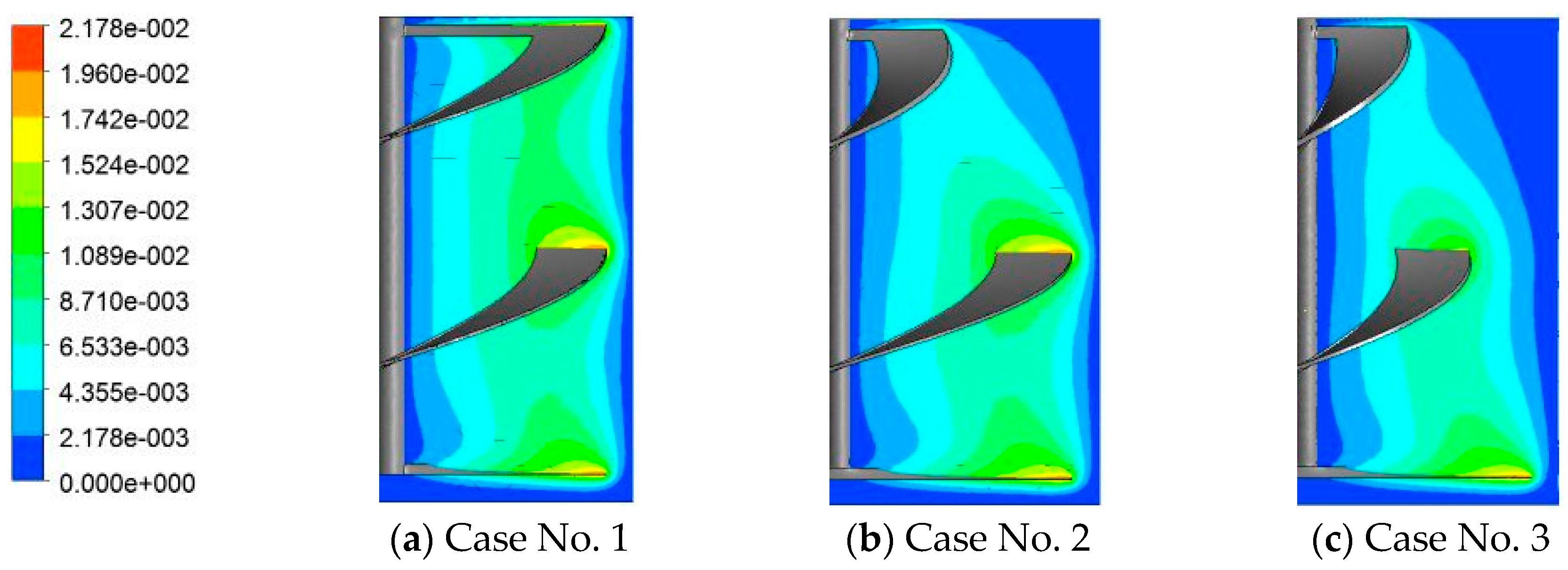
5.1. Effect of the Blade Width
5.2. Effect of the Bottom Shape
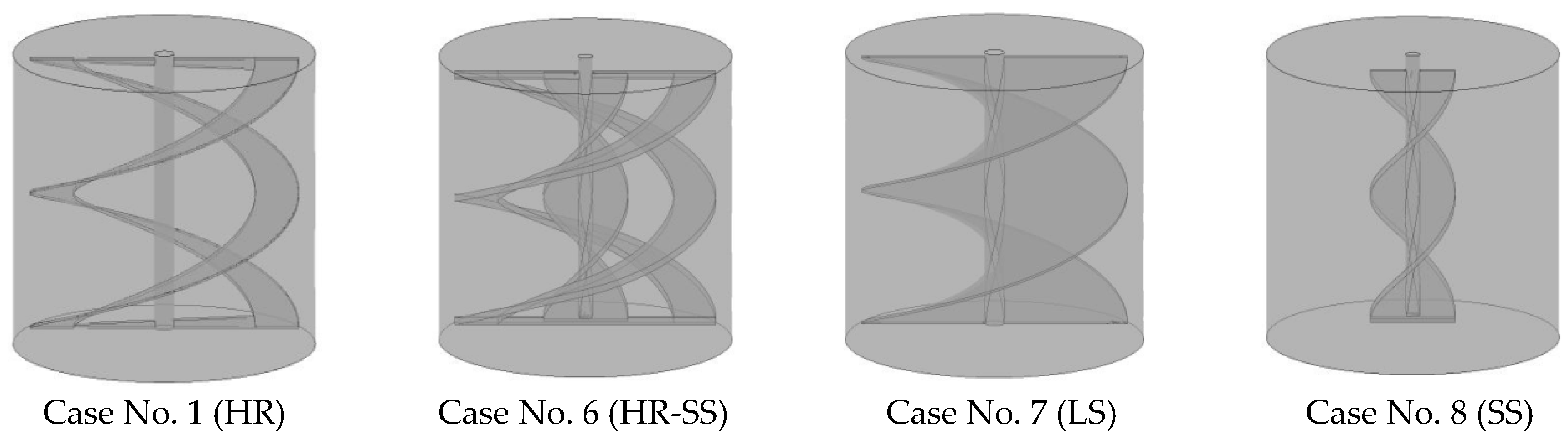
5.3. Comparison between the Helical Ribbon (HR), Small Screw (SS), Large Screw (LS), Helical Ribbon-Small Screw (HR-SS) Impellers
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Kuncewicz, C.; Stelmach, J. Optimization of geometric parameters of a ribbon impeller. Chem. Proc. Eng. 2017, 38, 491–502. [Google Scholar] [CrossRef]
- Gammoudi, A.; Ayadi, A.; Baccar, M. The hydrodynamic and thermal characterization of a yield stress fluid in stirred tanks equipped with simple helical ribbons with two stages. Meccanica 2017, 52, 1743–1766. [Google Scholar] [CrossRef]
- Mohd, S.M.; Rosfarizan, M.; Musaalbakri, A.; Arbakariya, B.A. Enhancement of red pigment production by monascuspurpureus FTC 5391 through retrofitting of helical ribbon impeller in stirred-tank fermenter. Food Bioproc. Technol. 2012, 5, 80–91. [Google Scholar]
- Yao, W.; Mishima, M.; Takahashi, K. Numerical investigation on dispersive mixing characteristics of Maxblend and double helical ribbons. Chem. Eng. J. 2001, 84, 565–571. [Google Scholar] [CrossRef]
- Ameur, H. Energy efficiency of different impellers in stirred tank reactors. Energy 2015, 93, 1980–1988. [Google Scholar] [CrossRef]
- Robinson, M.; Cleary, P.W. Flow and mixing performance in helical ribbon mixers. Chem. Eng. Sci. 2012, 84, 382–398. [Google Scholar] [CrossRef]
- Delaplace, G.; Guerin, R.; Leuliet, J.C.; Chhabra, R.P. An analytical model for the prediction of power consumption for shear thinning fluids with helical ribbon and helical screw ribbon impellers. Chem. Eng. Sci. 2006, 61, 3250–3259. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, L.; Jiang, B.; Yin, Y.; Li, X. Calculation of Metzner constant for double helical ribbon impeller by CFD method. Chin. J. Chem. Eng. 2008, 16, 686–692. [Google Scholar] [CrossRef]
- Ameur, H.; Kamla, Y.; Hadjeb, A.; Arab, I.M.; Sahel, D. Data on mixing of viscous fluids by helical screw impellers in cylindrical vessels. Data Brief 2016, 8, 220–224. [Google Scholar] [CrossRef] [PubMed]
- Ameur, H.; Kamla, Y.; Sahel, D. Performance of helical screw impellers for mixing of viscous liquids in cylindrical reactors. ChemistrySelect 2017, 2, 1891–1894. [Google Scholar] [CrossRef]
- Maingonnat, J.F.; Doublier, J.L.; Lefebvre, J.; Delaplace, G. Power consumption of a double ribbon impeller with Newtonian and shear thinning fluids and during the gelation of a iota-carrageenan solution. J. Food Eng. 2008, 87, 82–90. [Google Scholar] [CrossRef]
- Driss, Z.; Karray, S.; Kchaou, H.; Abid, M.S. CFD simulation of the laminar flow in stirred tanks generated by double helical ribbons and double helical screw ribbons impellers. Central Eur. J. Eng. 2011, 1, 413–422. [Google Scholar] [CrossRef]
- Ameur, H.; Bouzit, M.; Ghenaim, A. Hydrodynamics in a vessel stirred by simple and double helical ribbon impellers. Central Eur. J. Eng. 2013, 3, 87–98. [Google Scholar] [CrossRef]
- Anne-Archard, D.; Marouche, M.; Boisson, H.C. Hydrodynamics and Metzner–Otto correlation in stirred vessels for yield stress fluids. Chem. Eng. J. 2006, 125, 15–24. [Google Scholar] [CrossRef]
- Iranshahi, A.; Heniche, M.; Bertrand, F.; Tanguy, P.A. Numerical investigation of the mixing efficiency of the EkatoParavisc impeller. Chem. Eng. Sci. 2006, 61, 2609–2617. [Google Scholar] [CrossRef]
- Yu, L.; Ma, J.; Chen, S. Numerical simulation of mechanical mixing in high solid anaerobic digester. Bioresour. Technol. 2011, 102, 1012–1018. [Google Scholar] [CrossRef] [PubMed]
- Dieulot, J.Y.; Delaplace, G.; Guerin, R.; Brienne, J.P.; Leuliet, J.C. Laminar mixing performances of a stirred tank equipped with helical ribbon agitator subjected to steady and unsteady rotational speed. Chem. Eng. Res. Des. 2002, 80, 335–344. [Google Scholar] [CrossRef]
- Kuncewicz, C.; Szulc, K.; Kurasinski, T. Hydrodynamics of the tank with a screw impeller. Chem. Eng. Proc. 2005, 44, 766–774. [Google Scholar] [CrossRef]
- Masiuk, S.; Rakoczy, R. The entropy criterion for the homogenisation process in a multi-ribbon blender. Chem. Eng. Proc. 2006, 45, 500–506. [Google Scholar] [CrossRef]
- Rivera, C.A.; Heniche, M.; Takenaka, K.; Tanguy, P.A. Finite element modeling of the laminar and transition flow of the Super blend dual shaft coaxial mixer on parallel computers. Chem. Eng. Sci. 2009, 64, 4442–4456. [Google Scholar] [CrossRef]
- Bao, Y.; Lu, Y.; Liang, Q.; Li, L.; Gao, Z.; Huang, X.; Qin, S. Power demand and mixing performance of coaxial mixers in a stirred tank with CMC solution. Chin. J. Chem. Eng. 2015, 23, 623–632. [Google Scholar] [CrossRef]
- Gijón-Arreortúa, I.; Tecante, A. Mixing time and power consumption during blending of cohesive food powders with a horizontal helical double-ribbon impeller. J. Food Eng. 2015, 149, 144–152. [Google Scholar] [CrossRef]
- Oliva, A.M.; Hargrave, N.R.; Feys, D.; Park, J. Simulation of yield-stress fluid in a rotational rheometer: The effect of the vane geometry on cement flows. In Proceedings of the 2015 COMSOL Conference in Boston, Boston, MA, USA, 7–9 October 2015. [Google Scholar]
- Liu, B.; Wang, M.; Liu, J.L.; Qian, L.; Jin, Z. Experimental study on micromixing characteristics of novel large-double-blade impeller. Chem. Eng. Sci. 2015, 123, 641–647. [Google Scholar] [CrossRef]
- Patel, D.; Ein-Mozaffari, F.; Mehrvar, M. Using tomography to visualize the continuous-flow mixing of biopolymer solutions inside a stirred tank reactor. Chem. Eng. J. 2014, 239, 257–273. [Google Scholar] [CrossRef]
- Ameur, H. Mixing of shear thinning fluids in cylindrical tanks: Effect of the impeller blade design and operating conditions. Int. J. Chem. React. Eng. 2016, 14, 1025–1034. [Google Scholar] [CrossRef]
- Aubin, J.; Naud, I.; Xuereb, C.; Bertrand, J. Blending of Newtonian and shear-thinning fluids in a tank stirred with a helical screw agitator. Chem. Eng. Res. Des. 2000, 78, 1105–1114. [Google Scholar] [CrossRef]



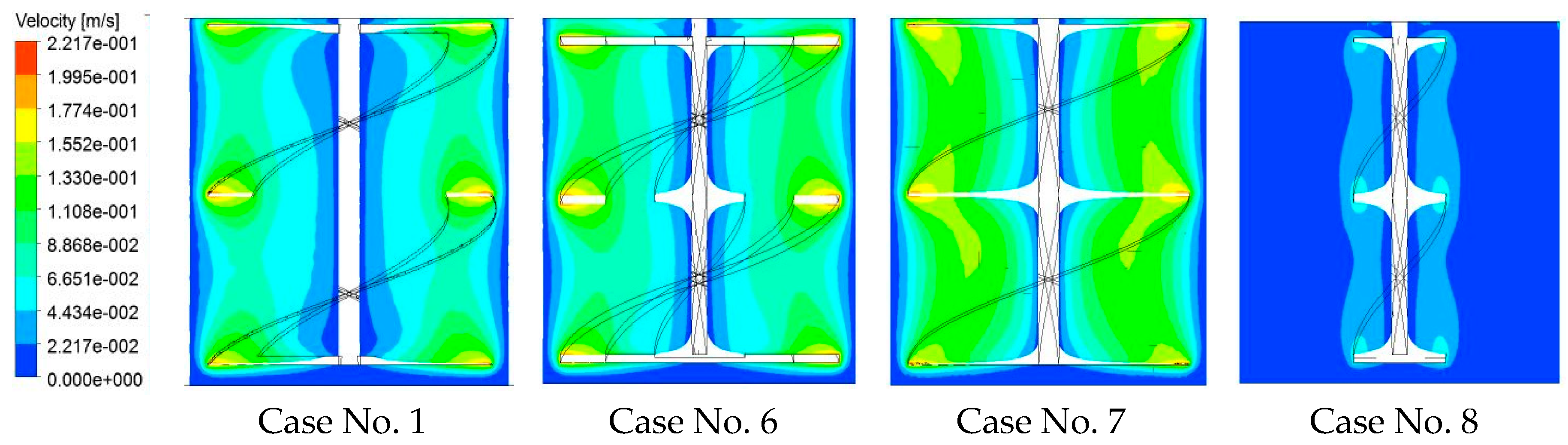
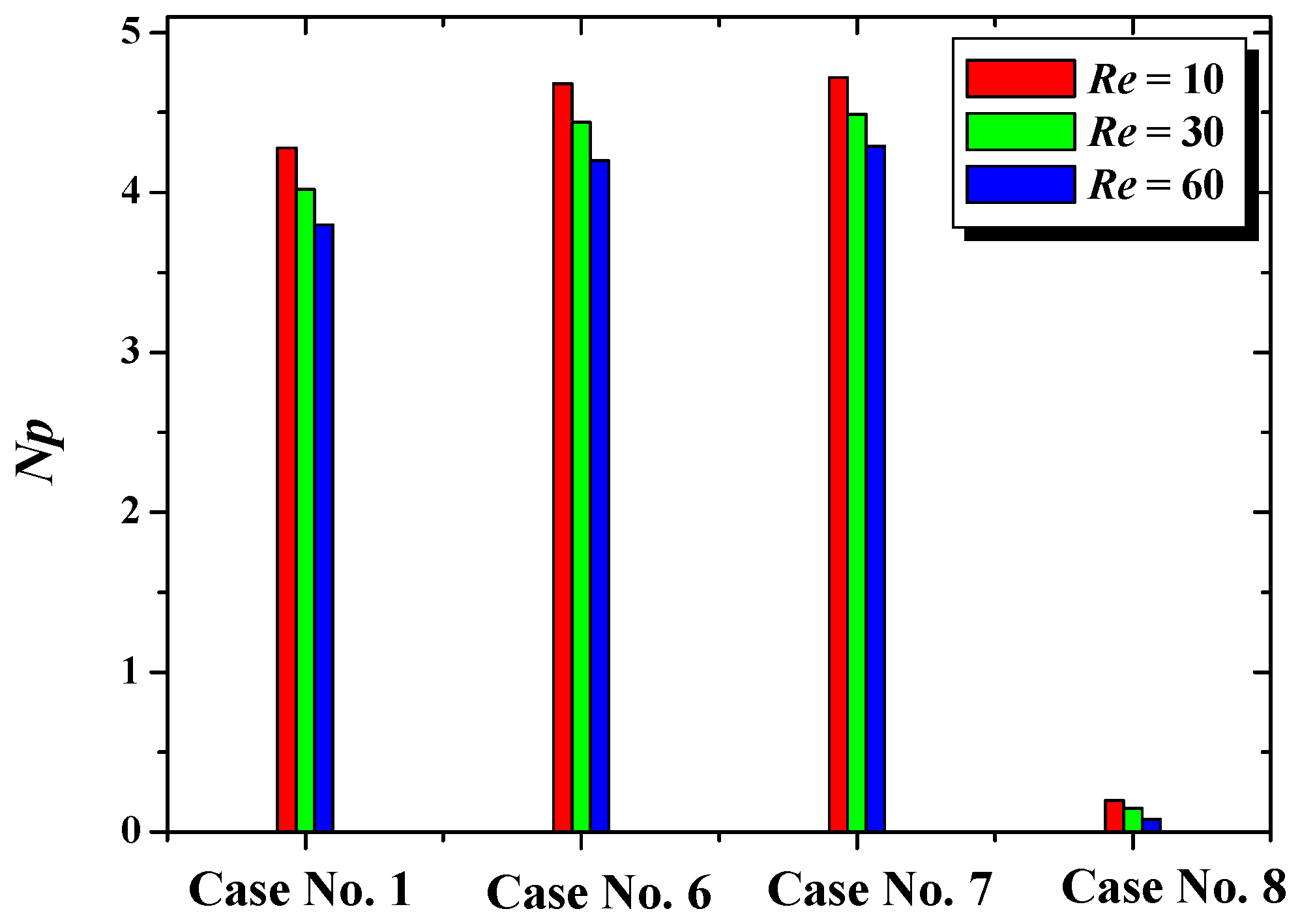
| Case | H/D | d1/D | d2/D | h1/D | h2/D | h3/D | c/D | ds/D |
|---|---|---|---|---|---|---|---|---|
| No. 1 | 1 | 0.89 | 0.89 | 0.445 | 0.445 | 0 | 0.052 | 0.033 |
| No. 2 | 1 | 0.4 | 0.89 | 0.445 | 0.445 | 0 | 0.052 | 0.033 |
| No. 3 | 1 | 0.4 | 0.89 | 0.779 | 0.111 | 0 | 0.052 | 0.033 |
| Case | H/D | d1/D | d2/D | h1/D | h2/D | h3/D | c/D | ds/D |
|---|---|---|---|---|---|---|---|---|
| No. 4 | 1 | 0.89 | 0.89 | 0.445 | 0.445 | 0.222 | 0.052 | 0.033 |
| No. 5 | 1 | 0.4 | 0.89 | 0.445 | 0.445 | 0.338 | 0.052 | 0.033 |
| Case | No. 1 | No. 2 | No. 3 |
|---|---|---|---|
| Np | 4.28 | 3.75 | 1.79 |
| Case | No. 4 | No. 5 |
|---|---|---|
| Np | 4.49 | 4.66 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ameur, H.; Kamla, Y.; Sahel, D. Performance of Helical Ribbon and Screw Impellers for Mixing Viscous Fluids in Cylindrical Reactors. ChemEngineering 2018, 2, 26. https://doi.org/10.3390/chemengineering2020026
Ameur H, Kamla Y, Sahel D. Performance of Helical Ribbon and Screw Impellers for Mixing Viscous Fluids in Cylindrical Reactors. ChemEngineering. 2018; 2(2):26. https://doi.org/10.3390/chemengineering2020026
Chicago/Turabian StyleAmeur, Houari, Youcef Kamla, and Djamel Sahel. 2018. "Performance of Helical Ribbon and Screw Impellers for Mixing Viscous Fluids in Cylindrical Reactors" ChemEngineering 2, no. 2: 26. https://doi.org/10.3390/chemengineering2020026
APA StyleAmeur, H., Kamla, Y., & Sahel, D. (2018). Performance of Helical Ribbon and Screw Impellers for Mixing Viscous Fluids in Cylindrical Reactors. ChemEngineering, 2(2), 26. https://doi.org/10.3390/chemengineering2020026




