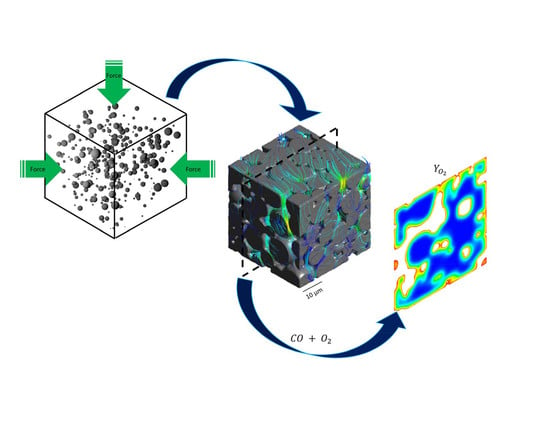
Resolved-Pore Simulation of CO Oxidation on Rh/Al2O3 in a Catalyst Layer
Abstract
:1. Introduction
2. Materials and Methods
2.1. Catalyst Reconstruction
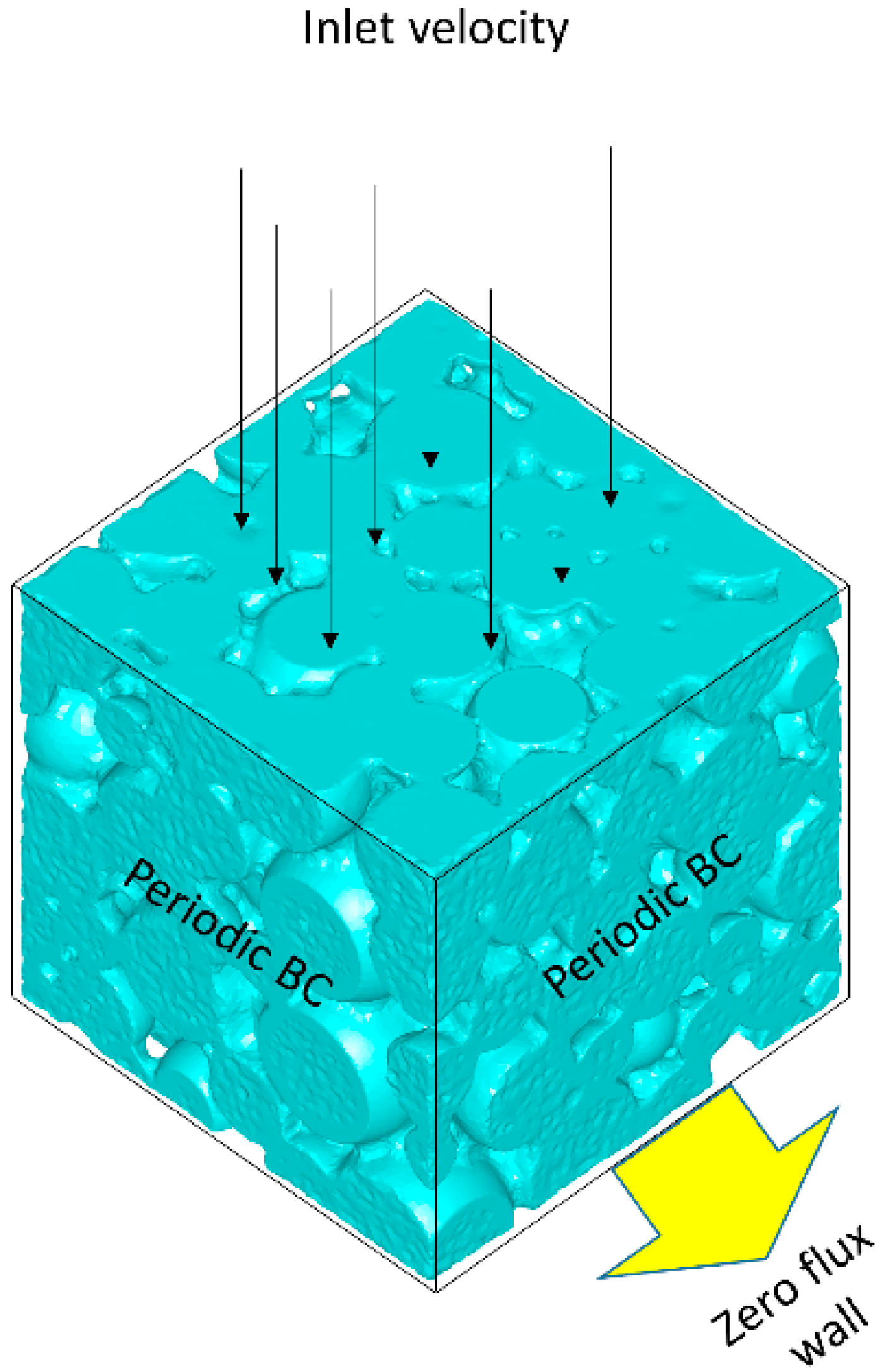
2.2. Mesh Generation
2.3. Reaction Kinetics
2.4. Governing Equations
2.5. Computational Parameters
2.5.1. Catalyst Construction Parameters
2.5.2. Mesh Parameters
2.5.3. Simulation Parameters
3. Results
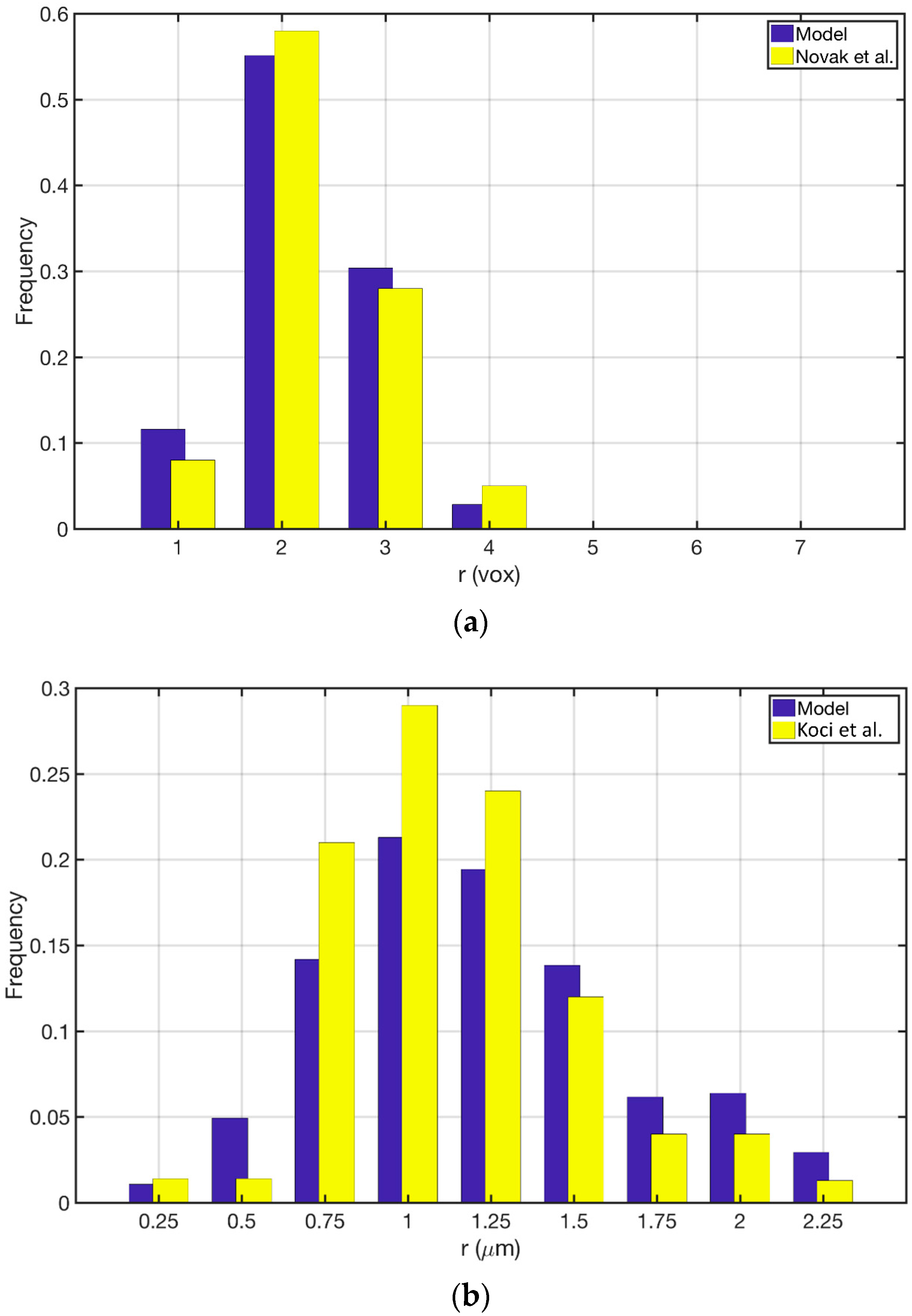
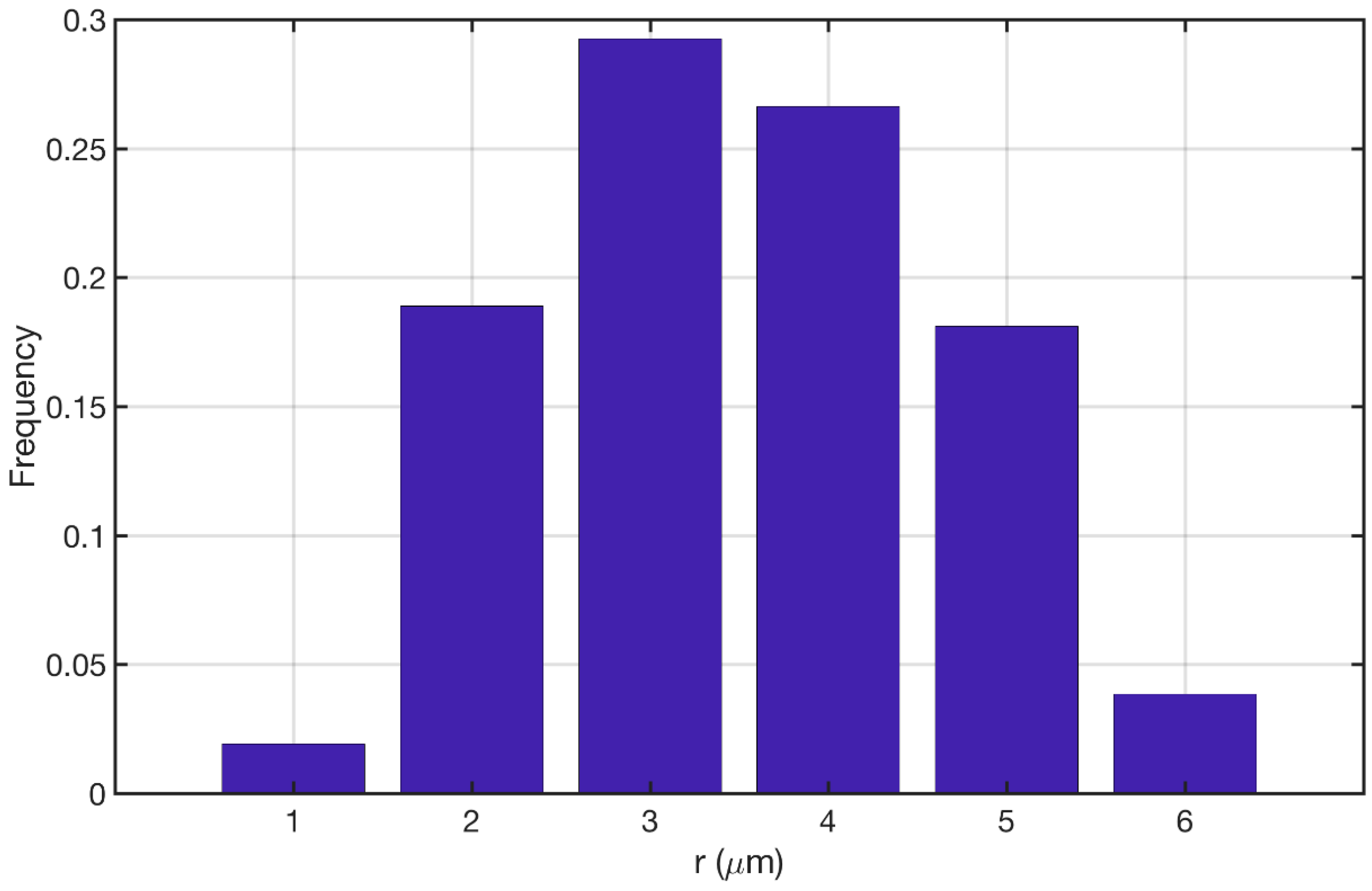
3.1. Reconstructed Catalyst Properties and Validation
3.2. Splines Accuracy
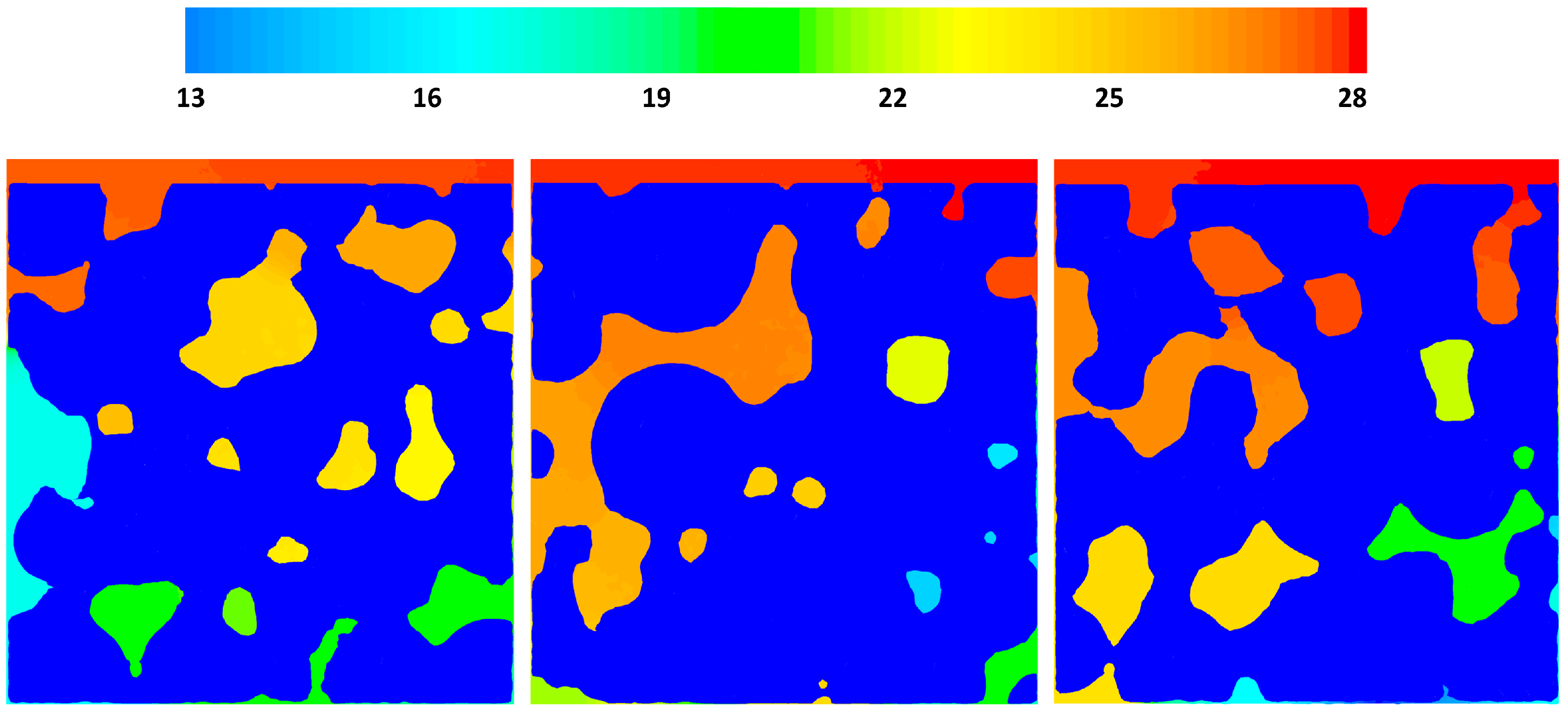
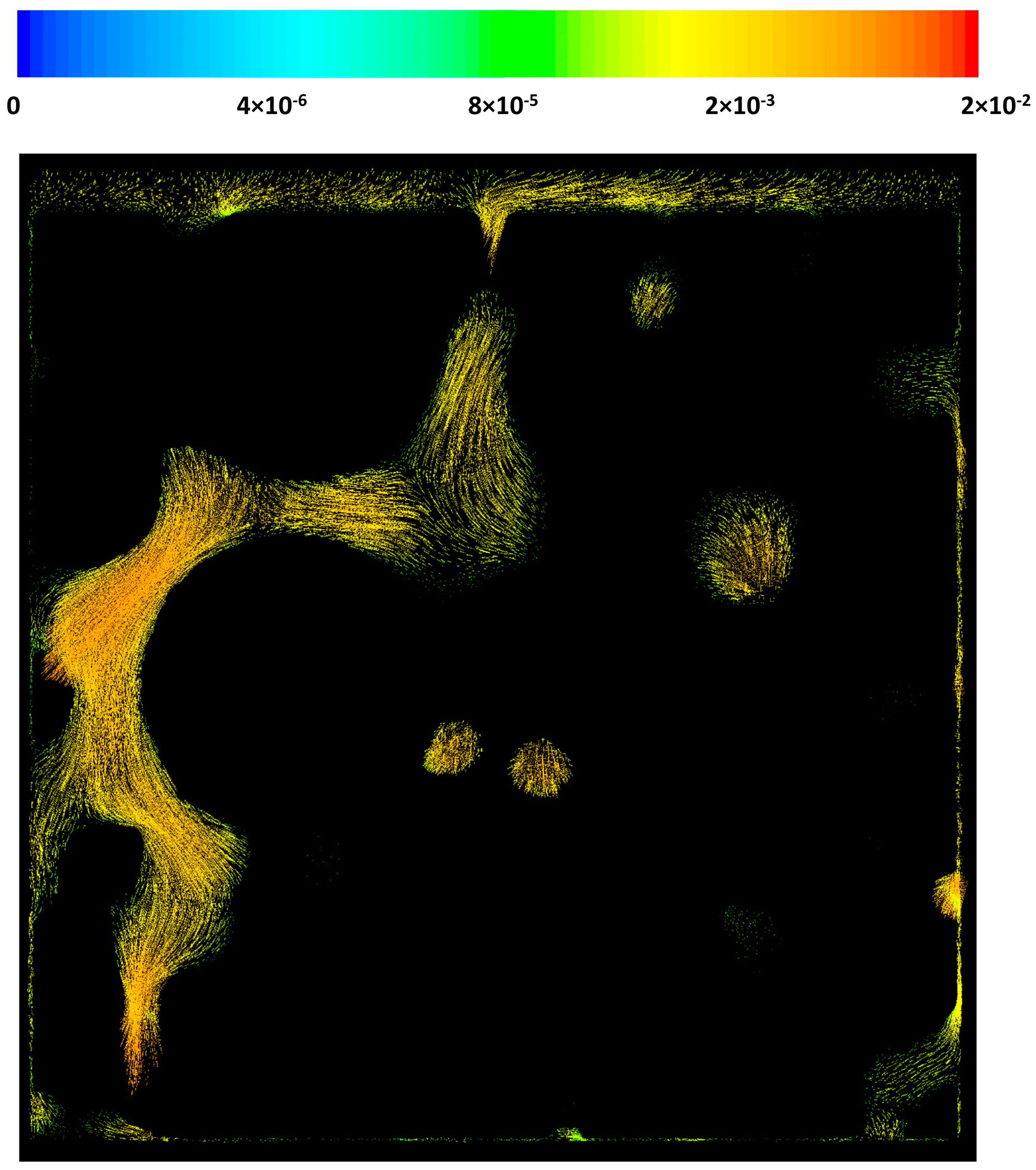
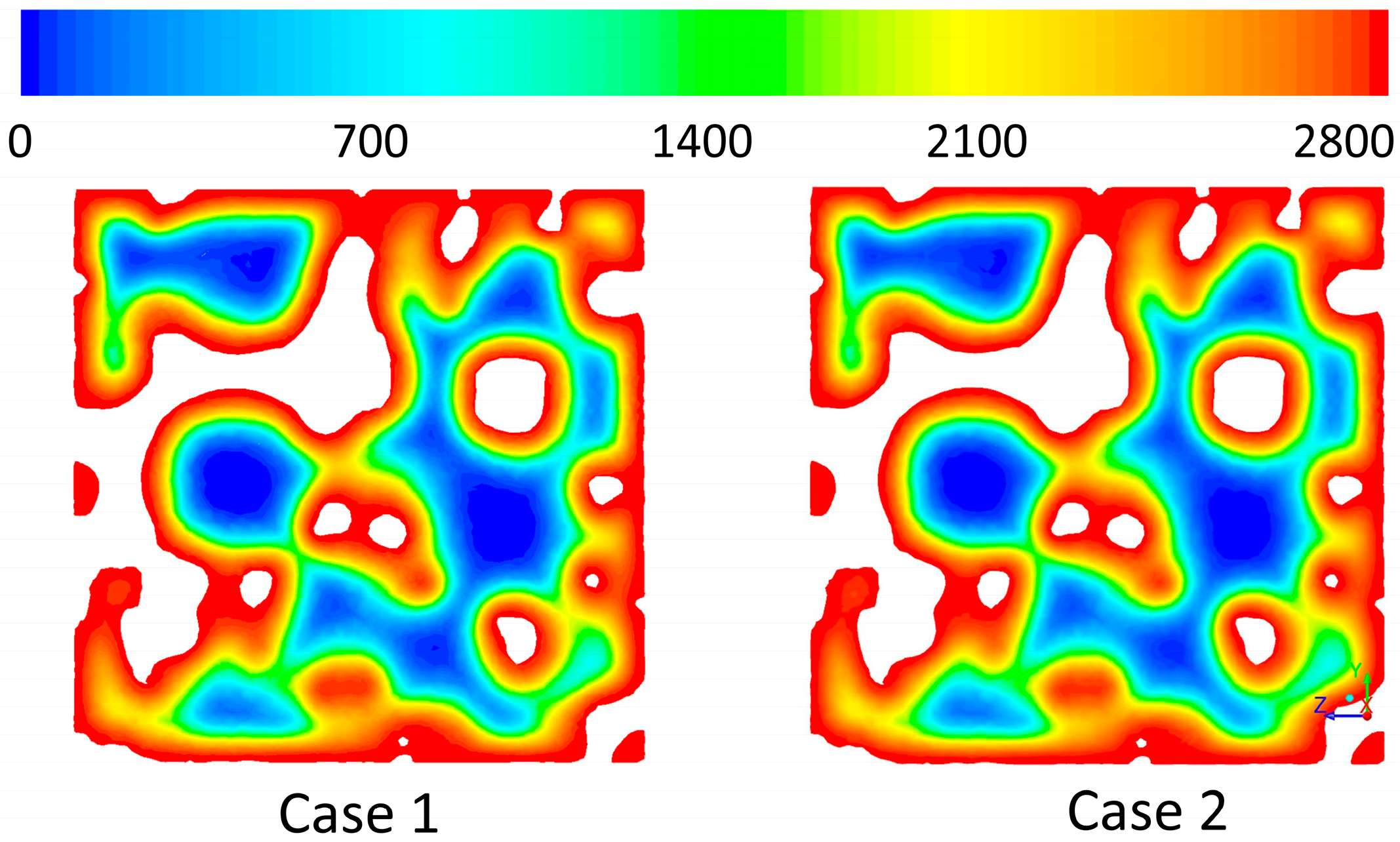
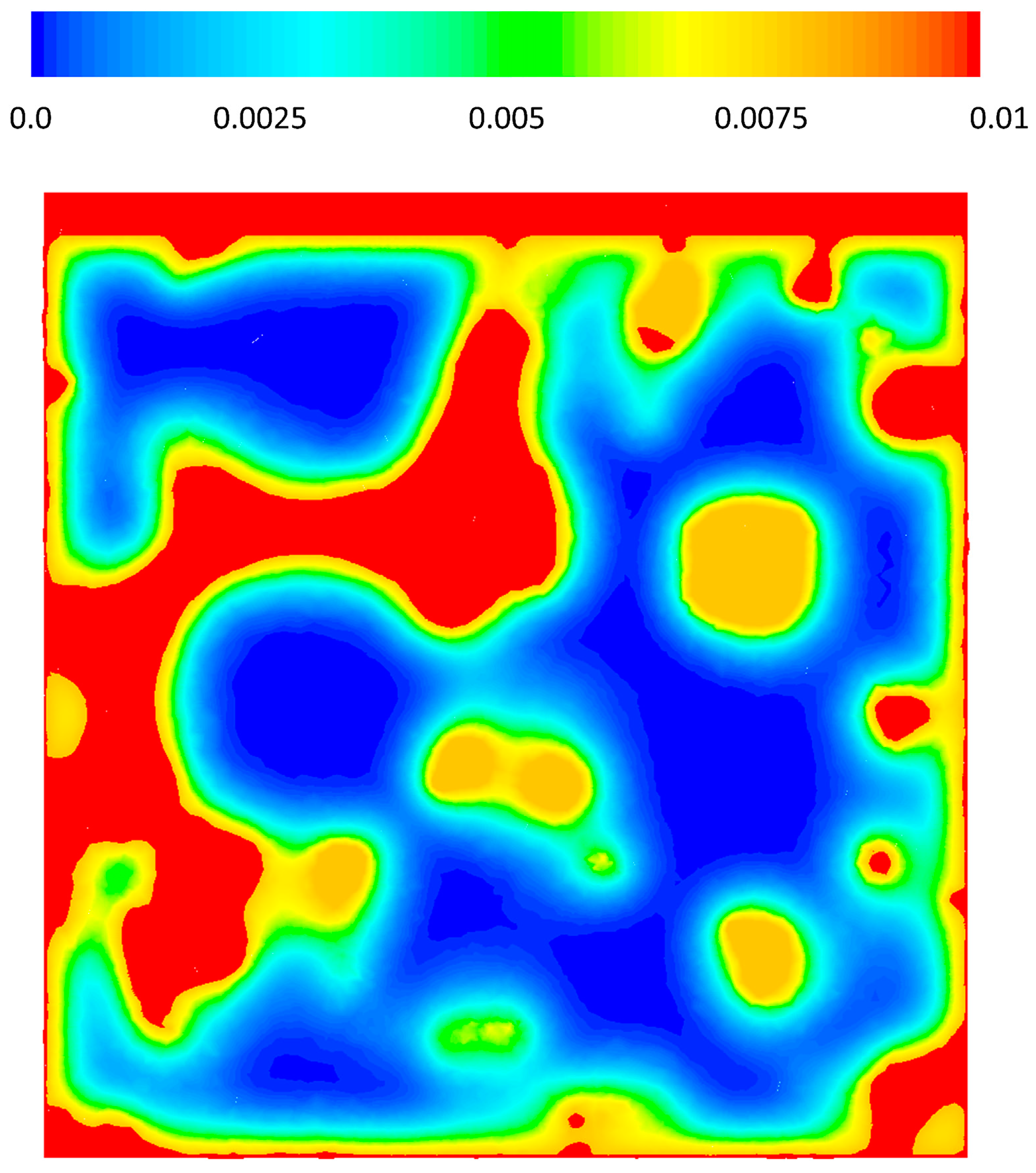
3.3. CFD Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Alavi, A.; Hu, P.; Deutsch, T.; Silvestrelli, P.L.; Hutter, J. CO oxidation on Pt(111): An Ab initio density functional theory study. Phys. Rev. Lett. 1998, 80, 3650–3653. [Google Scholar] [CrossRef]
- Chen, M.S.; Cai, Y.; Yan, Z.; Gath, K.K.; Axnanda, S.; Goodman, D.W. Highly active surfaces for CO oxidation on Rh, Pd, and Pt. Surf. Sci. 2007, 601, 5326–5331. [Google Scholar] [CrossRef]
- Carabineiro, S.A.C.; Silva, A.M.T.; Drazic, G.; Tavares, P.B.; Figueiredo, J.L. Effect of chloride on the sinterization of Au/CeO2 catalysts. Catal. Today. 2010, 154, 293–302. [Google Scholar] [CrossRef]
- Santos, V.P.; Carabineiro, S.A.C.; Bakker, J.J.W.; Soares, O.S.G.P.; Chen, X.; Pereira, M.F.R.; Orfao, J.J.M.; Figueiredo, J.L.; Gascon, J.; Kapteijn, F. Stablizied gold on cerium-modified cryotimelane: Highly active in low-temperature CO oxidation. J. Catal. 2014, 309, 58–65. [Google Scholar] [CrossRef]
- Rogal, J.; Reuter, K.; Scheffler, M. CO oxidation at Pd(100): A first-principles constrained thermodynamics study. Phys. Rev. B 2007, 75, 205433. [Google Scholar] [CrossRef]
- Rogal, J.; Reuter, K.; Scheffler, M. CO oxidation on Pd(100) at technologically relevant pressure conditions: First-principles kinetic Monte Carlo study. Phys. Rev. B 2008, 77, 155410. [Google Scholar] [CrossRef]
- Reuter, K.; Scheffler, M. First-principles kinetic Monte Carlo simulations for heterogeneous catalysis: Application to the CO oxidation at RuO2 (110). Phys. Rev. B 2006, 73, 045433. [Google Scholar] [CrossRef]
- Rogal, J.; Reuter, K.; Scheffler, M. First-principles statistical mechanics study of the stability of a subnanometer thin surface oxide in reactive environments: CO oxidation at Pd(100). Phys. Rev. Lett. 2007, 98, 046101. [Google Scholar] [CrossRef] [PubMed]
- Matera, S.; Reuter, K. First-principles approach to heat and mass transfer effects in model catalyst studies. Catal. Lett. 2009, 133, 156–159. [Google Scholar] [CrossRef]
- Matera, S.; Reuter, K. Transport limitations and bistability for in situ CO oxidation at RuO2 (110): First-principles based multiscale modeling. Phys. Rev. B 2010, 82, 085446. [Google Scholar] [CrossRef]
- Karadeniz, H.; Karakaya, C.; Tischer, S.; Deutschmann, O. Numerical modeling of stagnation-flows on porous catalytic surfaces: CO oxidation on Rh/Al2O3. Chem. Eng. Sci. 2013, 104, 899–907. [Google Scholar] [CrossRef]
- Montemore, M.M.; Montessori, A.; Succi, S.; Barroo, C.; Falcucci, G.; Bell, D.C.; Kaxiras, E. Effect of nanoscale flows on the surface structure of nanoporous catalysts. J. Chem. Phys. 2017, 146, 214703. [Google Scholar] [CrossRef] [PubMed]
- Roberts, A.P. Morphology and thermal conductivity of model organic aerogels. Phys. Rev. E 1996, 55, R1286–R1289. [Google Scholar] [CrossRef] [Green Version]
- Štěpánek, F.; Ansari, M.A. Computer simulation of granule microstructure formation. Chem. Eng. Sci. 2005, 60, 4019–4029. [Google Scholar] [CrossRef]
- Dudák, M.; Novák, V.; Kočí, P.; Marek, M.; Blanco-García, P.; Jones, G. Prediction of diffusivity and conversion of n-decane and CO in coated Pt/γ-Al2O3 catalyst depending on porous layer morphology. Appl. Catal. B Environ. 2014, 150–151, 446–458. [Google Scholar] [CrossRef]
- Dixon, A.G.; Nijemeisland, M. CFD as a design tool for fixed-bed reactors. Ind. Eng. Chem. Res. 2001, 40, 5246–5254. [Google Scholar] [CrossRef]
- Behnam, M.; Dixon, A.G.; Nijemeisland, M.; Stitt, E.H. A new approach to fixed bed radial heat transfer modeling using velocity fields from computational fluid dynamics simulations. Ind. Eng. Chem. Res. 2013, 52, 15244–15261. [Google Scholar] [CrossRef]
- Dixon, A.G.; Boudreau, J.; Rocheleau, A.; Troupel, A.; Taskin, M.E.; Nijemeisland, M.; Stitt, E.H. Flow, transport, and reaction interactions in shaped cylindrical particles for steam methane reforming. Ind. Eng. Chem. Res. 2012, 51, 15839–15854. [Google Scholar] [CrossRef]
- Wehinger, G.D.; Klippel, F.; Kraume, M. Modeling pore processes for particle-resolved CFD simulations of catalytic fixed-bed reactors. Comput. Chem. Eng. 2017, 101, 11–22. [Google Scholar] [CrossRef]
- Taskin, M.E.; Troupel, A.; Dixon, A.G.; Nijemeisland, M.; Stitt, E.H. Flow, transport, and reaction interactions for cylindrical particles with strongly endothermic reactions. Ind. Eng. Chem. Res. 2010, 49, 9026–9037. [Google Scholar] [CrossRef]
- Icardi, M.; Boccardo, G.; Marchisio, D.L.; Tosco, T.; Sethi, R. Pore-scale simulation of fluid flow and solute dispersion in three-dimensional porous media. Phys. Rev. E 2014, 90, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Novák, V.; Kočí, P.; Marek, M.; Štěpánek, F.; Blanco-García, P.; Jones, G. Multi-scale modelling and measurements of diffusion through porous catalytic coatings: An application to exhaust gas oxidation. Catal. Today 2012, 188, 62–69. [Google Scholar] [CrossRef]
- Kočí, P.; Novák, V.; Štěpánek, F.; Marek, M.; Kubíček, M. Multi-scale modelling of reaction and transport in porous catalysts. Chem. Eng. Sci. 2010, 65, 412–419. [Google Scholar] [CrossRef]
- Kočí, P.; Štěpánek, F.; Kubíček, M.; Marek, M. Meso-scale modelling of CO oxidation in digitally reconstructed porous Pt/γ-Al2O3 catalyst. Chem. Eng. Sci. 2006, 61, 3240–3249. [Google Scholar] [CrossRef]
- Dong, Y.; Keil, F.J.; Korup, O.; Rosowski, F.; Horn, R. Effect of the catalyst pore structure on fixed-bed reactor performance of partial oxidation of n-butane: A simulation study. Chem. Eng. Sci. 2015, 142, 299–309. [Google Scholar] [CrossRef]
- Bufe, A.; Klee, M.; Wehinger, G.; Turek, T. 3D Modeling of a Catalyst Layer with Transport Pore for Fischer-Tropsch Synthesis. Chem. Ing. Tech. 2017, 89, 1385–1390. [Google Scholar] [CrossRef]
- Novak, V.; Štěpánek, F.; Kočí, P.; Marek, M.; Kubicek, M. Evaluation of local pore sizes and transport properties in porous catalysts. Chem. Eng. Sci. 2010, 65, 2352–2360. [Google Scholar] [CrossRef]
- Partopour, B.; Dixon, A.G. An integrated workflow for resolved-particle packed bed models with complex particle shapes. Powder Technol. 2017, 322, 258–272. [Google Scholar] [CrossRef]
- Partopour, B.; Dixon, A.G. Computationally efficient incorporation of microkinetics into resolved-particle CFD simulations of fixed-bed reactors. Comput. Chem. Eng. 2016, 88, 126–134. [Google Scholar] [CrossRef]
- Tartakovsky, A.M. Langevin model for reactive transport in porous media. Phys. Rev. E 2010, 82, 026302. [Google Scholar] [CrossRef] [PubMed]
- Fuller, E.N.; Schettler, P.D.; Giddings, J.C. A new method for prediction of binary gas-phase diffusion coefficients. Ind. Eng. Chem. 1966, 16, 551. [Google Scholar] [CrossRef]
- Sobieski, W. The use of Path Tracking Method for determining the tortuosity field in a porous bed. Granul. Matter 2016, 18, 72. [Google Scholar] [CrossRef]


| Reaction | A (cm,mol,s) | β | Ea (kJ/mol) | |
|---|---|---|---|---|
| R1 | O2 + 2Rh(s) → 2O(s) | 1.00 | ||
| R2 | CO2 + Rh(s) → CO2(s) | 4.80 | ||
| R3 | CO + Rh(s) → CO(s) | 4.971 | ||
| R4 | 2O(s) → O2 + 2Rh(s) | 5.329 × 1022 | −0.137 | 387 |
| R5 | CO(s) → CO + Rh(s) | 1.300 × 1013 | 0.295 | 134 |
| R6 | CO2(s) → CO2 + Rh(s) | 3.920 × 1011 | 0.315 | 20.51 |
| R7 | CO2(s) + Rh(s) → CO(s) + O(s) | 5.735 × 1022 | −0.175 | 106.49 |
| R8 | CO(s) + O(s) → CO2(s) + Rh(s) | 6.183 × 1022 | 0.034 | 129.98 |
| R9 | CO(s) + Rh(s) → C(s) + O(s) | 6.290 × 1021 | 0.000 | 174.76 |
| R10 | C(s) + O(s) → CO(s) + Rh(s) | 1.173 × 1022 | 0.000 | 92.14 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Partopour, B.; Dixon, A.G. Resolved-Pore Simulation of CO Oxidation on Rh/Al2O3 in a Catalyst Layer. ChemEngineering 2018, 2, 2. https://doi.org/10.3390/chemengineering2010002
Partopour B, Dixon AG. Resolved-Pore Simulation of CO Oxidation on Rh/Al2O3 in a Catalyst Layer. ChemEngineering. 2018; 2(1):2. https://doi.org/10.3390/chemengineering2010002
Chicago/Turabian StylePartopour, Behnam, and Anthony G. Dixon. 2018. "Resolved-Pore Simulation of CO Oxidation on Rh/Al2O3 in a Catalyst Layer" ChemEngineering 2, no. 1: 2. https://doi.org/10.3390/chemengineering2010002