Glycerol Oxidation in the Liquid Phase over a Gold-Supported Catalyst: Kinetic Analysis and Modelling

Abstract

The present work deals with the kinetic analysis and modelling of glycerol (GLY) oxidation in the liquid phase over a supported gold catalyst. A Langmuir-Hinshelwood model was proposed, after considering the effect of the reaction temperature, the NaOH/GLY ratio and the initial concentrations of GLY and GLY-Product mixtures. The proposed model effectively predicted the experimental results, and both the global model and the individual parameters were statistically significant. The results revealed that the C–C cleavage to form glycolic and formic acids was the most important reaction without a catalyst. On the other hand, the supported Au catalyst promoted the GLY oxidation to glyceric acid and its further conversion to tartronic and oxalic acids. Regarding the adsorption terms, glyceric acid showed the highest constant value at 60 °C, whereas those of GLY and OH⁻ were also significant. Indeed, this adsorption role of OH⁻ seems to be the reason why the higher NaOH/GLY ratio did not lead to higher GLY conversion in the Au-catalysed reaction.

1. Introduction

During the past decade, the use of biofuels as an alternative energy source to fossil fuels has been established. In 2016, the total worldwide biofuels production reached 82 million tonnes of oil equivalent, this value being 2.6% higher than that of 2015. Moreover, it has been reported that the trend for biofuels production will be upwards until 2035 [1,2]. Among biofuels, the production of biodiesel, based on transesterification of vegetable oils from waste fats, leads to glycerol (GLY) as an inevitable by-product; over 100 kg of GLY is produced per tonne of biodiesel [3,4]. Therefore, the valorisation of GLY could improve the competitiveness of the biodiesel value chain. Considering these facts, the consumption volume of GLY is expected to increase from 2000 kt in 2011 to 3070 kt in 2018 [5].

GLY is, thanks to its three hydroxyl groups, a highly versatile C3 polyol that can be a starting material for the production of food additives, pharmaceuticals, polyethers, polyols, detergents, and many others. Nevertheless, the use of low-quality GLY obtained from the transesterification of biodiesel (the so-called crude glycerol or glycerine) is not recommended for most of these applications, even if some recent research shows the resistance of some formulations to the impurities [6,7]. Therefore, the application of impure GLY as a bio-building block seems a potential and promising route [8,9,10]. There are many GLY transformation pathways, and, among them, the catalytic oxidation in the liquid phase has gained a great deal of interest [11].

GLY oxidation in the liquid phase is an example of a catalytic process that opens possibilities for the production of highly valuable products, such as glyceric acid, tartronic acid, glycolic acid or oxalic acid [12]. This process can be carried out by low-cost, non-toxic oxidizing agents (oxygen, hydrogen peroxide). Most of the literature related to GLY oxidation reports the use of Pt, Pd, Au and their bi-metallic combinations as active phases [11,13,14,15,16]. These three metals are indeed active in this reaction, although Porta et al. [17] reported that catalysts based on Pt or Pd suffer from oxygen poisoning, so that a low partial pressure of oxygen should be used with these metals. Au appears to be more resistant to oxygen poisoning, but it is necessary to carry out the reaction in basic media when using this noble metal. The basic conditions are conventionally supposed to promote the hydrogen abstraction from the hydroxyl groups, which is the first step of the reaction mechanism [10,18]. Moreover, a recent study suggested that OH⁻ species can also attack C-H bonds in a side non-catalytic process [19].

Up until now, a few kinetic models of GLY oxidation in the liquid phase using Au-based catalysts have been reported. Demirel et al. [20] proposed a Langmuir-Hinshelwood kinetic model from the results obtained with a Au/C catalyst. They considered the effect of NaOH concentration and included the initial concentration as a constant term in the kinetic equations. The same approach was proposed by Gil et al. [4] using a Au/Graphite catalyst. None of these models considered either the occurrence of the non-catalysed reaction in basic media or the production of formic acid. Finally, in previous work by our group [21], unsupported Au nanoparticles were used as the active phase for this reaction, and a quasi-homogeneous kinetic model was proposed. All these studies concluded that the oxygen partial pressure did not affect the catalytic performance, therefore it was not included in these kinetic models.

The aim of this work is to develop a kinetic model of GLY oxidation in the liquid phase by using a Au/Al₂O₃ catalyst. Firstly, the influence of the reaction conditions (temperature, NaOH/GLY initial ratio, and species initial concentration) over the catalytic process was analysed. From these experimental results, a reaction scheme was proposed prior to kinetic modelling. The kinetic model presented in this work gives new insights into some important aspects of GLY oxidation, such as the role of NaOH and the species adsorption in the reaction.

2. Results

2.1. Influence of the Reaction Conditions

2.1.1. Reaction Temperature

To provide a sufficiently wide range of experimental data needed for kinetic modelling, four temperatures (40, 60, 80 and 100 °C) and four NaOH/GLY ratios (0, 1, 2 and 4 mol/mol in non-catalysed reactions and 0, 2, 4 and 6 mol/mol in Au-catalysed ones) were chosen. Moreover, two initial GLY concentrations (0.1 and 0.3 mol/L) and four initial GLY-Product mixtures (GLY-glyceric acid, GLY-tartronic acid, GLY-glycolic acid and GLY-formic acid) were tested to evaluate the influence of the species concentrations on the catalytic activity. The GLY/Au ratio, O₂ pressure and stirring speed were set as 3500 mol/mol, 5 bar and 1500 rpm, respectively. Regarding O₂ partial pressure, it has been reported previously [19] that its effect on catalytic activity is negligible if the experiments are conducted in the kinetic regime, as they were in this work (see below). Likewise, a stirring speed was selected that removed the external diffusion limitations. Figure 1 depicts the effect of the stirring speed over the catalytic conversion of GLY. It is clearly observed that, the catalytic activity was practically the same from 750 rpm to 1500 rpm. Taking into account the results, 1500 rpm was chosen as the stirring speed.

Firstly, the influence of the reaction temperature was studied by varying the values between 40 and 100 °C, keeping the other variables constant (NaOH/GLY = 4 mol/mol, C⁰_GLY = 0.3 mol/L). The results are listed in

Table 1. Experimental results obtained at different reaction conditions (pO₂ 5 bar, stirring speed 1500 rpm).

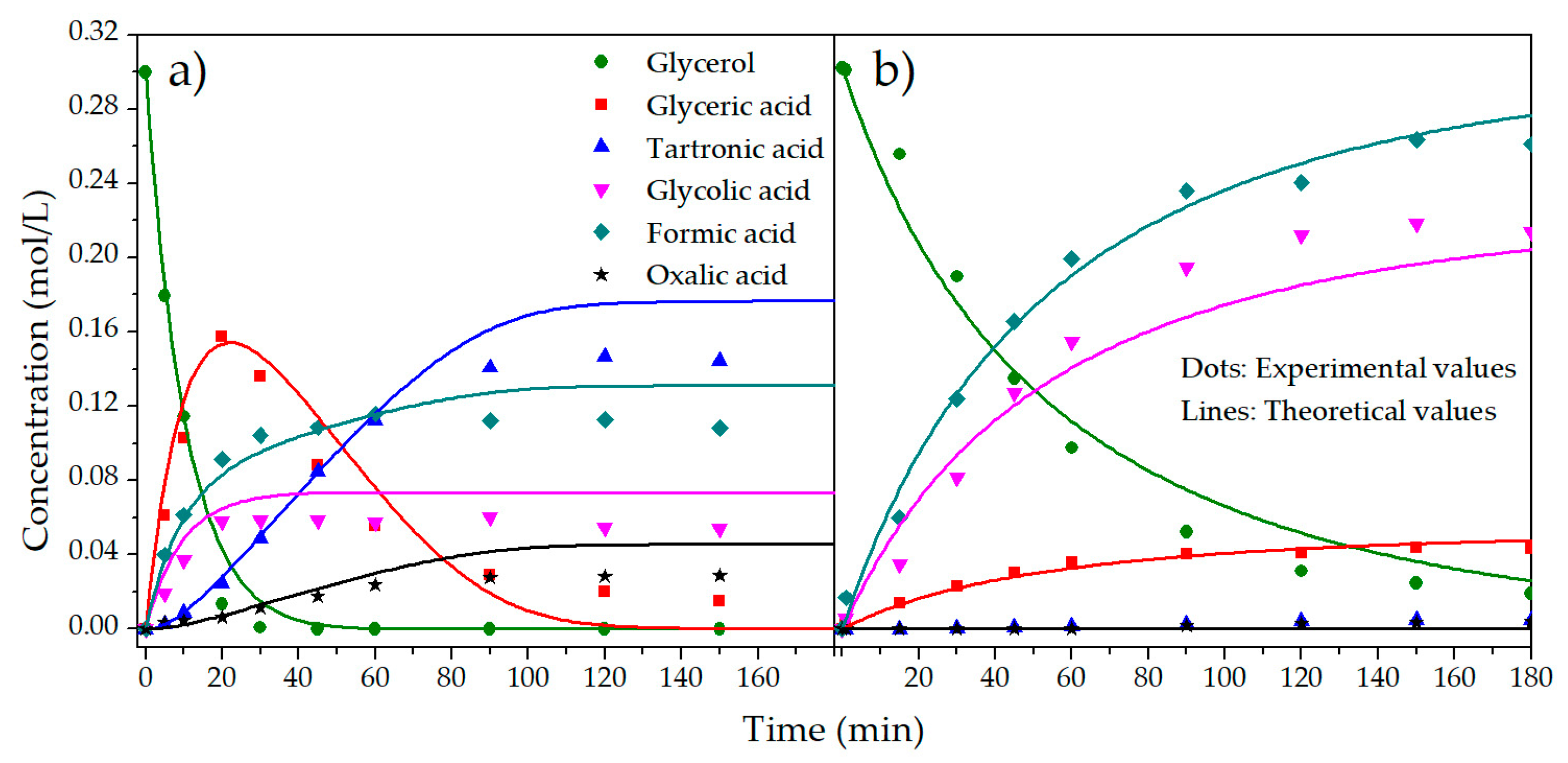
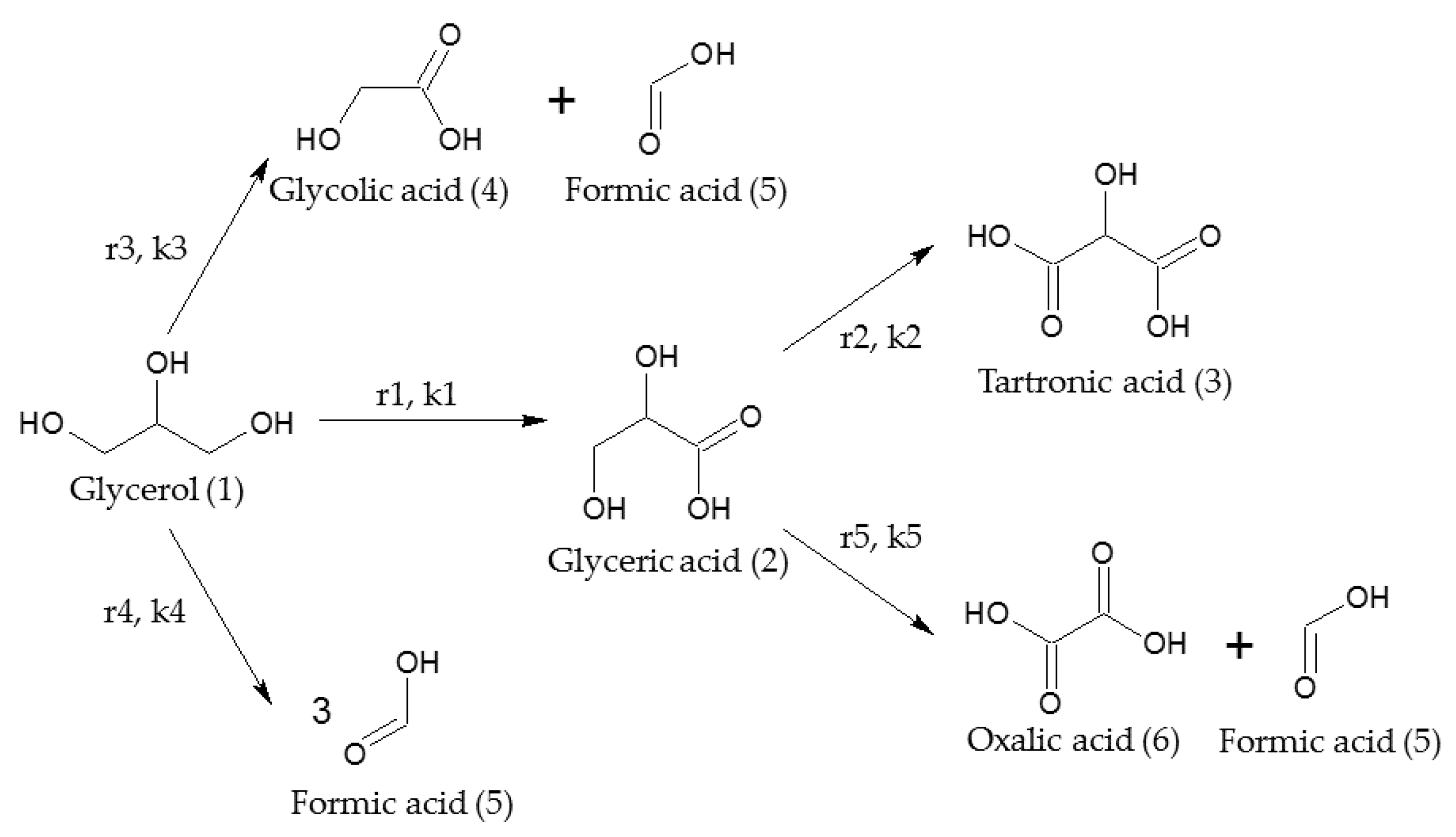
T (°C)	NaOH/GLY (mol/mol)	C0GLY (mol/L)	C0PRODUCTS (mol/L)	XGLY (%) a	Initial Reaction Rate b	SGLYCERIC (%) a	SGLYCOLIC (%) a
Without catalyst
40	4	0.3	-	0	0	-	-
60	4	0.3	-	3.6	4.9 × 10−4	33.3	29.5
80	4	0.3	-	18.5	4.3 × 10−3	24.9	40.1
100	4	0.3	-	68.0	1.7 × 10−2	17.2	49.9
60	0	0.3	-	0	0	-	-
60	1	0.3	-	1.6	2.0 × 10−4	48.7	13.9
60	2	0.3	-	1.8	3.4 × 10−4	51.0	19.2
Au-based catalyst (GLY/Au ratio 3500 mol/mol)
40	4	0.3	-	69.8	0.019	52.3	31.3
60	4	0.3	-	89.8	0.057	55.6	24.7
80	4	0.3	-	99.6	0.058	56.4	15.0
100	4	0.3	-	100	0.210	21.4	14.7
60	0	0.3	-	0	0	-	-
60	2	0.3	-	94.0	0.104	59.1	25.3
60	6	0.3	-	87.1	0.030	69.9	18.3
40	4	0.1	-	55.0	0.017	56.0	29.5
40	4	0.5	-	95.8	0.033	53.4	28.5
60	4	0.1	-	99.9	0.132	54.1	22.2
60	4	0.1	0.1 Glyceric acid	88.6	0.024	10.1	12.8
60	4	0.1	0.1 Tartronic acid	94.6	0.082	62.3	11.3
60	4	0.3	0.1 Glycolic acid	87.4	0.052	61.2	20.4
60	4	0.1	0.1 Formic acid	100	0.140	42.1	23.7

^a Conversion and selectivity after 60 min reaction.

^b [without catalyst] = mol/(L·min)/[Au-based catalyst] = mol/(L·g·min).

. As expected, it is clearly observed that the higher the reaction temperature, the higher the GLY conversion and initial reaction rate. Regarding selectivity, the trend showed for the reactions without a catalyst was opposite to that of the catalysed ones. This fact is explained according to the alcohol oxidation mechanism proposed by Davis et al. [18]. The second step of the reaction mechanism, β-hydride elimination, takes place over the catalyst surface. As this step promotes the formation of the corresponding carboxylic acid, the selectivity to glyceric acid using the Au-based catalyst is favoured.

Finally, it is worth mentioning that the selectivity to glyceric acid in the catalysed reaction performed at 100 °C was much lower than that observed at 80 °C. At the same time, tartronic and oxalic acids showed high selectivity values (43% and 6%, respectively), so it can be concluded that these products were obtained from glyceric acid.

2.1.2. NaOH/Glycerol Ratio

It is well known that Au-based catalysts are not able to carry out the proton abstraction that initiates the GLY oxidation, so a base is required for that purpose [18,19,20]. Results listed in Table 1 revealed the fact that, in absence of a base, the oxidation of GLY did not take place.

Regarding the results at different NaOH/GLY ratios, two different patterns were observed. The reactions without a catalyst showed that, the higher the NaOH/GLY ratio, the higher the initial reaction rate and the GLY conversion were, whereas the Au-catalysed ones showed the opposite trend. This fact, which was not reported previously, suggest that, although NaOH was necessary to initiate the reaction, an inhibition effect caused by its adsorption over the active sites took place and affected the catalytic performance. Therefore, the OH⁻ adsorption was taken into account in the kinetic model proposed hereafter.

2.1.3. Species Initial Concentration

Finally, the dependence of the reaction rate with respect to the species concentration was evaluated. Experiments with initial random GLY and product concentrations were performed at 40 and 60 °C, keeping the NaOH/GLY ratio constant at 4 mol/mol. Considering the influence of oxygen partial pressure as mentioned above, the concentration of this species was not expected to show a noticeable effect on the reaction rate, as all experiments were carried out in the kinetic regime (see hereafter).

Table 1 shows the experimental results obtained when different concentrations of GLY and the observed products (glyceric, tartronic, glycolic and formic acid) were added. Firstly, it was observed that, at 40 °C, the higher the initial GLY concentration, the higher the reaction rate was, with this increase being more pronounced between 0.3 and 0.5 mol/L. However, results at 60 °C revealed the opposite trend. Although it is difficult to establish an accurate conclusion from the experimental results (due to the presence of NaOH), it was demonstrated that the adsorption of GLY over the catalyst was considerable, so this was taken into account in the kinetic model proposed hereafter.

Also, the addition of product species in the reactant mixture revealed two trends. On the one hand, the presence of glyceric or tartronic acid led to a significant decrease in both GLY conversion and the initial reaction rate, as these products seemed to adsorb strongly on the catalyst surface and hinder the catalytic performance. Conversely, neither the presence of glycolic acid nor formic acid altered the conversion nor initial reaction rate values, so these species were presumed to adsorb weakly on the catalyst surface.

2.2. Kinetic Model

First of all, the internal diffusional constrains were evaluated by applying the Weisz-Prater criterion in each experiment. The Weisz-Prater number, N_W−P,i−j, was calculated using the following equation:

$$N_{W-P,i-j}=r·R_p^2/C_{Si}·D_{eff,i-j}\le 0.3$$

(1)

where, R_p is the catalyst average particle radius (25 µm), r is the reaction rate, and C_Si is the surface concentration of the species i (equal to the concentration in the reaction medium as there were no external diffusion limitations). According to M. Albert Vannice [22], the initial GLY concentration and consumption rate were respectively set as C_Si and r. The effective diffusivity of the species i over the solvent j (D_eff,i−j) was calculated as follows:

$$D_{eff,i-j}=D_{i-j}·\epsilon /\tau$$

(2)

where, D_i−j is the bulk diffusivity of the species, i over the solvent, j. The tortuosity (τ) and porosity (ε) values were not available, so they were set as 4 and 0.5, respectively [23]. In the oxidation of GLY, it was observed that O₂ was the limiting reactant since it presented low solubility in water. Henry’s Law was used to calculate the O₂ concentration in the reaction medium ($H_{{\mathrm{O}}_2/{\mathrm{H}}_2\mathrm{O}}$ (298.15 K) = 0.0012 mol/(kg·bar), ∆H/R = 1800 K). Due to the low concentration of GLY, all the calculations were performed considering the mixture O₂/H₂O. Bearing in mind all these points, the most restrictive N_W−P,i−j value (for the reaction performed at 100 °C) was 0.2236, so that internal diffusional constraints could be ruled out.

The reaction scheme was proposed on the basis of the experimental results. The C/t-profile of the reactions performed with and without a catalyst at 100 °C (Figure 2a,b) were similar to those reported previously [21], so that the same reaction scheme was proposed (Figure 3). The reaction pathways can be divided into two groups: oxidation reactions (r₁, r₂) and C–C cleavage reactions (r₃, r₄, r₅).

All the products listed in Figure 2 and Figure 3 were considered in the calculations. The effect of the base concentration was introduced into the kinetic model in the same way as the quasi-homogeneous one reported previously [21], and in agreement with the alcohol oxidation mechanism recently reported by Davis et al. [18]. This way, the role of the base in the GLY oxidation is evaluated in more detail than it was reported previously [4,20], where the NaOH concentration was included as a constant value.

A Langmuir-Hinshelwood model was proposed, by assuming the surface reaction as the rate-determining step (RDS), competitive adsorption, the occurrence of the non-catalysed reaction (which follows a power-law kinetic model), a partial 1^st order reaction of all the reactants and a carbon balance close to 100%. For instance, the carbon balances of the reactions showed in Figure 2 were 96 ± 3 and 102 ± 2, respectively. All the above-mentioned experiments were used to elaborate the kinetic model, by considering the influence of all the studied variables. The Langmuir-Hinshelwood model includes the adsorption-desorption equilibrium of the reaction species. It considers a single-step reversible reaction between the respective species with an unoccupied active site, which follows the Langmuir Isotherm. Therefore, the reaction rate equations can be written as the sum of the non-catalysed and catalysed ones, as follows:

$$r_1=k_1·C_1·C_{\mathrm{NaOH}}+w·k_{1,cat}·K_1·K_{\mathrm{OH}}·C_1·C_{\mathrm{NaOH}}/S$$

(3)

$$r_2=k_2·C_2·C_{\mathrm{NaOH}}+w·k_{2,cat}·K_2·K_{\mathrm{OH}}·C_2·C_{\mathrm{NaOH}}/S$$

(4)

$$r_3=k_3·C_1·C_{\mathrm{NaOH}}+w·k_{3,cat}·K_1·K_{\mathrm{OH}}·C_1·C_{\mathrm{NaOH}}/S$$

(5)

$$r_4=k_4·C_1·C_{\mathrm{NaOH}}+w·k_{4,cat}·K_1·K_{\mathrm{OH}}·C_1·C_{\mathrm{NaOH}}/S$$

(6)

$$r_5=k_5·C_2·C_{\mathrm{NaOH}}+w·k_{5,cat}·K_2·K_{\mathrm{OH}}·C_2·C_{\mathrm{NaOH}}/S$$

(7)

where w is the catalyst mass, C_i and C_NaOH the reactant concentrations, k_j and k_j,cat the non-catalysed and catalysed reaction rate constants, K_i and K_OH the reactant adsorption constants and S lumps the whole adsorption term, by considering competitive adsorption:

$$S={(1+K_1·C_1+K_2·C_2+K_3·C_3+K_4·C_4+K_5·C_5+K_6·C_6+K_{\mathrm{OH}}·C_{\mathrm{OH}})}^2$$

(8)

where K_i is the adsorption constants of all the species involved in the reaction. The rate and adsorption constants are given by the orthogonalised Arrhenius and Van’t Hoff equations, respectively [24]:

$$k_j={\overline{k}}_J\exp (-\frac{E_{a_j}}{R\theta })$$

(9)

$${\overline{k}}_J=k_{j,\infty }\exp (-\frac{E_{a_j}}{R\overline{T}})$$

(10)

$$K_i={\overline{K}}_{\tau }\exp (-\frac{\Delta H_i}{R\theta })$$

(11)

$${\overline{K}}_{\tau }=K_{i,\infty }\exp (-\frac{\Delta H_i}{R\overline{T}})$$

(12)

$$\frac{1}{\theta }=\frac{1}{T}-\frac{1}{\overline{T}}$$

(13)

where $E_{a_j}$ is the activation energy of the reaction, j, ∆H_i is the adsorption enthalpy of the component, i over the catalyst surface, and k_∞ and K_∞ are the corresponding pre-exponential factors. C_NaOH was calculated by the material balance proposed hereafter:

$$C_{\mathrm{NaOH}}=C_{\mathrm{NaOH}}^0-2·\left(C_1^0-C_1\right)-2·C_3-2·C_6$$

(14)

Using these rate equations, the mass balance equations for all the components of the reaction network are given by:

$$d{C}_1/dt=-\left(r_1+r_3+r_4\right)$$

(15)

$$d{C}_2/dt=r_1-r_2-r_5$$

(16)

$$d{C}_3/dt=r_2$$

(17)

$$d{C}_4/dt=r_3$$

(18)

$$d{C}_5/dt=r_3+3·r_4+r_5$$

(19)

$$d{C}_6/dt=r_5$$

(20)

Therefore, a kinetic model was proposed with 34 parameters (10 kinetic constants at a reference temperature of 60 °C, 10 activation energies, seven adsorption constants at the reference temperature and seven adsorption enthalpies). These parameters were estimated using an iterative non-linear regression procedure. The initial parameter estimates were obtained by the procedure described in the next section. The Residual Sum of Squares (RSS) between the theoretical and the experimental data was set as the objective function to be minimized:

$$\mathrm{RSS}={\displaystyle \sum }_{i=1}^n{\left(C_{exp,i}-C_{theo,i}\right)}^2$$

(21)

where n refers to the considered experimental data set. For given initial conditions, the MATLAB subroutine “ODE15S” was used to solve the system of ordinary differential equations. Then, the optimum kinetic parameters were determined by minimizing the objective function, using the MATLAB subroutine “LSQCURVEFIT” (Levenberg-Marquardt). The parameter estimation was performed by following a built-in option, i.e., by using the last estimation result as a starting point for the next one.

Once the kinetic model was established, the experimental results were analysed to remove the less influential parameters. For instance, Figure 2b reveals that the production of tartronic and oxalic acid was negligible without catalyst. Therefore, their corresponding parameters (k₂, $E_{a_2}$, k₅ and $E_{a_5}$) were removed from the kinetic model. Then, the simulated annealing algorithm was used to obtain the initial parameter estimates. By doing this, there were other parameters that could be removed, since they did not have any influence over the fitting procedure; those of the reaction r_4,cat (k_4,cat, $E_{a_{4,cat}}$) and the adsorption parameters of tartronic, glycolic, formic and oxalic acids (K₃, ∆H₃, K₄, ∆H₄, K₅, ∆H₅, K₆ and ∆H₆). This removal agreed with the experimental results obtained previously, except for the tartronic acid term which will be discussed in the next section. After the procedure described above, the number of parameters to be estimated was reduced to 20.

The results of the final kinetic model are shown in Figure 4 and Figure 5. The parity plot for prediction of the reactants and products concentrations (Figure 4), as well as the regression coefficient obtained (r², see

Table 2. Regression coefficient of the kinetic model and estimates of the kinetic parameters using all experimental data.

r2 = 0.9729
Parameter a	Estimate ± σ/1%σ|	t-Test b/Meaningful?
$\ln \left(k_1\left(\overline{T}\right)\right)$	−9.65 ± 0.11/1.14%	87.64 > 1.96/YES
$E_{a_1}/R\overline{T}$	35.58 ± 0.51/1.43%	69.72 > 1.96/YES
$\ln \left(k_3\left(\overline{T}\right)\right)$	−7.31 ± 0.05/0.69%	146.2 > 1.96/YES
$E_{a_3}/R\overline{T}$	27.35 ± 0.34/1.24%	80.44 > 1.96/YES
$\ln \left(k_4\left(\overline{T}\right)\right)$	−9.74 ± 0.10/0.98%	97.40 > 1.96/YES
$E_{a_4}/R\overline{T}$	30.13 ± 0.20/0.67%	150.65 > 1.96/YES
$\ln \left(k_{1,cat}\left(\overline{T}\right)+K_1+K_{\mathrm{NaOH}}\right)$	5.87 ± 0.13/2.14%	45.15 > 1.96/YES
$\left(E_{a_{{}_{1,cat}}}+\Delta H_1+\Delta H_{\mathrm{OH}}\right)/R\overline{T}$	−1.99 ± 0.27/13.65%	7.37 > 1.96/YES
$\ln \left(k_{2,cat}\left(\overline{T}\right)+K_2+K_{\mathrm{NaOH}}\right)$	3.60 ± 0.13/3.57%	27.69 > 1.96/YES
$\left(E_{a_{{}_{2,cat}}}+\Delta H_2+\Delta H_{\mathrm{OH}}\right)/R\overline{T}$	3.26 ± 0.48/14.82%	6.79 > 1.96/YES
$\ln \left(k_{3,cat}\left(\overline{T}\right)+K_1+K_{\mathrm{NaOH}}\right)$	5.09 ± 0.13/2.46%	39.15 > 1.96/YES
$\left(E_{a_{{}_{3,cat}}}+\Delta H_1+\Delta H_{\mathrm{OH}}\right)/R\overline{T}$	−10.38 ± 0.30/2.93%	34.6 > 1.96/YES
$\ln \left(k_{5,cat}\left(\overline{T}\right)+K_2+K_{\mathrm{NaOH}}\right)$	2.69 ± 0.18/6.83%	14.94 > 1.96/YES
$\left(E_{a_{{}_{5,cat}}}+\Delta H_2+\Delta H_{\mathrm{OH}}\right)/R\overline{T}$	−0.91 ± 0.59/64.49%	1.54 > 1.96/NO
$\ln \left(K_1\right)$	2.95 ± 0.13/4.43%	22.69 > 1.96/YES
$\Delta H_1/R\overline{T}$	−19.56 ± 0.22/1.14%	88.91 > 1.96/YES
$\ln \left(K_2\right)$	4.99 ± 0.08/1.62%	62.37 > 1.96/YES
$\Delta H_2/R\overline{T}$	−12.34 ± 0.45/3.63%	27.42 > 1.96/YES
$\ln \left(K_{\mathrm{OH}}\right)$	3.86 ± 0.07/1.77%	55.14 > 1.96/YES
$\Delta H_{\mathrm{OH}}/R\overline{T}$	−3.14 ± 0.19/6.10%	16.53 > 1.96/YES

^a $\overline{T}=60{}^{°}\mathrm{C};R=8.31\mathrm{J}/\left(\mathrm{mol}·\mathrm{K}\right)$.

^b $t \left(n-p,1-\alpha /2\right)=1.96$.

), suggested that the proposed heterogeneous Langmuir-Hinshelwood model, by considering the surface reaction as the rate determining step, the occurrence of the non-catalysed reaction, and competitive adsorption enabled a correct prediction of the experimental concentrations of all the components involved in the reaction. Additionally, Figure 2 shows an example of how good the prediction was. On the other hand, the measured residuals of the calculated concentrations (Figure 5) are small (less than 20%, except for a few values) and randomly distributed, so that there was no correlation between the calculated concentrations and their corresponding standard deviations.

Table 2 lists the final parameter estimation of the model, as well as the standard deviations and the students’ t-test results for each one. The t-test, performed according to the procedure described elsewhere [25], allows evaluation of the statistical significance of the estimated parameters. It is a statistical hypothesis test which follows the students’ t-distribution and allows verification if the estimate of the parameter, β_k differs from a reference value (generally zero). Thus, a parameter is statistically significant if the following inequality occurs:

$$t_{\beta i}=|{\beta }_k|·\sqrt{V{({\beta }_k)}_{nn}}>t(n-p;1-\frac{\alpha }{2})$$

(22)

where V(β_k)_nn represents the diagonal jth term of the covariance matrix, n − p the degrees of freedom, and α is the confidence interval (95%).

The results revealed that all the parameters except ($E_{a_{{}_5}}+\Delta H_2+\Delta H_{\mathrm{OH}}$) were statistically significant. This parameter, however, did not pass the t-test, since the estimated value was very close to zero. According to the estimation, the value of Ea₅ was equal to the absolute sum of the adsorption enthalpies ∆H₂ and ∆H_OH.

3. Discussion

In order to avoid possible correlation issues, the fitting procedure explained above was carried out by using lumped variables (see Table 2). The Arrhenius [k_j (60 °C) and $E_{a_j}$] and Van’t Hoff parameters [K_i (60 °C) and ∆H_i] obtained from those lumped variables, are listed in

Table 3. Arrhenius and Van’t Hoff parameters of all estimated reactions and components.

Reaction		kj (60 °C)		Activation Energy
Without catalyst	r1	6.51 × 10−5	L/(mol·min)	99	kJ/mol
	r3	6.69 × 10−4		76
	r4	5.89 × 10−5		83
Au-based catalyst	r1,cat	0.39	mol/(L·g·min)	57	kJ/mol
	r2,cat	5.25 × 10−3		52
	r3,cat	0.18		34
	r5,cat	2.11 × 10−3		40
Adsorption Terms		Kj (60 °C)		Adsorption Enthalpy
Glycerol		19.11	L/mol	−54	kJ/mol
Glyceric acid		146.94		−34
OH−		47.46		−9

.

As stated above, the reaction pathways illustrated in Figure 4 can be divided into oxidations (to produce glyceric and tartronic acids) and C–C cleavages, which lead to C2 (glycolic and oxalic) and C1 (formic) acids. As expected, ketone-based products, such as hydroxypyruvic and mesoxalic acid, were not observed in the reaction media [18,21]. On the other hand, CO₂ production was ruled out since no significant carbon balance decrease was observed. Regarding the reaction pathways, the oxidation reactions r₁ and r₂ followed the well-established mechanism reported by Davis et al. [18], whereas C–C cleavage reactions r₃, r₄ and r₅ were supposed to follow the reaction equation C_n-aldehyde → C_n−1-aldehyde + formic acid, like the mechanisms proposed by Isbell et al. [26,27] and Skrzyńska et al. [19], in agreement with the previous work of our group [21].

The k_j (60 °C) values of both non-catalysed (in basic media) and catalysed reactions are compared in Figure 6. On the one hand, the highest value among all the non-catalysed rate constants corresponds to k₃, which suggests that C–C cleavage did not necessarily require the presence of a catalyst, but a strong base like NaOH, as previously reported [19]. However, reactions r₂ and r₅ did not take place without a catalyst. Therefore, the production of tartronic and oxalic acid was practically absent. On the other hand, the Au-catalysed reaction promoted the formation of glyceric acid (k₁ presented the highest value) and to a lesser extent, its further reactions stimulated the formation of tartronic and oxalic acids.

Regarding the activation energies, Table 3 shows that, as expected, the $E_{a_j}$ values of the non-catalysed reaction were higher than those of the catalysed one. It was difficult to compare the obtained $E_{a_j}$ with the results reported in the literature, since the proposed reaction schemes are different to each other. Thus, the obtained $E_{a_{{}_{1,cat}}}$ was compared with those reported in the literature (see

Table 4. Comparison between the $E_{a_{{}_{1,cat}}}$ value and those reported in the literature.

Catalyst	${\mathit{E}}_{{\mathit{a}}_{1,\mathit{c}\mathit{a}\mathit{t}}}$ (kJ/mol) a	Reference
Au/Al2O3	57	This work
Au/C	50 b	[20]
Pt-Bi/C	67	[3]

^a Activation energy of the reaction Glycerol → Glyceric acid.

^b By considering the same Ea for all reaction pathways.

) [3,20], since this reaction pathway appeared in all of the proposed schemes. The results showed that the obtained $E_{a_{{}_{1,cat}}}$ value in the present work was slightly higher than that reported by Demirel [20] for a Au/C catalyst, and lower than that reported by Hu [3] for a Pt-based catalyst. Moreover, it is worth pointing out that the activation energies of the oxidation reactions ($E_{a_{{}_1}}$ and $E_{a_2}$) were higher than those of the C–C cleavage ($E_{a_{{}_3}}$ and $E_{a_{{}_5}}$), which confirmed that the latter group was less sensitive to temperature changes. Finally, the $E_{a_j}$ values corresponding to the non-catalysed reaction pathways could not be compared with other data, since there are no articles that deal with non-catalysed GLY oxidation.

The adsorption constants at 60 °C of GLY, glyceric acid and OH⁻, as well as their corresponding enthalpies, are listed in Table 3. As mentioned in the previous section, the first parameter fitting performed by simulated annealing revealed that the adsorption constants of glycolic, formic and oxalic acid had a negligible effect over the fitting procedure, and their values were much lower than that of glyceric acid. This fact was observed experimentally; neither the presence of glycolic acid nor formic acid influenced the catalytic activity. On the other hand, although the corresponding value of tartronic acid was expected to be significant in agreement to the experimental results, the very low tartronic acid concentration observed in most experiments, led to the product K₃∙C₃ not to have any influence over the parameter fitting.

Regarding the adsorption constants, the results listed in Table 3 reveal that the GLY value at 60 °C was lower than that of glyceric acid. This trend, which has been reported previously [3,20], revealed that GLY adsorption was weaker than that of some carboxylic acids, probably because the carboxylic acid group can be adsorbed onto the catalyst surface by chelation. As for the adsorption enthalpies, the obtained values were logical (the adsorption process is exothermic), but they could not be compared with the existing data, because there are only values for Pt-based catalysts, and these vary between 10 and 100 kJ/mol in both cases. It is worth noting that, to the best of our knowledge, this is the first kinetic model for GLY oxidation using Au-based catalysts that includes an estimation of the adsorption enthalpies.

Finally, the OH⁻ adsorption over the catalyst surface deserves a special mention. According to previous work, it is accepted that the higher the base/GLY ratio, the higher the catalytic activity. Indeed, experimental results of the non-catalytic GLY oxidation [19] agreed with this idea, as observed in Figure 7a. However, in the present work the results of the Au-catalysed reaction did not show this trend, as observed in Figure 7b. These results suggest the significant role of OH⁻ adsorption in GLY oxidation in the basic media. This OH⁻ adsorption has been described by Shang et al. [28]. They reported that OH⁻ adsorption led to negatively charged Au particles, which were responsible for O₂ reduction to a hydroperoxide adduct (OOH⁻). This H₂O₂-derived molecule is responsible for C–C cleavage reactions, according to the mechanism proposed by Isbell et al. [26,27], and as explained above. Indeed, Shang et al. calculated the adsorption energy of OH⁻ ions, as 30 kJ/mol, which has the same magnitude order as that obtained in this work, although the values were different.

Zope et al. [29] also reported that GLY oxidation by adsorbed OH⁻ species was more energetically favourable than by dissolved ones. Moreover, they asserted that the role of O₂ during alcohol oxidation is an indirect one that does not involve a reaction to form the acid products, but a reduction to form the hydroperoxide adduct OOH⁻, this is in agreement with the kinetic model proposed in the present work.

4. Materials and Methods

A commercial 1 wt % Au/Al₂O₃ catalyst (AUROlite^TM from Strem Chemicals (Newburyport, MA, USA)) was grounded and sieved to obtain a 50–125 μm fraction. No additional pre-treatment procedure was applied to this catalyst before testing. Characterization was carried out by Inductively Coupled Plasma Spectroscopy, X-ray Diffraction and Transmission Electron Microscopy, using the facilities and procedures described elsewhere [30]. The main characterization parameters are listed in

Table 5. Main characterization results of the catalyst used in this work.

Catalyst	Metal Loading (wt %)	Main Au Particle Diameter 1 (nm)	Theoretical Dispersion (%)
Au/Al2O3	0.98	4.7 ± 2.6	30

¹ Calculated by counting > 400 particles from TEM images.

.

Anhydrous glycerol 99% from Sigma-Aldrich was used for the catalytic tests. A typical experiment of the liquid phase GLY oxidation was carried out in a 300 cm³ semi-batch stainless steel reactor equipped with a gas-induced turbine, 4 baffles, a thermocouple, and a thermo-regulated oxygen supply system. In each experiment, 200 cm³ of a pure GLY solution was used. The products were periodically sampled and analysed with an Agilent 1200 HPLC equipped with a reflective index detector and a Rezex ROA-Organic Acid H⁺ column (300 × 7.8 mm). The identification and quantification of the obtained products was performed by comparison with the corresponding calibration curves established previously.

5. Conclusions

This work describes a kinetic model of the Au-catalysed GLY oxidation in the liquid phase. The results showed that the proposed Langmuir-Hinshelwood model, by considering the influence of the reaction temperature, the NaOH/GLY ratio and the initial concentrations of GLY and mixtures of GLY/products, effectively predicted the experimental concentrations. Both the global model and all fitted parameters were statistically significant, according to the results of the parity plot and the t-test, respectively. The occurrence of the non-catalysed reaction was also considered, and the results revealed that the direct GLY cleavage to glycolic and formic acid was the main reaction without a catalyst. The presence of a Au-based catalyst promoted all the reactions except for the direct GLY conversion to formic acid. Indeed, it promoted the GLY oxidation to glyceric acid and the conversion of the latter to tartronic and oxalic acids.

Regarding the adsorption group, results revealed that the highest adsorption constant corresponded to glyceric acid, since the carboxylic group interacts with the catalyst surface by chelation. The adsorption enthalpies, which have been estimated for the first time using a Au-based catalyst, showed that GLY and glyceric acid adsorption was strongly affected by the reaction temperature. Finally, the adsorption of OH⁻ ions were significant, as there was no clear increase in GLY conversion on increasing the NaOH/GLY ratio, unlike that observed in the non-catalysed reaction at 60 °C.