Composition of Probabilistic Preferences in Multicriteria Problems with Variables Measured in Likert Scales and Fitted by Empirical Distributions
Abstract
1. Introduction
2. Main Statistical Controversies
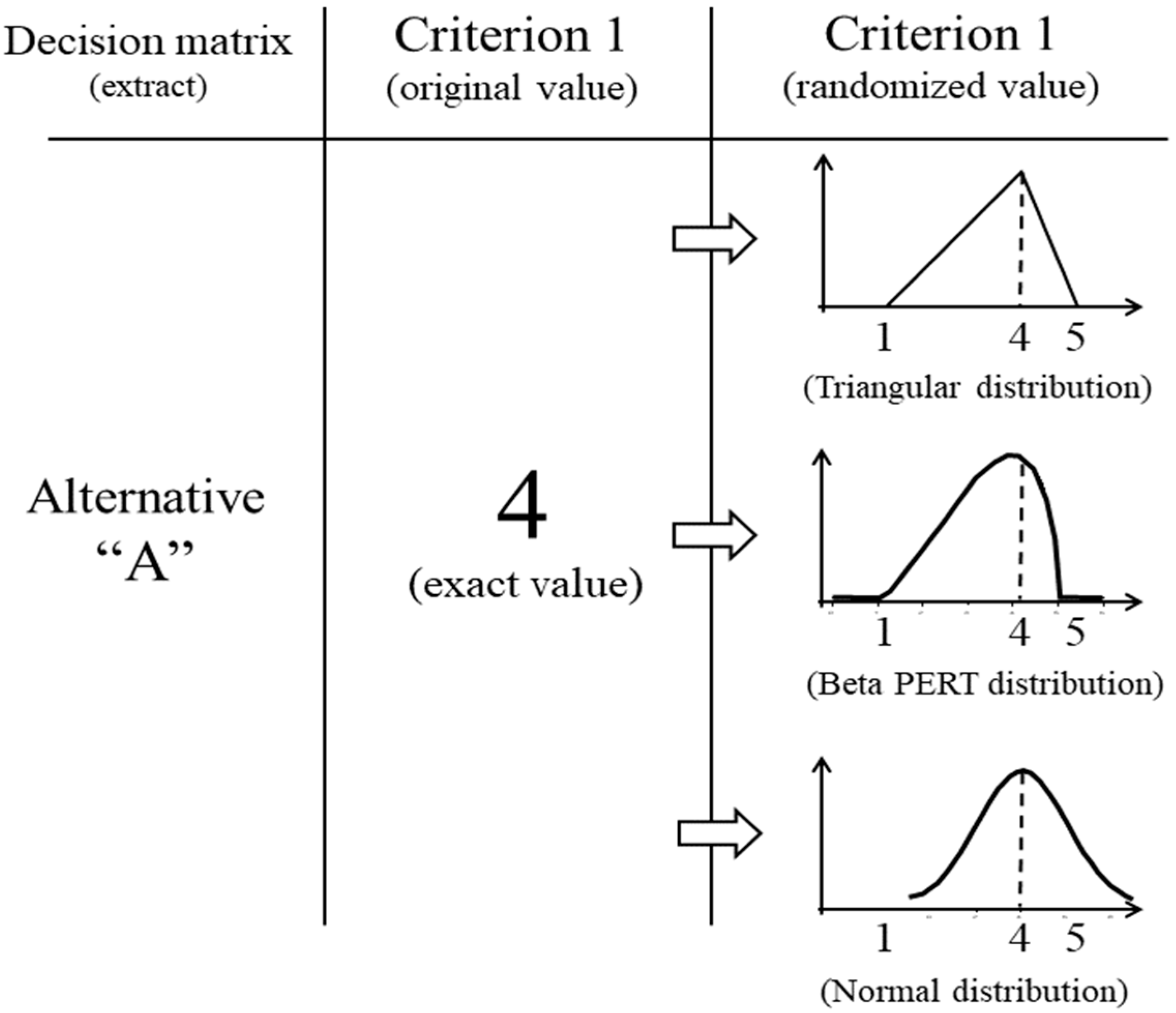
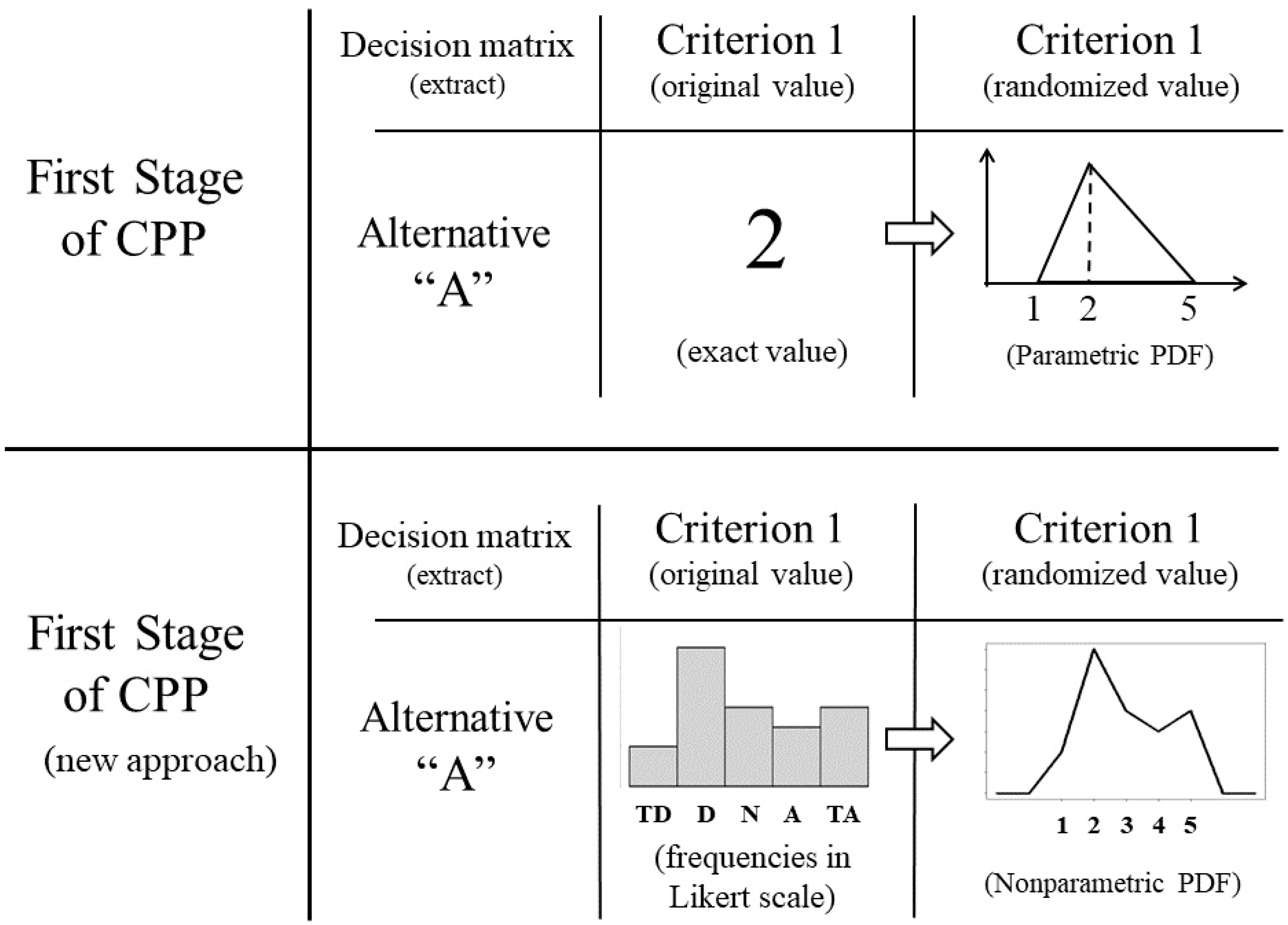
3. The Basics of CPP
4. Materials and Methods
5. Applications
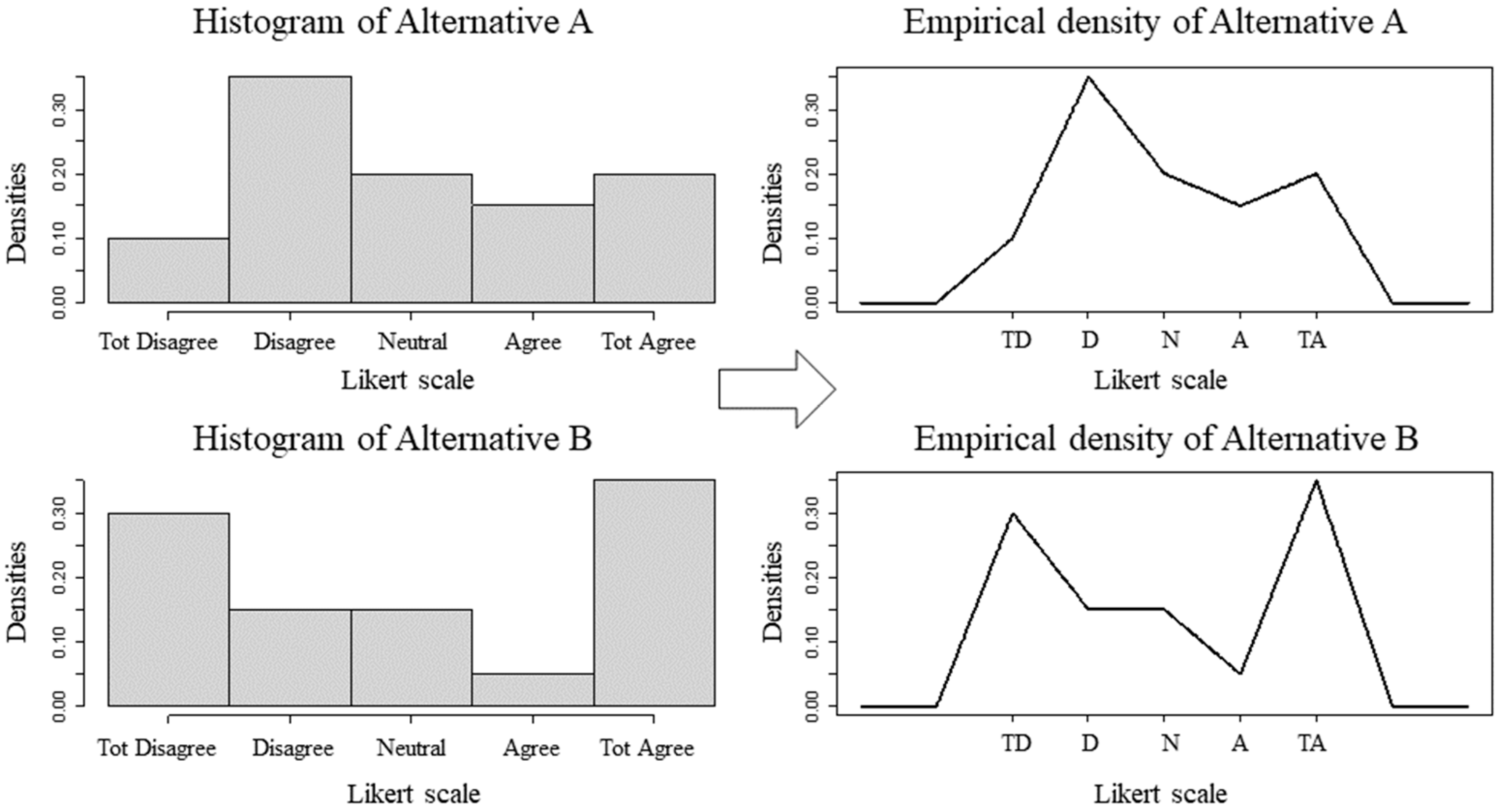
5.1. Dataset with the Same Means and Medians
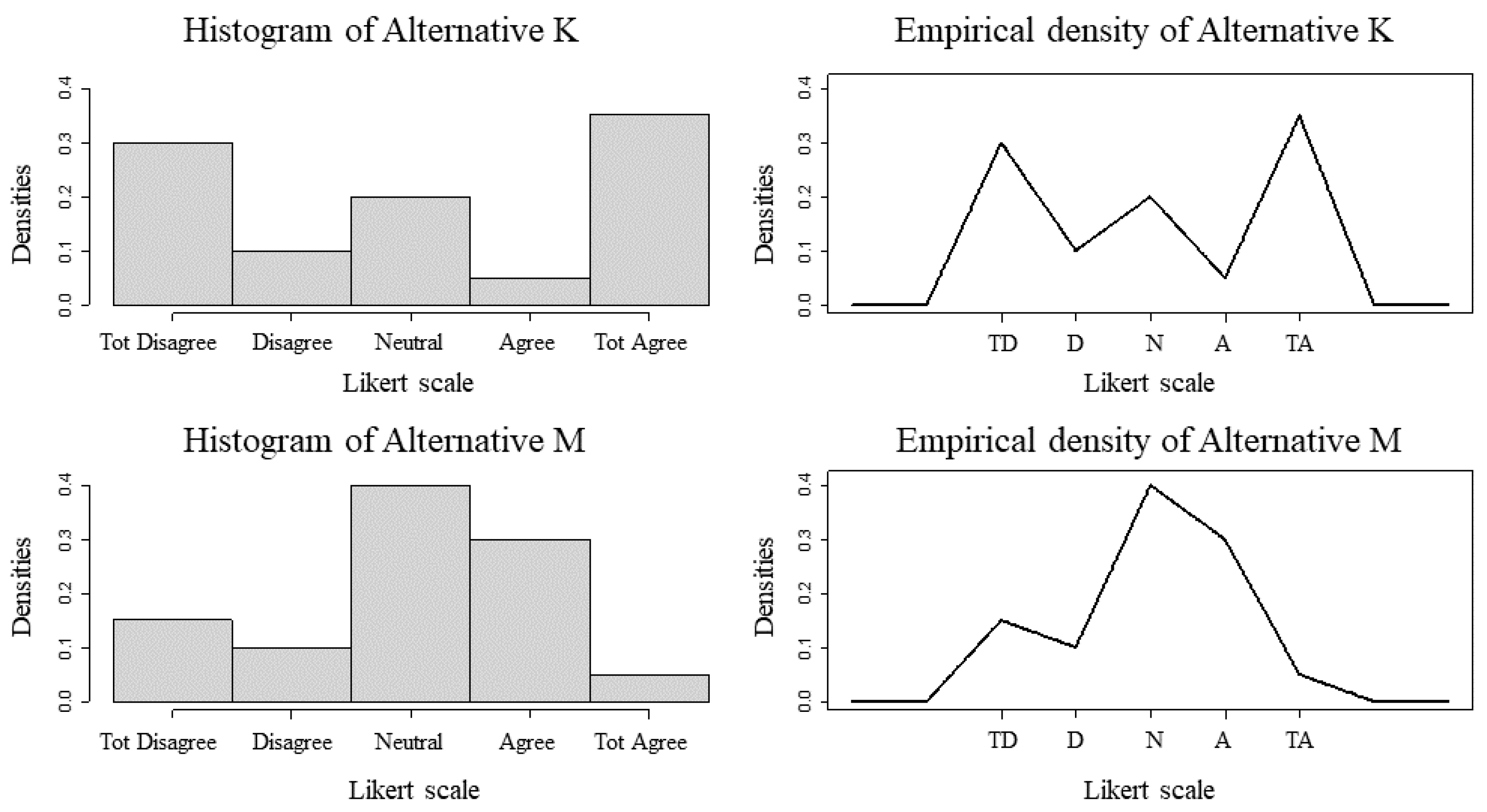
5.2. CPP Sensitivity to Likert Scale Cardinality
5.3. Unified Health System (SUS)
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Sant′Anna, A.P. Probabilistic Composition of Preferences, Theory and Applications, 1st ed.; Springer: New York, NY, USA, 2015. [Google Scholar]
- Gavião, L.O.; Sant’Anna, A.P.; Garcia, P.A.A.; Silva, L.C.E. Multi-criteria decision support to criminology by Graph Theory and Composition of Probabilistic Preferences. Pesqui. Oper. 2021, 41, e249751. [Google Scholar] [CrossRef]
- Likert, R. A technique for the measurement of attitudes. Arch. Psychol. 1932, 22, 5–55. [Google Scholar]
- Li, Q. A novel Likert scale based on fuzzy sets theory. Expert Syst. Appl. 2012, 40, 1609–1618. [Google Scholar] [CrossRef]
- Anjaria, K. Knowledge derivation from Likert scale using Z-numbers. Inf. Sci. 2022, 590, 234–252. [Google Scholar] [CrossRef]
- Karuppiah, K.; Sankaranarayanan, B. An integrated multi-criteria decision-making approach for evaluating e-waste mitigation strategies. Appl. Soft Comput. 2023, 144, 110420. [Google Scholar] [CrossRef]
- Alshamsi, A.M.; El-Kassabi, H.; Serhani, M.A.; Bouhaddioui, C. A multi-criteria decision-making (MCDM) approach for data-driven distance learning recommendations. Educ. Inf. Technol. 2023, 28, 1–38. [Google Scholar] [CrossRef]
- Daniel, M.; Ahammed, M.M.; Shaikh, I.N. Selection of Greywater Reuse Options Using Multi-criteria Decision-making Techniques. Water Conserv. Sci. Eng. 2023, 8, 2. [Google Scholar] [CrossRef]
- Wang, S.; Li, L.; Liu, C.; Huang, L.; Chuang, Y.-C.; Jin, Y. Applying a multi-criteria decision-making approach to identify key satisfaction gaps in hospital nurses’ work environment. Heliyon 2023, 9, e14721. [Google Scholar] [CrossRef]
- Stevens, S.S. On the Theory of Scales of Measurement. Science 1946, 103, 677–680. [Google Scholar] [CrossRef]
- Williams, M.N. Levels of measurement and statistical analyses. Meta-Psychology 2021, 5, 1–14. [Google Scholar] [CrossRef]
- Bishop, P.A.; Herron, R.L. Use and Misuse of the Likert Item Responses and Other Ordinal Measures. Int. J. Exerc. Sci. 2015, 8, 297–302. [Google Scholar]
- Tanujaya, B.; Prahmana, R.C.I.; Mumu, J. Likert scale in social sciences research: Problems and difficulties. FWU J. Soc. Sci. 2022, 16, 89–101. [Google Scholar]
- Hair, J.F.; Black, W.C.; Babin, B.J.; Anderson, R.E. Multivariate Data Analysis, 8th ed.; Cengage Learning EMEA: London, UK, 2018. [Google Scholar]
- Kuzon, W.; Urbanchek, M.; McCabe, S. The seven deadly sins of statistical analysis. Ann. Plast. Surg. 1996, 37, 265–272. [Google Scholar] [CrossRef]
- Wu, H.; Leung, S.-O. Can Likert Scales be Treated as Interval Scales?—A Simulation Study. J. Soc. Serv. Res. 2017, 43, 527–532. [Google Scholar] [CrossRef]
- Awang, Z.; Afthanorhan, A.; Mamat, M. The Likert scale analysis using parametric based Structural Equation Modeling (SEM). Comput. Methods Soc. Sci. 2016, 4, 13–21. [Google Scholar]
- Baran, T. Comparison of parametric and non-parametric methods to analyse the data gathered by a likert-type scale. In Handbook of Research on Applied Data Science and Artificial Intelligence in Business and Industry; IGI Global: Hershey, PA, USA, 2021; pp. 414–430. [Google Scholar]
- Norman, G. Likert scales, levels of measurement and the “laws” of statistics. Adv. Health Sci. Educ. 2010, 15, 625–632. [Google Scholar] [CrossRef]
- Harpe, S.E. How to analyze Likert and other rating scale data. Curr. Pharm. Teach Learn 2015, 7, 836–850. [Google Scholar] [CrossRef]
- Thomas, M.A. Mathematization, Not Measurement: A Critique of Stevens’ Scales of Measurement. J. Methods Meas. Soc. Sci. 2019, 10, 76–94. [Google Scholar] [CrossRef]
- Mircioiu, C.; Atkinson, J. A comparison of parametric and non-parametric methods applied to a Likert scale. Pharmacy 2017, 5, 26. [Google Scholar] [CrossRef]
- Pornel, J.B.; Saldaña, G.A. Four common misuses of the Likert scale. Philipp. J. Soc. Sci. Humanit. 2013, 18, 12–19. [Google Scholar]
- Jamieson, S. Likert scales: How to (ab) use them? Med. Educ. 2004, 38, 1217–1218. [Google Scholar] [CrossRef] [PubMed]
- Allen, I.E.; Seaman, C.A. Likert scales and data analyses. Qual. Prog. 2007, 40, 64–65. [Google Scholar]
- Sullivan, G.M.; Artino, A.R., Jr. Analyzing and interpreting data from Likert-type scales. J. Grad. Med. Educ. 2013, 5, 541–542. [Google Scholar] [CrossRef] [PubMed]
- Alabi, A.T.; Jelili, M.O. Clarifying likert scale misconceptions for improved application in urban studies. Qual. Quant. 2023, 57, 1337–1350. [Google Scholar] [CrossRef]
- Schrum, M.L.; Ghuy, M.; Hedlund-Botti, E.; Natarajan, M.; Johnson, M.J.; Gombolay, M.C. Concerning Trends in Likert Scale Usage in Human-robot Interaction: Towards Improving Best Practices. ACM Trans. Human-Robot Interact. 2023, 12, 1–32. [Google Scholar] [CrossRef]
- Gavião, L.O.; Sant′Anna, A.P.; Lima, G.B.A.; Garcia, P.A.A. Probabilistic Preferences of Likert Scale Data by Empirical Distributions; Version 2.0.; Zenodo.org: Geneve, Switzerland, 2023; p. 1. [Google Scholar]
- Sant′Anna, A.P.; Sant′Anna, L.A.F.P. Randomization as a stage in criteria combining. In Proceedings of the International Conference on Industrial Engineering and Operations Management—VII ICIEOM, Salvador, Brazil, 4–8 October 2001; pp. 248–256. [Google Scholar]
- Gavião, L.O.; Sant’Anna, A.P.; Lima, G.B.A.; de Almada Garcia, P.A.; de Sousa, A.M. Selecting distribution centers in disaster management by Network Analysis and Composition of Probabilistic Preferences. In Industrial Engineering and Operations Management; Amorim, A.M.T.T., Barbastefano, R.G., Scavarda, L.F., Reis, J.C.G.D., Amorim, M.P.C., Eds.; PUC-RJ: Rio de Janeiro, Brazil, 2020; pp. 1–11. [Google Scholar]
- de Souza, F.H.; Gavião, L.O.; Sant’Anna, A.P.; Lima, G.B. Prioritizing risks with composition of probabilistic preferences and weighting of FMEA criteria for fast decision-making in complex scenarios. Int. J. Manag. Proj. Bus. 2021, 15, 572–594. [Google Scholar] [CrossRef]
- Sant′anna, A.P.; Gavião, L.O.; Lima, G.B.A. Alternatives for the composition of interactive environmental impact factors. Pesqui. Oper. 2022, 42, e247786. [Google Scholar] [CrossRef]
- Sant′anna, A.P.; Gavião, L.O.; Sant’anna, T.L. Multi-criteria classification of reward collaboration proposals. IISE Trans. 2023. [Google Scholar] [CrossRef]
- Gavião, L.O.; Sant′anna, A.P.; Lima, G.B.A.; Garcia, P.A.A. Evaluation of soccer players under the Moneyball concept. J. Sports Sci. 2019, 38, 1221–1247. [Google Scholar] [CrossRef]
- Gavião, L.O.; Meza, L.A.; Lima, G.B.; Sant’Anna, A.P.; de Mello, J.C.B.S. Improving discrimination in efficiency analysis of bioethanol processes. J. Clean. Prod. 2017, 168, 1525–1532. [Google Scholar] [CrossRef]
- Gavião, L.O.; Sant′Anna, A.P.; Lima, G.B.A.; Garcia., P.A.A. CPP: Composition of Probabilistic Preferences; R Package Version 0.1.0.; R Foundation for Statistical Computing: Vienna, Austria, 2022; pp. 1–24. [Google Scholar]
- Wandresen, R.R.; Netto, S.P.; Koehler, H.S.; Sanquetta, C.R.; Behling, A. Nonparametric method: Kernel density estimation applied to forestry data. Floresta 2019, 49, 561–570. [Google Scholar] [CrossRef]
- Jiang, T.; Li, D. Approximation of Rectangular Beta-Laguerre Ensembles and Large Deviations. J. Theor. Probab. 2013, 28, 804–847. [Google Scholar] [CrossRef]
- Chalabi, Y.; Scott, D.J.; Würtz, D. The Generalized Lambda Distribution as an Alternative to Model Financial Returns. Inst Für Theor Phys Univ Auckland: Zürich, Auckland. Available online: www.Rmetrics.Org/Sites/Default/Files/Glambda.Pdf; www.rmetrics.org/sites/default/files/2009-01-glambdaDist.pdf (accessed on 30 June 2023).
- Zhou, Z.; Azam, S.S.; Brinton, C.; Inouye, D.I. Efficient Federated Domain Translation. In Proceedings of the International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023; pp. 1–31. [Google Scholar]
- Pouillot, R.; Delignette-Muller, M.L. Evaluating variability and uncertainty separately in microbial quantitative risk assessment using two R packages. Int. J. Food Microbiol. 2010, 142, 330–340. [Google Scholar] [CrossRef]
- Garcia, P.A.A.; Sant’Anna, A.P. Vendor and logistics provider selection in the construction sector: A Probabilistic Preferences Composition approach. Pesqui. Oper. 2015, 35, 363–375. [Google Scholar] [CrossRef]
- Sant′anna, A.P.; Meza, L.A.; Ribeiro, R.O.A. Probabilistic composition in quality management in the retail trade sector. Int. J. Qual. Reliab. Manag. 2014, 31, 718–736. [Google Scholar] [CrossRef]
- Gaviao, L.O.; Sant′Anna, A.P.; Lima, G.B.A.; Garcia, P.A.A.; Kostin, S.; Asrilhant, B. Selecting a Cargo Aircraft for Humanitarian and Disaster Relief Operations by Multicriteria Decision Aid Methods. IEEE Trans. Eng. Manag. 2019, 67, 631–640. [Google Scholar] [CrossRef]
- Sant′Anna, A.P.; Faria, F.; Costa, H.G. Aplicação da Composição Probabilística e do método das K-Médias à classificação de municípios quanto à oferta de creches. Cad. Do IME-Série Estatística 2013, 34, 17. [Google Scholar]
- Gavião, L.O.; Silva, R.F.d.; Sant’Anna, A.P.; Lima, G.B.A. Ordenação de Municípios por Potencial de Contaminação de Águas com Fármacos Oncológicos por Composição Probabilística de Preferências.; XLVIII Simpósio Brasileiro de Pesquisa Operacional: Vitória, Brazil, 2016; p. 12. [Google Scholar]
- Garcia, P.A.A.; Garcia, V.S.; Saldanha, P.L.C.; Jacinto, C.M.C. Combined use of composition of probabilistic preferences and entropy weighting for failure mode prioritization. In Proceedings of the European Safety and Reliability Conference—ESREL, Zurich, Switzerland, 7–10 September 2015; CRC Press: Boca Raton, FL, USA, 2015; pp. 381–386. [Google Scholar]
| Scale | Basic Empirical Operations | Permissible Statistics |
|---|---|---|
| Nominal | Determination of equality | Number of cases Mode Contingency correlation |
| Ordinal | Determination of greater or less | Median Percentiles |
| Interval | Determination of equality of intervals or differences | Mean Standard deviation Product-moment correlation |
| Ratio | Determination of equality of ratios | Coefficient of variation |
| Empirical Probabilities of Preference on Likert Scales |
|---|
| 1. Description: ranking alternatives evaluated on a criterion |
| 2. Variables >values—vector with numerical sequence of Likert scale options >freqs—Likert scale option frequency matrix: -matrix rows: problem alternatives -matrix columns: frequencies of Likert scale options |
| 3. Commands >open the R software console >install the R software “mc2d” library >load the database “values” and “freqs” >run the “PMax.Emp.Likert” function, for “benefit” type criteria >run the “PMin.Emp.Likert” function, for “cost” type criteria >rank alternatives in the criteria |
| 4. End |
| Alternative | PMax | PMin |
|---|---|---|
| A | 0.08981332 | 0.09327040 |
| B | 0.15662032 | 0.16098827 |
| C | 0.10803823 | 0.10993096 |
| D | 0.10599313 | 0.10154487 |
| E | 0.06747378 | 0.06140966 |
| F | 0.07062573 | 0.07502867 |
| G | 0.05176373 | 0.04871787 |
| H | 0.10671008 | 0.10557457 |
| I | 0.12501971 | 0.12782754 |
| J | 0.11794092 | 0.11570593 |
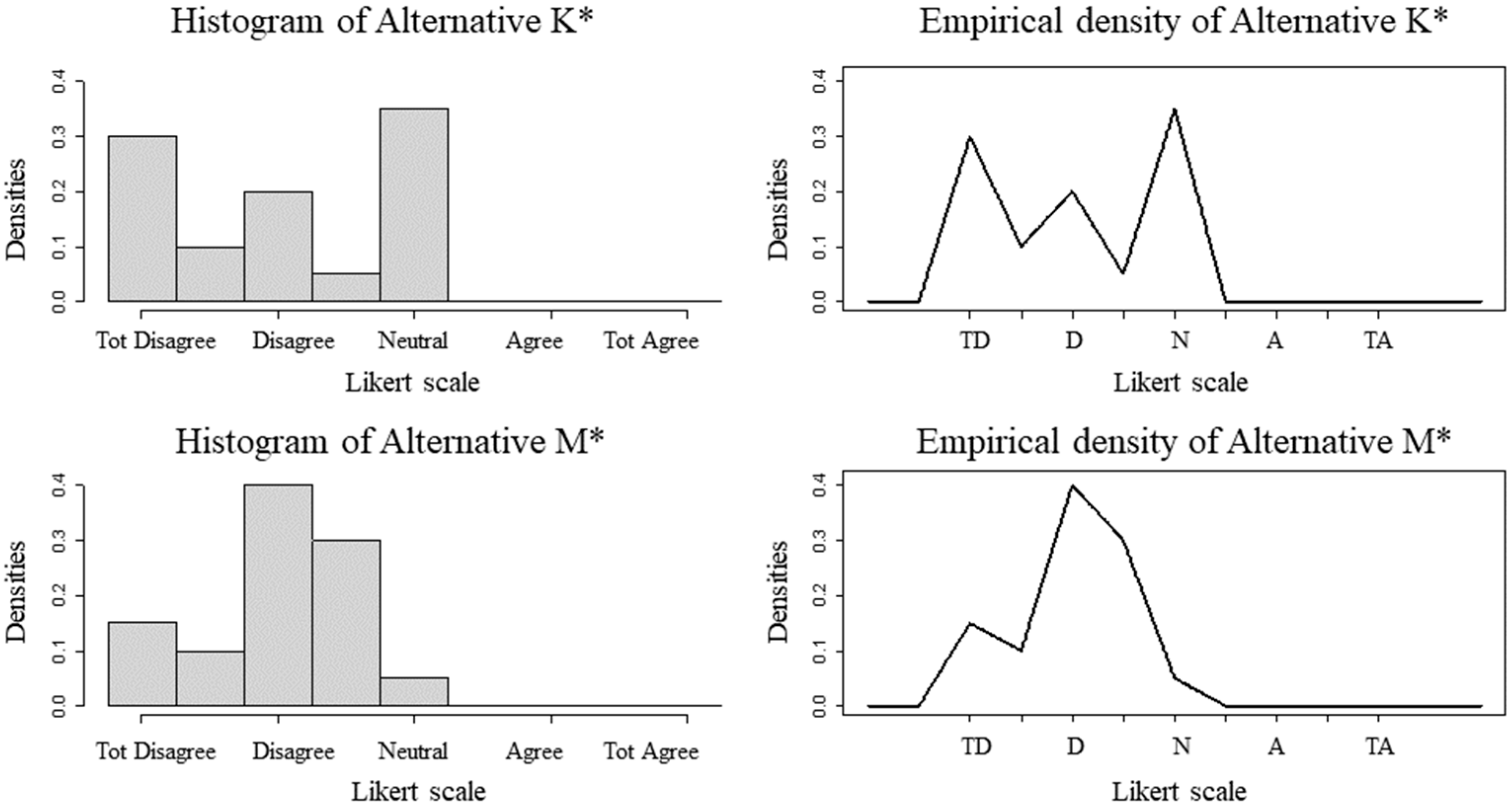
| Scales | Alternative | Median | Mean | Mode | PMax | PMin |
|---|---|---|---|---|---|---|
| 5 points | K | 3 | 3.05 | 5 | 0.4667357 | 0.5332673 |
| M | 3 | 3 | 3 | 0.5332673 | 0.4667357 | |
| 9 points | K* | 3 | 3.05 | 5 | 0.5637278 | 0.4362749 |
| M* | 3 | 3 | 3 | 0.4362749 | 0.5637278 |
| Hospital | Likert Scale (% of Evaluations) | PMax | Rank PMax | Rank Ebserh | Ebserh Result (%) | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |||||
| CHC-UFPR | 8 | 19 | 5 | 52 | 16 | 3.09 × 10−2 | 11 | 21 | 66.9 |
| CH-UFC | 6 | 7 | 6 | 57 | 25 | 4.61 × 10−2 | 3 | 5 | 82.2 |
| CHU-UFPA | 4 | 17 | 14 | 52 | 13 | 2.57 × 10−2 | 19 | 24 | 64.3 |
| HC-UFG | 7 | 16 | 10 | 52 | 14 | 2.79 × 10−2 | 15 | 22 | 66.3 |
| HC-UFMG | 4 | 11 | 5 | 61 | 19 | 3.66 × 10−2 | 7 | 8 | 79.9 |
| HC-UFPE | 5 | 19 | 9 | 58 | 9 | 2.09 × 10−2 | 27 | 20 | 67.3 |
| HC-UFTM | 8 | 11 | 11 | 56 | 14 | 2.85 × 10−2 | 14 | 18 | 70.1 |
| HC-UFU | 8 | 17 | 11 | 53 | 11 | 2.34 × 10−2 | 21 | 25 | 63.6 |
| HDT-UFT | 0 | 12 | 6 | 82 | 0 | 1.21 × 10−2 | 35 | 10 | 77.8 |
| HE-UFPEL | 22 | 31 | 3 | 25 | 19 | 3.37 × 10−2 | 8 | 34 | 44.4 |
| HUAB-UFRN | 6 | 8 | 12 | 54 | 21 | 3.86 × 10−2 | 5 | 15 | 72.2 |
| HUAC-UFCG | 0 | 12 | 5 | 67 | 17 | 3.33 × 10−2 | 10 | 6 | 81.4 |
| HUAP-UFF | 10 | 25 | 7 | 50 | 9 | 1.99 × 10−2 | 30 | 29 | 57.9 |
| HUB-UnB | 4 | 21 | 8 | 53 | 14 | 2.73 × 10−2 | 16 | 23 | 65.3 |
| HUCAM-UFES | 3 | 9 | 6 | 59 | 23 | 4.27 × 10−2 | 4 | 7 | 81.4 |
| HU-FURG | 13 | 19 | 9 | 44 | 16 | 3.00 × 10−2 | 12 | 28 | 59.4 |
| HUGD-UFGD | 17 | 28 | 10 | 38 | 7 | 1.59 × 10−2 | 33 | 35 | 44.1 |
| HUGG-Unirio | 8 | 23 | 15 | 48 | 8 | 1.78 × 10−2 | 31 | 31 | 55 |
| HUGV-UFAM | 11 | 24 | 9 | 51 | 5 | 1.47 × 10−2 | 34 | 32 | 54.3 |
| HUJB-UFCG | 0 | 11 | 0 | 78 | 11 | 2.65 × 10−2 | 17 | 1 | 88.9 |
| HUJM-UFMT | 7 | 11 | 4 | 69 | 9 | 2.30 × 10−2 | 22 | 9 | 78 |
| HUL-UFS | 19 | 38 | 10 | 29 | 5 | 1.15 × 10−2 | 36 | 36 | 31.8 |
| HULW-UFPB | 5 | 17 | 5 | 58 | 15 | 2.99 × 10−2 | 13 | 12 | 72.7 |
| HUMAP-UFMS | 7 | 17 | 3 | 64 | 9 | 2.22 × 10−2 | 23 | 13 | 72.5 |
| HUOL-UFRN | 6 | 16 | 10 | 55 | 13 | 2.65 × 10−2 | 18 | 19 | 67.8 |
| HUPAA-UFAL | 6 | 15 | 6 | 65 | 9 | 2.20 × 10−2 | 24 | 16 | 71.4 |
| HUPES-UFBA | 15 | 22 | 6 | 51 | 7 | 1.77 × 10−2 | 32 | 30 | 57 |
| HUSM-UFSM | 2 | 9 | 1 | 62 | 26 | 4.82 × 10−2 | 2 | 2 | 86.3 |
| HU-UFJF | 3 | 9 | 7 | 64 | 17 | 3.37 × 10−2 | 9 | 11 | 77.3 |
| HU-UFMA | 14 | 23 | 8 | 45 | 10 | 2.13 × 10−2 | 26 | 33 | 54.1 |
| HU-UFPI | 3 | 7 | 8 | 62 | 20 | 3.82 × 10−2 | 6 | 4 | 82.5 |
| HU-UFS | 1 | 17 | 8 | 64 | 9 | 2.17 × 10−2 | 25 | 14 | 72.4 |
| HU-UFSC | 7 | 22 | 7 | 56 | 9 | 2.06 × 10−2 | 29 | 26 | 63 |
| HU-UFSCar | 17 | 0 | 0 | 50 | 33 | 6.52 × 10−2 | 1 | 3 | 83.3 |
| HU-UNIVASF | 2 | 22 | 13 | 50 | 13 | 2.50 × 10−2 | 20 | 27 | 60.4 |
| MCO-UFBA | 8 | 21 | 0 | 63 | 8 | 2.07 × 10−2 | 28 | 17 | 70.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gavião, L.O.; Sant’Anna, A.P.; Lima, G.B.A.; Garcia, P.A.d.A. Composition of Probabilistic Preferences in Multicriteria Problems with Variables Measured in Likert Scales and Fitted by Empirical Distributions. Standards 2023, 3, 268-282. https://doi.org/10.3390/standards3030020
Gavião LO, Sant’Anna AP, Lima GBA, Garcia PAdA. Composition of Probabilistic Preferences in Multicriteria Problems with Variables Measured in Likert Scales and Fitted by Empirical Distributions. Standards. 2023; 3(3):268-282. https://doi.org/10.3390/standards3030020
Chicago/Turabian StyleGavião, Luiz Octávio, Annibal Parracho Sant’Anna, Gilson Brito Alves Lima, and Pauli Adriano de Almada Garcia. 2023. "Composition of Probabilistic Preferences in Multicriteria Problems with Variables Measured in Likert Scales and Fitted by Empirical Distributions" Standards 3, no. 3: 268-282. https://doi.org/10.3390/standards3030020
APA StyleGavião, L. O., Sant’Anna, A. P., Lima, G. B. A., & Garcia, P. A. d. A. (2023). Composition of Probabilistic Preferences in Multicriteria Problems with Variables Measured in Likert Scales and Fitted by Empirical Distributions. Standards, 3(3), 268-282. https://doi.org/10.3390/standards3030020








