Partial Order as Decision Support between Statistics and Multicriteria Decision Analyses

Abstract

Evaluation by ranking/rating of data based on a multitude of indicators typically calls for multi-criteria decision analyses (MCDA) methods. MCDA methods often, in addition to indicator values, require further information, typically subjective. This paper presents a partial-order methodology as an alternative to analyze multi-indicator systems (MIS) based on indicator values that are simultaneously included in the analyses. A non-technical introduction of main concepts of partial order is given, along with a discussion of the location of partial order between statistics and MCDA. The paper visualizes examples of a ‘simple’ partial ordering of a series of chemicals to explain, in this case, unexpected behavior. Further, a generalized method to deal with qualitative inputs of stakeholders/decision makers is suggested, as well as how to disclose peculiar elements/outliers. The paper finishes by introducing formal concept analysis (FCA), which is a variety of partial ordering that allows exploration and thus the generation of implications between the indicators. In the conclusion and outlook section, take-home comments as well as pros and cons in relation to partial ordering are discussed.

1. Introduction

A variety of methods for multi-criteria decision analyses (MCDA) exist [1], such as the ELECTRE family [2,3,4], different variants of PROMETHEE [5] or AHP [6]—just to mention a few, typically applied for decision analyses and/or ranking or rating tasks. The present paper focuses on an alternative methodology, i.e., partial ordering [7]. Thus, the immediate question to be asked is, “Why should one add another method, such as partial ordering?” A possible answer could be that partial ordering applied to indicator systems is simple from a mathematical point of view (cf. the methodology section), but obviously that is not an adequate answer.

The question “Why Partial Order?” is not asked for the importance of the corresponding mathematical field. Partial Order is in its own right a relevant area of discrete mathematics, and the number of books as well as the appearance of its own journal indicates this [7,8] (cf. also the extensive reference list at the end of the paper). Thus, when the question “Why Partial Order?” is posed, then this question aims at the application of partial order theory in decision making and evaluation. The background mathematics are simple, although they may not be part of the traditional knowledge of scientists and of most MCDA because it has not the arithmetic point of view but the relational one as its focus. Thus, it appears appropriate to present simple examples, one taken from the area of sociology, the well-being of children and young people, as a subject for illustration of the abilities of partial ordering, plus an example from the field of toxic chemicals.

1.1. An Exemplary Case

In 2007, UNICEF reported [9] on the well-being of children and young people. The study covered twenty-one nations and applied six indicators (

Table 1. Indicators of the UNICEF study concerning child well-being ¹.

Indicator	Abbreviation	Remarks
Material well-being	wb	Related to poverty, household equipment
Health and Safety	hs	Immunization, mortality
Educational well-being		Achievements
Family and peer relationships	fa	Family structure
Behavior and risks	br	Experience of violence
Subjective well-being	sub	Personal well-being

¹ For detailed information of this study cf. [7,9].

).

The overall objective of the study was the ranking of the twenty-one nations, and for that purpose, the final step was an aggregation of the six indicators to a composite indicator ci by summing the indicator values found for each nation:

ci(x) = ∑ g(j)·q(j)

(1)

with g(j) as the weight of the jth indicator, i.e., wb, hs, …, sub. The label “x” indicates one of the twenty-one nations. In the original study, all weights were selected to be “1”, i.e., the six indicators (Table 1) contribute to ci1 with the same weight, namely “1”.

For this exemplary didactic demonstration, three indicators, i.e., wb, hs and br, and arbitrarily eight nations, Sweden (SWE), Denmark (DNK), Finland (FIN), Norway (NOR), Ireland (IRE), Germany (DEU), France (FRA) and the Czech Republic (CZE) were selected. To illustrate the effect of different weight regimes, besides the regime of weights applied by the scientists of the study [9], i.e., ci: g(wb) = 1, g(hs) = 1, g(br) = 1, two further regimes were introduced: ci2: g(wb) = 3, g(hs) = 2, g(br) = 1 and ci3: g(wb) = 1, g(hs) = 2, g(br) = 3, applying Equation (1). The data are taken from the UNICEF study; they are summarized in

Table 2. Data for the exemplary case.

	Original Data			Aggregated Data
Nation	wb	hs	br	ci1	ci2	ci3
SWE	1	1	1	3	6	6
DNK	4	4	6	14	26	30
FIN	3	3	7	13	22	30
NOR	2	8	11	21	33	51
IRE	19	19	4	42	99	69
DEU	13	11	11	35	72	68
FRA	9	7	14	30	55	65
CZE	11	10	9	30	62	58

together with the aggregated data applying Equation (1) for the three weight regimes for the three indicators: wb, hs and br.

Based on the data given in Table 2, we can now rank the eight nations for each of the three weight regimes:

ci1: SWE < FIN < DNK < NOR < FRA = CZE < DEU < IRE

(2)

ci2: SWE < FIN < DNK < NOR < FRA < CZE < DEU < IRE

(3)

ci3: SWE < DNK = FIN < NOR < CZE < FRA < DEU < IRE

(4)

Looking at the ranking according to ci1 (Equation (2)), a nontrivial equivalence appears as FRA and CZE have the same ci1 value although they are clearly different countries! Thus, that FRA ≅ CZE means that there is equality of their ci1, only related to ci1.

It must be emphasized that the above-mentioned sequence expresses a < −relation without giving any indication whether the difference ci1(x)–ci1(y) may be large or small (in absolute terms). For example, FIN and DNK differ by one unit, whereas DNK and NOR differ by 7 units; nevertheless, FIN < DNK < NOR. The numerical point of view is only important to decide whether a < −relation can be established; all other metric details are ignored.

Turning to the ci2 regime (Equation (3)), where the weights are different from those of the UNICEF, the sequence changes. Thus, the equivalence FRA ≅ CZE is broken, but otherwise the relationships remain.

For the ci3 regime, again an equivalence (a tie) is noted; here DNK ≅ FIN, and further changes in the ordering are noted.

In the strict sense, only the sequence based on the ci2 regimes (Equation (3)) is a true ranking, since no equivalences (no ties) are found, whereas the two other sequences (Equations (2) and (4)) are called weak orders and may be seen as ranking with ties. However, does this justify the ci2 weight regime, denoted shortly as (3,2,1), as a better choice than the ci1 regime (1,1,1)? In general, selection of weights may be highly subjective, albeit weights express experience of stakeholders at least in a qualitative way. Therefore, loss of knowledge related to each single indicator due to the aggregation to a (one-dimensional) composite indicator, the knowledge of stakeholders, should not be ignored. However, the method to integrate this mathematically is the challenge.

Further, it can be seen that any of the three original indicators, wb, hs and br, may introduce their own, possible weak and different orders that can immediately be seen (Equations (5)–(7)).

wb:  SWE < NOR < FIN < DNK < FRA < CZE < DEU < IRE

(5)

hs:  SWE < FIN < DNK < FRA < NOR < CZE < DEU < IRE

(6)

br:  SWE < IRE < DNK < FIN < CZE < NOR = DEU < FRA

(7)

It is immediately noted that the positions of the nations change depending on the selection of indicators. Hence, the question arises: Which < -relations are common for all three indicators? This question brings the theory of partial order into play. To disclose what is common considering all (in the example, three) indicators simultaneously, there are two methods. One is to simply investigate the intersection of three sets of ordered pairs (see below) and may be called the set theoretical method; the other is to check the numerical values (see methods section) and may be denoted as the value-oriented method. The two methods are equivalent. Here, the first one, the set theoretic method, will be applied to continue with the logic of this section.

In order to construct the set of ordered pairs, the notation (a, b) is used to express a < b, where “a” and “b” stand for the objects under consideration, here the nations. For wb, the set of ordered pairs is

{(SWE, NOR), (SWE, FIN), (SWE, DNK),…,(FIN,DNK),…(NOR, FIN), (NOR, DNK), (NOR,FRA),…,(DEU,IRE)}.

For the indicator hs, it is found, besides others, {(SWE,NOR),…, (FIN,NOR),…}.

In common for wb and hs would be (SWE,NOR), but neither (FIN,NOR) nor (NOR,FIN), as due to wb: NOR < FIN, but due to hs: FIN < NOR. It is obviously a troublesome procedure to check all sets of ordered pairs manually (the number of sets equals the number of indicators—here three). Hence, a software package, “PyHasse”, was developed to disclose which relationships are in common for all three indicators (for details, see Section 4). The result of this exercise is shown in Figure 1.

This diagram in Figure 1 is known as a Hasse diagram. The diagram has 15 comparisons and 13 incomparisons and expresses that for nations linked by line-segments either only upwards or (exclusively) downwards, such as, e.g., SWE, FIN, DEU and CZE, a sequence, namely SWE < FIN < CZE < DEU can be stated, even when

• a simultaneous consideration of all three indicators is performed, i.e., independent of the specific indicator, and
• no aggregation to form a composite indicator is applied, and hence no weights are necessary.

Further, SWE < DNK < FRA can simultaneously be ordered by all three indicators. In other words: the indicator values along such sequences are co-monotone, i.e., if the value of one indicator increases, the other indicators increase as well or remain constant. In the terminology of partial order, objects (here the nations) that are connected by a line segment or a sequence of line segments (either up or down) are called comparable. Decision analysis aims at finding all objects under consideration as comparable, because then there will be a best, second best, etc., and a worst object (here nation).

Looking at Figure 1, the next question could be: What about IRE and, e.g., NOR? Considering the sequences (Equation (5a)–(5c)), IRE changes its position from the best (wb and hs) to a low position (5c). Whereas many nations are mutually comparable, IRE is incomparable with NOR, as for two indicators (wb and hs) IRE has high values whereas for one indicator, namely br, a low value. In contrast, NOR has a low value in wb, a medium value in hs and a value better than IRE in br. Thus, there is a conflict. IRE is good in two indicators, but bad in one, whereas NOR is worse than IRE in wb and hs, but remarkably better in br.

The key point is that when only one of the sequences (Equations (2)–(4)) is considered, this conflict is not visible. A decision maker may decide that IRE does not need any management, because it is anyway in a particularly good state despite a low ranking in br (cf. original data in Table 2).

A First (Preliminary) Conclusion

Partial order can be useful when multi-indicator systems are the basis for a decision (in contrast to methods based on probabilities) because it shows where indicator values are expressing a conflict, which, once identified, may cause appropriate management. Along with other scientists working with partial order, Roy and Vanderpooten [10], with their reflection about decision support systems, and Fishburn [11,12], who relates utility functions with partial order constructs, such as linear extensions, should be mentioned.

2. An Attempt for a Positioning of Partial Order

First, it should be mentioned that both ELECTRE [5] and PROMETHEE [2,3,4] use partial order methodology as an interim step. However, these methods apply further steps. Thus, partial order aspects do not play an essential role. On the other hand, other methods such as AHP [6] or TODIM [13] ignore at the very beginning partial order concepts. This intensifies the question, posed in the introduction: Why?

When the aim of MCDA is to provide a ranking to provide optimal and suboptimal options (in case of external constraints) for use in decision making, the concept of ranking is typically required to deliver a unique order among the options or objects. Hence, the resulting order should have neither several nontrivial equivalence classes (i.e., objects that have the same final ranking index without being identical (see Table 2, the composite indicator values ci1 for CZE and FRA)) nor, possibly more importantly, incomparabilities, i.e., objects that have some indicator(s) favorable in comparison to other objects, but other indicator(s) disadvantageous, at least in terms of ranking (see, for instance, NOR and IRE in Figure 1).

The typical result of a partial order is, unfortunately, to have incomparabilities. Thus, MCDMs must go beyond partial order to provide a ranking. There are three counterarguments that put partial order more into the foreground:

• The objective of any MCDA method is a ranking construct (by different and often highly sophisticated techniques) requiring a ranking index, which is a scalar as only a scalar can assure the absence of incomparabilities. Nevertheless, a scalar does not necessarily prevent the presence of nontrivial equivalence classes, and even if the unwanted effect of incomparabilities is avoided, the construction of a scalar from indicator values must take care to reduce as much as possible the ties with respect to the values of the scalar. However, the main point of construction of a scalar is the fact that incomparabilities are suppressed, although such incomparabilities indicate severe conflicts among the options or objects; disclosure of these conflicts should not be ignored.
• Any aggregation, mapping m indicators onto a one-dimensional scalar, such as one of the ci’s above, ignores specific information of the single indicators. In the final sequence, in ci1 it is no more evident that IRE is good with respect to wb and hs but strikingly bad with respect to br, which should evoke specific management plans. IRE is independent of the weight regime at the top of the sequences (2)–(4).
• The construction of a scalar is necessarily a mapping of a multidimensional system onto a one-dimensional quantity. Then, depending on the technical form of construction, compensation effects may develop [Munda, 2008], i.e., favorable indicator values may compensate for unfavorable ones. Accepting that partial order can deliver incomparabilities also means that in such cases compensation is conceptually eliminated; furthermore, conflicts are brought into the light. In light of the example above: IRE needs no management because IRE is at the top of sequence (2) (and the other two). Nevertheless, IRE has a deficit in br. This deficit is balanced out (compensated for) by the two good values in wb and hs.

2.1. Partial Order in Its Application on Multi-Indicator Systems (MIS)—An Attempt for a Localization within the Context of Other Mathematical Disciplines

The theory of partial order is relatively young and was invented with a pure algebraic/numeric theoretical approach at the end of 19th century [14,15,16]. At that time, partial order was as a theory of relations, an algebraic topic settled between graph theory, algebra and combinatorics. By the work of Garret Birkhoff [17] and Helmut Hasse [18], partial order received broader attention; however, it still remained a special topic in the field of pure mathematics. With the pioneering paper of Halfon and Reggiani [19], partial order entered the field of decision support, and hence, the question arises over how to localize partial order within operations research with MCDA as a special field, and with statistics, both traditionally disciplines in data analysis and decision support. Here may be the right place to check partial order with respect to three pillars of statistics:

Three Pillars of Statistics and the Partial Order Counterpart

Statistics can be seen as consisting of three pillars:

• Descriptive statistics
  Partial order (in its application to MIS) is based on standard statistics and does not add (at least up to now) its own concepts.
• Explorative statistics
  Partial order can explore data as to how much they contribute to a ranking. The background is its graph theoretical basis, which consequently leads to the question of why the graph induced by partial order has certain structures.
• Inference statistics
  Inference methods aim at a decision as to how far results from certain random sampling or spot tests can be extended to a universe. This important question should also be transferred to partial order applications. However, there the focus is on the objects for which a decision is to be found, and not on the generalization. Nevertheless, first attempts to judge the role of noise within partial order can be found in [20]. At least it cannot be claimed that a test theory in partial order applications is at hand.

In relation to exploration of the eminent, important branch of partial order, the theory of Formal Concept Analysis (FCA), founded in the 1980s by the group of H. Wille [21,22,23], must be mentioned. The basis for an analysis by FCA is the lattice theory, which can be considered as partial order additionally equipped with certain axioms. Each lattice is a partial order, but each partial order cannot be considered an outcome of lattice theory. So powerful is FCA, and so restrictive are the additional requirements on data, that FCA is not generally applicable. Recently, Kerber and Bruggemann [24] developed concepts to generalize FCA to continuous data. However, data statistics offers powerful methods for continuous data in concept, and it seems clear that an exploration will first apply well-known concepts of explorative statistics before the theoretically challenging methods of Kerber et al.

3. Basic Concepts of Partial Order in Application on MIS

3.1. Basic Equation

Whereas the mathematics of partial order can be overly complex, because graph theory, algebra and combinatorics are intertwingled, the mathematics of partial order applied on MIS is simple. Here is not the place for a formal introduction because there are several textbooks and many publications available (cf., e.g., [7]. Nevertheless, it is convenient to have some basics and some notations at hand. Most important is the basic equation of the value-based method to create a partial order:

• Objects: the items for which a decision is to be found, i.e., for which a ranking is the objective.
• Indicators: as most often the ranking objective, for example urban quality, cannot be directly measured, a set of indicators is defined that describe the important aspects of the wanted ranking. As several indicators are needed (as in the example above six indicators for child well-being), a multi-indicator system (MIS) is consequently found.

Let q(j,x) be the jth indicator of a MIS with a value for the object x. Then a < −relation between objects x and y is found when the following definition is fulfilled:

x ≤ y: if and only if q(j,x) ≤ q(j,y) for all j, i.e., for all the indicators of a MIS.

(8)

If q(j,x) = q(j,y) for all j, then objects x and y are equivalent, x ≅ y (with respect to the MIS).

If for some indicators q(j,x) < q(j,y) and for others q(j,x) > q(j,y) then objects x and y are mutually incomparable. Obviously by some indicators x is to be preferred, whereas for some other indicators y is to be preferred (the conflict situation). Clearly Equation (8) can also be applied to any single indicator. Thus, x and y may either be equivalent or x < y or x > y. One of these three possible cases will always prevail; hence, for a single indicator, always a set can be found, made of the pairs (x,y) with x < y (here the appearance of equivalences is suppressed in order to focus on the main logic). Hence, the set theoretical method is based on the value-based method taken for each single indicator.

3.2. Important Notations

Some notations simplify communication about results of partial order within the context of a MIS:

• Maximal element: If there is no y for which y > x is valid, then x is called a maximal element.
• Minimal element: If there is no y for which y < x is valid, then x is called a minimal element.
• If there is only one maximal (minimal) element, then this element is called a greatest (least) element.
• If x is at the same time a maximal and a minimal element, it is called an isolated element (from an explorative point of view, isolated elements indicate interesting data structures).
• Let X be the set of all objects of a study. Then X′ as a subset of X is called a chain if for every element of X′ it is found x < y or x > y.
• X″ is a subset of X called an antichain if for any two objects taken from X″ an incomparability is found.

With Figure 1 at hand, we can exemplify these few notation items:

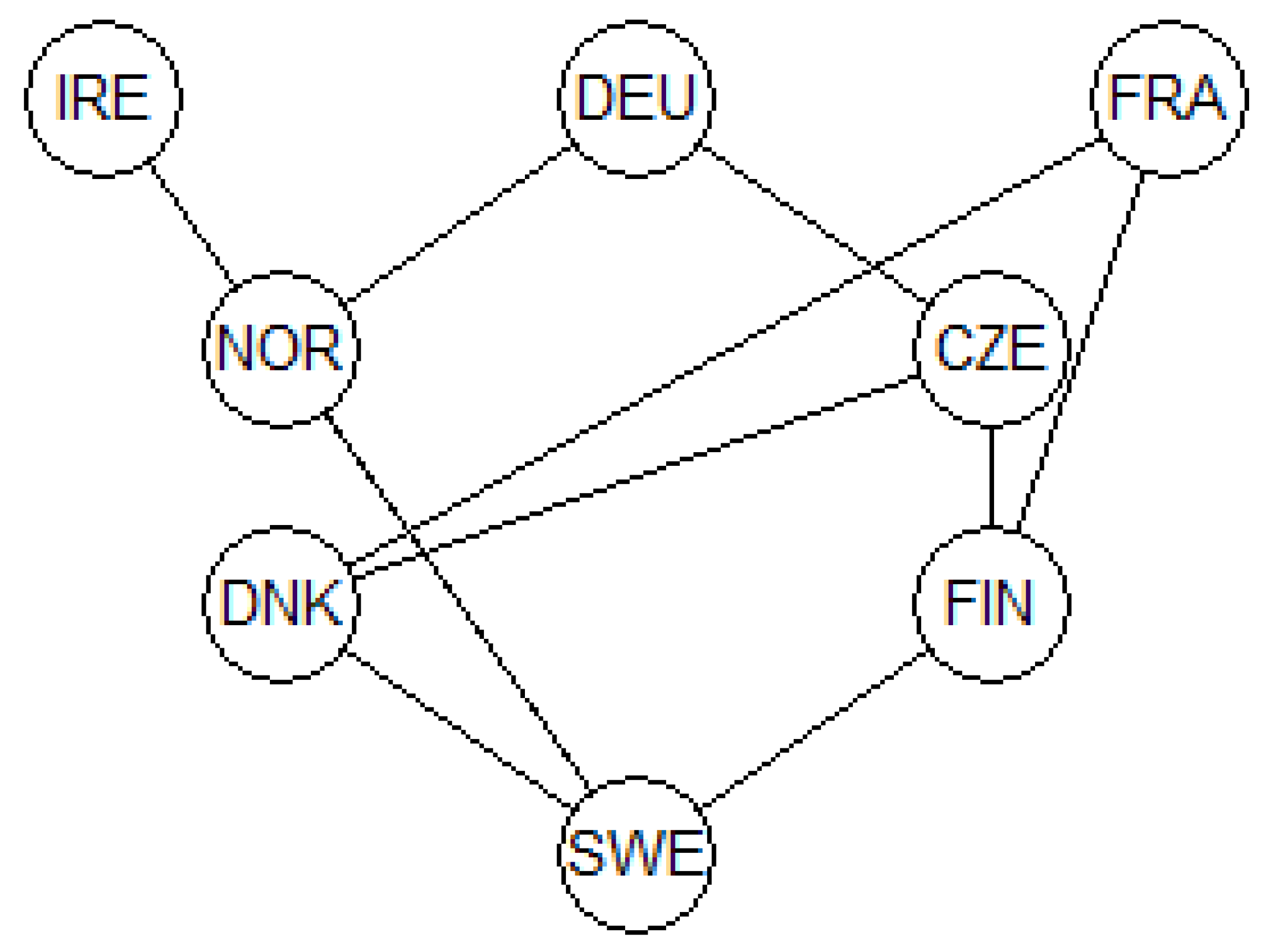
• IRE, DEU and FRA are maximal elements
• SWE is a minimal element: it is a least element because it is the only nation that is a minimal element.
• {SWE, DNK, DE, CZE} is an example of a chain. Indeed, it is found: SWE < DNK < CZE < DE
• {NOR, CZE, FRA} is one example of an antichain. Indeed, Equation (6) cannot be applied for any pair of objects taken from this subset.

It is particularly important to understand that classification of objects into chains or antichains or into the set of maximal or minimal elements is always to be seen as the background of the actually used MIS.

3.3. Generalized Linear Aggregation

As stated above, the knowledge of stakeholders, even though often arbitrary and subjective, is a part of experience that should not be ignored. The problem is the qualitative nature of weights, which induces in decision-making processes long and often controversial debates. As shown in the example of child well-being, a possible solution is to check alternatives for the weight values. Instead of only applying (1,1,1) as the weight regime, other weight regimes should be inspected to see how the final ranking is affected.

When a set of weights is written like a vectorial quantity (for example all weights are 1), then g1 = (1,1,1) (in the example) is applied to the matrix of indicator values. Written as a matrix equation:

$$\left(1,1,1\right)\left(\begin{array}{ccc}\mathrm{wb}\left(\mathrm{x}1\right),& \mathrm{wb}\left(\mathrm{x}2\right),& \dots \mathrm{wb}\left(\mathrm{xi}\right)\\ \mathrm{hs}\left(\mathrm{x}1\right),& \mathrm{hs}\left(\mathrm{x}2\right),& \dots \mathrm{hs}\left(\mathrm{xi}\right)\\ \mathrm{br}\left(\mathrm{x}1\right),& \mathrm{br}\left(\mathrm{x}2\right),& \dots \mathrm{br}\left(\mathrm{xi}\right)\end{array}\right)$$

Performing matrix multiplication leads to a one-dimensional quantity, the ci1 (as already mentioned).

Similarly, other weight regimes can be applied in the same manner.

Finally, there will be as many composite indicators, ci, as weight regimes that can be meaningfully applied. This means that by matrix multiplication a new MIS is obtained that needs the same partial order tools as the original one. Then, there will once again be conflicts, but usually much fewer conflicts than in partial orders obtained from the original MIS. One may see this as the consequence of the additional knowledge beyond the pure data matrix. Instead of performing the matrix multiplication for each weight regime separately, one can also condense all the additional knowledge (by the weights) by writing:

$$\left[\begin{array}{l}1,1,1\\ 3,2,1\\ 1,2,3\end{array}\right]\left[\begin{array}{l}\mathrm{wb}(\mathrm{x}1),\mathrm{wb}(\mathrm{x}2)\dots \mathrm{wb}(\mathrm{xi})\\ \mathrm{hs}(\mathrm{x}1),\mathrm{hx}(\mathrm{x}2)\dots \mathrm{hs}(\mathrm{xi})\\ \mathrm{br}(\mathrm{x}1),\mathrm{br}(\mathrm{x}2)\dots \mathrm{br}(\mathrm{xi})\end{array}\right]$$

maintaining the example of child well-being (see introduction; here subscript i equals eight for the eight nations).

This way of summarizing all stakeholder knowledge means that a matrix equation plays the key role. With G, a matrix organized as follows: Rows: different possible weight regimes, Columns: the single weights for each indicator, and the original MIS as a data matrix, the general equation is:

G·MIS(orig) = MIS(new)

(9)

Equation (9) does not only express in a clear and compact way the role of uncertainty with respect to the weights, but allows analysis of the role of weight regimes by statistical methods, now considering G as a data matrix in its own right. It should be noted that applying Equation (7) implies that the scaling level of the data of MIS(orig) allows such arithmetical operation. At least the data of the MIS(orig) must be carefully checked. Data ordinal in nature do not allow an operation such as Equation (9). When, nevertheless, Equation (7) is applied, then, for example, normalization of the data of MIS(orig) is a relevant step and must be at least explicitly mentioned. One should be aware that acting with ordinal data as if they are metric infers additional information into the dataset.

4. Software

Although the basis of partial order applied on MIS (Equation (6)) is conceptually quite simple, an analysis of m indicators and n objects becomes quickly tedious and error-prone. When n objects are present, then m n (n − 1)/2 pairs must be checked to decide whether Equation (6) is fulfilled.

Therefore, the support of appropriate software is needed. The software applied here is PyHasse (Hasse diagrams based on program codes of Python). Today, PyHasse contains more than 140 modules, comprising a few very specialized and rarely applied ones and others that are main workhorses. Details can be found in [25,26].

A new software package is under development and is available via the web. However, only a few modules are presently ready. It should be noted that other packages are recommended, for example PARSEC [27] and recently POSetR [28]. The original PyHasse software package is available from the second author.

5. Selected Examples of the Application of Partial Ordering

In the following, selected examples of the application of partial ordering for decision making and evaluation are described.

5.1. Novichok—Why the Skripals Did Not Die

On 4 March 2018, the former Russian spy Sergei Skripal and his daughter Yulia were poisoned in Salisbury by a nerve agent, later verified to be a member of the Novichok class, more precisely apparently A-234. Novichok (in Russian Hовичок = newbie or newcomer) is the name of a group of compounds that are closely related to the well-known nerve agents VX (CAS 050782-69-9) and VR (CAS 159939-87-4). For further structures, [29] should be consulted.

Fortunately, the Skripals did not die, which was somewhat surprising since A-234 was claimed to be even more toxic than the more well-known VX. Why did they not die? Several factors may come into play to explain this.

First, it should be mentioned that calculations determining the lethal concentration [29] have shown that A-234 is less toxic than VX (roughly by a factor of seven, which in this context probably is of minor importance. More important, it appears that factors such as skin penetration (J), evaporation (Evap), systemic absorption (Sys) and sorption in the outer layers of the skin (Cor) (

Table 3. Indicator values used for the Novichok study.

Compound #.	Name	Jmax	Sys	Evap	Cor
1	VX	1.537	90.5	8.8	0.73
2	VR	1.149	61.2	38.3	0.57
3	A-230	0.424	15.1	84.8	0.10
4	A-232	0.255	13.2	86.7	0.12
5	A-234	0.345	17.8	82.1	0.16
6	Novichok-5	0.250	51.8	39.9	8.51
7	Novichok-7	0.187	45.6	39.5	15.35
8	‘Iranian’	0.193	55.9	5.7	39.69
9	misc.	0.013	0.5	99.5	0.00

) play a role, too. The main reason for this selection of factors is that apparently Novichok was administrated by contaminating the door handle of the Skripal residence, i.e., the transfer to the Skripals was through skin contact.

A simple partial ordering based on these four factors as indicators for the nine Novichoks (for structures, etc., see [29]) unfortunately leads to an HD with a rather low level of information (Figure 2).

Obviously, the diagram has a rather low level of information, with only 5 comparisons and 31 incomparisons. However, virtually all data applied originate from calculations [29]. Thus, they should be taken with some caution. The dominance of incomparabilities is a clear signal that the calculated values [29] alone would mask the role of other factors. Here, two separate methods have been applied, both available as special modules of the PyHasse software: (1) introducing weight regimes and (2) introducing indicator noise/uncertainty.

(1) Introducing weight regimes is a way to say that maybe all values are not absolutely correct, but that they may be handled by using weights, e.g., 0.9–1.0, for all indicators. Doing so, a perfect linear ranking of the nine compounds is developed (Figure 3A), clearly demonstrating Novichok A-234 is not an ‘optimal choice’. Obviously, this can be explained by low skin penetration (J), higher evaporation (Evap) (handle concentration lower than expected), decreased systemic absorption (Sys) and increasing sorption to the outer parts of the skin (Cor) (in the palms).

(2) A similar result is obtained by applying noise/uncertainty as—again—the data may not be absolutely specific. Introducing 5% uncertainty for the four indicator values leads—again—to a ranking leaving A-234 (5) significantly lower than VX (1) and the Russian analogue (2) (Figure 3B); the overall ranking appears to be 1 > 2 > 3 > 5 > 8 > 4 > 6 > 9 > 7.

Hence, partial ordering constitutes a nice tool for such studies, here contributing to rationalization of the survival of the Skripals based on simultaneously taking all relevant factors into account in addition to considering data uncertainty/noise.

Later, another British lady was unfortunately exposed to the same Novichok, which turned out to be fatal. She got the poison in a perfume flacon that was found in the neighborhood. She sprayed the ‘perfume’ on herself; Thus, higher concentrations and possible inhalation of the highly toxic A-234, possibly combined with a more fragile general state of health may be the explanation for her death.

5.2. Stakeholders/Decision Makers Influence

If possible, the direct partial ordering of a series of objects by simultaneous inclusion of a number of indicators is a typical type of analysis. However, in many cases the resulting ordering does not lead to a sound foundation for decisions—the above Hasse diagram (Figure 1 and Figure 2) are examples of such a situation. However, despite the obvious problems with assigning weights to single indicators (cf. the above exemplary example), it may well be advantageous to bring stakeholders or decision makers into play in such situations.

Return to the example in the introduction with the eight nations and the three indicators: wb, hs and br. Let us assume that the three weight regimes are suggested by three stakeholders or decision makers. Thus, we now have the original MIS (Table 2 original data) and a weight matrix (

Table 4. Weight matrix for three stakeholders/decision makers to evaluate child well-being.

SH/DM	wb	Sh	br
SH1 (UNICEF)	1	1	1
SH2	3	2	1
SH3	1	2	3

).

Applying generalized linear aggregation (see Section 3.3) whereby the two matrices, i.e., the original MIS (Table 2) and the weight matrix (Table 4), are multiplied leads to a new MIS where all weight regimes are simultaneously brought into play (

Table 5. The new MIS based on the generalized aggregation method.

Nation	ci1	ci2	ci3
SWE	1.000	1.000	1.000
DNK	4.667	3.333	5.000
FIN	4.333	3.667	5.000
NOR	7.000	5.500	8.500
IRE	14.000	16.500	11.500
DEU	11.667	12.000	11.333
FRA	10.000	9.167	10.833
CZE	1.000	10.333	9.667

).

The resulting Hasse diagram visualized in Figure 4 displays a much higher level of information (with 23 comparisons and only 5 incomparisons) and thus a better background for decisions, both directly and indirectly, as every stakeholder/decision maker has made his/her footprint on the evaluation/ranking. FRA and CZE are, by this method, both ranked five (counted from the bottom), thus mimicking the weak order found applying the weight regime ci1 (cf. Equation (2)).

5.3. Peculiar Elements/Outliers

Analyzing data, the question of peculiar element or outliers often arises. Partial order methodology offers an efficient method to disclose such elements [30].

When data are [0,1] normalized (for each indicator, checking all objects), then the geometric view of a successful ranking is an ellipsoid, ranging from (0,0,…,0) to (1,1,…,1). These two special points in the m-dimensional space are denoted as “ranking points”. Within the ellipsoid, certainly objects will be incomparable, i.e., deviate from the ideal line connecting the two ranking points. The question is as to how far the objects deviate from that ideal line, or, taking the opposite point of view, how near are objects to those corners of the m-dimensional cube [0,1]^m (m indicators considered) that are not the ranking points. These corners are denoted as peculiar corners. Objects near the peculiar corners are called peculiar elements, and their data may be considered as interesting exceptions from the ideal line connecting the ranking points. The question is, when is a datapoint “near” the peculiar corners. Here a statistical point of view is taken, and a virtual m-dimensional ball is thought of, with one of the corners as center. The maximal Euclidean distance in an m-dimensional cube is √(m). Hence, a fraction of this maximal distance is an objective way to evaluate objects that are near a corner. This means it is not discussed but has a nearness based on a fraction of √(m). Most often the fraction is selected to be 0.05.

To illustrate the concept of peculiar elements/outliers, the 2017 data for gender equality within the European Union serve as an exemplary case [31]. The main indicators to elucidate gender equality according to Eurostat are summarized in

Table 6. Main indicators for disclosing gender equality.

Indicator	Short	Description	Orientation
sdg5_paygap	sdg5_pg	Unadjusted gender pay gap (% of gross male earnings)	Low better
sdg5_empgap	sdg5_eg	Gender employment gap (p.p.)	Low better
sdg5_caring	sdg5_car	Population inactive due to caring responsibilities (% of population aged 20 to 64)	Low better
sdg5_wparl	sdg5_wp	Seats held by women in national parliaments (%)	High better
sdg5_wmanage	sdg5_wsm	Positions held by women in senior management positions (%)	High better
sdg5_wsafe	sdg5_ws	Women who feel safe walking alone at night in the city or area where they live (%)	High better

[31].

Applying the partial order methodology, it was found that Finland is a peculiar element for the reason that the paygap for Finland is significantly lower than expected based on the indicator values for the 28 EU countries (note: prior to Brexit).

5.4. Formal Concept Analyses

A demonstration of Formal Concept Analysis (FCA) is difficult, because here a complete understanding would need to dive into depths of mathematics, especially in the theory of lattices, which are a special variant of partial order. Formal concept analysis combines both evaluation and—to some extent—exploration. The sections above already show the evaluative side of partial order, as any Hasse diagram visualizes the multitude of comparisons under the indicators, describing a ranking objective. Thus, demonstration of the exploration part remains.

The main reason behind binarization is that a certain element “possesses” the property q(j) if the value of qbin(j,x) = 1. The transformation equation can certainly be discussed because other variants are possible. However, the machinery of FCA is in focus here rather than a discussion of the details of the data (as, e.g., the statistical robustness or whether it fails to transform data in only a two-valued indicator).

At the heart of the exploration of FCA is the generation of implications. Consider the data given in

Table 7. A fictitious example.

Objects	Two Binary Indicators Case A		Two Binary Indicators, Case B
	q1bin	q2bin	q1bin	q2bin
a	1	1	1	0
b	0	1	0	1
c	0	0	0	0
d	1	1	1	1

.

In case A, it can be stated: if q1bin is a property of an object (such as for a and d, then q2bi is a property of the corresponding objects, too. In other words: q1bin implies q2bin (in case A, which is denoted as q1bin ⇒ q2bin). The reverse statement is not correct, because not all “1” of q2bin have a 1 as their counterpart in q1bin. In case B, q1bin does not imply q2bin, because q2bin(a) = 0 although q1bin(a) = 1.

Table 7 may be extended so that several indicators imply a subset of several others. Although this generalization sounds easy, it is in practice not an easy task to check a binary data matrix of, say, m indicators for implications of subsets of indicators. As 2^m subsets of indicators are possible, every set of 2^m subsets must be compared with every 2^m subsets taken from the set of m indicators. This comparison is to be performed over all objects; hence, the identification of implications is computationally challenging. There is an elegant solution of this problem by means of lattice theory; however, an explanation would be far beyond the main idea of the present paper; it is sufficient to understand the message derivable from consideration of Table 7.

Although formal concept analysis can conceptionally be applied to continuous indicators, the very theory needs discrete values. Hence, application of FCA, as in the case of twenty-eight nations of the EU, needs discretization. This can be done in various ways [21], which may be controversial as discussed by Kerber and Bruggemann [24,32]. In the present case, it is not possible to present the pros and cons; instead the data are simply transformed by:

$$\mathrm{qbin}(\mathrm{j},\mathrm{x})\left\{\begin{array}{l}=1 \mathrm{when} \mathrm{q}(\mathrm{j},\mathrm{x})>=\mathrm{mean}(\mathrm{j}) (\mathrm{take} \mathrm{over} \mathrm{the} \mathrm{values} \mathrm{of} \mathrm{q}(\mathrm{j}) \mathrm{of} \mathrm{all} \mathrm{objects}\\ \\ =0 \mathrm{else}\end{array}\right\}$$

The resulting data matrix is given in Appendix B.

As an illustrative example, data from the 2015 Fragile State Index [33] for the 28 EU member states (i.e., prior to Brexit) were studied (see Appendix A). The Fragile State Index applies 12 indicators for the evaluation of single nations and is comprised of Social indicators (d1: Mounting Demographic Pressures, d2: Massive Movement of Refugees or Internally Displaced Persons, d3: Legacy of Vengeance-Seeking Group Grievance or Group Paranoia, d4: Chronic and Sustained Human Flight); Economic indicators (d5: Uneven Economic Development Along Group Lines, d6: Sharp and/or Severe Economic Decline); and Political/Military Indicators (d7: Criminalization and/or Delegitimization of the State, d8: Progressive Deterioration of Public Services, d9: Suspension of the Rule of Law and Widespread Violation of Human Rights, d10: Security Apparatus Operates as a “State within a State”, d11: Rise of Factionalized Elites, d12: Intervention of Other States or External Political Actors) [34]. For a detailed description of the actual subjects being covered by the single descriptors, Baker [35] and/or The Fund for Peace [36] should be consulted.

Applying the 2015 data for the 28 member states of the EU under the 12 indicators, an approach similar to the above demonstrated by Table 7 leads to the following list (

Table 8. List of implications for the binary data, obtained by application of Equation (7).

No.	No of Objects	Realizations		Implications
1	6	d1 d2	→	d7
2	5	d1 d3	→	d7 d10 d11
3	9	d4	→	d7
4	4	d1 d6	→	d7 d9 d10
5	4	d2 d6	→	d7 d9
6	8	d3 d7	→	d11
7	8	d5 d7	→	d8
8	6	d1 d4 d7	→	d8
9	6	d1 d8	→	d4 d7
10	6	d2 d8	→	d4 d7
11	7	d3 d8	→	d5 d7 d11
12	8	d5 d8	→	d7
13	6	d1 d9	→	d7
14	7	d2 d9	→	d7
15	7	d7 d8 d9	→	d4
16	8	d10	→	d7
17	6	d7 d8 d10	→	d5
18	4	d6 d7 d9 d10	→	d1
19	6	d1 d11	→	d7
20	6	d2 d11	→	d7
21	8	d3 d11	→	d7
22	7	d5 d11	→	d3 d7 d8
23	7	d4 d7 d11	→	d8
24	9	d8 d11	→	d7
25	7	d9 d11	→	d7
26	5	d6 d7 d9 d11	→	d3
27	6	d7 d10 d11	→	d3
28	4	d3 d7 d9 d10 d11	→	d1
29	4	d2 d3 d7 d10 d11	→	d1
30	8	d12	→	d4 d7
31	7	d4 d7 d8 d12	→	d5
32	5	d1 d5	→	d4 d7 d8 d10 d12
33	5	d2 d5	→	d4 d7 d8 d12
34	5	d4 d6 d7	→	d5 d8 d9 d12
35	7	d4 d5 d7 d8	→	d12
36	6	d4 d7 d10	→	d12
37	5	d4 d5 d7 d8 d10 d12	→	d1

), where the notation should be read as—example—No 25, where ”25” is an enumeration and does not have a contextual meaning, ”7” is the number of objects for which the implication is realized, and “d9 d11 and → d7” indicates that when an object, here a nation “has” the property d9 and d11, then it also has the property d7.

In Table 7, from four objects, only two realize the implication q1bin → q2bin. In Table 8, the maximum and minimum of realizations are 9 (#24) and 4 (#18, #28, #29), respectively. Hence, this number indicates how important the generated implication is for the dataset under consideration.

More complex implications can be found, i.e., 22 with seven objects with two realizations (d5, d11) having three implications → (d3, d7, d8), which means that when objects simultaneously have d5 and d11 then they also have d3, d7 and d8. Back to the original data, this translates to when nations have values in d5 and d11 that are larger than the mean values of d5 and d11, respectively, they also have larger values in the three indicators d3, d7 and d8 in comparison to the respective mean values. Note that in contrast to correlation analysis, the implications shown in Table 8 are directed. Correlation measures are symmetrical; orientation requires a contextual analysis.

A couple of concrete examples illustrate the contextual interpretation of some implications, e.g., #1, where we find six countries scoring high, i.e., above average, for the indicators d1 (Mounting Demographic Pressures) and d2 (Massive Movement of Refugees or Internally Displaced Persons), indicating that countries scoring high on these indicators also will score, maybe not surprisingly, high on indicator d7 (Criminalization and/or Delegitimization of the State). A further example would be (cf. #30) that countries scoring high on d12 (Intervention of Other States or External Political Actors) causes high scores on d4 (Chronic and Sustained Human Flight) and d7 (Criminalization and/or Delegitimization of the State). In-depth analysis of all the above implications (Table 8) is outside the scope of this paper.

In some sense, the generation of implications is done artificially, which means that

(1)

the implication is to be considered a hypothesis, as it is only related to a sample;

(2)

any implication urgently needs a contextual interpretation;

(3)

any other discretization, say to d values, can change the result.

It should, however, be noted that these critical remarks are also relevant when statistical tools such as correlation or regression analysis are performed. The advantage of statistics is that it provides tests to evaluate the results (inference statistics). The mathematical method of partial order (and of lattice theory) is young, so it can be hoped that something such as inference methods will also be available in the future.

6. Conclusions and Outlook

6.1. Conclusions

Back to the preliminary conclusion

A preliminary conclusion was given at the end of the introduction. Now the question arises: Do we have to change this conclusion after demonstrating the application of partial order on MIS through examples from chemistry and sociology? The answer is: No. The use of diagrams is especially helpful to get deeper insight into the decision process. Mathematical concepts, namely comparability and incomparability, are at the heart of partial order theory applied to MIS. It is worthwhile to repeat the meaning of both of these concepts as “take-home messages”:

Take-home message

• Comparability: An increase in an indicator value is always accompanied by a non-decrease of all other indicators. For decision making, an overwhelming number of comparabilities is a comfortable situation, as a ranking is almost found. When all n objects are mutually comparable, then the limit of a ranking is reached.
• Incomparabilty: An increase in the values of some indicators is accompanied by a decrease of some others. This expresses a conflict because a preferred state due to some indicators is weakened by unpreferred values of other indicators. The evidence of conflicts is smashed out by aggregation methods to obtain a single quantity, which allows a ranking. However, in a public audit there is a great deal of resistance explainable by the loss of information about the inherent conflicts.

How to extend the framework of partial order theory?

When the number of incomparabilities overwhelms comparabilities, the situation becomes uncomfortable from a partial order point of view. This is certainly one reason why partial order concepts are ignored in many MCDAs. Very often, this unhandsome situation is the consequence of inherent trade-offs within the decision; thus, it may be wise to include qualitative knowledge of stakeholders. To our knowledge, most MCDAs include the knowledge of stakeholders. However, the methods are often so tricky that, once again, there is no real understanding by people involved in the decision process. Then, the simplest technique comes into play, i.e., the weighted sum. Although this concept is to be criticized because of compensation effect, and because “suddenly” performing the summing, the qualitative nature of weights must be ignored. In other words, weighted sums have

• an advantage, because they can be understood, but they have three
• disadvantages, namely:

  ○

  compensation effects,

  ○

  uncertainty in the weights themselves, “Is aspect x really more important than aspect y?”, and

  ○

  need of a numerical representation of qualitative knowledge by weights.

Here, the concept of an operator G may be helpful. Varying the weights, at least in discussing the result of a decision support system, is not new. However, condensing the different options of weighting into an operator, called G, infers a new quality: Now the manifold of points of view about weighting can be evaluated by examining G as a whole. Although the concept of G has some inherent difficulties (scaling level of data, i.e., as to how far it is acceptable to combine ordinal data with weights to obtain a sum), it may solve the problem of uncertainty of weights, but obviously not that of compensation. So what?

Independent of which of the many MCDA-methods is selected, it is recommended that the decision problem is checked by partial order methods; hence, often, but not always, a decision has already been found.

6.2. Limitations and Outlook

Clearly, partial order theory is relatively young (in comparison to statistics) and needs for its application on MIS further research.

(1)

The problem of noisy data is algorithmically solved; however, there is still the need of tests guaranteeing that there is a high probability for typical partial order theoretical results, such as “being a maximal element”. Up to now, only the relational point of view is considered. However, when the data matrix has noisy data, then there must be a statement possible such as: There is a probability of, e.g., p% that an object is a maximal element.

(2)

The above-mentioned problem of the scaling level of data. This problem can be circumvented by establishing preference functions (as done in many MCDA methods). Accepting the need to establish preference functions opens the door to many subsequent questions, such as: Which kind of preference function? How robust is the preference function in a statistical sense?

(3)

When partial order is applied on a MIS (without the use of matrix G), then the interpretation of incomparabilities can be directly traced back to single indicator values. However, when a new MIS is constructed in accordance with Equation (7), remaining incomparabilities are caused by two influences: (a) indicator values and (b) weights. An attempt to solve this problem is under work.

(4)

Partial order theory provides its own concept to obtain a weak order (average ranking). Although this concept is not specifically mentioned here, it plays a role as a mean for comparisons. How far does final ranking coincide with that provided by partial ordering? When this question appears, a subsequent problem arises: How far is any approximative construction of linear orders out of a poset exact? An exact linear ordering is most often computationally not tractable; hence, good approximations are needed.

(5)

Partial order theory delivers mathematical concepts. Many of them seem to have a seed for useful application with MIS. Identifying these and checking their role for application with MIS is a permanent task, as mathematicians really do not sleep!

7. Further Reading

Partial order methodology has, over the years, been applied in a variety of disciples, comprised of theory and mathematics [17,20,24,31,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53], decision support systems [54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70], biology and chemistry [71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94], formal concept analysis [95,96,97], sociology and economics [98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120], management (in its broadest sense) [121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137] and software [25,26,27,28,138].