Efficient Calibration of Groundwater Contaminant Transport Models Using Bayesian Optimization
Abstract
1. Introduction
2. Materials and Methods
2.1. Objective Function
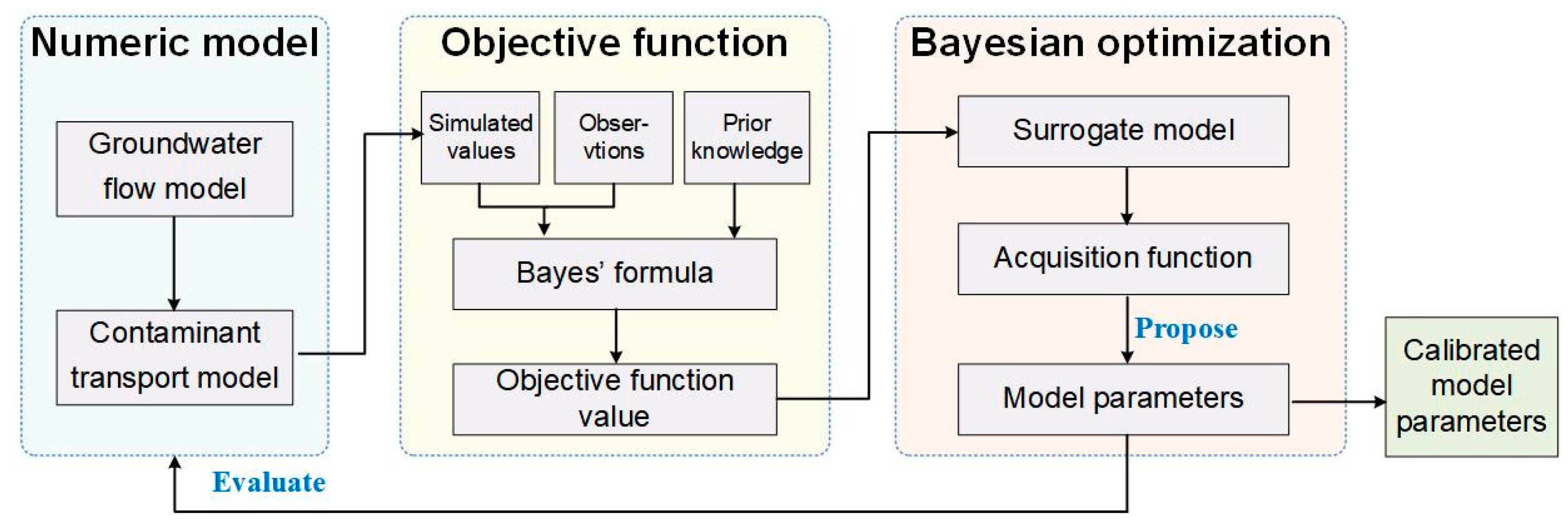
2.2. Bayesian Optimization
| Algorithm 1. Bayesian optimization for model calibration. |
| 01 Initialize sample set 02 03 Update probabilistic surrogate model with 04 Update acquisition function with 05 Select the new model parameters by maximizing the : 06 Compute simulation results 07 Compute the objective function with 08 09 end for 10 Output model parameters with the smallest |
2.3. Numerical Model
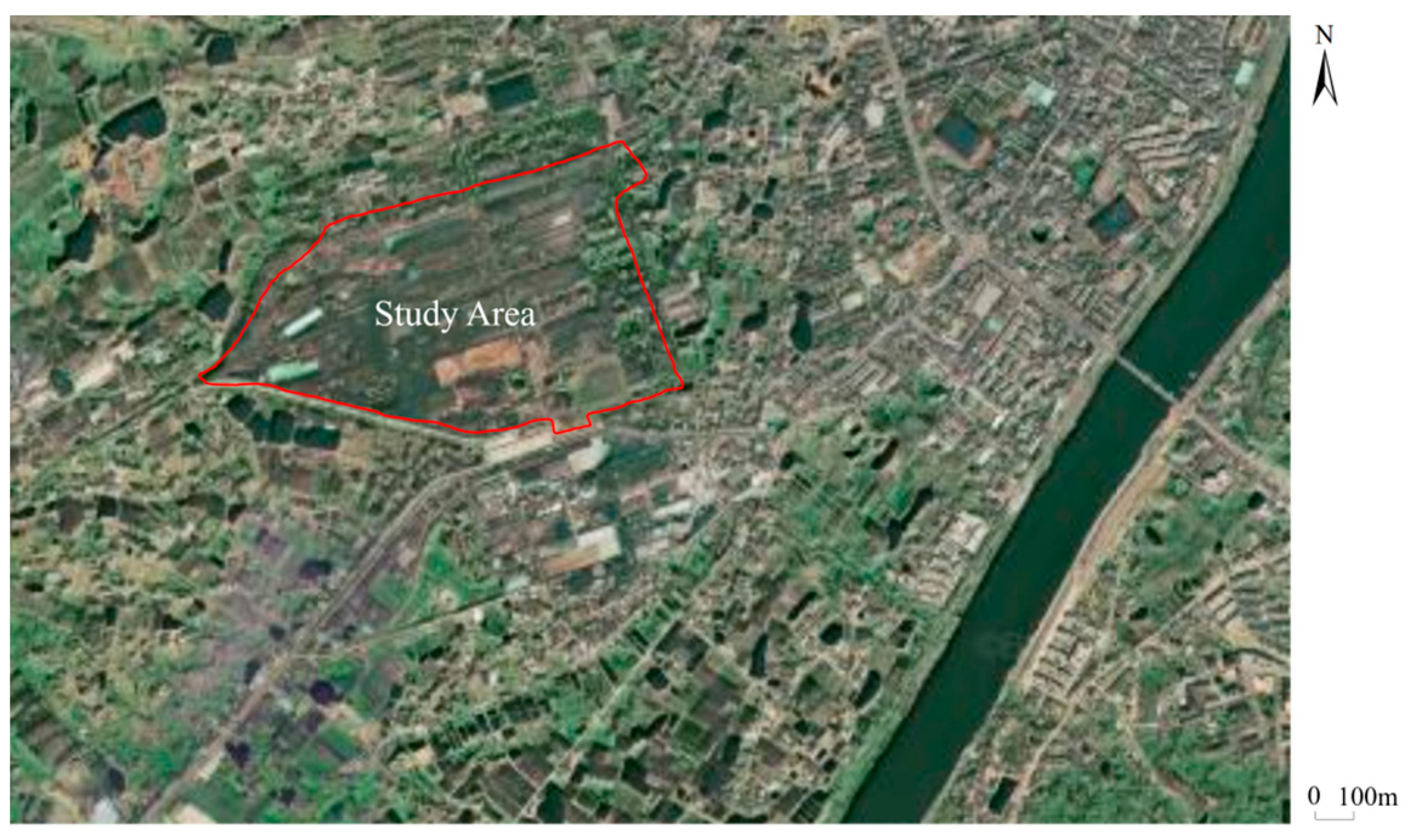
3. Study Area
4. Results
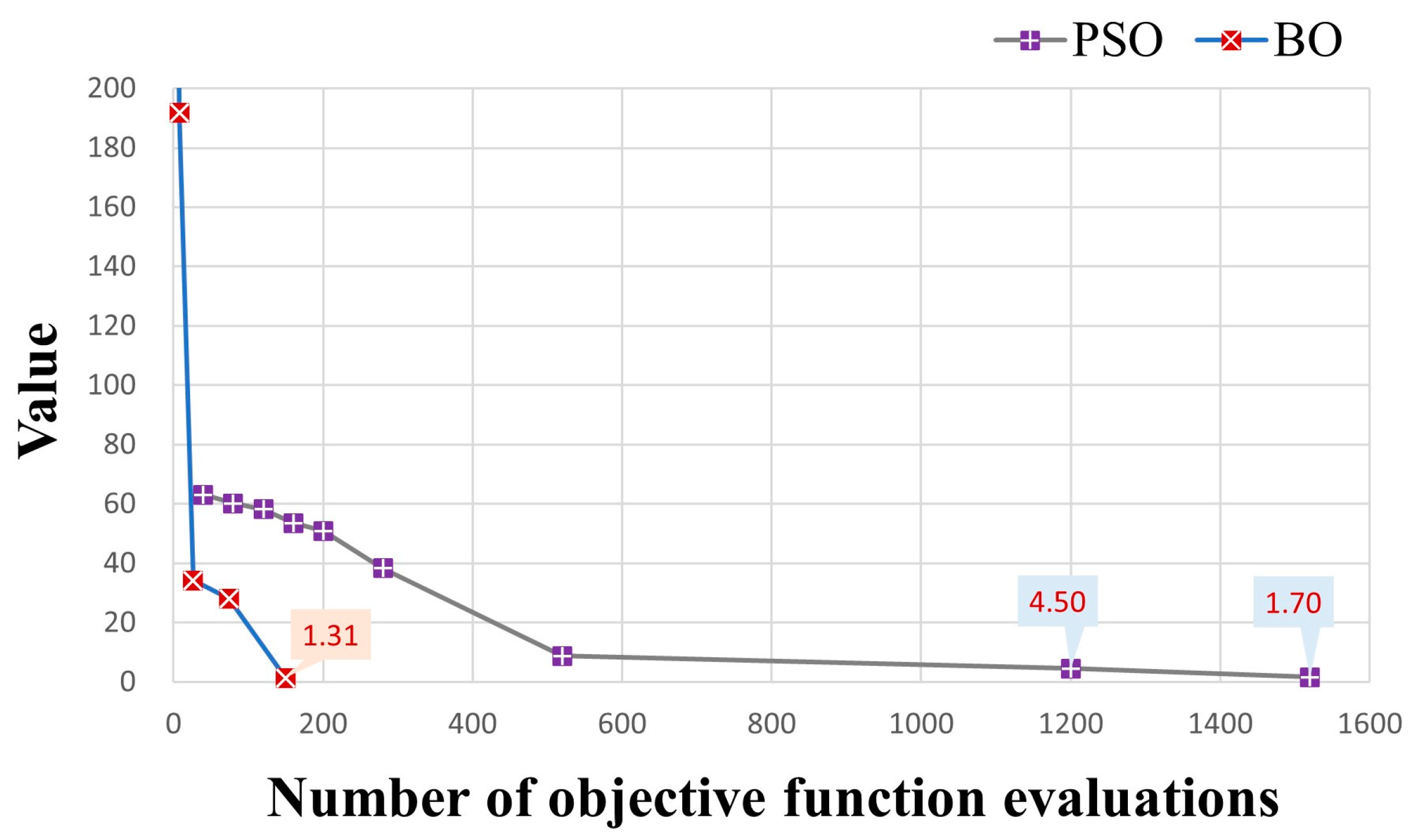
4.1. Setup
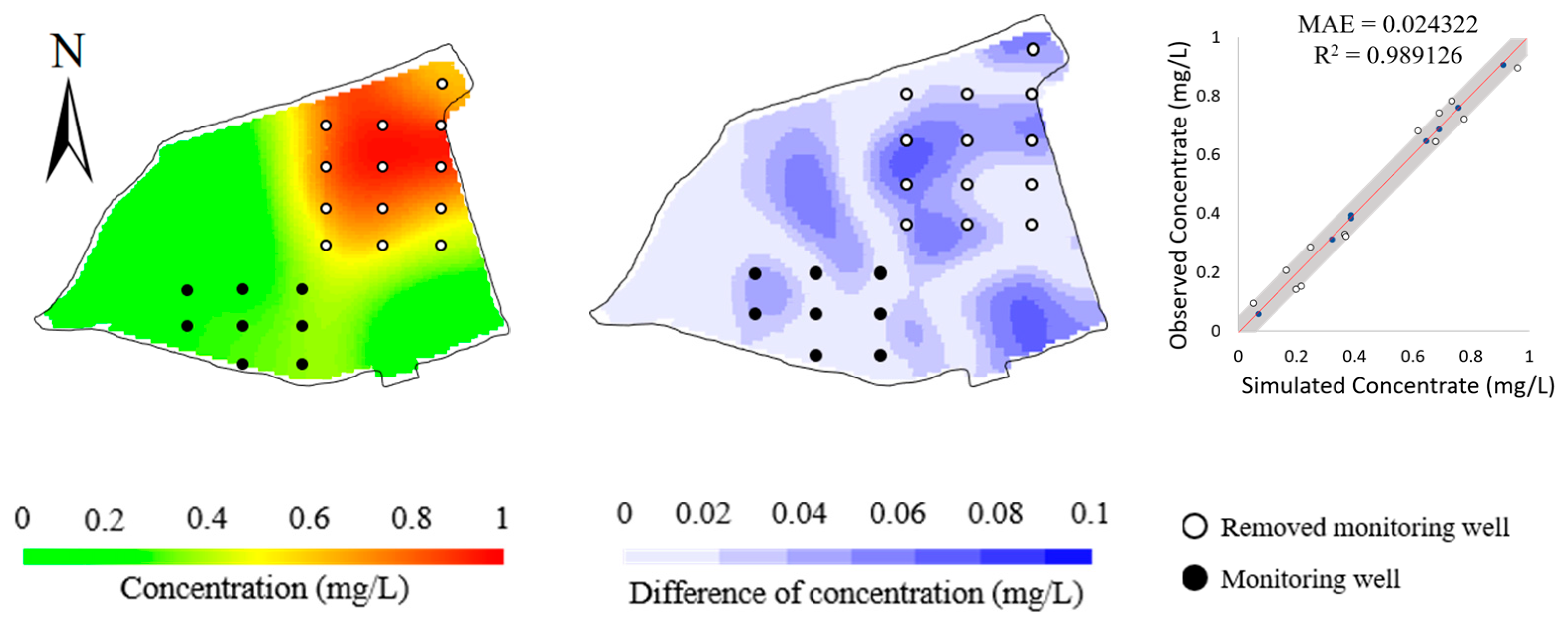
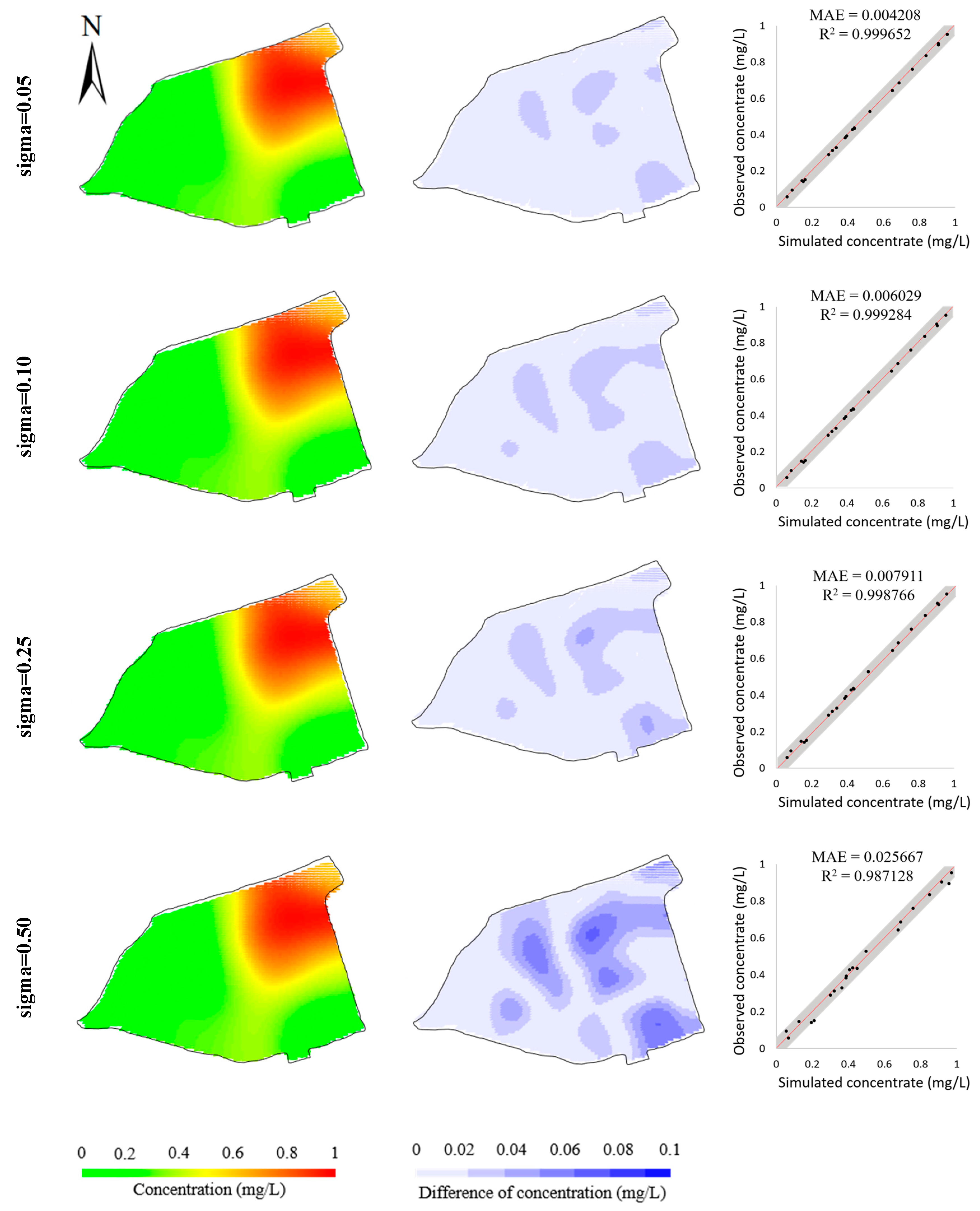
4.2. Hypothetical Case
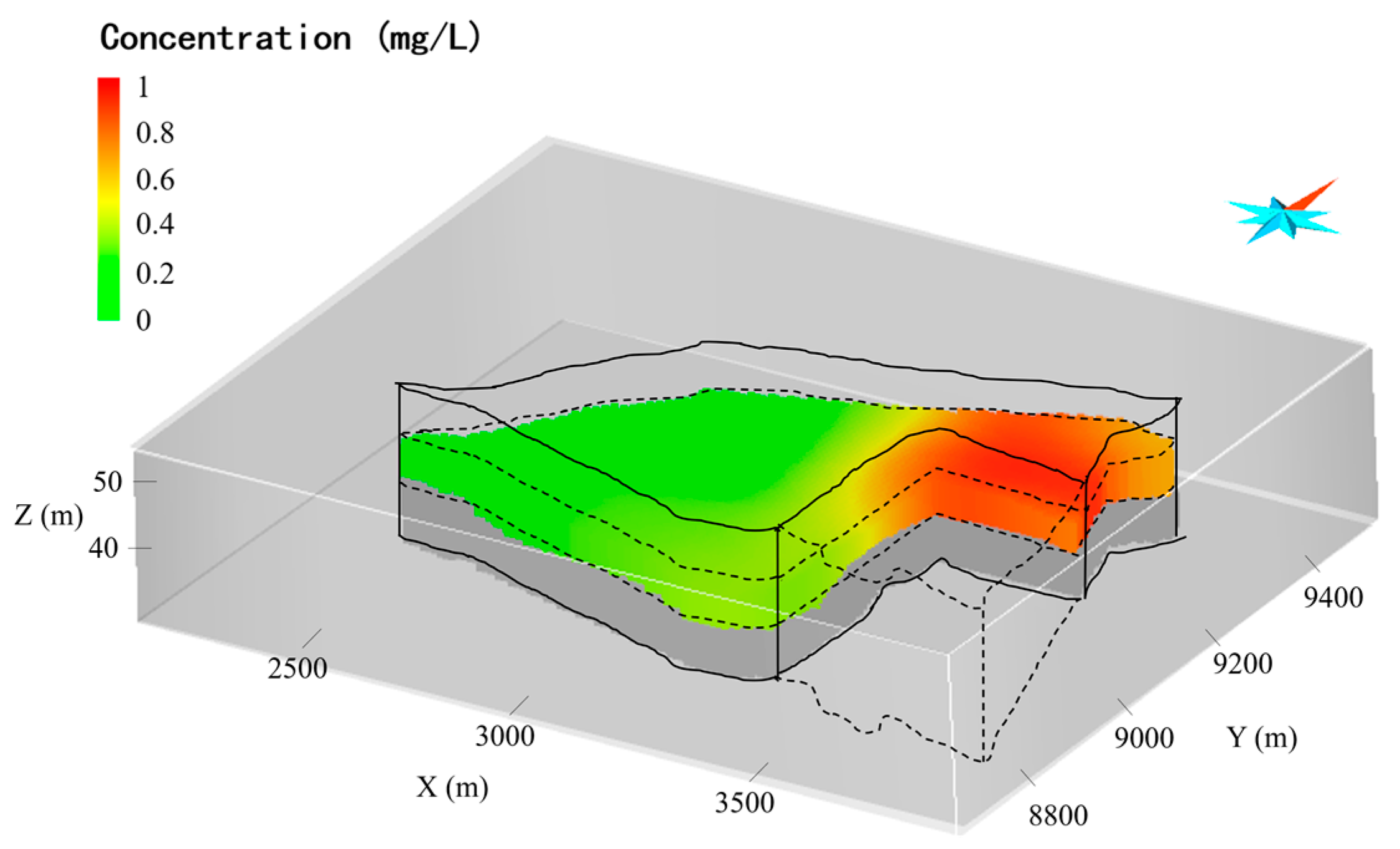
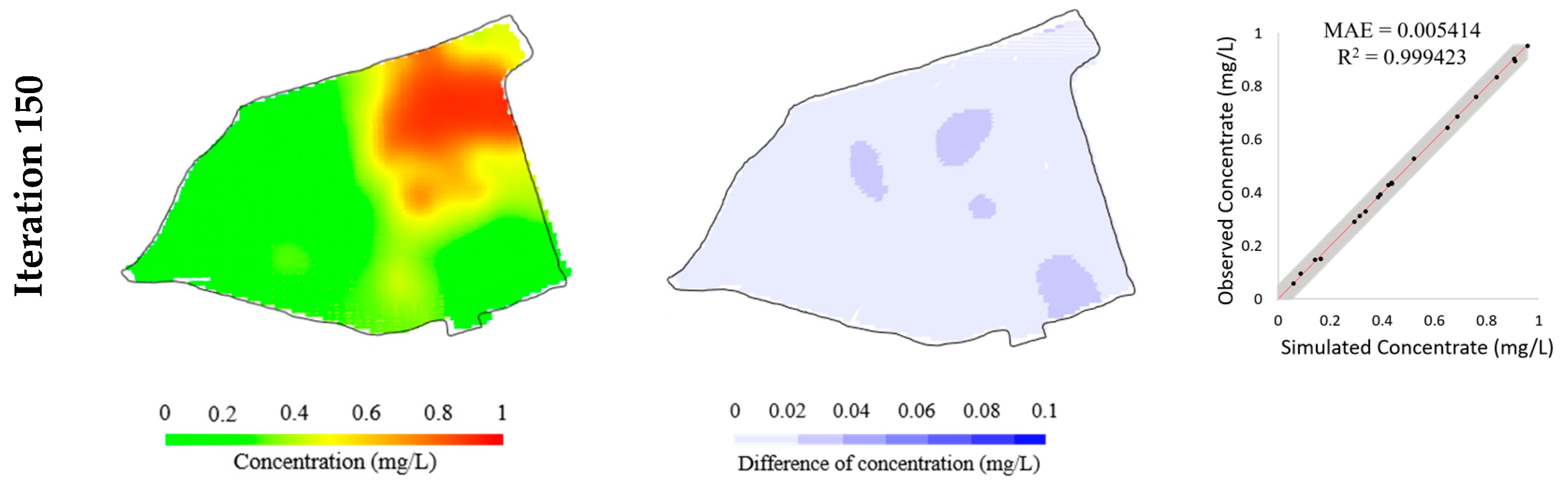
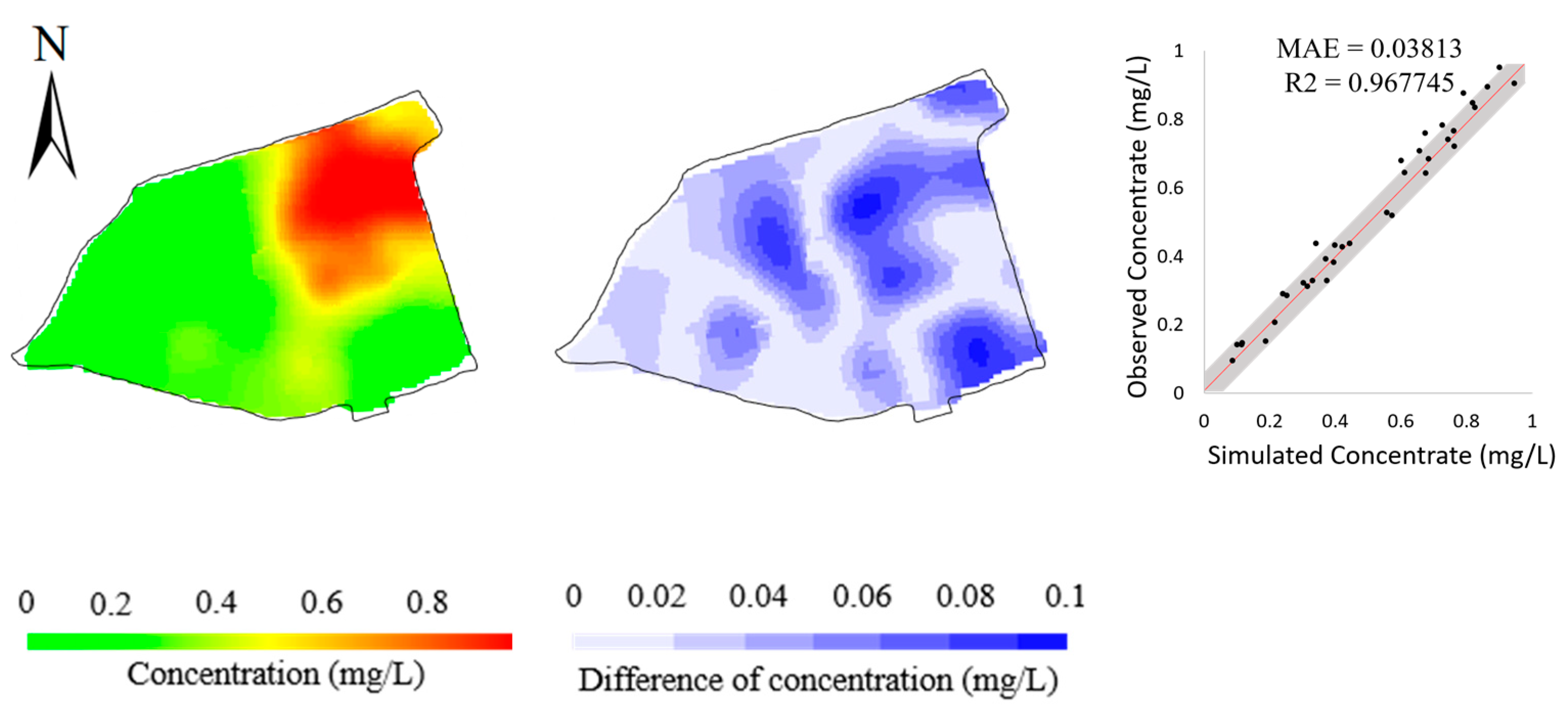
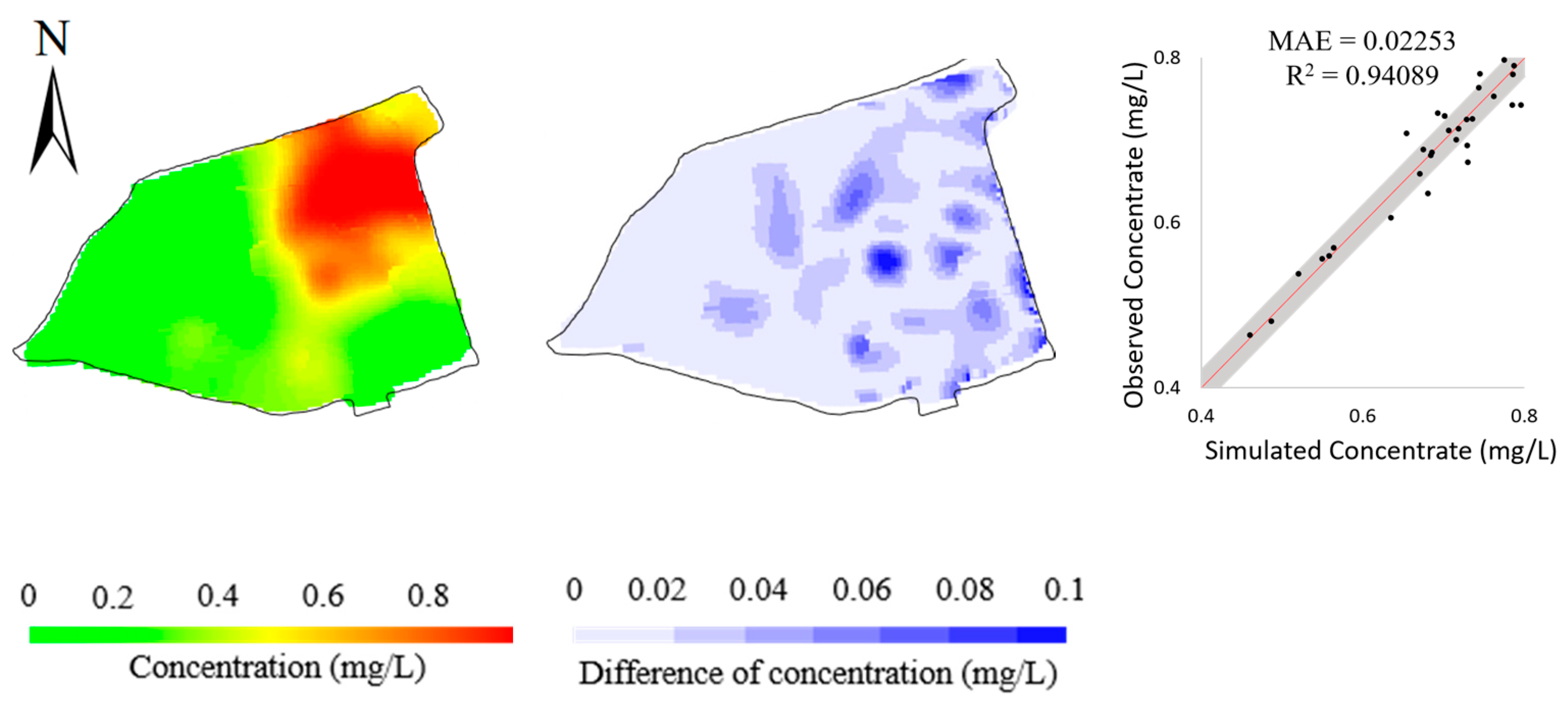
4.3. Real Case
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mackay, D.M.; Roberts, P.V.; Cherry, J.A. Transport of organic contaminants in groundwater. Environ. Sci. Technol. 1985, 19, 384–392. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; He, Y.; Hu, H.-P.; Lou, W.; Zhang, Z.; Zhang, K.-N.; Chen, Y.-G.; Ye, W.-M.; Sun, J. Laboratory investigation on the retention performance of a soil–bentonite mixture used as an engineered barrier: Insight into the effects of ionic strength and associated heavy metal ions. Environ. Sci. Pollut. Res. 2023, 30, 50162–50173. [Google Scholar] [CrossRef] [PubMed]
- United States Environmental Protection Agency; Office of Solid Waste, Emergency Response, & Environmental Management Support (Firm). Cleaning Up the Nation’s Waste Sites: Markets and Technology Trend; US Environmental Protection Agency, Office of Solid Waste and Emergency Response: Washington, DC, USA, 1997.
- He, Y.; Hu, G.; Wu, D.-Y.; Zhu, K.-F.; Zhang, K.-N. Contaminant migration and the retention behavior of a laterite–bentonite mixture engineered barrier in a landfill. J. Environ. Manag. 2022, 304, 114–338. [Google Scholar] [CrossRef] [PubMed]
- Gorelick, S.M.; Voss, C.I.; Gill, P.E.; Murray, W.; Saunders, M.A.; Wright, M.H. Aquifer Reclamation Design: The Use of Contaminant Transport Simulation Combined with Nonlinear Programing. Water Resour. Res. 1984, 20, 415–427. [Google Scholar] [CrossRef]
- Burnett, R.D.; Frind, E.O. Simulation of contaminant transport in three dimensions: 2. Dimensionality effects. Water Resour. Res. 1987, 23, 695–705. [Google Scholar] [CrossRef]
- Konikow, L.F.; Goode, D.J.; Hornberger, G.Z. A Three-Dimensional Method-of-Characteristics Solute-Transport Model (MOC3D); US Department of the Interior: Washington, DC, USA; US Geological Survey: Reston, VA, USA, 1996; Volume 96.
- Zheng, C.; Wang, P.P. MT3DMS: A Modular Three-Dimensional Multispecies Transport Model for Simulation of Advection, Dispersion, and Chemical Reactions of Contaminants in Groundwater Systems Documentation and User’s Guide; US Army Corps of Engineer: Washington, DC, USA, 1999.
- Greskowiak, J.; Hay, M.B.; Prommer, H.; Liu, C.; Post, V.E.A.; Ma, R.; Davis, J.A.; Zheng, C.; Zachara, J.M. Simulating adsorption of U(VI) under transient groundwater flow and hydrochemistry: Physical versus chemical nonequilibrium model. Water Resour. Res. 2011, 47, 118–132. [Google Scholar] [CrossRef]
- Steefel, C.I.; MacQuarrie, K.T. Approaches to modeling of reactive transport in porous media. React. Transp. Porous Media 2018, 34, 83–130. [Google Scholar]
- Seyedpour, S.; Kirmizakis, P.; Brennan, P.; Doherty, R.; Ricken, T. Optimal remediation design and simulation of groundwater flow coupled to contaminant transport using genetic algorithm and radial point collocation method (RPCM). Sci. Total Environ. 2019, 669, 389–399. [Google Scholar] [CrossRef]
- Locatelli, L.; Binning, P.J.; Sanchez-Vila, X.; Søndergaard, G.L.; Rosenberg, L.; Bjerg, P.L. A simple contaminant fate and transport modelling tool for management and risk assessment of groundwater pollution from contaminated sites. J. Contam. Hydrol. 2019, 221, 35–49. [Google Scholar] [CrossRef]
- Masum, S.A.; Zhang, Z.; Tian, G.; Sultana, M. Three-dimensional fully coupled hydro-mechanical-chemical model for solute transport under mechanical and osmotic loading conditions. Environ. Sci. Pollut. Res. 2023, 30, 5983–6000. [Google Scholar] [CrossRef]
- Doherty, J. PEST: A Unique Computer Program for Model-independent Parameter Optimisation. In Water Down Under 94: Groundwater/Surface Hydrology Common Interest Papers; Preprints of Papers: Groundwater/Surface Hydrology Common Interest Papers; Preprints of Papers; Institution of Engineers, Australia: Barton, Australia, 1994. [Google Scholar]
- Doherty, J. Ground Water Model Calibration Using Pilot Points and Regularization. Ground Water 2003, 41, 170–177. [Google Scholar] [CrossRef] [PubMed]
- Solomatine, D.P.; Dibike, Y.B.; Kukuric, N. Automatic calibration of groundwater models using global optimization techniques. Hydrol. Sci. J. 1999, 44, 879–894. [Google Scholar] [CrossRef]
- Mugunthan, P.; Shoemaker, C.A.; Regis, R.G. Comparison of function approximation, heuristic, and derivative-based methods for automatic calibration of computationally expensive groundwater bioremediation models. Water Resour. Res. 2005, 41, 134–152. [Google Scholar] [CrossRef]
- Hill, M.C.; Tiedeman, C.R. Effective Groundwater Model Calibration; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Shoemaker, C.A.; Regis, R.G.; Fleming, R.C. Watershed calibration using multistart local optimization and evolutionary optimization with radial basis function approximation. Hydrol. Sci. J. 2007, 52, 450–465. [Google Scholar] [CrossRef]
- Shafii, M.; De Smedt, F. Multi-objective calibration of a distributed hydrological model (WetSpa) using a genetic algorithm. Hydrol. Earth Syst. Sci. 2009, 13, 2137–2149. [Google Scholar] [CrossRef]
- Tang, G.; D’azevedo, E.F.; Zhang, F.; Parker, J.C.; Watson, D.B.; Jardine, P.M. Application of a hybrid MPI/OpenMP approach for parallel groundwater model calibration using multi-core computers. Comput. Geosci. 2010, 36, 1451–1460. [Google Scholar] [CrossRef]
- Gaganis, P.; Smith, L. A Bayesian approach to the quantification of the effect of model error on the predictions of groundwater models. Water Resour. Res. 2001, 37, 2309–2322. [Google Scholar] [CrossRef]
- Xu, T.; Valocchi, A.J.; Ye, M.; Liang, F. Quantifying model structural error: Efficient Bayesian calibration of a regional groundwater flow model using surrogates and a data-driven error model. Water Resour. Res. 2017, 53, 4084–4105. [Google Scholar] [CrossRef]
- Pang, M.; Shoemaker, C.A.; Bindel, D. Early termination strategies with asynchronous parallel optimization in application to automatic calibration of groundwater PDE models. Environ. Model. Softw. 2022, 147, 105–237. [Google Scholar] [CrossRef]
- Dai, Z.; Samper, J. Inverse problem of multicomponent reactive chemical transport in porous media: Formulation and applications. Water Resour. Res. 2004, 40, 407–425. [Google Scholar] [CrossRef]
- EL Harrouni, K.; Ouazar, D.; Wrobel, L.; Cheng, A.-D. Groundwater parameter estimation by optimization and DRBEM. Eng. Anal. Bound. Elements 1997, 19, 97–103. [Google Scholar] [CrossRef]
- Lin, A.C.; Yeh, W.W.G. Identification of parameters in an inhomogenous aquifer by the use of the maximum priciple of optimal control and quasi-linearization. Water Resour. Res. 1974, 10, 829–838. [Google Scholar] [CrossRef]
- Poeter, E.P.; Hill, M.C.; Lu, D.; Tiedeman, C.R.; Mehl, S. UCODE_2014, with new capabilities to define parameters unique to predictions, calculate weights using simulated values, estimate parameters with SVD, evaluate uncertainty with MCMC, and more. Integr. Groundw. Model. Cent. Rep. Number GWMI 2022, 2, 2014. [Google Scholar]
- Adams, B.M.; Bohnhoff, W.J.; Dalbey, K.R.; Ebeida, M.S.; Eddy, J.P.; Eldred, M.S.; Hooper, R.W.; Hough, P.D.; Hu, K.T.; Jakeman, J.D.; et al. Dakota, A Multilevel Parallel Object-Oriented Framework for Design Optimization, Parameter Estimation 2020, Uncertainty Quantification, and Sensitivity Analysis: Version 6.13 User’s Manual (No. SAND2020-12495); Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2020. [Google Scholar]
- Giacobbo, F.; Marseguerra, M.; Zio, E. Solving the inverse problem of parameter estimation by genetic algorithms: The case of a groundwater contaminant transport model. Ann. Nucl. Energy 2002, 29, 967–981. [Google Scholar] [CrossRef]
- Zheng, C.; Wang, P. Parameter structure identification using tabu search and simulated annealing. Adv. Water Resour. 1996, 19, 215–224. [Google Scholar] [CrossRef]
- Duan, Q.Y.; Gupta, V.K.; Sorooshian, S. Shuffled complex evolution approach for effective and efficient global minimization. J. Optim. Theory Appl. 1993, 76, 501–521. [Google Scholar] [CrossRef]
- Braak, C.J.T. A Markov Chain Monte Carlo version of the genetic algorithm Differential Evolution: Easy Bayesian computing for real parameter spaces. Stat. Comput. 2006, 16, 239–249. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M.; Rojas, R. A model-independent Particle Swarm Optimisation software for model calibration. Environ. Model. Softw. 2013, 43, 5–25. [Google Scholar] [CrossRef]
- Wang, Z.; Lu, W.; Chang, Z.; Wang, H. Simultaneous identification of groundwater contaminant source and simulation model parameters based on an ensemble Kalman filter—Adaptive step length ant colony optimization algorithm. J. Hydrol. 2022, 605, 127–352. [Google Scholar] [CrossRef]
- Laloy, E.; Rogiers, B.; Vrugt, J.A.; Mallants, D.; Jacques, D. Efficient posterior exploration of a high-dimensional groundwater model from two-stage Markov chain Monte Carlo simulation and polynomial chaos expansion. Water Resour. Res. 2013, 49, 2664–2682. [Google Scholar] [CrossRef]
- Xu, T.; Valocchi, A.J. A Bayesian approach to improved calibration and prediction of groundwater models with structural error. Water Resour. Res. 2015, 51, 9290–9311. [Google Scholar] [CrossRef]
- Xu, T.; Valocchi, A.J.; Ye, M.; Liang, F.; Lin, Y.F. Bayesian calibration of groundwater models with input data uncertainty. Water Resour. Res. 2017, 53, 3224–3245. [Google Scholar] [CrossRef]
- Zhang, J.; Man, J.; Lin, G.; Wu, L.; Zeng, L. Inverse modeling of hydrologic systems with adaptive multifidelity Markov chain Monte Carlo simulations. Water Resour. Res. 2018, 54, 4867–4886. [Google Scholar] [CrossRef]
- Sun, X.; Zeng, X.; Wu, J.; Wang, D. A Two-Stage Bayesian Data-Driven Method to Improve Model Prediction. Water Resour. Res. 2021, 57, e2021WR030436. [Google Scholar] [CrossRef]
- Yang, H.Q.; Zhang, L.; Xue, J.; Zhang, J.; Li, X. Unsaturated soil slope characterization with Karhunen–Loève and polynomial chaos via Bayesian approach. Eng. Comput. 2019, 35, 337–350. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Ter Braak, C.J.; Clark, M.P.; Hyman, J.M.; Robinson, B.A. Treatment of input uncertainty in hydrologic modeling: Doing hydrology backward with Markov chain Monte Carlo simulation. Water Resour. Res. 2008, 44, 720–735. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Ter Braak, C.J.F. DREAM (D): An adaptive Markov Chain Monte Carlo simulation algorithm to solve discrete, noncontinuous, and combinatorial posterior parameter estimation problems. Hydrol. Earth Syst. Sci. 2011, 15, 3701–3713. [Google Scholar] [CrossRef]
- Chen, M.; Izady, A.; Abdalla, O.A. An efficient surrogate-based simulation-optimization method for calibrating a regional MODFLOW model. J. Hydrol. 2017, 544, 591–603. [Google Scholar] [CrossRef]
- Kourakos, G.; Mantoglou, A. Pumping optimization of coastal aquifers based on evolutionary algorithms and surrogate modular neural network models. Adv. Water Resour. 2009, 32, 507–521. [Google Scholar] [CrossRef]
- Stone, N. Gaussian Process Emulators for Uncertainty Analysis in Groundwater Flow. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2011. [Google Scholar]
- Garcet, J.D.P.; Ordonez, A.; Roosen, J.; Vanclooster, M. Metamodelling: Theory, concepts and application to nitrate leaching modelling. Ecol. Model. 2006, 193, 629–644. [Google Scholar] [CrossRef]
- Regis, R.G.; Shoemaker, C.A. Constrained global optimization of expensive black box functions using radial basis functions. J. Glob. Optim. 2005, 31, 153–171. [Google Scholar] [CrossRef]
- Yoon, H.; Jun, S.C.; Hyun, Y.; Bae, G.O.; Lee, K.K. A comparative study of artificial neural networks and support vector machines for predicting groundwater levels in a coastal aquifer. J. Hydrol. 2011, 396, 128–138. [Google Scholar] [CrossRef]
- Fallah-Mehdipour, E.; Haddad, O.B.; Mariño, M.A. Prediction and simulation of monthly groundwater levels by genetic programming. J. Hydro Environ. Res. 2013, 7, 253–260. [Google Scholar] [CrossRef]
- Hoffman, M.W.; Shahriari, B.; Freitas, N.D. On correlation and budget constraints in model-based bandit optimization with application to automatic machine learning. In Proceedings of the Seventeenth International Conference on Artificial Intelligence and Statistics, Reykjavik, Iceland, 22–25 April 2014; pp. 365–374. [Google Scholar]
- Zhang, Y.; Sohn, K.; Villegas, R.; Pan, G.; Lee, H. Improving object detection with deep convolutional networks via Bayesian optimization and structured prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 249–258. [Google Scholar]
- Frazier, P.I.; Wang, J. Bayesian optimization for materials design. In Information Science for Materials Discovery and Design; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Vanchinathan, H.P.; Nikolic, I.; Bona, F.D.; Krause, A. Explore-Exploit in top-n recommender systems via Gaussian processes. In Proceedings of the 8th ACM Conference on Recommender systems, Foster City, CA, USA, 6–10 October 2014; Volume 31. [Google Scholar]
- Nadarajah, S. A generalized normal distribution. J. Appl. Stat. 2005, 32, 685–694. [Google Scholar] [CrossRef]
- Chen, Y.-C. A tutorial on kernel density estimation and recent advances. Biostat. Epidemiology 2017, 1, 161–187. [Google Scholar] [CrossRef]
- Frazier, P.I. A tutorial on Bayesian optimization. arXiv 2018, arXiv:1807.02811. [Google Scholar]
- Pelikan, M.; Goldberg, D.E.; Cantú-Paz, E. BOA: The Bayesian optimization algorithm. In Proceedings of the genetic and evolutionary computation conference GECCO-99, Orlando, FL, USA, 13–17 July 1999; Volume 1, pp. 525–532. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 2012, 25, 1–9. [Google Scholar]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge MA, USA, 2006. [Google Scholar]
- Mockus, J. The application of Bayesian methods for seeking the extremum. Towards Glob. Optim. 1998, 2, 117. [Google Scholar]
- Bull, A.D. Convergence rates of efficient global optimization algorithms. J. Mach. Learn. Res. 2011, 12, 2879–2904. [Google Scholar]
- Snoek, J.R. Bayesian Optimization and Semiparametric Models with Applications to Assistive Technology. Ph.D. Thesis, University of Toronto, Toronto, Canada, 2013. [Google Scholar]
- Zheng, C.; Bennett, G.D. Applied Contaminant Transport Modeling; Wiley-Interscience: New York, NY, USA, 2002. [Google Scholar]
- Harbaugh, A.W.; Banta, E.R.; Hill, M.C.; McDonald, M.G. Modflow-2000, the U. S. Geological Survey Modular Ground-Water Model-User Guide to Modularization Concepts and the Ground-Water Flow Process; USGS: Reston, VA, USA, 2000.
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Poli, R. Analysis of the Publications on the Applications of Particle Swarm Optimisation. J. Artif. Evol. Appl. 2008, 2008, 685175. [Google Scholar] [CrossRef]
- Asher, M.J.; Croke, B.F.W.; Jakeman, A.J.; Peeters, L.J. A review of surrogate models and their application to groundwater modeling. Water Resour. Res. 2015, 51, 5957–5973. [Google Scholar] [CrossRef]

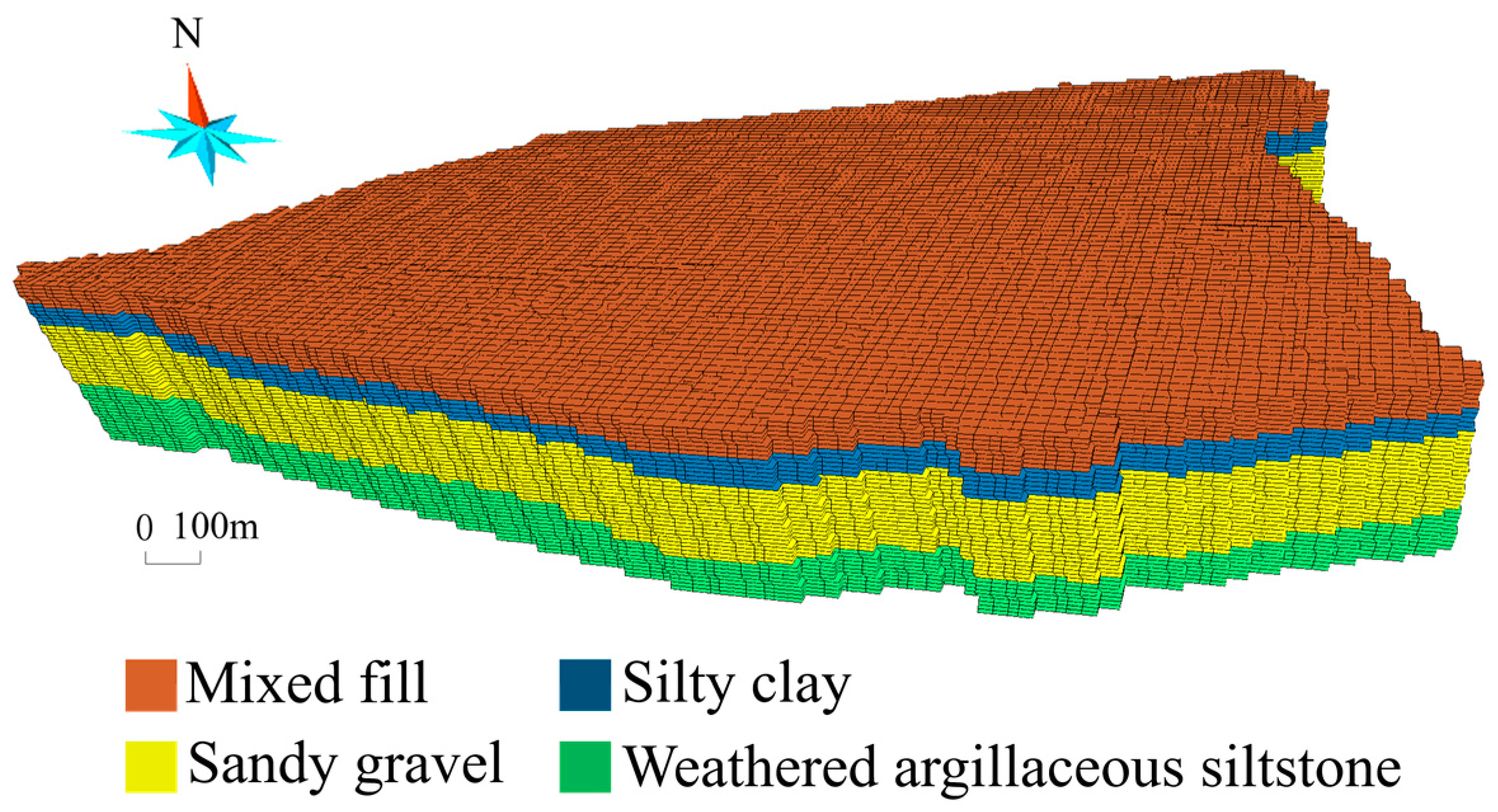

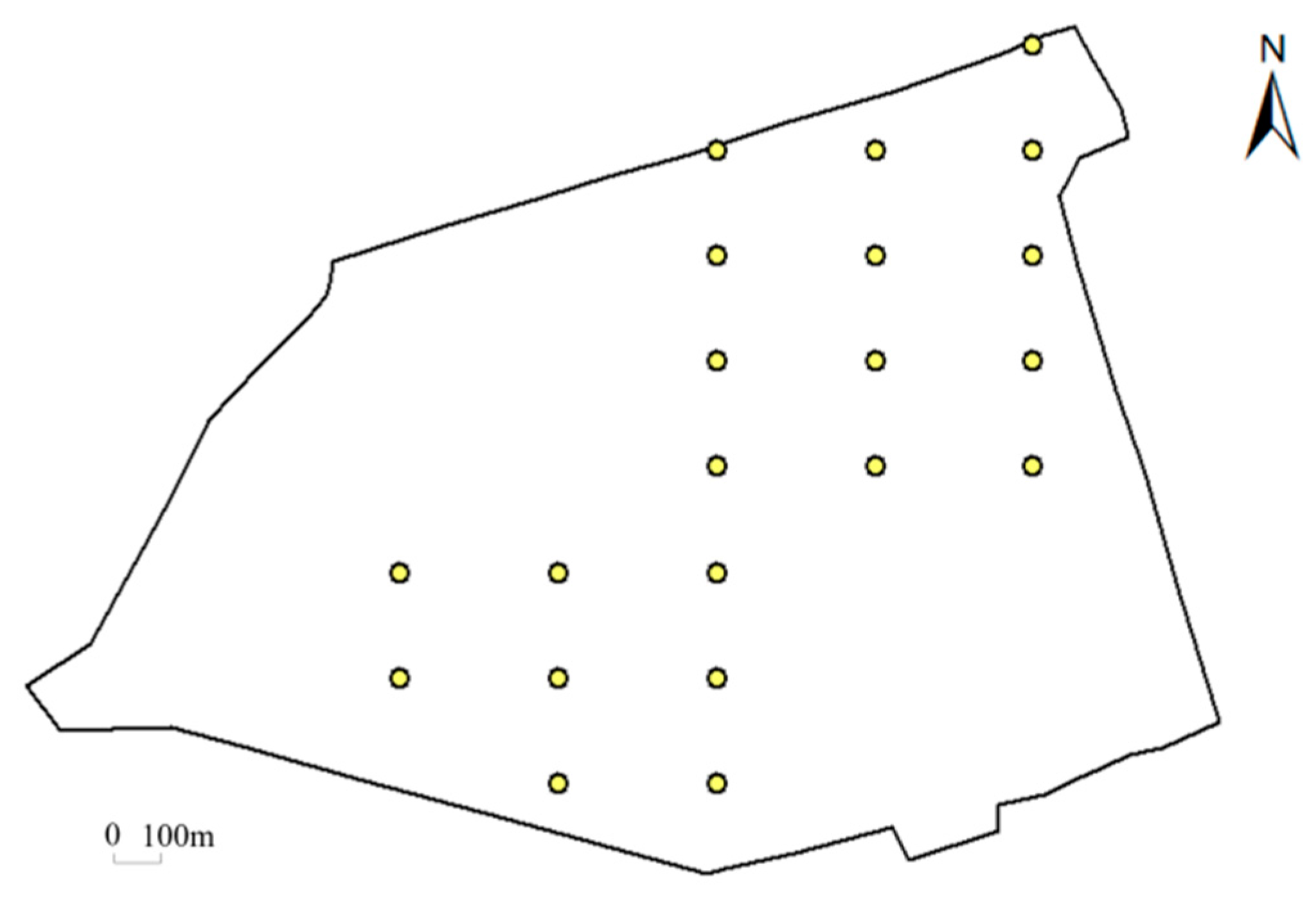


| Layer | Thickness | Water Permeability |
|---|---|---|
| Mixed fill | 3~4 m | Strong permeability |
| Silty clay | 2~4 m | Weak permeability |
| Sandy gravel | 3~4 m | Medium permeability |
| Weathered argillaceous siltstone | 9~10 m | Weak permeability |
| Model Parameter | Value |
|---|---|
| Releasing water (m−1) | 0.0~ |
| Effective porosity | 0.10~0.60 |
| Dispersity (m2 s−1) | 0.0~ |
| Retardation factor | 1.00~5.00 |
| Horizontal permeability (m s−1) | ~ |
| Vertical permeability (m s−1) | ~ |
| Model Parameter | Value |
|---|---|
| Releasing water (m−1) | 1.0 |
| Effective porosity | 0.30 |
| Dispersity (m2 s−1) | 1.00 |
| Retardation factor | 2.00 |
| Horizontal permeability (m s−1) | 6.97 |
| Vertical permeability (m s−1) | 4.37 |
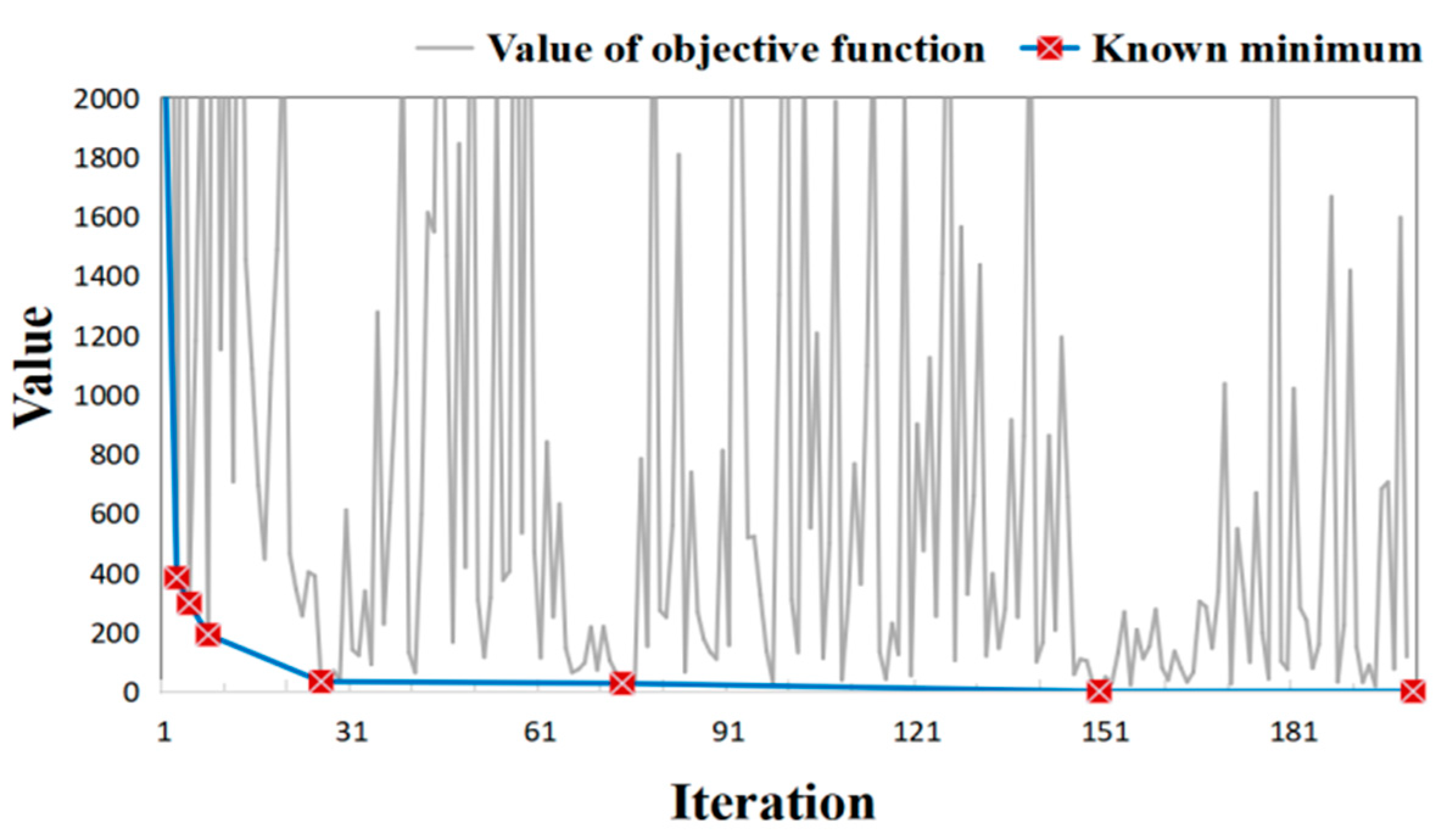
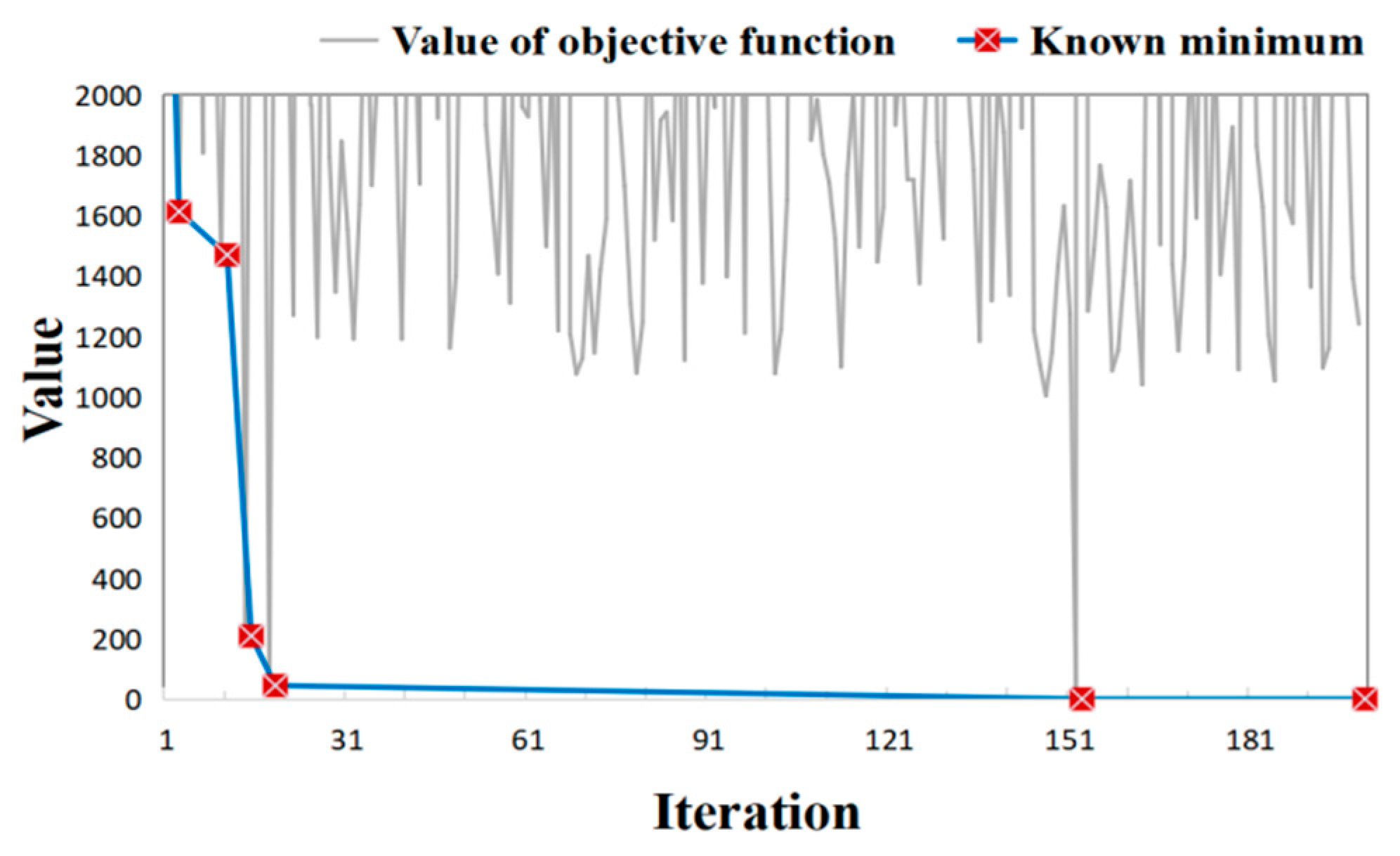
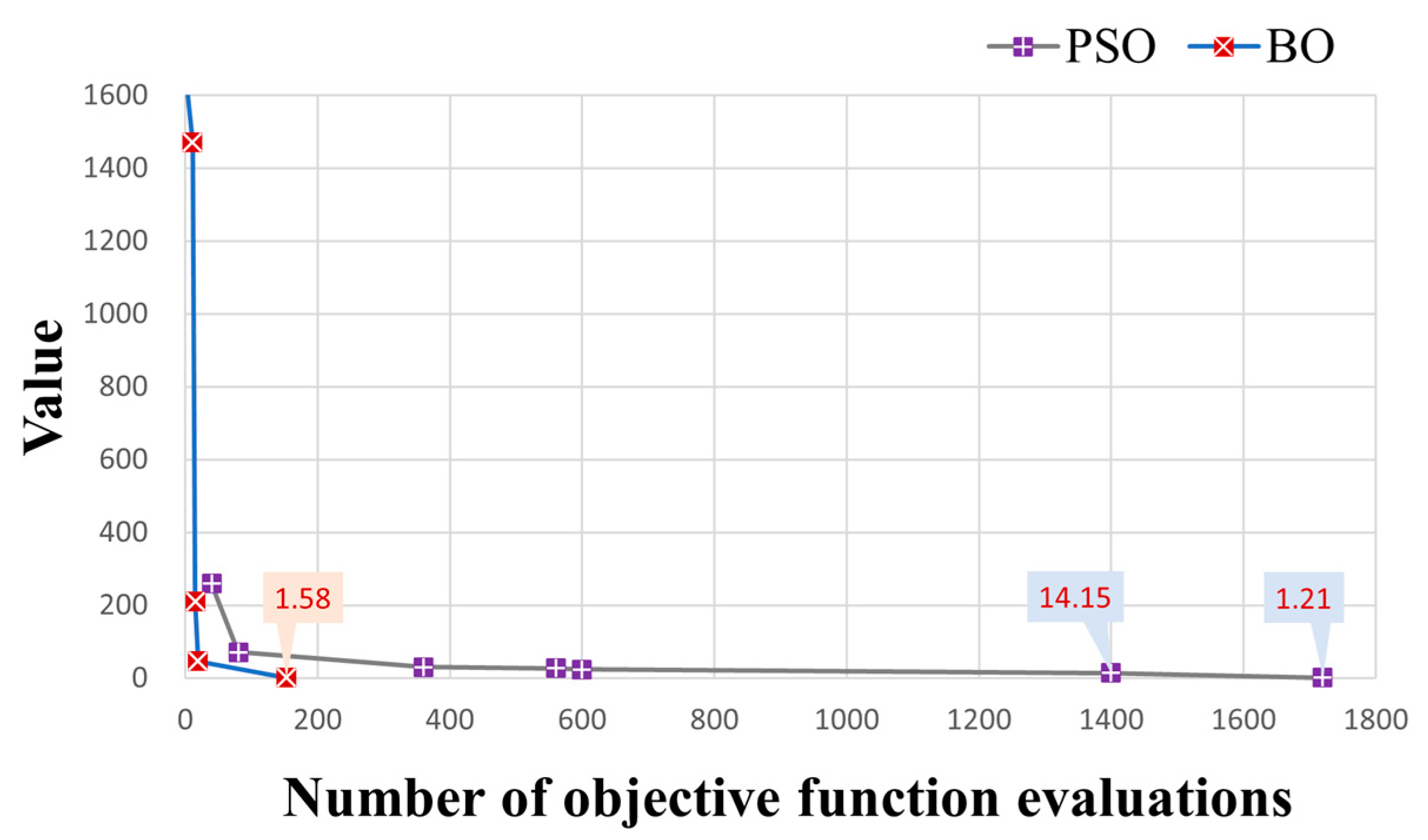
| Iteration | 1 | 3 | 5 | 8 | 26 | 74 | 150 |
|---|---|---|---|---|---|---|---|
| Minimum | 2284.01 | 383.84 | 297.55 | 191.93 | 34.18 | 28.09 | 1.31 |
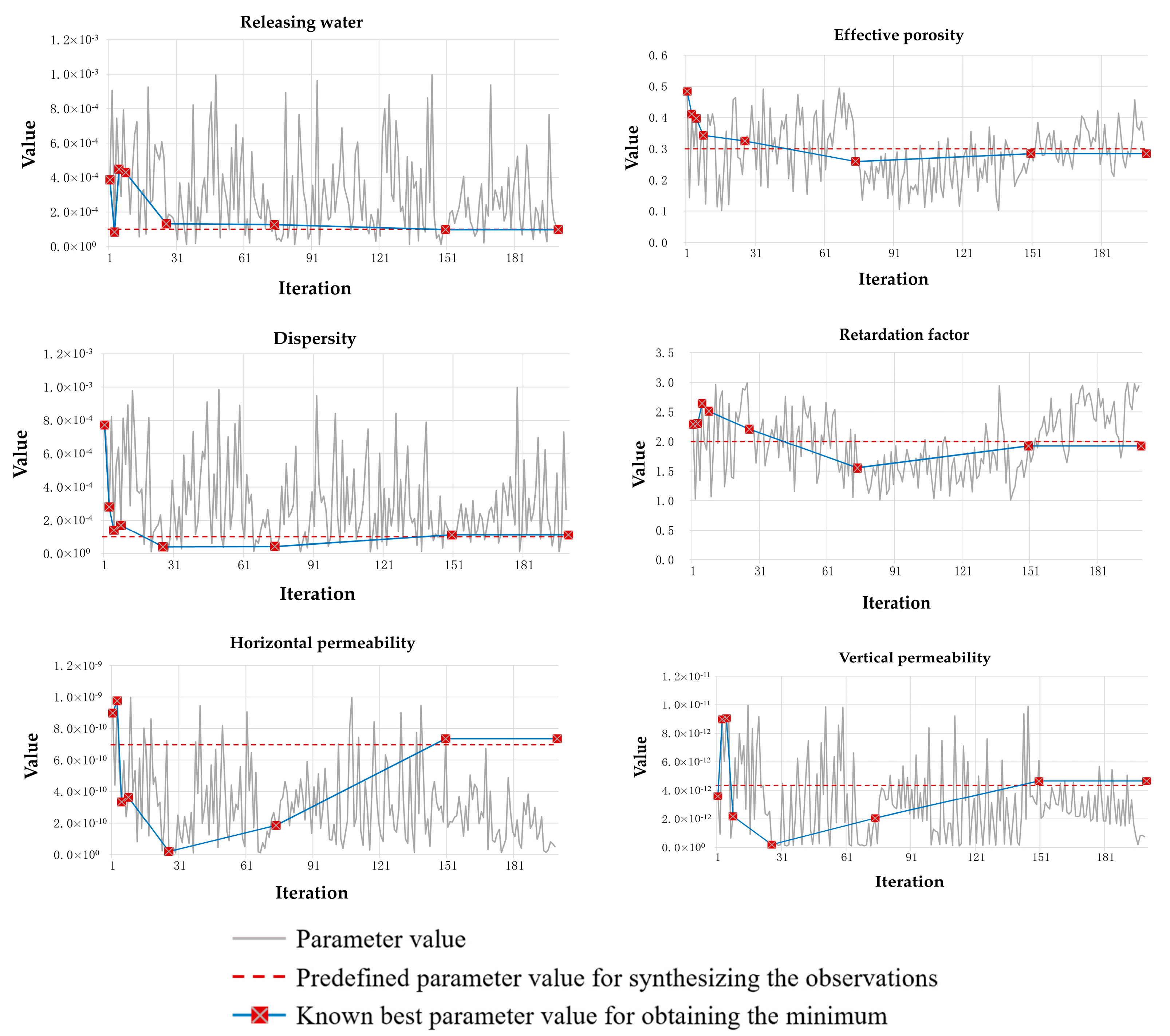
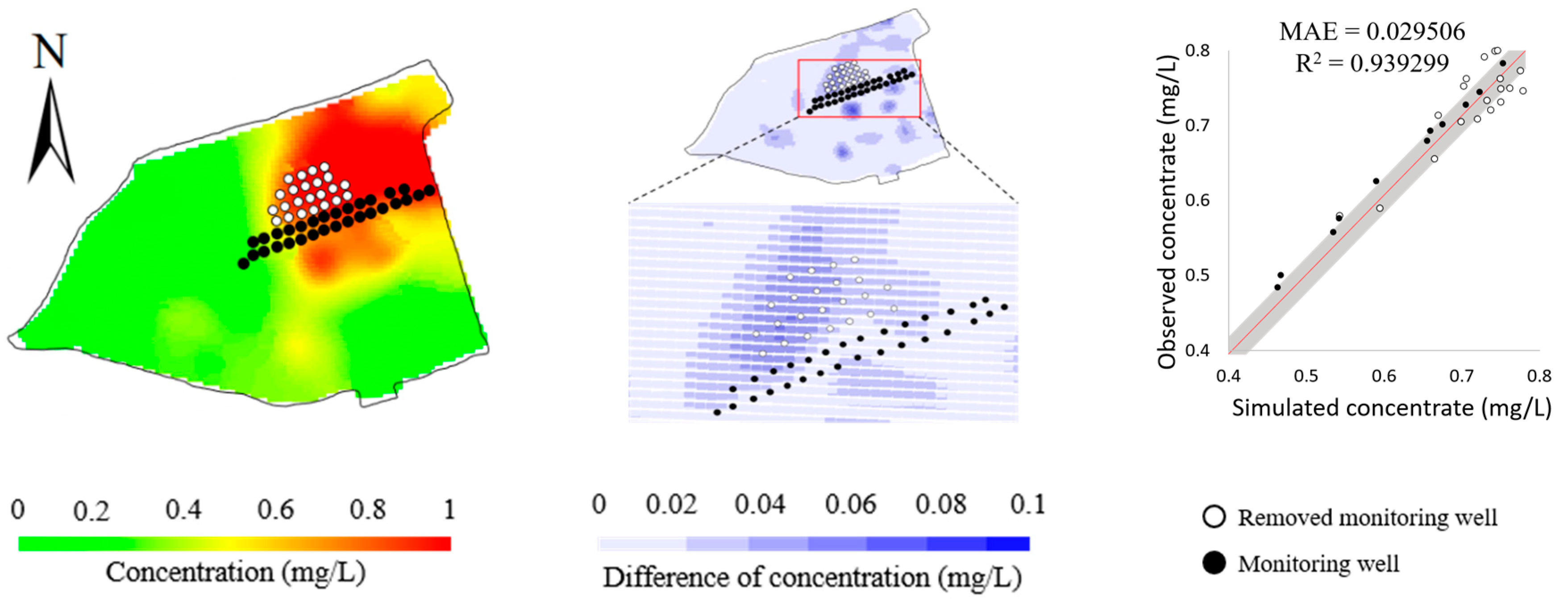
| Model Parameter | Partial Data | Full Data | Target Parameters |
|---|---|---|---|
| Releasing water (m−1) | 9.00 | 1.00 | 1.0 |
| Effective porosity | 0.31 | 0.28 | 0.30 |
| Dispersity (m2 s−1) | 1.10 | 1.10 | 1.00 |
| Retardation factor | 1.90 | 1.92 | 2.00 |
| Horizontal permeability (m s−1) | 3.58 | 7.35 | 6.97 |
| Vertical permeability (m s−1) | 1.82 | 6.07 | 4.37 |
| Objective function value | 9.87 | 1.31 | - |
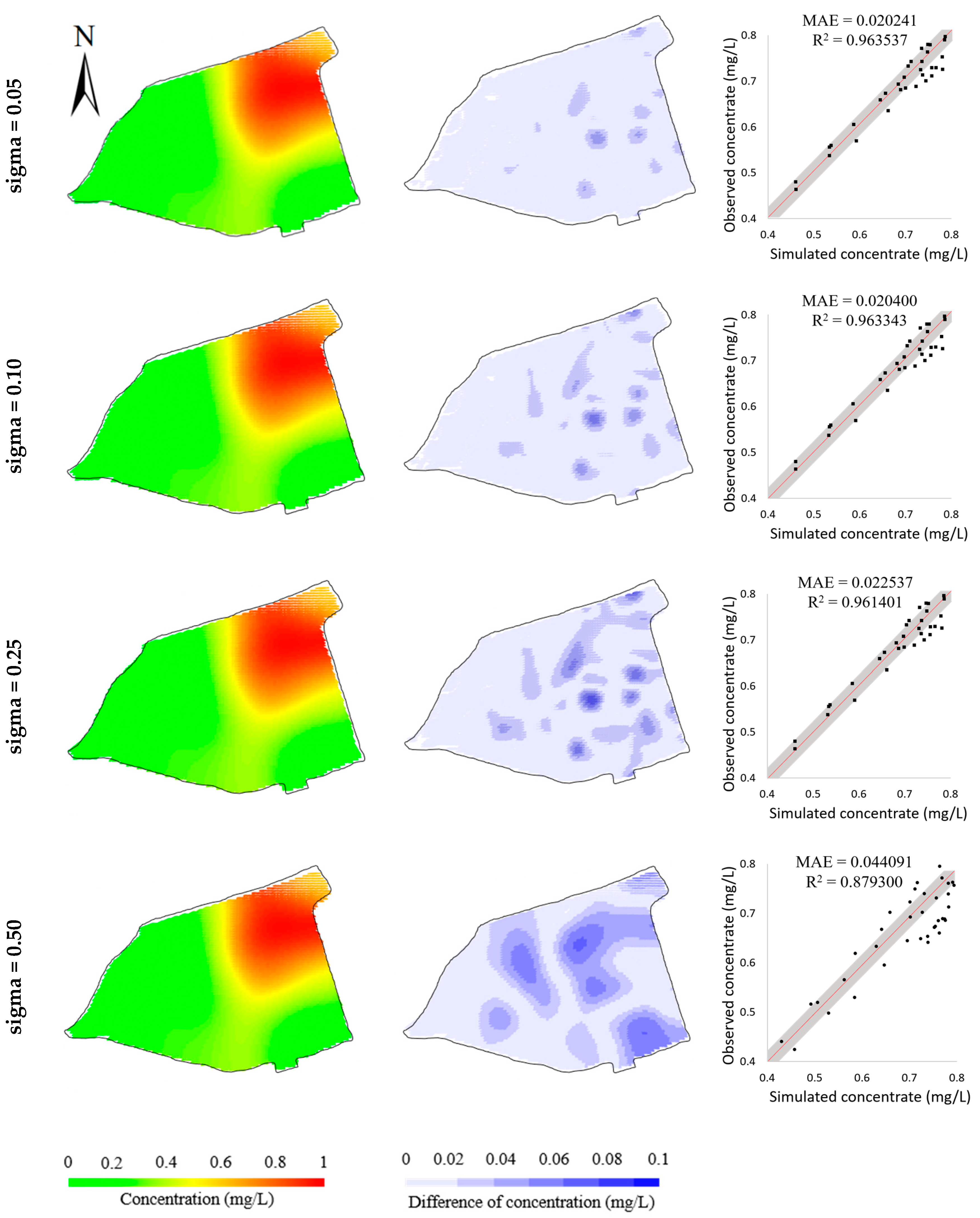
| Model Parameter | Sigma = 0.05 | Sigma = 0.10 | Sigma = 0.25 | Sigma = 0.50 | Target Parameters |
|---|---|---|---|---|---|
| Releasing water (m−1) | 1.10 | 1.0 | 1.10 | 1.1 | 1.0 |
| Effective porosity | 0.30 | 0.31 | 0.30 | 0.31 | 0.30 |
| Dispersity (m2 s−1) | 1.00 | 1.20 | 1.0 | 1.00 | 1.00 |
| Retardation factor | 1.96 | 1.98 | 1.95 | 2.08 | 2.00 |
| Horizontal permeability (m s−1) | 5.71 | 5.88 | 7.84 | 6.02 | 6.97 |
| Vertical permeability (m s−1) | 4.80 | 6.06 | 3.98 | 4.87 | 4.37 |
| Objective function value | 1.79 | 2.64 | 1.63 | 1.92 | - |
| Iteration | 1 | 3 | 11 | 15 | 19 | 153 |
|---|---|---|---|---|---|---|
| Known minimum | 2975.10 | 1614.30 | 1470.65 | 210.01 | 46.03 | 1.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, H.; Zhou, S.; He, Y.; Lan, Z.; Zou, Y.; Mao, X. Efficient Calibration of Groundwater Contaminant Transport Models Using Bayesian Optimization. Toxics 2023, 11, 438. https://doi.org/10.3390/toxics11050438
Deng H, Zhou S, He Y, Lan Z, Zou Y, Mao X. Efficient Calibration of Groundwater Contaminant Transport Models Using Bayesian Optimization. Toxics. 2023; 11(5):438. https://doi.org/10.3390/toxics11050438
Chicago/Turabian StyleDeng, Hao, Shengfang Zhou, Yong He, Zeduo Lan, Yanhong Zou, and Xiancheng Mao. 2023. "Efficient Calibration of Groundwater Contaminant Transport Models Using Bayesian Optimization" Toxics 11, no. 5: 438. https://doi.org/10.3390/toxics11050438
APA StyleDeng, H., Zhou, S., He, Y., Lan, Z., Zou, Y., & Mao, X. (2023). Efficient Calibration of Groundwater Contaminant Transport Models Using Bayesian Optimization. Toxics, 11(5), 438. https://doi.org/10.3390/toxics11050438









