1. Introduction
Heavy metal contamination is a vital environmental concern in most developing countries, causing soil and air pollution, disrupting ecosystems, and threatening human health. Copper, which is one of the most common heavy metals, is primarily derived from industrial wastewater [
1], mineral processing [
2], agricultural practices [
3], and landfills [
4]. Groundwater contaminated by Cu and other heavy metals can be contained and remediated using permeable reactive barriers (PRBs), which were used in several studies and led to satisfactory results [
5,
6,
7,
8]. Activated carbon (AC), which is one of the most common barrier materials, is frequently used as a cost-effective adsorbent for pollutants, including heavy metals and dissolved organic and inorganic species [
9].
The adsorption mechanism of AC is determined by its physical properties (i.e., pore size distribution and specific surface area) and the nature of its surface chemicals (i.e., functional groups) [
10]. The mechanisms include surface complexation, electrostatic interaction, physical adsorption, and ion exchange [
11,
12]. Rio [
13] demonstrated that the removal of Cu(II) using biochar was dominated by ion exchange with Ca(II) on the biochar surface. Xie [
11] showed that ion exchange may be considered the main mechanism in the adsorption of Cu(II) on the AC surface, and the carboxyl and hydroxyl groups are mainly responsible for this process. However, to the best of our knowledge, the dynamic evolution during the adsorption process has not been revealed yet. Real-time monitoring of heavy metal remediation should be further studied.
Emerging electrical geophysical methods have been widely used to study the hydraulic–physical–chemical properties and reaction process of porous media, such as direct-current (DC) electrical resistivity, induced polarization (IP), and spectral induced polarization (SIP). The latter is a promising, real-time, and nondestructive technique that can reveal the electrical properties of a porous medium to reflect its characterization information and monitor its physical–chemical–biological interaction processes at low frequency (i.e., in the range of 0.01–1000 Hz). Compared with other existing methods, such as DC electrical resistivity and IP, SIP provides information on the electrical properties of the porous media, which demonstrates electrical conduction (charge carrier electromigration) and polarization effects (energy storage) in the real and imaginary parts of the complex conductivity [
14,
15]. SIP has been widely used to study microbial growth and biofilm formation [
16,
17,
18], biochar remediation and characterization [
19,
20,
21], calcite precipitation [
22,
23], and organic pollution [
24,
25]. It also has high potential in the in situ detection and monitoring of contaminant transport, chemical reactions due to the sensitivity to interfacial properties (i.e., ionic mobility and surface charge density) of porous media, and conditions of the aqueous phase such as the salinity, saturation, and temperature. Thus, the application of SIP has high potential for monitoring the remediation process.
The cationic contaminants remediated by porous media have strong SIP signatures, which makes real-time monitoring by SIP feasible. Several studies monitored the adsorption of contaminants using porous materials. For instance, Masi et al. [
26] studied the electrokinetic remediation processes of heavy metal-contaminated fine-grained marine sediments using SIP. They deduced that pH is one of the most important parameters affecting the polarization mechanism. In addition, they observed a linear link between the total chargeability and the pH. Ben Moshe et al. [
27] performed SIP on a soil sample to demonstrate the ion exchange process (Na
+-Ca
2+, Na
+-Zn
2+). This was strongly related to ion mobility and Stern layer polarization, and it was reflected through the variation of the imaginary conductivity. Hao et al. [
28] presented the processes of Pb
2+ and Cd
2+ flow-through on loess using SIP. They differentiated the adsorption mechanisms between loess and Pb
2+/Cd
2+ using SIP signals and correlated the decrease of the imaginary conductivity and reduced total polarizable surface charges with the shift of the characteristic frequency and calcite dissolution. Siddiq et al. [
29] studied the process of SIP detection in biochar-based As remediation. They deduced that the real and imaginary components will be affected by the amount of As adsorption caused by the interaction with surface functional groups. To the best of our knowledge, research on the SIP responses of the AC-based Cu remediation process is scarce. In addition, knowledge of the mechanisms of Cu–AC interaction evolution during the adsorption process incorporating SIP technology is still lacking.
The goal of this study is to innovatively incorporate the SIP method in monitoring the process of Cu2+ adsorption onto AC in a column test setup. The objectives are as follows: (1) Perform a flow-through test under 1, 5, and 10 mmol/L CuCl2 concentrations with SIP monitoring, (2) Perform thermodynamic experiments and propose a kinetic equation, (3) Perform microscopic and physicochemical experiments to elucidate the fundamental mechanisms of Cu–AC interactions, (4) Examine the SIP signals and analyze correlations to the quantity and the signature sizes of the Cu–AC units, and then evaluate the feasibility of SIP as a monitoring technique in a permeable reactive barrier or in contaminated land near a copper mine waste dump.
2. Background of SIP
SIP is a noninvasive geophysical method for measuring the electrical properties and polarization phenomena of porous media. It can be expressed by the complex conductivity (
) or resistivity (
), which is its inverse. The complex conductivity is expressed as [
30,
31]:
where
(S/m) is the real or in-phase conductivity representing the energy loss of charge carrier electromigration,
(S/m) is the imaginary or quadrature conductivity representing the energy storage of charge carrier polarization,
is the magnitude of
,
(rad/s) is the angular frequency, and
denotes the imaginary number.
Three main mechanisms (Stern layer, diffuse layer, and membrane polarizations) were observed in the SIP measurements that are closely related to the dispersion of the complex conductivity caused by the polarization of the electrical double layer (EDL) at the solid–liquid interface at a low frequency (<1 MHz) [
32]. When an external alternating electrical field is applied, the counterions in the EDL move in the direction of the electric field and accumulate at the edge of the grain. Once the injected current is shut off, the charges will balance to the previous status through ion diffusion [
30].
To evaluate the performance of the SIP method in monitoring the copper ion adsorption process on AC at CuCl2 concentrations ranging between 1 mmol/L and 10 mmol/L, the following tasks were conducted: (1) Chemical analytical techniques were performed to study the possible mechanisms of copper adsorption on AC. A combination of breakthrough column experiments and an adsorption kinetic model was performed to predict and reflect the evolutions of the geochemical process with time. (2) The real and imaginary conductivities were measured using SIP to study the copper adsorption mechanism. (3) The double Cole–Cole model was used to fit the SIP experiment data for comparison and further discussion.
The SIP data acquired from experiments mostly follow a Cole–Cole distribution and have been widely analyzed with the Cole–Cole model in resistivity or conductivity forms. In this study, the Cole–Cole model was used in its conductivity form and an overlay of two individual Cole–Cole terms according to the bimodal SIP response. The double Cole–Cole model is expressed as:
where
is the chargeability [
33,
34,
35],
and
(S/m) are respectively the electrical conductivities at low (DC) and high frequencies,
and
are the time constants, and
and
are the Cole–Cole exponents that reflect the broadness of the relaxation time distribution [
36].
For simplification, the normalized chargeability (
), which is equal to the conductivity difference at high-limit and low-limit frequencies, is widely used to quantify the degree of polarization [
34,
37,
38].
According to the Schwartz equation [
31], the average particle size (
d) in the porous media can be calculated from the peak frequency (
) as:
where
(
) is the time constant and
(
) denotes the diffusion coefficient of counterions in the Stern layer, which is related to the mobility of the counterions in the Stern layer based on the Nernst–Einstein relation (
).
The ion mobility in the Stern layer is a reduction of the corresponding value in the diffuse layer by a factor of 10 (). In other words, , where is the diffusion coefficient in the diffuse layer.
3. Materials and Methodology
AC samples made from coconut shells with particle sizes in the range of 1–2 mm were provided by the Henan province of China and produced by physical steam activation at 1000 °C. The sample was directly rinsed with deionized (DI) water until the electrical conductivity of the supernatant became less than 100 μS/cm. In addition, air bubbles residing in activated carbon were removed to ensure full saturation by DI water.
The mercury intrusion porosimetry (MIP) (Micromeritics, AutoPore IV 9510) was used to measure the pore size distribution, and multipoint Brunauer–Emmett–Teller (BET) specific surface area of the samples was analyzed by nitrogen adsorption (Quantachrome, Autosorb-iQ2-mp). SEM and energy-dispersive spectroscopy (EDS) were used to observe the morphology and elemental composition of the surface using an FEI Nova 450 and Raith Elphy Quanta. X-ray diffraction (XRD) and FTIR spectroscopy were performed to obtain the crystallographic information and functional groups of the AC samples using an Escalab 250Xi spectrometer and a Thermo Scientific Nicolet iS50 FTIR.
The copper adsorption performance of AC was analyzed through batch experiments. About 10 g of AC samples was added to 250mL of a copper solution with concentrations from 20 to 700 mg L−1 and shaken at a rate of 110 rpm in a constant temperature shaker incubator. The adsorption kinetics experiments were conducted to study the factor of contact time (5, 10, 20, 30, 40, 60, 80, 130, 200, and 300 min) at 298 K with Cu(II) concentration of 60, 300, 700 mg L−1. The adsorption isotherms experiments were performed to investigate the effect of the initial concentrations (20, 40, 60, 100, 200, 300, 500, and 700 mg L−1) at the temperatures of 298, 308, 318 K. The Erlenmeyer flasks were kept shaking for 24 h to achieve equilibrium. The influence of temperature was analyzed based on the adsorption isotherms experiments.
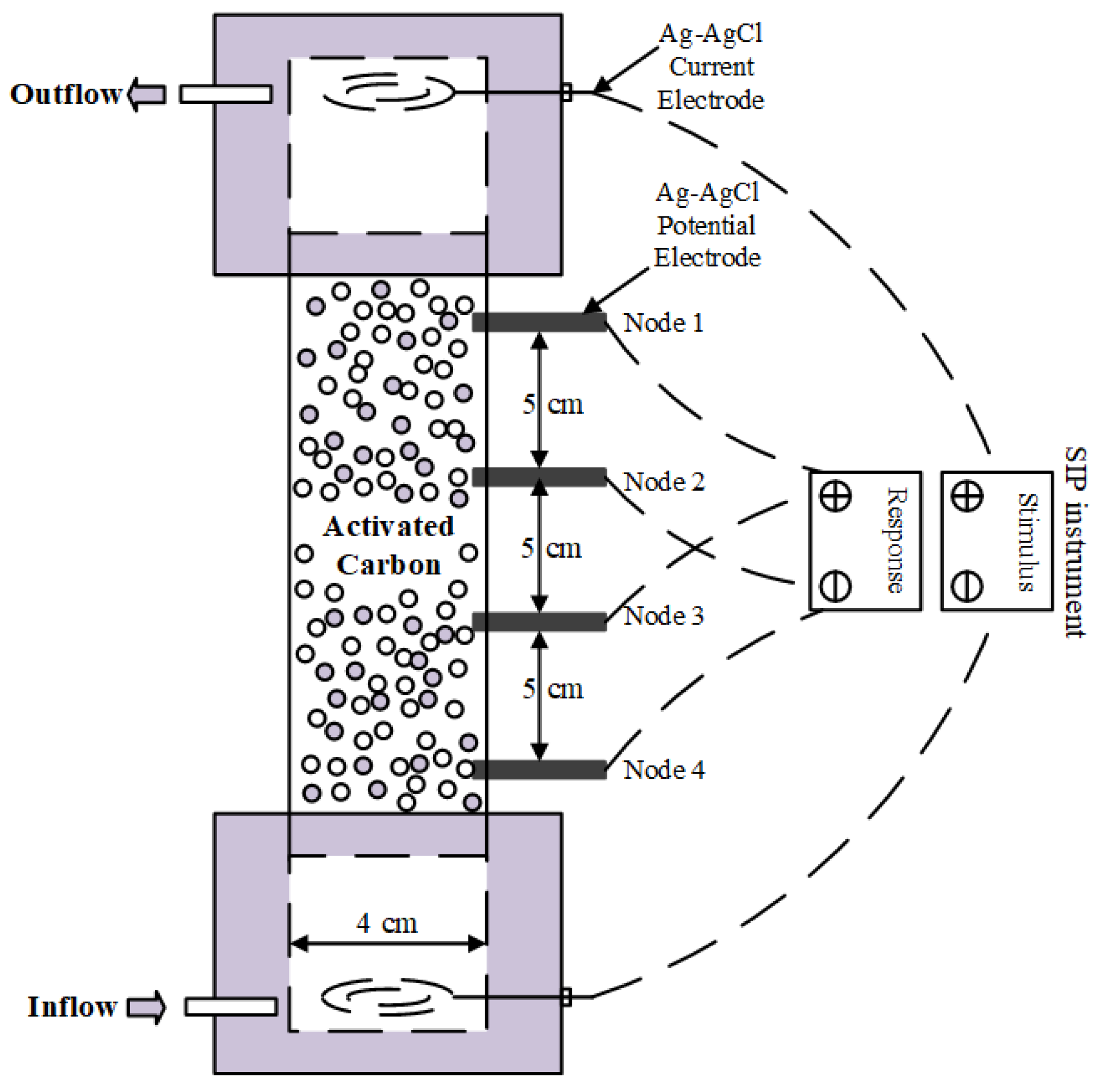
The column flow-through test was conducted as follows. The AC samples were first transferred into a SIP column of size 210 × 40 × 10 mm (length × inner diameter × thickness) using the wet packing filling method, as shown in
Figure 1. DI water was then injected into the sample with a peristaltic pump through the bottom of the column until it was fully immersed. Afterwards, three sets of experiments were performed, in which CuCl
2 solutions having concentrations of 1, 5, and 10 mmol/L were injected into the columns for 60, 30, and 30 h, respectively. During the fluid injections, SIP signals were measured using the PSIP instrument (Ontash & Ermac, Inc., River Edge, NJ, USA) within a frequency range of 0.01–1000 Hz (
Figure 1). Two pairs of electrodes were used to measure the potentials of upper (Node 1–2) and bottom (Node 3–4) of the column. The obtained complex conductivities were then further analyzed through Equations (1)–(3) in
Section 2. A constant flow rate of 1 mL/min was maintained, and the temperature was set to 25 °C. Finally, the outflow solutions were collected using an automatic collection device, and the concentrations of metal ions were measured by ICP-OES (Avio 220 Max ICP-OES Scott).
4. Results and Discussion
4.1. Characterization of AC Samples
SEM–EDS. The images of uncontaminated AC (
Figure 2) show honeycomb pores with two main pore sizes of approximately 1 μm and 20 μm (
Figure 3a,b, respectively). After the Cu
2+ contamination, Cu spots were evenly distributed on the AC surface, as shown in
Figure 2c. The EDS results show spikes in the magnitudes of Cu and Cl. The weight percentage of the chemical element constituents (
Figure 2d) shows a decrease in Al (1.35%–0.46%) and Ca (0.74%–0.52%) and an increase in Cu (0%–2.43%). This indicates that Ca
2+ was displaced by Cu
2+, most probably through a cation exchange reaction [
39], and no precipitation or crystallization occurred.
BET and MIP. The surface areas calculated using the BET and MIP methods were 132.653 m
2/g and 230 m
2/g, respectively. The pore size distribution of the AC sample obtained using MIP was trimodal, with major peaks at approximately 0.01, 1, and 100 μm, which did not change after the Cu(II) uptake, as shown in
Figure 3a. BJH and DFT methods were employed to determine the mesopore and microspore distributions in
Figure 3b. Obvious peak at 0.01 μm can be observed, which corresponds to the results in MIP methods (
Figure 3a). ImageJ was used for the pore size distribution analysis on the SEM images of the AC (
Figure 3c). This indicates the limited copper crystals or precipitate generation. The analysis results of ImageJ are consistent with the MIP results. That is, 1 μm and 10 μm were the dominant pore diameters, as shown in
Figure 3.
FTIR spectroscopy. Figure 4a shows the FTIR spectroscopy results for the pure and 10-mM contaminated AC within the wavenumber range of 400–4000 cm
−1. The adsorption at approximately 1033 cm
−1 and 1165 cm
−1 was assigned to the C–O stretching in alcohols, phenols, and carboxylic acid groups [
40,
41]. In addition, a strong bond around 1583 cm
−1 corresponded to the C=C stretching [
41,
42]. The peaks around 1687 cm
−1 were ascribed to the stretching of C=O groups [
11]. Moreover, two small peaks of absorption at 2850 cm
−1 and 2922 cm
−1 were ascribed to the asymmetric and symmetric C–H stretching, respectively [
43] (p. 283). Furthermore, another strong band at approximately 3450 cm
−1 was attributed to the vibrations of the O–H groups [
44]. After the flow-through of Cu, the results of the variations show that three main functional groups (O–H, C=C, and C=O) participated in the Cu(II) adsorption process [
12,
45].
XRD. In the XRD results shown in
Figure 4b, two broad peaks at approximately
and
, corresponding to the (0 0 2) and (1 0 0) graphitic structures [
46], were observed. A small and sharp peak at
representing the CaCO
3 crystalline phase [
47] was detected for the pure and contaminated AC. A sharp peak at
was observed in the 1-mmol/L CuCl
2 sample, which is attributed to the quartz that may originally exist in AC [
48].
4.2. Adsorption Performance
4.2.1. Adsorption Isotherms
To better understand the adsorption isotherms, Langmuir and Freundlich models are employed to fit the adsorption results by following equations:
where
and
(mg g
−1) are respectively the amounts of copper adsorbed at equilibrium and maximum adsorption capacity,
(mg L
−1) is the equilibrium concentration of adsorbate,
(L g
−1) and
(L g
−1) are Langmuir and Freundlich equilibrium constants, and 1/n is the Freundlich coefficient.
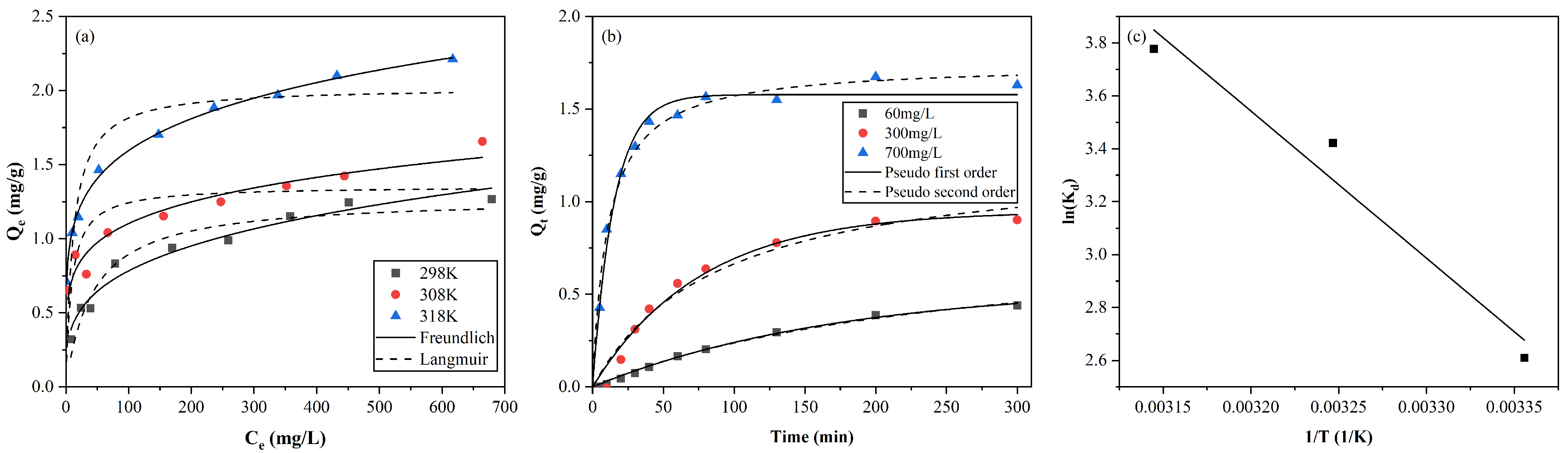
Nonlinear fitting results for the adsorption isotherms at 298 K, 308 K, 318 K were plotted in
Figure 5a with detailed parameters tabulated in
Table 1. The adsorption capacities of AC increased with the initial concentration and gradually reached equilibrium at high concentrations. It is shown that the Freundlich model represents better correlation coefficient than the Langmuir model, suggesting the adsorption process is mainly multilayer. A comparison with the maximum capacity of other adsorbents for copper adsorption is shown in
Table 2.
4.2.2. Adsorption Kinetics
The rate-determining step of adsorption process was studied using pseudo-first-order and pseudo-second-order models:
where
and
(mg/g) are respectively the amounts of copper adsorbed at time
and at equilibrium.
(min
−1) and
(g mg
−1min
−1) are the adsorption rate constants of the first-order and second-order reactions, respectively.
The adsorption kinetics fitting results of two common models are shown in
Figure 5b and the corresponding parameters were tabulated in
Table 3. In the existing experiments on the adsorption of copper by activated carbon [
49], the pseudo-second-order model exhibits better agreement with experiments results than pseudo-first-order. According to the correlation coefficients (
R2), it can be observed that the two models perform similar fitting results and both well described the kinetics processes.
4.2.3. Adsorption Thermodynamics
The relation thermodynamics parameters, such as the change in enthalpy (
, kJ mol
−1), entropy (
, kJ K
−1 mol
−1), and Gibbs energy change (
, kJ mol
−1) are calculated as follows:
where
is the thermodynamic equilibrium constant,
is constant of the best isotherm model fitted (
is replaced here),
(1 mol L
−1) is the standard concentration of the adsorbate,
(g.mol
−1) is the molecular weight of adsorbate,
(8.314 J mol
−1 K
−1) is the universal gas constant, and T (K) is the absolute temperature of the solution.
The Van ’t Hoff graph is shown in
Figure 5c and values of
and
were obtained from the slope and the intercept of line of
versus
. Detailed thermodynamic parameters are shown in
Table 4. The negative
and positive
indicate that the adsorption process of Cu
2+ is thermodynamic spontaneous and endothermic, which means that the increase in temperature benefits the adsorption process. This is consistent with the previous results of thermodynamic experiments [
49,
50]. The positive
indicates that the degree of disorder at the solid–liquid interface increases at higher temperatures, and the AC has high affinity for Cu
2+ in aqueous solution [
51].
Table 2.
Copper adsorption capacities for different adsorbents.
Table 2.
Copper adsorption capacities for different adsorbents.
| Adsorbent | Capacity (mg/g) | References |
|---|
| Granular activated carbon | 5.845 | [52] |
| Coconut shell-based carbon | 7.04 | [53] |
| Orange peel | 44.28 | [54] |
| Chitosan-coated perlite bead | 104 | [55] |
| Carbon nanofibers | 8.8 | [56] |
| Bottom ash of expired drugs incineration | 13.335 | [57] |
| Biochar made from pinewood pyrolysis | 2.73 | [58] |
| Biochar produced from wood waste | 2.9 | [59] |
| Cellulose hydrogel | 52.3 | [60] |
| Activated carbon | 2.078 | This study |
Table 3.
Kinetics parameters of Cu(II) adsorption onto AC.
Table 3.
Kinetics parameters of Cu(II) adsorption onto AC.
| Kinetics Models | Parameters | Value |
|---|
| 60 mg/L | 300 mg/L | 700 mg/L |
|---|
| Pseudo-first-order | qe (mg.g−1) | 0.546 | 0.949 | 1.578 |
| K1 (min−1) | 0.00579 | 0.0131 | 0.06536 |
| R2 | 0.995 | 0.969 | 0.988 |
| Pseudo-second-order | qe (mg.g−1) | 0.842 | 1.256 | 1.744 |
| K2 (g.mg−1min−1) | 0.00467 | 0.00894 | 0.05187 |
| R2 | 0.993 | 0.957 | 0.990 |
4.3. Geochemical Process
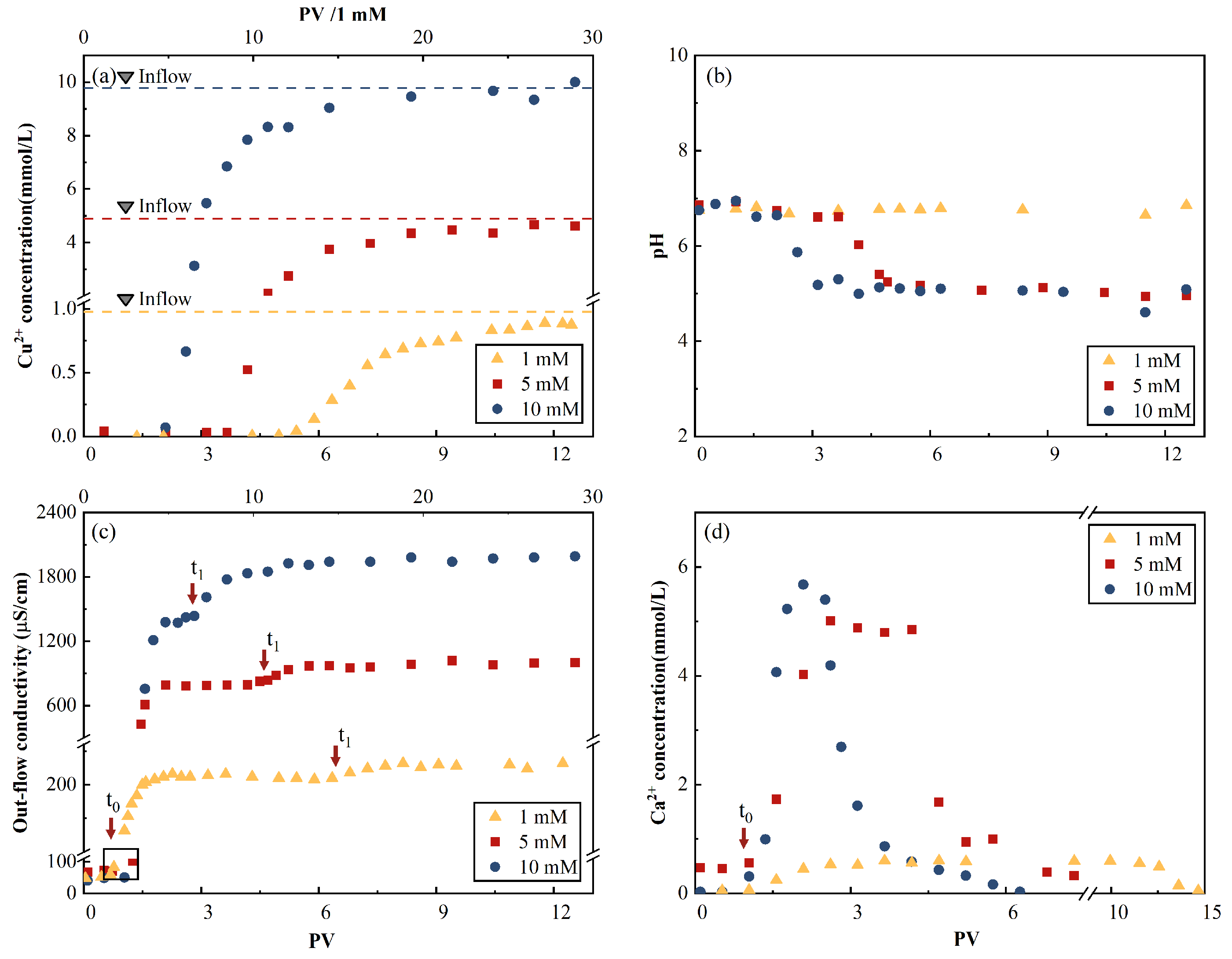
The breakthrough curve (BTC) of Cu
2+ had an S shape with a sharp initial concentration increase for the three inflow concentrations, as shown in
Figure 6. The results of cation displacement are shown in
Figure 6d. The breakthrough onset occurred at 2.2 pore volume (PV).
The effluent Ca
2+ concentrations first reached their peak values, then decreased to zero. This indicates the replacement of Ca
2+ by Cu
2+ through an ion exchange reaction in the AC matrix. Considering the 10-mM CuCl
2 influent case as an example, the peak Ca
2+ concentration occurred at 2.1 PV, which was close to the onset of the Cu
2+ breakthrough (2.1 PV) and before the inflection point (i.e., the maximal concentration increases point) of the Cu
2+ BTC (2.5 PV). A similar occurrence sequence of the peak Ca
2+ concentration, followed by the onset of the Cu
2+ breakthrough, was observed for the 1-mM and 5-mM CuCl
2 influence cases. The results indicate that after displacing a major portion of Ca
2+, which was originally in the AC samples, insufficient adsorption sites were available to contain Cu
2+. Note that this portion was approximately 50%, corresponding to the peak Ca
2+ concentration if a Gaussian distribution was assumed for the effluent Ca
2+ concentration curve. The total amounts of displaced Ca(II) ion calculated using the curve are presented in
Table 5. The ratios of the total Ca(II) ion concentration to the total adsorbed Cu(II) ion concentration were 47%, 74%, and 25%, which indicates that the Ca
2+-Cu
2+ ion exchange participated in a part of the adsorption process.
The curves of the electrical conductivity time evolution in
Figure 6c reflected the cation exchange and adsorption processes. Considering the 10-mM Cu
2+ inflow case as an example, the first electrical conductivity plateau of 2.1 PV coincided with the peak of effluent Ca
2+ concentration, and its decline almost neutralized the effluent Cu
2+ concentration, which results in a period of constant electrical conductivity (2.1–2.8 PV), as shown in
Figure 6c. The second plateau value was obtained when the effluent Cu
2+ concentration reached its maximum value of 4.2 PV.
The pH of the effluent solutions evolved from 6.7 to 7.0 to be close to that of the influent, as shown in
Table 6. This process corresponds to the previously discussed chemical reactions. Minimal variations in the 1-mmol/L concentration and fluctuations around 6.7 were observed. This can be explained by the comparable pH values of the inflow fluid and the original DI water-saturated AC background liquid of 6.09 and 6.7, respectively. Similar degrees of decline were observed from approximately 6.7 to 5 within the ranges of 2–3.6 and 3.6–5 PV for the 5-mmol/L and 10-mmol/L cases, respectively.
4.4. Adsorption Mechanism
Through the SEM–EDS methods, it can be observed that Cu2+ spots were evenly distributed on the surface of AC after adsorption. The pore size distribution measured using MIP methods remains unchanged before and after adsorption, indicating that no precipitation is formed, and the XRD results show no copper-related crystal is formed. The decrease in Ca2+ amount and increase in Cu2+ amount in EDS element analysis after contamination by copper ions indicate the ion exchange of metal ions. The increments of Ca2+ and Cu2+ ions in the effluent fluids in the column experiments further confirmed the process of ion exchange. In addition, the FTIR spectroscopy suggests that O–H, C=C, and C=O participated in the adsorption process. These function groups indicated that surface complexation could be one of the adsorption mechanisms of AC.
4.5. Typical SIP Responses
The evolution of
and
, respectively, is plotted (
Figure 7) at 1.21 Hz and 1000 Hz, where the peak responses of relaxation were not close. The typical SIP responses for three different contamination solutions are shown in
Figure 8 and
Figure 9.
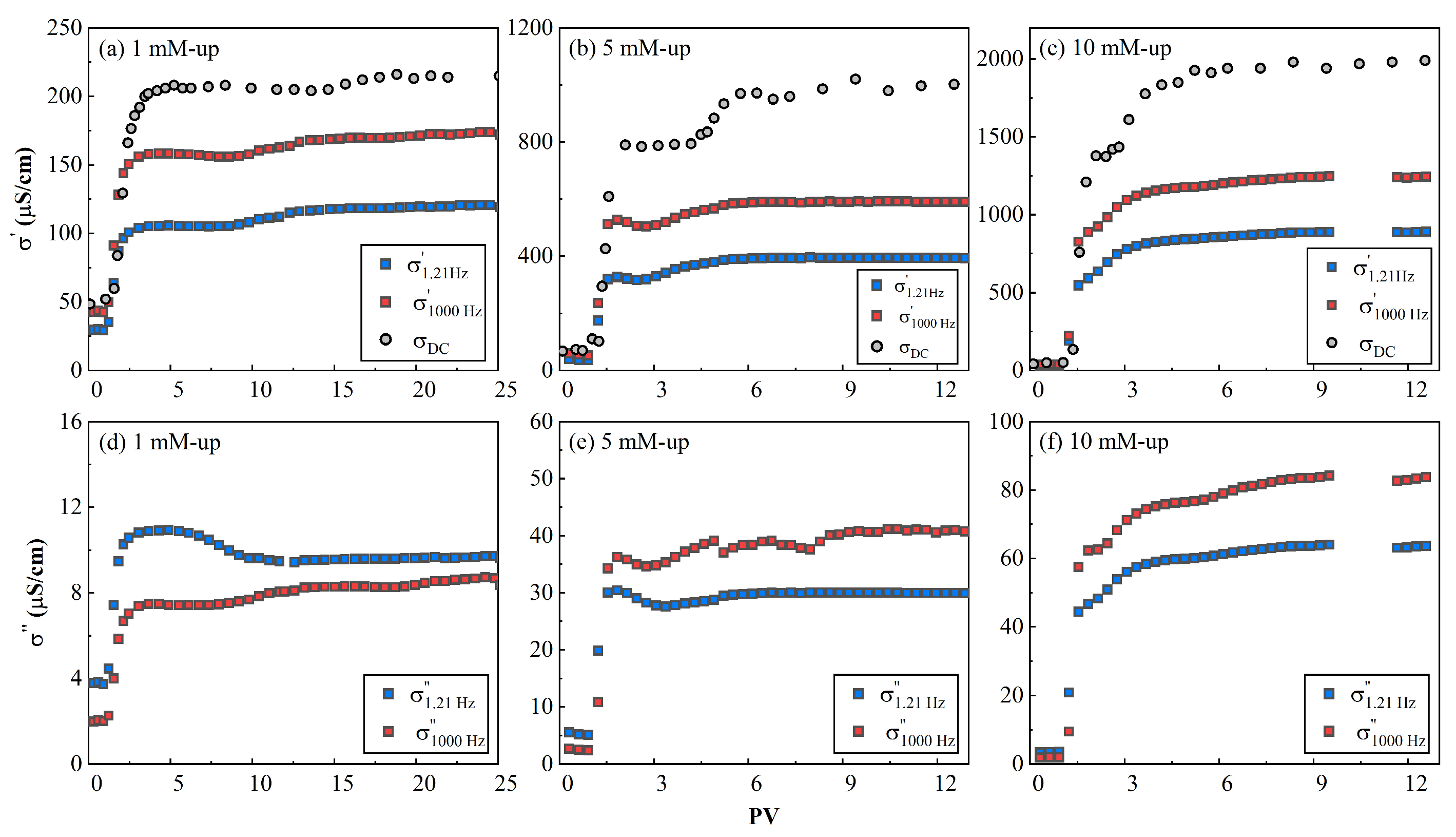
It can be seen that the value of real conductivity increased with the injection of CuCl
2 fluids (
Figure 7); that is, with the increase of salinity. After the first PV, the real conductivity (
) rapidly increased to a steady-state value, roughly from the second to the third PV (
Figure 7). Afterwards, the real conductivity steadily reached a plateau value. The increase of the inflow salinity (primarily from the CuCl
2 solutions) added more ions, which endowed the entire porous media with more conductivity. This trend was similar to that of the DC conductivity, as the real part is dominated by the pore fluid conductivity [
28]. The real component can be written as:
where
denotes the surface conductivity [
61] and
is the intrinsic formation factor.
Note that
corresponds to the EDL and comprised two parts. The first part is from the frequency-independent diffuse layer, and the second one is from the frequency-dependent Stern layer [
62]. The real part (
) had a temporal pattern, which indicates that the ion exchange process occurred before the chemical reaction reached equilibrium. It can be deduced that
can be used as an alternative method to replace the outflow conductivity and provide more real-time feedback on the inflow process.
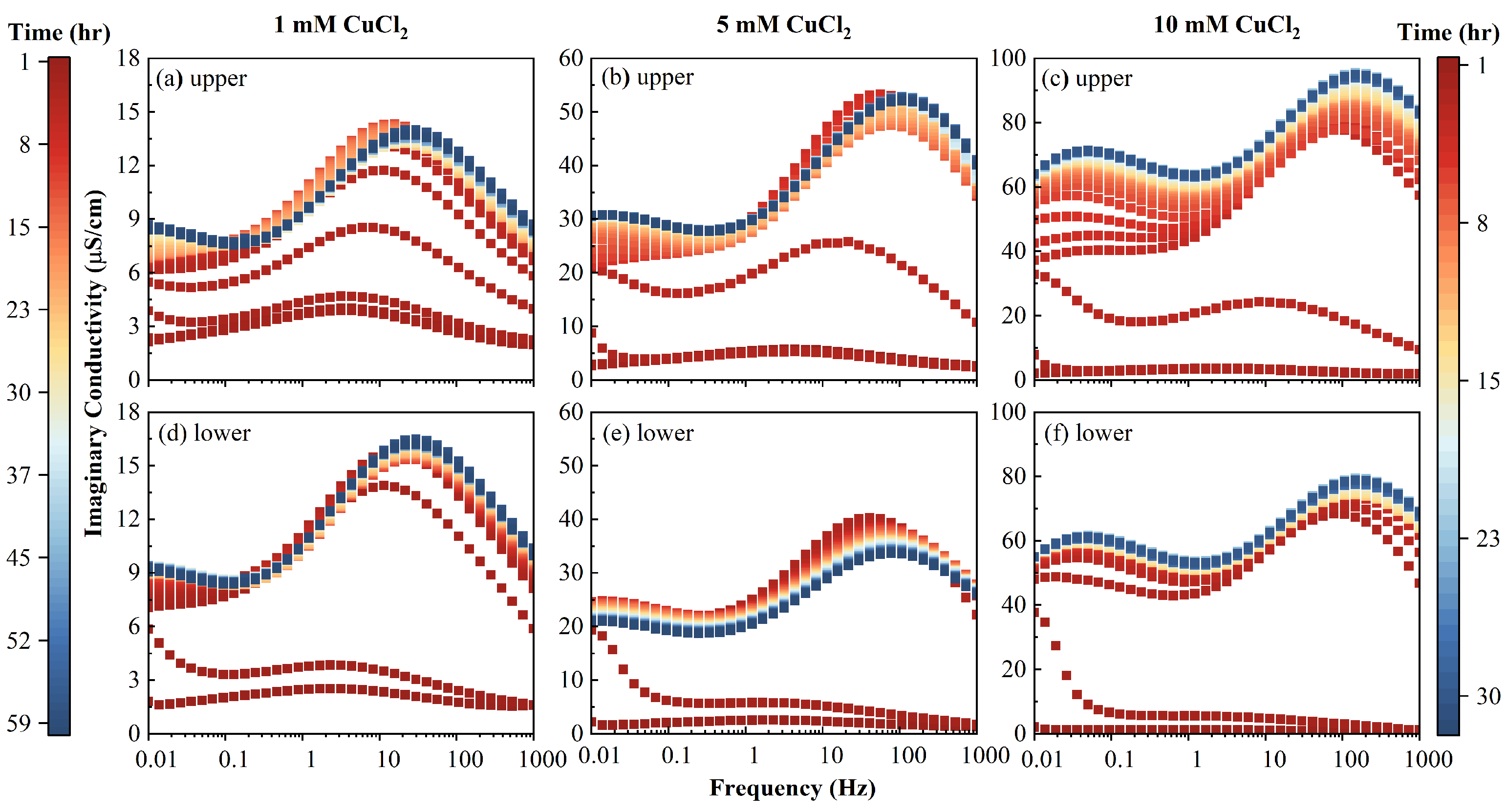
The clean initial AC imaginary conductivity had a single peak around 3 Hz. With the injection of inflow fluid,
transformed from unimodal distribution into a bimodal one, and when the PV increased, the peak frequencies shifted to high frequencies, as shown in
Figure 8. At a steady state, the characteristic frequencies at the two peaks increased with the increase of the inflow salinity, as shown in
Figure 8. For example, the peak frequencies increased from 30 to 106, then to 147 Hz, and from a value less than 0.01 to 0.01, then to 0.05 Hz, for those two peaks, respectively. When the PV increased, the magnitude of the imaginary conductivity increased for the two peaks. It can be seen from
Figure 7 that the magnitude of
was lower than that of
at a concentration of 1 mM, while that of
exceeded that of
, with an inflow salinity greater than 5 mM. This phenomenon demonstrates that Cu
2+ was mainly adsorbed and distributed in macrospores (1.21 Hz) at low salinity, as the value of imaginary conductivity reflected the polarizable charges on the surface of the porous medium.
It can be observed that
increased with the PV for most of the inflow concentrations and upper/lower portions. The only exception was the case of the 5 mM of the lower column portion shown in
Figure 8, where
first increased until 2 h, then decreased. With a continuous influent injection, the adsorbed Cu
2+ content continuously increased. This led to the increase of the number of polarizable units, which is due to the fact that the Cu
2+ adsorbed the AC macropores. A detailed discussion on the latter phenomenon is presented in
Section 4.6. A further injection of Cu
2+ can lead to a plateau in the magnitude of
and even to the decrease of
. This was possibly due to the connection of polarizable units or the diffuse layer between the AC macropores, which neutralized the dipoles comprising the EDL.
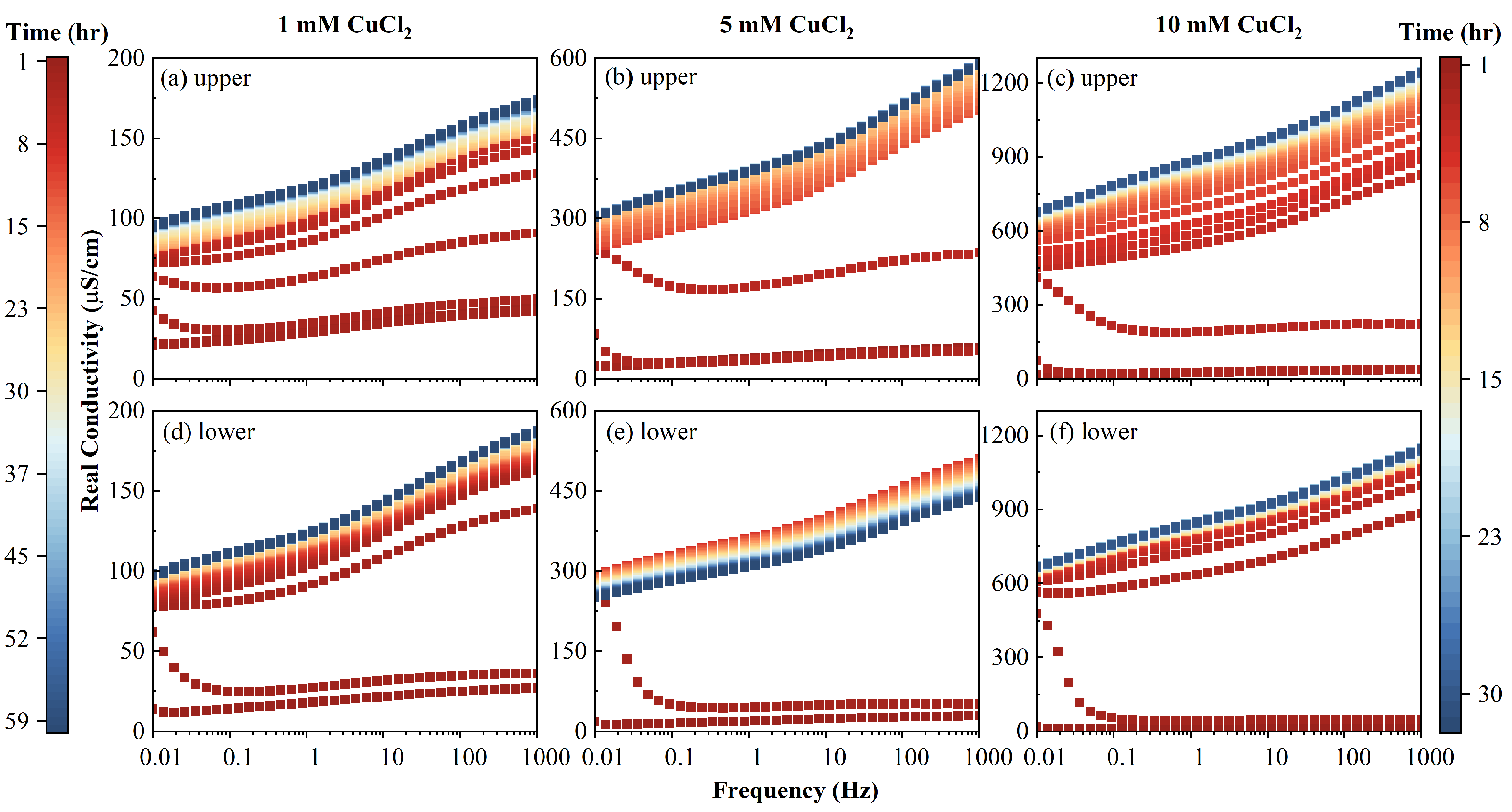
4.6. Cole–Cole Models
It can be seen from
Figure 8 and
Figure 9 that the SIP signals of the column at upper part (1–2) and lower part (3–4) show similarity, and the upper part (1–2) exhibits better performance, which is gradual. This is due to the fact that the upper part of the column is slowly infiltrated by the inflow solutions compared to the lower part. Therefore, the signals in the upper part (1–2) were employed to fit the double Cole–Cole model. The fitting results of lower part (3–4) are plotted and discussed in the
Supplementary Materials.
The time evolution of the fitting parameters for the double Cole–Cole model (Equation (2)) is shown in
Figure 10. The normalized chargeability, which represents the polarization magnitude, first increased with the inflow of CuCl
2 solution, and then became almost stable after 3–7 PVs, as shown in
Figure 10a,d. This indicates the saturation of Cu
2+ adsorption on AC. It is also deduced that the Cu
2+ BTCs reached the inflow concentration (C
0) after 4–8 PVs, which were more delayed than the
,
, and
curves. In addition,
increased with the increase of the pore fluid conductivity, which is consistent with the results obtained by previous studies [
18,
34]. The relaxation times
and
first decreased and reached equilibrium within 9–12 PVs. Similar
trends suggested a similar broadness of the relaxation time distribution in the three inflow solutions.
4.7. Discussion
4.7.1. The Normalized Chargeability vs. Content
The relationship between
and the adsorbed capacity at three salinities is shown in
Figure 11.
Figure 11a reflects the relationship between the adsorption capacity and the normalized chargeability when the adsorption reaches equilibrium. It can be seen that (1) the normalized chargeability (
) at equilibrium (
Figure 11a), which represents the content of polarizable units at the pore scale (1.7–0.6 µm) at equilibrium, was linearly proportional to the adsorbed Cu(II) (= 0.998). Similarly, the normalized chargeability (
), which represents the content of polarizable units at the macrospore scale (99–54 µm), was also linearly proportional to the adsorbed Cu(II) (
= 0.999). The linearity validated that the chargeability revealed the adsorbed Cu
2+ content at macrospores. In addition, this linearity was reported for the processes of cations adsorbed on soil, clay, and sand [
34,
63]. (2) The Cu
2+ uptakes at two scale pores were simultaneous (
Figure 11a), which indicates that when the influent concentration is increased, the distribution of the adsorbed Cu
2+ between two scales pores becomes constant. (3) The time evolution of
and
at
PV (shown in
Figure 10a,d) further corroborated the aforementioned observation, as the relative positions of
and
were maintained (i.e.,
>
) and the chargeability at a high adsorbed Cu
2+ content was high.
Figure 11b presents the evolution of the amount of adsorbate with the normalized chargeability under the three concentrations, which exhibits the effect of ion strength on
during the adsorption process compared to
Figure 11a. It can be seen that at the same adsorbed Cu
2+ content, the normalized chargeability at a high influent conductivity was also high (
Figure 11b). These mechanisms were attributed to the influence of the ionic strength of the pore fluid on the chargeability and the delayed Cu
2+ adsorption equilibrium or the early attainment of the
plateau value.
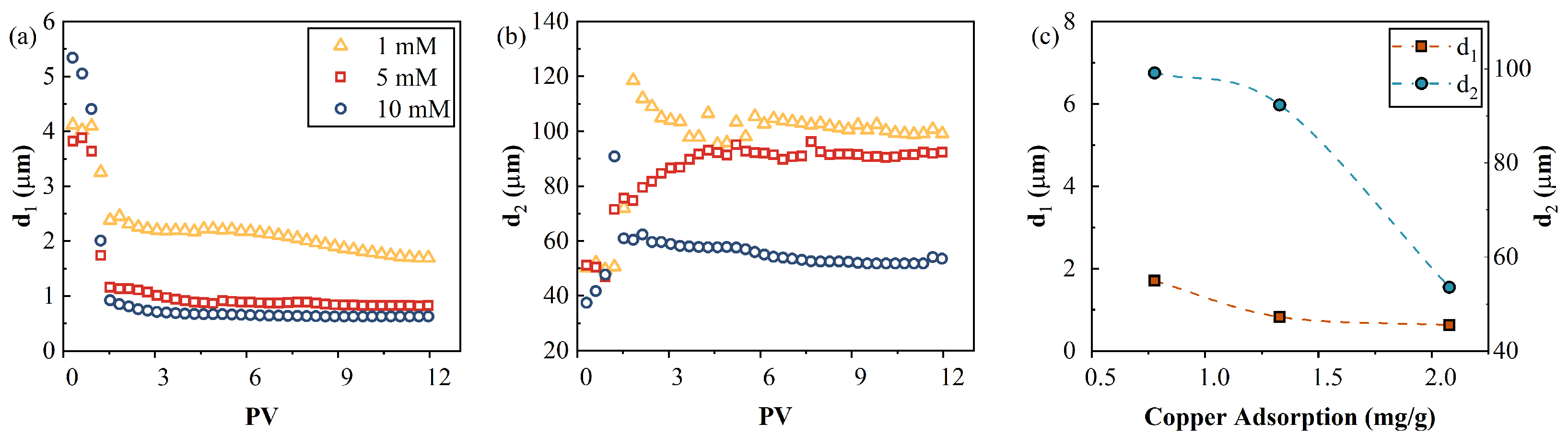
4.7.2. Calculated Pore Sizes
The characteristic polarizing unit size can be calculated using the Schwartz equation (Equation (3)) with a CuCl
2 diffusion coefficient of 1.290 × 10
−9 m
2/s [
64] at 25 °C. The average pore sizes of the imaginary conductivities at low frequencies were approximately in the ranges of 100–110, 80–90, and 53–60 µm for the 1, 5, and 10 mM influents, respectively. This falls into the average pore size range of 100 μm measured by MIP, as shown in
Figure 3. When the calculated Cu
2+ increased, the size of the characteristic polarizing units (
) decreased from 99 µm to 54 µm, as shown in
Figure 12c. No crystals were observed by SEM. Therefore, the characteristic polarizing unit should be the pores with adsorbed Cu
2+. Thus, the decreased
indicates that the adsorbed Cu
2+ migrated to small pores when the Cu
2+ influx increased. Similarly, the calculated average pore sizes (.
.) of the contaminated AC were 2, 0.8, and 0.6 µm at high frequencies of imaginary conductivities for the 1, 5, and 10mM influents, which is consistent with the average pore size of 1 μm measured by MIP in
Figure 3. The decrease of
can also be attributed to the migration of adsorbed Cu
2+ into small pores. In addition, the shrinkage of the electric diffuse layer caused by the increased ionic strength of the pore fluid may lead to the disconnection of the electric diffuse layer of adjacent pores and, consequently, a reduced polarizable unit size. The decrease of the size (corresponding to the characteristic increase of the frequency) with an increased fluid salinity is consistent with previous studies [
65,
66,
67].
5. Future Outlook
Real groundwater contaminated by mining operations is often a multi-ion system [
68], as opposed to the single-cation system analyzed in this study. The behavior of the ions may differ from that of the single-ion system. (1) In a multi-component system, the competitive adsorption effects will result in reducing the Cu
2+ uptake. (2) In general, the adsorbents obey an adsorption selectivity sequence or lyotropic series [
69]. For instance, Xue et al. [
70] conducted batch experiments to study the removal characteristics of multi-ion by basic oxygen furnace slag, and the selectivity for adsorption isotherms follows the order Cu > Cd > Pb > Zn. Park et al. [
71] evaluated the adsorption of multi-element onto sesame straw biochar with the selectivity sequence of Pb > Cu > Cr > Zn > Cd. (3) The pH will play an essential role in multi-ion systems as the proton can also compete with the adsorption [
72]. Consequently, when studying the influence of multi-ion adsorption on the SIP signal, the above factors should be considered.
6. Conclusions
This study demonstrates the ability of SIP measurements to monitor the adsorption process on AC. The batch experiments and chemical analysis were conducted to study the adsorption performance. Three concentration cases of column experiments were performed. The following conclusions were drawn:
(1) The adsorption isotherms of copper on AC follows the Freundlich model. The adsorption kinetics both follow PFO and PSO models. The adsorption thermodynamics demonstrates that the process is spontaneous and endothermic.
(2) The real and DC conductivities of effluents with 3 Cu2+ inflow concentrations showed similar trends. The electrical conductivity curves that had a temporary plateau reflected the cation exchange and adsorption processes.
(3) The normalized chargeability was proportional to the copper adsorption capacity, at either the micropores or mesopores. During the adsorption process, the distribution of adsorbed Cu2+ between the mesopores and micropores was constant.
(4) The calculated pore sizes at the 1-µm and 100-µm scales from the relaxation time of the SIP measurements were consistent with the average pore size obtained from the SEM and MIP tests. The observed decrease of the calculated size was attributed to the migration of adsorbed Cu2+ into small pores.
(5) SIP method is a viable emerging monitoring technique for monitoring the copper adsorption onto AC process, and is able to shed light on the content, signature size, and the affiliation form of Cu2+.
Author Contributions
Conceptualization, B.B.; methodology, B.B.; software, Y.Y.; validation, C.Z.; formal analysis, J.C. (Jingjing Cao); investigation, Y.Y.; resources, J.C. (Jingjing Cao); data curation, J.C. (Jingjing Cao); writing—original draft preparation, J.C. (Jingjing Cao); writing—review and editing, S.Z.; supervision, J.C. (Junnan Cao); project administration, B.B.; funding acquisition, B.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [Ministry of Science and Technology] grant number [2019YFC1805002, 2018YFC1802300], [National Natural Science Foundation of China] grant number [42177118, 51779219, 51988101], [Overseas Expertise Introduction Center for Discipline Innovation] grant number [B18047].
Data Availability Statement
Data sharing not applicable.
Acknowledgments
We sincerely acknowledge for the insightful comments of three anonymous reviewers during the process.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
An example of the 10-mM concentration fitting results is shown in
Figure A1, where the basic six Cole–Cole parameters are presented. The algorithm was coded using the Python language and modified using the pyGIMLi package, which is a Python-based open-source library for modeling and inversion. The open-source code for fitting SIP bimodal signals is available on the GitHub repository:
https://github.com/bluspi/The-double-cole-cole-model-of-SIP-based-on-pygimli (accessed on 1 January 2023). It is recommended to follow the steps and to clone the repository to your system. In addition, a simple example for the simulation of multiple sets of SIP data is provided.
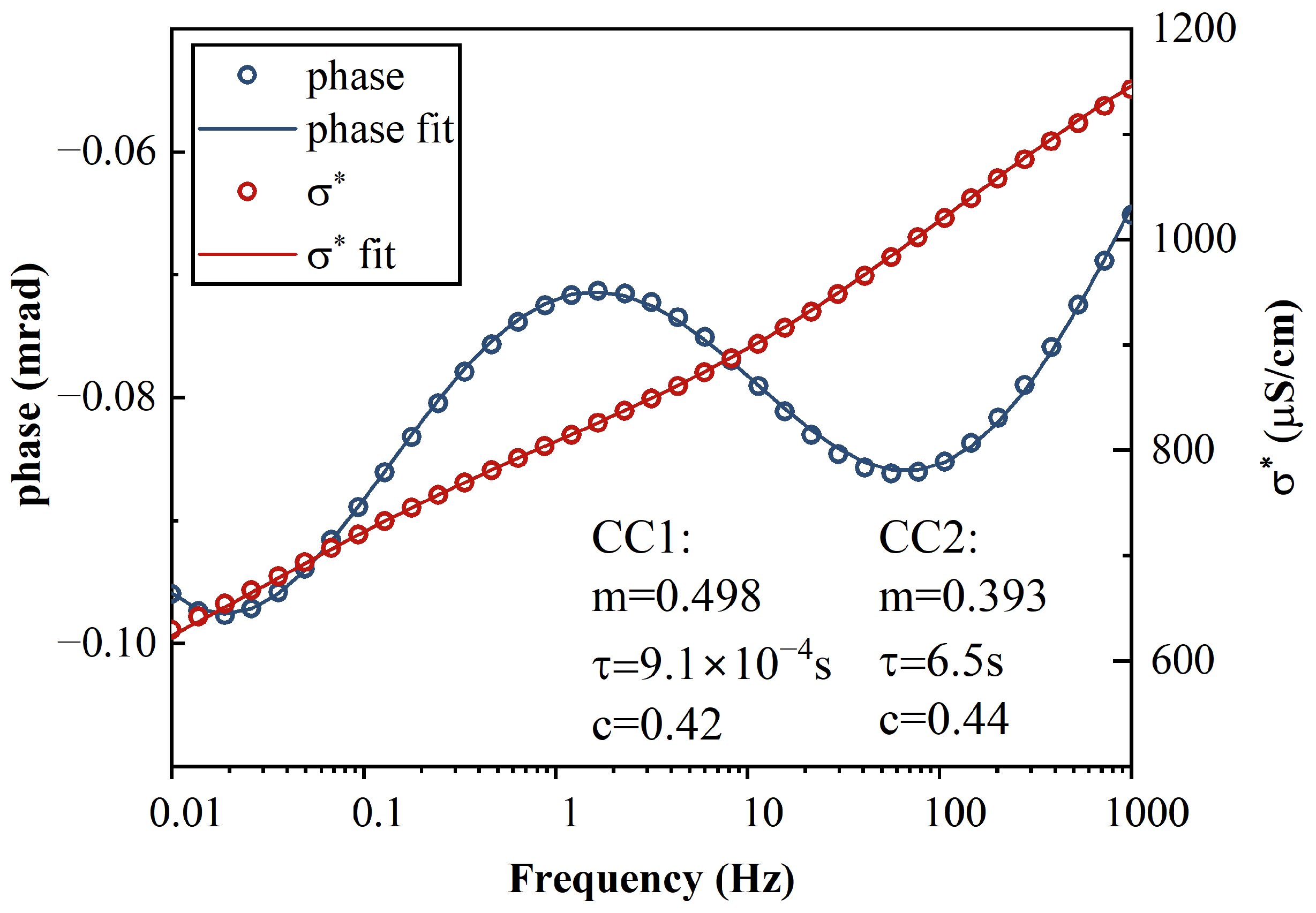
Figure A1.
Example of the fitting results and SIP responses at 10 mM equilibrium. Two sets of Cole–Cole parameters are presented.
Figure A1.
Example of the fitting results and SIP responses at 10 mM equilibrium. Two sets of Cole–Cole parameters are presented.
References
- Chen, C.-W.; Chen, C.-F.; Dong, C.-D. Copper Contamination in the Sediments of Salt River Mouth, Taiwan. Energy Procedia 2012, 16, 901–906. [Google Scholar] [CrossRef]
- Xie, S.; Yu, C.; Peng, B.; Xiao, H.; Zhang, W.; Zhou, Z.; Åström, M.E. A re-assessment of metal pollution in the Dexing mining area in Jiangxi province, China: Current status, hydro-geochemical controls, and effectiveness of remediation practices. Int. J. Environ. Sci. Technol. 2022, 19, 10707–10722. [Google Scholar] [CrossRef]
- Apori, O.S.; Hanyabui, E.; Asiamah, Y.J. Remediation Technology for Copper Contaminated Soil: A Review. Asian Soil Res. J. 2018, 8, 1–7. [Google Scholar] [CrossRef]
- Long, Y.-Y.; Hu, L.-F.; Jiang, C.-J.; Fang, C.-R.; Wang, F.-P.; Shen, D.-S. Releasing behavior of copper in recirculated bioreactor landfill. Bioresour. Technol. 2009, 100, 2419–2424. [Google Scholar] [CrossRef]
- Poudel, M.B.; Awasthi, G.P.; Kim, H.J. Novel insight into the adsorption of Cr(VI) and Pb(II) ions by MOF derived Co-Al layered double hydroxide @hematite nanorods on 3D porous carbon nanofiber network. Chem. Eng. J. 2021, 417, 129312. [Google Scholar] [CrossRef]
- Selvi, A.; Rajasekar, A.; Theerthagiri, J.; Ananthaselvam, A.; Sathishkumar, K.; Madhavan, J.; Rahman, P.K. Integrated Remediation Processes Toward Heavy Metal Removal/Recovery From Various Environments-A Review. Front. Environ. Sci. 2019, 7, 66. [Google Scholar] [CrossRef]
- Zhao, S.; Fan, L.; Zhou, M.; Zhu, X.; Li, X. Remediation of Copper Contaminated Kaolin by Electrokinetics Coupled with Permeable Reactive Barrier. Procedia Environ. Sci. 2016, 31, 274–279. [Google Scholar] [CrossRef]
- Han, Z.Y.; Lv, X.B.; Di, L. Experiment study on the remediation effects of Copper Polluted Groundwater by PRB with the volcanic as reactive medium. In Advances in Engineering Research, Proceedings of the 2018 7th International Conference on Energy and Environmental Protection (ICEEP 2018), Shenzhen, China, 14–15 July 2018; Atlantis Press: Amsterdam, The Netherlands, 2018; pp. 904–911. ISBN 978-94-6252-558-0. [Google Scholar]
- Menéndez, J.A.; Phillips, J.; Xia, B.; Radovic, L.R. On the Modification and Characterization of Chemical Surface Properties of Activated Carbon: In the Search of Carbons with Stable Basic Properties. Langmuir 1996, 12, 4404–4410. [Google Scholar] [CrossRef]
- Gundogdu, A. A new low-cost activated carbon produced from tea-industry waste for removal of Cu(II) ions from aqueous solution: Equilibrium, kinetic and thermodynamic evaluation. Karadeniz Chem. Sci. Technol. 2018, 2, 1–10. [Google Scholar]
- Xie, R.; Jin, Y.; Chen, Y.; Jiang, W. The importance of surface functional groups in the adsorption of copper onto walnut shell derived activated carbon. Water Sci. Technol. 2017, 76, 3022–3034. [Google Scholar] [CrossRef]
- Yang, X.; Wan, Y.; Zheng, Y.; He, F.; Yu, Z.; Huang, J.; Wang, H.; Ok, Y.S.; Jiang, Y.; Gao, B. Surface functional groups of carbon-based adsorbents and their roles in the removal of heavy metals from aqueous solutions: A critical review. Chem. Eng. J. 2019, 366, 608–621. [Google Scholar] [CrossRef] [PubMed]
- Rio, S.; Faur-Brasquet, C.; Le Coq, L.; Le Cloirec, P. Structure Characterization and Adsorption Properties of Pyrolyzed Sewage Sludge. Environ. Sci. Technol. 2005, 39, 4249–4257. [Google Scholar] [CrossRef] [PubMed]
- Leroy, P.; Li, S.; Jougnot, D.; Revil, A.; Wu, Y. Modeling the evolution of complex conductivity during calcite precipitation on glass beads. Geophys. J. Int. 2017, 209, 123–140. [Google Scholar] [CrossRef]
- Xing, L.; Niu, J.; Zhang, S.; Cao, S.; Wang, B.; Lao, L.; Wei, W.; Han, W.; Ge, X.; Wei, Z. Experimental study on hydrate saturation evaluation based on complex electrical conductivity of porous media. J. Pet. Sci. Eng. 2022, 208, 109539. [Google Scholar] [CrossRef]
- Albrecht, R.; Gourry, J.C.; Simonnot, M.-O.; Leyval, C. Complex conductivity response to microbial growth and biofilm formation on phenanthrene spiked medium. J. Appl. Geophys. 2011, 75, 558–564. [Google Scholar] [CrossRef]
- Davis, C.A.; Atekwana, E.; Atekwana, E.; Slater, L.D.; Rossbach, S.; Mormile, M.R. Microbial growth and biofilm formation in geologic media is detected with complex conductivity measurements. Geophys. Res. Lett. 2006, 33, L18403. [Google Scholar] [CrossRef]
- Joo, H.-W.; Kwon, T.-H.; Lee, S.-R.; Wu, Y. Relaxation behavior in low-frequency complex conductivity of sands caused by bacterial growth and biofilm formation by Shewanella oneidensis under a high-salinity condition. Geophysics 2021, 86, B389–B400. [Google Scholar] [CrossRef]
- Gao, Z.; Haegel, F.-H.; Huisman, J.A.; Esser, O.; Zimmermann, E.; Vereecken, H. Spectral induced polarization for the characterisation of biochar in sand. Near Surf. Geophys. 2017, 15, 645–656. [Google Scholar] [CrossRef]
- Hao, N.; Cao, J.; Ye, J.; Zhang, C.; Li, C.; Bate, B. Content and morphology of lead remediated by activated carbon and biochar: A spectral induced polarization study. J. Hazard. Mater. 2021, 411, 124605. [Google Scholar] [CrossRef]
- Kirmizakis, P.; Kalderis, D.; Ntarlagiannis, D.; Soupios, P. Preliminary assessment on the application of biochar and spectral-induced polarization for wastewater treatment. Near Surf. Geophys. 2020, 18, 109–122. [Google Scholar] [CrossRef]
- Bate, B.; Cao, J.; Zhang, C.; Hao, N. Spectral induced polarization study on enzyme induced carbonate precipitations: Influences of size and content on stiffness of a fine sand. Acta Geotech. 2021, 16, 841–857. [Google Scholar] [CrossRef]
- Wu, Y.; Hubbard, S.; Williams, K.; Ajo-Franklin, J. On the complex conductivity signatures of calcite precipitation. J. Geophys. Res. Biogeosciences 2010, 115. [Google Scholar] [CrossRef]
- Ben Moshe, S.; Furman, A. Real-time monitoring of organic contaminant adsorption in activated carbon filters using spectral induced polarization. Water Res. 2022, 212, 118103. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, N.; Furman, A. Spectral induced polarization signature of soil contaminated by organic pollutant: Experiment and modeling. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Masi, M.; Losito, G. Spectral induced polarization for monitoring electrokinetic remediation processes. J. Appl. Geophys. 2015, 123, 284–294. [Google Scholar] [CrossRef]
- Ben Moshe, S.; Kessouri, P.; Erlich, D.; Furman, A. Geophysically based analysis of breakthrough curves and ion exchange processes in soil. Hydrol. Earth Syst. Sci. 2021, 25, 3041–3052. [Google Scholar] [CrossRef]
- Hao, N.; You, Y.; Zhan, L.-T.; Bate, B. Evaluation of aqueous Cd2+ and Pb2+ removal by natural loess using spectral induced polarization and microscopic characterization. Environ. Sci. Pollut. Res. 2022, 29, 50500–50514. [Google Scholar] [CrossRef]
- Siddiq, M.; Tawabini, B.; Kirmizakis, P.; Kalderis, D.; Ntarlagiannis, D.; Soupios, P. Combining geophysics and material science for environmental remediation: Real-time monitoring of Fe-biochar arsenic wastewater treatment. Chemosphere 2021, 284, 131390. [Google Scholar] [CrossRef]
- Revil, A.; Florsch, N. Determination of permeability from spectral induced polarization in granular media. Geophys. J. Int. 2010, 181, 1480–1498. [Google Scholar] [CrossRef]
- Schwarz, G. A THEORY OF THE LOW-FREQUENCY DIELECTRIC DISPERSION OF COLLOIDAL PARTICLES IN ELECTROLYTE SOLUTION 1,2. J. Phys. Chem. 1962, 66, 2636–2642. [Google Scholar] [CrossRef]
- Bücker, M.; Orozco, A.F.; Undorf, S.; Kemna, A. On the Role of Stern- and Diffuse-Layer Polarization Mechanisms in Porous Media. J. Geophys. Res. Solid Earth 2019, 124, 5656–5677. [Google Scholar] [CrossRef]
- Revil, A.; Florsch, N.; Camerlynck, C. Spectral induced polarization porosimetry. Geophys. J. Int. 2014, 198, 1016–1033. [Google Scholar] [CrossRef]
- Revil, A.; Coperey, A.; Shao, Z.; Florsch, N.; Fabricius, I.L.; Deng, Y.; Delsman, J.R.; Pauw, P.S.; Karaoulis, M.; De Louw, P.G.B.; et al. Complex conductivity of soils. Water Resour. Res. 2017, 53, 7121–7147. [Google Scholar] [CrossRef]
- Seigel, H.O. Mathematical Formulation and Type Curves for Induced Polarization. Geophysics 1959, 24, 547–565. [Google Scholar] [CrossRef]
- Tarasov, A.; Titov, K. On the use of the Cole–Cole equations in spectral induced polarization. Geophys. J. Int. 2013, 195, 352–356. [Google Scholar] [CrossRef]
- Gao, Z.; Haegel, F.; Esser, O.; Zimmermann, E.; Vereecken, H.; Huisman, J. Spectral Induced Polarization of Biochar in Variably Saturated Soil. Vadose Zone J. 2019, 18, 1–13. [Google Scholar] [CrossRef]
- Weller, A.; Slater, L.; Nordsiek, S.; Ntarlagiannis, D. On the estimation of specific surface per unit pore volume from induced polarization: A robust empirical relation fits multiple data sets. Geophysics 2010, 75, WA105–WA112. [Google Scholar] [CrossRef]
- Mariana, M.; HPS, A.K.; Mistar, E.; Yahya, E.B.; Alfatah, T.; Danish, M.; Amayreh, M. Recent advances in activated carbon modification techniques for enhanced heavy metal adsorption. J. Water Process Eng. 2021, 43, 102221. [Google Scholar] [CrossRef]
- Allwar, A. Characteristics of Pore Structures and Surface Chemistry of Activated Carbons by Physisorption, Ftir and Boehm Methods. IOSR J. Appl. Chem. 2012, 2, 09–15. [Google Scholar] [CrossRef]
- Bakti, A.I.; Gareso, P.L. Characterization of Active Carbon Prepared from Coconuts Shells using FTIR, XRD and SEM Techniques. J. Ilm. Pendidik. Fis. Al-Biruni 2018, 7, 33–39. [Google Scholar] [CrossRef]
- Mopoung, S.; Moonsri, P.; Palas, W.; Khumpai, S. Characterization and Properties of Activated Carbon Prepared from Tamarind Seeds by KOH Activation for Fe(III) Adsorption from Aqueous Solution. Sci. World J. 2015, 2015, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Ali, R.; Aslam, Z.; Shawabkeh, R.A.; Asghar, A.; Hussein, I.A. BET, FTIR, and RAMAN characterizations of activated carbon from wasteoil fly ash. Turk. J. Chem. 2020, 44, 279–295. [Google Scholar] [CrossRef] [PubMed]
- Demiral, I.; Samdan, C.; Demiral, H. Enrichment of the surface functional groups of activated carbon by modification method. Surfaces Interfaces 2020, 22, 100873. [Google Scholar] [CrossRef]
- Hotová, G.; Slovák, V.; Zelenka, T.; Maršálek, R.; Parchaňská, A. The role of the oxygen functional groups in adsorption of copper (II) on carbon surface. Sci. Total. Environ. 2019, 711, 135436. [Google Scholar] [CrossRef]
- Omri, A.; Benzina, M. Characterization of activated carbon prepared from a new raw lignocellulosic material: Ziziphus spina-christi seeds. J. De La Société Chim. De Tunis. 2012, 14, 175–183. [Google Scholar]
- Luo, X.; Song, X.; Cao, Y.; Song, L.; Bu, X. Investigation of calcium carbonate synthesized by steamed ammonia liquid waste without use of additives. RSC Adv. 2020, 10, 7976–7986. [Google Scholar] [CrossRef]
- Peternela, J.; Silva, M.F.; Vieira, M.; Bergamasco, R.; Vieira, A.M.S. Synthesis and Impregnation of Copper Oxide Nanoparticles on Activated Carbon through Green Synthesis for Water Pollutant Removal. Mater. Res. 2017, 21. [Google Scholar] [CrossRef]
- Chen, W.-S.; Chen, Y.-C.; Lee, C.-H. Modified Activated Carbon for Copper Ion Removal from Aqueous Solution. Processes 2022, 10, 150. [Google Scholar] [CrossRef]
- Demiral, H.; Güngör, C. Adsorption of copper(II) from aqueous solutions on activated carbon prepared from grape bagasse. J. Clean. Prod. 2016, 124, 103–113. [Google Scholar] [CrossRef]
- Poudel, M.B.; Shin, M.; Kim, H.J. Interface engineering of MIL-88 derived MnFe-LDH and MnFe2O3 on three-dimensional carbon nanofibers for the efficient adsorption of Cr(VI), Pb(II), and As(III) ions. Sep. Purif. Technol. 2022, 287, 120463. [Google Scholar] [CrossRef]
- Sulaymon, A.H.; Abid, B.A.; Al-Najar, J.A. Removal of lead copper chromium and cobalt ions onto granular activated carbon in batch and fixed-bed adsorbers. Chem. Eng. J. 2009, 155, 647–653. [Google Scholar] [CrossRef]
- Chu, K.H.; Hashim, M.A. Adsorption of copper(II) and EDTA-chelated copper(II) onto granular activated carbons. J. Chem. Technol. Biotechnol. 2000, 75, 1054–1060. [Google Scholar] [CrossRef]
- Feng, N.-C.; Guo, X. Characterization of adsorptive capacity and mechanisms on adsorption of copper, lead and zinc by modified orange peel. Trans. Nonferrous Met. Soc. China 2012, 22, 1224–1231. [Google Scholar] [CrossRef]
- Hasan, S.; Ghosh, T.K.; Viswanath, D.S.; Boddu, V.M. Dispersion of chitosan on perlite for enhancement of copper(II) adsorption capacity. J. Hazard. Mater. 2007, 152, 826–837. [Google Scholar] [CrossRef] [PubMed]
- García-Díaz, I.; López, F.A.; Alguacil, F.J. Carbon Nanofibers: A New Adsorbent for Copper Removal from Wastewater. Metals 2018, 8, 914. [Google Scholar] [CrossRef]
- Benzaoui, T.; Selatnia, A.; Djabali, D. Adsorption of copper (II) ions from aqueous solution using bottom ash of expired drugs incineration. Adsorpt. Sci. Technol. 2017, 36, 114–129. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, F.-S.; Wu, J. Characterization and application of chars produced from pinewood pyrolysis and hydrothermal treatment. Fuel 2010, 89, 510–514. [Google Scholar] [CrossRef]
- Tomczyk, A.; Sokołowska, Z.; Boguta, P. Biomass type effect on biochar surface characteristic and adsorption capacity relative to silver and copper. Fuel 2020, 278, 118168. [Google Scholar] [CrossRef]
- Teow, Y.H.; Kam, L.M.; Mohammad, A.W. Synthesis of cellulose hydrogel for copper (II) ions adsorption. J. Environ. Chem. Eng. 2018, 6, 4588–4597. [Google Scholar] [CrossRef]
- Niu, Q.; Revil, A.; Saidian, M. Salinity dependence of the complex surface conductivity of the Portland sandstone. Geophysics 2016, 81, D125–D140. [Google Scholar] [CrossRef]
- Ghorbani, A.; Revil, A.; Coperey, A.; Soueid Ahmed, A.S.; Roque, S.; Heap, M.J.; Grandis, H.; Viveiros, F. Complex conductivity of volcanic rocks and the geophysical mapping of alteration in volcanoes. J. Volcanol. Geotherm. Res. 2018, 357, 106–127. [Google Scholar] [CrossRef]
- Ahmed, A.S.; Revil, A.; Abdulsamad, F.; Steck, B.; Vergniault, C.; Guihard, V. Induced polarization as a tool to non-intrusively characterize embankment hydraulic properties. Eng. Geol. 2020, 271, 105604. [Google Scholar] [CrossRef]
- Ribeiro, A.; Esteso, M.A.; Lobo, V.; Valente, A.; Simoes, S.; Sobral, A.; Burrows, H. Diffusion Coefficients of Copper Chloride in Aqueous Solutions at 298.15 K and 310.15 K. J. Chem. Eng. Data 2005, 50, 1986–1990. [Google Scholar] [CrossRef]
- Feng, L.; Li, Q.; Cameron, S.D.; He, K.; Colby, R.; Walker, K.M.; Deckman, H.W.; Ertaş, D. Quantifying Induced Polarization of Conductive Inclusions in Porous Media and Implications for Geophysical Measurements. Sci. Rep. 2020, 10, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Gurin, G.; Titov, K.; Ilyin, Y.; Tarasov, A. Induced polarization of disseminated electronically conductive minerals: A semi-empirical model. Geophys. J. Int. 2015, 200, 1555–1565. [Google Scholar] [CrossRef]
- Martin, T.; Weller, A.; Behling, L. Desaturation effects of pyrite–sand mixtures on induced polarization signals. Geophys. J. Int. 2021, 228, 275–290. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, P.; Gojenko, B.; Yu, J.; Wei, L.; Luo, D.; Xiao, T. A review of water pollution arising from agriculture and mining activities in Central Asia: Facts, causes and effects. Environ. Pollut. 2021, 291, 118209. [Google Scholar] [CrossRef] [PubMed]
- Jalali, M.; Arian, T.M.; Ranjbar, F. Selectivity coefficients of K, Na, Ca, and Mg in binary exchange systems in some calcareous soils. Environ. Monit. Assess. 2020, 192, 1–14. [Google Scholar] [CrossRef]
- Xue, Y.; Hou, H.; Zhu, S. Competitive adsorption of copper(II), cadmium(II), lead(II) and zinc(II) onto basic oxygen furnace slag. J. Hazard. Mater. 2009, 162, 391–401. [Google Scholar] [CrossRef]
- Park, J.-H.; Ok, Y.S.; Kim, S.-H.; Cho, J.-S.; Heo, J.-S.; Delaune, R.D.; Seo, D.-C. Competitive adsorption of heavy metals onto sesame straw biochar in aqueous solutions. Chemosphere 2016, 142, 77–83. [Google Scholar] [CrossRef]
- Mahdi, Z.; Yu, Q.J.; El Hanandeh, A. Competitive adsorption of heavy metal ions (Pb2+, Cu2+, and Ni2+) onto date seed biochar: Batch and fixed bed experiments. Sep. Sci. Technol. 2018, 54, 888–901. [Google Scholar] [CrossRef]
Figure 1.
SIP column for the flow-through experiment.
Figure 1.
SIP column for the flow-through experiment.
Figure 2.
SEM images of the (a,b) pores on the pure AC. (c) SEM–EDS images of AC contaminated by 10-mM Cu. (d) EDS analysis of pure and contaminated AC samples.
Figure 2.
SEM images of the (a,b) pores on the pure AC. (c) SEM–EDS images of AC contaminated by 10-mM Cu. (d) EDS analysis of pure and contaminated AC samples.
Figure 3.
Pore size distribution of (a) clean and polluted AC during 5-mmol/L adsorption using MIP and (b) clean AC sample using BJH and DFT measurements (represented by the left and right vertical axes, respectively). (c) ImageJ analysis of SEM results for the clean AC sample.
Figure 3.
Pore size distribution of (a) clean and polluted AC during 5-mmol/L adsorption using MIP and (b) clean AC sample using BJH and DFT measurements (represented by the left and right vertical axes, respectively). (c) ImageJ analysis of SEM results for the clean AC sample.
Figure 4.
(a) FTIR results of AC permeated with CuCl2 solutions. (b) XRD image of AC at different Cu(II) concentrations.
Figure 4.
(a) FTIR results of AC permeated with CuCl2 solutions. (b) XRD image of AC at different Cu(II) concentrations.
Figure 5.
Adsorption (a) isotherms at 298, 308, 318 K, and (b) kinetic, and (c) thermodynamics studies for adsorption of Cu(II) on AC.
Figure 5.
Adsorption (a) isotherms at 298, 308, 318 K, and (b) kinetic, and (c) thermodynamics studies for adsorption of Cu(II) on AC.
Figure 6.
Time evolution of the outflow properties. (a) Cu2+ concentration, (b) pH, (c) electrical conductivity, and (d) Ca2+ concentration. Note: the two-segment x-axis scale is used for a better illustration of the results for the 1-mM CuCl2 influent case.
Figure 6.
Time evolution of the outflow properties. (a) Cu2+ concentration, (b) pH, (c) electrical conductivity, and (d) Ca2+ concentration. Note: the two-segment x-axis scale is used for a better illustration of the results for the 1-mM CuCl2 influent case.
Figure 7.
Evolution of the (a–c) real and (d–f) imaginary conductivities with time of the column at upper part in three different concentration solutions at 1.21 Hz and 1000 Hz. Note: the x-axis scale used for the 1-mM CuCl2 case is different from that used for the other cases.
Figure 7.
Evolution of the (a–c) real and (d–f) imaginary conductivities with time of the column at upper part in three different concentration solutions at 1.21 Hz and 1000 Hz. Note: the x-axis scale used for the 1-mM CuCl2 case is different from that used for the other cases.
Figure 8.
Evolutions of imaginary conductivities versus time measured of the column at (a–c) upper part using electrodes 1–2, and (d–f) lower part using electrodes 3–4. Time scale of 60 h for 1 mM and 30 h for 5 and 10 mM.
Figure 8.
Evolutions of imaginary conductivities versus time measured of the column at (a–c) upper part using electrodes 1–2, and (d–f) lower part using electrodes 3–4. Time scale of 60 h for 1 mM and 30 h for 5 and 10 mM.
Figure 9.
Evolutions of real conductivities versus time measured of the column at (a–c) upper part using electrodes 1–2, and (d–f) lower part using electrodes 3–4. Time scale of 60 h for 1 mM and 30 h for 5 and 10 mM.
Figure 9.
Evolutions of real conductivities versus time measured of the column at (a–c) upper part using electrodes 1–2, and (d–f) lower part using electrodes 3–4. Time scale of 60 h for 1 mM and 30 h for 5 and 10 mM.
Figure 10.
Parameters of the double Cole–Cole model function of time. (a,d) the normalized chargeability (), (b,e) the relaxation time (), and (c,f) the exponent at high and low peak frequencies, respectively.
Figure 10.
Parameters of the double Cole–Cole model function of time. (a,d) the normalized chargeability (), (b,e) the relaxation time (), and (c,f) the exponent at high and low peak frequencies, respectively.
Figure 11.
(a) Relationships between the copper adsorption capacity and normalized chargeability, and (the dotted line shows the linear fitting results). (b) The dynamic evolution process of , and versus the copper uptake at each concentrations.
Figure 11.
(a) Relationships between the copper adsorption capacity and normalized chargeability, and (the dotted line shows the linear fitting results). (b) The dynamic evolution process of , and versus the copper uptake at each concentrations.
Figure 12.
(a,b) Two scale pores calculated using the Cole–Cole model as a function of PV, and (c) relationship between the pore sizes ( and ) and the copper adsorption content at equilibrium. Note that the dotted lines are an eye guide.
Figure 12.
(a,b) Two scale pores calculated using the Cole–Cole model as a function of PV, and (c) relationship between the pore sizes ( and ) and the copper adsorption content at equilibrium. Note that the dotted lines are an eye guide.
Table 1.
Fitting parameters of Langmuir and Freundlich isotherm models.
Table 1.
Fitting parameters of Langmuir and Freundlich isotherm models.
| Isotherm Models | Parameters | Temperature |
|---|
| 298 K | 308 K | 318 K |
|---|
| Langmuir | qm (mg g−1) | 1.28 | 1.354 | 2.023 |
| KL (L g−1) | 0.02332 | 0.11145 | 0.08725 |
| R2 | 0.941 | 0.600 | 0.793 |
| Freundlich | n | 3.556 | 5.569 | 5.484 |
| KF (L g−1) | 0.214 | 0.482 | 0.689 |
| R2 | 0.968 | 0.939 | 0.997 |
Table 4.
Thermodynamics parameters of Cu(II) adsorption on AC.
Table 4.
Thermodynamics parameters of Cu(II) adsorption on AC.
| | ΔG (kJ mol−1) | ΔH (kJ mol−1) | ΔS (J mol−1K−1) |
|---|
| 298 K | −6.46 | 46.24 | 177.41 |
| 308 K | −8.76 |
| 318 K | −9.99 |
Table 5.
Calculated amount of Ca2+ displaced by Cu2+.
Table 5.
Calculated amount of Ca2+ displaced by Cu2+.
| | Concentration | Ca (mg/g) |
|---|
| Parameters | |
|---|
| 1 mmol/L | 0.226 |
| 5 mmol/L | 0.616 |
| 10 mmol/L | 0.316 |
Table 6.
Parameters of different concentrations of inflow CuCl2 solutions.
Table 6.
Parameters of different concentrations of inflow CuCl2 solutions.
| | Concentration | 1 mmol/L | 5 mmol/L | 10 mmol/L |
|---|
| Parameters | |
|---|
| DC conductivity (μS/cm) | 221 | 983 | 2040 |
| pH | 6.092 | 5.308 | 5.143 |
| Concentration (mg/L) | 62.56 | 312.7 | 625.8 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).