Reducing Virus Transmission from Heating, Ventilation, and Air Conditioning Systems of Urban Subways
Abstract
1. Introduction
2. Numerical Method and Simulation Setup
2.1. Formulation of the Subway HVAC Air Flows in the Cabin
2.2. Numerical Technique and Boundary Conditions
2.3. Numerical Technique and Boundary Conditions
2.4. Modelling of Aerosol
3. Results and Discussion
3.1. Infected Individual Breathing near the Supply and Exhaust Ducts (Cases 1 and 2)
3.2. Infected Individual Breathing near the Fresh-Air Ducts (Cases 3 and 4)
3.3. Infected Individual Breathes near the Recirculated Ducts (Cases 5 and 6)
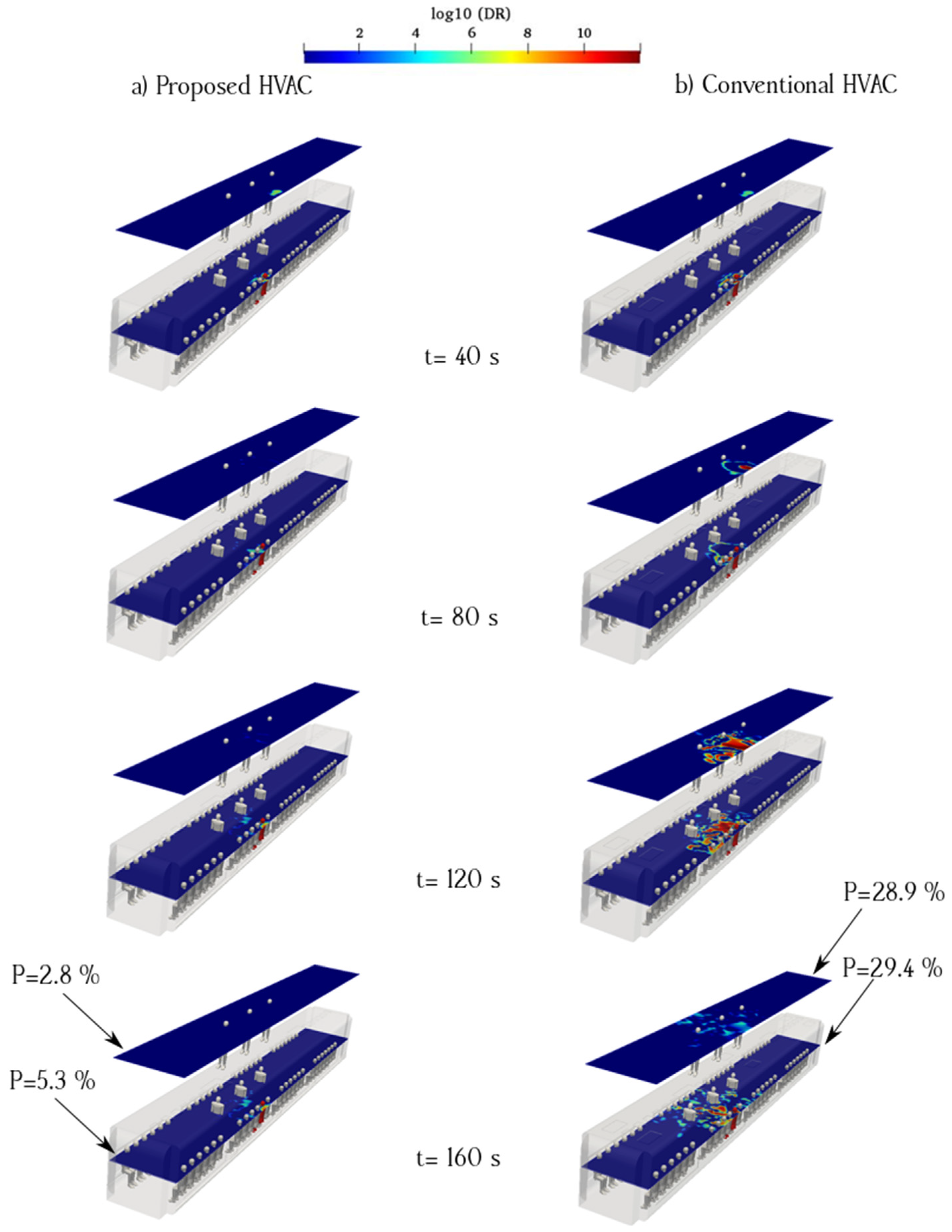
3.4. General Comparison of Cases 1 to 6
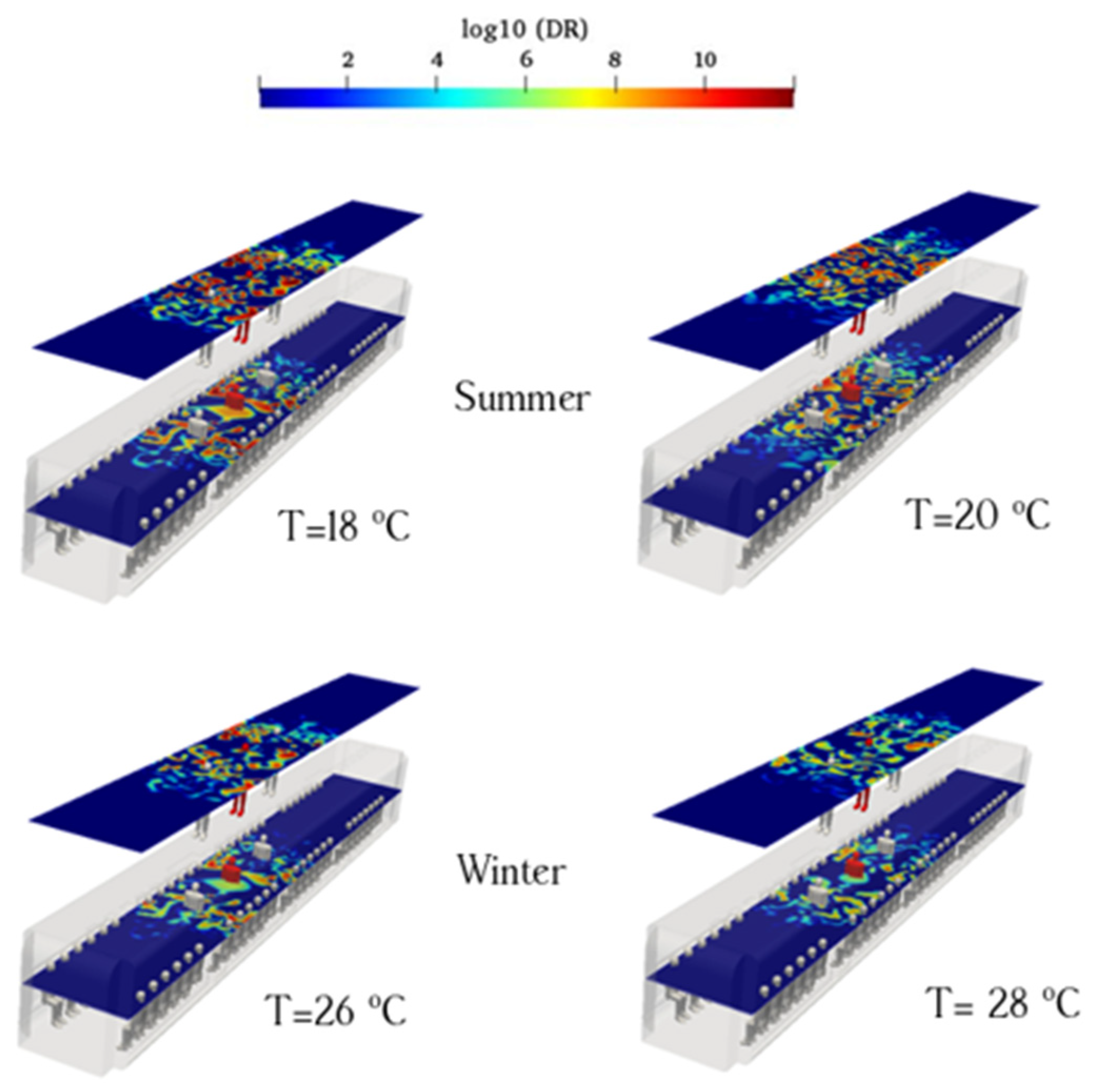
3.5. Effect of Supply Temperature of HVAC for Case 3
3.6. Effect of Supply Air change Rate (ACR) of HVAC for Case 3
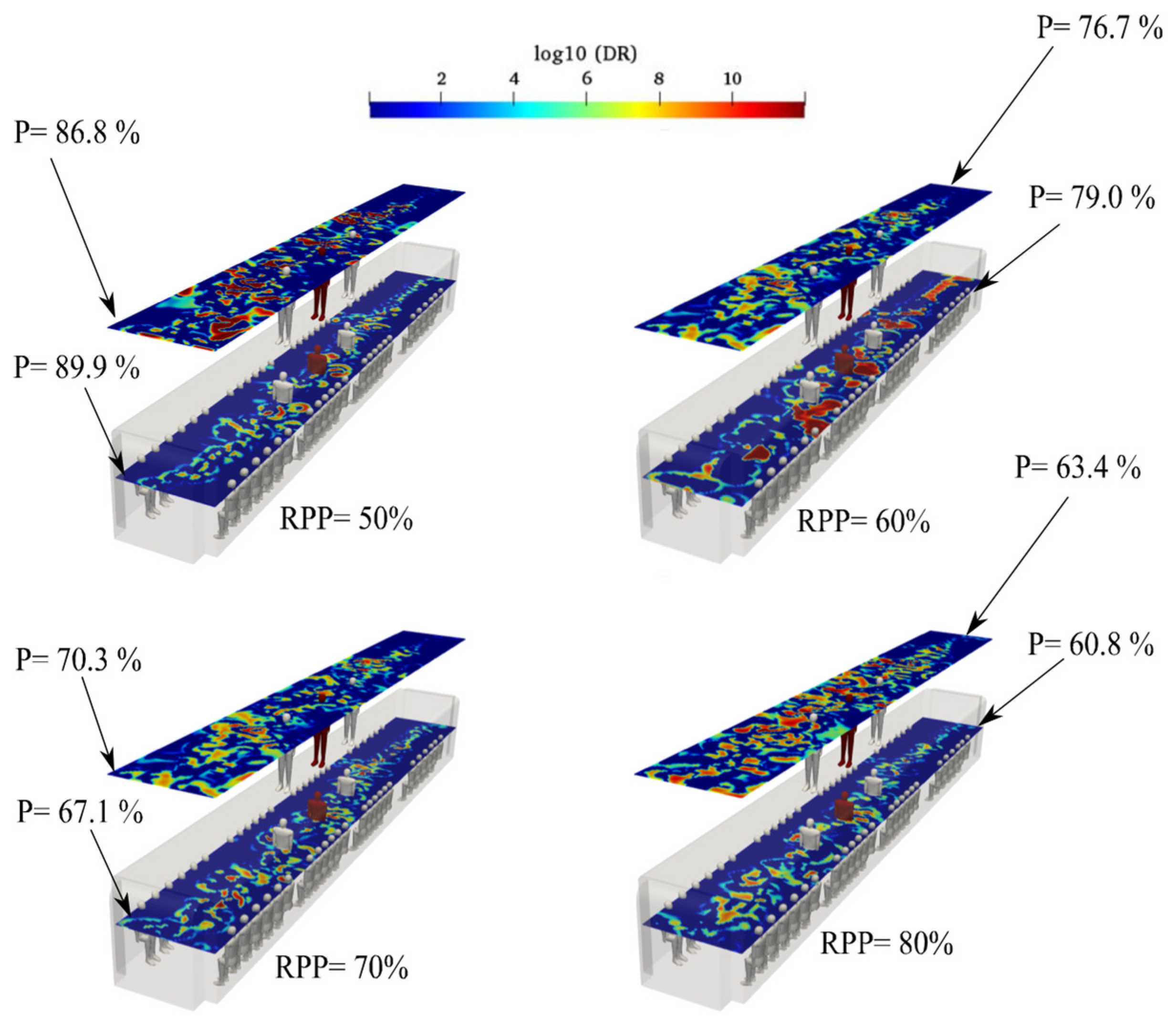
3.7. Effect of Imperfect Filtration of HVAC for Case 3
4. Conclusions
4.1. Concluding Remarks
4.2. Practical Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Johns Hopkins University and Medicine. COVID-19 Mortality Rate. 2022. Available online: https://coronavirus.jhu.edu/map.html (accessed on 6 June 2022).
- Rakhsha, A.; Azghandi, S.; Taghizadeh-Hesary, F. COVID-19 pandemic and patients with cancer: The protocol of a clinical oncology center in Tehran, Iran. Rep. Pract. Oncol. Radiother. 2020, 25, 765–767. [Google Scholar] [CrossRef] [PubMed]
- Siavashpour, Z.; Taghizadeh-Hesary, F.; Rakhsha, A. Recommendations on management of locally advanced rectal cancer during the COVID-19 pandemic: An Iranian consensus. J. Gastrointest. Cancer 2020, 51, 800–804. [Google Scholar] [CrossRef] [PubMed]
- Rakhsha, A.; Azghandi, S.; Taghizadeh-Hesary, F. Decision on chemotherapy amidst COVID-19 pandemic: A review and a practical approach from Iran. Infect. Chemother. 2020, 52, 496. [Google Scholar] [CrossRef] [PubMed]
- Fazilat-Panah, D.; Fallah Tafti, H.; Rajabzadeh, Y.; Fatemi, M.A.; Ahmadi, N.; Jahansouz, D.; Tabasi, M.; Javadinia, S.A.; Joudi, M.; Harati, H.; et al. Clinical Characteristics and Outcomes of COVID-19 in 1290 New Cancer Patients: Single-center, Prospective Cohort Study from Iran. Cancer Investig. 2022, 40, 1–3. [Google Scholar] [CrossRef] [PubMed]
- Rabaan, A.A.; Al-Ahmed, S.H.; Al-Malkey, M.K.; Alsubki, R.A.; Ezzikouri, S.; Al-Hababi, F.H.; Sah, R.; Al Mutair, A.; Alhumaid, S.; Al-Tawfiq, J.A.; et al. Airborne transmission of SARS-CoV-2 is the dominant route of transmission: Droplets and aerosols. Infez Med. 2021, 29, 10–19. [Google Scholar] [PubMed]
- Agrawal, A.; Bhardwaj, R. Probability of COVID-19 infection by cough of a normal person and a super-spreader. Phys. Fluids 2021, 33, 031704. [Google Scholar] [CrossRef]
- Avni, O.; Dagan, Y. Dynamics of Evaporating Respiratory Droplets in the Vicinity of Vortex Dipoles. arXiv 2021, arXiv:210807068. [Google Scholar] [CrossRef]
- Dbouk, T.; Drikakis, D. On respiratory droplets and face masks. Phys. Fluids 2020, 32, 063303. [Google Scholar] [CrossRef]
- Bergmans, B.; Cattaneo, A.; Duarte, R.M.; Gomes, J.F.; Saraga, D.; Rodenas Garcia, M.; Querol, X.; Liotta, L.F.; Safell, J.; Spinazzé, A.; et al. Particulate matter indoors: A strategy to sample and monitor size-selective fractions. Appl. Spectrosc. Rev. 2022, 57, 675–704. [Google Scholar] [CrossRef]
- Kaewrat, J.; Janta, R.; Sichum, S.; Rattikansukha, C.; Tala, W.; Kanabkaew, T. Human Health Risks and Air Quality Changes Following Restrictions for the Control of the COVID-19 Pandemic in Thailand. Toxics 2022, 10, 520. [Google Scholar] [CrossRef]
- Hossain, M.; Faisal, N.H. Modeling aerosol cloud aerodynamics during human coughing, talking, and breathing actions. AIP Adv. 2021, 11, 045111. [Google Scholar] [CrossRef]
- Manoj, M.G.; Satheesh Kumar, M.K.; Valsaraj, K.T.; Vijayan, S.K.; Nishanth, T. Exacerbation of Fatality Rates Induced by Poor Air Quality Due to Open-Air Mass Funeral Pyre Cremation during the Second Wave of COVID-19. Toxics 2022, 10, 306. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.S.; Larpruenrudee, P.; Paul, A.R.; Paul, G.; Gemci, T.; Gu, Y.; Saha, S.C. SARS CoV-2 aerosol: How far it can travel to the lower airways? Phys. Fluids 2021, 33, 061903. [Google Scholar] [CrossRef] [PubMed]
- Jiang, G.; Li, F.; Hu, T. Transport Characteristics and Transmission Risk of Virus-Containing Droplets from Coughing in Outdoor Windy Environment. Toxics 2022, 10, 294. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Allahyari, M.; Salinas, J.S.; Zgheib, N.; Balachandar, S. Peering inside a cough or sneeze to explain enhanced airborne transmission under dry weather. Sci. Rep. 2021, 11, 1–9. [Google Scholar] [CrossRef]
- Mohammadi Nafchi, A.; Blouin, V.; Kaye, N.; Metcalf, A.; Van Valkinburgh, K.; Mousavi, E. Room HVAC influences on the removal of airborne particulate matter: Implications for school reopening during the COVID-19 pandemic. Energies 2021, 14, 7463. [Google Scholar] [CrossRef]
- Nazari, A.; Jafari, M.; Rezaei, N.; Arash-Azad, S.; Talati, F.; Nejad-Rahim, R.; Taghizadeh-Hesary, F.; Taghizadeh-Hesary, F. Effects of High-Speed Wind, Humidity, and Temperature on the Generation of a SARS-CoV-2 Aerosol; a Novel Point of View. Aerosol Air Qual. Res. 2021, 21, 200574. [Google Scholar] [CrossRef]
- Stadnytskyi, V.; Anfinrud, P.; Bax, A. Breathing, speaking, coughing or sneezing: What drives transmission of SARS-CoV-2? J. Intern. Med. 2021, 290, 1010–1027. [Google Scholar] [CrossRef]
- Ju, M.J.; Oh, J.; Choi, Y.H. Changes in air pollution levels after COVID-19 outbreak in Korea. Sci. Total Environ. 2021, 750, 141521. [Google Scholar] [CrossRef]
- Zhou, M.; Zou, J. A dynamical overview of droplets in the transmission of respiratory infectious diseases. Phys. Fluids 2021, 33, 031301. [Google Scholar] [CrossRef]
- Akagi, F.; Haraga, I.; Inage, S.-i.; Akiyoshi, K. Effect of sneezing on the flow around a face shield. Phys. Fluids 2020, 32, 127105. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Li, Z.; Zhang, X.; Zhu, L.; Liu, Y.; Wang, S. The motion of respiratory droplets produced by coughing. Phys. Fluids 2020, 32, 125102. [Google Scholar] [CrossRef] [PubMed]
- Zeng, G.; Chen, L.; Yuan, H.; Yamamoto, A.; Maruyama, S. Evaporation flow characteristics of airborne sputum droplets with solid fraction: Effects of humidity field evolutions. Phys. Fluids 2021, 33, 123308. [Google Scholar] [CrossRef]
- Li, L.; He, R.; Kong, M.; Eilts, S.M.; Hong, J.; Hogan Jr, C.J.; Pope, Z.C. Effect of low-cost recirculating portable air filtration on aerosol particle deposition and concentration in a conference room: Experiment, theory, and simulation comparison. J. Aerosol Sci. 2022, 166, 106048. [Google Scholar] [CrossRef]
- He, R.; Gao, L.; Trifonov, M.; Hong, J. Aerosol generation from different wind instruments. J. Aerosol Sci. 2021, 151, 105669. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Leong, F.Y.; Xu, G.; Ge, Z.; Kang, C.W.; Lim, K.H. Dispersion of evaporating cough droplets in tropical outdoor environment. Phys. Fluids 2020, 32, 113301. [Google Scholar] [CrossRef] [PubMed]
- Nazari, A.; Jafari, M.; Rezaei, N.; Taghizadeh-Hesary, F.; Taghizadeh-Hesary, F. Jet fans in the underground car parking areas and virus transmission. Phys. Fluids 2021, 33, 013603. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; He, S.; Shen, L.; Hong, J. Simulation-based study of COVID-19 outbreak associated with air-conditioning in a restaurant. Phys. Fluids 2021, 33, 023301. [Google Scholar] [CrossRef]
- Li, Y.-y.; Wang, J.-X.; Chen, X. Can a toilet promote virus transmission? From a fluid dynamics perspective. Phys. Fluids 2020, 32, 065107. [Google Scholar] [CrossRef]
- Schreck, J.H.; Lashaki, M.J.; Hashemi, J.; Dhanak, M.; Verma, S. Aerosol generation in public restrooms. Phys. Fluids 2021, 33, 033320. [Google Scholar] [CrossRef]
- Wang, J.-X.; Li, Y.-Y.; Liu, X.-D.; Cao, X. Virus transmission from urinals. Phys. Fluids 2020, 32, 081703. [Google Scholar] [CrossRef] [PubMed]
- Dbouk, T.; Drikakis, D. On airborne virus transmission in elevators and confined spaces. Phys. Fluids 2021, 33, 011905. [Google Scholar] [CrossRef] [PubMed]
- Vranay, F.; Pirsel, L.; Kacik, R.; Vranayova, Z. Adaptation of HVAC Systems to Reduce the Spread of COVID-19 in Buildings. Sustainability 2020, 12, 9992. [Google Scholar] [CrossRef]
- Rezaei, N.; Jafari, M.; Nazari, A.; Salehi, S.; Talati, F.; Torab, R.; Nejad-Rahim, R. A novel methodology and new concept of SARS-CoV-2 elimination in heating and ventilating air conditioning systems using waste heat recovery. AIP Adv. 2020, 10, 085308. [Google Scholar] [CrossRef]
- Zhang, Z.; Han, T.; Yoo, K.H.; Capecelatro, J.; Boehman, A.L.; Maki, K. Disease transmission through expiratory aerosols on an urban bus. Phys. Fluids 2021, 33, 015116. [Google Scholar] [CrossRef]
- Abuhegazy, M.; Talaat, K.; Anderoglu, O.; Poroseva, S.V. Numerical investigation of aerosol transport in a classroom with relevance to COVID-19. Phys. Fluids 2020, 32, 103311. [Google Scholar] [CrossRef]
- Burgmann, S.; Janoske, U. Transmission and reduction of aerosols in classrooms using air purifier systems. Phys. Fluids 2021, 33, 033321. [Google Scholar] [CrossRef]
- He, R.; Liu, W.; Elson, J.; Vogt, R.; Maranville, C.; Hong, J. Airborne transmission of COVID-19 and mitigation using box fan air cleaners in a poorly ventilated classroom. Phys. Fluids 2021, 33, 057107. [Google Scholar] [CrossRef]
- Narayanan, S.R.; Yang, S. Airborne transmission of virus-laden aerosols inside a music classroom: Effects of portable purifiers and aerosol injection rates. Phys. Fluids 2021, 33, 033307. [Google Scholar] [CrossRef]
- Foster, A.; Kinzel, M. Estimating COVID-19 exposure in a classroom setting: A comparison between mathematical and numerical models. Phys. Fluids 2021, 33, 021904. [Google Scholar] [CrossRef]
- Wu, L.; Liu, X.; Yao, F.; Chen, Y. Numerical study of virus transmission through droplets from sneezing in a cafeteria. Phys. Fluids 2021, 33, 023311. [Google Scholar] [CrossRef] [PubMed]
- Talaat, K.; Abuhegazy, M.; Mahfoze, O.A.; Anderoglu, O.; Poroseva, S.V. Simulation of aerosol transmission on a Boeing 737 airplane with intervention measures for COVID-19 mitigation. Phys. Fluids 2021, 33, 033312. [Google Scholar] [CrossRef] [PubMed]
- Jia, D.; Lee Baker, J.; Rameau, A.; Esmaily, M. Simulation of a vacuum helmet to contain pathogen-bearing droplets in dental and otolaryngologic outpatient interventions. Phys. Fluids 2021, 33, 013307. [Google Scholar] [CrossRef] [PubMed]
- Baudet, A.; Baurès, E.; Blanchard, O.; Le Cann, P.; Gangneux, J.P.; Florentin, A. Indoor carbon dioxide, fine particulate matter and total volatile organic compounds in private healthcare and elderly care facilities. Toxics 2022, 10, 136. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, X.; Wu, T.; Zhu, L.; Qin, J.; Yang, X. Effects of slope and speed of escalator on the dispersion of cough-generated droplets from a passenger. Phys. Fluids 2021, 33, 041701. [Google Scholar] [CrossRef] [PubMed]
- Abraham, A.; He, R.; Shao, S.; Kumar, S.S.; Wang, C.; Guo, B.; Trifonov, M.; Placucci, R.G.; Willis, M.; Hong, J. Risk assessment and mitigation of airborne disease transmission in orchestral wind instrument performance. J. Aerosol Sci. 2021, 157, 105797. [Google Scholar] [CrossRef]
- Duarte, R.M.; Gomes, J.F.; Querol, X.; Cattaneo, A.; Bergmans, B.; Saraga, D.; Maggos, T.; Di Gilio, A.; Rovelli, S.; Villanueva, F. Advanced instrumental approaches for chemical characterization of indoor particulate matter. Appl. Spectrosc. Rev. 2022, 57, 705–745. [Google Scholar] [CrossRef]
- Shao, X.; Li, X. COVID-19 transmission in the first presidential debate in 2020. Phys. Fluids 2020, 32, 115125. [Google Scholar] [CrossRef] [PubMed]
- Arias, F.J.; De Las Heras, S. The mechanical effect of moisturization on airborne COVID-19 transmission and its potential use as control technique. Environ. Res. 2021, 197, 110940. [Google Scholar] [CrossRef]
- Baboli, Z.; Neisi, N.; Babaei, A.A.; Ahmadi, M.; Sorooshian, A.; Birgani, Y.T.; Goudarzi, G. On the airborne transmission of SARS-CoV-2 and relationship with indoor conditions at a hospital. Atmos. Environ. 2021, 118563. [Google Scholar] [CrossRef]
- Rowe, B.R.; Canosa, A.; Drouffe, J.-M.; Mitchell, J. Simple quantitative assessment of the outdoor versus indoor airborne transmission of viruses and covid-19. Environ. Res. 2021, 198, 111189. [Google Scholar] [CrossRef] [PubMed]
- Moreno, T.; Pintó, R.M.; Bosch, A.; Moreno, N.; Alastuey, A.; Minguillón, M.C.; Anfruns-Estrada, E.; Guix, S.; Fuentes, C.; Buonanno, G.; et al. Tracing surface and airborne SARS-CoV-2 RNA inside public buses and subway trains. Environ. Int. 2021, 147, 106326. [Google Scholar] [CrossRef] [PubMed]
- Chang, Z.; Yi, K.; Liu, W. A new ventilation mode of air conditioning in subway vehicles and its air distribution performance. Energy Built Environ. 2021, 2, 94–104. [Google Scholar] [CrossRef]
- Gröndahl, M.; Goldbaum, C.; White, J. What Happens to Viral Particles on the Subway. 2021. Available online: www.nytimes.com/interactive/2020/08/10/nyregion/nyc-subway-coronavirus.html (accessed on 10 August 2020).
- Tao, Y.; Yang, M.; Qian, B.; Wu, F.; Wang, T. Numerical and experimental study on ventilation panel models in a subway passenger compartment. Engineering 2019, 5, 329–336. [Google Scholar] [CrossRef]
- Shao, S.; Zhou, D.; He, R.; Li, J.; Zou, S.; Mallery, K.; Kumar, S.; Yang, S.; Hong, J. Risk assessment of airborne transmission of COVID-19 by asymptomatic individuals under different practical settings. J. Aerosol Sci. 2021, 151, 105661. [Google Scholar] [CrossRef]
- Chia, P.Y.; Coleman, K.K.; Tan, Y.K.; Ong, S.W.X.; Gum, M.; Lau, S.K.; Lim, X.F.; Lim, A.S.; Sutjipto, S.; Lee, P.H.; et al. Detection of air and surface contamination by SARS-CoV-2 in hospital rooms of infected patients. Nat. Commun. 2020, 11, 2800. [Google Scholar] [CrossRef]
- Li, C.; Wang, H.; Yu, C.W.; Xie, D. Diffusion characteristics of the industrial submicron particle under Brownian motion and turbulent diffusion. Indoor Built Environ. 2022, 31, 17–30. [Google Scholar] [CrossRef]
- Kanso, M.; Chaurasia, V.; Fried, E.; Giacomin, A. Peplomer bulb shape and coronavirus rotational diffusivity. Phys. Fluids 2021, 33, 033115. [Google Scholar] [CrossRef]
- Kanso, M.; Naime, M.; Chaurasia, V.; Tontiwattanakul, K.; Fried, E.; Giacomin, A.J. Coronavirus Pleomorphism. Phys. Fluids 2022, 34, 063101. [Google Scholar] [CrossRef]
- Yan, Y.; Li, X.; Shang, Y.; Tu, J. Evaluation of airborne disease infection risks in an airliner cabin using the Lagrangian-based Wells-Riley approach. Build. Environ. 2017, 121, 79–92. [Google Scholar] [CrossRef]
- Amri, H.; Hofstädter, R.N.; Kozek, M. Energy efficient design and simulation of a demand-controlled heating and ventilation unit in a metro vehicle. In Proceedings of the 2011 IEEE Forum on Integrated and Sustainable Transportation Systems, Vienna, Austria, 29 June–1 July 2011. [Google Scholar]
- Ventilation for Acceptable Indoor Air Quality. Standard 62-1999; American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 1999.
- Popov, T.; Kralimarkova, T.; Dimitrov, V. Measurement of exhaled breath temperature in science and clinical practice. Breathe 2012, 8, 186–192. [Google Scholar] [CrossRef]
- Das Neves Almeida, M.; de Paula Xavier, A.A.; Michaloski, A.O. A Review of Thermal Comfort Applied in Bus Cabin Environments. Appl. Sci. 2020, 10, 8648. [Google Scholar] [CrossRef]
- Ergonomics of the Thermal Environment: Estimation of the Thermal Insulation and Evaporative Resistance of a Clothing Ensembles. ISO 9920; International Standard Organization: Geneva, Switzerland, 1995.
- ASHRAE. Handbook of Fundamentals: Physiological Principles, Comfort Health; ASHRAE: New York, NY, USA, 1997. [Google Scholar]
- Angelova, R.A. Numerical simulation of the thermoregulation of clothed human body: Skin and clothing temperatures. J. Braz. Soc. Mech. Sci. Eng. 2015, 37, 297–303. [Google Scholar] [CrossRef]
- Stefanitsis, D.; Koukouvinis, P.; Nikolopoulos, N.; Gavaises, M. Numerical Investigation of the Aerodynamic Droplet Breakup at Mach Numbers Greater Than 1. J. Energy Eng. 2021, 147, 04020077. [Google Scholar] [CrossRef]
- Magnini, M.; Pulvirenti, B.; Thome, J. Characterization of the velocity fields generated by flow initialization in the CFD simulation of multiphase flows. Appl. Math. Model. 2016, 40, 6811–6830. [Google Scholar] [CrossRef]
- Yin, Y.; Gupta, J.K.; Zhang, X.; Liu, J.; Chen, Q. Distributions of respiratory contaminants from a patient with different postures and exhaling modes in a single-bed inpatient room. Build. Environ. 2011, 46, 75–81. [Google Scholar] [CrossRef]
- Zhu, S.; Kato, S.; Murakami, S.; Hayashi, T. Study on inhalation region by means of CFD analysis and experiment. Build. Environ. 2005, 40, 1329–1336. [Google Scholar] [CrossRef]
- Gorbunov, B. Aerosol particles generated by coughing and sneezing of a SARS-CoV-2 (COVID-19) host travel over 30 m distance. Aerosol Air Qual. Res. 2021, 21, 200468. [Google Scholar] [CrossRef]
- Kolinski, J.M.; Schneider, T.M. Superspreading events suggest aerosol transmission of SARS-CoV-2 by accumulation in enclosed spaces. Phys. Rev. E 2021, 103, 033109. [Google Scholar] [CrossRef]
- Bhardwaj, R.; Agrawal, A. Tailoring surface wettability to reduce chances of infection of COVID-19 by a respiratory droplet and to improve the effectiveness of personal protection equipment. Phys. Fluids 2020, 32, 081702. [Google Scholar] [CrossRef]
- Liu, Y.; Shen, L.; Zamansky, R.; Coletti, F. Life and death of inertial particle clusters in turbulence. J. Fluid Mech. 2020, 902. [Google Scholar] [CrossRef]
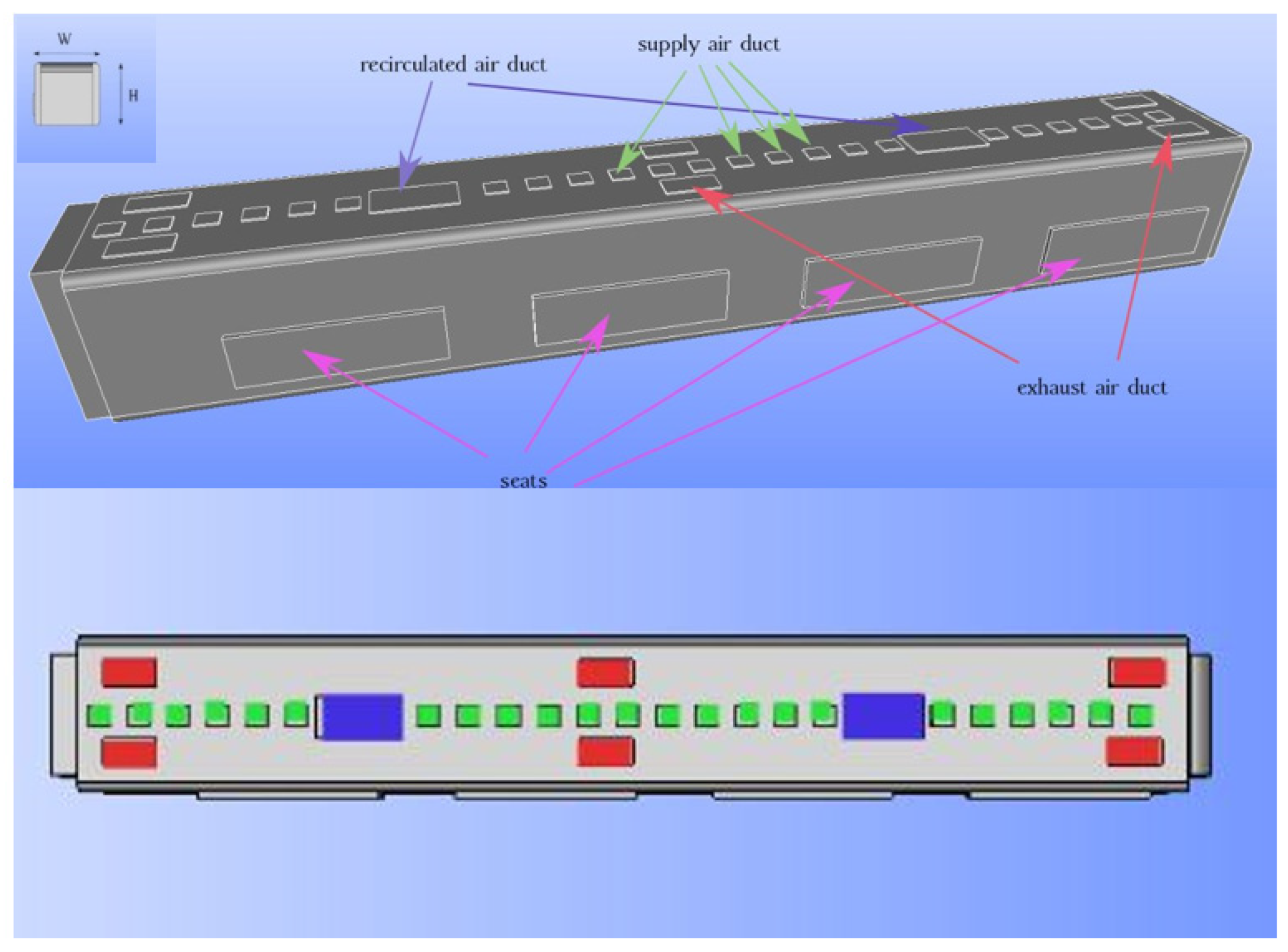





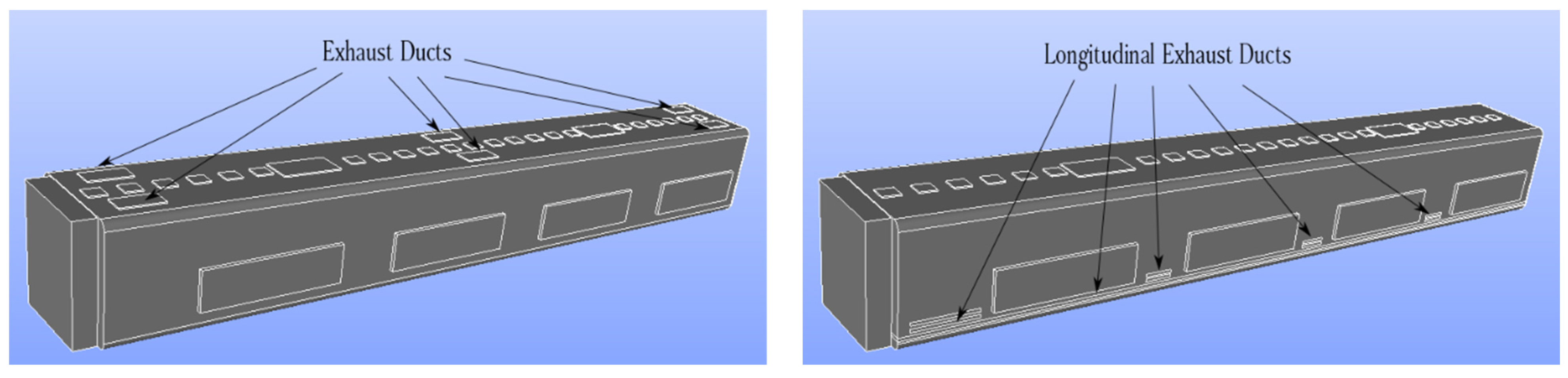








| No. Case Study | Different Inputs | Common Inputs |
|---|---|---|
| The conventional HVAC system (Case studies 1, 2, 3, 4, 5 and 6) | The length and width of exhaust ducts are 2.5 m and 1.6 m, respectively. The number of exhaust ducts is 6, | Air change rate is 10 hr−1. The temperature values of the supply air, human breath, ambiance, and other cabin interior surfaces (such as mannequins, seats, and walls) are set at 20 °C, 30 °C, 25 °C, and 27 °C, respectively. |
| The proposed HVAC system (Case studies 1, 2, 3, 4, 5 and 6) | The length and width of exhaust ducts are 4 m and 0.6 m, respectively. The number of ducts is 12. | ν = 1.5 × 10−5 m2/s, T0 = 20 °C, β = 3 × 10−3 K−1, Pr = 0.71, Prt = 0.9, g = 9.81 m/s2, Sc = 1, Sct = 1, clothing insulation of mannequins is 0.60 clo. |
| Values | Experimental Data | Present Work (RSM) | Present Work (k–ε) | Present Work (k-ε RNG) | Present Work (k–ω) | Present Work (k–ω SST) |
|---|---|---|---|---|---|---|
| va (average velocity) | 0.170 | 0.168 | 0.168 | 0.168 | 0.160 | 0.161 |
| vx (horizontal velocity) | 0.250 | 0.248 | 0.248 | 0.247 | 0.240 | 0.242 |
| vz (vertical velocity) | 0.590 | 0.578 | 0.578 | 0.578 | 0.562 | 0.560 |
| Ta (average temperature) | 26.90 | 26.85 | 27.00 | 27.00 | 24.00 | 24.00 |
| Tx (horizontal temperature) | 06.68 | 06.65 | 06.80 | 06.80 | 05.71 | 05.81 |
| Tz (vertical temperature) | 06.94 | 06.94 | 07.02 | 07.02 | 06.07 | 06.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nazari, A.; Hong, J.; Taghizadeh-Hesary, F.; Taghizadeh-Hesary, F. Reducing Virus Transmission from Heating, Ventilation, and Air Conditioning Systems of Urban Subways. Toxics 2022, 10, 796. https://doi.org/10.3390/toxics10120796
Nazari A, Hong J, Taghizadeh-Hesary F, Taghizadeh-Hesary F. Reducing Virus Transmission from Heating, Ventilation, and Air Conditioning Systems of Urban Subways. Toxics. 2022; 10(12):796. https://doi.org/10.3390/toxics10120796
Chicago/Turabian StyleNazari, Ata, Jiarong Hong, Farzad Taghizadeh-Hesary, and Farhad Taghizadeh-Hesary. 2022. "Reducing Virus Transmission from Heating, Ventilation, and Air Conditioning Systems of Urban Subways" Toxics 10, no. 12: 796. https://doi.org/10.3390/toxics10120796
APA StyleNazari, A., Hong, J., Taghizadeh-Hesary, F., & Taghizadeh-Hesary, F. (2022). Reducing Virus Transmission from Heating, Ventilation, and Air Conditioning Systems of Urban Subways. Toxics, 10(12), 796. https://doi.org/10.3390/toxics10120796









