Abstract
Background: Increasing regulatory pressure for maritime decarbonization (e.g., IMO CII, FuelEU) drives adoption of low-carbon fuels and prompts reassessment of regional ports’ competitiveness. This study aims to evaluate the economic and environmental viability of rerouting deep-sea container services to regional ports in a decarbonizing world. Methods: A scenario-based analysis is used to evaluate total costs and CO2 emissions across the entire container shipping supply chain, incorporating deep-sea shipping, port operations, feeder services, and inland rail/road transport. The Port of Liverpool serves as the primary case study for rerouting Asia–Europe services from major ports. Results: Analysis indicates Liverpool’s competitiveness improves with shipping lines’ slow steaming, growth in hinterland shipment volume, reductions in the emission factors of alternative low-carbon fuels, and an increased modal shift to rail matching that of competitor ports (e.g., Southampton). A dual-port strategy, rerouting services to call at both Liverpool and Southampton, shows potential for both economic and environmental benefits. Conclusions: The study concludes that rerouting deep-sea services to regional ports can offer cost and emission advantages under specific operational and market conditions. Findings on factors and conditions influencing competitiveness and the dual-port strategy provide insights for shippers, ports, shipping lines, logistics agents, and policymakers navigating maritime decarbonization.
1. Introduction
Regional or secondary container ports refer to less prominent ports, often located off mainstream shipping routes, that complement primary or major container ports. These ports are generally less attractive to global shipping lines and typically handle lower volumes of container traffic compared to primary ports. Such regional ports are under-studied compared to major container ports [1]. However, with increasing concerns about maritime decarbonization, regional ports may become more competitive due to their proximity to hinterland and transshipment markets and reduced congestion.
The shipping industry is under increasing pressure to decarbonize. Several maritime decarbonization regulations have been introduced in recent years, such as the IMO’s Carbon Intensity Indicator (CII) and the European Union’s FuelEU initiative. In response, the industry has begun adopting low-carbon alternative fuels (e.g., LNG, biofuels, methanol). Within this new paradigm of alternative fuel adoption, it is timely to revisit the role of regional or secondary ports.
In the container shipping sector, shipping lines frequently adjust their service routes, particularly during periods of strategic alliance restructuring. Maersk and MSC have announced they will dissolve their 2 M Alliance in January 2025. Starting in February 2025, Maersk and Hapag-Lloyd will form a new alliance called Gemini Cooperation, while another new alliance, the Premier Alliance, comprising Ocean Network Express, Yang Ming, and HMM, will also emerge in 2025. Following these shipping alliance restructurings, many service routes will be redesigned or adjusted in 2025. For instance, the Gemini Cooperation plans to adopt a hub-and-spoke system, averaging only seven port calls per loop, while MSC will operate independently, focusing on multi-port direct services to smaller destinations, including secondary ports [2]. Specifically, in North Europe, the port of Antwerp will lose four Asia–North Europe calls due to the Gemini Cooperation’s departure from the port. Hamburg will gain one call, Bremerhaven will lose one, and Le Havre will gain one. In the UK, the port of Felixstowe will lose two calls, while London Gateway will gain two calls. MSC has added the Port of Liverpool to one of its Asia–Europe service routes from July 2024.
Many factors affect shipping lines’ choice of ports, e.g., port tariffs, port infrastructure, cargo volume, inland distance, port location, intermodal connectivity, port productivity, environmental issues, and the total portfolio of the port [3,4,5]. Several empirical studies have examined the competitiveness of container ports. For example, Tongzon and Heng [6] used a sample of container terminals around the world to identify the determinants of port competitiveness. It showed that private sector participation in the port industry and the adaptability to the customers’ demand can increase port competitiveness. Yeo et al. [7] studied the competitiveness of container ports in the regions of Korea and China and evaluated the determining factors influencing port competitiveness through a regional survey of shipping companies. Notteboom and Yap [8] discussed port competition and competitiveness in a region where several ports possess largely overlapping hinterlands. Cantillo et al. [5] analyzed the competitiveness of four major public ports in Colombia and showed that freight rates are the most relevant factor in port choice. However, empirical research usually does not quantify the economic and environmental impacts of port choices.
From a modeling perspective, there is a rich and varied body of literature on port competition and competitiveness. Discrete choice theory has been widely used for port choice analysis [9]. Lagoudis et al. [10] reported that discrete choice modeling was used in approximately 20% of studies on port choice published between 1981 and 2009. Data Envelopment Analysis (DEA) and Stochastic Frontier Analysis (SFA) are also commonly employed to evaluate the performance and relative competitiveness of ports (e.g., [6,11]). Game theory is another popular approach used to investigate port competition, especially in ports’ pricing decisions (e.g., [12,13,14,15,16]). Pujats et al. [17] reviewed 33 studies on the topic of container port competition and cooperations that used game theory models, published between 2008 and 2019. However, most port competition models developed to date primarily focus on port performance and strategic decisions, such as pricing, investment, and demand catchment, while often neglecting shipping lines’ decisions and lacking the consideration of supply chain perspective.
Another research stream on port selection adopts the perspective of shipping lines, focusing on optimizing shipping service routes and service network design. Various mathematical models have been developed in this area (e.g., [18,19,20,21,22]). Most studies in this stream emphasize seaborne transportation decisions, such as route design, port selection, fleet deployment, ship scheduling, and container movements, aiming to meet port-to-port trade demands while minimizing operational costs and/or environmental impacts. This stream of studies often ignores inland transportation.
It is important to note that inland transportation is an essential part of container shipping supply chains. Since inland transportation often incurs high costs and emissions, it is desirable to model port choice within the context of the global shipping supply chain, incorporating deep-sea services, feeder services, port operations, and hinterland transport simultaneously [23]. This aligns with the practices of major shipping lines like Maersk and Hapag-Lloyd, which are pursuing end-to-end supply chain integration by expanding into the inland logistics sector.
Academically, several studies have designed shipping service routes and port choices from a global shipping supply chain perspective, explicitly considering both seaborne and inland transportation (e.g., [24,25,26,27]). The total transport chain’s cost is regarded as the most important determinant for shipping lines or shippers’ port choice [21,25]. These studies primarily focused on economic costs without explicitly considering environmental impacts or alternative marine fuels.
To the best of our knowledge, no existing study has comprehensively assessed the cost and emission impacts of an integrated supply chain adopting low-carbon alternative fuels. In this study, we conduct a scenario-based analysis to analyze the total costs and CO2 emissions of container shipping supply chains under alternative fuel adoption, taking into account deep-sea services, port operations, feeder services, and inland rail and road transportation. The objective is to evaluate the economic and environmental viability of rerouting deep-sea shipping services to call at regional ports in a decarbonizing world, using the Port of Liverpool and the Asia–Europe service route as a case study.
The rest of the paper is organized as follows: Section 2 describes the case study context and highlights the need for this research. Section 3 explains the three scenarios of container shipping supply chains in the case study and outlines the approach to estimate the total relevant costs and carbon emissions across these scenarios, incorporating deep-sea services, port operations, feeder services, and inland rail and road transportation. Section 4 presents a series of sensitivity analyses evaluating how the relative performance between rerouted shipping supply chains and the base scenario responds to key parameters. Managerial insights and policy implications are summarized. Finally, Section 5 provides the conclusions and directions for further research.
2. Case Study Description
The Port of Liverpool, located on the River Mersey in Merseyside, is considered a secondary or regional container port compared to major UK hubs like Felixstowe and Southampton. However, it plays a vital role in supporting trade for the Northwest of England, North Wales, and parts of Scotland and Ireland. Its strategic location establishes it as a key gateway for transatlantic trade and regional supply chains. Nevertheless, its competitiveness on Asia–Europe shipping routes remains debatable, as it is situated off the mainstream shipping routes for this trade.
Infrastructurally, the GBP 400 million Liverpool2 project has added a new deep-water container terminal to the Port of Liverpool since 2016. This terminal can accommodate mega-containerships of up to 20,000 TEUs (https://www.placenorthwest.co.uk/liverpool-2-mega-cranes-arrive-from-china/, accessed on 1 June 2025), covering the majority of container vessels worldwide, including those deployed on Asia–Europe routes. The primary motivation behind the Liverpool2 project is that 50% of the UK’s container demand is located closer to Liverpool than to southern ports, yet over 90% of deep-sea containers enter the UK through southern ports [28].
The Liverpool2 deep-water terminal can offer an alternative for bringing cargo to the hinterland market more efficiently, with reduced overland transport costs and emissions. Compared to southern ports such as Felixstowe and Southampton, Liverpool experiences less congestion, both at the port itself and within the surrounding transport networks. Additionally, the Port of Liverpool offers competitive handling charges, making it appealing to businesses seeking to optimize logistics costs. Furthermore, Liverpool’s designation as part of the Liverpool City Region Freeport enhances its attractiveness to international investors and shippers.
However, these benefits would largely depend on whether shipping lines are willing to adjust their deep-sea service routes to call at Liverpool directly. It is widely agreed that the Liverpool2 deep-water terminal is well-positioned to attract trans-Atlantic trade due to its strategic location on the west coast of England. However, shipping lines hold differing views on the viability of rerouting Asia–Europe services to include Liverpool. Combined with the conservative and risk-averse behavior of shipping lines, only one Asia–Europe shipping service route has directly called at the Port of Liverpool since the Liverpool2 terminal opened in 2016.
Nevertheless, with the growing emphasis on maritime decarbonization by the IMO and national governments in recent years (such as the 2023 IMO GHG Strategy and the UK’s Maritime 2050 Strategy), and the increasing adoption of alternative fuels, it is essential to evaluate the cost and emission viability of rerouting shipping service routes to call directly at Liverpool from a supply chain perspective, taking into account deep-sea services, port operations, feeder services, and inland rail and road transportation. This issue is significant for both industry professionals and scholars. From the shipping industry’s perspective, a comprehensive cost and emissions analysis is necessary to quantitatively understand the matter and identify opportunities for sustainable development. From an academic perspective, the issue is closely related to port choice and competitiveness, particularly for regional and secondary ports, which constitute a significant portion of ports worldwide but remain under-studied.
3. Supply Chain Rerouting Scenarios and Methodology
To achieve this objective, we employ a scenario-based approach to model the integrated container shipping supply chains, covering deep-sea shipping, port operations, feeder services, and inland rail/road transport. This method systematically evaluates rerouting scenarios as a strategic planning tool while providing shipping companies and policymakers with a flexible, practical framework for exploring additional potential scenarios.
Consider a base scenario of a container shipping supply chain (CSSC), in which an Asia–Europe deep-sea service route calls at the Port of Southampton (a major port) to serve the UK hinterland market via road and rail transport. Additionally, it serves the transshipment markets, including Scotland, Ireland, and Northern Ireland, through feeder vessels connected to the Port of Southampton. The base scenario is termed Scenario 1.
The rerouting scenarios would modify the base scenario by introducing calls at the regional port. We propose two alternative supply chain scenarios where Asia–Europe deep-sea shipping services are rerouted to the Port of Liverpool. These scenarios have been widely discussed in industry since the opening of the Liverpool2 deep-water terminal, yet perspectives on their viability diverge significantly. The adoption of low-carbon alternative fuels adds a new factor to complicate the perspectives. A comprehensive quantitative analysis is therefore needed to resolve this divergence. Two rerouting scenarios are described below:
- The first alternative (termed Scenario 2) involves replacing the Port of Southampton with the Port of Liverpool on the deep-sea service route. In this case, the UK hinterland market would be served via road and rail transport from Liverpool, while transshipment markets in Scotland, Ireland, and Northern Ireland would be served via feeder vessels from Liverpool.
- The second alternative (termed Scenario 3) involves the deep-sea service route calling at both Liverpool and Southampton. Under this arrangement, the UK markets closer to Southampton would be served by road and rail transport from Southampton, while the UK markets closer to Liverpool would be served by road or rail transport from Liverpool. Additionally, as Scotland, Ireland, and Northern Ireland are significantly closer to Liverpool than Southampton, these transshipment markets would be served via feeder vessels from Liverpool.
The feeder services from the Port of Southampton and from the Port of Liverpool are shown in Figure 1. The three scenarios of container shipping supply chains are illustrated in Figure 2, where Base CSSC represents Scenario 1, Regional port CSSC represents Scenario 2, and Dual port CSSC represents Scenario 3.
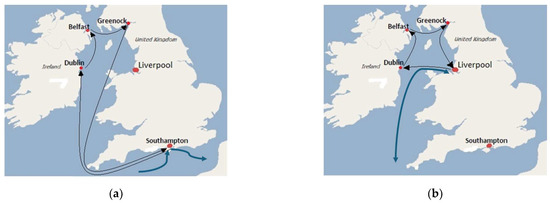
Figure 1.
Feeder service routes: (a) from Southampton; (b) from Liverpool.
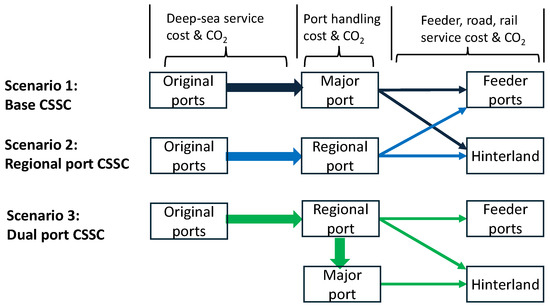
Figure 2.
Three container shipping supply chain (CSSC) scenarios.
To evaluate the viability of rerouting the Asia–Europe shipping services to the regional port in Scenarios 2 and 3, compared to the base scenario, we exclude the hinterland transport logistics associated with the original ports (i.e., foreign ports). This is because the related costs and CO2 emissions will be identical across all three scenarios in the segment of the supply chain from original hinterland to original ports (Figure 2).
Our analysis focuses on the costs and CO2 emissions in the supply chain segments from the original ports to the final inland destinations, including deep-sea services, port operations, feeder services, and inland rail and road transport, as shown in Figure 2. Specifically, the scenario evaluation includes the following steps:
- Step 1. Calculate deep-sea service costs and CO2 emissions in Section 3.2.
- Step 2. Calculate port handling costs and CO2 emissions in Section 3.3.
- Step 3. Calculate feeder service costs and CO2 emissions in Section 3.4.
- Step 4. Calculate inland rail and road transportation costs and CO2 emissions in Section 3.5.
- Step 5. Obtain total relevant costs and CO2 emissions for three scenarios and calculate the performance differences between rerouting scenarios and the base scenario in Section 3.6.
We make the following assumptions:
Assumption 1. The deep-sea shipping services and feeder services operate on a weekly schedule. The round-trip journey times for both the deep-sea service routes and feeder services are consistent across the three scenarios, which will be achieved by appropriately adjusting vessel sailing speeds in the proposed scenarios.
Assumption 2. The vessel’s port times at non-UK ports are identical across all three scenarios. In Scenario 3, the combined container handling time at Southampton and Liverpool is equal to the port handling time at Southampton in the base scenario (Scenario 1) and the port handling time at Liverpool in Scenario 2. At any specific port, container loading and unloading handling charges are identical across the three scenarios. All containers are measured in TEUs (20-foot equivalent units), with one FEU (40-foot equivalent unit) counted as two TEUs.
Assumption 3. All vessels deployed for the same service are of a similar type and size.
Assumption 4. The number of containers flowing into a port by sea is the same as the number of containers flowing out of the port by sea.
Assumption 1 implies that the same number of deep-sea vessels (and feeder vessels) are deployed across all three scenarios. Note that the total sailing distances for the round-trip journey differ in each scenario. Therefore, the sailing speeds of the vessels will vary to maintain the same journey time for a round-trip. It should be noted that the adjustments of sailing speeds will have a significant impact on fuel consumption and on CO2 emissions. Assumption 2 is reasonable under the assumption that two ports have similar handling rates and the total loading and unloading activities (for both laden and empty containers) are very similar across scenarios. Assumption 3 is common in practice because sister vessels are often deployed on the same service route. Assumption 4 follows the common principle of container flow balancing in the literature (e.g., [29]).
3.1. Notation
We introduce the following notation:
h: the UK hinterland shipment volume in TEUs in the dominant direction.
hi: the UK hinterland shipment volume in TEUs at inland location i, i = 1, 2, …, N, h = ∑i hi.
d1i, d2i: the distances in km from inland location i to Southampton and Liverpool, respectively, i = 1, 2,…, N.
θ1i: the proportion of the UK hinterland shipment volume at inland location i transported by road haulers via Southampton in Scenario 1, i = 1, 2, …, N; while (1 − θ1i) is the proportion transported by rail services in Scenario 1.
θ2i: the proportion of the UK hinterland shipment volume at inland location i transported by road haulers via Liverpool in Scenario 2, i = 1, 2, …, N; while (1 − θ2i) is the proportion transported by rail services in Scenario 2.
θ3,1i, θ3,2i: the proportions of the UK hinterland shipment volume at inland location i transported by road haulers via Southampton and Liverpool in Scenario 3, i = 1, 2, …, N.
δ3,1i, δ3,2i: the proportions of the UK hinterland shipment volume at inland location i transported by rail services via Southampton and Liverpool in Scenario 3, where θ3,1i + θ3,2i + δ3,1i + δ3,2i = 1, for i = 1, 2, …, N.
g: the transshipment volume in TEUs in the dominant direction.
Ch: the unit transportation cost per km in USD in the hinterland by road haulers.
Cr: the unit transportation cost per km in USD in the hinterland by rail services.
Crt: the unit handling cost in USD at seaport rail terminal or inland rail terminal.
W1, W2: the terminal handling charge per TEU in USD at Southampton and Liverpool.
Y(V): the fixed vessel berthing costs per call at a port, where V represents the vessel capacity.
Z1, Z2: the congestion cost per TEU in USD at Southampton and Liverpool.
Cfuel: the marine fuel cost per tonne in USD.
Vd: the vessel carrying capacity in TEUs in the deep-sea service.
Vf: the vessel carrying capacity in TEUs in the feeder service.
sd0: the designed speed in knots of the deep-sea vessels.
sf0: the designed speed in knots of the feeder vessels.
sd1, sd2, sd3: the sailing speed in knots of the deep-sea vessels in Scenarios 1, 2, and 3.
sf1, sf2, sf3: the sailing speed in knots of the feeder vessels in Scenarios 1, 2 and 3.
dd1, dd2, dd3: the sailing distance in nautical miles of the round-trip journey of the deep-sea service route in Scenarios 1, 2 and 3.
df1, df2, df3: the sailing distance in nautical miles of the round-trip journey of the feeder service route in Scenarios 1, 2 and 3.
Fd: the fuel consumption in tonnes per day when a vessel in the deep-sea service sails at its designed speed.
Ff: the fuel consumption in tonnes per day when a vessel in the feeder service sails at its designed speed.
Gd(sdj): the fuel consumption in tonnes per day when a vessel in the deep-sea service sails at the speed sdj.
Gf(sfj): the fuel consumption in tonnes per day when a vessel in the feeder service sails at the speed sfj.
Km: the emission factor that converts the consumed marine fuel into the emissions, which represents the tonnes of CO2 emitted per tonne of marine fuel burned by the engine.
Kw1, Kw2: the CO2 emissions in grams per container caused by port congestion at Southampton and Liverpool, respectively.
Krt: the CO2 emissions in grams per container handled at seaport rail terminal or inland rail terminal.
Kh: the CO2 emissions in grams per tonne-km (g CO2/tkm) by road haulers.
Kr: the CO2 emissions in grams per tonne-km (g CO2/tkm) by rail services.
3.2. Deep-Sea Service Costs and CO2 Emissions
The operating costs of deep-sea services primarily include vessel chartering, crew salaries, and fuel consumption. Since all three scenarios involve the same number and type of vessels with identical round-trip journey times, the chartering and crew costs remain constant and can therefore be excluded. Consequently, only fuel consumption costs need to be evaluated, as vessel speeds vary across the three scenarios. The relevant deep-sea service cost for scenario j, denoted by RCdj, is given by
RCdj = Cfuel · Gd(sdj) · ddj/(24sdj), for j = 1, 2, 3.
Note that the deep-sea service in Scenario 2 differs from that in Scenario 1 only by replacing Southampton with Liverpool. This implies that the number of port calls and the number of container loading/unloading activities in the deep-sea service remain the same in both scenarios, although the total sailing distances in two scenarios are different. As a result, the total time a vessel spends at ports during a round trip on the deep-sea service route is identical in Scenario 1 and Scenario 2. Therefore, the sailing speeds in Scenario 2 can be determined by ensuring that the total sailing time at sea remains the same as in Scenario 1, in order to maintain the same overall round-trip duration, i.e.,
sd2 = dd2 · sd1/dd1.
The deep-sea service in Scenario 3 differs from that in Scenario 1 by adding Liverpool to the route. This change not only increases the total sailing distance but also adds additional port call time (e.g., for vessel mooring and casting off at Liverpool). We assume the additional port call time to be 8 h [4]. Consequently, the deep-sea vessel must operate at a higher sailing speed to compensate for the extra distance and time, in order to maintain the same overall round-trip duration as in Scenario 1. Based on this, the sailing speeds in Scenario 3 can be determined as follows:
sd3 = dd3/(dd1/sd1 − 8).
It is widely accepted that a vessel’s fuel consumption follows a cubic relationship with its sailing speed (e.g., [4,30]). It follows that
Gd(sdj): = Fd · (sdj/sd0)3, for j = 1, 2, 3.
The CO2 emissions can be estimated from marine fuel consumption by multiplying it by the emission factor Km. The emission factor is an empirical mean value that depends on the specific fuel used. Hence, the relevant CO2 emissions of a vessel in deep-sea service, REdj for scenario j, are given by
REdj = Km · Gd(sdj) · ddj/(24sdj), for j = 1, 2, 3.
3.3. Port Handling Costs and CO2 Emissions
Three types of port handling costs will be considered: the fixed vessel berthing costs per call at a port, the terminal handling charges, and the port congestion costs.
We assume that the fixed vessel berthing costs per call at a port only depends on vessel capacity. According to Shintani et al. [31], we have Y(V) = 1.95*V + 5200. In all three scenarios, the fixed vessel berthing costs for feeder services are the same. However, for the deep-sea service, it should be noted that both Southampton and Liverpool are called in Scenario 3, where only Southampton is called in Scenario 1 and only Liverpool is called in Scenario 2.
Terminal handling charges primarily arise from quay crane operations when containers are lifted on or off vessels. Port congestion costs are associated with yard density levels and are incurred due to unproductive yard equipment activities and vehicle waiting. In the base CSSC scenario, all hinterland shipments and transshipments are unloaded from deep-sea vessels to storage yards at Southampton. According to Assumption 4, the same number of shipments and transshipments (including both laden and empty containers) will later be loaded onto deep-sea vessels. For transshipments, double handling is required due to the use of feeder vessels. Therefore, in Scenario 1, the number of handlings for hinterland shipments equals 2h containers, while the number of handlings for transshipments equals 4g. The numbers of container handlings for Scenario 2 and Scenario 3 can be analyzed similarly. Consequently, we have the relevant port handling costs in three scenarios, RCpj for j = 1, 2, 3, as follows:
where h3,1 = Σi hi · (θ3,1i + δ3,1i) represents the hinterland shipment volume handled at the port of Southampton in Scenario 3.
RCp1 = Y(Vd) + Y(Vf) + (W1 + Z1) · (2h + 4g),
RCp2 = Y(Vd) + Y(Vf) + (W2 + Z2) · (2h + 4g),
RCp3 = 2Y(Vd) + Y(Vf) + (W1 + Z1) · 2h3,1 + (W2 + Z2) · (2h − 2h3,1 + 4g).
Regarding CO2 emissions at ports, since the total berthing time of the vessels is consistent across the three scenarios, the emissions from the vessels, primarily caused by their auxiliary engines, remain unchanged and can be excluded from the comparison. However, as two ports may experience different levels of port congestion, external trucks, yard cranes, and internal trucks may generate different amounts of CO2 emissions when handling hinterland shipments. It is worth noting that transshipment operations at ports are less affected by yard congestion, and their emissions are therefore excluded from the analysis. We use REpj for j = 1, 2, 3 to denote the relevant port operations emissions as follows:
REp1 = Kw1 · 2h,
REp2 = Kw2 · 2h,
RCp3 = Kw1 · 2h3,1 + Kw2 · 2(h − h3,1).
3.4. Feeder Service Costs and CO2 Emissions
Similar to the deep-sea service cost, the feeder service costs can focus on the fuel consumption costs of feeder vessels. The relevant feeder service cost for scenario j, denoted by RCfj, is given by
where
RCfj = Cfuel · Gf(sfj) · dfj/(24sfj), for j = 1, 2, 3.
sfj = dfj · sf1/df1, for j = 1, 2, 3.
Gf(sfj): = Ff · (sfj/sf0)3, for j = 1, 2, 3.
The relevant CO2 emissions of a vessel in feeder service, REfj for scenario j, are given by
REfj = Km · Gf(sfj) · dfj/(24sfj), for j = 1, 2, 3.
3.5. Inland Rail and Road Transportation Costs and CO2 Emissions
It is assumed that the UK hinterland shipments are distributed over N inland locations with {hi: i = 1, 2, …, N; Σi hi = h}. For road haulage, the containers can be delivered directly between the port and customers. However, for rail services, the containers must be handled at both seaport rail terminal and inland rail terminal, and further transported by trucks between inland rail terminals and customers. For simplicity, we assume there is an average of 30 km between inland rail terminals and customers. The relevant hinterland transportation costs by road haulers and rail services for three scenarios, denoted by RChj for j = 1, 2, 3, can be calculated as follows:
RCh1 = Ch · Σi (θ1i · 2hi · d1i) + Σi 2hi· (1 − θ1i) · (Cr·d1i + 2Crt + 30Ch);
RCh2 = Ch · Σi (θ2i · 2hi · d2i) + Σi 2hi · (1 − θ2i) · (Cr·d2i + 2Crt + 30Ch);
RCh3 = Ch · Σi (θ3,1i · 2hi · d1i + θ3,2i · 2hi · d2i)
+ Σi 2hi· δ3,1i · (Cr·d1i + 2Crt + 30Ch) + Σi 2hi· δ3,2i · (Cr·d2i + 2Crt + 30Ch).
+ Σi 2hi· δ3,1i · (Cr·d1i + 2Crt + 30Ch) + Σi 2hi· δ3,2i · (Cr·d2i + 2Crt + 30Ch).
The average weight per container in both directions (to and from ports) can be estimated at 15 tonnes, considering both laden and empty containers. The CO2 emissions per tonne-kilometer by road haulers, Kh, are approximately 106.5 g CO2/tkm [32]. The CO2 emissions per tonne-kilometer by rail services, Kr, are approximately 26.5 g CO2/tkm in the UK [33]. For rail services, the emissions from container handling at both seaport rail terminal and inland rail terminal, Krt, are about 8040 g CO2 per container. Therefore, the relevant CO2 emissions in tonnes from hinterland transportation by road haulers and rail services for three scenarios, denoted by REhj for j = 1, 2, 3, can be calculated as follows:
REh1 = 15Kh · Σi (θ1i · 2hi · d1i) · 10−6 + Σi (1 − θ1i)·2hi·(15Kr ·d1i + 2Krt + 15Kh ·30) · 10−6;
REh2 = 15Kh · Σi (θ2i · 2hi · d2i) · 10−6 + Σi (1 − θ2i)·2hi·(15Kr ·d2i + 2Krt + 15Kh ·30) · 10−6;
REh3 = 15Kh · Σi (θ3,1i·2hi·d1i + θ3,2i·2hi·d2i)·10−6 + Σi [δ3,1i·2hi·(10Kr ·d1i + 2Krt + 15Kh ·30)
+ δ3,2i·2hi·(15Kr ·d2i + 2Krt + 15Kh ·30)]·10−6.
+ δ3,2i·2hi·(15Kr ·d2i + 2Krt + 15Kh ·30)]·10−6.
3.6. Total Relevant Costs and CO2 Emissions in Three Scenarios
In summary, the total relevant costs and CO2 emissions in three CSSC scenarios, denoted by TRCj and TREj for j = 1, 2, 3, are given by
TRCj = RCdj + RCpj + RCfj + RChj, for j = 1, 2, 3.
TREj = REdj + REpj + REfj + REhj, for j = 1, 2, 3.
Using the base CSSC scenario (i.e., Scenario 1) as the reference point, we can obtain the relative total relevant costs and CO2 emissions between Scenarios 2 and 3 compared to Scenario 1 as follows:
TRC2 − TRC1 = Cfuel · Fd · sd12 (dd23 − dd13)/(24 · dd12 · sd03)
+ (W2 + Z2 − W1 − Z1) · (2h + 4g)
+ Cfuel · Ff · sf12 (df23 – df13)/(24 · df12 · sf03)
+ Ch·Σi 2hi·(θ2i·d2i − θ1i·d1i) + Σi 2hi·Cr·[(1 − θ2i)·d2i − (1 − θ1i)·d1i]
+ Σi 2hi·(θ1i − θ2i) · (2Crt + 30Ch).
+ (W2 + Z2 − W1 − Z1) · (2h + 4g)
+ Cfuel · Ff · sf12 (df23 – df13)/(24 · df12 · sf03)
+ Ch·Σi 2hi·(θ2i·d2i − θ1i·d1i) + Σi 2hi·Cr·[(1 − θ2i)·d2i − (1 − θ1i)·d1i]
+ Σi 2hi·(θ1i − θ2i) · (2Crt + 30Ch).
TRC3 − TRC1 = Cfuel · Fd · (sd32·dd3 − sd12·dd1)/(24 · sd03)
+ Y(Vd) + (W2 + Z2 − W1 − Z1)· (2h − 2h3,1 + 4g)
+ Cfuel · Ff · sf12 (df33 − df13)/(24 · df12 · sf03)
+ Ch·Σi 2hi·(θ3,1i·d1i + θ3,2i·d2i − θ1i·d1i) + Σi 2hi·Cr·[δ3,1i·d1i + δ3,2i·d2i − (1 − θ1i)·d1i]
+ Σi 2hi· (δ3,1i + δ3,2i − 1 + θ1i) · (2Crt + 30Ch).
+ Y(Vd) + (W2 + Z2 − W1 − Z1)· (2h − 2h3,1 + 4g)
+ Cfuel · Ff · sf12 (df33 − df13)/(24 · df12 · sf03)
+ Ch·Σi 2hi·(θ3,1i·d1i + θ3,2i·d2i − θ1i·d1i) + Σi 2hi·Cr·[δ3,1i·d1i + δ3,2i·d2i − (1 − θ1i)·d1i]
+ Σi 2hi· (δ3,1i + δ3,2i − 1 + θ1i) · (2Crt + 30Ch).
TRE2 − TRE1 = Km · Fd · sd12 (dd23 − dd13)/(24 · dd12 · sd03)
+ 2h · (Kw2 − Kw1) · 10−6
+ Km · Ff · sf12 (df23 − df13)/(24 · df12 · sf03)
+ 15Kh·Σi 2hi·(θ2i·d2i − θ1i·d1i) · 10−6 + ∑i 2hi· 15Kr·[(1 − θ2i)·d2i − (1 − θ1i)·d1i)] · 10−6
+ Σi 2hi·[(θ1i − θ2i) · (2Krt + 15Kh ·30)] · 10−6.
+ 2h · (Kw2 − Kw1) · 10−6
+ Km · Ff · sf12 (df23 − df13)/(24 · df12 · sf03)
+ 15Kh·Σi 2hi·(θ2i·d2i − θ1i·d1i) · 10−6 + ∑i 2hi· 15Kr·[(1 − θ2i)·d2i − (1 − θ1i)·d1i)] · 10−6
+ Σi 2hi·[(θ1i − θ2i) · (2Krt + 15Kh ·30)] · 10−6.
TRE3 − TRE1 = Km · Fd · (sd32·dd3 − sd12·dd1)/(24 · sd03)
+ 2(h − h3,1) · (Kw2 − Kw1) · 10−6
+ Km · Ff · sf12 (df33 − df13)/(24 · df12 · sf03)
+ 15Kh·∑i2hi·(θ3,1i·d1i + θ3,2i·d2i − θ1i·d1i) · 10−6 + Σi2hi·15Kr·[δ3,1i·d1i + δ3,2i·d2i − (1 − θ1i)·d1i] · 10−6
+ Σi2hi·[(δ3,1i + δ3,2i − (1 − θ1i)) · (2Krt + 15Kh ·30)] · 10−6.
+ 2(h − h3,1) · (Kw2 − Kw1) · 10−6
+ Km · Ff · sf12 (df33 − df13)/(24 · df12 · sf03)
+ 15Kh·∑i2hi·(θ3,1i·d1i + θ3,2i·d2i − θ1i·d1i) · 10−6 + Σi2hi·15Kr·[δ3,1i·d1i + δ3,2i·d2i − (1 − θ1i)·d1i] · 10−6
+ Σi2hi·[(δ3,1i + δ3,2i − (1 − θ1i)) · (2Krt + 15Kh ·30)] · 10−6.
Proposition 1.
Suppose that the major port (Southampton) has a closer proximity to maritime routes (dd3 > dd2 > dd1), while the regional port (i.e., Liverpool) has a closer proximity to transshipment markets (df3 = df2 < df1). Additionally, the regional port (Liverpool) has lower terminal handling charges (W1 > W2) and lower port congestion costs (Z1 > Z2). Under these conditions, we have the following results regarding the relative total relevant costs:
- (i)
- TRC2–TRC1 and TRC3–TRC1 are increasing in sd1 but decreasing in sf1.
- (ii)
- TRC2–TRC1 and TRC3–TRC1 are decreasing in dd1.
- (iii)
- TRC2–TRC1 and TRC3–TRC1 are decreasing in W1 − W2 and Z1 − Z2.
- (iv)
- TRC2–TRC1 and TRC3–TRC1 are decreasing in g.
The results in Proposition 1 can be derived from (24) and (25). Proposition 1(i) follows from the conditions dd3 > dd2 > dd1 and df3 = df2 < df1. This implies that a smaller sd1 or a larger sf1 tends to increase the competitiveness of rerouting to Liverpool. Proposition 1(ii) implies that a longer round-trip journey distance in the base CSSC scenario tends to increase the competitiveness of rerouting to Liverpool. Proposition 1(iii) arises from the conditions W1 > W2 and Z1 > Z2. This is intuitive as lower terminal handling charges and reduced port congestion at Liverpool encourage rerouting to Liverpool. Finally, Proposition 1(iv) indicates that the volume of transshipments (g) has a positive impact on rerouting to Liverpool. This follows from the conditions W1 > W2 and Z1 > Z2.
Proposition 2.
Suppose that the major port (Southampton) has a closer proximity to maritime routes (dd3 > dd2 > dd1), while the regional port (i.e., Liverpool) has a closer proximity to transshipment markets (df3 = df2 < df1). Additionally, the regional port (Liverpool) is less congested (Kw2 < Kw1). We have the following results regarding the relative total CO2 emissions:
- (i)
- TRE2–TRE1 and TRE3–TRE1 are increasing in sd1 but decreasing in sf1.
- (ii)
- TRE2–TRE1 and TRE3–TRE1 are decreasing in dd1.
- (iii)
- TRC2–TRC1 and TRC3–TRC1 are decreasing in (Kw2 − Kw1).
The results in Proposition 2 can similarly be derived from Equations (26) and (27). Notably, Propositions 2(i–iii) align with Proposition 1(i–iii), indicating that the relative costs and CO2 emissions exhibit similar sensitivities to these factors in Proposition 2. However, the results in both Proposition 1 and Proposition 2 are qualitative. A more insightful analysis involves quantitatively evaluating these sensitivities, which will be explored in the next section.
4. Numerical Experiments and Sensitivity Analysis
The system parameters can be classified into several categories: shipping service-related, port-related, and hinterland transport-related parameters. Shipping service-related parameters are set as follows. The deep-sea vessel has capacity Vd = 10,000 TEUs with a designed speed sd0 = 23 knots; the feeder vessel has a capacity Vf = 600 TEUs with a designed speed sf0 = 18 knots; it is assumed that in the base scenario the feeder vessel’s sailing speed is 5 knots less than the deep-sea vessel, i.e., sf1 = sd1 − 5.
Biofuel, as a drop-in fuel, is considered one of the most promising low-carbon alternative fuels. In this study, we assume that both deep-sea vessels and feeder vessels operate using biofuel. The deep-sea vessel’s fuel consumption per day at designed speed Fd = 205 tonnes; the feeder vessel’s fuel consumption per day at designed speed Ff = 33 tonnes. The biofuel cost Cfuel = USD 1000/tonne. The fuel emission factor Km = 1.2 g CO2/g [34].
To calculate the differences in sailing distances for deep-sea services across three scenarios, we use the following Asia–Europe service route as an example, omitting several Far East ports at the beginning and end of the port rotation:
Scenario 1 (base): Far East ports–Singapore–Rotterdam–Hamburg–Southampton–Singapore–Far East ports.
Scenario 2: Far East ports–Singapore–Rotterdam–Hamburg–Liverpool–Singapore–Far East ports.
Scenario 3: Far East ports–Singapore–Liverpool–Rotterdam–Hamburg–Southampton–Singapore–Far East ports.
According to HiFleet [35], the relevant port-to-port distances in nautical miles can be obtained as follows:
- Singapore–8436–Rotterdam–314–Hamburg–521–Southampton–8214–Singapore.
- Singapore–8436–Rotterdam–314–Hamburg–903–Liverpool–8335–Singapore.
- Singapore–8335–Liverpool–706–Rotterdam–314–Hamburg–521–Southampton–8214–Singapore.
Therefore, the round-trip journey distances for the deep-sea services in Scenario 2 and Scenario 3 are 503 and 605 nautical miles longer, respectively, than in the base scenario, i.e., dd2 = dd1 + 503, dd3 = dd1 + 605. The round-trip journey distance in the feeder service in the base scenario (Southampton–583–Greenock–97–Belfast–115–Dublin–432–Southampton) is df1 = 1227. The round-trip journey distances in the feeder services in Scenario 2 and Scenario 3 (Liverpool feeder route: Liverpool–203–Greenock–97–Belfast–115–Dublin–134–Liverpool) are df2 = df3 = 549 nautical miles.
Port-related parameters are set as follows. Currently, Liverpool (port 2) is less congested and has a lower terminal handling charge compared to Southampton (port 1). For example, according to CMA CGM, its terminal handling charge at Liverpool is GBP 15 less than that at Southampton. We therefore assume the following: W2 − W1 = USD −15; Z2 − Z1 = USD −10; Kw2 − Kw1 = −1072 g CO2 per container, where the last equation represents the amount of CO2 emissions for additional 10~15 min waiting at ports for an external truck [36]. The fixed vessel berthing costs per call at a port is given by Y(V) = 1.95*V + 5200, where V represents the vessel capacity in TEUs.
Hinterland transport-related parameters are set as follows. The cost of transporting a container by truck Ch = USD 2.5/km; the cost of transporting a container by rail Cr = USD 0.3/km. However, for rail containers, it incurs handling costs at both seaport and inland rail terminals, i.e., Crt = USD 187.5 per container at each rail terminal. In addition, the inland rail terminals are often some distance from customer locations. It is assumed that the distance between inland terminals and customers is 30 km, with deliveries made by trucks. Let Kh = 106.5 g CO2 per tonne-km by truck; Kr = 26 g CO2 per tonne-km by rail; Krt = 8040 g CO2 per container handled at rail terminals; and the average container weight is 15 tonnes [37].
According to Rodrigues et al. [38], hinterland shipment locations in the UK can be categorized into nine regions, with reference cities listed in Table 1. To account for the influence of the Ports of Felixstowe and London Gateway on the East of England and South East regions, we halve the shipment volumes in these two regions relative to the data from [38]. The distribution of container volumes across these locations is presented in Table 1, where the last two columns indicate the distances from the ports of Southampton and Liverpool to each location, respectively.

Table 1.
Hinterland shipment distribution in the UK with distances from ports of Southampton and Liverpool in km.
It is assumed that the farthest inland locations are prioritized for rail service, as it is common practice for road transport to be less competitive than rail for long-distance deliveries. In Scenario 1, the Port of Southampton has a rail-to-road modal split of 0.3:0.7, while the Port of Liverpool has a modal split of 0.1:0.9 in Scenario 2. These modal splits reflect the current practices. In Scenario 3, the modal split at both ports remains unchanged. However, hinterland regions are assigned exclusively to their nearest port: shipments closer to Liverpool route solely through Liverpool, while those nearer to Southampton use Southampton exclusively.
In the following, we will examine the impact of key system parameters (including deep-sea vessel speed sd1, the round-trip distance in deep-sea service dd1, the hinterland shipment volume h, the CO2 emission factor of marine fuel Km, the marine fuel cost per tonne Cfuel, the reduction in terminal handling charge at Liverpool W1 − W2, and the modal split at Liverpool modalSplit2) on the relative costs and CO2 emissions between Scenarios 2 and 3 and the base Scenario 1 one by one. The selections of these parameters are explained as follows. The varying deep-sea vessel speed can represent shipping companies’ different levels of slow steaming practices. The varying round-trip distance in deep-sea service represents deep-sea service’s different route structures, e.g., via Suez Canal or the Cape of Good Hope. The varying hinterland shipment volume represents the potential growth of the UK trade market. The varying CO2 emission factors of marine fuel represent the different levels of carbon reduction for alternative fuels. The varying marine fuel cost per tonne can represent different cost scenarios of alternative ship fuels. The reduction in terminal handling charge at Liverpool can reflect the economy of scale at the port of Liverpool, i.e., as port handling volumes grow, the unit cost of handling would reduce. The rising modal share of rail transport in Liverpool shows that rail usage is increasing to levels matching those in Southampton.
The performance differences between Scenarios 2 and 3 compared to Scenario 1 in the experiments are presented in Table 2, Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8. Specifically, the last columns in Table 2, Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8 give the total relevant costs or CO2 emissions of Scenario 2 and Scenario 3 minus that of Scenario 1, i.e., TRC2–TRC1, or TRC3–TRC1, or TRE2–TRE1, or TRE3–TRE1. Negative numbers in Table 2, Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8 indicate the rerouting scenarios outperform the base scenario. The experiments below also demonstrate the sensitivity of the performance differences to those key parameters. Following the sensitivity analysis, the managerial insights and policy implications on the viability of rerouting to regional ports are summarized in Section 4.8.

Table 2.
Performance differences between scenarios with varying deep-sea vessel speed.

Table 3.
Performance differences between scenarios with varying round-trip distance in deep-sea service.

Table 4.
Performance differences between scenarios with varying hinterland shipment volume.

Table 5.
Performance differences between scenarios with varying marine-fuel emission factor.

Table 6.
Performance differences between three scenarios with varying marine fuel unit cost.

Table 7.
Performance differences between scenarios with varying THC reduction at Liverpool.

Table 8.
Performance differences between scenarios with varying modal-split at Liverpool.
4.1. Sensitivity of Performance Differences to the Deep-Sea Vessel Speed
In this subsection, the deep-sea vessel’s sailing speed sd1 varies from 22, 20, 18, 16, to 14 knots. Lower speeds represent the slower steaming practices that shipping lines may adopt in response to the IMO’s decarbonization requirements. Other parameters are fixed as follows: dd1 = 26,000, h = 2000, Km = 1.2, Cfuel = 1000, W1 − W2 = 15, modalSplit2 = 0.1. Table 2 gives the performance differences between Scenarios 2 and 3 compared to Scenario 1 for individual cost components, total relevant cost, individual CO2 emission components, and total relevant CO2 emissions. To visualize the trend with respect to deep-sea vessel speed more intuitively, the total cost differences (i.e., TRC2−TRC1, TRC3−TRC1) are shown in Figure 3a, and the total emission differences (i.e., TRE2−TRE1, TRE3−TRE1) are shown in Figure 3b.
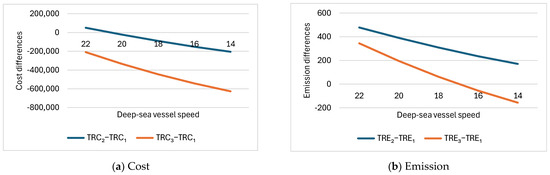
Figure 3.
Total relevant cost and emission differences between Scenarios 2 and 3 compared to Scenario 1 with varying deep-sea vessel speed.
Table 2 and Figure 3a show that as the deep-sea vessel speed in the base scenario decreases, the total relevant cost and CO2 emissions for Scenarios 2 and 3 compared to the base scenario also decrease. This observation supports Proposition 1(i) and Proposition 2(i). The results indicate that slower steaming practices would favor rerouting to regional ports from both economic and emissions perspectives.
Economically, the base scenario is more favorable than Scenario 2 when sd1 is 22 knots. However, Scenario 2 outperforms the base scenario when sd1 is 20 knots or less. This is because extra slow steaming reduces marine fuel costs, making the deviation of the Asia–Europe route to Liverpool economically viable. Scenario 3 outperforms the base scenario for all sailing speeds in the experiments.
From the emissions perspective, Table 2 and Figure 3b show that the base scenario outperforms Scenario 2 in all sailing speeds, emitting 170 to 478 tonnes less CO2. It also outperforms Scenario 3 when sd1 is 18 knots or above. However, Scenario 3 outperforms the base scenario at sd1 = 16 knots or less. In Scenario 2, the Asia–Europe service route calls at Liverpool instead of Southampton. The results in Table 2 indicate that this rerouting option would increase emissions from deep-sea services and road transport while reducing emissions from port operations, feeder services, and rail transport. However, the increase in deep-sea and road transport emissions outweighs the decreases in other areas, resulting in an overall increase in total CO2 emissions across the entire CSSC. The increase in road transport emissions and the decrease in rail transport emissions are partially due to the significantly lower percentage of rail transport usage at Liverpool. Note that Liverpool’s rail modal shift is only 10%, compared to Southampton’s 30%. In contrast, in Scenario 3, where the Asia–Europe service route calls at both Liverpool and Southampton, the CO2 emissions from ports, feeder services, road transport, and rail transport are all lower than that in the base scenario, except for the deep-sea service emissions.
4.2. Sensitivity of Performance Differences to the Round-Trip Distance in Deep-Sea Service
In this subsection, the round-trip journey distance for the deep-sea service dd1 varies from 22,000, 24,000, 26,000, 28,000 and 30,000 nautical miles. Lower distances represent shipping routes via Suez Canal; higher distances represent shipping routes via Cape of Good Hope. Other parameters are fixed as follows: sd1 = 18, h = 2000, Km = 1.2, Cfuel = 1000, W1 − W2 = 15, modalSplit2 = 0.1. Table 3 gives the performance differences between Scenarios 2 and 3 compared to Scenario 1 for individual cost components, total relevant cost, individual CO2 emission components, and total relevant CO2 emissions. To visualize the sensitivity of the performance differences to deep-sea route round-trip distance more intuitively, the total cost differences (i.e., TRC2−TRC1, TRC3−TRC1) are shown in Figure 4a, and the total emission differences (i.e., TRE2−TRE1, TRE3−TRE1) are shown in Figure 4b.
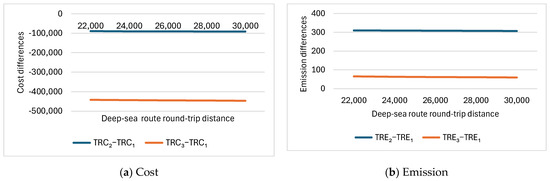
Figure 4.
Total relevant cost and emission differences between Scenarios 2 and 3 compared to Scenario 1 with varying deep-sea route round-trip distance.
Table 3 shows that as the round-trip journey distance in the base scenario increases, the total relevant costs and CO2 emissions for Scenarios 2 and 3 compared to the base scenario decrease. This observation supports Proposition 1(ii) and Proposition 2(ii). However, the impacts are minor as shown in Figure 4. This indicates that the relative performances between scenarios are less sensitive to the deep-sea route round-trip distance. In all cases, both Scenario 2 and Scenario 3 outperform the base scenario economically but underperform the base scenario in terms of CO2 emissions. The rerouting Scenario 3 is significantly better than the rerouting Scenario 2 both economically and environmentally.
4.3. Sensitivity of Performance Differences to the Hinterland Shipment Volume
In this subsection, the hinterland shipment volume h varies from 2000, 2500, 3000, to 3500 TEUs. Other parameters are fixed as follows: sd1 = 18, dd1 = 26,000, Km = 1.2, Cfuel = 1000, W1 − W2 = 15, modalSplit2 = 0.1. Table 4 gives the performance differences between Scenarios 2 and 3 compared to Scenario 1 for individual cost components, total relevant cost, individual CO2 emission components, and total relevant CO2 emissions. The total cost differences (i.e., TRC2−TRC1, TRC3−TRC1) are visualized in Figure 5a, and the total emission differences (i.e., TRE2−TRE1, TRE3−TRE1) are shown in Figure 5b.
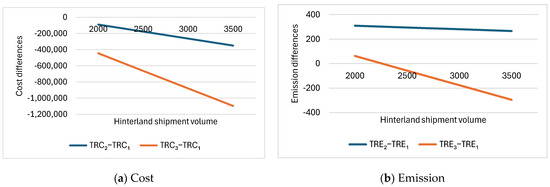
Figure 5.
Total relevant cost and emission differences between Scenarios 2 and 3 compared to Scenario 1 with varying hinterland shipment volume.
It can be observed from Table 4 and Figure 5 that, as the volume of hinterland shipments increases, the total relevant costs and CO2 emissions for Scenario 2 and Scenario 3 compared to the base scenario are decreasing, while the performance difference between Scenario 3 and the base scenario is significantly more sensitive than that between Scenario 2 and Scenario 1. A higher hinterland shipment volume would favor rerouting to regional ports from both economic and emissions perspectives.
Economically, both Scenario 2 and Scenario 3 outperform the base scenario in all cases. However, from the emission perspective, the base scenario outperforms Scenario 2 in all cases. In contrast, Scenario 3 outperforms the base scenario environmentally when hinterland shipment volume increases to 2500 TEUs or above.
4.4. Sensitivity of Performance Differences to Marine-Fuel Emission Factor
In this subsection, the marine-fuel emission factor Km varies from 1.2, 1.0, 0.8, to 0.6 gCO2/g, representing different levels of carbon emissions from low-carbon fuels. Other parameters are fixed as follows: sd1 = 18, dd1 = 26,000, h = 2000, Cfuel = 1000, W1 − W2 = 15, modalSplit2 = 0.1. Table 2 gives the performance differences between Scenarios 2 and 3 compared to Scenario 1 for individual cost components, total relevant cost, individual CO2 emission components, and total relevant CO2 emissions. The total emission differences (i.e., TRE2−TRE1, TRE3−TRE1) are visualized in Figure 6.
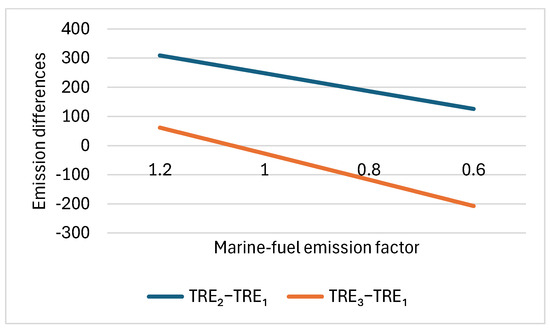
Figure 6.
Total relevant emission differences between Scenarios 2 and 3 compared to Scenario 1 with varying marine-fuel emission factor.
From Table 5, it can be observed that as the marine-fuel emission factor decreases, the cost differences between the rerouting scenarios and the base scenario remain unchanged; Scenarios 2 and 3 are consistently more economically favorable than the base scenario across all cases. From an emissions perspective, the emission difference decreases as the marine-fuel emission factor decreases (Table 5 and Figure 6). This indicates that a lower marine fuel emission factor would favor rerouting to regional ports from an emissions perspective. The base scenario outperforms Scenario 2 in all cases. In contrast, Scenario 3 becomes environmentally preferable to the base scenario when the emission factor drops to 1.0 or below.
4.5. Sensitivity of Performance Differences to Marine-Fuel Unit Cost
In this subsection, the marine-fuel unit cost Cfuel varies from 1000, 900, 800, to 700 USD/ton. Lower unit costs represent that low-carbon alternative fuels might become cheaper as they scale up in the future. Other parameters are fixed as follows: sd1 = 18, dd1 = 26,000, h = 2000, Km = 1.2, W1 − W2 = 15, modalSplit2 = 0.1. Table 6 gives the performance differences between Scenarios 2 and 3 compared to Scenario 1 for individual cost components, total relevant cost, individual CO2 emission components, and total relevant CO2 emissions. The total cost differences (i.e., TRC2−TRC1, TRC3−TRC1) are visualized in Figure 7.
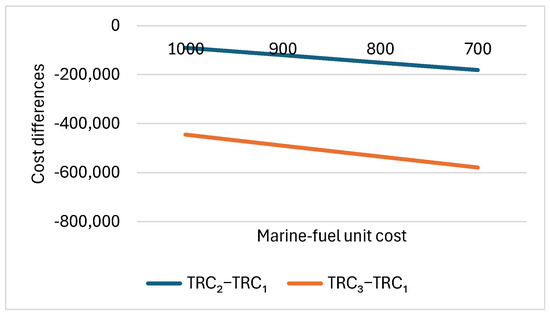
Figure 7.
Total relevant cost differences between Scenarios 2 and 3 compared to Scenario 1 with varying marine-fuel unit cost.
As the marine-fuel unit cost decreases, the cost differences between the rerouting scenarios and the base scenario decrease (Table 6 and Figure 7), while the emission differences remain unchanged (Table 6). This indicates that a lower marine-fuel unit cost would favor rerouting to regional ports from an economic perspective. Both Scenario 2 and Scenario 3 are more economically favorable than the base scenario in all tested cases. From an emissions perspective, the base scenario outperforms both Scenarios 2 and 3 in all cases.
4.6. Sensitivity of Performance Differences to THC Reduction at Liverpool
In this subsection, the terminal handling charge reduction at Liverpool W1 − W2 varies from 15, 20, 25, to 30 USD/TEU. The reduction in THC at Liverpool can reflect the economy of scale at the port of Liverpool, i.e., as port handling volumes grow due to rerouting, the unit cost of handling would reduce. Other parameters are fixed as follows: sd1 = 18, dd1 = 26,000, h = 2000, Km = 1.2, Cfuel = 1000, modalSplit2 = 0.1. Table 7 gives the performance differences between Scenarios 2 and 3 compared to Scenario 1 for individual cost components, total relevant cost, individual CO2 emission components, and total relevant CO2 emissions. In addition, the total cost differences (i.e., TRC2−TRC1, TRC3−TRC1) are visualized in Figure 8.
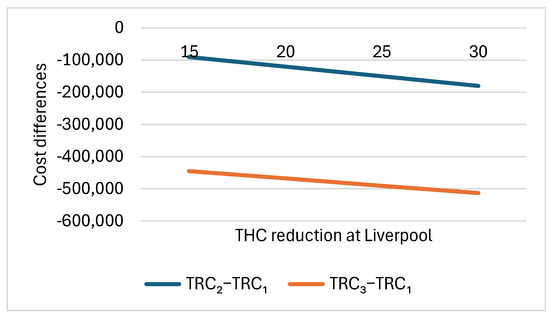
Figure 8.
Total relevant cost differences between Scenarios 2 and 3 compared to Scenario 1 with varying THC reduction at Liverpool.
As the THC reduction at Liverpool increases, the cost differences between the rerouting scenarios and the base scenario decrease (Table 7 and Figure 8), while the emission differences remain unchanged (Table 7). This indicates that a higher THC reduction at Liverpool would favor rerouting to regional ports from an economic perspective. Economically, both Scenarios 2 and 3 are more favorable than the base scenario in all cases. On the other hand, from an emissions perspective, the base scenario outperforms both Scenarios 2 and 3 in all cases.
4.7. Sensitivity of Performance Differences to Modal-Split at Liverpool
In this subsection, the rail modal rate modalSplit2 varies from 0.1, 0.2, to 0.3. Low level 0.1 represents the current situation at Liverpool, while high level 0.3 represents the current situation at Southampton. Other parameters are fixed as follows: sd1 = 18, dd1 = 26,000, h = 2000, Km = 1.2, Cfuel = 1000, W1 − W2 = 15. Table 8 gives the performance differences between Scenarios 2 and 3 compared to Scenario 1 for individual cost components, total relevant cost, individual CO2 emission components, and total relevant CO2 emissions. The total cost differences (i.e., TRC2−TRC1, TRC3−TRC1) are visualized in Figure 9a, and the total emission differences (i.e., TRE2−TRE1, TRE3−TRE1) are shown in Figure 9b.
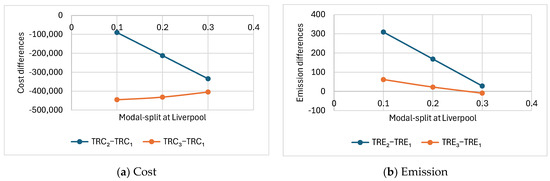
Figure 9.
Total relevant cost and emission differences between Scenarios 2 and 3 compared to Scenario 1 with varying modal-split at Liverpool.
It can be observed from Table 8 and Figure 9 that, economically, as the rail usage at Liverpool increases towards the level at Southampton, the relative total relevant cost between Scenario 2 and the base scenario decreases, while the relative total relevant cost between Scenario 3 and the base scenario slightly increases. Both Scenario 2 and Scenario 3 significantly outperform the base scenario in all cases. From the emission perspective, as the rail usage at Liverpool increases towards the level at Southampton, the relative total relevant emissions between Scenarios 2 and 3 compared to the base scenario are decreasing. The base scenario outperforms the rerouting scenarios in all cases except the case when the rail usage at Liverpool matches the level at Southampton under Scenario 3. In general, a higher rail usage at Liverpool would favor rerouting to regional ports from both economic and emissions perspectives.
4.8. Managerial Insights and Policy Implications: Viability of Rerouting to Regional Ports
Key findings under baseline parameters
The following parameter setting reflects near-current operations: deep-sea vessel speed sd1 = 18 knots, the round-trip distance in deep-sea service dd1 = 26,000 nautical miles, the hinterland shipment volume h = 2000 TEUs, the CO2 emission factor of marine fuel Km = 1.2 gCO2/g, the marine fuel cost per tonne Cfuel = 1000 USD/ton, the reduction in terminal handling charge at Liverpool W1 − W2 = 15 USD/TEU, and the modal split at Liverpool modalSplit2 = 0.1. Under this parameter setting, the key findings include the following:
- Economic viability: Rerouting to Liverpool yields significant cost savings under both scenarios, saving USD 90,201 in Scenario 2 and USD 445,060 in Scenario 3. This confirms commercial viability under current market conditions.
- Environmental trade-off: Rerouting increases total supply chain CO2 emissions by 309 tonnes and 62 tonnes more for Scenario 2 and Scenario 3, respectively. This creates a cost–emissions trade-off for decision-makers.
Strategic levers for enhancing rerouting viability
Slower steaming practices, higher hinterland shipment volume, and increasing rail usage at Liverpool have a significant positive impact on the competitiveness of regional ports, both economically and environmentally. This implies that extra slowing steaming, increasing hinterland shipment volume, and increasing rail modal shift would favor rerouting to regional ports from both economic and emissions perspectives.
The use of alternative marine fuels with lower carbon emission factors would favor rerouting to regional ports from an emissions perspective. This implies that as near or net zero marine fuels are adopted in the future, rerouting to regional ports tends to be more favorable environmentally.
Decreasing marine-fuel unit cost or reducing terminal handling charge at Liverpool will favor rerouting to Liverpool from an economic perspective.
The relative performances between the rerouting scenarios and the base scenario are less sensitive to the deep-sea route round-trip distance. A longer distance of the deep-sea service route has a minor positive impact on the competitiveness of regional ports, both economically and environmentally.
The above findings can be summarized in Table 9.

Table 9.
Key factors influencing costs and emissions of rerouting to Liverpool.
Managerial and policy recommendations
Prioritize dual-benefit levers: Investing in rail infrastructure, incentivizing slower steaming, and fostering hinterland cargo consolidation can improve both cost and emissions performance simultaneously.
Accelerate greener fuel adoption: Policy support (subsidies, mandates) for near-zero emission marine fuels is essential to resolve the emissions trade-off and make rerouting environmentally sustainable.
Optimize port economics: Regional ports should strategically improve efficiency and offer competitive terminal handling charges to attract deep-sea services.
Implement a consolidated UK service model: An alternative rerouting scenario can be designed by introducing a rotating call pattern alternating between Southampton and Liverpool on a single Asia–Europe service. This new alternative is highly likely to be both economically and environmentally viable, allowing UK hinterland shipments to be consolidated and served more efficiently based on their proximity to these two ports. However, this scenario implies that shippers will be served bi-weekly rather than weekly.
5. Conclusions
This paper adopts a container shipping supply chain perspective to analyze the total costs and CO2 emissions, and to evaluate the economic and environmental viability of rerouting shipping services to call at regional or secondary container ports in the era of adopting low-carbon alternative fuels. The Port of Liverpool and Asia–Europe service routes are used as a case study. The main contributions and managerial insights of this study are summarized as follows:
- We present a straightforward and practical approach based on scenario analysis to evaluate the viability of rerouting shipping services to regional or secondary ports from a container shipping supply chain perspective. This scenario-based analysis approach is broadly applicable to regional and secondary ports beyond the case study and is easy for shipping lines to implement, enabling incremental adjustments to their existing service routes. For example, our analysis is based on the use of biofuel, and it can be easily extended to other alternative fuels such as LNG and methanol.
- The results reveal that shipping lines’ slow steaming practices, the hinterland shipment volume, and the modal shift at regional ports can significantly influence the competitiveness of regional ports, both economically and environmentally.
- Two rerouting options are compared to the base scenario in the case study. The first option (Scenario 2) involves replacing Southampton with Liverpool in the Asia–Europe service routes. The second option (Scenario 3) adjusts the Asia–Europe service routes to call at both Liverpool and Southampton. The experiments show that both rerouting scenarios are economically viable in all tested cases except for one case (where sd1 = 22 knots in Scenario 2). From the emissions perspective, Scenario 2 is not viable in all tested cases, while Scenario 3 becomes environmentally viable when the deep-sea vessel speed is less than 16 knots, or the hinterland shipment volume reaches 2500 TEUs, or the marine-fuel emission factor is less than 1.0, or Liverpool’s rail usage matches Southampton’s level. Combining these factors would further enhance Scenario 3′s environmental viability relative to the base scenario.
- A two-port strategy, either in the form of Scenario 3 or by alternating calls between Southampton and Liverpool, is a preferable rerouting option. Such a strategy would offer more economic benefits than Scenario 2 and is likely to achieve environmental benefits compared to the base scenario. This may explain recent industrial practices, such as MSC launching a new Asia–Europe service route (termed the Britannia Service) that simultaneously calls at Liverpool and London Gateway, which started in July 2024. It also aligns with the views of some UK retailers who are urging shipping lines to adopt a two-port strategy—calling at both northern and southern ports—to save costs and reduce emissions [39].
It should be noted that this study has several implications that require further research. Firstly, the hinterland shipment distribution is based on the entire UK container import market across all shipping service routes [38], which may not accurately represent the Asia–Europe shipping route. Secondly, our inland container transport analysis relies on rail–road modal splits of 0.3:0.7 at Southampton and 0.1:0.9 at Liverpool. In practice, ports may implement incentive schemes to encourage a modal shift towards rail. For example, Southampton increased the share of rail freight from 21% to 30% through the launch of the Modal Shift Programme in September 2023, offering a GBP 70 subsidy for each container transported by rail within a range of 225 km. It is plausible that other ports may introduce similar schemes. The impact of such incentives on shipping service rerouting warrants further investigation. Thirdly, greater granularity in data would enable a more accurate comparison between different scenarios, e.g., inland container transportation between ports and customers, and port handling times. Fourthly, our study adopts scenario-based analysis; it does not involve advanced optimization of ship routing and scheduling, fleet deployment, and alternative fuel selection [40]. Further research could be conducted in this direction.
Funding
This work was partially supported by the UK Department for Transport, as part of the UK Shipping Office for Reducing Emissions (UK SHORE) Programme and the UK Engineering and Physical Sciences Research Council (EPSRC) [Grant No: EP/Y024605/1], and a combined EPSRC and ESRC Impact Acceleration Account grant: EP/X525741/1 and ES/X004910/1.
Data Availability Statement
Data can be provided upon request.
Conflicts of Interest
The author declares no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| CSSC | Container Shipping Supply Chain |
| IMO | International Maritime Organization |
| LNG | Liquefied Natural Gas |
| CII | Carbon Intensity Indicator |
| MSC | Mediterranean Shipping Company |
| HMM | Hyundai Merchant Marine |
| TEU | Twenty-foot Equivalent Unit |
References
- Svindland, M.; Monios, J.; Hjelle, H.M. Port rationalization and the evolution of regional port systems: The case of Norway. Marit. Policy Manag. 2019, 46, 613–629. [Google Scholar] [CrossRef]
- Van Marle, G. Singapore to Gain Six Asia-North Europe Calls in Alliance Reshuffle. The Loadstar. 2024. Available online: https://theloadstar.com/singapore-to-gain-six-asia-north-europe-calls-in-alliance-reshuffle/ (accessed on 18 September 2024).
- Wiegmans, B.W.; Hoest, A.V.D.; Notteboom, T.E. Port and terminal selection by deep-sea container operators. Marit. Policy Manag. 2008, 35, 517–534. [Google Scholar] [CrossRef]
- Song, D.P. Container Logistics and Maritime Transport; Routledge: London, UK, 2021. [Google Scholar]
- Cantillo, J.; Cantillo-García, V.; Cantillo, V.; Arellana, J. Port choice using aggregate open data: An application to Colombian port zones. Marit. Econ. Logist. 2023, 25, 520–548. [Google Scholar] [CrossRef]
- Tongzon, J.; Heng, W. Port privatization, efficiency and competitiveness: Some empirical evidence from container ports (terminals). Transp. Res. Part A 2005, 39, 405–424. [Google Scholar] [CrossRef]
- Yeo, G.T.; Roe, M.; Dinwoodie, J. Evaluating the competitiveness of container ports in Korea and China. Transp. Res. Part A 2008, 42, 910–921. [Google Scholar] [CrossRef]
- Notteboom, T.; Yap, W.Y. Port competition and competitiveness. In The Blackwell Companion to Maritime Economics; Tally, W., Ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2012; pp. 549–570. [Google Scholar]
- Caballé Valls, J.; de Langen, P.W.; García Alonso, L.; Vallejo Pinto, J.A. Understanding Port Choice Determinants and Port Hinterlands: Findings from an Empirical Analysis of Spain. Marit. Econ. Logist. 2020, 22, 53–67. [Google Scholar] [CrossRef]
- Lagoudis, I.N.; Theotokas, I.; Broumas, D. A literature review of port competition research. Int. J. Shipp. Transp. Logistics. 2017, 9, 724–762. [Google Scholar] [CrossRef]
- Lee, P.W.; Lam, J. Container port competition and competitiveness analysis: Asian major ports. In Handbook of Ocean Container Transport Logistics; Lee, C.Y., Meng, Q., Eds.; International Series in Operations Research & Management Science; Springer International Publishing AG: Cham, Switzerland, 2015; Volume 220. [Google Scholar]
- Cullinane, K.; Teng, Y.; Wang, T.F. Port competition between Shanghai and Ningbo. Marit. Policy Manag. 2005, 32, 331–346. [Google Scholar] [CrossRef]
- De Borger, B.; Proost, S.; Van Dender, K. Private port pricing and public investment in port and hinterland capacity. J. Transp. Econ. Policy 2008, 42, 527–561. [Google Scholar] [CrossRef]
- Li, J.B.; Oh, Y.S. A research on competition and cooperation between Shanghai port and Ningbo-Zhoushan port. Asian J. Shipp. Logist. 2010, 26, 67–91. [Google Scholar] [CrossRef]
- Luo, M.; Liu, L.; Gao, F. Post-entry container port capacity expansion. Transp. Res. Part B 2012, 46, 120–138. [Google Scholar] [CrossRef]
- Song, D.; Lyons, A.; Li, D.; Sharifi, H. Modelling port competition from a transport chain perspective. Transp. Res. Part E Logist. Transp. Rev. 2016, 87, 75–96. [Google Scholar] [CrossRef]
- Pujats, K.; Golias, M.; Konur, D. A review of game theory applications for seaport cooperation and competition. J. Mar. Sci. Eng. 2020, 8, 100. [Google Scholar] [CrossRef]
- Brouer, B.D.; Alvarez, J.F.; Plum, C.E.M.; Pisinger, D.; Sigurd, M.M. A base integer programming model and benchmark suite for liner-shipping network design. Transp. Sci. 2014, 48, 281–312. [Google Scholar] [CrossRef]
- Meng, Q.; Wang, S.; Andersson, H.; Thun, K. Containership routing and scheduling in liner shipping: Overview and future research directions. Transp. Sci. 2014, 48, 265–280. [Google Scholar] [CrossRef]
- Tran, N.K.; Haasis, H.D. Literature survey of network optimization in container liner shipping. Flex. Serv. Manuf. J. 2015, 27, 139–179. [Google Scholar] [CrossRef]
- Lee, C.Y.; Song, D. Ocean Container Transport in Global Supply Chains: Overview and Research Opportunities. Transp. Res. Part B Methodol. 2017, 95, 442–474. [Google Scholar] [CrossRef]
- Mollaoglu, M.; Altay, B.C.; Balin, A. Bibliometric review of route optimization in maritime transportation: Environmental sustainability and operational efficiency. Transp. Res. Rec. 2023, 2677, 879–890. [Google Scholar] [CrossRef]
- Song, D. A literature review, container shipping supply chain: Planning problems and research opportunities. Logistics 2021, 5, 41. [Google Scholar] [CrossRef]
- Tavasszy, L.A.; Minderhoud, M.; Perrin, J.-F.; Notteboom, T. A strategic network choice model for global container flows: Specification, estimation and application. J. Transp. Geogr. 2011, 19, 1163–1172. [Google Scholar] [CrossRef]
- Liu, Z.; Meng, Q.; Wang, S.; Sun, Z. Global intermodal liner shipping network design. Transp. Res. Part E 2014, 61, 28–39. [Google Scholar] [CrossRef]
- Tran, N.; Haasis, H.D.; Buer, T. Container shipping route design incorporating the costs of shipping, inland/feeder transport, inventory and CO2 emission. Marit. Econ. Logist. 2017, 19, 667–694. [Google Scholar] [CrossRef]
- De Almeida Rodrigues, T.; Maria de Miranda Mota, C.; Ojiako, U.; Chipulu, M.; Dweiri, F.; Marshall, A. Competitiveness throughout the seaport-hinterland: A container shipping analysis. Marit. Policy Manag. 2023, 51, 1170–1189. [Google Scholar] [CrossRef]
- CILT. Peel’s Liverpool2 Project to Cut Carbon Emissions. Available online: https://ciltuk.org.uk/News/News-Centre/ArtMID/7018/ArticleID/6269/Peel%e2%80%99s-Liverpool2-project-to-cut-carbon-emissions (accessed on 6 May 2015).
- Song, D.P.; Dong, J.X. Long-haul liner service route design with ship deployment and empty container repositioning. Transp. Res. Part B 2013, 55, 188–211. [Google Scholar] [CrossRef]
- Ronen, D. The effect of oil price on containership speed and fleet size. J. Oper. Res. Soc. 2011, 62, 211–216. [Google Scholar] [CrossRef]
- Shintani, K.; Imai, A.; Nishimura, E.; Papadimitriou, S. The container shipping network design problem with empty container repositioning. Transp. Res. Part E 2007, 43, 39–59. [Google Scholar] [CrossRef]
- Samuelson, R.D.; Wang, H. Comparing freight transport emissions by mode. In Proceedings of the Transportation 2021 Conference, Hilton Auckland, New Zealand, 9–12 May 2021. [Google Scholar]
- ORR. Rail Emissions 2020-21. Office of Rail and Road. 2021. Available online: https://dataportal.orr.gov.uk/media/1993/rail-emissions-2020-21.pdf (accessed on 1 August 2024).
- DNV. Biofuels in Shipping. White Paper. 2025. Available online: https://www.naucher.com/wp-content/uploads/2025/01/Biofuel_whitepaper_2025.pdf (accessed on 1 May 2025).
- HiFleet. 2025. Available online: http://www.hifleet.com (accessed on 1 June 2025).
- Starcrest Consulting Group. Inventory of Air Emissions 2023 for the Port of Los Angeles, Technical Report. 2024. Available online: https://kentico.portoflosangeles.org/getmedia/3fad9979-f2cb-4b3d-bf82-687434cbd628/2023-air-emissions-inventory (accessed on 1 May 2025).
- UK Department for Energy Security & Net Zero. Government Conversion Factors for Company Reporting of Greenhouse Gas Emissions. 2013. Available online: https://www.gov.uk/government/collections/government-conversion-factors-for-company-reporting (accessed on 1 May 2025).
- Rodrigues, V.S.; Beresford, A.; Pettit, S.; Bhattachary, S.; Harris, I. Assessing the cost and CO2e impacts of rerouteing UK import containers. Transp. Res. Part A Policy Pract. 2014, 61, 53–67. [Google Scholar] [CrossRef]
- Goldstone, C. UK Retailers Call for Two-port Strategy to Save Costs and Emissions, The Loadstar. 2024. Available online: https://theloadstar.com/uk-retailers-call-for-two-port-strategy-to-save-costs-and-emissions/ (accessed on 6 March 2024).
- Wang, Y.; Iris, C. Transition to near-zero emission shipping fleet powered by alternative fuels under uncertainty. Transp. Res. Part D Transp. Environ. 2025, 142, 104689. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).