Gresilient Supplier Evaluation and Selection under Uncertainty Using a Novel Streamlined Full Consistency Method

Abstract

Background: Supply chain management (SCM) plays a fundamental role in the progress and success of organizations and has continuously evolved to better adapt to today’s complex business environments. Consequently, the issue of supplier evaluation and selection (SES), which is one of the most critical decisions in SCM, has gained special significance and has been examined from various perspectives. The concept of green and resilient (gresilient) SCM has emerged in response to recent concerns about environmentally friendly production and operations, as well as organizations’ ability to cope with crises and disasters. In the rapidly growing construction industry, applying gresilient principles can ensure green operations and help overcome future challenges. Methods: This study focuses on gresilient SES in a real-world construction case study, proposing a streamlined FUCOM (S-FUCOM) approach. The proposed method streamlines traditional FUCOM processes to solve decision-making problems in deterministic and uncertain environments. Several numerical examples are provided to illustrate its applicability. Results: the case study results identify air emissions, environmental management systems, and restorative capacity as the most critical gresilient SES criteria. Conclusions: The third supplier emerged as the top performer based on decision-making indicators. Finally, a sensitivity analysis was conducted across 20 scenarios, demonstrating that S-FUCOM is robust and provides stable results.

1. Introduction

Green and resilient (gresilient) supplier evaluation and selection (SES) is a crucial strategic decision. This is because adhering to gresilient principles has become a key strategic focus in business organizations for improving the environment, economic performance, and resilience to crises [1,2]. Green supply chain management (SCM) is defined as a set of processes and flows considering environmental aspects throughout the supply chain [3]. Also, resilient SCM reflects the adaptive capacity of the supply chain to prepare for unexpected events, respond to disruptions, return to desirable conditions while maintaining operational continuity, and exert maximum control over structure and performance [4]. The green and resilience paradigms have an interdependent relationship and should be considered simultaneously [5,6].

Organizations that utilize green suppliers who also satisfy resilience principles not only address environmental and green requirements but have also become more resistant to numerous challenges and obstacles. Suppliers are the primary drivers of production processes and operations, acting as the input to the supply chain. Consequently, an SCM system that leverages suppliers committed to green and resilience principles against crises takes a significant step towards achieving gresilient supply chain management (GSCM). The process of evaluating and selecting gresilient suppliers, although potentially costly for the organization, should be considered a forward-looking investment. Over the past two decades, businesses have experienced several transformations and changes that have increasingly exposed companies to new challenges, such as globalization. Consequently, the market has become highly challenging and competitive, necessitating modern SCM to adapt to dynamic business environments. Evaluating and selecting suppliers, as one of the critical decisions in SCM, requires strengthening the structure and the execution process [7,8].

Due to the expansion of sourcing processes on a global scale, supply chain risks have also increased correspondingly. The processes within the supply chain, from the first supplier to the end consumer, are influenced by crises and unexpected events such as pandemics, floods, earthquakes, and more. Therefore, supply chains (SCs) aim to confront these challenges and minimize the unforeseen damages to production and supply processes [9]. To address these challenges, one effective approach within SCs is implementing gresilient strategies, which incorporate green and resilience criteria throughout the chain. In this way, manufacturing organizations and factories across various industries are obliged to implement and adhere to principles of greenness and resilience. For example, by considering green criteria, SCs prioritize purchasing environmentally friendly raw materials, and to mitigate risks associated with unexpected disruptions and future crises, they utilize resilience principles [6,10]. Green SCM is recognized as a convergence point alongside resilience in the supply chain [11,12,13]. The results of studies examining organizations that have developed their SCM within the gresilient context indicate that the integration of greenness and resilience has led to significant synergy and convergence in organizational processes and operations. Not only has the organization’s overall operation become more environmentally conscious and green-oriented, but its resilience and ability to cope with crises have also been enhanced.

Several research gaps remain unresolved in the SES issue. The vast majority of studies in the field of SES have considered the dimensions of greenness and resilience as two separate branches. However, the performance of a green supply chain is exposed to multiple potential internal and external risks. In fact, green SCM is constrained by numerous inevitable disruptions, increasing the need for a flexible framework that can withstand these challenges [14]. Therefore, an integrated approach combining gresilient aspects is essential for the evolution of SCs [15]. Additionally, each supply chain and industry require unique research to identify gresilient supplier evaluation criteria and analyze the relevant results. Brandenburg and Rebs [16] conducted a review study on SCs, examining 185 articles over the past 20 years that utilized quantitative models. They highlighted the need for future research to focus on integrating greenness, resilience, and sustainability in SCs using quantitative approaches. Additionally, the methodologies employed to address the issue of SES are still evolving to better handle uncertainties and ambiguities in information. Developing effective and efficient methodologies that can successfully manage the SES process and produce and analyze reliable results remains a significant research gap in this field.

The issue of SES is inherently a multi-criteria decision-making (MCDM) problem [17]. In SES, multiple suppliers are typically evaluated and prioritized based on various criteria. Organizations leverage their sourcing experts to identify, evaluate, select, and contract with suppliers. Given that SES is a critical decision, potentially accounting for up to 70% of total costs [18], this process necessitates the use of appropriate tools, effective decision-support frameworks, and consideration of all deterministic factors as well as the anticipation of as many uncertain factors as possible. The use of MCDM methods in SES is particularly valued for their ability to support decision makers and aid them in making appropriate decisions [19].

The main objective of this study is to address the SES issue by introducing a novel approach based on the full consistency method (FUCOM) proposed by [20]. FUCOM is a pairwise comparison-based MCDM approach that offers several advantages over other pairwise comparison-based methods. A significant reduction in the number of pairwise comparisons required, less need for information to conduct the decision-making process, and comprehensible steps are among the benefits of this approach. In this study, a streamlined version of FUCOM (S-FUCOM) is developed, and the steps of its implementation are described. The proposed approach is a simplified version of FUCOM that preserves all its advantages and eliminates the need for formulating and solving mathematical optimization models. Additionally, it can determine the final weights of decision criteria using simple algebraic relationships and operators, providing results consistent with the original FUCOM. This simplification facilitates the decision-making process, adding a significant advantage over the original FUCOM. Moreover, to address the uncertainties inherent in the SES process, the S-FUCOM method utilizes triangular fuzzy numbers (TFNs) in fuzzy environments. The details and comprehensive explanation of the proposed approach are presented in Section 3. To illustrate the proposed approach and demonstrate its applicability and capabilities, several numerical examples are used. Additionally, the proposed approach is employed in a real-world case study to address the SES issue in a company operating in the construction industry, and the results are analyzed. Considering the aforementioned points, the contributions and innovations of this study are summarized as follows:

• The identification and prioritization of gresilient supplier evaluation criteria in a real-world case study in the construction industry, achieved through a literature review and the input of experienced experts in the field.
• The introduction of a novel approach, based on FUCOM, to prioritize decision-making criteria and rank suppliers without the need for formulating and solving mathematical optimization models, featuring simplified calculations and reduced complexity.
• The development of a streamlined decision support system for solving various MCDM problems in both deterministic and non-deterministic environments, with the capability to adapt to a wide range of linguistic terms and their precise and imprecise numerical counterparts.
• The validation and assessment of the proposed approach’s applicability through multiple numerical examples and a real-world case study, including a sensitivity analysis of the research results across 20 different scenarios.

Based on the discussed research gaps and the characteristics of this study, the main research questions are formulated as follows:

• RQ1: What are the criteria for evaluating and selecting gresilient suppliers in the construction industry?
• RQ2: How is the process of weighting evaluation criteria and prioritizing suppliers conducted?
• RQ3: How will the development of the streamlined FUCOM approach be structured, what are its steps, and how will it be implemented?

The remainder of the paper is structured as follows: Section 2 reports the literature review on the issue of gresilient SES, highlighting key points and details of the research conducted in this field. Section 3 explains the proposed approach and demonstrates the steps required for the decision-making process. Numerous numerical examples in deterministic and non-deterministic decision-making spaces are provided in Section 4. Section 5 elaborates on the real-world case study concerning the gresilient SES issue, focusing on the weighting of criteria and ranking of suppliers. Section 6 analyzes the sensitivity of the research results. The research results are discussed in Section 7, and, finally, Section 8 presents the conclusions, limitations, and directions for future research.

2. Literature Review

The primary objective of this research is to evaluate and select gresilient suppliers using the proposed S-FUCOM approach. Integrating the green aspects of the supply chain with the resilience aspects can lead to better long-term performance of the supply chain. Therefore, the concept of gresilient SCs will offer superior performance compared to traditional SCs [21]. Understanding this reality entails acknowledging that environmental sustainability seeks to maintain services while balancing conventional business responsibilities and complying with green development regulations. Meanwhile, resilience emphasizes the prevention or mitigation of the effects of anticipated or unforeseen disruptions, or, at the very least, reducing their adverse impacts, to achieve the optimal goal of environmental sustainability. Consequently, resilience and greenness are the ultimate objectives of an effective SCM. To develop a supply chain capable of sustaining its capabilities, it is essential to consider both aspects concurrently [22]. It is evident that concurrently considering both green and resilience principles in SCs makes the evaluation and selection of suppliers more challenging. Therefore, the need for advanced and suitable methodologies can alleviate these challenges and facilitate the decision-making process. Therefore, this section reviews recent literature on the evaluation and selection of gresilient suppliers using MCDM approaches. By reviewing the literature in the field of gresilient SES (GSES) and the approaches employed for this purpose, the evaluation criteria for GSES are identified, and insights into the MCDM methods used are obtained. Subsequently, several conducted studies are examined, and the characteristics of each are elaborated.

Mahmoudi et al. [21] examined the impact of COVID-19 on SCs, focusing on disruptions in essential and non-essential goods. They developed a decision-making framework for supplier selection within “gresilient” SCM, integrating green and resilience aspects. Using data from a manufacturing firm, they extended the ordinal priority approach (OPA) to a fuzzy OPA (OPA-F) to address imprecise and incomplete reports, aiding procurement managers in evaluating suppliers and preparing for future disruptions. Çalık [23] developed a new group decision-making approach integrating AHP and TOPSIS under a Pythagorean fuzzy environment to select green suppliers. Their method utilized Industry 4.0 components, leveraging advanced technologies and traditional criteria. This approach expressed expert judgments using linguistic terms based on Pythagorean fuzzy numbers and applied interval-valued Pythagorean fuzzy AHP to determine criteria weights. Pythagorean fuzzy TOPSIS was used to rank suppliers. The effectiveness and accuracy of this method were validated through a real case study in an agricultural tools and machinery company. Mohammed et al. [22] studied the re-engineering of SCs to enhance both green initiatives and resilience against disruptions, emphasizing the strategic role of supplier selection. They developed an integrated framework using the analytical hierarchy process (AHP) and the technique for order of preference by similarity to the ideal solution (TOPSIS) to evaluate suppliers based on traditional, green, and resilience criteria. The study employed a multi-objective programming model and the ε-constraint method for order allocation, demonstrating this approach’s effectiveness through a real case study, aiding managers in improving supply chain resilience and sustainability.

Ghosh et al. [24] proposed a green SCM framework to evaluate supplier organizations across three industrial segments in India. They identified six key criteria encompassing environmental, economic, and operational aspects, gathering data via expert surveys. An integrated MCDM approach was employed, using the entropy method for criteria weights and various ranking techniques. The results identify the manufacturing organization as the benchmark, highlighting ‘Total energy consumption’, ‘Total scrap material generation’, and ‘Renewable energy utilization’ as critical for green supplier selection. This framework aids policymakers in developing sustainable sourcing strategies. In another study, the challenge of integrating green and resilience aspects in supplier selection was addressed by coining the term “gresilient” SCM. This study aimed to explore, identify, and quantify greenness and resilience in supplier selection, developing a framework that includes criteria like development, agility, robustness, sensing, and flexibility (DARSF). Using MCDM algorithms, a method was proposed to evaluate suppliers’ gresilience performance. The research yielded a comprehensive gresilient supplier evaluation framework and a decision-making tool, providing insights into the advantages of gresilient SCs in a competitive business environment [14]. Ecer [25] examined the application of an interval type-2 fuzzy analytical hierarchy process (IT2FAHP) model for green supplier selection, addressing ambiguity in decision making. Their study, conducted on a home appliance manufacturer, highlighted cleaner production, energy/material saving, green packaging, remanufacturing, and environmental management systems as critical factors. They demonstrated the IT2FAHP model’s effectiveness through a real case application, supported by comparison and sensitivity analyses showing consistency with existing literature models. Their findings underscore the positive impact of green product initiatives, cleaner production practices, green designs, and eco-friendly packaging on the performance of green suppliers. Javad et al. [26] investigated green supplier selection, focusing on the innovation abilities of the Khouzestan Steel Company (KSC). Their study identified alternative suppliers and determined key criteria for selection using the BWM. They applied fuzzy TOPSIS to rank suppliers based on these criteria, highlighting the importance of green innovation in supplier selection. Their findings emphasize the need for KSC to prioritize green innovation criteria. The study’s framework offers insights for selecting suppliers across various categories, including spare parts and technical services. A sensitivity analysis ensured robustness, while limitations and future research directions were discussed.

Rajesh and Ravi [27] investigated the role of suppliers as external risks in modern SCs, emphasizing the importance of resilience in supplier selection. They employed a grey relational analysis to evaluate suppliers based on qualitative and quantitative attributes, using a linguistic assessment to calculate possibility values for prioritizing suppliers. A case study in the electronic supply chain context, involving six suppliers, illustrated this method. The sensitivity analysis identified resilience attributes where suppliers excelled, and comparisons with AHP and ANP methods highlighted the grey methodology’s effectiveness. Their findings support strategic decision making in selecting resilient suppliers. In another research study, the complex proportional assessment (COPRAS) approach for MCDM under intuitionistic fuzzy information was introduced, with a novel formula developed for criterion weights, which incorporates objective weights derived from a divergence measure method. This study addressed the uncertainty inherent in MCDM problems, proposing that the COPRAS approach is a valuable tool for decision making in uncertain environments. A case study on green supplier selection demonstrated this method’s applicability, including comparisons with existing methods and sensitivity analyses to ensure stability across varying criterion weights [28]. Leong et al. [29] explored the impact of global disruptions on SCM, focusing on resilient supplier selection. They proposed combining the grey relational analysis (GRA), best–worst method (BWM), and TOPSIS to evaluate suppliers based on seven resilience criteria: Quality, Lead Time, Cost, Flexibility, Visibility, Responsiveness, and Financial Stability. Five experts provided judgments, and this method was validated through a case study in a food manufacturing company, evaluating and ranking ten suppliers. Their proposed GRA–BWM–TOPSIS method proved effective for resilient supplier selection amid uncertainties and incomplete data.

Rouyendegh et al. [30] explored green supplier selection (GSS) to enhance competitive pressures under changing competition conditions favoring environmentalism. They addressed GSS criteria by focusing on lean, agile, environmentally sensitive, sustainable, and durable practices, which differed from classical supplier selection regarding carbon footprints, water consumption, environmental applications, and recycling. Utilizing TOPSIS combined with the intuitionistic fuzzy approach, they aimed to mitigate ambiguity and instability in MCDM. Their hybrid method proved effective for selecting suitable suppliers and is adaptable to similar decision-making problems. Afrasiabi et al. [31] addressed the sustainable-resilient supplier selection problem in their study, focusing on economic, environmental, and social indicators combined with resilience, particularly in light of the COVID-19 pandemic’s impact on SCs. They proposed a hybrid fuzzy MCDM method, utilizing the fuzzy best–worst method to determine criteria importance and combining the grey relational analysis with TOPSIS to evaluate suppliers in a fuzzy environment. TFNs were used to handle ambiguity and uncertainty. Sensitivity analyses validated the framework’s robustness by altering criteria weights, comparing with other methods, and modifying the decision matrix components. Mohammed et al. [32] examined the need for food industry associations to establish gresilient SCs post-epidemic. They proposed a hybrid methodology using a fuzzy multi-objective mixed integer linear programming model (FMOMILPM) to address G-resilient supplier selection and order allocation under uncertain demands and cost conditions. Their approach included a multi-criteria framework integrating traditional, green, and resilient criteria for evaluating suppliers. FMOMILPM utilized fuzzy group decision-making and optimization techniques to minimize costs and transportation time while maximizing G-resilient purchasing values. LP metrics and ϵ-constraint methods were applied to derive Pareto solutions, validated through a UK halal food industry case study.

Hasan et al. [33] explored resilient supplier selection in Logistic 4.0 using a fuzzy MADM approach. They developed a decision support system to handle imprecise, heterogeneous data for ranking suppliers. Their framework generated TFNs from large-scale temporal data using the probability–possibility consistency principle and processed qualitative attributes through fuzzy linguistic variables. They utilized the fuzzy TOPSIS method to rank suppliers, followed by a multi-choice goal programming model to optimize order allocation. Wang et al. [34] addressed supplier selection in resilient SCM, a multi-attribute decision-making problem. They proposed using Dombi operational laws based on complex intuitionistic fuzzy (CIF) information. They introduced CIF Dombi prioritized averaging (CIFDPA) and CIF weighted Dombi prioritized averaging (CIFWDPA) operators, enhancing traditional aggregation operators for various fuzzy information types. The operators were evaluated through an applicational example for resilient green supplier selection, with a comparative analysis demonstrating the proposed method’s advantages and effectiveness. In another study, a decision-making framework was developed for selecting suppliers who are Green, Resilient, and embrace Inclusive Development (GRID). This framework included a GRID-based criteria system and utilized an enhanced BWM and TOPSIS methodology. The study employed Scenario-Varying Z-numbers (SVZs) and reversed PageRank and SVZ Preference Relations (SVZPRs) to enhance the evaluation accuracy. Dependent uncertain events were incorporated using the Stratification Theory with Z-numbers. BWM was used to determine criteria weights, and TOPSIS with SVZs ranked the suppliers accordingly. This approach was validated through comparative and sensitivity analyses [35].

Pamucar et al. [36] aimed to mitigate supply chain risks and disturbances by proposing a fuzzy neutrosophic decision-making approach for resilient SES. Their model introduced a new weight aggregator using pairwise comparisons with a Dombi aggregator, enhancing the flexibility of information aggregation through adjustable parameters. This model used an MABAC tool for analysis. This approach addressed the complexities in qualitative performance evaluations by experts through pairwise comparisons and Dombi aggregation operators. Sonar et al. [37] explored supplier selection in the LARGS (Lean, Agile, Resilient, Green, and Sustainable) paradigm amid the COVID-19 outbreak. They identified 22 key criteria for supplier selection and developed a hierarchical model using interpretive structural modelling (ISM) based on data from 12 experts. Geographic location emerged as the most crucial criterion, followed by lead time. Their findings aid practitioners in formulating strategies to enhance supply chain robustness and resilience, making this the first study to apply the LARGS paradigm for sustainable supplier selection. Xiong et al. [38] addressed the need to select resilient green suppliers for sustainable SCM. They proposed a hybrid method integrating BWM, the weighted aggregated sum product assessment (WASPAS), and TOPSIS. BWM was used to weigh the criteria, while intuitionistic fuzzy numbers aided in the ranking stage. WASPAS and TOPSIS were combined to rank alternatives and select the optimal resilient green supplier. An illustrative example demonstrated the feasibility and effectiveness of their approach.

Nasrollahi et al. [39] aimed to identify and analyze resilient supplier selection criteria in the desalination supply chain. They initially identified 89 criteria from the literature, narrowing them down to 19 main criteria. Using ISM and fuzzy DEMATEL, they identified key driving criteria. Their findings provide a framework for prioritizing criteria in resilient supplier selection, contributing to decision making in the desalination supply chain. Hailiang et al. [40] proposed a multi-stage fuzzy sustainable supplier index for supplier selection, emphasizing its importance for supply chain performance, especially during lockdowns. Their method used triple bottom-line criteria and integrated fuzzy membership functions to address uncertainties. This approach aimed to enhance selection accuracy by employing an ordered mean integration representation method. A practical case study validated this model’s effectiveness and applicability, showing its impact on improving supplier selection accuracy and contributing to the SCM literature by addressing the computational difficulties of previous methods. Taghavi et al. [41] addressed the integration of gresilient supplier selection and order allocation with vehicle routing under disruptions in SCs. They proposed a multi-product, two-stage, risk-averse mixed-integer stochastic linear programming model that considers resilient strategies like multiple sourcing and supplier fortification. The objective was to minimize the total mean-risk cost and greenhouse emissions using conditional value at risk (CvaR). Key decisions included optimal supplier determination, vehicle routing under disruption, and inventory management. Numerical examples and sensitivity analyses using the GAMS software (47.2.0) validated this model, revealing that increased risk factors and shortage costs significantly impacted the mean CVaR objective function cost, highlighting this model’s effectiveness and application. Abedian et al. [42] explored supplier selection in the electronic industry, focusing on gresilient principles. They developed an integrated decision-making method using the fuzzy set theory and data envelopment analysis (DEA). The fuzzy set theory analyzed supplier indicator weights and performance, while DEA ranked the suppliers using one dummy input and three output variables. A sensitivity analysis and validation against existing models demonstrated the effectiveness of their DEA-based approach. Their model is adaptable to various numbers of suppliers, criteria, and sub-criteria, enhancing its applicability in different contexts.

Pamucar et al. [43] addressed the critical supplier selection for medical face masks and shields during the COVID-19 pandemic, focusing on healthcare centers facing shortages. Their study developed a novel decision-making approach using measuring attractiveness through a categorical-based evaluation technique (MACBETH) and a new combinative distance-based assessment (CODAS) method. They implemented this approach under fuzzy rough numbers to handle high uncertainty and incomplete information. In another study, a decision support framework (DSF) was developed for selecting robust suppliers under lean, agile, resilient, and green (LARG) practices in the manufacturing sector. This study, conducted on the Indian automotive industry, integrated AHP, DEMATEL, ANP, Extended MOORA, and SAW techniques to evaluate suppliers. It identified 63 measures across LARG practices, with significant metrics including internal communication agility, interchangeability to personnel resources, and manufacturing flexibility. The importance of these metrics in supplier selection was highlighted, emphasizing this framework’s effectiveness in handling imprecise and uncertain decision making [44].

A summary of the reviewed studies, along with their characteristics, is presented in

Table 1. Some studies on gresilient suppliers’ evaluation and selection.

Study	Year	SES Aspect			MCDM Approach	Information Form	Application
		Green	Resilient	Gresilient
[27]	2015	□	■	□	Grey relational analysis	Grey numbers	Electronic industry
[33]	2020	□	■	□	F-TOPSIS and Goal programming	Triangular fuzzy numbers	Illustrative example
[36]	2020	□	■	□	MABAC	Trapezoidal fuzzy neutrosophic numbers	Construction industry
[38]	2020	□	□	■	BWM, WASPAS, and TOPSIS	Intuitionistic fuzzy numbers	Illustrative example
[26]	2020	■	□	□	BWM and FTOPSIS	Triangular fuzzy numbers	Steel industry
[28]	2020	■	□	□	IF-COPRAS	Intuitionistic fuzzy numbers	Illustrative example
[30]	2020	■	□	□	IF-TOPSIS	Intuitionistic fuzzy numbers	Illustrative example
[14]	2020	□	□	■	DEMATEL and VIKOR	Deterministic	Chemical industry
[23]	2021	■	□	□	FAHP and FTOPSIS	Pythagorean fuzzy numbers	Agricultural tools industry
[22]	2021	□	□	■	AHP and TOPSIS	Deterministic	Measurement equipment industry
[25]	2022	■	□	□	IT2FAHP	Interval type-2 fuzzy numbers	Home appliance industry
[31]	2022	□	■	□	FBWM, GRA, and TOPSIS	Triangular fuzzy numbers	Valves, fittings, and pipes industry
[21]	2022	□	□	■	Fuzzy OPA	Triangular fuzzy numbers	Kitchen utensils industry
[29]	2022	□	■	□	GRA–BWM–TOPSIS	Deterministic	Food industry
[24]	2023	■	□	□	Entropy, TOPSIS, an GRA	Deterministic	Several industries
[44]	2023	□	□	■	Hybrid MCDM approach	Triangular fuzzy numbers	Automotive industry
[40]	2023	□	□	■	Fuzzy BWM	Trapezoidal fuzzy numbers	Oil industry
[41]	2023	□	□	■	Stochastic linear programming model	Deterministic	Illustrative example
[42]	2023	□	□	■	DEA	Triangular fuzzy numbers	Electronic industry
[32]	2023	□	□	■	FMOMILPM	Triangular fuzzy numbers	Food industry
[34]	2023	□	□	■	Dombi operational operators	Intuitionistic fuzzy numbers	Illustrative example
[39]	2023	□	■	□	Fuzzy DEMATEL	Triangular fuzzy numbers	Desalination company
[43]	2023	□	■	□	MACBETH and CODAS	Fuzzy rough numbers	Healthcare sector
[35]	2024	□	□	■	S-BWM and TOPSIS	SVZs and SVZPRs	Illustrative example
This study	---	□	□	■	Streamlined FUCOM	Triangular fuzzy numbers	Construction industry

.

The results from the literature review on the issue of gresilient supplier evaluation and selection, as shown in Table 1, indicate that although previous studies have largely relied on MCDM approaches, challenges such as computational complexity, the high number of pairwise comparisons, the formulation and solving of mathematical optimization models, and the type of input data have been problematic. For instance, studies [26,31,35,38] which employed various BWM approaches not only required more pairwise comparisons compared to the approach proposed in this research but also had to formulate and solve mathematical optimization models. As the number of pairwise comparisons increases, the amount of information needed for the decision-making process also rises, thereby adding to the complexity of the problem. Studies [22,23,25] which utilized the AHP method to address the SES problem also encountered a significant increase in the number of pairwise comparisons. Each study, depending on the type of input data and the methodology employed, had its unique advantages and disadvantages. Studies that used the AHP method conducted more pairwise comparisons to prioritize the criteria, while studies that employed the BWM method, despite requiring fewer pairwise comparisons, still needed to formulate and solve mathematical optimization models. Overall, in this study, by utilizing FUCOM and developing a streamlined version of FUCOM, there are fewer pairwise comparisons compared to other approaches and no need to formulate or solve mathematical optimization models. As a result, the decision-making processes regarding criteria and alternatives have been significantly simplified and made more efficient.

On the other hand, the criteria for evaluating and selecting gresilient suppliers in the reviewed studies have almost been similar, with significant differences observed only in studies that considered green and resilient aspects separately. It is important to note that the evaluation criteria can vary according to the gresilient principles applied in different industries. Additionally, the importance of the same criteria may vary across different studies, as the significance of each criterion is determined by its application and the nature of the industry.

Numerous research gaps have been highlighted from the results of this literature review. There is a need for comprehensive studies that simultaneously examine the evaluation criteria for green and resilience in SES issues through real-world case studies. Despite researchers’ focus on gresilient criteria and the specific studies conducted in this domain, there remains a need for further research across various industries with different characteristics. This will help in forming well-rounded comparative analyses. On the other hand, while the methodologies used in SES issues are often applied under conditions of uncertainty, the inherent complexities of some approaches make the decision-making process difficult. Integrating MCDM approaches with uncertainty theories empowers these approaches to handle ambiguity in information, insufficient knowledge, complexities, and vagueness, thereby assisting decision makers in the decision-making process. However, if the developed approaches for addressing uncertainties have fewer inherent complexities and simplify the decision-making process, they will undoubtedly have better efficiency and effectiveness, and decision makers will face minimal intrinsic challenges from the methodologies employed.

In this study, aiming to evaluate and select gresilient suppliers, the streamlined FUCOM (S-FUCOM) approach is proposed in an uncertain environment. As a simplified method, the proposed approach can handle the decision-making process under uncertainty with minimal complexities and significantly aid decision makers in achieving their objectives. Five reasons for the presence of uncertainty in the decision-making process in MCDM approaches are identified as follows [45]:

• Uncertainty due to human error;
• Uncertainty related to data collection instruments and methodologies;
• Uncertainty associated with the collected data;
• Uncertainty regarding data analysis tools and methodologies;
• Uncertainty in the interpretation of results.

As it is impossible to claim that any approach can address all the reasons for uncertainty in the decision-making process mentioned above, the proposed approach also cannot handle all factors of uncertainty simultaneously. However, given its streamlined structure and facilitated processes, it can control a significant portion of the reasons for uncertainty. The proposed approach, with its simplified structure, reduces human errors, makes the process of obtaining expert preferences more efficient, and simplifies data analysis and result interpretation through straightforward and understandable algebraic relationships.

3. Materials and Methods

In this section, the steps of the traditional full consistency method (FUCOM) are first presented and explained. Then, the streamlined full consistency method (S-FUCOM), in a deterministic environment, is proposed, and its steps are explained. Finally, the fuzzy streamlined FUCOM (FS-FUCOM), in an uncertain environment, is described.

3.1. Full Consistency Method (FUCOM)

FUCOM is an MCDM method introduced by Pamučar et al. [20]. It is capable of calculating the final weights of criteria based on the subjective judgments of the decision maker and performing pairwise comparisons between the decision-making criteria. FUCOM has several advantages over other decision-making methods based on pairwise comparisons, such as AHP and BWM, which have attracted the attention of many academics and researchers [46,47,48]. The advantages of FUCOM include (1) a significant reduction in the number of pairwise comparisons (n − 1), where n represents the number of criteria; (2) less information required to carry out the decision-making process; (3) the validation of results by calculating the deviation from full consistency (DFC); (4) a facilitation of the pairwise comparison process by disregarding unnecessary comparisons; (5) simplified steps and mathematical relations to increase the efficiency of the decision-making process; and (6) the definition of effective constraints in the process of calculating the final weights of criteria. The following explains the steps of FUCOM to obtain the final weights of the decision-making criteria.

Step 1. First, the decision-making criteria are defined as $C=\left\{C_1,C_2,\dots ,C_n\right\}$. Then, the decision maker ranks the criteria based on subjective judgments. The criteria ranking is performed from the most important to the least important, as shown in Equation (1), where $k$ represents the rank of the given criterion. The ranking starts with the criterion that is expected to have the highest weight based on the decision maker’s knowledge and continues with the symbol “>” towards the criterion that is expected to be the least important. Additionally, if two or more criteria are considered equally important by the decision maker, the symbol “=” is used between them.

$$C_{j\left(1\right)}\left(〈>〉\bigvee 〈=〉\right)C_{j\left(2\right)}\left(〈>〉\bigvee 〈=〉\right)\dots (〈>〉\bigvee 〈=〉)C_{j\left(k\right)}$$

(1)

Step 2. In this step, pairwise comparisons between the criteria ranked in Step 1 are conducted. The priority of each criterion over another is determined using the comparative priority $\left({\mathcal{p}}_{k/\left(k+1\right)}, k=\mathrm{1,2},\dots , n\right)$, where $k$ denotes the rank of the criteria. The comparative priority $\left({\mathcal{p}}_{k/\left(k+1\right)}\right)$ indicates the superiority of criterion $C_{j\left(k\right)}$ over criterion $C_{j(k+1)}$. This way, the vector of comparative priorities for the decision-making criteria is obtained, as shown in Equation (2).

$$\mathcal{P}=\left({\mathcal{p}}_{1/2},{\mathcal{p}}_{2/3},\dots ,{\mathcal{p}}_{k/\left(k+1\right)}\right)$$

(2)

In the FUCOM model, the comparative priorities between criteria $\left({\mathcal{p}}_{k/\left(k+1\right)}\right)$ can be exact numbers, decimal numbers, or other predefined scales. Figure 1 illustrates the pairwise comparison process among criteria in FUCOM.

Step 3. This step calculates the final weights of the decision criteria ${\left({\mathcal{W}}_1,{\mathcal{W}}_2{,\dots ,\mathcal{W}}_n\right)}^T$. Two prerequisites must be satisfied to calculate the final weights in FUCOM. Equations (3) and (4) show the first and second prerequisites, respectively.

Prerequisite 1. The ratio of the weight coefficients and the comparative priority between them $\left({\mathcal{p}}_{k/\left(k+1\right)}\right)$, as determined in Step 2, must be equal. Therefore, we have the following:

$${\displaystyle \frac{{\mathcal{W}}_k}{{\mathcal{W}}_{\left(k+1\right)}}}={\mathcal{p}}_{k/\left(k+1\right)}$$

(3)

Prerequisite 2. The ratio of the final weights of the decision-making criteria must satisfy mathematical transitivity, such that ${\mathcal{p}}_{k/\left(k+1\right)}.{\mathcal{p}}_{\left(k+1\right)/\left(k+2\right)}={\mathcal{p}}_{k/\left(k+2\right)}$ when ${\mathcal{p}}_{k/\left(k+1\right)}={\displaystyle \frac{{\mathcal{W}}_k}{{\mathcal{W}}_{\left(k+1\right)}}}$ and ${\mathcal{p}}_{\left(k+1\right)/\left(k+2\right)}={\displaystyle \frac{{\mathcal{W}}_{\left(k+1\right)}}{{\mathcal{W}}_{\left(k+2\right)}}}$, resulting in ${\displaystyle \frac{{\mathcal{W}}_k}{{\mathcal{W}}_{\left(k+1\right)}}}.{\displaystyle \frac{{\mathcal{W}}_{\left(k+1\right)}}{{\mathcal{W}}_{\left(k+2\right)}}}={\displaystyle \frac{{\mathcal{W}}_k}{{\mathcal{W}}_{\left(k+2\right)}}}$. To achieve these settings, the following equation must also be satisfied to obtain the final weights of the criteria under conditions of maximum consistency.

$${\displaystyle \frac{{\mathcal{W}}_k}{{\mathcal{W}}_{\left(k+2\right)}}}={\mathcal{p}}_{k/\left(k+1\right)}.{\mathcal{p}}_{\left(k+1\right)/\left(k+2\right)}$$

(4)

Given the above prerequisites, full consistency or minimum DFC $\left(\mathcal{Z}\right)$ is achieved when Prerequisites (1) and (2) are fully satisfied. In other words, when DFC is $\mathcal{Z}=0$, this indicates that full consistency is achieved in the process of obtaining the final weights of the criteria. In this regard, Equation (5) shows the final model for obtaining the weights of the criteria.

$$\begin{gathered} \min \mathcal{Z} \\ S.T.\left\{\begin{array}{c}\left|{\displaystyle \frac{{\mathcal{W}}_{jk}}{{\mathcal{W}}_{j\left(k+1\right)}}}-{\mathcal{p}}_{k/\left(k+1\right)}\right|\le Z, \forall j\hfill \\ \left|{\displaystyle \frac{{\mathcal{W}}_{jk}}{{\mathcal{W}}_{j\left(k+2\right)}}}-{\mathcal{p}}_{k/\left(k+1\right)}.{\mathcal{p}}_{\left(k+1\right)/\left(k+2\right)}\right|\le Z, \forall j\hfill \\ {\displaystyle \sum _{j=1}^n}{\mathcal{W}}_j=1,\forall j\hfill \\ {\mathcal{W}}_j\ge 0,\forall j\hfill \end{array}\right. \end{gathered}$$

(5)

By solving the above model, the final weights of the decision-making criteria ${\left({\mathcal{W}}_1,{\mathcal{W}}_2{,\dots ,\mathcal{W}}_n\right)}^T$ and DFC $\left(\mathcal{Z}\right)$ will be obtained. When FUCOM is employed to evaluate criteria and alternatives, after obtaining the final weights of the criteria, Equation (6) can be used to evaluate the alternatives based on each criterion’s weight and prioritize the alternatives. In this way, FUCOM can address a multi-criterion, multi-alternative decision-making problem.

$${\mathcal{S}}_i=\sum _{j=1}^n{w}_j{x}_{ij},where w_j\ge 0 and {\sum }_{j=1}^n{w}_j=1.$$

(6)

where $w_j$ is the final weight of each criterion, and $x_{ij}$ is the final score of each alternative relative to each criterion in the initial decision matrix $X={\left[x_{ij}\right]}_{m\times n}$.

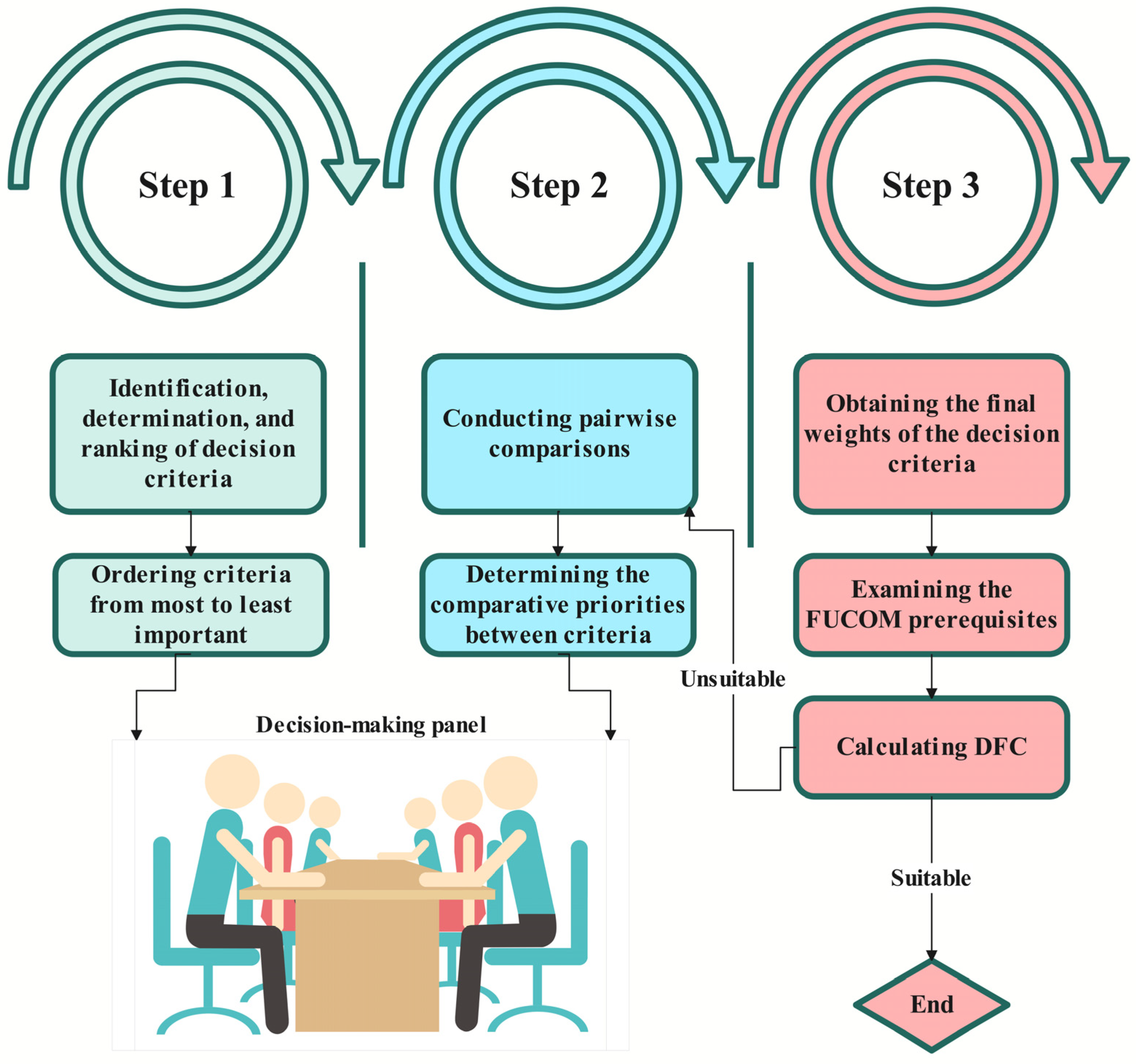
3.2. The Proposed Streamlined FUCOM (S-FUCOM)

FUCOM, compared to other decision-making methods based on pairwise comparisons, does not require the calculation of a consistency ratio, because fully consistent comparisons are a prerequisite for obtaining the decision criteria weights in FUCOM. In FUCOM, the initial ranking of the criteria (Step 1) and obtaining the comparative priority between criteria (Step 2) are influenced by two specific prerequisites. If the specified prerequisites are not satisfied, the comparisons deviate from full consistency. In some FUCOM extensions and depending on the nature of the input data, the DFC value will not always be exactly zero. It is noteworthy that the smaller the DFC value, the greater the consistency of the comparisons. In other words, the smaller the DFC value, the more the weights obtained from the FUCOM process align with the decision maker’s subjective preferences.

On the other hand, FUCOM has garnered the attention of many researchers due to its numerous advantages over other pairwise comparison-based methods like AHP and BWM, and it has been applied in various decision-making and management issues. The significant reduction in the number of comparisons and the simplified calculations for determining the final weights of the criteria are among the most important advantages of FUCOM. The complexity of calculations in FUCOM may only arise in Step 3, during the formulation and solving of the mathematical programming model, particularly when the number of decision-making criteria increases. In such cases, formulating the mathematical programming model and solving it using various software packages can be time-consuming and may affect the efficiency of this approach.

In this way, we aim to propose a streamlined FUCOM (S-FUCOM) approach, which considers FUCOM without the need to formulate mathematical programming models and software packages, thereby significantly enhancing its efficiency. Despite the lack of necessity for formulating and solving various mathematical optimization models in S-FUCOM, the proposed approach calculates the final weights of the criteria by considering the consistency of the first and second FUCOM prerequisites and is also capable of calculating the DFC. Since the proposed approach is an approximate method that does not require formulating precise optimization models, there may be slight deviations from complete consistency, similar to what might occur in the original FUCOM. Generally, the smaller the deviation from complete consistency, the higher the consistency of the comparisons. More specifically, the results of the proposed approach completely align with the results of FUCOM. Still, there is no need to formulate and solve an optimization model to obtain the final weights of the criteria. Additionally, all previous advantages of the FUCOM method are preserved. This way, a major advantage is added to the existing benefits of FUCOM, making this approach richer for solving decision-making problems. Figure 2 illustrates the stages of the proposed approach.

The steps of the proposed S-FUCOM approach are as follows:

Step A1. Identification, determination, and ranking of decision criteria: In this step, the decision criteria are identified and determined as $C^{\prime }=\left\{C_1^{\prime },C_2^{\prime },\dots , C_n^{\prime }\right\}$. Then, the decision maker ranks the criteria based on their knowledge, ordering them from the most important to the least important. The superiority and equality between criteria are denoted by the symbols “$>$” and “$=$”, respectively, as shown in Equation (7), where $k$ represents the rank of the given criterion.

$$C_{j\left(1\right)}^{\prime }\left(〈>〉\bigvee 〈=〉\right)C_{j\left(2\right)}^{\prime }\left(〈>〉\bigvee 〈=〉\right)\dots (〈>〉\bigvee 〈=〉)C_{j\left(k\right)}^{\prime }$$

(7)

Step A2. In this step, pairwise comparisons between the criteria ranked in Step A1 are conducted. The priority of each criterion relative to the other criteria $({\mathcal{p}}_{k\left(k+1\right)}^{\prime },k=\mathrm{1,2},\dots , n)$, where k denotes the rank of the criteria, is determined by the decision maker, and different scales can be used to determine the priority between criteria, such as [1 9]. This way, the vector of priorities for the decision-making criteria is obtained as $\left({\mathcal{p}}_{12}^{\prime }, {\mathcal{p}}_{23}^{\prime }, \dots , {\mathcal{p}}_{k\left(k+1\right)}^{\prime }\right)$. Then, the comparative priority of the criteria $\left({\mathcal{p}}_{k/\left(k+1\right)}^{\prime }\right)$ is calculated, expressed as $\left({\mathcal{p}}_{k/\left(k+1\right)}^{\prime }, k=\mathrm{1,2},\dots , n\right)$, where k denotes the rank of the criteria. The comparative priority $\left({\mathcal{p}}_{k/\left(k+1\right)}^{\prime }\right)$ indicates the superiority of criterion $C_{j\left(k\right)}^{\prime }$ over criterion $C_{j\left(k+1\right)}^{\prime }$. This way, the vector of comparative priorities for the decision-making criteria is obtained, as shown in Equation (8).

$${\mathcal{P}}^{\prime }=\left({\mathcal{p}}_{1/2}^{\prime },{\mathcal{p}}_{2/3}^{\prime },\dots ,{\mathcal{p}}_{k/\left(k+1\right)}^{\prime }\right)$$

(8)

In this step, the comparative priorities $\left({\mathcal{p}}_{k/\left(k+1\right)}^{\prime }\right)$ can take various forms, such as decimal numbers, exact numbers, or other predefined scales based on the priority of each criterion relative to the other criteria $\left({\mathcal{p}}_{k\left(k+1\right)}^{\prime }\right)$. Next, the second comparative priority of the criteria $\left({\mathcal{p}}_{(k+1)/\left(k+2\right)}^{\prime }\right)$ is also calculated to evaluate the satisfaction of the second FUCOM prerequisite (mathematical transitivity).

Step A3. Obtaining the final weights of the decision criteria and confirming the prerequisites: In this step, the final weights of the criteria ${\left({\mathcal{W}}_1^{\prime },{\mathcal{W}}_2^{\prime },\dots ,{\mathcal{W}}_n^{\prime }\right)}^T$ are calculated using Equations (9) and (10). ${\mathcal{W}}_1^{\prime }$ represents the weight of the most important criterion from the decision-maker’s perspective, which is identified as the first criterion $C_{j\left(1\right)}^{\prime }$ in Step A1 and is predicted to have the highest importance among all criteria. Using Equation (9), the final weight of the most important criterion is calculated first. Then, using Equation (10), by dividing the weight of most important criterion $\left({\mathcal{W}}_I^{\prime }\right)$ by the priorities of the other criteria $\left({\mathcal{p}}_{k\left(k+1\right)}^{\prime }\right)$, the final weights of the remaining criteria are calculated.

$$\sum _k{\displaystyle \frac{1}{{\mathcal{p}}_{k\left(k+1\right)}^{\prime }}}{\mathcal{W}}_I^{\prime }=1\Rightarrow {\mathcal{W}}_I^{\prime }={\displaystyle \frac{1}{\sum _k\frac{1}{{\mathcal{p}}_{k\left(k+1\right)}^{\prime }}}},\forall k.$$

(9)

$${\mathcal{W}}_I^{\prime }-{\mathcal{p}}_{k\left(k+1\right)}^{\prime }{\mathcal{W}}_k^{\prime }=0\Rightarrow {\mathcal{p}}_{k\left(k+1\right)}^{\prime }{\mathcal{W}}_k^{\prime }={\mathcal{W}}_I^{\prime }\Rightarrow {\mathcal{W}}_k^{\prime }={\displaystyle \frac{{\mathcal{W}}_I^{\prime }}{{\mathcal{p}}_{k\left(k+1\right)}^{\prime }}},\forall k.$$

(10)

Definition 1.

According to Pamučar et al. [20], in FUCOM, full consistency (DFC is $\mathcal{Z}=0$) is achieved only when the first and second prerequisites are fully satisfied. Therefore, when the final weights obtained from Step A3 are substituted into Equations (11) and (12), which correspond to the first and second FUCOM prerequisites, respectively, and these equations hold true, full consistency is achieved, and DFC is $\mathcal{Z}=0$. Otherwise, if DFC is $\mathcal{Z}\ne 0$, the smaller the DFC, the lower the total deviation from complete consistency, indicating a higher reliability of the results.

$${\displaystyle \frac{{\mathcal{W}}_k^{\prime }}{{\mathcal{W}}_{(k+1)}^{\prime }}}={\mathcal{p}}_{k/\left(k+1\right)}^{\prime }⟹{\displaystyle \frac{{\mathcal{W}}_k^{\prime }}{{\mathcal{W}}_{(k+1)}^{\prime }}}-{\mathcal{p}}_{k/\left(k+1\right)}^{\prime }=0$$

(11)

$${\displaystyle \frac{{\mathcal{W}}_k^{\prime }}{{\mathcal{W}}_{(k+2)}^{\prime }}}={\mathcal{p}}_{k/\left(k+1\right)}^{\prime }.{\mathcal{p}}_{(k+1)/\left(k+2\right)}^{\prime }⟹{\displaystyle \frac{{\mathcal{W}}_k^{\prime }}{{\mathcal{W}}_{(k+2)}^{\prime }}}-{\mathcal{p}}_{k/\left(k+1\right)}^{\prime }.{\mathcal{p}}_{(k+1)/\left(k+2\right)}^{\prime }=0$$

(12)

In some FUCOM extensions, and depending on the nature of the input data, the DFC value might not be exactly zero, as seen in the fuzzy extension of FUCOM [48]. However, logically, the smaller the DFC value, the more effective the method and the higher the consistency of the results with the decision-maker’s preferences. Since S-FUCOM does not involve formulating and solving an optimization model, DFC can be calculated using Equation (13), where n − 1 is the total number of pairwise comparisons conducted by the FUCOM approach. In pairwise comparison-based approaches, the total deviation is divided by the number of pairwise comparisons required in each approach. For example, the total deviation in AHP and BWM is divided by n² and 2n, respectively [49]. In the S-FUCOM approach, which is considered a simplified and approximate method, the lower the DFC value, the greater the consistency of the comparisons.

$$DFC={\displaystyle \frac{1}{n-1}}\sum _k{\left({\displaystyle \frac{{\mathcal{W}}_k^{\prime }}{{\mathcal{W}}_{(k+1)}^{\prime }}}-{\mathcal{p}}_{k/\left(k+1\right)}^{\prime }\right)}^2$$

(13)

According to Definition 1, if the final weights of the decision criteria are obtained using the proposed approach without the need to formulate and solve mathematical optimization models and satisfy all the prerequisites and structural equations of FUCOM, there will be no difference between the final weights obtained from traditional FUCOM and S-FUCOM. Therefore, by substituting the final weights of the decision criteria into Equations (11) and (12), if the equations hold true, the FUCOM prerequisites are fully confirmed. Otherwise, if DFC is $\mathcal{Z}\ne 0$, the smaller the DFC, the lower the total deviation from complete consistency, indicating a higher reliability of the results. Since the proposed approach is an approximate method that does not require formulating precise optimization models, there may be slight deviations from complete consistency, similar to what might occur in the original FUCOM. Generally, the smaller the deviation from complete consistency, the higher the consistency of the comparisons and the FUCOM prerequisites are better satisfied. The proposed approach significantly reduces the computational process of FUCOM. Numerical examples and further details are provided in Section 4.

3.3. Fuzzy Streamlined FUCOM (FS-FUCOM)

In MCDM problems, especially in approaches based on pairwise comparisons and subjective judgments, the decision-making environment often faces uncertainty, and decision makers prefer to express their preferences using imprecise numbers and linguistic terms corresponding to them [50]. The fuzzy set theory introduced by Zadeh [51] can address the uncertainty in the decision-making environment, enabling MCDM approaches to handle decisions under uncertain conditions. Ambiguity in information, the lack of information, insufficient knowledge, complexity, and vagueness can impact the decision-making environment, so precise preferences in these environments do not lead to reliable results [52]. Therefore, in this section, we propose the S-FUCOM approach using TFNs to cope with the uncertainty prevailing in the decision-making environment. FS-FUCOM is a fuzzy extension of S-FUCOM that retains all its advantages while enabling it to handle decision-making problems in uncertain environments. FS-FUCOM also does not require the formulation and solving of mathematical optimization models to obtain the final fuzzy weights of the criteria. Compared to other fuzzy FUCOM approaches available in the literature [46,47,48], it significantly reduces the computations needed to determine the fuzzy weights of the decision criteria. The steps of FS-FUCOM are the same as those of S-FUCOM, with the difference that decision-makers’ preferences are expressed as TFNs, and the calculations are also performed based on the operations of TFNs, as shown in Definitions 2 and 3.

Definition 2.

Let $\mathcal{X}=\left\{{\mathcal{x}}_1,{\mathcal{x}}_2,\dots ,{\mathcal{x}}_n\right\}$ be the set of elements denoted by ${\mathcal{x}}_i$. A fuzzy set $\tilde{\mathcal{A}}$ in $\mathcal{X}$ is represented as $\mathcal{A}=\left\{\left({\mathcal{x}}_i,{\mu }_{\tilde{\mathcal{A}}}\left({\mathcal{x}}_i\right)\right)|{\mathcal{x}}_i\in \mathcal{X}\right\}$, where ${\mu }_{\tilde{\mathcal{A}}}$ is the membership function of the fuzzy set $\tilde{\mathcal{A}}$. The value ${\mu }_{\tilde{\mathcal{A}}}\left(x_i\right)$ indicates the grade of membership of the element ${\mathcal{x}}_i$ associated with $\tilde{\mathcal{A}}$ and ${\mu }_{\tilde{\mathcal{A}}}\left({\mathcal{x}}_i\right)\in \left[\mathrm{0,1}\right]$ [53].

Definition 3.

A triangular fuzzy number (TFN) is a specific type of fuzzy number denoted by $\tilde{\mathcal{A}}=\left({\mathcal{a}}^L,{\mathcal{a}}^M,{\mathcal{a}}^U\right)$. Here, $\tilde{\mathcal{A}}$ is a fuzzy set defined in the set $\mathbb{R}$ of real numbers. The membership function ${\mu }_{\tilde{\mathcal{A}}}\left({\mathcal{x}}_i\right)$ for the TFN can be defined as shown in Equation (14).

$${\mu }_{\tilde{\mathcal{A}}}\left({\mathcal{x}}_i\right)\left\{\begin{array}{c}{\displaystyle \frac{{\mathcal{a}}^U-\mathcal{x}}{{\mathcal{a}}^U-{\mathcal{a}}^M}}, if {\mathcal{a}}^M\le x\le {\mathcal{a}}^U\\ {\displaystyle \frac{\mathcal{x}-{\mathcal{a}}^L}{{\mathcal{a}}^M-{\mathcal{a}}^L}}, if {\mathcal{a}}^L\le x\le {\mathcal{a}}^M\\ 0, if x<{\mathcal{a}}^L or x>{\mathcal{a}}^U\end{array}\right.$$

(14)

In this context, ${\mathcal{a}}^L$, ${\mathcal{a}}^M$, and ${\mathcal{a}}^U$ are referred to as the lower bound, the modal, and the upper bound of the TFN $\tilde{\mathcal{A}}=\left({\mathcal{a}}^L,{\mathcal{a}}^M,{\mathcal{a}}^U\right)$, respectively, with the condition ${\mathcal{a}}^L\le {\mathcal{a}}^M\le {\mathcal{a}}^U$. If ${\mathcal{a}}^L\ge 0$, then the TFN is called a positive TFN. Conversely, if ${\mathcal{a}}^U\le 0$, then the TFN is termed a negative TFN. Figure 3 shows a graphical representation of fully positive and fully negative TFNs. The relationships, mathematical operators, and normalization for TFNs, $\tilde{\mathcal{A}}=\left({\mathcal{a}}^L,{\mathcal{a}}^M,{\mathcal{a}}^U\right)$ and $\tilde{\mathcal{B}}=\left({\beta }^L,{\beta }^M,{\beta }^U\right)$, are as follows (Equation (15)) [53]:

$$\begin{gathered} \tilde{\mathcal{A}}⨁\tilde{\mathcal{B}}=\left({\mathcal{a}}^L+{\beta }^L,{\mathcal{a}}^M+{\beta }^M,{\mathcal{a}}^U+{\beta }^U\right) \\ \tilde{\mathcal{A}}\ominus \tilde{\mathcal{B}}=\left({\mathcal{a}}^L-{\beta }^U,{\mathcal{a}}^M-{\beta }^M,{\mathcal{a}}^U-{\beta }^L\right) \\ \tilde{\mathcal{A}}\otimes \tilde{\mathcal{B}}\cong \left({\mathcal{a}}^L{\beta }^L,{\mathcal{a}}^M{\beta }^M,{\mathcal{a}}^U{\beta }^U\right) \\ \tilde{\mathcal{A}}\oslash \tilde{\mathcal{B}}\cong \left({\displaystyle \frac{{\mathcal{a}}^L}{{\beta }^U}},{\displaystyle \frac{{\mathcal{a}}^M}{{\beta }^M}},{\displaystyle \frac{{\mathcal{a}}^U}{{\beta }^L}}\right) \\ {\displaystyle \frac{1}{\tilde{\mathcal{A}}}}\cong \left({\displaystyle \frac{1}{{\mathcal{a}}^U}},{\displaystyle \frac{1}{{\mathcal{a}}^M}},{\displaystyle \frac{1}{{\mathcal{a}}^L}}\right) \\ {\tilde{\mathcal{A}}}_{Norm}=\left({\displaystyle \frac{{\mathcal{a}}_{ij}^L}{{Max,\mathcal{a}}_j^U}},{\displaystyle \frac{{\mathcal{a}}_{ij}^M}{{Max,\mathcal{a}}_j^U}},{\displaystyle \frac{{\mathcal{a}}_{ij}^U}{{Max,\mathcal{a}}_j^U}}\right) (j \mathrm{is} \mathrm{a} \mathrm{positive} \mathrm{criteria}) \\ {\tilde{\mathcal{A}}}_{Norm}=\left({\displaystyle \frac{{Min,\mathcal{a}}_j^L}{{\mathcal{a}}_{ij}^U}},{\displaystyle \frac{{Min,\mathcal{a}}_j^L}{{\mathcal{a}}_{ij}^M}},{\displaystyle \frac{{Min,\mathcal{a}}_j^L}{{\mathcal{a}}_{ij}^L}}\right) (j \mathrm{is} \mathrm{a} \mathrm{negative} \mathrm{criteria}) \\ \tilde{\mathcal{A}}\otimes \lambda =\left({\mathcal{a}}^L\lambda ,{\mathcal{a}}^M\lambda ,{\mathcal{a}}^U\lambda \right), where \lambda \ge 0. \end{gathered}$$

(15)

Definition 4.

To defuzzify TFNs, we can use the graded mean integration representation (GMIR). Suppose $a_j=(L_j,M_j,U_j)$ is a TFN, in which case $GMIR\left(a_j\right)$ of $a_j$ can convert the TFN into a crisp number using $GMIR\left(a_j\right)={\displaystyle \frac{L_j+{4M}_j+U_j}{6}}$ [54].

Definition 5.

To integrate multiple TFNs, their average can be used. In MCDM problems, when multiple decision makers express their preferences regarding several alternatives for each criterion, it is usually necessary to integrate the decision-makers’ preferences. For this purpose, the average of multiple TFNs can be used. Suppose $\tilde{\mathcal{A}}=\left({\mathcal{a}}_{ijk}^L,{\mathcal{a}}_{ijk}^M,{\mathcal{a}}_{ijk}^U\right)$ is a TFN, where $i$th alternative, $j$th criterion, and $k$th decision-maker are involved. The average of the fuzzy numbers, given that the decision makers have equal weights, is calculated as follows: ${\tilde{\mathcal{A}}}_{ij}=\left({\displaystyle \frac{1}{K}}{\sum }_{k=1}^K{\mathcal{a}}_{ijk}^L,{\displaystyle \frac{1}{K}}{\sum }_{k=1}^K{\mathcal{a}}_{ijk}^M,{\displaystyle \frac{1}{K}}{\sum }_{k=1}^K{\mathcal{a}}_{ijk}^U\right)$, where K is the number of decision makers [55].

The following outlines the steps of the FS-FUCOM approach to obtain the final fuzzy weights of the decision-making criteria.

Step B1. Identification, determination, and ranking of decision criteria: In this step, the decision criteria are identified and determined as $C^{″}=\left\{C_1^{″},C_2^{″},\dots , C_n^{″}\right\}$. Then, the decision maker ranks the criteria based on their knowledge, ordering them from the most important to the least important. The superiority and equality between criteria are denoted by the symbols “$>$” and “$=$”, respectively, as shown in Equation (16), where $k$ represents the rank of the given criterion.

$$C_{j\left(1\right)}^{″}\left(〈>〉\bigvee 〈=〉\right)C_{j\left(2\right)}^{″}\left(〈>〉\bigvee 〈=〉\right)\dots (〈>〉\bigvee 〈=〉)C_{j\left(k\right)}^{″}$$

(16)

Step B2. In this step, pairwise comparisons between the criteria ranked in Step B1 are conducted. The fuzzy priority of each criterion relative to the other criteria $({\tilde{\mathcal{p}}}_{k\left(k+1\right)},k=\mathrm{1,2},\dots , n)$, where k denotes the rank of the criteria, is determined by the decision maker, and different fuzzy scales can be used to determine the priority between criteria. This way, the vector of fuzzy priorities for the decision-making criteria is obtained, as shown in Equation (17). Then, the comparative priority of the criteria $\left(\left({\mathcal{p}}_{k/\left(k+1\right)}^{\prime }\right)\right)$ is calculated, expressed as $\left(\left({\mathcal{p}}_{k/\left(k+1\right)}^{\prime }\right), k=\mathrm{1,2},\dots , n\right)$, where k denotes the rank of the criteria. The comparative priority $\left({\mathcal{p}}_{k/\left(k+1\right)}^{\prime }\right)$ indicates the superiority of criterion $C_{j\left(k\right)}^{″}$ over criterion $C_{j\left(k+1\right)}^{″}$. Next, the second comparative priority of the criteria $\left({\mathcal{p}}_{(k+1)/\left(k+2\right)}^{\prime }\right)$ is also calculated to evaluate the satisfaction of the second FUCOM prerequisite (mathematical transitivity).

$$\tilde{\mathcal{P}}=\left({\tilde{\mathcal{p}}}_{12}, {\tilde{\mathcal{p}}}_{23}, \dots , {\tilde{\mathcal{p}}}_{k\left(k+1\right)}\right)$$

(17)

In this step, the fuzzy comparative priorities $\left({\tilde{\mathcal{p}}}_{k/\left(k+1\right)}\right)$ can take various fuzzy scales based on the fuzzy priority of each criterion relative to the other criteria $\left({\tilde{\mathcal{p}}}_{k\left(k+1\right)}\right)$.

Step B3. Obtaining the final fuzzy weights of the decision criteria: In this step, the final fuzzy weights of the criteria ${\left({\tilde{\mathcal{W}}}_1,{\tilde{\mathcal{W}}}_2,\dots ,{\tilde{\mathcal{W}}}_n\right)}^T$ are calculated using Equations (18) and (19). ${\tilde{\mathcal{W}}}_1$ represents the fuzzy weight of the most important criterion from the decision-maker’s perspective, which is identified as the first criterion $C_{j\left(1\right)}^{″}$ in Step B1 and is predicted to have the highest importance among all criteria. Using Equation (18), the final fuzzy weight of the most important criterion is calculated first. Then, using Equation (19), by dividing the fuzzy weight of most important criterion $\left({\tilde{\mathcal{W}}}_I\right)$ by the priorities of the other criteria $\left({\tilde{\mathcal{p}}}_{k\left(k+1\right)}\right)$, the final fuzzy weights of the remaining criteria are calculated.

$$\sum _k{\displaystyle \frac{1}{{\tilde{\mathcal{p}}}_{k\left(k+1\right)}}}{\tilde{\mathcal{W}}}_I=1\Rightarrow {\tilde{\mathcal{W}}}_I={\displaystyle \frac{1}{\sum _k\frac{1}{{\tilde{\mathcal{p}}}_{k\left(k+1\right)}}}},\forall k.$$

(18)

$${\tilde{\mathcal{W}}}_I-{\tilde{\mathcal{p}}}_{k\left(k+1\right)}{\tilde{\mathcal{W}}}_k=0\Rightarrow {\tilde{\mathcal{p}}}_{k\left(k+1\right)}{\tilde{\mathcal{W}}}_k={\tilde{\mathcal{W}}}_I\Rightarrow {\tilde{\mathcal{W}}}_k={\displaystyle \frac{{\tilde{\mathcal{W}}}_I}{{\tilde{\mathcal{p}}}_{k\left(k+1\right)}}},\forall k.$$

(19)

After obtaining the final fuzzy weights, the first and second prerequisites of FUCOM are reviewed for validation to ensure the reliability of the results. Since the consistency of linguistic evaluations is independent of the degree of fuzziness of the membership functions, consistency evaluations can be conducted with the crisp equivalents of linguistic statements [56]. Therefore, in FS-FUCOM, the evaluation of FUCOM prerequisites and the consistency of comparisons can be performed using the crisp values of the obtained weights and the crisp values of the fuzzy comparative priorities. Therefore, when the final weights obtained are substituted into Equations (20) and (21), which correspond to the first and second FUCOM prerequisites, respectively, and these equations hold true, full consistency is achieved, and DFC is $\mathcal{Z}=0$. Otherwise, if DFC is $\mathcal{Z}\ne 0$, the smaller the DFC, the lower the total deviation from complete consistency, indicating a higher reliability of the results. Generally, smaller deviations indicate higher consistency in comparisons and better satisfaction of FUCOM prerequisites. The DFC in FS-FUCOM can be calculated using Equation (22), where n − 1 is the total number of pairwise comparisons conducted by the FUCOM approach.

$${\displaystyle \frac{{\tilde{\mathcal{W}}}_k}{{\tilde{\mathcal{W}}}_{(k+1)}}}={\tilde{\mathcal{p}}}_{k/\left(k+1\right)}⟹{\displaystyle \frac{{\tilde{\mathcal{W}}}_k}{{\tilde{\mathcal{W}}}_{(k+1)}}}-{\tilde{\mathcal{p}}}_{k/\left(k+1\right)}=0$$

(20)

$${\displaystyle \frac{{\tilde{\mathcal{W}}}_k}{{\tilde{\mathcal{W}}}_{(k+2)}}}={\tilde{\mathcal{p}}}_{k/\left(k+1\right)}.{\tilde{\mathcal{p}}}_{(k+1)/\left(k+2\right)}⟹{\displaystyle \frac{{\tilde{\mathcal{W}}}_k}{{\tilde{\mathcal{W}}}_{(k+2)}}}-{\tilde{\mathcal{p}}}_{k/\left(k+1\right)}.{\tilde{\mathcal{p}}}_{(k+1)/\left(k+2\right)}=0$$

(21)

The DFC in FS-FUCOM can be calculated using Equation (22), where n − 1 is the total number of pairwise comparisons conducted by the FUCOM approach. In the next section, numerical examples are provided to demonstrate the applicability of this approach and to validate the results obtained from FS-FUCOM.

$$DFC={\displaystyle \frac{1}{n-1}}\sum _k{\left({\displaystyle \frac{{\mathcal{W}}_k^{\prime }}{{\mathcal{W}}_{(k+1)}^{\prime }}}-{\mathcal{p}}_{k/\left(k+1\right)}^{\prime }\right)}^2$$

(22)

4. Numerical Examples

In this section, four numerical examples are provided to demonstrate the applicability and capabilities of the proposed approach. The first two numerical examples employ S-FUCOM to solve decision-making problems in a deterministic environment, while the next two examples evaluate FS-FUCOM under conditions of uncertainty. All numerical examples utilize data from relevant articles, thus enabling an appropriate comparative analysis of the results.

4.1. Numerical Example 1

This example is of a car buyer from the FUCOM base article [20], where a car buyer evaluated the alternatives using the following five criteria: Quality (C₁), Price (C₂), Comfort (C₃), Safety Level (C₄), and Interior (C₅).

In Step A1, the decision-maker identifies and selects the criteria for purchasing a car, then ranks the criteria based on subjective judgments. Here, the decision-maker prioritizes the criteria as $C_2>C_1>C_4>C_3>C_5$. Based on this judgment, it is predicted that criterion $C_2$will be the most important and will obtain the highest weight, while criterion $C_5$ is considered the least important and will receive the lowest weight.

In Step A2, pairwise comparisons are made between the criteria ranked in Step A1. The decision maker can express their preferences for the criteria using various scales, with the [1 9] scale being used in this example. After performing the pairwise comparisons between the criteria, the priority of each criterion relative to another $\left({\mathcal{p}}_{k\left(k+1\right)}^{\prime }\right)$, the comparative priority between criteria $\left({\mathcal{p}}_{k/\left(k+1\right)}^{\prime }\right)$ for evaluating the first prerequisite, and the comparative priority $\left({\mathcal{p}}_{(k+1)/\left(k+2\right)}^{\prime }\right)$ for evaluating the second prerequisite (mathematical transitivity) will be obtained, as shown in

Table 2. Pairwise comparisons and comparative priorities between the criteria (example 1).

Main	Criteria
	C2	C1	C4	C3	C5
${\mathcal{p}}_{k\left(k+1\right)}^{\prime }$	1	2.1	3	3	7
${\mathcal{p}}_{k/\left(k+1\right)}^{\prime }$	---	2.1	1.43	1	2.33
${\mathcal{p}}_{(k+1)/\left(k+2\right)}^{\prime }$	---	---	3	1.43	2.33

.

In Step 3A, the final weights of the criteria are calculated using Equations (9) and (10), and ultimately, the FUCOM prerequisites are evaluated to determine their satisfaction. Equations (23) and (24) illustrate how the final weights of the criteria are calculated. First, the weight of the most important criterion, which is predicted to have the highest weight, is calculated, and then the weights of the other criteria are determined based on the weight of the most important criterion. Here, C₂ is identified as the most important criterion.

$$\left({\mathcal{W}}_I^{\prime }={\displaystyle \frac{1}{\sum _k\frac{1}{{\mathcal{p}}_{k\left(k+1\right)}^{\prime }}}},\forall k.\right)⟹\left[{\mathcal{W}}_2^{\prime }={\displaystyle \frac{1}{\frac{1}{1}+\frac{1}{2.1}+\frac{1}{3}+\frac{1}{3}+\frac{1}{7}}}\right]=0.438$$

(23)

$$\left({\mathcal{W}}_k^{\prime }={\displaystyle \frac{{\mathcal{W}}_I^{\prime }}{{\mathcal{p}}_{k\left(k+1\right)}^{\prime }}},\forall k.\right)⟹w_k\left\{\begin{array}{c}{\mathcal{W}}_1^{\prime }={\displaystyle \frac{0.438}{2.1}}=0.208\\ {\mathcal{W}}_4^{\prime }={\displaystyle \frac{0.438}{3}}=0.146\\ {\mathcal{W}}_3^{\prime }={\displaystyle \frac{0.438}{3}}=0.146\\ {\mathcal{W}}_5^{\prime }={\displaystyle \frac{0.438}{7}}=0.063\end{array}\right.$$

(24)

After obtaining the decision criteria weights, it is time to evaluate the FUCOM prerequisites. Therefore, the first and second FUCOM prerequisites are assessed based on the obtained weights to determine their confirmation or rejection. Using Equations (11) and (12), which correspond to the first and second FUCOM prerequisites, respectively, the evaluation result is determined. If these equations are satisfied, maximum consistency (DFC is $\mathcal{Z}=0$) will be achieved. Otherwise, if DFC is $\mathcal{Z}\ne 0$, the smaller the DFC, the lower the total deviation from complete consistency, indicating a higher reliability of the results. Equations (25) and (26) illustrate how the first and second FUCOM prerequisites are calculated and evaluated.

$${\displaystyle \frac{{\mathcal{W}}_k^{\prime }}{{\mathcal{W}}_{(k+1)}^{\prime }}}-{\mathcal{p}}_{{\displaystyle \frac{k}{\left(k+1\right)}}}^{\prime }⟹ Prerequisite (1)\left\{\begin{array}{c}{\displaystyle \frac{w_2:0.438}{w_1:0.208}}-2.1=0\\ {\displaystyle \frac{w_1:0.208}{w_4:0.146}}-1.43=0\\ {\displaystyle \frac{w_4:0.146}{w_3:0.146}}-1.00=0\\ {\displaystyle \frac{w_3:0.146}{w_5:0.063}}-2.33=0.012\end{array}\right.$$

(25)

$${\displaystyle \frac{{\mathcal{W}}_k^{\prime }}{{\mathcal{W}}_{(k+2)}^{\prime }}}-{\mathcal{p}}_{k/\left(k+1\right)}^{\prime }.{\mathcal{p}}_{(k+1)/\left(k+2\right)}^{\prime }⟹Prerequisite (2)\left\{\begin{array}{c}{\displaystyle \frac{w_2:0.438}{w_4:0.146}}-2.1\times 1.43=0\\ {\displaystyle \frac{w_1:0.208}{w_3:0.146}}-1.43\times 1=0\\ {\displaystyle \frac{w_4:0.146}{w_5:0.063}}-1\times 2.33=0.012\end{array}\right.$$

(26)

Table 3. Comparison of the final criteria weights and the status of prerequisites (example 1).

Criteria	Weights		Prerequisites
	S-FUCOM	FUCOM	(1)	(2)	Status
C1	0.208	0.208	2–1 1–4 4–3 3–5	2–4 1–3 4–5	Confirmed
C2	0.437	0.437
C3	$0.146$	$0.146$
C4	$0.146$	$0.146$
C5	$0.063$	$0.063$
DFC	$\cong 0$

shows the results of the proposed approach, along with the status of the FUCOM prerequisites, and compares them with the results obtained from the traditional FUCOM. As evident from the results, the FUCOM prerequisites in the proposed approach are fully satisfied, and complete consistency is achieved. The obtained weights are entirely consistent with the traditional FUCOM approach, without the need to formulate and solve mathematical optimization models. The proposed approach computes the results while ensuring full consistency and significantly reduces the computational effort.

4.2. Numerical Example 2

In this example, one of the examples presented in the original FUCOM article is used to compare the results obtained from the proposed approach with those from the traditional FUCOM [57]. This example examines eight criteria for addressing the issue of task-oriented resource allocation in cloud computing, where the decision maker has initially ranked the criteria as $C_3=C_5=C_7>C_1>C_2=C_4=C_6=C_6$. The preferences between the criteria have been specified using Saaty’s nine-point scale, and the comparative preferences between the criteria can be seen in

Table 4. Pairwise comparisons and comparative priorities between the criteria (example 2).

Main	Criteria
	C3	C5	C7	C1	C2	C4	C6	C8
${\mathcal{p}}_{k\left(k+1\right)}^{\prime }$	1	1	1	2	4	4	4	4
${\mathcal{p}}_{k/\left(k+1\right)}^{\prime }$	---	1	1	2	2	1	1	1
${\mathcal{p}}_{(k+1)/\left(k+2\right)}^{\prime }$	---	---	1	2	4	2	1	1

. Solving this decision-making problem and obtaining the final weights of the criteria using traditional FUCOM requires formulating and solving a mathematical optimization model with 13 main constraints and 8 main variables. However, using the S-FUCOM approach, it is observed that without the need for optimization models and software packages and only with simple algebraic calculations, results completely consistent with traditional FUCOM, along with a full satisfaction of its prerequisites, are obtained.

Below, the final weights of the criteria are calculated using Equations (9) and (10), and the FUCOM prerequisites are subsequently evaluated to determine their satisfaction. Equations (27) and (28) demonstrate the process of calculating the final weights of the criteria. First, the weight of the most important criterion, which is predicted to have the highest weight, is calculated. Then, the weights of the other criteria are determined based on this most important criterion. In this case, C₃ is identified as the most important criterion.

$$\left({\mathcal{W}}_I^{\prime }={\displaystyle \frac{1}{\sum _k\frac{1}{{\mathcal{p}}_{k\left(k+1\right)}^{\prime }}}},\forall k.\right)⟹\left[{\mathcal{W}}_3^{\prime }={\displaystyle \frac{1}{\frac{1}{1}+\frac{1}{1}+\frac{1}{1}+\frac{1}{2}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}}}\right]=0.222$$

(27)

$$\left({\mathcal{W}}_k^{\prime }={\displaystyle \frac{{\mathcal{W}}_I^{\prime }}{{\mathcal{p}}_{k\left(k+1\right)}^{\prime }}},\forall k.\right)⟹w_k\left\{\begin{array}{c}{\mathcal{W}}_5^{\prime }={\displaystyle \frac{0.222}{1}}=0.222\\ {\mathcal{W}}_7^{\prime }={\displaystyle \frac{0.222}{1}}=0.222\\ {\mathcal{W}}_1^{\prime }={\displaystyle \frac{0.222}{2}}=0.111\\ {\mathcal{W}}_2^{\prime }={\displaystyle \frac{0.222}{4}}=0.055\\ {\mathcal{W}}_4^{\prime }={\displaystyle \frac{0.222}{4}}=0.055\\ {\mathcal{W}}_6^{\prime }={\displaystyle \frac{0.222}{4}}=0.055\\ {\mathcal{W}}_8^{\prime }={\displaystyle \frac{0.222}{4}}=0.055\end{array}\right.$$

(28)

Using Equations (11) and (12), which correspond to the first and second FUCOM prerequisites, respectively, the evaluation result is determined. If these equations are satisfied, maximum consistency (DFC is $\mathcal{Z}=0$) will be achieved. Otherwise, if DFC is $\mathcal{Z}\ne 0$, the smaller the DFC, the lower the total deviation from complete consistency, indicating a higher reliability of the results. Equations (29) and (30) illustrate how the first and second FUCOM prerequisites are calculated and evaluated.

Table 5. Comparison of the final criteria weights and the status of prerequisites (example 2).

Criteria	Weights		Prerequisites
	S-FUCOM	FUCOM	(1)	(2)	Status
C1	0.111	0.111	3–5 5–7 7–1 1–2 2–4 4–6 6–8	3–7 5–1 7–2 1–4 2–6 4–8	Confirmed
C2	0.055	0.055
C3	0.222	0.222
C4	0.055	0.055
C5	0.222	0.222
C6	0.055	0.055
C7	0.222	0.222
C8	0.055	0.055
DFC	0

shows the results of the proposed approach, along with the status of the FUCOM prerequisites, and compares them with the results obtained from the traditional FUCOM.

$${\displaystyle \frac{{\mathcal{W}}_k^{\prime }}{{\mathcal{W}}_{(k+1)}^{\prime }}}-{\mathcal{p}}_{k/\left(k+1\right)}^{\prime }⟹Prerequisite (1)\left\{\begin{array}{c}{\displaystyle \frac{w_3:0.222}{w_5:0.222}}-1=0\\ {\displaystyle \frac{w_5:0.222}{w_7:0.222}}-1=0\\ {\displaystyle \frac{w_7:0.222}{w_1:0.111}}-2=0\\ {\displaystyle \frac{w_1:0.111}{w_2:0.055}}-2=0\\ {\displaystyle \frac{w_2:0.055}{w_4:0.055}}-1=0\\ {\displaystyle \frac{w_4:0.055}{w_6:0.055}}-1=0\\ {\displaystyle \frac{w_6:0.055}{w_8:0.055}}-1=0\end{array}\right.$$

(29)

$${\displaystyle \frac{{\mathcal{W}}_k^{\prime }}{{\mathcal{W}}_{(k+2)}^{\prime }}}-{\mathcal{p}}_{k/\left(k+1\right)}^{\prime }.{\mathcal{p}}_{(k+1)/\left(k+2\right)}^{\prime }⟹Prerequisite (2)\left\{\begin{array}{c}{\displaystyle \frac{w_3:0.222}{w_7:0.222}}-1\times 1=0\\ {\displaystyle \frac{w_5:0.222}{w_1:0.111}}-1\times 2=0\\ {\displaystyle \frac{w_7:0.222}{w_2:0.055}}-2\times 2=0\\ {\displaystyle \frac{w_1:0.111}{w_4:0.055}}-2\times 1=0\\ {\displaystyle \frac{w_2:0.055}{w_6:0.055}}-1\times 1=0\\ {\displaystyle \frac{w_4:0.055}{w_8:0.055}}-1\times 1=0\end{array}\right.$$

(30)

4.3. Numerical Example 3

In this section, the applicability and capabilities of FS-FUCOM are evaluated for addressing decision-making problems in uncertain environments. To this end, the problem of hospital performance evaluation with five main decision-making criteria presented by Amiri et al. [58] is discussed and analyzed. In their study, the experts’ preferences were elicited using linguistic terms and their corresponding TFNs. However, in this example, by utilizing FS-FUCOM, we demonstrate that even in decision-making environments characterized by uncertainty, incomplete information, or data shortages, S-FUCOM can determine the final fuzzy weights of the decision criteria without the need to formulate and solve mathematical optimization models in FUCOM. Using simple fuzzy operators and algebraic operations, the proposed approach significantly reduces and simplifies computations to address the uncertainty prevalent in the decision-making environment.

Step B1. At this stage, the decision-making criteria are first identified and selected. Then, the decision maker ranks the criteria from the most important to the least important based on their subjective judgments, specifying the superiority and equality between the criteria.

Step B2. After the initial ranking of the criteria by the decision maker, pairwise comparisons between the criteria are conducted using linguistic terms and their corresponding TFNs. The fuzzy priority of each criterion over another $\left({\tilde{\mathcal{p}}}_{k\left(k+1\right)}\right)$ is determined. Subsequently, the vectors of comparative fuzzy priorities $\left({\tilde{\mathcal{p}}}_{k/\left(k+1\right)}, {\tilde{\mathcal{p}}}_{(k+1)/\left(k+2\right)}\right)$are calculated.

Table 6. Fuzzy linguistic terms.

Linguistic Variables	TFNs
Equal importance (EI)	(1, 1, 1)
Lower importance (LI)	(1, 2, 3)
Moderate importance (MI)	(2, 3, 4)
Moderate plus importance (MP)	(3, 4, 5)
Strong importance (SI)	(4, 5, 6)
Strong plus importance (SP)	(5, 6, 7)
Very strong importance (VS)	(6, 7, 8)
Extreme importance (EX)	(7, 8, 9)

shows the linguistic terms and corresponding TFNs used for the fuzzy pairwise comparisons between the criteria [58]. Additionally,

Table 7. Fuzzy pairwise comparisons and comparative priorities between the criteria (example 3).

Main	Criteria
	C3	C2	C1	C5	C4
${\tilde{\mathcal{p}}}_{k\left(k+1\right)}$	(1, 1, 1)	(1, 2, 3)	(3, 4, 5)	(3, 4, 5)	(6, 7, 8)
${\tilde{\mathcal{p}}}_{k/\left(k+1\right)}$	---	(1, 2, 3)	(1, 2, 5)	(0.6, 1, 1)	(1.2, 1.75, 2.66)
${\tilde{\mathcal{p}}}_{(k+1)/\left(k+2\right)}$	---	---	(1, 4, 15)	(0.6, 2, 5)	(0.72, 1.75, 2.67)

presents the initial ranking of the criteria, the fuzzy priorities between them, and the comparative fuzzy priorities. In this example, it is assumed that the decision maker has initially ranked the five decision criteria as $C_3>C_2>C_1>C_5>C_4$ and has expressed the priority of each criterion over the others $\left({\tilde{\mathcal{p}}}_{k\left(k+1\right)}\right)$ in the order of EI, LI, MP, MP, and VS.

Step B3. After performing pairwise comparisons and obtaining the fuzzy priorities among the criteria, the final fuzzy weights of the decision-making criteria are calculated using Equations (18) and (19). Equations (31) and (32) illustrate how to calculate the fuzzy weights of the most important criterion and the other criteria, respectively. Subsequently, the FUCOM prerequisites are evaluated to confirm the conditions for full consistency. In this example, C₃ is identified as the most important criterion.

$$\begin{gathered} \left({\tilde{\mathcal{W}}}_I={\displaystyle \frac{1}{\sum _k\frac{1}{{\tilde{\mathcal{p}}}_{k\left(k+1\right)}}}},\forall k.\right)⟹\left[{\tilde{\mathcal{W}}}_3={\displaystyle \frac{1}{\frac{1}{\left(1,1,1\right)}+\frac{1}{\left(1,2,3\right)}+\frac{1}{\left(3,4,5\right)}+\frac{1}{\left(3,4,5\right)}+\frac{1}{\left(6,7,8\right)}}}\right] \\ =(0.353,0.466,0.538) \end{gathered}$$

(31)

$$\left({\tilde{\mathcal{W}}}_k={\displaystyle \frac{{\mathcal{W}}_I^{\prime }}{{\tilde{\mathcal{p}}}_{k\left(k+1\right)}}},\forall k.\right)⟹{\tilde{\mathcal{W}}}_k\left\{\begin{array}{c}{\tilde{\mathcal{W}}}_2={\displaystyle \frac{(0.353,0.466,0.538)}{(1,2,3)}}=(0.117, 0.233, 0.538)\\ {\tilde{\mathcal{W}}}_1={\displaystyle \frac{(0.353,0.466,0.538)}{(3,4,5)}}=(0.070, 0.116, 0.179)\\ {\tilde{\mathcal{W}}}_5={\displaystyle \frac{(0.353,0.466,0.538)}{(3,4,5)}}=(0.070, 0.116, 0.179)\\ {\tilde{\mathcal{W}}}_4={\displaystyle \frac{(0.353,0.466,0.538)}{(6,7,8)}}=(0.044, 0.066, 0.089)\end{array}\right.$$

(32)

After calculating the fuzzy weights of the criteria, the first and second FUCOM prerequisites are evaluated using Equations (20) and (21) to determine whether they are satisfied. Equations (33) and (34) show how to calculate and evaluate the first and second FUCOM prerequisites, respectively. If DFC is $\mathcal{Z}\ne 0$, the smaller the DFC, the lower the total deviation from complete consistency, indicating a higher reliability of the results.

Table 8. Fuzzy and crisp weights of decision criteria and their final ranking.

Criteria	Weights		Order
	Fuzzy	Crisp
C1	(0.070, 0.116, 0.179)	0.119	3
C2	(0.117, 0.233, 0.538)	0.264	2
C3	(0.353, 0.466, 0.538)	0.459	1
C4	(0.044, 0.066, 0.089)	0.066	4
C5	(0.070, 0.116, 0.179)	0.119	3
DFC	0.021

presents the fuzzy weights of the criteria, the defuzzified weights, and the final ranking of the criteria. However, it should be noted that the mathematical optimization model was neither formulated nor solved.

$${\displaystyle \frac{{\tilde{\mathcal{W}}}_k}{{\tilde{\mathcal{W}}}_{(k+1)}}}-{\tilde{\mathcal{p}}}_{k/\left(k+1\right)}⟹Prerequisite (1)\left\{\begin{array}{c}{\displaystyle \frac{w_3:(0.353,0.466,0.538)}{w_2:(0.117,0.233,0.538)}}-\left(1,2,3\right)=-0.209\\ {\displaystyle \frac{w_2:(0.117,0.233,0.538)}{w_1:(0.070,0.116,0.179)}}-\left(1,2,5\right)=-0.107\\ {\displaystyle \frac{w_1:(0.070,0.116,0.179)}{w_5:(0.070,0.116,0.179)}}-(0.6, 1, 1)=0.066\\ {\displaystyle \frac{w_5:(0.070,0.116,0.179)}{w_4:(0.044,0.066,0.089)}}-\left(1.2,1.75,2.67\right)=-0.015\end{array}\right.$$

(33)

$${\displaystyle \frac{{\tilde{\mathcal{W}}}_k}{{\tilde{\mathcal{W}}}_{(k+2)}}}-{\tilde{\mathcal{p}}}_{k/\left(k+1\right)}.{\tilde{\mathcal{p}}}_{(k+1)/\left(k+2\right)}⟹Prerequisite (2)\left\{\begin{array}{c}{\displaystyle \frac{w_3:(0.353,0.466,0.538)}{w_1:(0.070,0.116,0.179)}}-(1, 4, 15)=-1.042\\ {\displaystyle \frac{w_2:(0.117,0.233,0.538)}{w_5:(0.070,0.116,0.179)}}-(0.6, 2, 5)=-0.040\\ {\displaystyle \frac{w_1:(0.070,0.116,0.179)}{w_4:(0.044,0.066,0.089)}}-\left(0.72,1.75,2.66\right)=0.065\end{array}\right.$$

(34)

The FS-FUCOM results indicate that the fuzzy weights of the criteria were calculated with complete alignment with the decision-maker’s preferences. In this example, the DFC value is calculated as 0.021, indicating the high consistency of the comparisons and a high level of reliability in the results. As previously mentioned, the consistency of linguistic terms and expert preferences is independent of the degree of fuzziness in the membership functions, and the obtained DFC reflects this fact. Otherwise, the DFC would be calculated as zero. The fuzzy calculations and defuzzification processes impact the DFC value and the status of the FUCOM prerequisites in fuzzy extensions of FUCOM. If, in this example, the fuzzy preferences of the decision maker were first defuzzified, and then the final weights were calculated, complete consistency with $DFC=0$ would be observed, and the FUCOM prerequisites would show a high level of consistency.

4.4. Numerical Example 4

This example is based on the study by Simić et al. [46], and it compares the results obtained from fuzzy FUCOM and FS-FUCOM. They focused on assessing the condition of road sections from a traffic safety perspective, using four evaluation criteria: traffic accidents with fatalities (C₁), traffic accidents with severe injuries (C₂), traffic accidents with minor injuries (C₃), and traffic accidents with material damage (C₄). The decision-making criteria weights were obtained using the fuzzy FUCOM approach. They gathered preferences from several experts, with their integrated preferences shown in

Table 9. Fuzzy pairwise comparisons and comparative priorities between the criteria (example 4).

Main	Criteria
	C1	C2	C3	C4
${\tilde{\mathcal{p}}}_{k\left(k+1\right)}$	(1, 1, 1)	(1.02, 1.14, 1.47)	(1.09, 1.29, 1.47)	(1.55, 1.79, 1.99)
${\tilde{\mathcal{p}}}_{k/\left(k+1\right)}$	---	(1.02, 1.14, 1.47)	(0.743, 1.131, 1.44)	(1.053, 1.387, 1.836)
${\tilde{\mathcal{p}}}_{(k+1)/\left(k+2\right)}$	---	---	(0.757, 1.289, 2.11)	(0.782, 1.569, 2.644)

. In this example, the initial ranking of the criteria is considered as $C_1>C_2>C_3>C_4$, with C₁ being selected as the most important criterion. Subsequently, this problem is solved using the FS-FUCOM approach, and the steps and results are explained to enable a comparative analysis.

Step C1. At this stage, the decision-making criteria are first identified and selected. Subsequently, the decision maker ranks these criteria from most to least important based on their subjective judgments, indicating the relative importance and equality among the criteria.

Step C2. At this step, the fuzzy priority of each criterion relative to others is expressed using linguistic terms and their corresponding TFNs. In this example, the experts’ opinions have been aggregated and are shown in Table 9. Subsequently, the comparative fuzzy priorities $\left({\tilde{\mathcal{p}}}_{k/\left(k+1\right)}, {\tilde{\mathcal{p}}}_{(k+1)/\left(k+2\right)}\right)$ are calculated. Criterion C₁ is considered the most important criterion in the road safety assessment problem.

Step C3. Following the pairwise comparisons and determination of fuzzy priorities among the criteria, the final fuzzy weights are computed using Equations (18) and (19). Equations (35) and (36) demonstrate the method for calculating the fuzzy weights of the most important criterion and the remaining criteria, respectively. Thereafter, the FUCOM prerequisites are assessed and DFC determined.

$$\begin{gathered} \left({\tilde{\mathcal{W}}}_I={\displaystyle \frac{1}{\sum _k\frac{1}{{\tilde{\mathcal{p}}}_{k\left(k+1\right)}}}},\forall k.\right)⟹\left[{\tilde{\mathcal{W}}}_1={\displaystyle \frac{1}{\frac{1}{\left(1,1,1\right)}+\frac{1}{\left(1.02,1.14,1.47\right)}+\frac{1}{\left(1.09,1.29,1.47\right)}+\frac{1}{\left(1.55,1.79,1.99\right)}}}\right] \\ =(0.282,0.311,0.349) \end{gathered}$$

(35)

$$\left({\tilde{\mathcal{W}}}_k={\displaystyle \frac{{\mathcal{W}}_I^{\prime }}{{\tilde{\mathcal{p}}}_{k\left(k+1\right)}}},\forall k.\right)⟹{\tilde{\mathcal{W}}}_k\left\{\begin{array}{c}{\tilde{\mathcal{W}}}_2={\displaystyle \frac{(0.282,0.311,0.349)}{(1.02,1.14,1.47)}}=(0.192, 0.273, 0.342)\\ {\tilde{\mathcal{W}}}_3={\displaystyle \frac{(0.282,0.311,0.349)}{(1.09,1.29,1.47)}}=(0.192, 0.241, 0.320)\\ {\tilde{\mathcal{W}}}_4={\displaystyle \frac{(0.282,0.311,0.349)}{(1.55,1.79,1.99)}}=(0.141, 0.173, 0.225)\end{array}\right.$$

(36)

After calculating the fuzzy weights of the criteria, the first and second FUCOM prerequisites are evaluated using Equations (20) and (21). Equations (37) and (38) illustrate the calculation and evaluation process for these prerequisites. If DFC is $\mathcal{Z}\ne 0$, a smaller DFC indicates a lower total deviation from complete consistency, thus suggesting a higher reliability of the results.

Table 10. Comparison of fuzzy and crisp weights of decision criteria and their final ranking.

Criteria	FS-FUCOM			Fuzzy FUCOM
	Fuzzy Weights	Crisp	Order	Fuzzy Weights	Crisp	Order
C1	(0.282, 0.311, 0.349)	0.313	1	(0.284, 0.323, 0.404)	0.330	1
C2	(0.192, 0.273, 0.342)	0.271	2	(0.241, 0.241, 0.350)	0.259	2
C3	(0.192, 0.241, 0.320)	0.246	3	(0.212, 0.216, 0.294)	0.228	3
C4	(0.141, 0.173, 0.225)	0.177	4	(0.144, 0.176, 0.244)	0.182	4
DFC	0.001			0.2

presents the fuzzy weights of the criteria, the defuzzified weights, and the final ranking of the criteria according to both FS-FUCOM and fuzzy FUCOM. However, it should be noted that the mathematical optimization model was neither formulated nor solved.

$$\begin{gathered} {\displaystyle \frac{{\tilde{\mathcal{W}}}_k}{{\tilde{\mathcal{W}}}_{(k+1)}}}-{\tilde{\mathcal{p}}}_{k/\left(k+1\right)}⟹ \\ Prerequisite (1)\left\{\begin{array}{c}{\displaystyle \frac{w_1:(0.282,0.311,0.349)}{w_2:(0.192,0.273,0.342)}}-(1.02, 1.14, 1.47)=0.026\\ {\displaystyle \frac{w_2:(0.192,0.273,0.342)}{w_3:(0.192,0.241,0.320)}}-\left(0.743,1.131,1.44\right)=0.034\\ {\displaystyle \frac{w_3:(0.192,0.241,0.320)}{w_4:(0.141,0.173,0.225)}}-\left(1.053,1.387,1.836\right)=0.043\end{array}\right. \end{gathered}$$

(37)

$$\begin{gathered} {\displaystyle \frac{{\tilde{\mathcal{W}}}_k}{{\tilde{\mathcal{W}}}_{(k+2)}}}-{\tilde{\mathcal{p}}}_{k/\left(k+1\right)}.{\tilde{\mathcal{p}}}_{(k+1)/\left(k+2\right)}⟹ \\ Prerequisite (2)\left\{\begin{array}{c}{\displaystyle \frac{w_1:(0.282,0.311,0.349)}{w_3:(0.192,0.241,0.320)}}-\left(0.757,1.289,2.11\right)=-0.025\\ {\displaystyle \frac{w_2:(0.192,0.273,0.342)}{w_4:(0.141,0.173,0.225)}}-\left(0.782,1.569,2.644\right)=-0.018\end{array}\right. \end{gathered}$$

(38)

As can be seen, FS-FUCOM calculates the fuzzy weights of the criteria in complete alignment with the decision-maker’s preferences without the need to formulate and solve a mathematical optimization model. In this example, the DFC value calculated by FS-FUCOM is 0.001, whereas the DFC value in the traditional FUCOM is reported to be 0.2. This indicates a high consistency of the comparisons and a high level of reliability in the results obtained from the proposed approach. Various fuzzy scales and the consistency in pairwise comparisons affect the results of FS-FUCOM. It is recommended to use standard fuzzy scales and ensure that the pairwise comparisons accurately reflect the initial ranking of the criteria.

5. Case Study

In this section, a real-world case study is conducted to evaluate and select gresilient suppliers in the construction industry using the FS-FUCOM approach. A holding company active in the construction industry is examined for this purpose. This company is involved in technical services, consulting, and research for various projects in the fields of designing and constructing residential buildings and administrative and commercial centers. It also has a track record of creating and operating numerous construction projects. The senior managers of this company have recently sought to prioritize some of their main suppliers based on gresilient criteria, as the company is highly committed to environmental protection, preventing pollution, avoiding the waste of raw materials, and other green industry indicators as part of its core mission. Selecting resilient suppliers can significantly bolster supply chain processes, thereby improving both competitiveness and customer satisfaction by fostering the development of management capabilities [59,60]. Given the high sensitivity of the construction industry and existing requirements, supplier resilience is also considered one of the most important evaluation criteria.

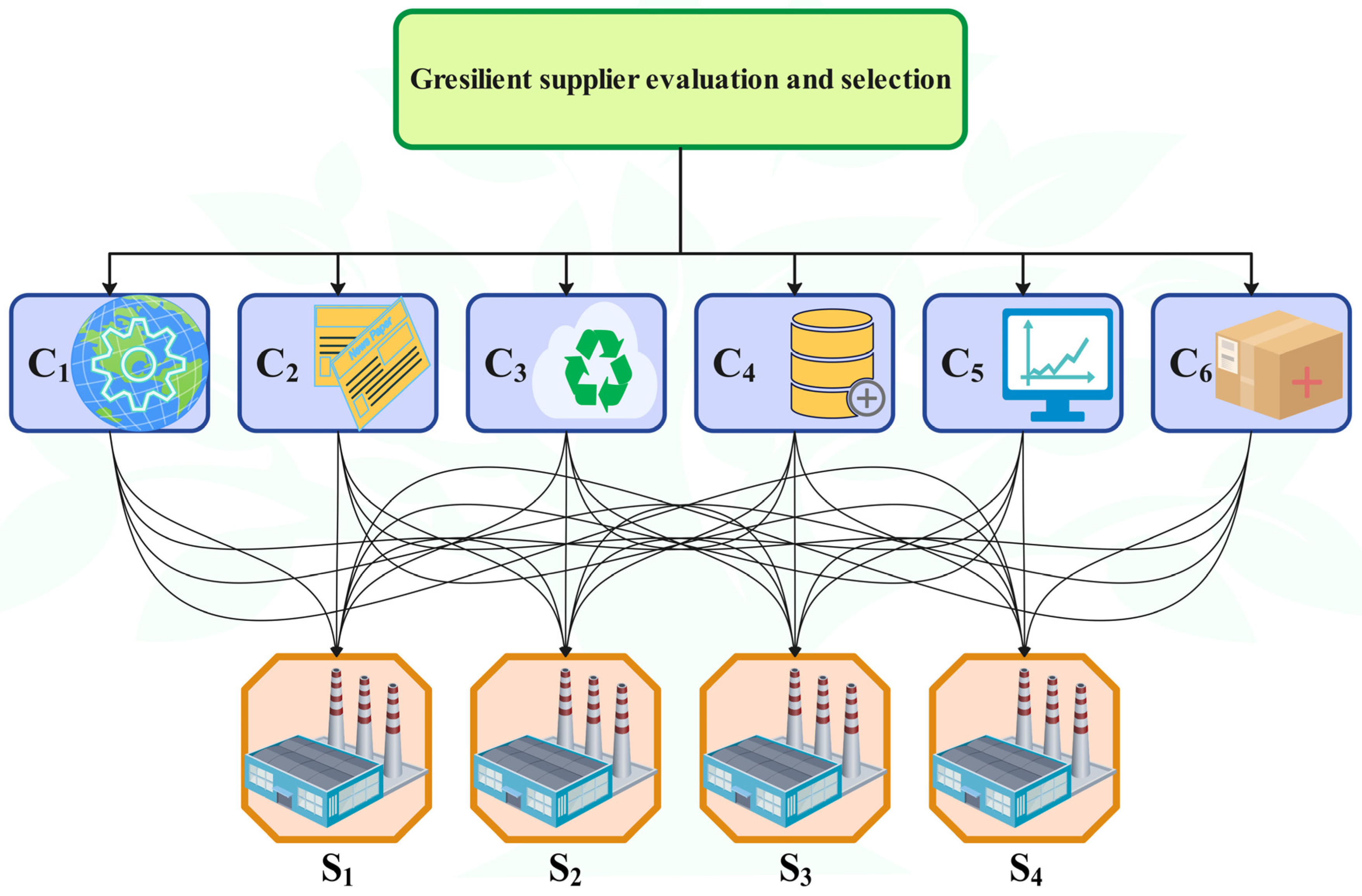
A group of three decision makers, all active professionals in the construction industry, was selected to evaluate the issue of gresilient supplier selection. Their details are shown in

Table 11. Characteristics of decision panel members.

Experts	Education		Specialized Area	Position	Experience
	Ph.D.	MA
Expert 1	✓		Supply chain management	Supplier relations manager	13+
Expert 2		✓	Environmental management	Environmental specialist	9+
Expert 3		✓	Project management	Planning and scheduling specialist	12+

. After reviewing the literature and company information regarding suppliers, the decision makers agreed on six evaluation criteria, three green indicators, and three resilience indicators, listed with brief descriptions in

Table 12. Evaluation criteria in gresilient SES with a brief description.

GSES Criteria	Brief Description	References
Environmental management systems (C1)	The supplier’s environmental policies and objectives, as well as their procedures for evaluating and controlling environmental activities.	[22,31,61]
Green certification (C2)	The supplier’s capability to obtain green-related certifications for the production of necessary materials.	[13,14,17,32,62]
Air emissions (C3)	The supplier’s ability to control the level of harmful emissions during the production of required materials.	[32,63,64]
Restorative capacity (C4)	The supplier’s capacity to implement repair or reconstruction protocols to recover from threats and return to normal conditions.	[31,33,65,66]
Vulnerability detection and reaction plans (C5)	The supplier’s ability to identify and respond to various potential threats through a resilient and well-structured sales and operations planning scheme.	[31,67,68]
Surplus inventory (C6)	Additional inventory available for use during crises or emergencies.	[66,69,70]

. The evaluation criteria, which include environmental management systems (C₁), green certification (C₂), air emissions (C₃), restorative capacity (C₄), vulnerability detection and reaction plans (C₅), and surplus inventory (C₆), were identified and validated based on the company’s requirements, a literature review, and expert opinions. As previously mentioned, these criteria focus on two main aspects: the greenness and resilience of suppliers. The criteria C₁ to C₃, which assess greenness, respectively focus on the suppliers’ ability in environmental control systems and policies, adherence to green certifications and their requirements, and the management of air pollution and toxic gas emissions. The criteria C₄ to C₆, which evaluate supplier resilience, respectively focus on the suppliers’ ability to return to normal or improved conditions, anticipate potential damages and plan appropriate responses, and maintain surplus inventory to aid in crisis recovery. Considering the decision-makers’ views that the decision-making space was uncertain, FS-FUCOM was used first to examine the evaluation criteria to determine their weights. Then, the four main suppliers of the construction company were prioritized based on the evaluation criteria weights. The hierarchical structure of the gresilient SES problem is shown in Figure 4. The following sections detail the steps of assigning importance to the evaluation criteria, prioritizing suppliers using FS-FUCOM, and analyzing the results.

5.1. Calculating the Evaluation Criteria Weights in Gresilient SES

In this section, the fuzzy weights of the evaluation criteria are calculated using the FS-FUCOM approach and the preferences of three experts. Then, in the next section, the prioritization of suppliers based on the obtained weights of the evaluation criteria and each supplier’s score in each criterion will be specified. Subsequently, the steps for calculating the criteria weights are explained, and the results are analyzed.

Step D1. First, the evaluation criteria for suppliers are identified and selected, as shown in Table 12. Then, the initial ranking of the criteria is performed by the decision maker, who arranges them from the most important criterion to the least important criterion. In this process, the opinions of three experts are used, whose preferences regarding the criteria may differ, but there is agreement on the initial criteria ranking. The fuzzy preferences of the experts regarding the criteria can be integrated using common TFN aggregation operators, and here, the simple average is used [71]. Table 6 shows the linguistic terms used in the gresilient SES problem. Additionally,

Table 13. Integration of the fuzzy preferences of evaluation criteria.

Criteria	Expert 1	Expert 2	Expert 3	$\mathit{A}\mathit{V}\mathit{G}{\tilde{\mathcal{p}}}_{\mathit{k}\left(\mathit{k}+1\right)}$
C3	EI	EI	EI	(1,1,1)
C1	MI	LI	MI	(1.667, 2.667, 3.667)
C4	MP	MP	SI	(3.333, 4.333, 5.333)
C2	SP	SI	SP	(4.667, 5.667, 6.667)
C6	SP	SP	EX	(5.667, 6.667, 7.667)
C5	EX	SP	EX	(6.333, 7.333, 8.333)
Order	C3 > C1 > C4 > C2 > C6 > C5

presents the results of integrating the experts’ fuzzy preferences regarding the evaluation criteria. In this case, the initial ranking of the criteria is obtained as $C_3>C_1>C_4>C_2>C_6>C_5$.

Step D2. After determining the initial ranking of the criteria and the fuzzy preferences, the fuzzy comparative preferences of each criterion relative to another criterion $\left({\tilde{\mathcal{p}}}_{k/\left(k+1\right)}, {\tilde{\mathcal{p}}}_{(k+1)/\left(k+2\right)}\right)$are also calculated.

Table 14. Fuzzy pairwise comparisons and comparative priorities between the criteria (case study).

Main	Criteria
	C3	C1	C4	C2	C6	C5
${\tilde{\mathcal{p}}}_{k\left(k+1\right)}$	(1, 1, 1)	(1.667, 2.667, 3.667)	(3.333, 4.333, 5.333)	(4.667, 5.667, 6.667)	(5.667, 6.667, 7.667)	(6.333, 7.333, 8.333)
${\tilde{\mathcal{p}}}_{k/\left(k+1\right)}$	---	(1.667, 2.667, 3.667)	(0.909, 1.625, 3.2)	(0.875, 1.307, 2)	(0.85, 1.176, 1.642)	(0.826, 1.1, 1.470)
${\tilde{\mathcal{p}}}_{(k+1)/\left(k+2\right)}$	---	---	(1.515, 4.34, 11.733)	(0.795, 2.125, 6.4)	(0.744, 1.538, 3.285)	(0.702, 1.294, 2.416)

shows the fuzzy preference of each criterion relative to another criterion and the fuzzy comparative preferences. Here, the opinions of all three experts have been integrated to evaluate the decision-making criteria, and the final weights of the criteria can be calculated based on the obtained preferences.

Step D2. In this step, the fuzzy weights of the evaluation criteria for the gresilient SES problem are determined. After pairwise comparisons and establishing the fuzzy priorities among the criteria, the final fuzzy weights of the decision-making criteria are calculated using Equations (18) and (19). Equations (39) and (40) demonstrate computing the fuzzy weight of the most important criterion and the subsequent criteria, respectively. Criterion C₃ is considered the most important criterion in the gresilient SES problem.

$$\begin{gathered} \left({\tilde{\mathcal{W}}}_I={\displaystyle \frac{1}{\sum _k\frac{1}{{\tilde{\mathcal{p}}}_{k\left(k+1\right)}}}}, \forall k.\right) ⟹ \\ \left[{\tilde{\mathcal{W}}}_3={\displaystyle \frac{1}{\frac{1}{\left(1, 1, 1\right)}+\frac{1}{(1.667,2.667,3.667)}+\frac{1}{(3.333,4.333,5.333)}+\frac{1}{(4.667,5.667,6.667)}+\frac{1}{(5.667,6.667,7.667)}+\frac{1}{(6.333,7.333,8.333)}}}\right] \\ =(0.408, 0.483, 0.537) \end{gathered}$$

(39)

$$\left({\tilde{\mathcal{W}}}_k={\displaystyle \frac{{\mathcal{W}}_I^{\prime }}{{\tilde{\mathcal{p}}}_{k\left(k+1\right)}}},\forall k.\right)⟹{\tilde{\mathcal{W}}}_k\left\{\begin{array}{c}{\tilde{\mathcal{W}}}_1={\displaystyle \frac{(0.408,0.483,0.537)}{(1.667,2.667,3.667)}}=(0.111, 0.181, 0.322)\hfill \\ {\tilde{\mathcal{W}}}_4={\displaystyle \frac{(0.408,0.483,0.537)}{(3.333,4.333,5.333)}}=(0.076, 0.111, 0.161)\hfill \\ {\tilde{\mathcal{W}}}_2={\displaystyle \frac{(0.408,0.483,0.537)}{(4.667,5.667,6.667)}}=\left(0.061,0.085,0.115\right)\hfill \\ {\tilde{\mathcal{W}}}_6={\displaystyle \frac{(0.408,0.483,0.537)}{(5.667,6.667,7.667)}}=\left(0.053,0.072,0.094\right)\hfill \\ {\tilde{\mathcal{W}}}_5={\displaystyle \frac{(0.408,0.483,0.537)}{(6.333,7.333,8.333)}}=(0.049, 0.065, 0.085)\hfill \end{array}\right.$$

(40)

After determining the fuzzy weights of the gresilient SES criteria, the first and second FUCOM prerequisites are evaluated to ensure the consistency and reliability of the results. This evaluation is performed using Equations (20) and (21), while Equations (41) and (42) detail the specific calculation and evaluation process for these prerequisites.

Table 15. The final weights of the evaluation criteria for the gresilient SES problem.

Criteria	FS-FUCOM
	Fuzzy Weights	Crisp	Order
C1	(0.111, 0.181, 0.322)	0.191	2
C2	(0.061, 0.085, 0.115)	0.086	4
C3	(0.408, 0.483, 0.537)	0.469	1
C4	(0.076, 0.111, 0.161)	0.114	3
C5	(0.049, 0.065, 0.085)	0.066	6
C6	(0.053, 0.072, 0.094)	0.073	5
DFC	0.008

summarizes the fuzzy weights of the criteria, the defuzzified weights of the criteria, and the final criteria ranking based on these weights.

$$\begin{gathered} {\displaystyle \frac{{\tilde{\mathcal{W}}}_k}{{\tilde{\mathcal{W}}}_{(k+1)}}}-{\tilde{\mathcal{p}}}_{k/\left(k+1\right)}⟹ \\ Prerequisite(1)\left\{\begin{array}{c}{\displaystyle \frac{w_3:(0.408,0.483,0.537)}{w_1:(0.111,0.181,0.322)}}-(1.515, 4.34, 11.733)=0.126\\ {\displaystyle \frac{w_1:(0.111,0.181,0.322)}{w_4:(0.076,0.111,0.161)}}-(0.909, 1.625, 3.2)=0.132\\ {\displaystyle \frac{w_4:(0.076,0.111,0.161)}{w_2:\left(0.061,0.085,0.115\right)}}-(0.875, 1.307, 2)=0.070\\ {\displaystyle \frac{w_2:\left(0.061,0.085,0.115\right)}{w_6:\left(0.053,0.072,0.094\right)}}-(0.85, 1.176, 1.642)=0.052\\ {\displaystyle \frac{w_6:\left(0.053,0.072,0.094\right)}{w_5:(0.049,0.065,0.085)}}-(0.826, 1.1, 1.470)=0.044\end{array}\right. \end{gathered}$$

(41)

$$\begin{gathered} {\displaystyle \frac{{\tilde{\mathcal{W}}}_k}{{\tilde{\mathcal{W}}}_{(k+2)}}}-{\tilde{\mathcal{p}}}_{k/\left(k+1\right)}.{\tilde{\mathcal{p}}}_{(k+1)/\left(k+2\right)}⟹ \\ Prerequisite(2)\left\{\begin{array}{c}{\displaystyle \frac{w_3:(0.408,0.483,0.537)}{w_4:(0.076,0.111,0.161)}}-\left(0.757,1.289,2.11\right)=-0.616\\ {\displaystyle \frac{w_1:(0.111,0.181,0.322)}{w_2:\left(0.061,0.085,0.115\right)}}-\left(0.795,2.125,6.4\right)=-0.160\\ {\displaystyle \frac{w_4:(0.076,0.111,0.161)}{w_6:\left(0.053,0.072,0.094\right)}}-\left(0.744,1.538,3.285\right)=-0.032\\ {\displaystyle \frac{w_2:\left(0.061,0.085,0.115\right)}{w_5:(0.049,0.065,0.085)}}-\left(0.702,1.294,2.416\right)=-0.007\end{array}\right. \end{gathered}$$

(42)

The results show that criterion C₃, with a significant margin over the other criteria, is selected as the most important criterion for evaluating and selecting the gresilient supplier, with a weight of 0.469. Subsequently, criteria C₁, C₄, C₂, C₆, and C₅ are ranked second to sixth with final weights of 0.191, 0.114, 0.086, 0.073, and 0.066, respectively. Additionally, the DFC value is calculated to be 0.008, indicating the consistency of the comparisons and the alignment of the experts’ fuzzy preferences with the results obtained from the FS-FUCOM approach. In the proposed approach, the evaluation criteria for suppliers are prioritized using only algebraic relationships and fuzzy operators, and other advantages of FUCOM, such as fewer pairwise comparisons, also significantly impact the effectiveness of the proposed approach. In the next section, the four suppliers considered by the company will be prioritized based on the criteria weights using the proposed approach.

5.2. Prioritization of Gresilient Suppliers Based on the Importance of Evaluation Criteria

In this section, the alternatives to the decision-making problem, which include the four main suppliers of the mentioned company, are prioritized based on the fuzzy weights of the decision-making criteria. Here, the opinions of all three experts are also used for the prioritization of suppliers. The experts provide their fuzzy preferences regarding the superiority of each supplier in each criterion using the linguistic terms in Table 6. Then, the average of the experts’ fuzzy preferences is calculated using Definition 5 to form the integrated fuzzy decision matrix. Subsequently, according to Definition 3 and considering that all decision-making criteria are positive, the integrated fuzzy preferences of the experts are normalized. Then, the fuzzy weights of the decision-making criteria are applied to the normalized matrix to determine the final score of each supplier in each criterion $\left(x_{ij}\right)$. Finally, using Equation (6), the final scores and prioritization of the suppliers will be obtained.

Table 16. The fuzzy preference of each supplier in each criterion by each expert.

Experts	Suppliers	Criteria
		C1	C2	C3	C4	C5	C6
Expert 1	S1	MP	SP	MP	SP	VS	MP
	S2	MI	MI	SI	MP	SI	SI
	S3	VS	SI	EX	SP	SP	EX
	S4	MP	SP	VS	MI	LI	SI
Expert 2	S1	SI	VS	SI	EX	EX	SP
	S2	MI	MI	SP	VS	MP	SI
	S3	SP	EX	SP	MP	MI	SP
	S4	EX	MI	SP	LI	MI	EX
Expert 3	S1	VS	SP	EX	MP	MP	MI
	S2	MP	SI	MP	SP	SP	VS
	S3	SI	EX	SI	VS	VS	MI
	S4	SP	SI	SP	VS	MP	MP

shows the experts’ fuzzy preferences regarding the priority of each supplier in each criterion.

The experts’ fuzzy evaluations regarding the score of each supplier in each criterion are aggregated according to Definition 5 to form the initial fuzzy decision matrix.

Table 17. Fuzzy initial decision matrix.

Main	Criteria
	C1	C2	C3	C4	C5	C6
	${\mathit{w}}_1:$ (0.111, 0.181, 0.322)	${\mathit{w}}_2:$ (0.061, 0.085, 0.115)	${\mathit{w}}_3:$ (0.408, 0.483, 0.537)	${\mathit{w}}_4:$ (0.076, 0.111, 0.161)	${\mathit{w}}_5:$ (0.049, 0.065, 0.085)	${\mathit{w}}_6:$ (0.053, 0.072, 0.094)
S1	(4.33, 5.33, 6.33)	(5.33, 6.33, 7.33)	(4.66, 5.66, 6.66)	(5, 6, 7)	(5.33, 6.33, 7.33)	(3.33, 4.33, 5.33)
S2	(2.33, 3.33, 4.33)	(2.66, 3.66, 4.66)	(4, 5, 6)	(4.66, 5.66, 6.66)	(4, 5, 6)	(4.66, 5.66, 6.66)
S3	(5, 6, 7)	(6, 7, 8)	(5.33, 6.33, 7.33)	(4.66, 5.66, 6.66)	(4.33, 5.33, 6.33)	(4.66, 5.66, 6.66)
S4	(5, 6, 7)	(3.66, 4.66, 5.66)	(5.33, 6.33, 7.33)	(3, 4, 5)	(2, 3, 4)	(4.66, 5.66, 6.66)

shows the results of this aggregation.

Next, a normalization of the fuzzy decision matrix is carried out. In this normalization process, the values in the matrix are adjusted to fall within a standardized range, typically between 0 and 1, for each row or column. This normalization ensures that the elements of the decision matrix do not disproportionately affect the analysis. After normalizing the decision matrix, the fuzzy weights of the evaluation criteria for suppliers, obtained in the previous section through the FS-FUCOM approach, are applied to the normalized matrix to form the weighted fuzzy decision matrix.

Table 18. Fuzzy normalized decision matrix.

Suppliers	Criteria
	C1	C2	C3	C4	C5	C6
S1	(0.619, 0.742, 0.905)	(0.667, 0.792, 0.917)	(0.636, 0.773, 0.909)	(0.714, 0.857, 1)	(0.727, 0.864, 1)	(0.5, 0.65, 0.8)
S2	(0.333, 0.476, 0.619)	(0.333, 0.458, 0.583)	(0.545, 0.682, 0.818)	(0.667, 0.810, 0.952)	(0.545, 0.682, 0.818)	(0.7, 0.85, 1)
S3	(0.714, 0.857, 1)	(0.750, 0.875, 1)	(0.724, 0.864, 1)	(0.667, 0.810, 0.952)	(0.591, 0.727, 0.864)	(0.7, 0.85, 1)
S4	(0.714, 0.857, 1)	(0.458, 0.583, 0.708)	(0.724, 0.864, 1)	(0.429, 0.571, 0.714)	(0.273, 0.409, 0.545)	(0.7, 0.85, 1)

and

Table 19. Fuzzy weighted normalized decision matrix.

Suppliers	Criteria
	C1	C2	C3	C4	C5	C6
S1	(0.068, 0.138, 0.291)	(0.041, 0.067, 0.105)	(0.260, 0.373, 0.488)	(0.054, 0.095, 0.161)	(0.036, 0.056, 0.085)	(0.026, 0.047, 0.075)
S2	(0.023, 0.066, 0.180)	(0.020, 0.039, 0.067)	(0.223, 0.329, 0.439)	(0.051, 0.090, 0.153)	(0.027, 0.044, 0.070)	(0.037, 0.061, 0.094)
S3	(0.079, 0.155, 0.322)	(0.046, 0.074, 0.115)	(0.297, 0.417, 0.537)	(0.051, 0.090, 0.153)	(0.029, 0.047, 0.073)	(0.037, 0.061, 0.094)
S4	(0.079, 0.155, 0.322)	(0.028, 0.050, 0.081)	(0.297, 0.417, 0.537)	(0.033, 0.063, 0.115)	(0.013, 0.027, 0.046)	(0.037, 0.061, 0.094)

show the normalized decision matrix and the weighted normalized decision matrix, respectively.

After calculating the weighted normalized decision matrix, the scores for each supplier in each criterion are defuzzified using Definition 4 to obtain precise values. Subsequently, the final scores for the suppliers are calculated using Equation (6), and the suppliers are ranked based on their final scores.

Table 20. Final scores and prioritization of gresilient suppliers.

Suppliers	Criteria						$\sum {\mathit{x}}_{\mathit{i}\mathit{j}}{\mathit{w}}_{\mathit{j}}$	Rank
	C1	C2	C3	C4	C5	C6
S1	0.152	0.069	0.373	0.099	0.058	0.048	0.800	2
S2	0.078	0.041	0.330	0.094	0.046	0.063	0.650	4
S3	0.170	0.076	0.417	0.094	0.049	0.063	0.869	1
S4	0.170	0.051	0.417	0.067	0.028	0.063	0.796	3

shows the final rankings and scores of the suppliers.

The results in Table 20 show that the final prioritization of suppliers is S₃ > S₁ > S₄ > S₂, with supplier S₃ having the highest capacity in gresilient principles. Additionally, suppliers S₁, S₄, and S₃ have been selected as the second to fourth suppliers, respectively. The suppliers were compared based on the gresilient evaluation criteria, and those performed better in criteria with higher weights were selected as the top suppliers. For example, criteria C₁, C₃, and C₄ were considered the most important criteria, and the first and third suppliers, who performed better in these criteria, were introduced as the selected suppliers. The results obtained from FS-FUCOM indicate that this approach, while maintaining the other advantages of FUCOM and without the need to formulate and solve mathematical optimization models, is a comprehensive approach capable of calculating the final weights of criteria in both deterministic and non-deterministic environments. It can provide accurate results for the problem of SES. Since the requirements of FUCOM are also examined in the proposed approach, and the DFC value is calculated, the decision-maker is able to modify the pairwise comparisons between criteria and the preferences of experts until a reliable and trustworthy result is achieved.

Additionally, to better evaluate the results of assigning importance to the evaluation criteria, the construction company in question has stated the need for an analysis and validation of the research results. For this purpose, in the next section, a sensitivity analysis of the final weights of the criteria obtained from the FS-FUCOM approach will be conducted to confirm the validity and robustness of the results.

6. Sensitivity Analysis

The evaluation and selection process of gresilient suppliers under uncertainty is considered a complex process due to the presence of multiple criteria and alternatives with different characteristics, as well as the need for subjective judgments by the decision-making group. Therefore, after calculating the final weights of the evaluation criteria for gresilient suppliers using FS-FUCOM and prioritizing the desired suppliers, a sensitivity analysis of the research results is conducted to assess their robustness and validity. A sensitivity analysis examines the sensitivity of the results obtained from MCDM methods to slight adjustments, thereby determining their robustness. Various approaches have been employed in the literature to perform sensitivity analyses, and this analysis is usually carried out on the key results of a research project [72]. Some of the approaches to conducting a sensitivity analysis include making adjustments to the weight coefficients of the criteria by generating different sets of weights based on the main criteria weights, changing linguistic terms and their numerical scales to obtain experts’ preferences, changing the nature of criteria from positive to negative or vice versa, the application of dynamic matrices, comparative analyses between different approaches, etc. [73]. The purpose of a sensitivity analysis of the results is to evaluate the impact of the most important criterion on the performance ranking of the proposed approach [74].

Here, to analyze the sensitivity of the research results, the most important outputs, namely the final weights of the criteria and the prioritization of the suppliers, are evaluated. For this purpose, the sensitivity analysis approach based on the variation of the weight coefficients of the criteria is used [48,75,76]. In FUCOM, before conducting pairwise comparisons, the initial ranking of criteria is specified by the decision maker, and the most important criterion, which is expected to have the highest weight, is determined. In the sensitivity analysis approach of the variation of criterion weights, the set of changes for other criteria is considered based on the weight of the most important criterion. This demonstrates the high compatibility of this sensitivity analysis approach with the FUCOM structure.

To conduct a sensitivity analysis on the main research results, the sensitivity of the fuzzy weight of the most important criterion, C₃, to changes in the final ranking of alternatives is first considered. Then, using Equation (43), different scenarios, i.e., different sets of fuzzy weights for the criteria, are derived. In this analysis, 20 different scenarios are examined. In the first scenario, the fuzzy weight of the most important criterion is reduced by 5%, and the adjusted fuzzy weights of the other criteria are calculated proportionally based on the fuzzy weight of the most important criterion using Equation (43).

$${\tilde{W}}_R^C=\left(\left(1-{\tilde{W}}_R^{MC}\right){\displaystyle \frac{{\tilde{W}}^C}{\left(1-{\tilde{W}}^{MC}\right)}}\right)$$

(43)

where ${\tilde{W}}_R^C$ is the adjusted fuzzy weight coefficient of the other criteria, ${\tilde{W}}_R^{MC}$ is the reduced fuzzy weight coefficient of the most important criterion, ${\tilde{W}}^C$ is the original fuzzy weight coefficient of the criterion to be adjusted, and ${\tilde{W}}^{MC}$ is the original fuzzy weight coefficient of the most important criterion, which in this case is C₃.

In the subsequent scenarios, the fuzzy weight of criterion C₃ is similarly reduced, and the generated fuzzy weights of the other criteria are calculated based on the reduced weight of criterion C₃. In all scenarios, the final fuzzy weights satisfy the condition ${\sum }_{j=1}^n{w}_j=1$. This process results in 20 different scenarios, each comprising vectors of fuzzy weight coefficients for the supplier selection criteria, as shown in

Table 21. Changes in the fuzzy weights of evaluation criteria in 20 different scenarios.

Scenarios	Criteria Weight Adjustments
	C1	C2	C3	C4	C5	C6
Main	(0.111, 0.181, 0.322)	(0.061, 0.085, 0.115)	(0.408, 0.483, 0.537)	(0.076, 0.111, 0.161)	(0.049, 0.065, 0.085)	(0.053, 0.072, 0.094)
Sce. 1	(0.103, 0.196, 0.418)	(0.056, 0.092, 0.149)	(0.418, 0.473, 0.518)	(0.071, 0.120, 0.209)	(0.045, 0.071, 0.110)	(0.049, 0.078, 0.123)
Sce. 2	(0.109, 0.205, 0.434)	(0.060, 0.096, 0.155)	(0.396, 0.448, 0.490)	(0.075, 0.126, 0.217)	(0.048, 0.074, 0.114)	(0.052, 0.082, 0.127)
Sce. 3	(0.115, 0.214, 0.450)	(0.063, 0.101, 0.160)	(0.374, 0.423, 0.463)	(0.079, 0.132, 0.225)	(0.050, 0.078, 0.118)	(0.055, 0.085, 0.132)
Sce. 4	(0.120, 0.224, 0.466)	(0.066, 0.105, 0.166)	(0.352, 0.398, 0.436)	(0.083, 0.137, 0.233)	(0.053, 0.081, 0.122)	(0.057, 0.089, 0.137)
Sce. 5	(0.126, 0.233, 0.482)	(0.069, 0.109, 0.172)	(0.330, 0.373, 0.409)	(0.087, 0.143, 0.241)	(0.055, 0.084, 0.126)	(0.060, 0.093, 0.141)
Sce. 6	(0.132, 0.242, 0.497)	(0.072, 0.114, 0.177)	(0.308, 0.348, 0.381)	(0.091, 0.149, 0.248)	(0.058, 0.088, 0.131)	(0.063, 0.097, 0.146)
Sce. 7	(0.138, 0.252, 0.513)	(0.076, 0.118, 0.183)	(0.286, 0.324, 0.354)	(0.095, 0.155, 0.256)	(0.060, 0.091, 0.135)	(0.066, 0.100, 0.151)
Sce. 8	(0.144, 0.261, 0.529)	(0.079, 0.122, 0.189)	(0.264, 0.299, 0.327)	(0.099, 0.160, 0.264)	(0.063, 0.095, 0.139)	(0.069, 0.104, 0.155)
Sce. 9	(0.150, 0.270, 0.545)	(0.082, 0.127, 0.194)	(0.242, 0.274, 0.299)	(0.103, 0.166, 0.272)	(0.066, 0.098, 0.143)	(0.071, 0.108, 0.160)
Sce. 10	(0.156, 0.279, 0.561)	(0.085, 0.131, 0.200)	(0.220, 0.249, 0.272)	(0.107, 0.172, 0.280)	(0.068, 0.101, 0.147)	(0.074, 0.111, 0.165)
Sce. 11	(0.161, 0.289, 0.577)	(0.089, 0.136, 0.206)	(0.198, 0.224, 0.245)	(0.111, 0.177, 0.288)	(0.071, 0.105, 0.151)	(0.077, 0.115, 0.169)
Sce. 12	(0.167, 0.298, 0.592)	(0.092, 0.140, 0.211)	(0.176, 0.199, 0.218)	(0.115, 0.183, 0.296)	(0.073, 0.108, 0.156)	(0.080, 0.119, 0.174)
Sce. 13	(0.173, 0.307, 0.608)	(0.095, 0.144, 0.217)	(0.154, 0.174, 0.190)	(0.119, 0.189, 0.304)	(0.076, 0.111, 0.160)	(0.083, 0.123, 0.179)
Sce. 14	(0.179, 0.317, 0.624)	(0.098, 0.149, 0.223)	(0.132, 0.149, 0.163)	(0.123, 0.195, 0.312)	(0.078, 0.115, 0.164)	(0.085, 0.126, 0.183)
Sce. 15	(0.185, 0.326, 0.640)	(0.101, 0.153, 0.228)	(0.110, 0.124, 0.136)	(0.127, 0.200, 0.320)	(0.081, 0.118, 0.168)	(0.088, 0.130, 0.188)
Sce. 16	(0.191, 0.335, 0.656)	(0.105, 0.157, 0.234)	(0.088, 0.099, 0.109)	(0.131, 0.206, 0.328)	(0.084, 0.122, 0.172)	(0.091, 0.134, 0.193)
Sce. 17	(0.196, 0.344, 0.672)	(0.108, 0.162, 0.240)	(0.066, 0.074, 0.081)	(0.135, 0.212, 0.336)	(0.086, 0.125, 0.176)	(0.094, 0.137, 0.197)
Sce. 18	(0.202, 0.354, 0.687)	(0.111, 0.166, 0.245)	(0.044, 0.049, 0.054)	(0.139, 0.218, 0.343)	(0.089, 0.128, 0.181)	(0.097, 0.141, 0.202)
Sce. 19	(0.208, 0.363, 0.703)	(0.114, 0.171, 0.251)	(0.022, 0.024, 0.027)	(0.143, 0.223, 0.351)	(0.091, 0.132, 0.185)	(0.099, 0.145, 0.207)
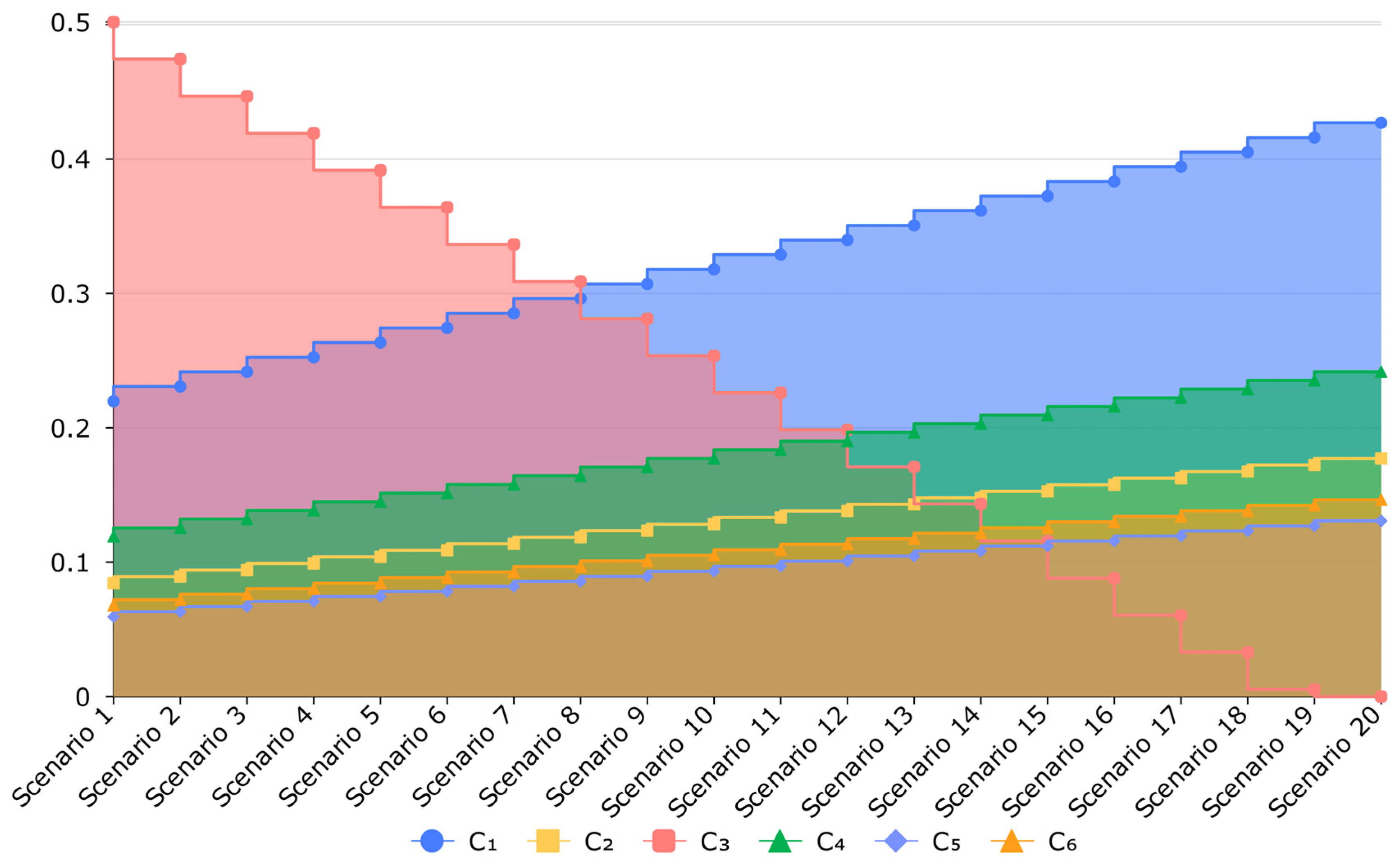
Sce. 20	(0.214, 0.372, 0.719)	(0.117, 0.175, 0.257)	(0.011, 0.012, 0.013)	(0.147, 0.229, 0.359)	(0.094, 0.135, 0.189)	(0.102, 0.149, 0.211)

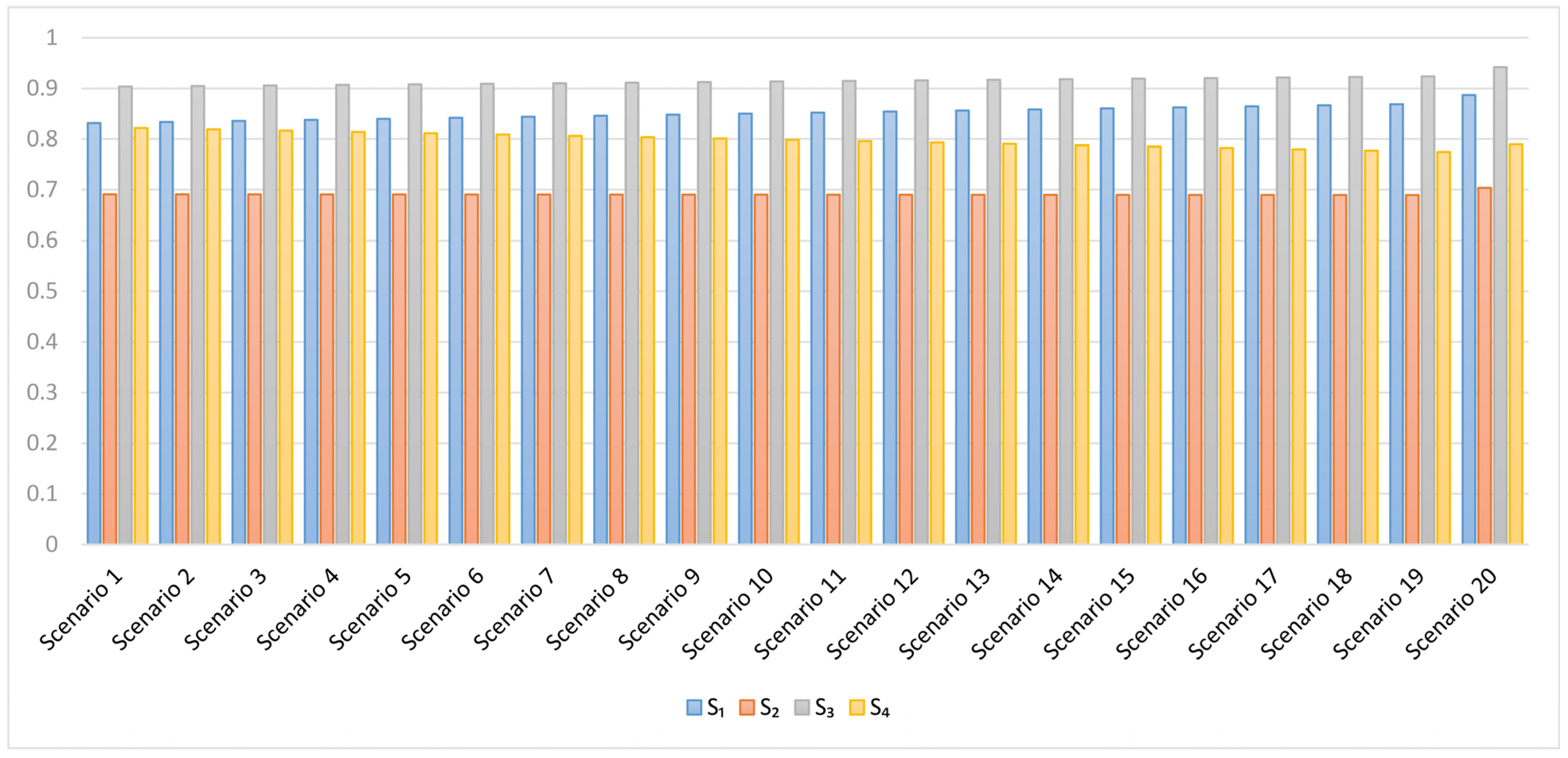
. Each of the generated fuzzy weight vectors is examined in the SES problem using the FS-FUCOM approach. Figure 5 and Figure 6, respectively, illustrate the changes in the weight coefficients of the criteria and the changes in the ranking of the alternatives across the 20 different scenarios. Additionally,

Table 22. Changes in the ranking of suppliers during the sensitivity analysis.

Scenarios	Supplier Ranking				Order
	S1	S2	S3	S4
Main	2	4	1	3	S3 > S1 > S4 > S2
Scenario 1	2	4	1	3	S3 > S1 > S4 > S2
Scenario 2	2	4	1	3	S3 > S1 > S4 > S2
…	…	…	…	…	…
Scenario 20	2	4	1	3	S3 > S1 > S4 > S2

shows the changes in the ranking of the suppliers in the various scenarios.

The results of the sensitivity analysis indicate that, in addition to the best supplier (S₃) maintaining its rank in all scenarios, the other suppliers (S₁, S₂, and S₄) also retain their ranks. This demonstrates the stability and robustness of the proposed approach against changes in the criteria weights. In other words, changes in the weights of the criteria do not significantly affect the final ranking of the construction company’s suppliers, indicating that the results are stable. Additionally, the sensitivity analysis results suggest that the proposed approach is a reliable and robust tool for addressing managerial issues and challenges.

7. Discussion

The main objective of this research was to address the problem of evaluating and selecting gresilient suppliers under uncertainty using the proposed approach, FS-FUCOM. FUCOM offers many advantages over other pairwise comparison-based decision-making approaches, such as significantly reducing the number of pairwise comparisons, requiring less information for the decision-making process, validating results with the ability to calculate DFC, and featuring simple and comprehensible mathematical steps and relationships. In this research, a streamlined version of FUCOM was proposed, which retains all the previous advantages of the approach while eliminating the need to formulate and solve mathematical optimization models. Therefore, another major advantage was added to this approach, making FUCOM more powerful for tackling various decision-making problems. Initially, the S-FUCOM approach was discussed in a deterministic environment, and it was shown that the proposed approach provides similar answers to the original FUCOM, with the difference being a simplified process that does not require mathematical programming models. Additionally, FUCOM’s requirements were well met, and the capability to calculate DFC was maintained. Then, FS-FUCOM was proposed to address decision-making environments under uncertainty using TFNs. In FS-FUCOM, experts’ preferences were expressed using linguistic terms and their corresponding TFNs. The final fuzzy weights of the decision-making criteria were evaluated using fuzzy operators and algebraic relationships. The results demonstrate the appropriate performance of the proposed approach in uncertain environments. Compared to pairwise comparison-based approaches such as AHP and BWM, the proposed FS-FUCOM approach operates more effectively in uncertain environments. The proposed approach is capable of adapting to various schemes of linguistic terms, and their corresponding fuzzy numbers and can assign weights to criteria and prioritize alternatives using basic fuzzy operators, even under conditions of uncertainty. Additionally, the proposed FS-FUCOM approach significantly reduces the number of pairwise comparisons compared to other approaches and decreases the complexities associated with fuzzy computations. For example, in the fuzzy BWM approach, after receiving experts’ fuzzy preferences, a mathematical optimization model with fuzzy parameters is formulated and solved. Compared to the deterministic case, the number of model constraints increases, resulting in higher computational complexity. In the original FUCOM, decision-making under uncertain conditions also leads to an increase in model constraints and complexity. However, in the proposed approach, these challenges are significantly mitigated, and even under uncertain conditions, decision makers can address various decision-making problems using a streamlined fuzzy approach.

The proposed approach was applied in a real-world case study concerning evaluating and selecting gresilient suppliers in the construction industry. A company active in the construction sector aimed to prioritize some of its leading suppliers based on green and resilience principles. The senior managers of this construction holding believed that the most important criteria for evaluating their suppliers, given the nature of the industry and current conditions, were gresilient criteria. The company’s suppliers, mainly providing raw materials such as gypsum, cement, and prefabricated structures, must consider chemical pollutants and their environmental impacts in their production processes. On the other hand, given the existing deadlines and the construction industry’s high sensitivity, suppliers’ resilience criteria in various conditions are also of great importance. Therefore, in this research, the evaluation criteria for suppliers adhering to gresilient principles were selected through a literature review and in-depth expert opinions. Then, these criteria were weighted and utilized to select suppliers using the proposed approach.

Six criteria were selected for evaluating and selecting suppliers, including environmental management systems (C₁), green certification (C₂), air emissions (C₃), restorative capacity (C₄), vulnerability detection and reaction plans (C₅), and surplus inventory (C₆). The importance of each criterion was determined using the proposed approach. Air emissions (C₃) was chosen as the most important criterion with a final weight of 0.469, significantly higher than the other criteria. The environmental management system (C₁) and restorative capacity (C₄) ranked second and third with final weights of 0.191 and 0.114, respectively. Green certification (C₂), surplus inventory (C₆), and vulnerability detection and reaction plans (C₅) ranked fourth to sixth with final weights of 0.086, 0.073, and 0.066, respectively. The supplier selection process has begun integrating various environmental dimensions over the past decade. Decision-making models in this area have necessarily become more complex due to the expansion of new dimensions created by green supply chain initiatives [77]. As the climate change movement gains momentum, it is essential to consider greenhouse gas emission indicators alongside economic efficiency and resilience indicators. Organizations must strive to increase suppliers’ awareness of carbon emissions and select environmentally friendly suppliers [78]. On the other hand, resilience in suppliers is a crucial factor for organizations and manufacturing companies to withstand crises. A resilient supplier typically has a high adaptive capacity to reduce vulnerability to disruptions, absorb the impacts of disasters, and quickly recovers from disruptions to ensure an optimal level of operational continuity after a crisis [33,79].

Following the determination of the importance of evaluation criteria and based on expert opinions, supplier S₃ was selected as the top supplier with a final score of 0.869 for alignment with green principles and resilience. Supplier S₃ demonstrated superior performance across the evaluation criteria, particularly excelling in air emissions (C₃), environmental management systems (C₁), and restorative capacity (C₄). Additionally, the performance of supplier S₁ in criteria C₁ to C₃ led to its selection as the second supplier with a score of 0.800 based on the evaluation criteria. Suppliers S₄ and S₂ followed with final scores of 0.796 and 0.650, respectively, securing third and fourth positions. Given the construction company’s focus on selecting gresilient suppliers, those demonstrating a balanced trade-off between the most important green and resilience criteria were chosen as top suppliers. With the increasing public awareness of environmental protection, green practices have become a public demand. Manufacturing companies are progressing towards green principles, which are becoming ingrained in corporate culture [80]. Selecting and evaluating resilient and green suppliers is crucial for establishing environmentally compatible SCs. Choosing resilient suppliers enables organizations to ensure the long-term sustainability of their SCs and identify suitable suppliers aligned with green and resilience objectives [81].

After prioritizing the criteria and selecting gresilient suppliers using the proposed approach, a sensitivity analysis was conducted to validate the results obtained from FS-FUCOM. In this analysis, various scenarios were considered, and in each scenario, the final weights of the criteria and the ranking of suppliers were examined. The results demonstrate that the proposed approach provides robust and reliable outcomes despite simplifying the original FUCOM and omitting its optimization model. FS-FUCOM can thus be considered a streamlined MCDM tool with significant advantages.

8. Concluding Remarks

Evaluating and selecting suppliers is a strategic decision-making process for organizations, because through this process, they add new members to their supply chain. If the selected suppliers are aligned with the organization’s goals and characteristics, they act as enablers, helping the organization face various challenges. Conversely, if the selected suppliers are in conflict with the organization’s goals and characteristics, they become obstacles and limitations in achieving the organization’s objectives. On the one hand, concerns about the environment and pollutants produced by industrial companies have increased, making the adoption of environmentally friendly technologies and products a public demand. Organizations and manufacturing companies are seeking suppliers who adhere to green principles. On the other hand, alongside economic efficiency, organizations are increasingly focusing on their suppliers’ ability to cope with crises and unforeseen issues. They prefer suppliers who can fulfill their commitments during critical conditions and help the organization navigate out of the crisis and return to optimal conditions. Therefore, suppliers with higher resilience capabilities are considered more reliable and are preferred by organizations.

The main objective of this study was to evaluate and select gresilient suppliers under uncertainty in a construction company using the streamlined FUCOM approach. Initially, S-FUCOM was introduced and evaluated for addressing decision-making problems under certain conditions. Subsequently, FS-FUCOM was developed to solve various decision-making problems under uncertainty using TFNs. FUCOM offers significant advantages over other pairwise comparison-based approaches, such as a substantial reduction in pairwise comparisons and the simplification of gathering expert preferences. These benefits make it an effective approach for addressing decision-making problems. The proposed approach in this study retains all the previous advantages of FUCOM while eliminating the need to formulate and solve mathematical optimization models. This significantly simplifies and streamlines the decision-making process, adding another major advantage to FUCOM and making it more powerful for dealing with decision-making issues. To demonstrate the capabilities and applicability of the proposed approach, several different numerical examples were evaluated, and the results were analyzed. In the numerical examples, various decision-making problems and their data were adapted from previous studies to be analyzed using the proposed approach, enabling a comparative analysis. The results show that the proposed approach, despite omitting the mathematical programming model of FUCOM, could provide results consistent with the original FUCOM. Subsequently, the proposed approach was applied in a real-world case study for selecting a gresilient supplier in the construction industry. A three-member expert group used the proposed approach to determine the final weights of the criteria and the prioritization of the suppliers. The results indicate that the criteria of air emissions, environmental management systems, and restorative capacity were identified as the most important criteria for evaluating and selecting a gresilient supplier. The third supplier demonstrated the best performance in these evaluation criteria and was thus identified as the top supplier. To validate and ensure the robustness of the results obtained from the proposed approach, a sensitivity analysis was conducted with 20 different scenarios. The results show that the proposed approach is robust and provides reliable outcomes.

The practical implications of this research, derived from the application of the proposed approach in a case study within the construction industry, can be summarized in several key points. The findings related to the identification and weighting the criteria and the prioritization of suppliers can serve as a basis for comparing the results of gresilient supplier evaluation and selection across different industries. Companies operating in the construction sector can also benefit from these results for their own evaluations in identifying gresilient supplier evaluation criteria. Organizations that focus separately on the greenness and resilience of their supply chains can use the integrated analysis of criteria importance and supplier prioritization to enhance their supplier evaluation policies. Moreover, the framework proposed in this study, which includes a methodology developed for uncertain conditions and the derived weights for gresilient supplier evaluation criteria, can be adapted by various organizations across different industries for use in both short-term and long-term evaluation processes.

There were limitations in this study that affected its execution. The expert group was selected from the company’s internal specialists, and despite their different capabilities, equal weight was assigned to them. Additionally, the suppliers evaluated were former suppliers of the company, limiting the opportunity to assess new suppliers. The necessary consensus on the initial ranking of criteria in FUCOM also posed challenges for decision makers. Moreover, access to some supplier information, such as green certifications and related inquiries, was another limitation of this study.

Several recommendations for future studies are envisioned. Since the approach presented in this research introduces a new version of FUCOM, future studies can apply this approach to various decision-making problems and analyze the results. Additionally, different linguistic terms and various scales of fuzzy numbers can be explored using the proposed approach. Integrating expert preferences and consolidating input data will also be important topics in this context. Finally, by combining other MCDM methods with the proposed approach, further simplified decision-making frameworks can be developed and introduced, transitioning from complex to simplified decision-making processes. Moreover, this study focused on the evaluation and selection of gresilient suppliers from the perspective of a construction company. Future research could also examine the priorities of different suppliers in providing services to companies and organizations committed to green principles.