Design and Evaluation of an Integrated Autonomous Control Method for Automobile Terminals
Abstract
1. Introduction
2. State of the Art
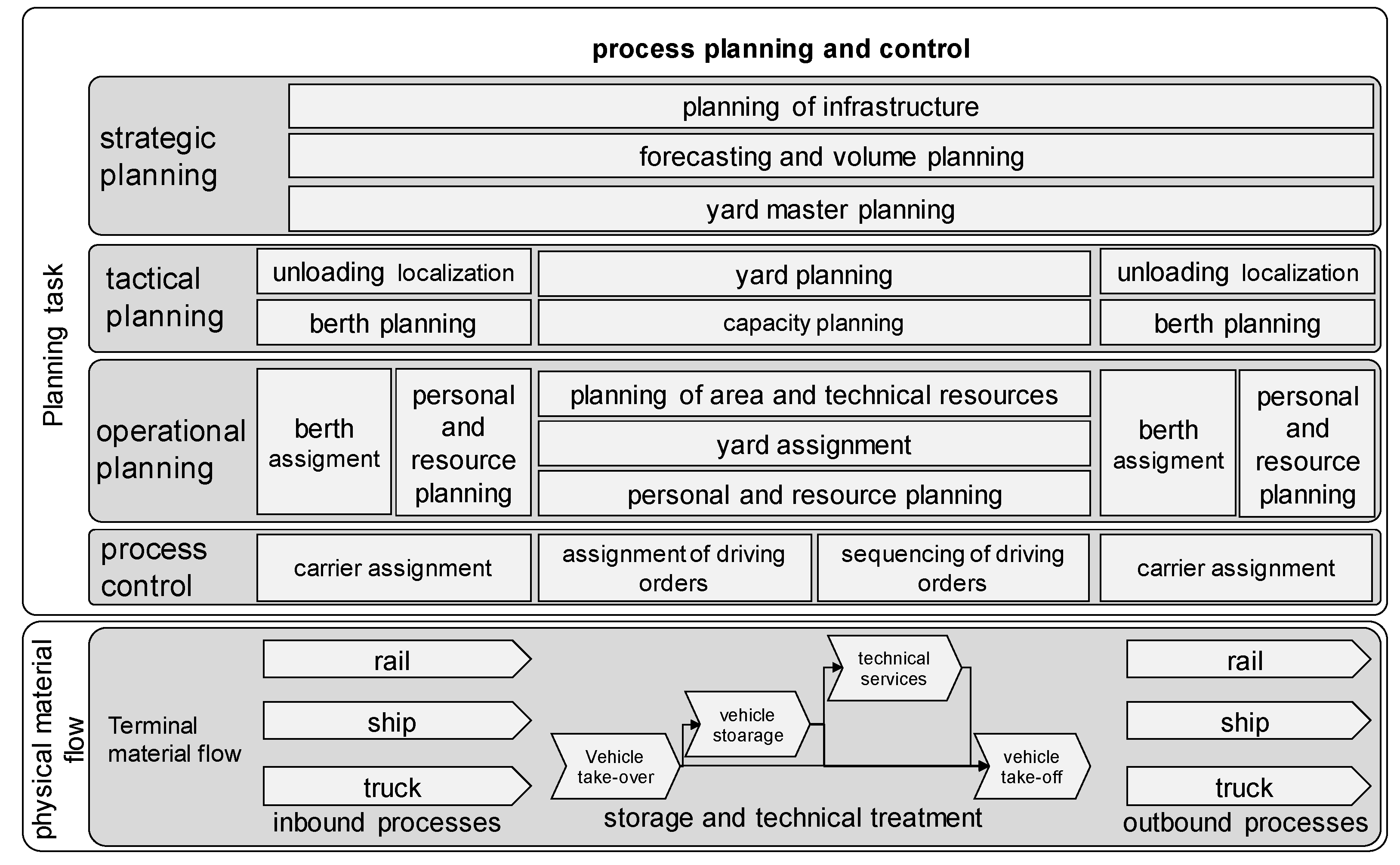
2.1. Planning Process of Automobile Terminals
2.2. Autonomous Control for Coping with Dynamics and Complexity
3. Materials and Methods
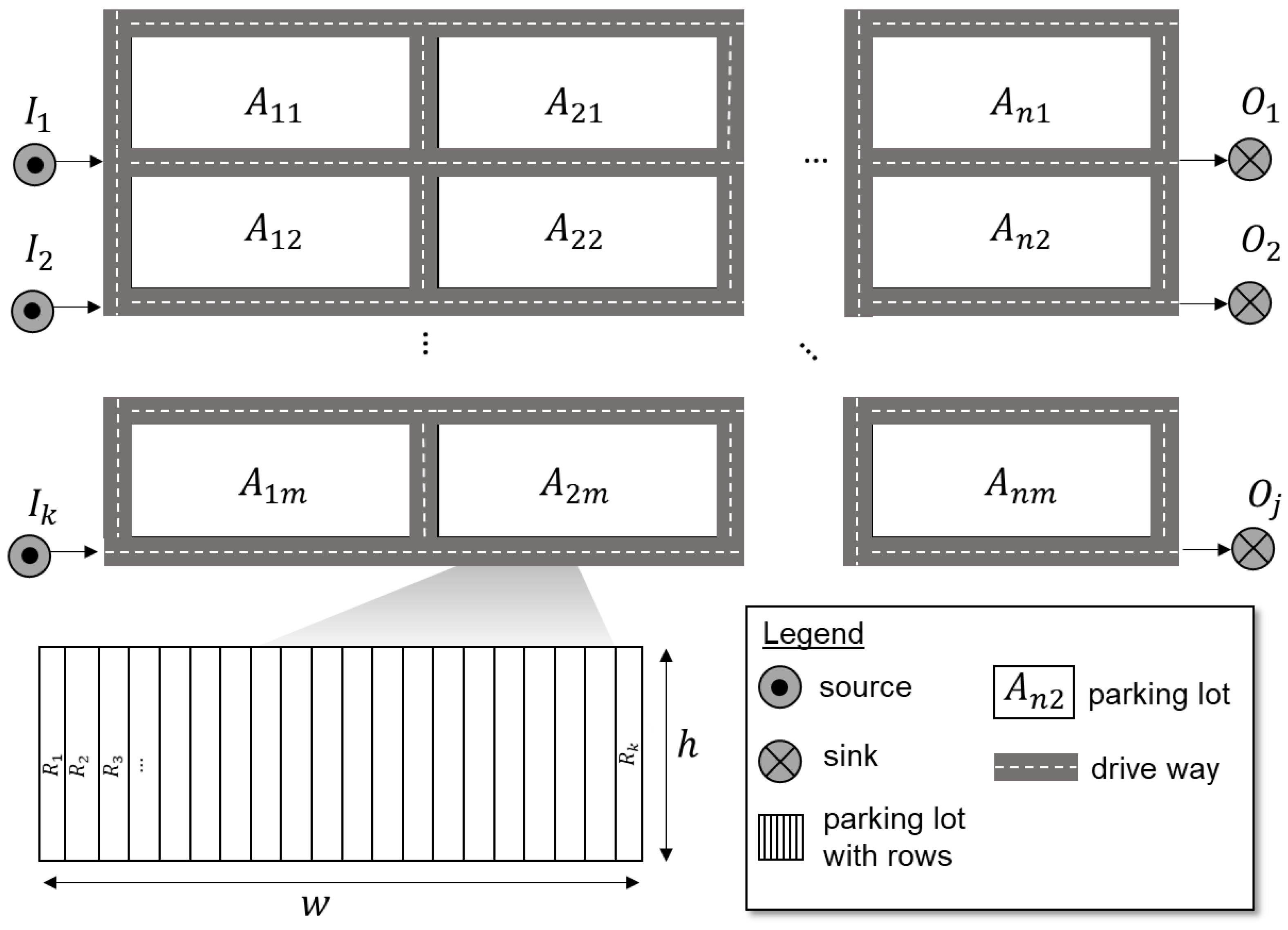
3.1. Generic Terminal Model
3.1.1. Structure and Parameters of the Generic Model
3.1.2. Evaluation of KPIs for the Generic Model
3.1.3. Benchmarks Planning Methods
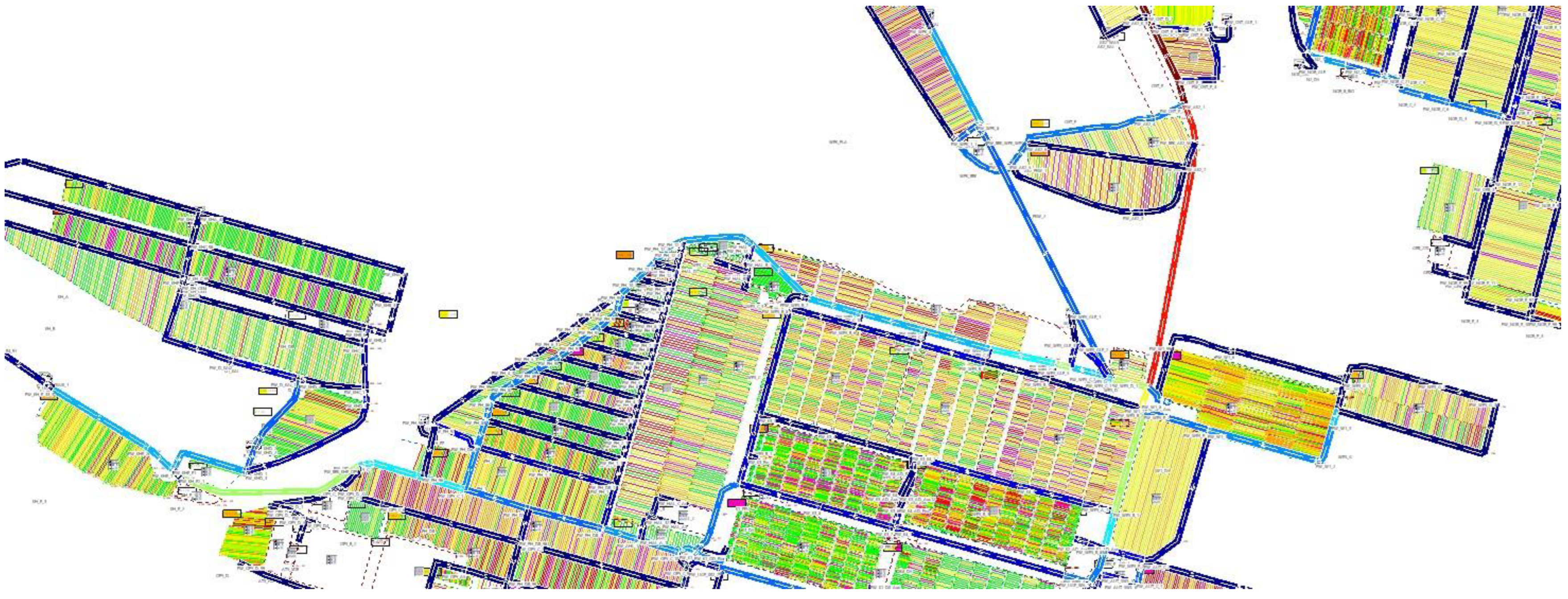
3.2. Real-World Scenario
3.2.1. Automobile Terminal Scenario and Simulation Model
3.2.2. Evaluation Benchmark for the Real-World Case
3.3. Deriving an Integrated Autonomous Control Method for Automobile Terminals
3.3.1. Pheromone-Based Method for Yard Assignment
3.3.2. Pheromone-Based Method for Berth Assignment
3.4. Experimental Design
3.5. Simulation Implementation and Validation
4. Results and Discussion
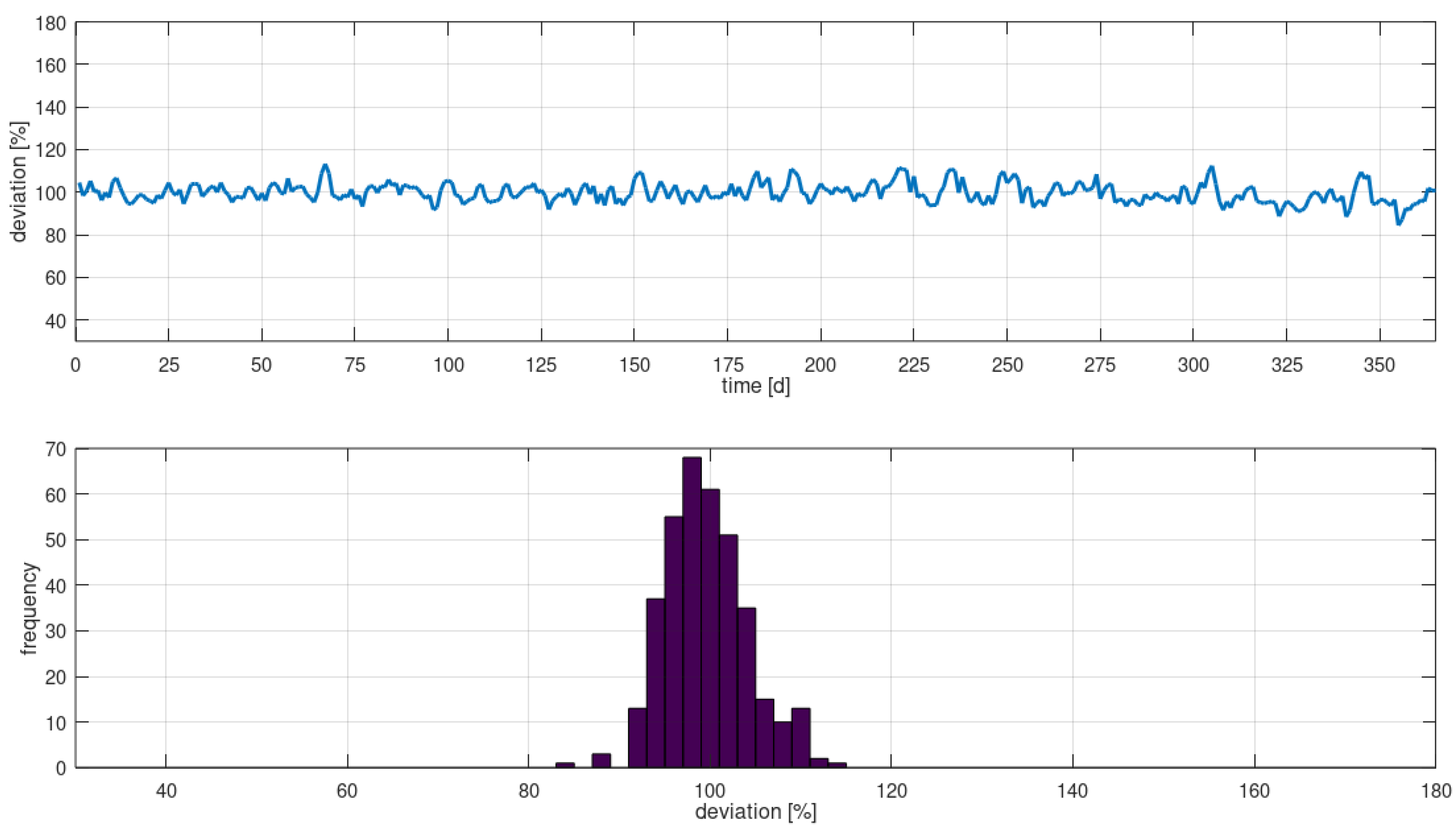
4.1. Performance Evaluation of Generic Scenario
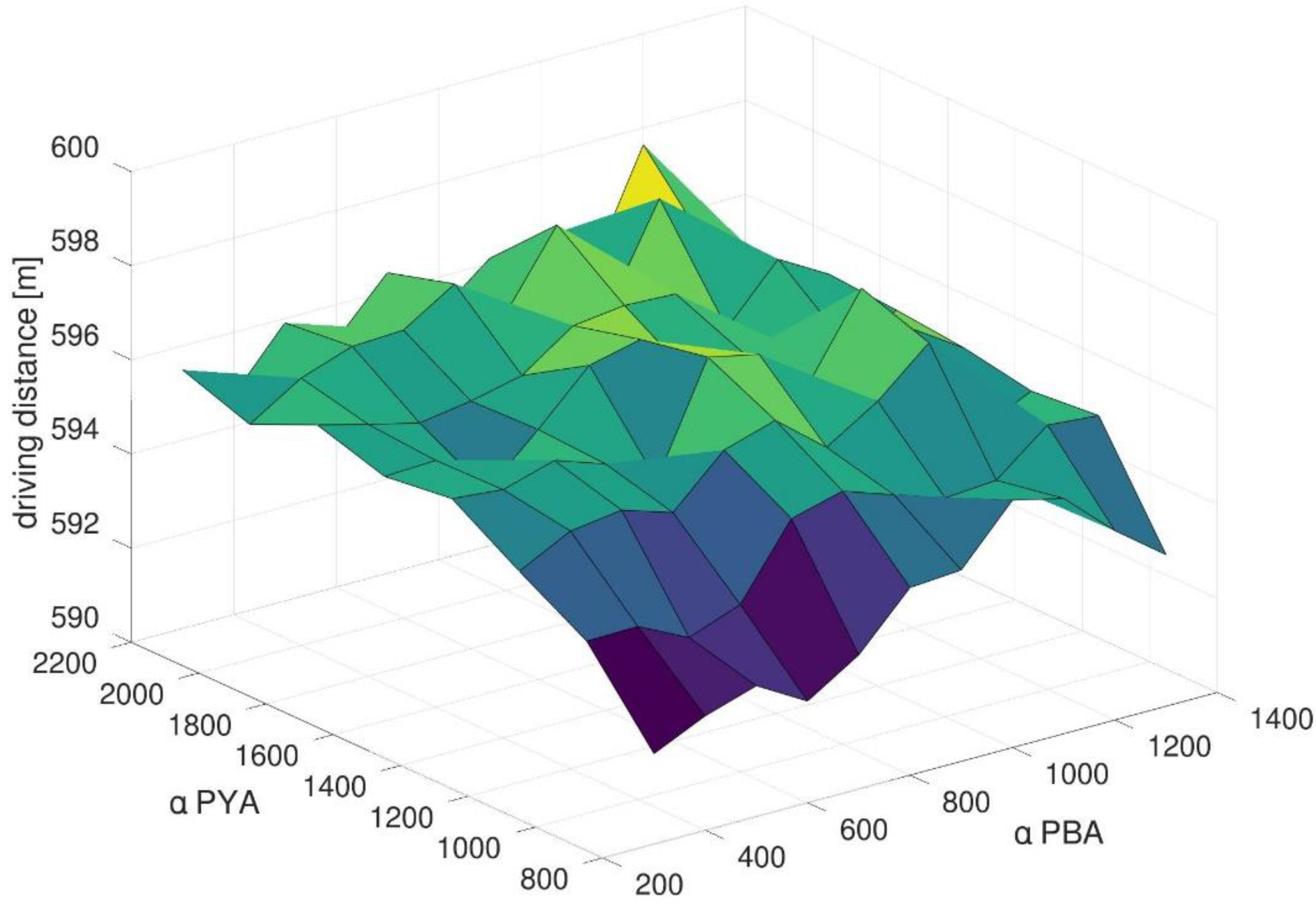
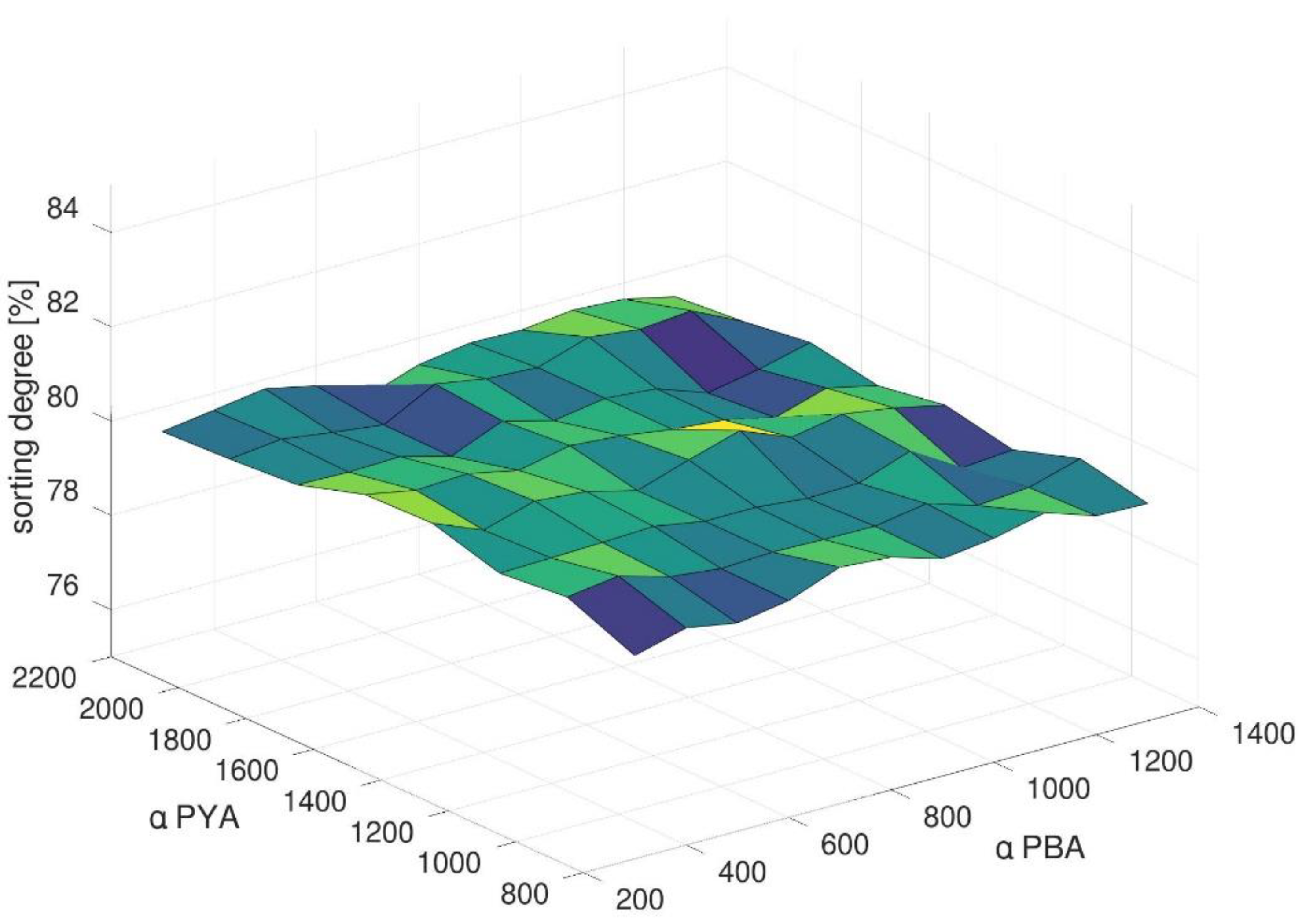
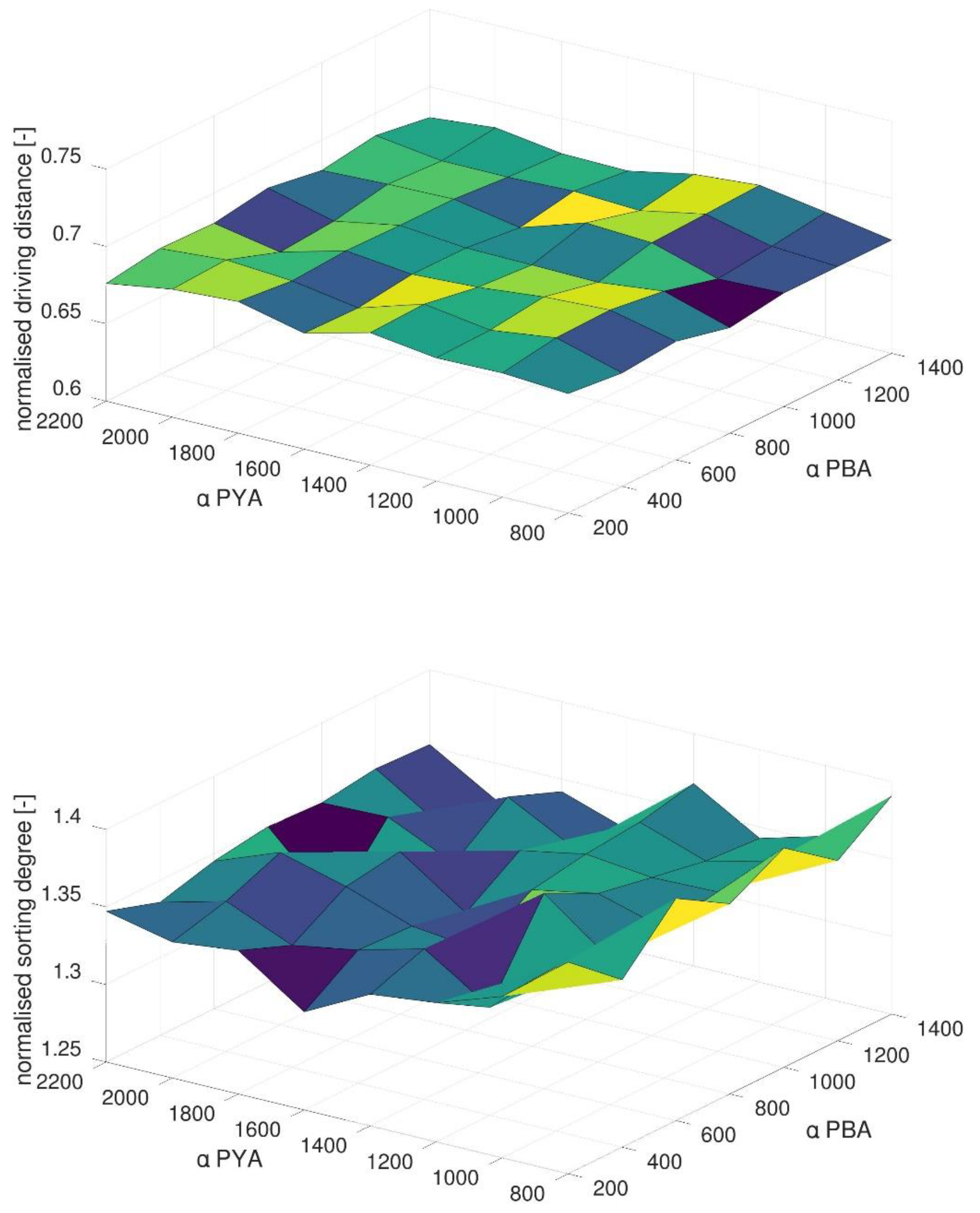
4.2. Impact of Methods Parameters in the Generic Scenario
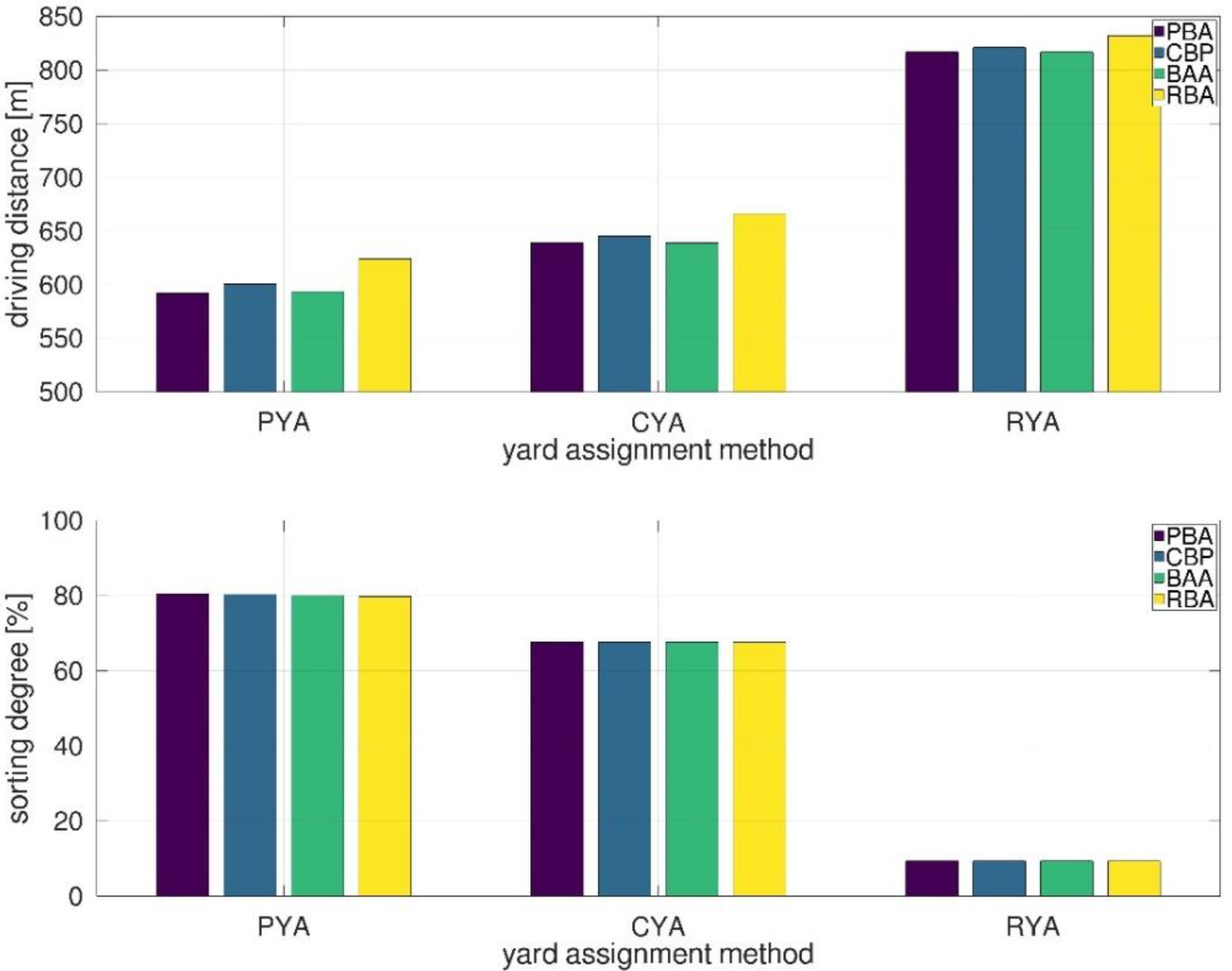
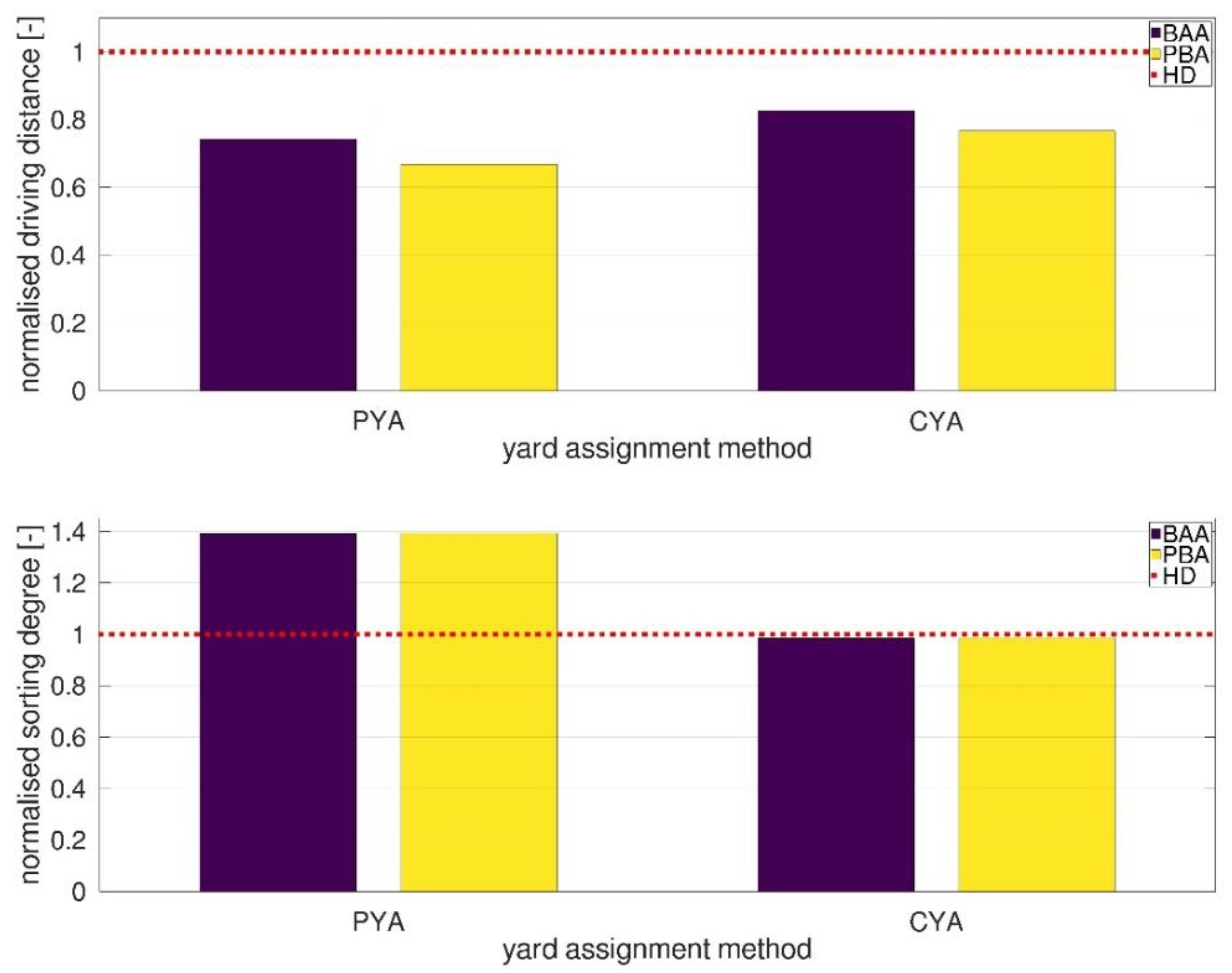
4.3. Performance Evaluation of Real-Word Scenario
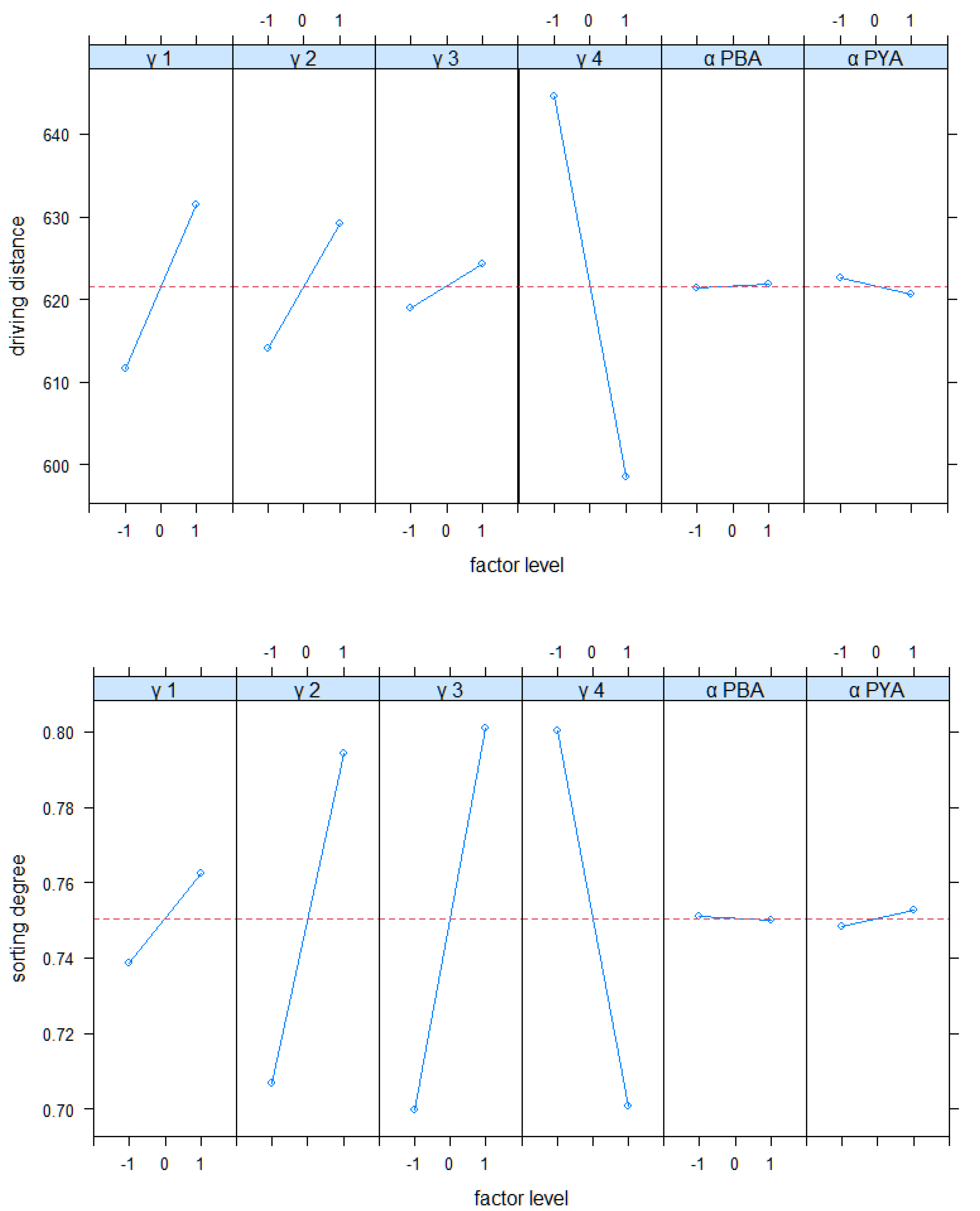
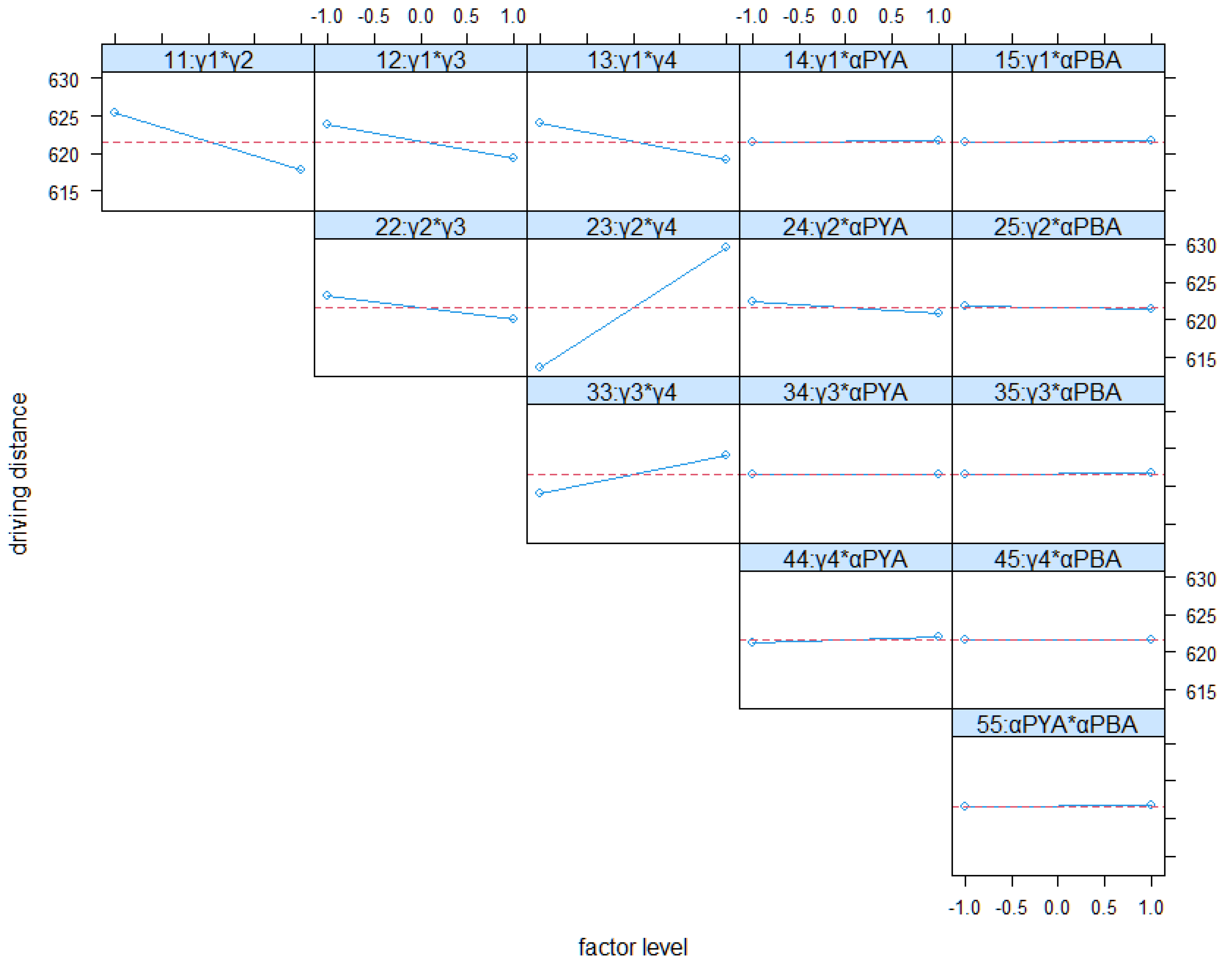
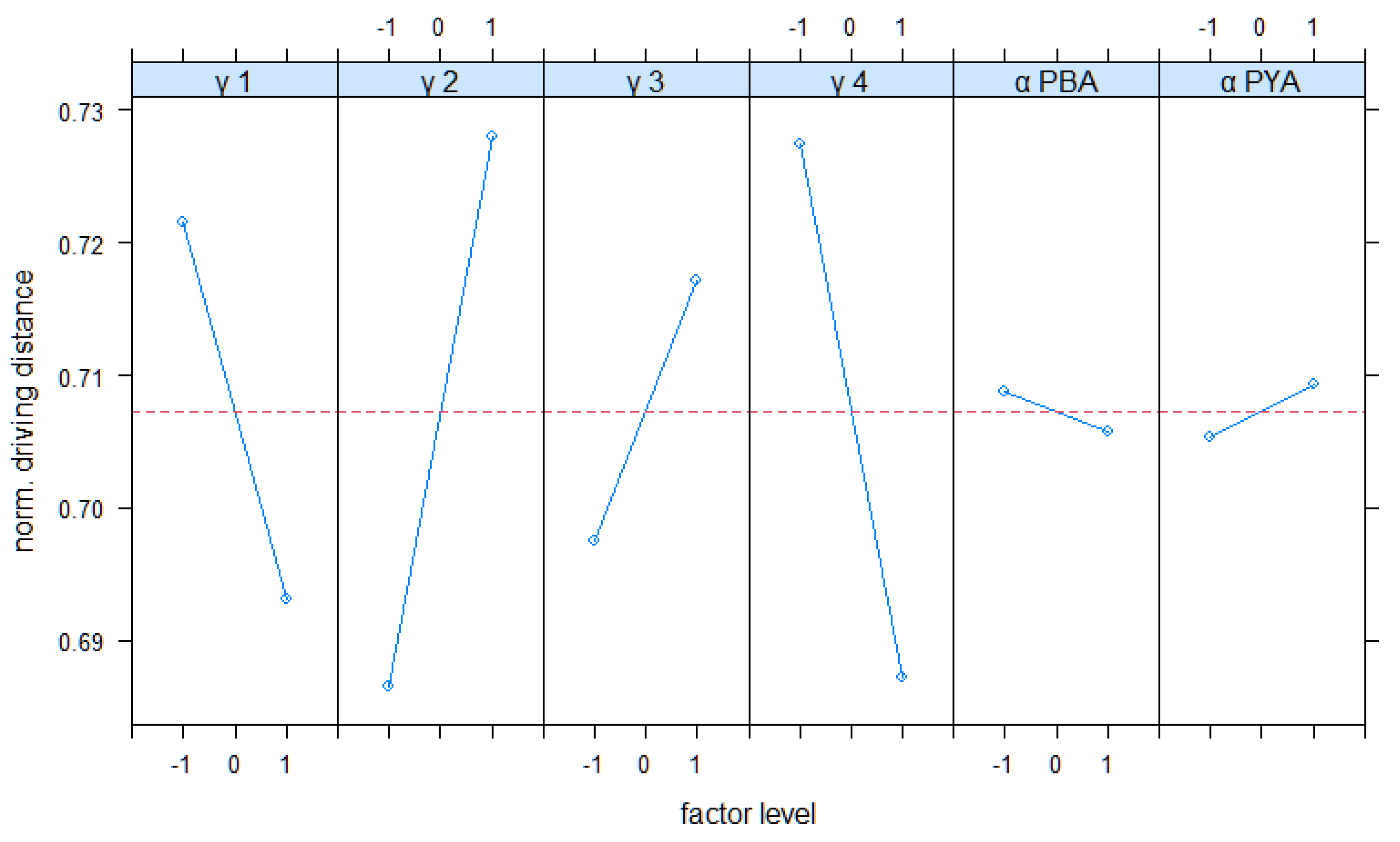
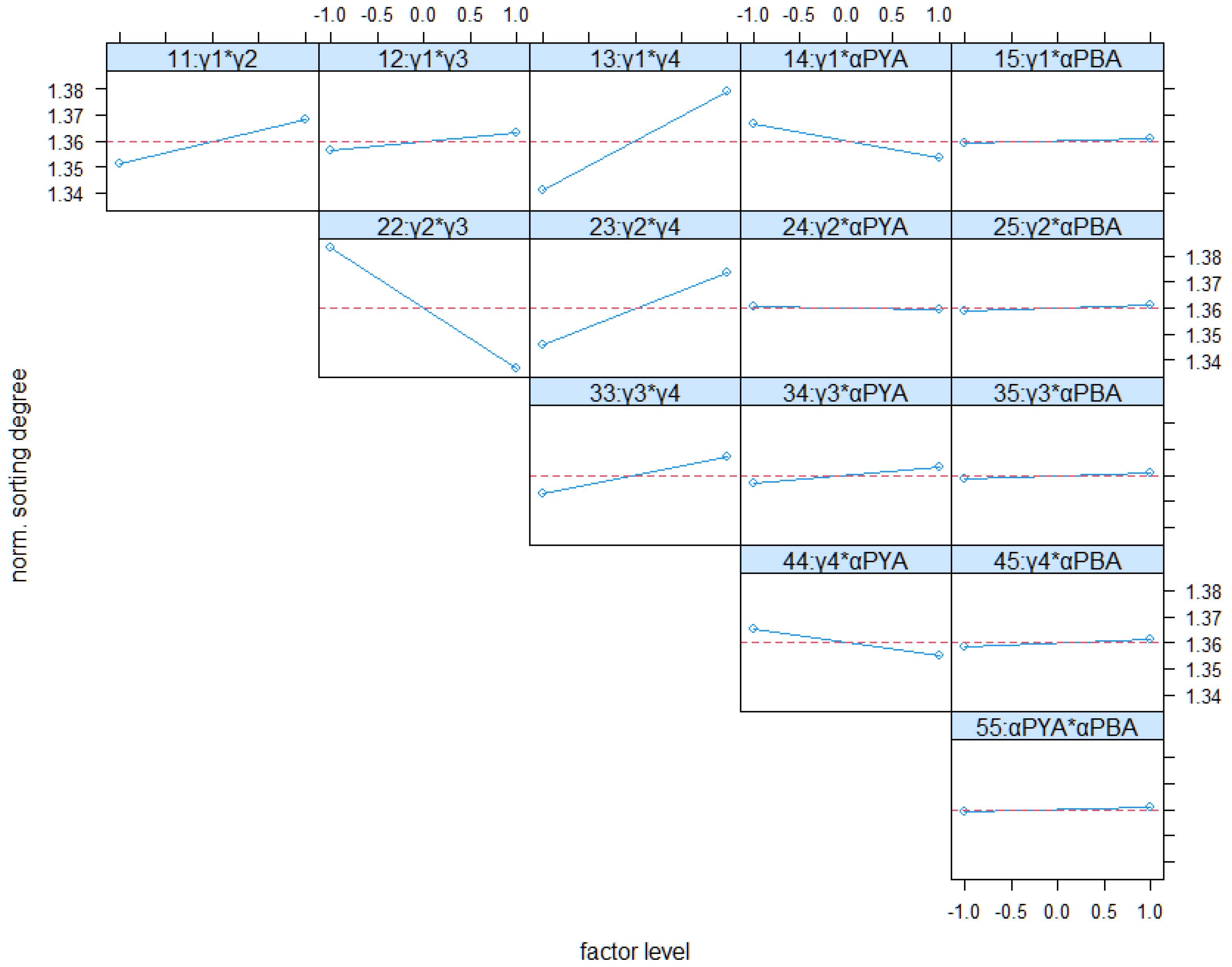
4.4. Full Factorial Analysis of Real-Word Scenario
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nayak, J.; Mishra, M.; Naik, B.; Swapnarekha, H.; Cengiz, K.; Shanmuganathan, V. An Impact Study of COVID-19 on Six Different Industries: Automobile, Energy and Power, Agriculture, Education, Travel and Tourism and Consumer Electronics. Expert Syst. 2021, 39, e12677. [Google Scholar] [CrossRef]
- Esteve-Pérez, J.; Gutiérrez-Romero, J.E.; Mascaraque-Ramírez, C. Performance of the Car Carrier Shipping Sector in the Iberian Peninsula under the COVID-19 Scenario. JMSE 2021, 9, 1295. [Google Scholar] [CrossRef]
- Belhadi, A.; Kamble, S.; Jabbour, C.J.C.; Gunasekaran, A.; Ndubisi, N.O.; Venkatesh, M. Manufacturing and Service Supply Chain Resilience to the COVID-19 Outbreak: Lessons Learned from the Automobile and Airline Industries. Technol. Forecast. Soc. Chang. 2021, 163, 120447. [Google Scholar] [CrossRef]
- Carbone, V.; Martino, M.D. The Changing Role of Ports in Supply-Chain Management: An Empirical Analysis. Marit. Policy Manag. 2003, 30, 305–320. [Google Scholar] [CrossRef]
- Mattfeld, D.C. The Management of Transshipment Terminals: Decision Support for Terminal Operations in Finished Vehicle Supply Chains; Operations Research/Computer Science Interfaces Series; Springer Science + Business Media: New York, NY, USA, 2006; ISBN 978-0-387-30853-1. [Google Scholar]
- Dias, J.C.Q.; Calado, J.M.F.; Mendonça, M.C. The Role of European «ro-Ro» Port Terminals in the Automotive Supply Chain Management. J. Transp. Geogr. 2010, 18, 116–124. [Google Scholar] [CrossRef]
- Görges, M.; Freitag, M. Dynamisierung von Planungsaufgaben Auf Automobilterminals-Potenziale Selbststeuernder Logistischer Prozesse Zur Flexibilisierung Der Flächenmasterplanung. Ind. 4.0 Manag. 2019, 35, 23–26. [Google Scholar]
- Cordeau, J.-F.; Laporte, G.; Moccia, L.; Sorrentino, G. Optimizing Yard Assignment in an Automotive Transshipment Terminal. Eur. J. Oper. Res. 2011, 215, 149–160. [Google Scholar] [CrossRef]
- Dkhil, H.; Diarrassouba, I.; Benmansour, S.; Yassine, A. Modelling and Solving a Berth Allocation Problem in an Automotive Transshipment Terminal. J. Oper. Res. Soc. 2021, 72, 580–593. [Google Scholar] [CrossRef]
- Mattfeld, D.C.; Orth, H. The Allocation of Storage Space for Transshipment in Vehicle Distribution. OR Spectr. 2006, 28, 681–703. [Google Scholar] [CrossRef]
- Böse, F.; Piotrowski, J.; Scholz-Reiter, B. Autonomously Controlled Storage Management in Vehicle Logistics-Applications of RFID and Mobile Computing Systems. Int. J. RF Technol. Res. Appl. 2009, 1, 57–76. [Google Scholar] [CrossRef]
- Görges, M.; Freitag, M. Modeling Autonomously Controlled Automobile Terminal Processes. In Proceedings of the Hamburg International Conference of Logistics (HICL), Hamburg, Germany, 26 September 2019. [Google Scholar]
- Görges, M.; Freitag, M. On the Influence of Structural Complexity on Autonomously Controlled Automobile Terminal Processes. In Dynamics in Logistics; Freitag, M., Haasis, H.-D., Kotzab, H., Pannek, J., Eds.; Lecture Notes in Logistics; Springer International Publishing: Cham, Switzerland, 2020; pp. 42–51. ISBN 978-3-030-44782-3. [Google Scholar]
- Mattfeld, D.C.; Kopfer, H. Terminal Operations Management in Vehicle Transshipment. Transp. Res. Part A Policy Pract. 2003, 37, 435–452. [Google Scholar] [CrossRef]
- Hoff-Hoffmeyer-Zlotnik, M.; Schukraft, S.; Werthmann, D.; Oelker, S.; Freitag, M. Interactive Planning and Control for Finished Vehicle Logistics; epubli: Hamburg, Germany, 2017. [Google Scholar] [CrossRef]
- Beškovnik, B.; Twrdy, E. Managing Maritime Automobile Terminals: An Approach toward Decision-Support Model for Higher Productivity. Int. J. Nav. Archit. Ocean Eng. 2011, 3, 233–241. [Google Scholar] [CrossRef]
- Chen, X.; Li, F.; Jia, B.; Wu, J.; Gao, Z.; Liu, R. Optimizing Storage Location Assignment in an Automotive Ro-Ro Terminal. Transp. Res. Part B Methodol. 2021, 143, 249–281. [Google Scholar] [CrossRef]
- Bierwirth, C.; Meisel, F. A Follow-up Survey of Berth Allocation and Quay Crane Scheduling Problems in Container Terminals. Eur. J. Oper. Res. 2015, 244, 675–689. [Google Scholar] [CrossRef]
- Huang, K.; Suprayogi; Ariantini. A Continuous Berth Template Design Model with Multiple Wharfs. Marit. Policy Manag. 2016, 43, 763–775. [Google Scholar] [CrossRef]
- Lv, X.; Jin, J.G.; Hu, H. Berth Allocation Recovery for Container Transshipment Terminals. Marit. Policy Manag. 2020, 47, 558–574. [Google Scholar] [CrossRef]
- Zhen, L.; Lee, L.H.; Chew, E.P. A Decision Model for Berth Allocation under Uncertainty. Eur. J. Oper. Res. 2011, 212, 54–68. [Google Scholar] [CrossRef]
- Fischer, T.; Gehring, H. Planning Vehicle Transhipment in a Seaport Automobile Terminal Using a Multi-Agent System. Eur. J. Oper. Res. 2005, 166, 726–740. [Google Scholar] [CrossRef]
- Fischer, T.; Gehring, H. Business Process Support in a Seaport Automobile Terminal—A Multi-Agent Based Approach. In Multiagent Based Supply Chain Management; Chaib-draa, B., Müller, J.P., Eds.; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2006; Volume 28, pp. 373–394. ISBN 978-3-540-33875-8. [Google Scholar]
- Olhager, J. The Role of Decoupling Points in Value Chain Management. In Modelling Value; Jodlbauer, H., Olhager, J., Schonberger, R.J., Eds.; Contributions to Management Science; Physica-Verlag HD: Heidelberg, Germany, 2012; pp. 37–47. ISBN 978-3-7908-2746-0. [Google Scholar]
- Wikner, J.; Johansson, E. Inventory Classification Based on Decoupling Points. Prod. Manuf. Res. 2015, 3, 218–235. [Google Scholar] [CrossRef]
- Windt, K.; Böse, F.; Philipp, T. Autonomy in Production Logistics: Identification, Characterisation and Application. Robot. Comput.-Integr. Manuf. 2008, 24, 572–578. [Google Scholar] [CrossRef]
- Windt, K.; Hülsmann, M. Changing Paradigms in Logistics—Understanding the Shift from Conventional Control to Autonomous Cooperation and Control. In Understanding Autonomous Cooperation and Control in Logistics; Hülsmann, M., Windt, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 1–16. ISBN 978-3-540-47449-4. [Google Scholar]
- Armbruster, D.; de Beer, C.; Freitag, M.; Jagalski, T.; Ringhofer, C. Autonomous Control of Production Networks Using a Pheromone Approach. Phys. A Stat. Mech. Its Appl. 2006, 363, 104–114. [Google Scholar] [CrossRef]
- Martins, L.; Varela, M.L.R.; Fernandes, N.O.; Carmo–Silva, S.; Machado, J. Literature Review on Autonomous Production Control Methods. Enterp. Inf. Syst. 2020, 14, 1219–1231. [Google Scholar] [CrossRef]
- Scholz-Reiter, B.; De Beer, C.; Freitag, M.; Jagalski, T. Bio-Inspired and Pheromone-Based Shop-Floor Control. Int. J. Comput. Integr. Manuf. 2008, 21, 201–205. [Google Scholar] [CrossRef]
- Scholz-Reiter, B.; Rekersbrink, H.; Görges, M. Dynamic Flexible Flow Shop Problems—Scheduling Heuristics vs. Autonomous Control. CIRP Ann. 2010, 59, 465–468. [Google Scholar] [CrossRef]
- Rekersbrink, H.; Makuschewitz, T.; Scholz-Reiter, B. A Distributed Routing Concept for Vehicle Routing Problems. Logist. Res. 2009, 1, 45–52. [Google Scholar] [CrossRef]
- Martins, L.M.; Fernandes, N.O.G.; Varela, M.L.R.; Dias, L.M.S.; Pereira, G.A.B.; Silva, S.C. Comparative Study of Autonomous Production Control Methods Using Simulation. Simul. Model. Pract. Theory 2020, 104, 102142. [Google Scholar] [CrossRef]
- Scholz-Reiter, B.; Jagalski, T.; Bendul, J.C. Autonomous Control of a Shop Floor Based on Bee’s Foraging Behaviour. In Dynamics in Logistics; Kreowski, H.-J., Scholz-Reiter, B., Haasis, H.-D., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 415–423. ISBN 978-3-540-76861-6. [Google Scholar]
- 35. BLG LOGISTICS GROUP AG & Co. KG BLG-AutoTerminal Bremerhaven. Available online: https://www.blg-logistics.com/autoterminal-bremerhaven (accessed on 1 September 2022).
- Van Dyke Parunak, H. “Go to the Ant”: Engineering Principles from Natural Multi-Agent Systems. Ann. Oper. Res. 1997, 75, 69–101. [Google Scholar] [CrossRef]
- Chen, Y.; Li, K.W.; Marc Kilgour, D.; Hipel, K.W. A Case-Based Distance Model for Multiple Criteria ABC Analysis. Comput. Oper. Res. 2008, 35, 776–796. [Google Scholar] [CrossRef]
- Gutenschwager, K.; Rabe, M.; Spieckermann, S.; Wenzel, S. Grundlagen der ereignisdiskreten Simulation. In Simulation in Produktion und Logistik; Springer: Berlin/Heidelberg, Germany, 2017; pp. 51–84. ISBN 978-3-662-55744-0. [Google Scholar]
- Durakovic, B. Design of Experiments Application, Concepts, Examples: State of the Art. Period. Eng. Nat. Sci. 2017, 5, 421–439. [Google Scholar] [CrossRef]
- Czitrom, V. One-Factor-at-a-Time versus Designed Experiments. Am. Stat. 1999, 53, 126. [Google Scholar] [CrossRef]
- Jankovic, A.; Chaudhary, G.; Goia, F. Designing the Design of Experiments (DOE)–An Investigation on the Influence of Different Factorial Designs on the Characterization of Complex Systems. Energy Build. 2021, 250, 111298. [Google Scholar] [CrossRef]
- Law, A.M. Simulation Modeling and Analysis, 5th ed.; McGraw-Hill Series in Industrial Engineering and Management Science; McGraw-Hill Education: Dubuque, IA, USA, 2013; ISBN 978-0-07-340132-4. [Google Scholar]
- Law, A.M. A Tutorial on Design of Experiments for Simulation Modeling. In Proceedings of the 2017 Winter Simulation Conference (WSC), Savannah, GA, USA, 7–10 December 2014; IEEE: Las Vegas, NV, USA, 2017; pp. 550–564. [Google Scholar]
- Guthrie, W.F. NIST/SEMATECH e-Handbook of Statistical Methods (NIST Handbook 151); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2020.
- Banks, J. Discrete-Event System Simulation; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]



| OEM | Destination | Ship Group | Avg. Arrival Rate [Cars/Day] | Amplitude [Cars/Day] | Relative Phase Shift [−] | Avg. Turnover Time [d] |
|---|---|---|---|---|---|---|
| OEM 1 | D1 | R3 | 47.62 | 45.24 | 0 | 10 |
| D2 | R3 | 38.10 | 36.20 | 0.2 | 15 | |
| D3 | R2 | 28.57 | 27.14 | 0.4 | 20 | |
| D4 | R2 | 19.05 | 18.10 | 0.6 | 25 | |
| D5 | R1 | 9.52 | 9.04 | 0.8 | 30 | |
| D6 | R1 | 57.14 | 54.28 | 1 | 5 | |
| OEM 2 | D1 | R3 | 38.10 | 36.20 | 0 | 15 |
| D2 | R3 | 28.57 | 27.14 | 0.2 | 20 | |
| D3 | R2 | 19.05 | 18.10 | 0.4 | 25 | |
| D4 | R2 | 9.52 | 9.04 | 0.6 | 30 | |
| D5 | R1 | 57.14 | 54.28 | 0.8 | 5 | |
| D6 | R1 | 47.62 | 45.24 | 1 | 10 | |
| OEM 3 | D1 | R3 | 28.57 | 27.14 | 0 | 20 |
| D2 | R3 | 19.05 | 18.10 | 0.2 | 25 | |
| D3 | R2 | 9.52 | 9.04 | 0.4 | 30 | |
| D4 | R2 | 57.14 | 54.28 | 0.6 | 5 | |
| D5 | R1 | 47.62 | 45.24 | 0.8 | 10 | |
| D6 | R1 | 38.10 | 36.20 | 1 | 15 | |
| OEM 4 | D1 | R3 | 19.05 | 18.10 | 0 | 25 |
| D2 | R3 | 9.52 | 9.04 | 0.2 | 30 | |
| D3 | R2 | 57.14 | 54.28 | 0.4 | 5 | |
| D4 | R2 | 47.62 | 45.24 | 0.6 | 10 | |
| D5 | R1 | 38.10 | 36.20 | 0.8 | 15 | |
| D6 | R1 | 28.57 | 27.14 | 1 | 20 | |
| OEM 5 | D1 | R3 | 9.52 | 9.04 | 0 | 30 |
| D2 | R3 | 57.14 | 54.28 | 0.2 | 5 | |
| D3 | R2 | 47.62 | 45.24 | 0.4 | 10 | |
| D4 | R2 | 38.10 | 36.20 | 0.6 | 15 | |
| D5 | R1 | 28.57 | 27.14 | 0.8 | 20 | |
| D6 | R1 | 19.05 | 18.10 | 1 | 25 | |
| OEM 6 | D1 | R3 | 57.14 | 54.28 | 0 | 5 |
| D2 | R3 | 47.62 | 45.24 | 0.2 | 10 | |
| D3 | R2 | 38.10 | 36.20 | 0.4 | 15 | |
| D4 | R2 | 28.57 | 27.14 | 0.6 | 20 | |
| D5 | R1 | 19.05 | 18.10 | 0.8 | 25 | |
| D6 | R1 | 9.52 | 9.04 | 1 | 30 |
| Ship Group | Avg. Number of Cars per Journey | Standard Deviation | Destinations |
|---|---|---|---|
| R1 | 1000 | 150 | D5, D6 |
| R2 | 1000 | 150 | D3, D4 |
| R3 | 1000 | 150 | D1, D2 |
| Generic Scenario | Real-World Scenario | |
|---|---|---|
| Annual volume | 456,202 | 1,765,787 |
| Number of parking rows | 1692 | 18,825 |
| Terminal capacity | 21,996 | 104,478 |
| Annual ship arrivals | 447 | 1245 |
| Groups of cars | 36 | 7073 |
| Number berth | 5 | 11 |
| Parameter Value | Factor Level | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # | Runs | γ1 | γ2 | γ3 | γ4 | αf | αs | γ1 | γ2 | γ3 | γ4 | αf | αs |
| 1 | 10 | 0.05 | 0.05 | 0.05 | 0.05 | 500 | 200 | −1 | −1 | −1 | −1 | −1 | −1 |
| 2 | 10 | 0.95 | 0.05 | 0.05 | 0.05 | 500 | 200 | 1 | −1 | −1 | −1 | −1 | −1 |
| 3 | 10 | 0.05 | 0.95 | 0.05 | 0.05 | 500 | 200 | −1 | 1 | −1 | −1 | −1 | −1 |
| 4 | 10 | 0.95 | 0.95 | 0.05 | 0.05 | 500 | 200 | 1 | 1 | −1 | −1 | −1 | −1 |
| 5 | 10 | 0.05 | 0.05 | 0.95 | 0.05 | 500 | 200 | −1 | −1 | 1 | −1 | −1 | −1 |
| 6 | 10 | 0.95 | 0.05 | 0.95 | 0.05 | 500 | 200 | 1 | −1 | 1 | −1 | −1 | −1 |
| 7 | 10 | 0.05 | 0.95 | 0.95 | 0.05 | 500 | 200 | −1 | 1 | 1 | −1 | −1 | −1 |
| 8 | 10 | 0.95 | 0.95 | 0.95 | 0.05 | 500 | 200 | 1 | 1 | 1 | −1 | −1 | −1 |
| 9 | 10 | 0.05 | 0.05 | 0.05 | 0.95 | 500 | 200 | −1 | −1 | −1 | 1 | −1 | −1 |
| 10 | 10 | 0.95 | 0.05 | 0.05 | 0.95 | 500 | 200 | 1 | −1 | −1 | 1 | −1 | −1 |
| 11 | 10 | 0.05 | 0.95 | 0.05 | 0.95 | 500 | 200 | −1 | 1 | −1 | 1 | −1 | −1 |
| 12 | 10 | 0.95 | 0.95 | 0.05 | 0.95 | 500 | 200 | 1 | 1 | −1 | 1 | −1 | −1 |
| 13 | 10 | 0.05 | 0.05 | 0.95 | 0.95 | 500 | 200 | −1 | −1 | 1 | 1 | −1 | −1 |
| 14 | 10 | 0.95 | 0.05 | 0.95 | 0.95 | 500 | 200 | 1 | −1 | 1 | 1 | −1 | −1 |
| 15 | 10 | 0.05 | 0.95 | 0.95 | 0.95 | 500 | 200 | −1 | 1 | 1 | 1 | −1 | −1 |
| 16 | 10 | 0.95 | 0.95 | 0.95 | 0.95 | 500 | 200 | 1 | 1 | 1 | 1 | −1 | −1 |
| 17 | 10 | 0.05 | 0.05 | 0.05 | 0.05 | 2500 | 200 | −1 | −1 | −1 | −1 | 1 | −1 |
| … | |||||||||||||
| 64 | 10 | 0.95 | 0.95 | 0.95 | 0.95 | 2500 | 1500 | 1 | 1 | 1 | 1 | 1 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Görges, M.; Freitag, M. Design and Evaluation of an Integrated Autonomous Control Method for Automobile Terminals. Logistics 2022, 6, 73. https://doi.org/10.3390/logistics6040073
Görges M, Freitag M. Design and Evaluation of an Integrated Autonomous Control Method for Automobile Terminals. Logistics. 2022; 6(4):73. https://doi.org/10.3390/logistics6040073
Chicago/Turabian StyleGörges, Michael, and Michael Freitag. 2022. "Design and Evaluation of an Integrated Autonomous Control Method for Automobile Terminals" Logistics 6, no. 4: 73. https://doi.org/10.3390/logistics6040073
APA StyleGörges, M., & Freitag, M. (2022). Design and Evaluation of an Integrated Autonomous Control Method for Automobile Terminals. Logistics, 6(4), 73. https://doi.org/10.3390/logistics6040073









