Evaluation of the Strontium Isotope Ratios in Soil–Plant–Fruit: A Comprehensive Study on Vignola Cherry (Ciliegia di Vignola PGI)
Abstract
1. Introduction
2. Materials and Methods
2.1. Reagents and Materials
2.2. Instrumentation
2.3. Sampling and Samples Pretreatment
2.3.1. Soil Sampling
2.3.2. Branches and Cherries Sampling
2.4. Experimental—Sample Processing
2.4.1. Soil Samples
2.4.2. Cherry Branches and Cherries
2.4.3. Removing of the Isobaric Interferences: Sr/Rb Separation
2.4.4. Delta Notation
2.4.5. Mass Bias Correction
3. Results and Discussion
3.1. Mass Bias Correction Procedure
3.2. Reproducibility of Measurements
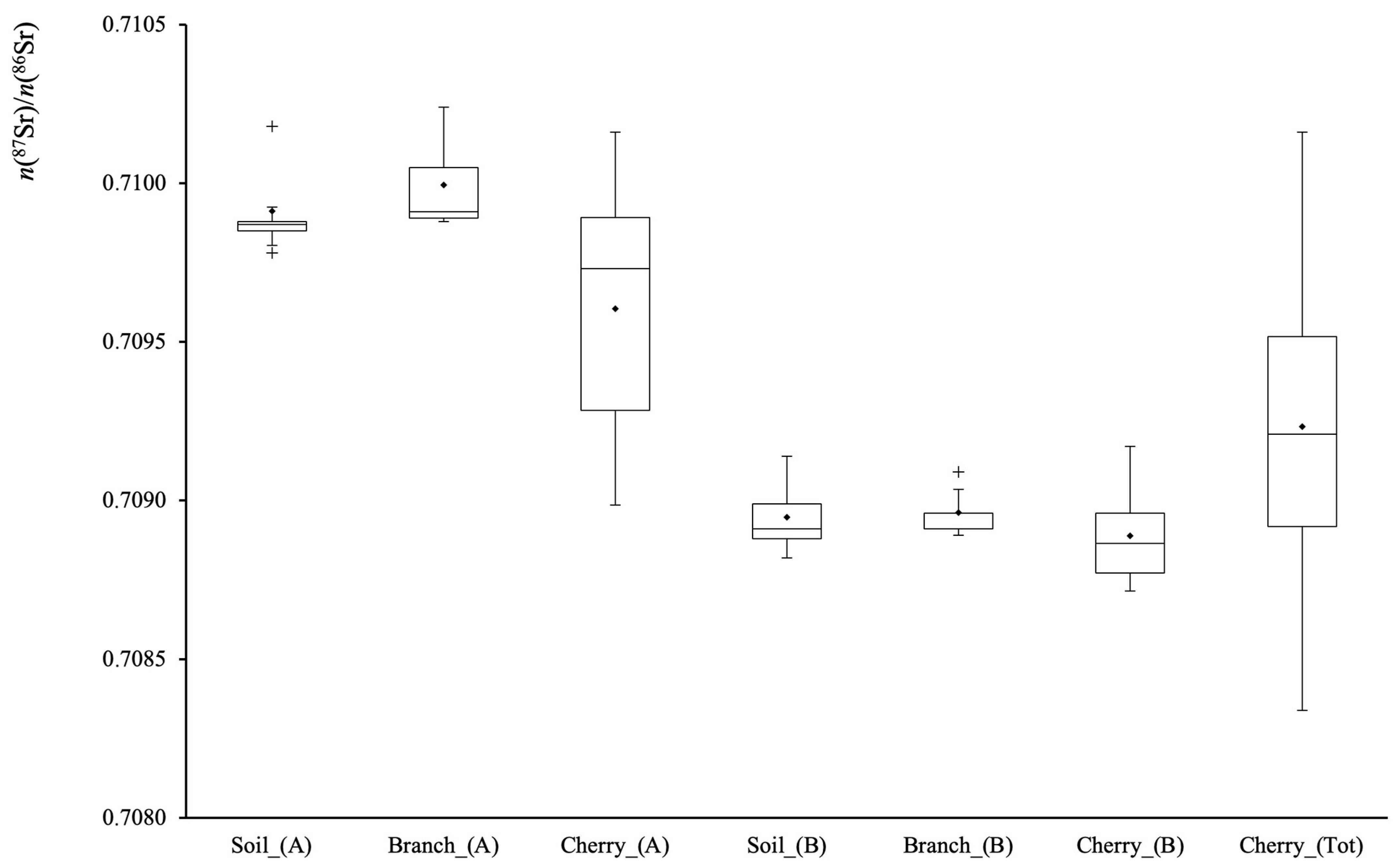
3.3. Soil, Branches and Cherry Samples
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PDO | Protected Designation of Origin |
| PGI | Protected Geographical Indication |
| ICP/qMS | inductively coupled plasma/quadrupolar mass spectrometer |
| MC-ICP/MS | multi-collector—inductively coupled plasma/mass spectrometer |
References
- Badia-Melis, R.; Mishra, P.; Ruiz-García, L. Food traceability: New trends and recent advances. A review. Food Control 2015, 57, 393–401. [Google Scholar] [CrossRef]
- Castañeda, F.N.; Vidal, R.B.P.; Aspromonte, J. Untargeted chromatographic methods coupled with chemometric strategies for the analysis of food and related samples. TrAC Trends Anal. Chem. 2024, 173, 117650. [Google Scholar] [CrossRef]
- Drakopoulou, S.; Orfanakis, E.; Karagiannaki, I.; Gaitis, F.; Skoulika, S.; Papaioannou, A.; Boukouvalas, G.; Petropoulos, G.; Katsoudas, V.; Kontzedaki, R.; et al. Comparative Evaluation of Different Targeted and Untargeted Analytical Approaches to Assess Greek Extra Virgin Olive Oil Quality and Authentication. Molecules 2022, 27, 1350. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Xu, Z.; Liao, X. A review of fruit juice authenticity assessments: Targeted and untargeted analyses. Crit. Rev. Food Sci. Nutr. 2021, 62, 6081–6102. [Google Scholar] [CrossRef]
- Mialon, N.; Roig, B.; Capodanno, E.; Cadiere, A. Untargeted metabolomic approaches in food authenticity: A review that showcases biomarkers. Food Chem. 2023, 398, 133856. [Google Scholar] [CrossRef]
- Durante, C.; Bertacchini, L.; Bontempo, L.; Camin, F.; Manzini, D.; Lambertini, P.; Marchetti, A.; Paolini, M. From soil to grape and wine: Variation of light and heavy elements isotope ratios. Food Chem. 2016, 210, 648–659. [Google Scholar] [CrossRef]
- Lees, M. (Ed.) Food Authenticity and Traceability, 1st ed.; Woodhead Publishing Ltd.: Cambridge, UK, 2003; ISBN 9781855735262. [Google Scholar]
- Izzo, F.; Di Renzo, V.; Langella, A.; D’Antonio, M.; Tranfa, P.; Widory, D.; Salzano, L.; Germinario, C.; Grifa, C.; Varricchio, E.; et al. Investigating strontium isotope linkage between biominerals (uroliths), drinking water and environmental matrices. Environ. Pollut. 2024, 344, 123316. [Google Scholar] [CrossRef]
- Yang, D.; Podkovyroff, K.; Uno, K.T.; Bowen, G.J.; Fernandez, D.P.; Cerling, T.E. Strontium isotope mapping of elephant enamel supports an integrated microsampling-modeling workflow to reconstruct herbivore migrations. Commun. Biol. 2025, 8, 274. [Google Scholar] [CrossRef]
- Aguzzoni, A.; Giammarchi, F.; Mundo, I.A.; Voto, G.; Tonon, G.; Tirler, W.; Tomelleri, E. Enhancing timber traceability via multielement and strontium isotope ratio: An example from the Eastern Alps. BioRxiv 2024. [Google Scholar] [CrossRef]
- Rossi, M.; Iacumin, P.; Venturelli, G. 87Sr/86Sr Isotope Ratio as a Tool in Archaeological Investigation: Limits and Risks. Quaternary 2024, 7, 6. [Google Scholar] [CrossRef]
- Kelly, S.; Heaton, K.; Hoogewerff, J. Tracing the geographical origin of food: The application of multi-element and multi-isotope analysis. Trends Food Sci. Technol. 2005, 16, 555–567. [Google Scholar] [CrossRef]
- Wang, S.; Chen, P.; Liu, Y.; Chen, C.; Tian, J.; Liu, Z.; Li, B.; Mei, X.; Chen, Y.; Zhang, Y.; et al. Geographical origin traceability of sweet cherry (Prunus avium (L.) Moench) in China using stable isotope and multi-element analysis with multivariate modeling. Food Chem. X 2024, 23, 101477. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.; Zhang, J.; Wang, L.; Jin, G.; Zhang, A. Signature of Sr isotope ratios and the contents of elements as a tool to distinguish wine regions in China. Food Chem. 2024, 446, 138812. [Google Scholar] [CrossRef]
- Epova, E.N.; B’erail, S.; S’eby, F.; Vacchina, V.; Bareille, G.; M’edina, B.; Sarthou, L.; Donard, O.F.X. Strontium elemental and isotopic signatures of Bordeaux wines for authenticity and geographical origin assessment. Food Chem. 2019, 294, 35–45. [Google Scholar] [CrossRef]
- Su, Y.; Li, Y.; Zhang, J.; Wang, L.; Rengasamy, K.R.R.; Ma, W.; Zhang, A. Analysis of soils, grapes, and wines for Sr isotope characterisation in Diqing Tibetan Autonomous Prefecture (China) and combining multiple elements for wine geographical traceability purposes. J. Food Comp. Anal. 2023, 122, 105470. [Google Scholar] [CrossRef]
- Tescione, I.; Casalini, M.; Marchionni, S.; Braschi, E.; Mattei, M.; Conticelli, S. Conservation of 87Sr/86Sr during wine-making of white wines: A geochemical fingerprint of geographical provenance and quality production. Frontiers 2020, 8, 153. [Google Scholar] [CrossRef]
- Petrini, R.; Sansone, L.; Slejko, F.F.; Buccianti, A.; Marcuzzo, P.; Tomasi, D. The 87Sr/86Sr strontium isotopic systematics applied to Glera vineyards: A tracer for the geographical origin of the Prosecco. Food Chem. 2015, 170, 138–144. [Google Scholar] [CrossRef]
- Nasr, E.G.; Epova, E.N.; Barre, J.; Sebilo, M.; de Diego, A.; Souissi, R.; Abderrazak, H.; Donard, O.F.X. Combined use of 87Sr/86Sr and carbon isotopes with multielemental analysis for the geographical authentication of Tunisian and European olive oils. Food Chem. 2023, 426, 136487. [Google Scholar] [CrossRef]
- Nasr, E.G.; Epova, E.; Souissi, R.; Abderrazak, H.; Sebilo, M.; Donard, O.F.X. Conservative Behavior of 87Sr/86Sr Isotope Ratios from Soil to Olive Oil in Tunisia: A Tool for Geographical Traceability. J. Agric. Food Chem. 2025, 73, 6151–6157. [Google Scholar] [CrossRef]
- Zannella, C.; Carucci, F.; Aversano, R.; Prohaska, T.; Vingiani, S.; Carputo, D.; Adamo, P. Genetic and geochemical signatures to prevent frauds and counterfeit of high-quality asparagus and pistachio. Food Chem. 2017, 237, 545–552. [Google Scholar] [CrossRef]
- Torres-Cobos, B.; Rosell, M.; Soler, A.; Rovira, M.; Romero, A.; Guardiola, F.; Vichi, S.; Tres, A. Investigating isotopic markers for hazelnut geographical authentication: Promising variables and potential applications. Food Chem. 2024, 449, 139083. [Google Scholar] [CrossRef] [PubMed]
- Podio, N.S.; Baroni, M.V.; Badini, R.G.; Inga, M.; Ostera, H.A.; Cagnoni, M.; Gautier, E.A.; García, P.P.; Hoogewerff, J.; Wunderlin, D.A. Elemental and Isotopic Fingerprint of Argentinean Wheat. Matching Soil, Water, and Crop Composition to Differentiate Provenance. J. Agric. Food Chem. 2013, 61, 3763–3773. [Google Scholar] [CrossRef]
- Dehelean, A.; Feher, I.; Romulus, P.; Magdas, D.A.; Covaciu, F.-D.; Kasza, A.M.; Curean, V.; Cristea, G. Influence of Geographical Origin on Isotopic and Elemental Compositions of Pork Meat. Foods 2023, 12, 4271. [Google Scholar] [CrossRef] [PubMed]
- Varrà, M.O.; Zanardi, E.; Serra, M.; Conter, M.; Ianieri, A.; Ghidini, S. Isotope Fingerprinting as a Backup for Modern Safety and Traceability Systems in the Animal-Derived Food Chain. Molecules 2023, 28, 4300. [Google Scholar] [CrossRef] [PubMed]
- Avigliano, E.; Chung, M.T.; Pouilly, M.; Huang, K.F.; Casalinuovo, M.; Dominino, J.; Silva, N.; Sánchez, S.; Facetti, J.F.; Volpedo, A.V. Strontium isotope mapping and its application to study the fish life history (Salminus brasiliensis) in semi-fragmented rivers (La Plata Basin, South America). Fish. Res. 2023, 265, 106741. [Google Scholar] [CrossRef]
- Stevenson, R.; Desrochers, S.; Hélie, J.F. Stable and radiogenic isotopes as indicators of agri-food provenance: Insights from artisanal cheeses from Quebec, Canada. Int. Dairy J. 2015, 49, 37–45. [Google Scholar] [CrossRef]
- White, W.M. Geochemistry, 2nd ed.; Chapter 8—Radiogenic Isotope Geochemistry; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2020; ISBN 978-1-119-43805-2. [Google Scholar]
- Balcaen, L.; Moens, L.; Vanhaecke, F. Determination of isotope ratios of metals (and metalloids) by means of inductively coupled plasma mass spectrometry for provenancing purposes. A review. Spectrochim. Acta Part B 2010, 65, 769–786. [Google Scholar] [CrossRef]
- Lewis, J.; Pike, A.W.G.; Coath, C.D.; Evershed, R.P. Strontium concentration, radiogenic (87Sr/86Sr) and stable (δ88Sr) strontium isotope systematics in a controlled feeding study. STAR Sci. Technol. Archaeol. Res. 2017, 3, 45–57. [Google Scholar] [CrossRef]
- Fietzke, J.; Eisenhauer, A. Determination of temperature-dependent stable strontium isotope (88Sr/86Sr) fractionation via bracketing standard MC-ICP-MS. Geochem. Geophys. Geosyst. 2006, 7, Q08009. [Google Scholar] [CrossRef]
- Yoshimura, T.; Wakaki, S.; Kawahata, H.; Hossain, H.M.Z.; Manaka, T.; Suzuki, A.; Ishikawa, T.; Ohkouchi, N. Stable strontium isotopic compositions of river water, groundwater and sediments from the Ganges–Brahmaputra–Meghna River system in Bangladesh. Front. Earth Sci. 2021, 9, 592062. [Google Scholar] [CrossRef]
- Yang, L.; Peter, C.; Panne, U.; Sturgeon, R.E. Use of Zr for mass bias correction in strontium isotope ratio determinations using MC-ICP/MS. J. Anal. At. Spectrom. 2008, 23, 1269–1274. [Google Scholar] [CrossRef]
- Choi, H.-B.; Shin, W.-J.; Liu, H.-C.; Chen, Y.-H.; Hsieh, J.-Y.; Lee, K.-S. Stable strontium isotope fractionation in hydroponically grown mung and soy bean sprouts. J. Food Compos. Anal. 2023, 116, 105081. [Google Scholar] [CrossRef]
- Liu, H.-C.; Chung, C.-H.; You, C.-F.; Chiang, Y.-H. Determination of 87Sr/86Sr and δ88/86Sr ratios in plant materials using MC-ICP-MS. Anal. Bioanal. Chem. 2016, 408, 387–397. [Google Scholar] [CrossRef] [PubMed]
- Irrgeher, J.; Prohaska, T.; Sturgeon, R.E.; Mester, Z.; Yang, L. Determination of strontium isotope ratios in a biological tissue using mc-icpms. Anal. Methods 2013, 5, 1687–1694. [Google Scholar] [CrossRef]
- Gazzetta Ufficiale dell’Unione Europea, C 52/17. 22 February 2012. Available online: https://eur-lex.europa.eu/legal-content/IT/TXT/HTML/?uri=OJ:C:2012:052:FULL (accessed on 2 April 2025).
- Martini, S.; Conte, A.D. Tagliazucchi. Phenolic compounds profile and antioxidant properties of six sweet cherry (Prunus avium) cultivars. Food Res. Int. 2017, 97, 15–26. [Google Scholar] [CrossRef]
- Filaferro, M.; Codeluppi, A.; Brighenti, V.; Cimurri, F.; González-Paramás, A.M.; Santos-Buelga, C.; Bertelli, D.; Pellati, F.; Vitale, G. Disclosing the Antioxidant and Neuroprotective Activity of an Anthocyanin-Rich Extract from Sweet Cherry (Prunus avium L.) Using In Vitro and In Vivo Models. Antioxidants 2022, 11, 211. [Google Scholar]
- Moore, L.J.; Murphy, T.J.; Barnes, I.L.; Paulsen, P.J. Absolute isotopic abundance ratios and atomic weight of a reference sample of Strontium. J. Res. Natl. Bur. Stand. 1982, 87, 1–8. [Google Scholar] [CrossRef]
- Stein, M.; Starinsky, A.; Katz, A.; Goldstein, S.L.; Machlus, M.; Schramm, A. Strontium isotopic, chemical and sedimentological evidence for the evolution of lake Lisan and the Dead sea. Geochim. Cosmochim. Acta 1997, 61, 3975–3992. [Google Scholar] [CrossRef]
- Bohlkea, J.K.; Horan, M. Strontium isotope geochemistry of ground waters and streams affected by agriculture, Locust Grove, MD. Appl. Geochem. 2000, 15, 599–609. [Google Scholar] [CrossRef]
- Durante, C.; Bertacchini, L.; Cocchi, M.; Manzini, D.; Marchetti, A.; Rossi, M.C.; Tassi, S.S.L. Development of 87Sr/86Sr maps as targeted strategy to support wine quality. Food Chem. 2018, 255, 139–146. [Google Scholar] [CrossRef]
- DIN ISO 19730 (2009-07); Soil Quality—Extraction of Trace Elements from Soil Using Ammonium Nitrate Solution. ISO: Geneva, Switzerland, 2009.
- Horwitz, E.P.; Chiarizia, R.; Dietz, M.L. A novel strontium-selective extraction chromatographic resin. Solvent Extr. Ion Exch. 1992, 10, 313–336. [Google Scholar] [CrossRef]
- Durante, C.; Baschieri, C.; Bertacchini, L.; Cocchi, M.; Sighinolfi, S.; Silvestri, M.; Marchetti, A. Geographical traceability based on 87Sr/86Sr indicator: A first approach for PDO Lambrusco wines from Modena. Food Chem. 2013, 141, 2779–2787. [Google Scholar] [CrossRef] [PubMed]
- Brenna, J.T.; Corso, T.N.; Tobias, H.J.; Caimi, R.J. High-precision continuous-flow isotope ratio mass spectrometry. Mass Spectrom. Rev. 1997, 16, 227–258. [Google Scholar] [CrossRef]
- Steiger, R.H.; Jager, E. Subcommission on geochronology: Convention on the use of decay Constants in geo- and cosmochronology. Earth Planet. Sci. Lett. 1977, 36, 359. [Google Scholar] [CrossRef]
- Russell, W.A.; Papanastassiou, D.A.; Tombrello, T.A. Ca isotope fractionation on the earth and other solar system materials. Geochim. Cosmochim. Acta 1978, 42, 1075–1090. [Google Scholar] [CrossRef]
- Berni, A.; Baschieri, C.; Covelli, S.; Emili, A.; Marchetti, A.; Manzini, D.; Berto, D.; Rampazzo, F. DoE optimization of a mercury isotope ratio determination method for environmental studies. Talanta 2016, 152, 179–187. [Google Scholar] [CrossRef]
- Johnson, C.M.; Beard, B.L.; Albarède, F. Geochemistry of Non-Traditional Stable Isotopes, Vol. 55 in the Series: Reviews in Mineralogy & Geochemistry; De Gruyter: Berlin, Germany; Boston, MA, USA, 2004; ISSN 1529-6466. [Google Scholar]
- Yang, L. Accurate and precise determination of isotopic ratios by MC-ICP-MS: A review. Mass Spectrom. Rev. 2009, 28, 990–1011. [Google Scholar] [CrossRef]
- Albarède, F.; Telouk, P.; Blichert-Toft, J.; Boyet, M.; Agranier, A.; Nelson, B. Precise and accurate isotopic measurements using multiple-collector ICPMS. Geochim. Cosmochim. Acta 2004, 68, 2725–2744. [Google Scholar] [CrossRef]
- White, W.M.; Albarède, F.; Télouk, P. High-precision analysis of Pb isotope ratios by multi-collector ICP-MS. Chem. Geol. 2000, 167, 257–270. [Google Scholar] [CrossRef]
- Lancellotti, L.; Sighinolfi, S.; Marchetti, A.; Tassi, L. Use of Lead Isotopic Ratios as Geographical Tracer for Lambrusco PDO Wines. Molecules 2020, 25, 1641. [Google Scholar] [CrossRef]
- Durante, C.; Bertacchini, L.; Marchetti, A. Heavy isotopes: A powerful tool to support geographical traceability of food. In Food Authentication: Management, Analysis, Regulation and Consumers; Georgiou, C.A., Ed.; Wiley-Blackwell: Oxford, UK, 2017; ISBN 978-1-118-81026-2. [Google Scholar]
- Sahoo, S.K.; Masuda, A. Precise measurement of zirconium isotopes by thermal ionization mass spectrometry. Chem. Geol. 1997, 141, 117–126. [Google Scholar] [CrossRef]
- Sanloup, C.; Blichert, T.J.; Gillet, P.; Albarède, F. Zr isotope anomalies in chondrites and the presence of 92Nb in the early solar system. Earth Planet. Sci. Lett. 2000, 184, 75–81. [Google Scholar]
- Ingle, C.P.; Sharp, B.L.; Horstwood, M.S.A.; Parrish, R.R.; Lewisc, D.J. Instrument response functions, mass bias and matrix effects in isotope ratio measurements and semi-quantitative analysis by single and multi-collector ICP-MS. J. Anal. At. Spectrom. 2003, 18, 219–229. [Google Scholar] [CrossRef]
- De Souza, G.F.; Reynolds, B.C.; Kiczka, M.; Bourdon, B. Evidence for mass-dependent isotopic fractionation of strontium in a glaciated granitic watershed. Geochim. Cosmochim. Acta 2010, 74, 2596–2614. [Google Scholar] [CrossRef]
- Oeser, R.A.; Von Blanckenburg, F. Strontium isotopes trace biological activity in the Critical Zone along a climate and vegetation gradient. Chem. Geol. 2020, 558, 119861. [Google Scholar] [CrossRef]

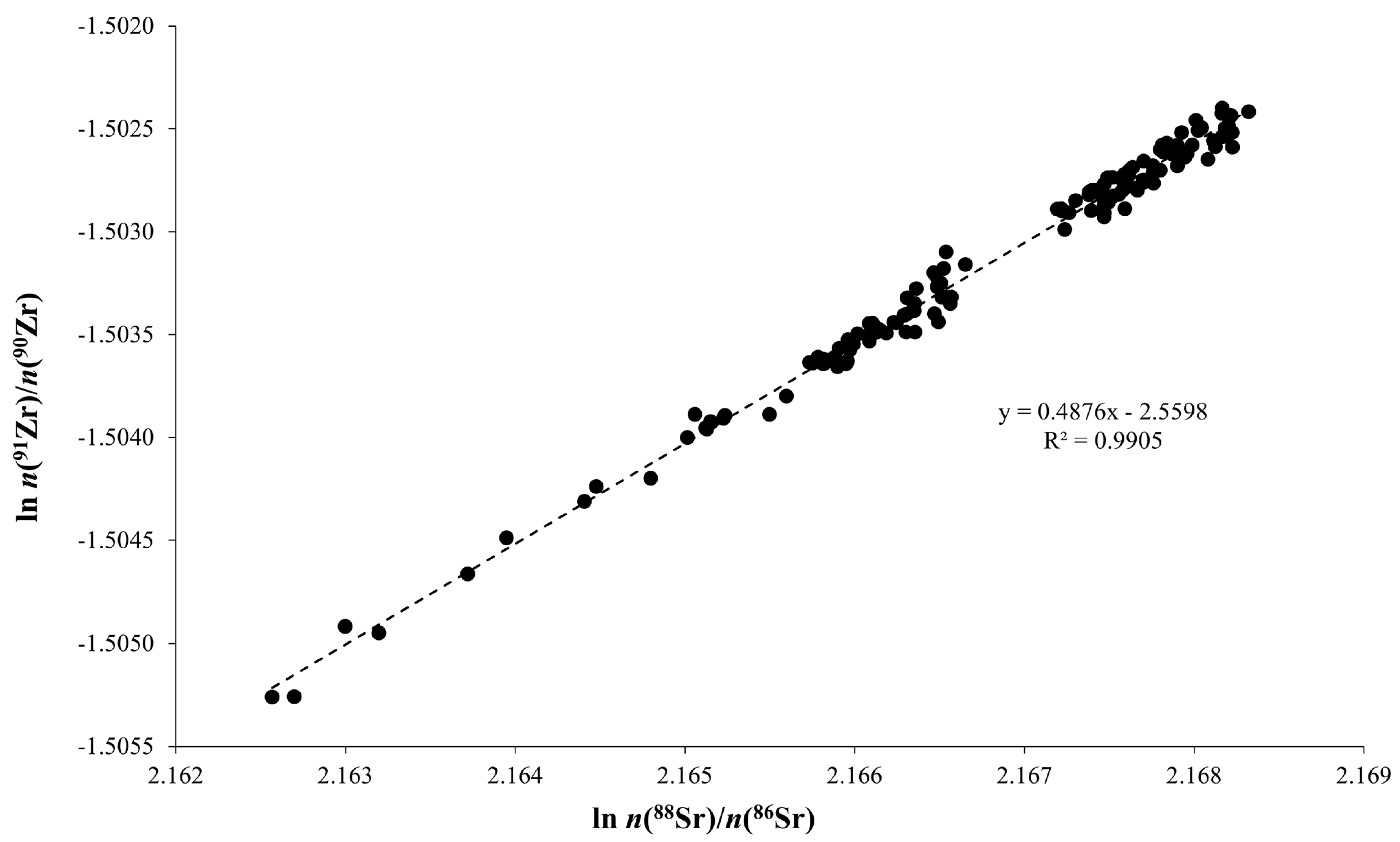

| Slope | sd | Intercept | sd | r2 | Theoretical Slope | |
|---|---|---|---|---|---|---|
| ln n(88Sr)/n(86Sr) | 0.488 | 0.004 | −2.560 | 0.008 | 0.9905 | 0.4820 |
| ln n(87Sr)/n(86Sr) | 0.967 | 0.008 | −1.193 | 0.003 | 0.9896 | 0.9571 |
| 87Sr/86Sr ± Sd | 88Sr/86Sr ± Sd | δ88Sr * ± Sd | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Soil(4) # | 0.70875 | ± | 0.00003 | 8.3758 | ± | 0.0003 | −0.33 | ± | 0.03 |
| Branch(3) | 0.71022 | ± | 0.00001 | 8.3784 | ± | 0.0004 | −0.04 | ± | 0.04 |
| Cherry(5) | 0.70960 | ± | 0.00006 | 8.3758 | ± | 0.0003 | −0.34 | ± | 0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lancellotti, L.; D’Eusanio, V.; Manzini, D.; Durante, C.; Marchetti, A.; Tassi, L. Evaluation of the Strontium Isotope Ratios in Soil–Plant–Fruit: A Comprehensive Study on Vignola Cherry (Ciliegia di Vignola PGI). Foods 2025, 14, 1492. https://doi.org/10.3390/foods14091492
Lancellotti L, D’Eusanio V, Manzini D, Durante C, Marchetti A, Tassi L. Evaluation of the Strontium Isotope Ratios in Soil–Plant–Fruit: A Comprehensive Study on Vignola Cherry (Ciliegia di Vignola PGI). Foods. 2025; 14(9):1492. https://doi.org/10.3390/foods14091492
Chicago/Turabian StyleLancellotti, Lisa, Veronica D’Eusanio, Daniela Manzini, Caterina Durante, Andrea Marchetti, and Lorenzo Tassi. 2025. "Evaluation of the Strontium Isotope Ratios in Soil–Plant–Fruit: A Comprehensive Study on Vignola Cherry (Ciliegia di Vignola PGI)" Foods 14, no. 9: 1492. https://doi.org/10.3390/foods14091492
APA StyleLancellotti, L., D’Eusanio, V., Manzini, D., Durante, C., Marchetti, A., & Tassi, L. (2025). Evaluation of the Strontium Isotope Ratios in Soil–Plant–Fruit: A Comprehensive Study on Vignola Cherry (Ciliegia di Vignola PGI). Foods, 14(9), 1492. https://doi.org/10.3390/foods14091492







