Optimizing Commercial-Scale Storage for Chinese Cabbage (Brassica rapa L. ssp. Pekinensis): Integrating Morphological Classification, Respiratory Heat Effects, and Computational Fluid Dynamics for Enhanced Cooling Efficiency
Abstract
1. Introduction
2. Materials and Methods
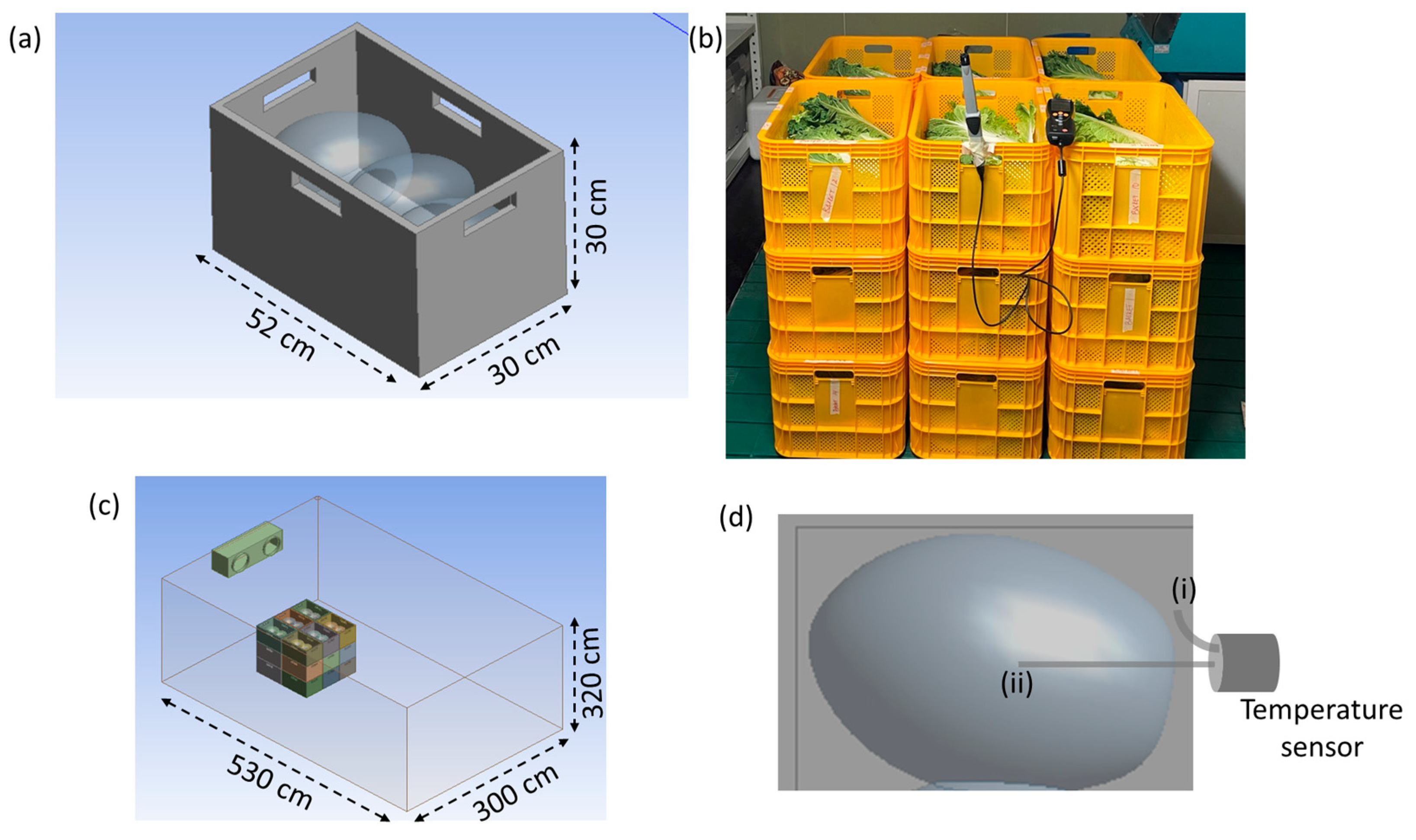
2.1. Sample Preparation
2.2. Measurement of CC Respiration Rate
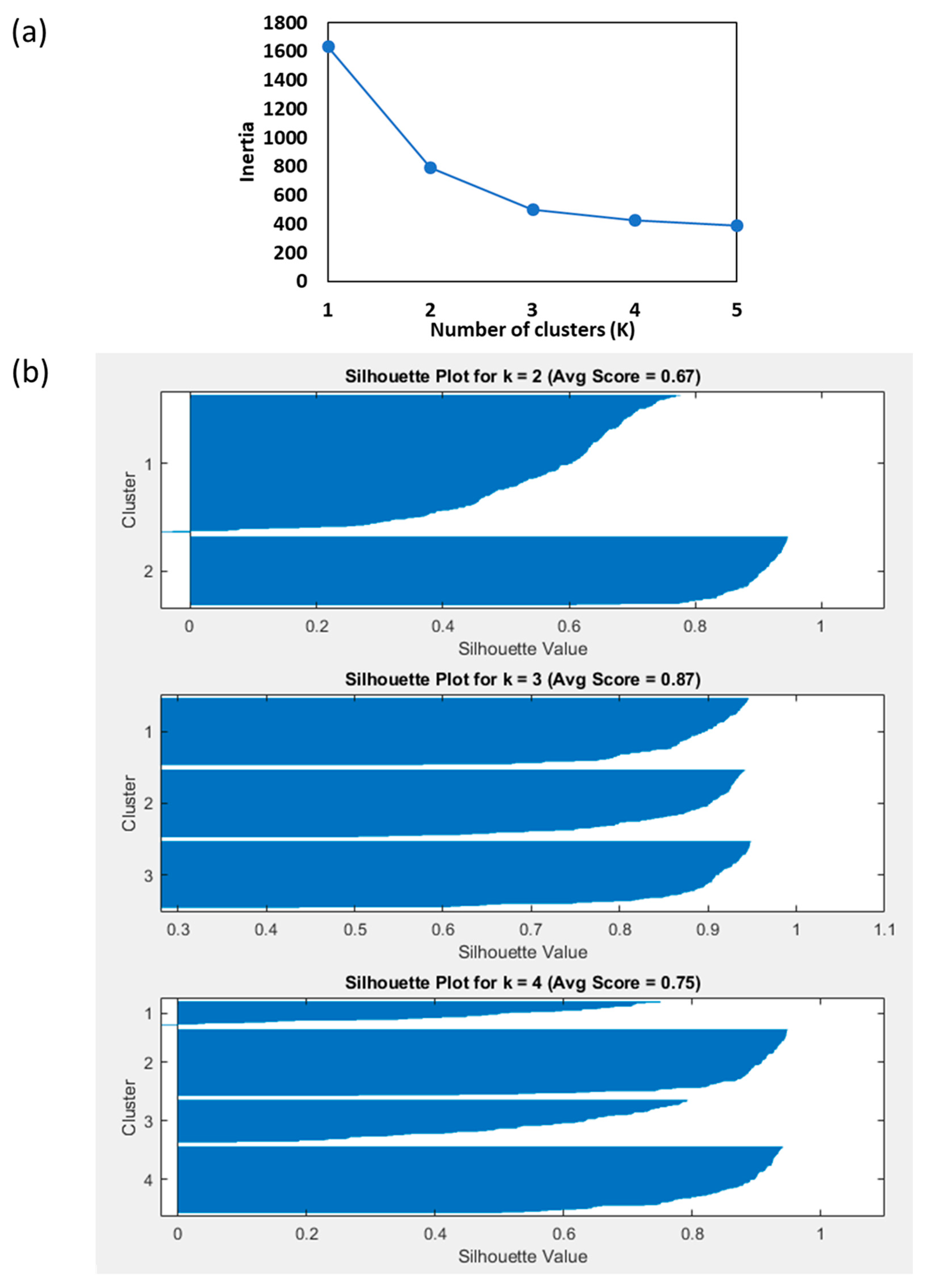
2.3. K-Means Clustering
2.4. Numerical Model
2.4.1. CFD Simulation Setup
2.4.2. Porous Media Model
2.4.3. Transient Heat Conduction Model
2.4.4. Boundary Conditions
- 1.
- Initial condition:
- 2.
- The boundary conditions included the following:
- Symmetry at the center (r = 0): Due to spherical symmetry, the temperature gradient at the center is zero:
- The convective heat transfer at the CC surface (r = R), modeled as a heat exchange between the cabbage and the surrounding environment (e.g., refrigeration or air):
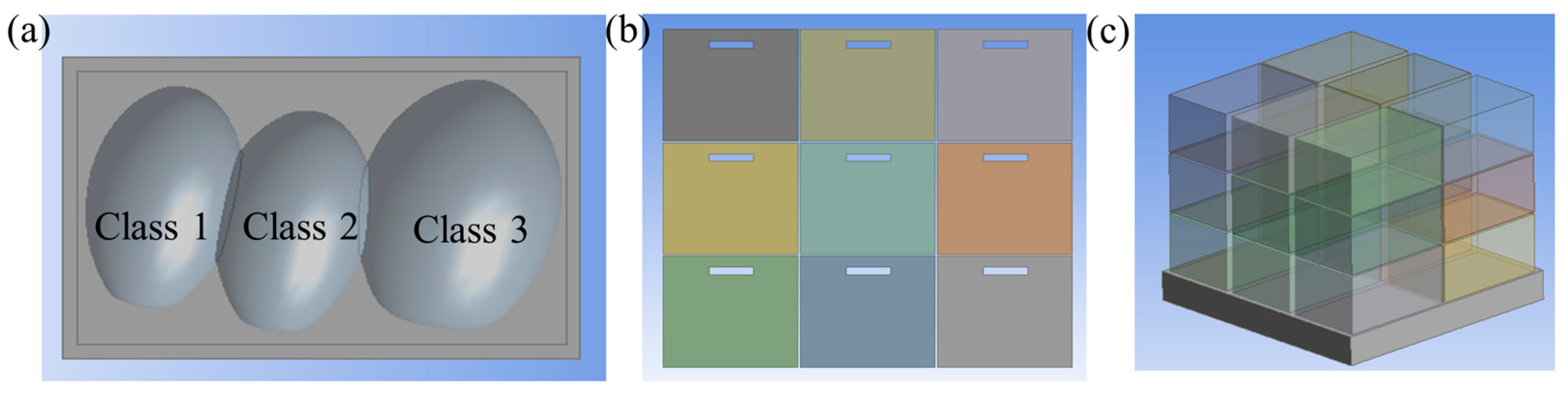
2.4.5. Model Geometry Simplification for Commercial-Scale Storage Facility
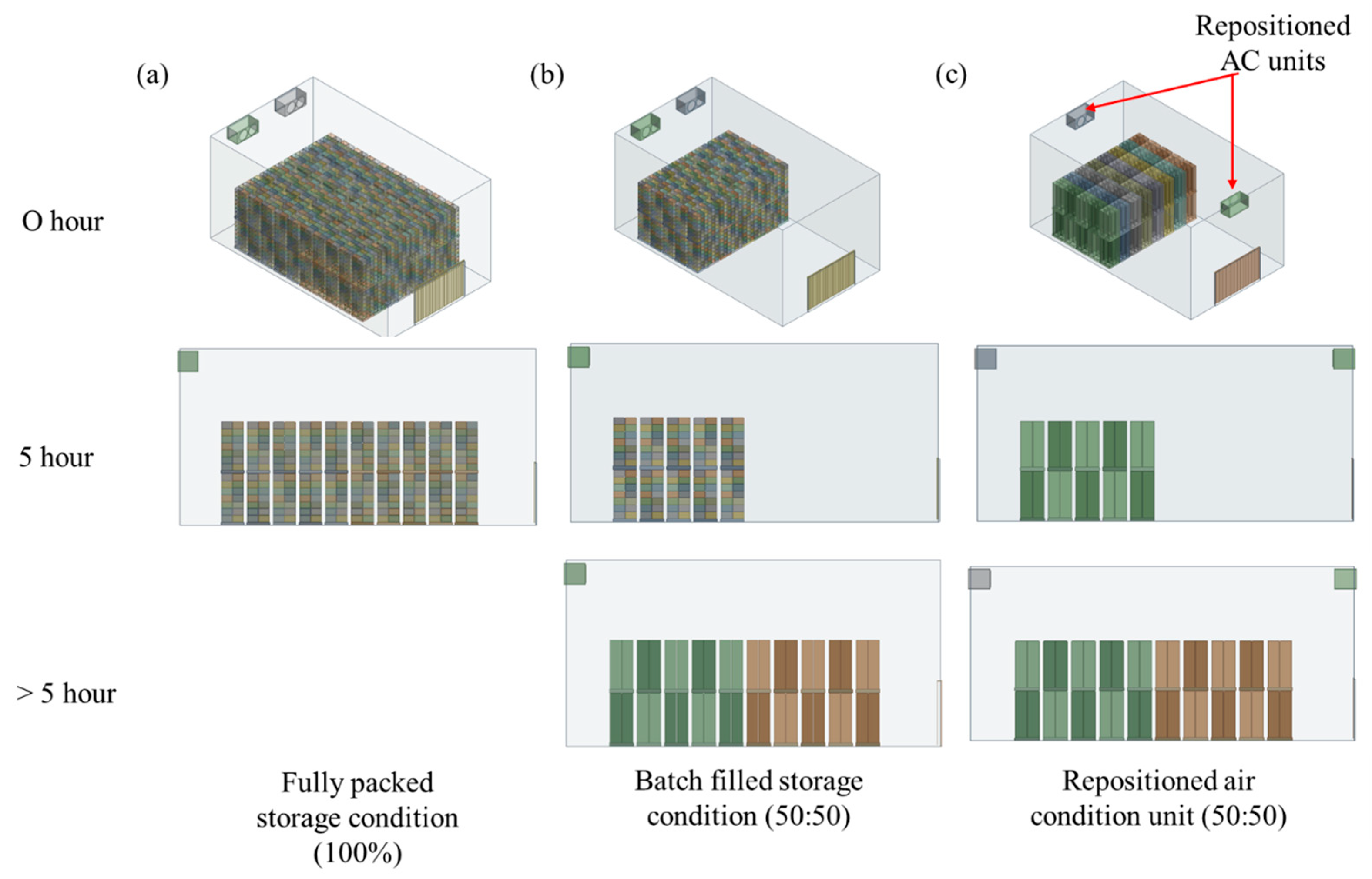
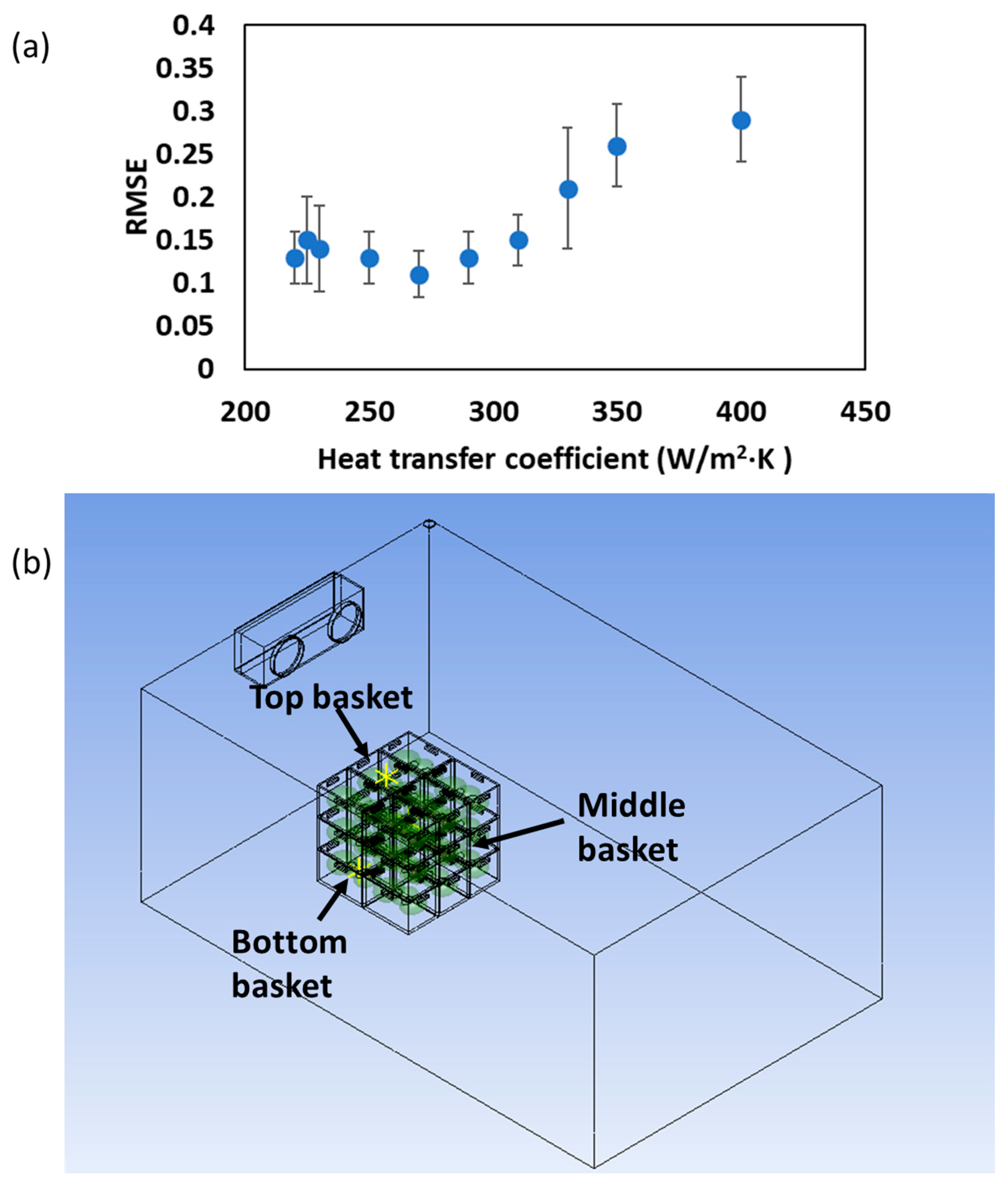
2.5. Optimization of Commercial-Scale CC Storage Room Design
3. Results and Discussion
3.1. K-Means Clustering Analysis of CC
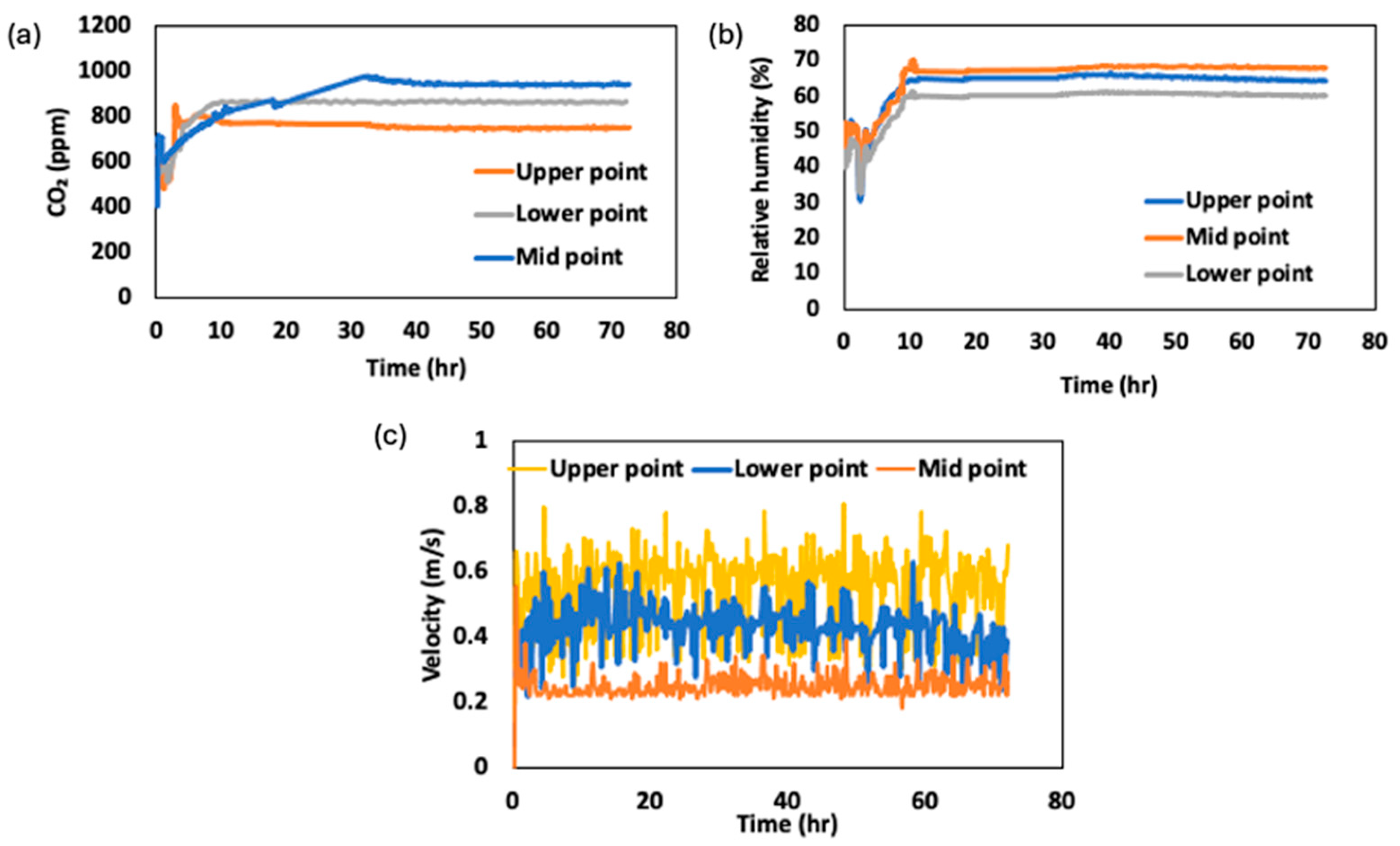
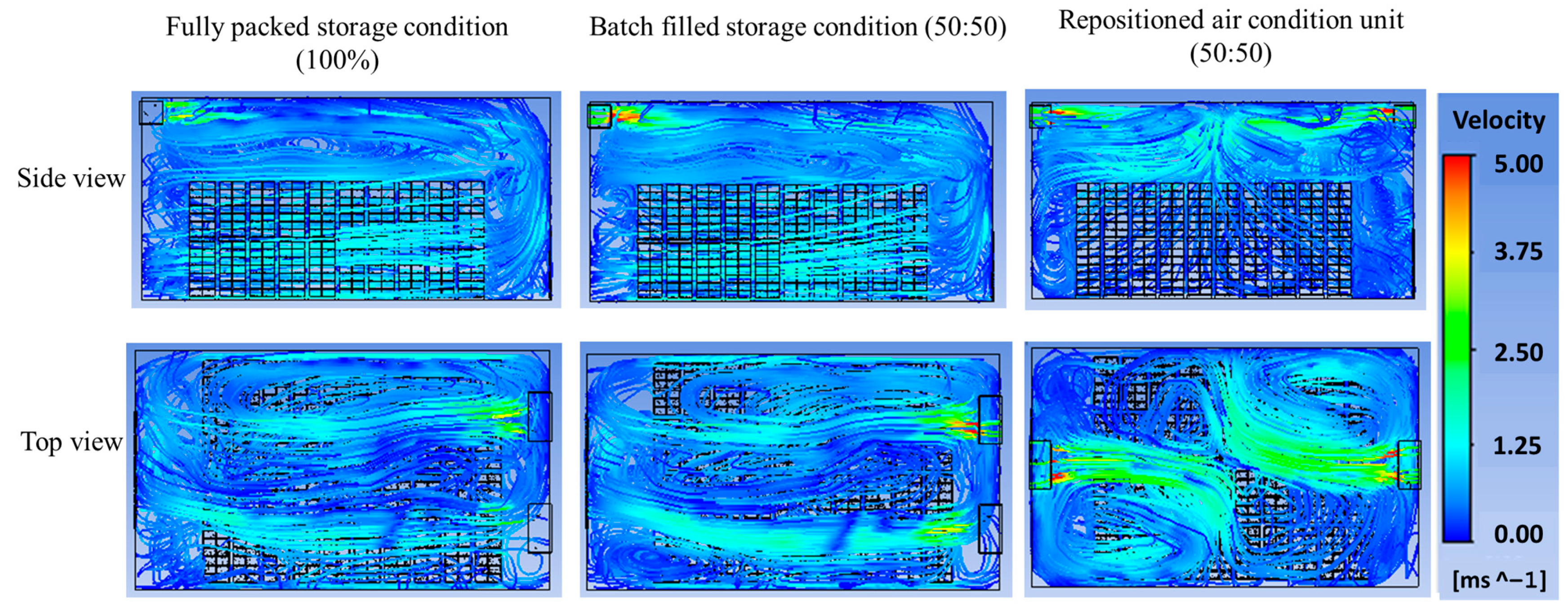
3.2. CO2, Relative Humidity, and Velocity in Storage Facility
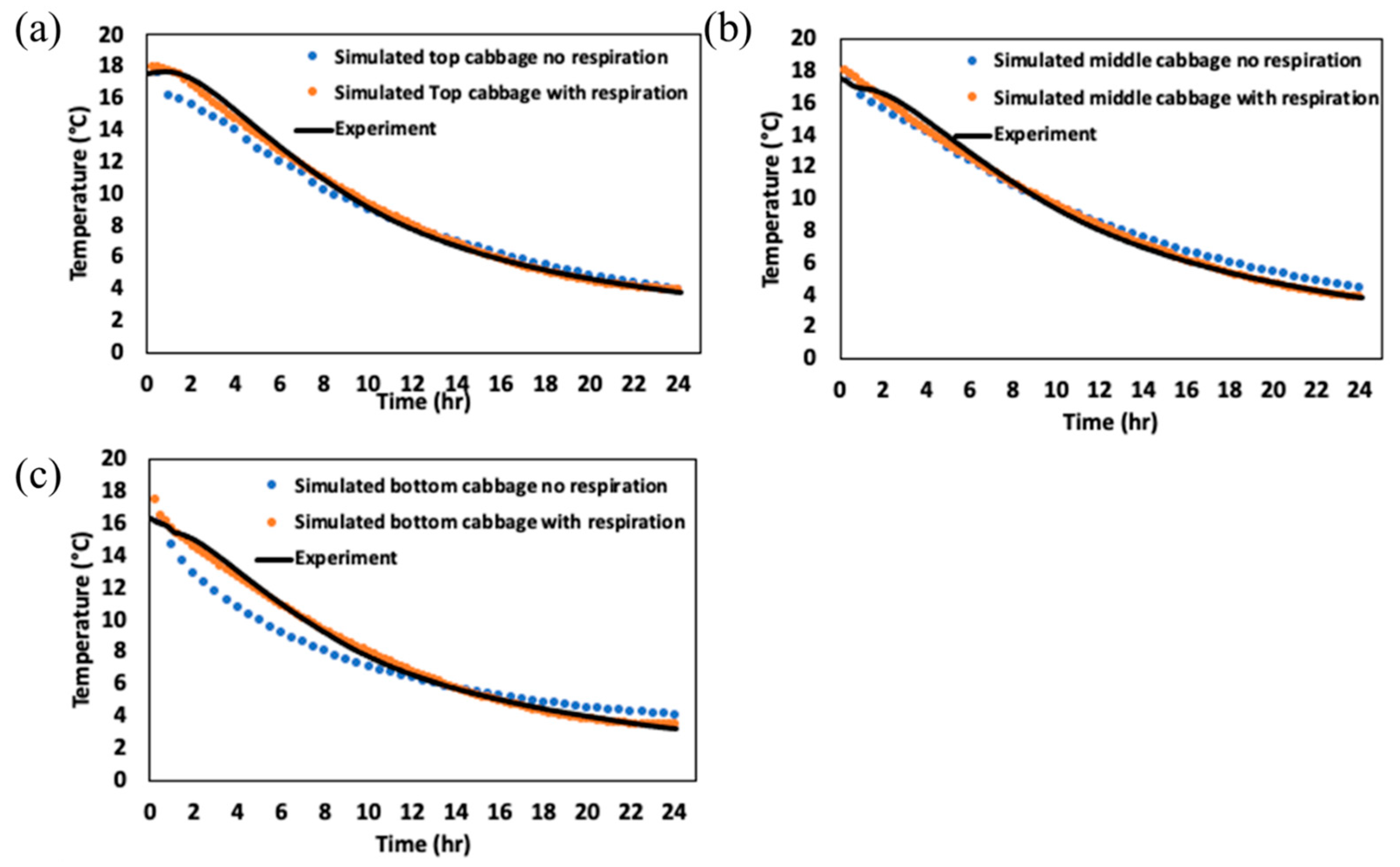
3.3. Effects of CC Heat of Respiration on the Heat Transfer Model in Storage Facility
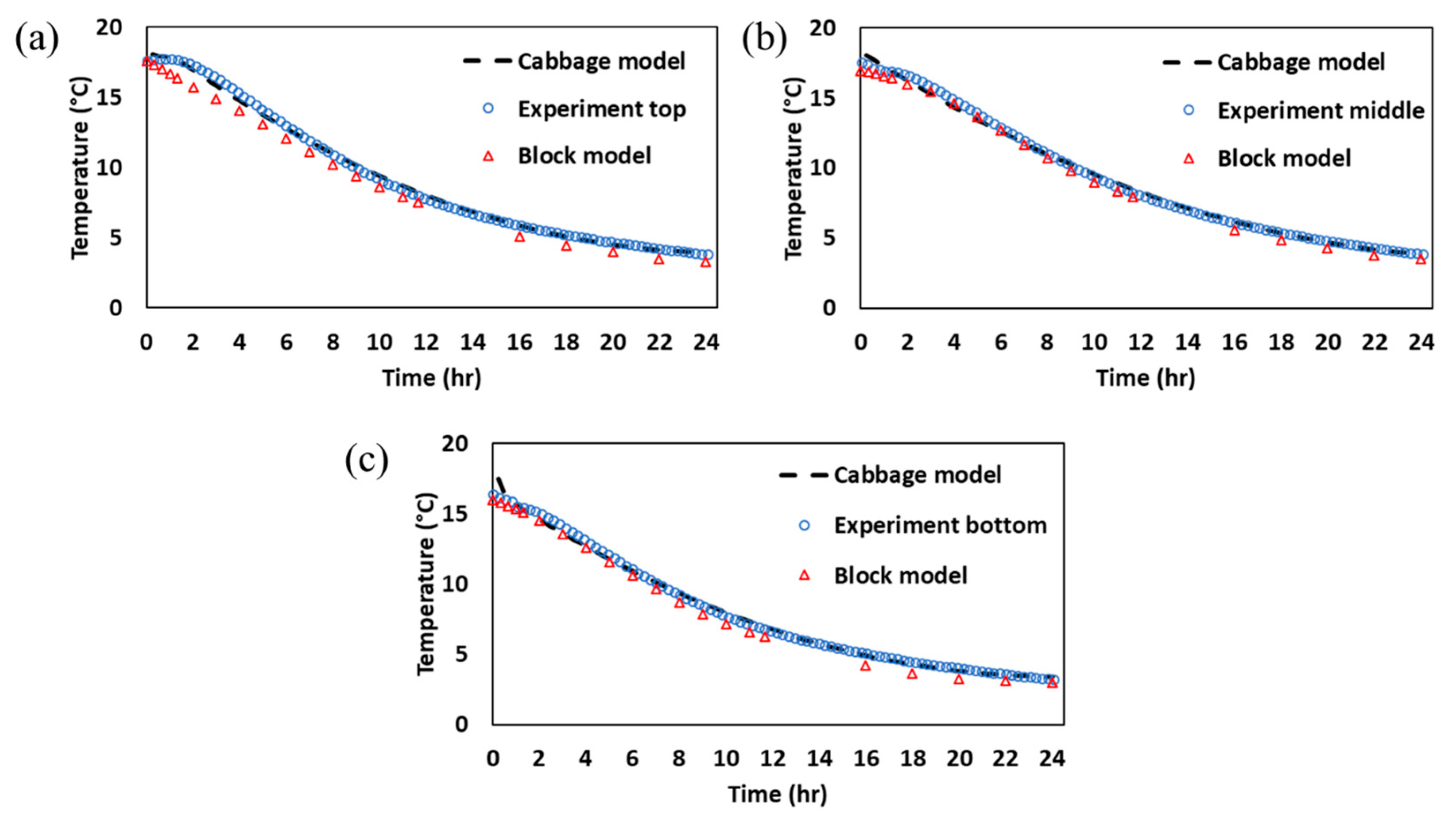
3.4. Model Simplification for Storage Facility Scale-Up and Computational Efficiency
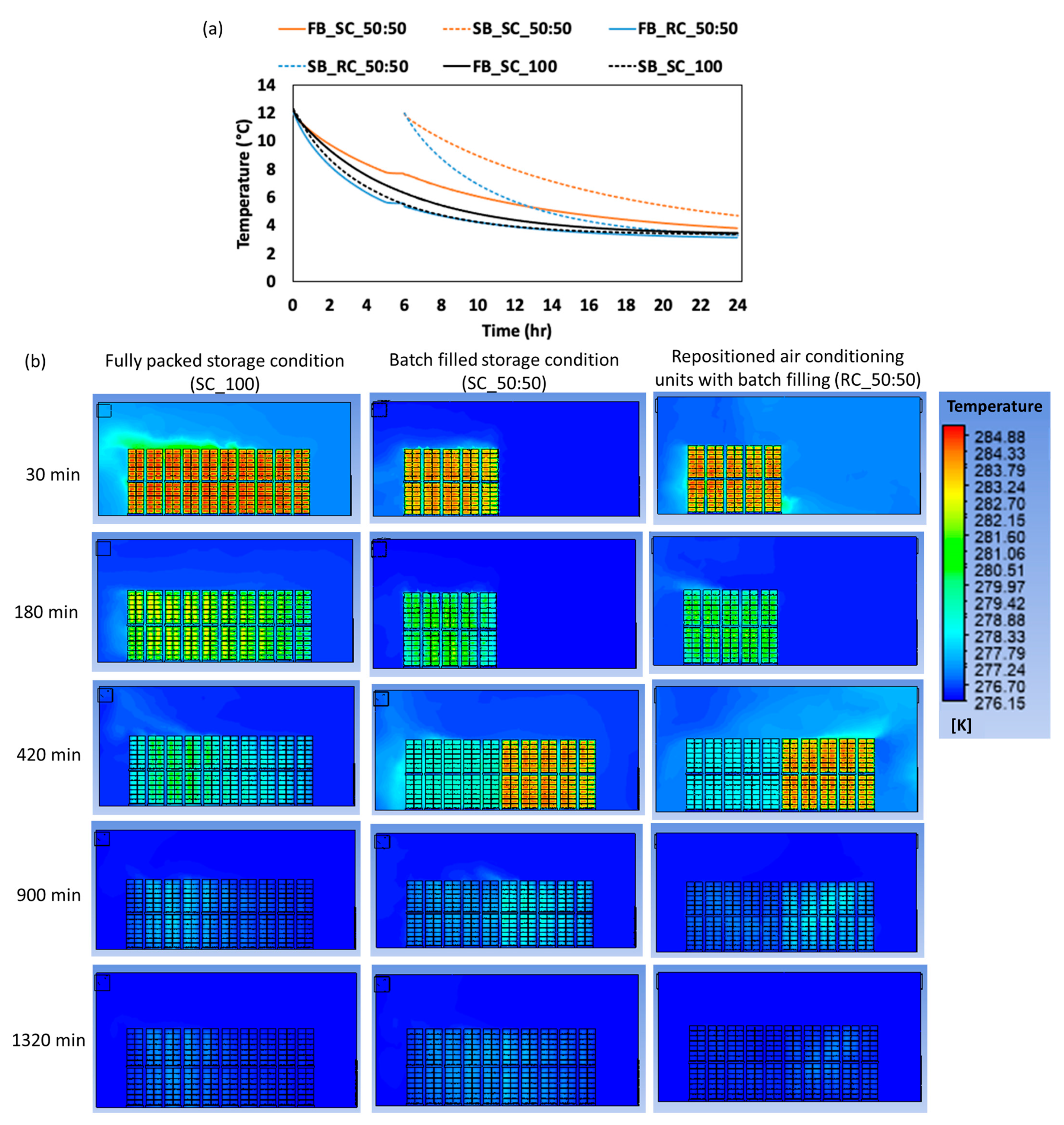
3.5. Evaluating Storage Conditions for Optimal Design of Commercial-Scale CC Storage Room
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dahiru, S.; Salele, Y.; Japhet, A.T.; Abubakar, M.Y.; Adam, A.B. Nutritional status and risk characterization of red pepper, cabbage, lettuce and spinach grown at Ajiwa, Batagarawa, Lambun Sarki and Kofar Marusa vegetable farms, Katsina State, Nigeria. Earthline J. Chem. Sci. 2024, 11, 539–552. [Google Scholar] [CrossRef]
- Zhang, R.; He, Q.; Pan, Q.; Feng, Y.; Shi, Y.; Li, G.; Khan, A. Blue-green light treatment enhances the quality and nutritional value in postharvest Chinese cabbage (Brassica rapa L. ssp. pekinensis). Food Chem. X 2024, 24, 102004. [Google Scholar] [CrossRef]
- Ta-Oun, P.; Suwakrai, K.; Hongpakdee, P.; Nimkingrat, P. The impact of bio-control management, storage temperature and packaging on postharvest characterization of Chinese flowering cabbage. Acta Hortic. 2021, 1336, 229–234. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, W.; Cheng, S.; Liu, Y.; Yang, W.; Wang, Y.; Chen, G. Postharvest storage at near-freezing temperature maintained the quality and antioxidant properties of Prunus domestica L. cv. Ximei fruit. Sci. Hortic. 2022, 293, 110720. [Google Scholar] [CrossRef]
- Lim, K.T.; Kim, J.; Chung, J.H. Development of Long-Term Storage Technology for Chinese Cabbage—Physiological Characteristics of Postharvest Freshness in a Cooler with a Monitoring and Control Interface. J. Biosyst. Eng. 2014, 39, 194–204. [Google Scholar] [CrossRef]
- Oyinloye, T.M.; Yoon, W.B. Analysis of Mass Transfer and Shrinkage Characteristics of Chinese Cabbage (Brassica rapa L. ssp. pekinensis) Leaves during Osmotic Dehydration. Foods 2024, 13, 332. [Google Scholar] [CrossRef]
- Chaves, P.J.L.; Cepeda, J.T.; Álvarez, F.J.G.; Orzáez, M.J.H. Influence of moisture, temperature and microbial activity in biomass sustainable storage. Special Focus on Olive Biomasses. Int. J. Environ. Sci. Nat. Res. 2020, 25, 556165. [Google Scholar]
- Alexander, L.D.; Jakhar, S.; Dasgupta, M.S. Optimizing cold storage for uniform airflow and temperature distribution in apple preservation using CFD simulation. Sci. Rep. 2024, 14, 25402. [Google Scholar] [CrossRef]
- Getahun, S.T. Investigating Cooling Performance and Energy Utilization of Refrigerated Shipping Container Packed with Fresh Fruit Using Computational Fluid Dynamics Modelling. Ph.D. Thesis, Stellenbosch University, Stellenbosch, South Africa, 2017. [Google Scholar]
- Arpaci, E.; Atayılmaz, Ş.Ö.; Gemici, Z. Exploring Mathematical Modeling and CFD in Convective Drying of Fruits and Vegetables: A Review. Food Bioprocess Technol. 2024, 1–28. [Google Scholar] [CrossRef]
- Yin, J.; Guo, M.; Liu, G.; Ma, Y.; Chen, S.; Jia, L.; Liu, M. Research progress in simultaneous heat and mass transfer of fruits and vegetables during precooling. Food Eng. Rev. 2022, 14, 307–327. [Google Scholar] [CrossRef]
- Prukwarun, W.; Khumchoo, W.; Seancotr, W.; Phupaichitkun, S. CFD simulation of fixed bed dryer by using porous media concepts: Unpeeled longan case. Int. J. Agric. Biol. Eng. 2013, 6, 100–110. [Google Scholar]
- Halder, A. A Framework for Multiphase Heat and Mass Transport in Porous Media with Applications to Food Processes. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, May 2010. [Google Scholar]
- Sajadiye, S.M.; Ahmadi, H.; Zolfaghari, M.; Mohtasebi, S.S.; Mostofi, Y.; Raja, A. A multi-scale three-dimensional CFD model of a full loaded cool storage. Int. J. Food Eng. 2013, 9, 163–178. [Google Scholar] [CrossRef]
- Worasawate, D.; Sakunasinha, P.; Chiangga, S. Automatic classification of the ripeness stage of mango fruit using a machine learning approach. AgriEngineering 2022, 4, 32–47. [Google Scholar] [CrossRef]
- Liming, X.; Yanchao, Z. Automated strawberry grading system based on image processing. Comput. Electron. Agric. 2010, 71, S32–S39. [Google Scholar] [CrossRef]
- Kolodziejczyk, M.; Butrymowicz, D.; Smierciew, K.; Gagan, J. Numerical Modelling of Heat and Mass Transfer Processes in Chinese Cabbage Cold Storage Chamber. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 11–14 July 2016; Available online: https://docs.lib.purdue.edu/iracc/1829/ (accessed on 4 March 2024).
- Priss, O.; Yevlash, V.; Zhukova, V.; Kiurchev, S.; Verkholantseva, V.; Kalugina, I.; Bandurenko, H. Investigation of the respiration rate during storage of fruit vegetables under the influence of abiotic factors. EUREKA Life Sci. 2017, 10–15. [Google Scholar] [CrossRef][Green Version]
- González-Buesa, J.; Salvador, M.L. An Arduino-based low cost device for the measurement of the respiration rates of fruits and vegetables. Comput. Electron. Agric. 2019, 162, 14–20. [Google Scholar] [CrossRef]
- Kandasamy, P. Respiration rate of fruits and vegetables for modified atmosphere packaging: A mathematical approach. J. Postharvest Technol. 2022, 10, 88–102. [Google Scholar]
- Al-Ati, T.; Hotchkiss, J.H. Application of packaging and modified atmosphere to fresh-cut fruits and vegetables. In Fresh-Cut Fruits and Vegetables: Science, Technology, and Market; CRC Press: Boca Raton, FL, USA, 2002; pp. 305–338. [Google Scholar]
- ASHRAE. Thermal properties of foods, In Handbook—Refrigeration; ASHRAE: Peachtree Corners, GA, USA, 2006; Chapter 9; pp. 9.1–9.31. [Google Scholar]
- ANSYS Inc. ANSYS FLUENT 12.0 User’s Guide. Section 7.2.2 Solid Conditions. 2009. Available online: https://www.afs.enea.it/project/neptunius/docs/fluent/html/ug/node232.htm (accessed on 6 February 2025).
- Bazgaou, A.; Fatnassi, H.; Bouharroud, R.; Tiskatine, R.; Wifaya, A.; Demrati, H.; Bouirden, L. CFD modeling of the microclimate in a greenhouse using a rock bed thermal storage heating system. Horticulturae 2023, 9, 183. [Google Scholar] [CrossRef]
- Oyinloye, T.M.; An, S.; Cho, C.W.; Yoon, W.B. Optimization of Steaming Conditions for Bellflower Root (Platycodon grandiflorus) Using K-Means Clustering-Based Morphological Grading System. Processes 2024, 12, 2347. [Google Scholar] [CrossRef]
- Zhao, Y.; Xie, J. Practical applications of vacuum impregnation in fruit and vegetable processing. Trends Food Sci. Tech. 2004, 15, 434–451. [Google Scholar] [CrossRef]
- Park, S.H.; Seo, D.H.; Jeong, J.H. Experimental and numerical analysis of thermal flow in open-cell porous metal during Darcy-Forchheimer transition regime. Appl. Therm. Eng. 2020, 181, 116029. [Google Scholar] [CrossRef]
- Kosari, E.; Vafai, K. Synthesis of flow and thermal transport in porous media as applied to biological applications. J. Heat Transf. 2021, 143, 062701. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Merliana, N.P.E.; Santoso, A.J. Analisa Penentuan Jumlah Cluster Terbaik pada Metode K-Means Clustering. In Proceedings of the National Seminar on Multidisciplinary Science, Semarang, Indonesia, 28 July 2015; Available online: https://scholar.google.com/scholar?hl=en&as_sdt=0%2C5&q=Merliana%2C+N.P.%3B+Santoso%2C+A.J.+Analisa+Penentuan+Jumlah+Cluster+Terbaik+pada+Metode+K-means+Clustering.+2015.&btnG= (accessed on 10 January 2024).
- Mahajan, P.V.; Caleb, O.J.; Singh, Z.; Watkins, C.B.; Geyer, M. Postharvest treatments of fresh produce. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372, 20130309. [Google Scholar] [CrossRef]
- Rao, C.G. Engineering for Storage of Fruits and Vegetables: Cold Storage, Controlled Atmosphere Storage, Modified Atmosphere Storage; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Thompson, A.K.; Prange, R.K.; Bancroft, R.; Puttongsiri, T. Controlled Atmosphere Storage of Fruit and Vegetables; CABI: Wallingford, UK, 2018. [Google Scholar]
- Praeger, U.; Jedermann, R.; Sellwig, M.; Neuwald, D.A.; Hartgenbusch, N.; Borysov, M.; Geyer, M. Airflow distribution in an apple storage room. J. Food Eng. 2020, 269, 109746. [Google Scholar] [CrossRef]
- Benítez, S.; Chiumenti, M.; Sepulcre, F.; Achaerandio, I.; Pujolá, M. Modeling the effect of storage temperature on the respiration rate and texture of fresh cut pineapple. J. Food Eng. 2012, 113, 527–533. [Google Scholar] [CrossRef]
- Hoang, M.L.; Verboven, P.; Baelmans, M.; Nicolaï, B.M. A continuum model for airflow, heat and mass transfer in bulk of chicory roots. Trans. ASAE 2003, 46, 1603–1611. [Google Scholar] [CrossRef]
- Ferrua, M.J.; Singh, R.P. Modeling the forced-air cooling process of fresh strawberry packages, Part II: Experimental validation of the flow model. Int. J. Refrig. 2009, 32, 349–358. [Google Scholar] [CrossRef]
- Xin, S.; Xu, H.; Li, S.; Wang, W.; Guo, J.; Yang, W. Efficiency evaluation of a floor standing air conditioner with different installation positions and air supply parameters applied to a large laboratory. J. Build. Eng. 2020, 32, 101701. [Google Scholar] [CrossRef]
- Nalbandi, H.; Seiiedlou, S.; Ghasemzadeh, H.R.; Rangbar, F. Innovative parallel airflow system for forced-air cooling of strawberries. Food Bioprod. Process. 2016, 100, 440–449. [Google Scholar] [CrossRef]


| Properties | Class 1 | Class 2 | Class 3 |
|---|---|---|---|
| Thermal conductivity (k) (W/m·K) | 8.1 × 10−5 T + 2.2 × 10−2 | 8.3 × 10−5 T + 2.27 × 10−2 | 8.5 × 10−5 T + 2.3 × 10−2 |
| Specific heat (CP) (J/kg·K) | −0.0048 T2 + 1.76 T + 1770 | −0.00475 T2 + 1.765 T + 1775 | −0.0047 T2 + 1.78 T + 1780 |
| Density (ρ) (kg/m3) | 601.64 ± 42.68 | 675.70 ± 38.59 | 754.34 ± 35.34 |
| Properties | Class 1 | Class 2 | Class 3 | |
|---|---|---|---|---|
| Max | 79 | 84 | 93 | |
| Length circumference (cm) | Min | 68 | 80 | 85 |
| Average | 73.32 ± 3.34 | 82.67 ± 1.17 | 89.17 ± 2.45 | |
| Max | 48 | 54 | 61 | |
| Width circumference (cm) | Min | 44 | 49 | 55 |
| Average | 46.73 ± 2.24 | 51.89 ± 2.37 | 58.67 ± 2.77 | |
| Max | 1783.26 | 2483.57 | 3112.85 | |
| Weight (g) | Min | 1306.39 | 1795.23 | 2484.77 |
| Average | 1503.20 ± 118.39 | 2132.48 ± 127.16 | 2826.37 ± 121.25 |
| Properties | Cabbage Model | Block Model | Reduction (%) |
|---|---|---|---|
| Number of mesh element | 2,694,876 | 2,102,003 | 22 |
| Convergence time (h) | 2.1 | 1.3 | 38 |
| Simulation time (h) | 4.5 | 2.7 | 40 |
| RAM uasge (GB) | 32 | 22.4 | 30 |
| Loading Process | Model | Temperature Gradient | Equilibrium Temperature | ||
|---|---|---|---|---|---|
| Time | Temp (°C) | Time | Temp (°C) | ||
| Fully packed storage condition | First block | 12 h 55 min | 4.25 °C | 21 h 30 min | 4.1 °C |
| Second block | 15 h 30 min | 4.25 °C | |||
| Batch-filled storage condition (50:50) | First block | 12 h 05 min | 4.25 °C | 18 h 40 min | 4.1 °C |
| Second block | 14 h 35 min | 4.25 °C | |||
| Repositioned air condition unit with batch filling (50:50) | First block | 11 h 10 min | 4.25 °C | 17 h 15 min | 4.1 °C |
| Second block | 11 h 10 min | 4.25 °C | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Min, S.G.; Oyinloye, T.M.; Chung, Y.B.; Yoon, W.B. Optimizing Commercial-Scale Storage for Chinese Cabbage (Brassica rapa L. ssp. Pekinensis): Integrating Morphological Classification, Respiratory Heat Effects, and Computational Fluid Dynamics for Enhanced Cooling Efficiency. Foods 2025, 14, 879. https://doi.org/10.3390/foods14050879
Min SG, Oyinloye TM, Chung YB, Yoon WB. Optimizing Commercial-Scale Storage for Chinese Cabbage (Brassica rapa L. ssp. Pekinensis): Integrating Morphological Classification, Respiratory Heat Effects, and Computational Fluid Dynamics for Enhanced Cooling Efficiency. Foods. 2025; 14(5):879. https://doi.org/10.3390/foods14050879
Chicago/Turabian StyleMin, Sung Gi, Timilehin Martins Oyinloye, Young Bae Chung, and Won Byong Yoon. 2025. "Optimizing Commercial-Scale Storage for Chinese Cabbage (Brassica rapa L. ssp. Pekinensis): Integrating Morphological Classification, Respiratory Heat Effects, and Computational Fluid Dynamics for Enhanced Cooling Efficiency" Foods 14, no. 5: 879. https://doi.org/10.3390/foods14050879
APA StyleMin, S. G., Oyinloye, T. M., Chung, Y. B., & Yoon, W. B. (2025). Optimizing Commercial-Scale Storage for Chinese Cabbage (Brassica rapa L. ssp. Pekinensis): Integrating Morphological Classification, Respiratory Heat Effects, and Computational Fluid Dynamics for Enhanced Cooling Efficiency. Foods, 14(5), 879. https://doi.org/10.3390/foods14050879







