3.1. Dynamic Conditional Correlations between Global and Local Wheat Prices
Figure 1 shows the movement in the logarithmic returns of global and local wheat prices. Both global and local wheat prices volatilize mainly within a range of ±20% during the entire sample period and experienced large price volatility after the 2008 Global Financial Crisis.
Table 3 reports the descriptive statistics and the augmented Dicky–Fuller (ADF) test statistics of wheat price returns. Both the global price and local prices in most importer countries averagely increased from January 2008 to December 2018, except South Korea and Peru. The augmented Dicky–Fuller (ADF) test on global and all local price returns rejects the null hypothesis that there is a unit root at a 1% significant level, showing stationarity at the level.
In addition, we applied the Granger causality test between global and local price returns by country to find the causality with one- or two-period (month) lag. The results in
Table 4 shows that, for most wheat importer countries, there is significant Granger causality from the global price return to local price returns, expressing the large dominant power of the global price on local prices. For Armenia, Brazil, and South Korea, there are significant Granger causalities from local price returns to global returns, showing the local prices of importer countries could even affect the global price. Conversely, for Japan and South Africa, there are no significant Granger causalities.
Regarding the stationarity and Granger causality of sample data, we estimated four types of DCC-GARCH models, as mentioned in the methodology: the DCC-GARCH model, the DCC-GARCH model with autoregressive effect in mean equation (AR-DCC-GARCH), the ADCC-GARCH model, and the ADCC-GARCH model with autoregressive effect in the mean equation (AR-ADCC-GARCH).
Table 5 reports the DCC-GARCH model selection by Bayesian information criterion (BIC). It is notable that, for some model settings, dynamic conditional correlation could not be estimated by the maximum likelihood method, possibly due to the small sample size. After excluding the inestimable model settings (represented by a hyphen in
Table 5), the best model selections for countries were chosen by BIC: DCC-GARCH models for Cameroon, Japan, and Kyrgyzstan; an AR-DCC-GARCH model for South Korea; ADCC-GARCH models for Brazil, Georgia, and South Africa; AR-ADCC-GARCH models for Armenia, Mexico, and Peru.
Table 6 presents the estimation results of the parameter metrics for the DCC models with specifications selected by BIC, which are shown in
Table 5. First, every model specification fits the condition of
λ1 +
λ2 ≤ 1, indicating that the dynamic conditional correlation for all pairs of global and domestic wheat prices is mean reverting (convergent). Second, the coefficient
λ2 is observed to be positive and significant for most model specifications, showing the autoregressive effect that the lagged dynamic conditional correlation significantly affects the current dynamic conditional correlations. Third, the asymmetric coefficients,
δ, are found to be positive, indicating the asymmetric response in the correlation between global and domestic wheat prices, although it is not statistically significant at a 10% significant level for all selected model specifications possibly due to the limitation on data size.
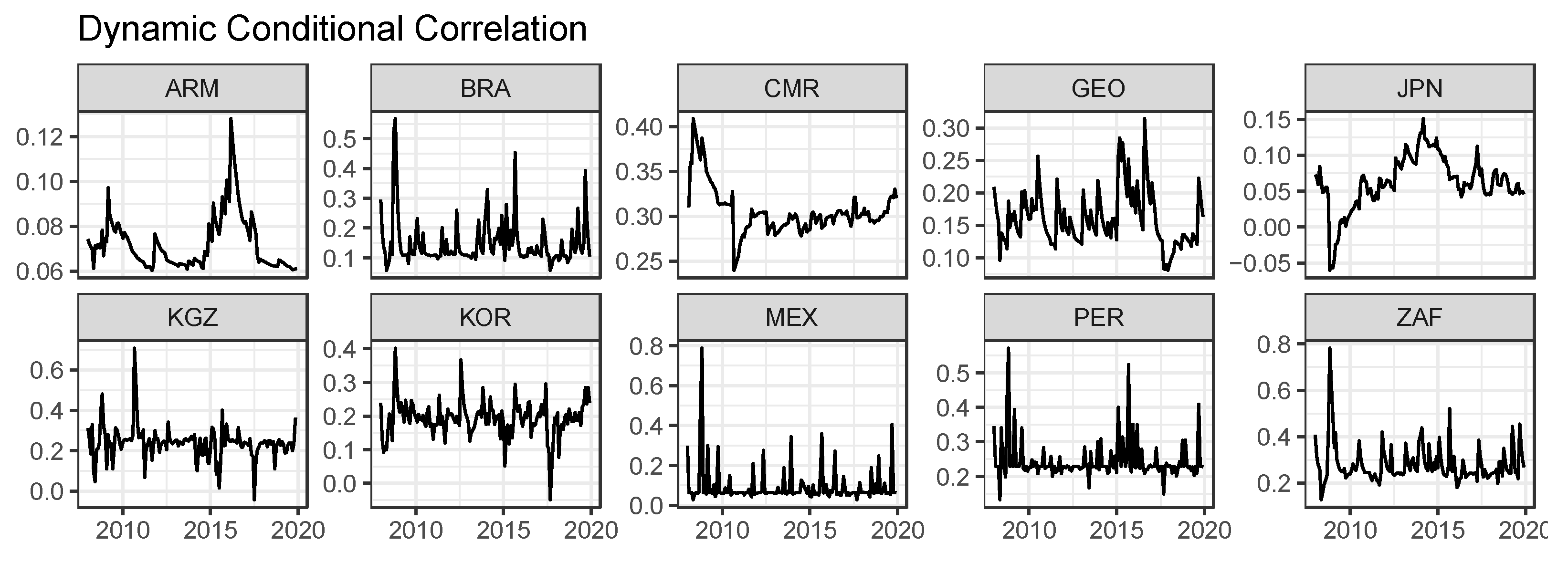
Figure 2 represents the estimated dynamic conditional correlations between global and domestic prices, following the model specifications selected by BIC.
Overall, the movements in dynamic conditional correlations show strong time variability in the sample period and considerable country dependence. For almost the entire sample period, dynamic conditional correlations are positive for sample countries, showing that the high volatility of the global wheat price could lead to an increase in the volatility of local wheat prices. Further, we also found that the dynamic conditional correlations could become negative in a very short time after shocks. For example, the DCC for Japan became negative after the 2008 Global Financial Crisis, showing the different movements between global and local prices. The same scenario also happened in Kyrgyzstan and South Korea after the shock in 2017. Therefore, shocks could affect the conditional correlation between global and local prices, showing the different responses of global and local wheat markets. Finally, we found a significant time trend of the dynamic conditional correlation in some sample countries such as Armenia, Cameroon, and Japan. For example, the DCC in Cameroon experienced a sharp decrease after the 2008 Global Financial Crisis and then stabilized around 0.3 from 2012 to 2018.
Further,
Table 7 indicates the descriptive statistics of monthly DCC between global and local wheat prices. We found that, during the sample period, all country DCCs have positive means, displaying the increasing volatility spillovers between global and local wheat prices in import countries. The ranges of DCCs largely varied depending on the country. For example, the Armenian DCC range was 0.068, while the Mexican DCC range was 0.759, showing the different movements of DCC.
Figure 2 signifies the DCC pairs between the global wheat price and retail wheat flour prices. It is observed that the DCCs for all regions over the sample period never take negative values, except those for Japan in the food crisis (2007–2008) period and Kyrgyzstan and South Korea around 2017. This suggests that greater price volatility in the global market tends to cause larger price volatility in local markets. It is interesting that the dynamic correlations dramatically fluctuate around the 2008 food price surges in most of the nations (Armenia, Brazil, Cameroon, Mexico, South Korea, Peru, and South Africa), while the connectedness largely varies over time and across regions. The mean of the correlations is positive in all regions. Cameroon has the highest average estimate of the DCC (0.306), while Armenia shows the lowest value (0.072).
3.3. Policy Implications
Our results indicate that reducing the foreign dependency on wheat could significantly abate the conveyance of international market shocks to indigenous markets. This partially bolsters the efficacy of the food self-sufficiency policy that gained the attention of food-deficit nations especially after the 2008 food price spikes. For instance, since the Second World War, the food self-sufficiency of Japan on a calorie basis has almost halved to approximately 40%, and the central government has long attempted to push up its food autarky rate by protecting domestic markets from global markets. Because the wheat self-sufficiency in Japan is achieved with around 10% imported from major exporters such as the US, Australia, and Canada, reducing reliance on foreign suppliers could stabilize local prices. After the global commodity boom in 2008, many developing countries suffered the price spikes of bread, a primary diet commodity, and people sparked off food riots [
25]. Egypt, the largest importer of wheat, experienced food riots in 2011 and 2017 [
26,
27], which may have been prevented with the policy measure.
Due to the discovery of cows with bovine spongiform enteropathy in the United States around 2004, Japan’s government restricted beef imports from the country, which caused substitutive behavior with many restaurants replacing beef meals with pork ones immediately after the event. In this context, our analysis uncovered that substitutive grain consumption behavior was not useful for alleviating shocks from external markets. However, the result explains only the short-term impact, and long-term effects may be different. Namely, cereal substitution could occur in the long run, mitigating price volatility transmission from world markets. However, the diversification of food consumption patterns must be beneficial in terms of financial risk management for households. Consumers who have eating habits of just wheat-based products are economically susceptible to wheat price fluctuations, compared with those who consume a variety of grain-based food products. Japan is a good example of diversifying food goods. Before the end of the Second World War, the citizens of Japan depended only on traditional Japanese meals. This was largely changed with the introduction of Western-style foods to school lunches by the General Headquarters of the Supreme Commander of Allied Powers that reigned over the nation. Consequently, the population in the country consumes a wide range of international meals today. Although it would take a long time to actualize food consumption diversity, the policy implementation cost to maintain the eating habits of nationals does not seem to be large once it is realized.
Food security comprises four aspects: “availability”, “access”, “stability”, and “utilization”. From these viewpoints, our results suggest that, assuming that domestic wheat production is boosted by, for instance, a higher import tariff or additional farming subsidy, the reduction of food supply dependency improves “availability”. The resulting lower external supply dependency could improve “stability”. From the perspective of farmers, the reduction of price volatility under the autarky system improves their price forecast, which increases farmers’ expected utility levels.