Exploring the Hjif-Index, an Analogue to the H-Like Index for Journal Impact Factors
Abstract
1. Introduction and Objectives
- (a)
- To calculate a hjif-index defined in a manner similar to the h-index. This indicator was obtained for each JCR group with two versions of the JIF: the usual one calculated with a 2-year window (JIF2), and a newer one calculated with a five-year window (JIF5).
- (b)
- To explore the distribution of JCR groups according to the two hjif-indices calculated here.
- (c)
- To explore the distribution of JCR groups according to the percentage of journals included in the hjif-core (see below).
- (d)
- To compare the behavior of the hjif-indices based on the JIF2 and the JIF5.
2. Method
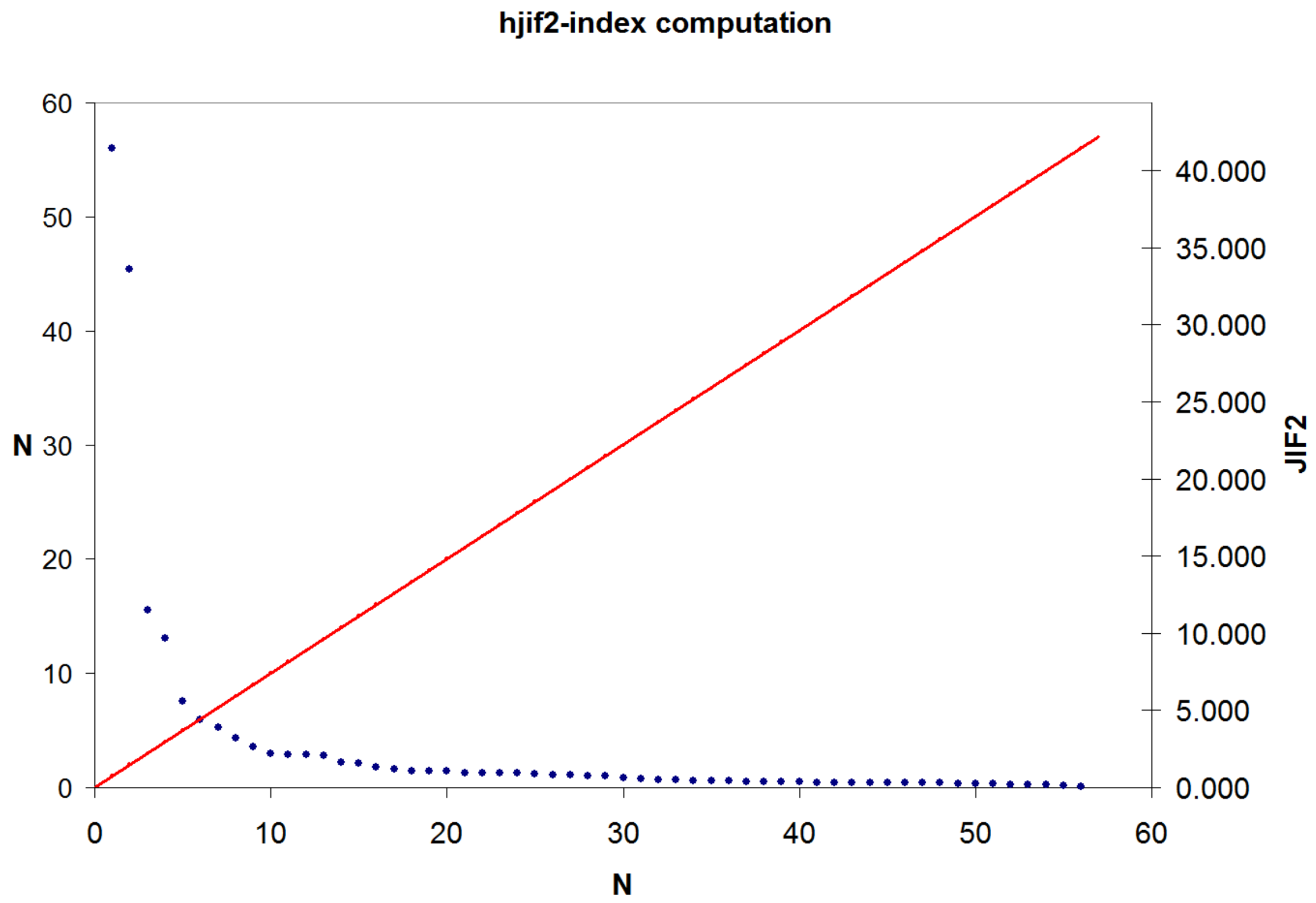
2.1. Calculation of Hjif-Indices and Hjif-Core
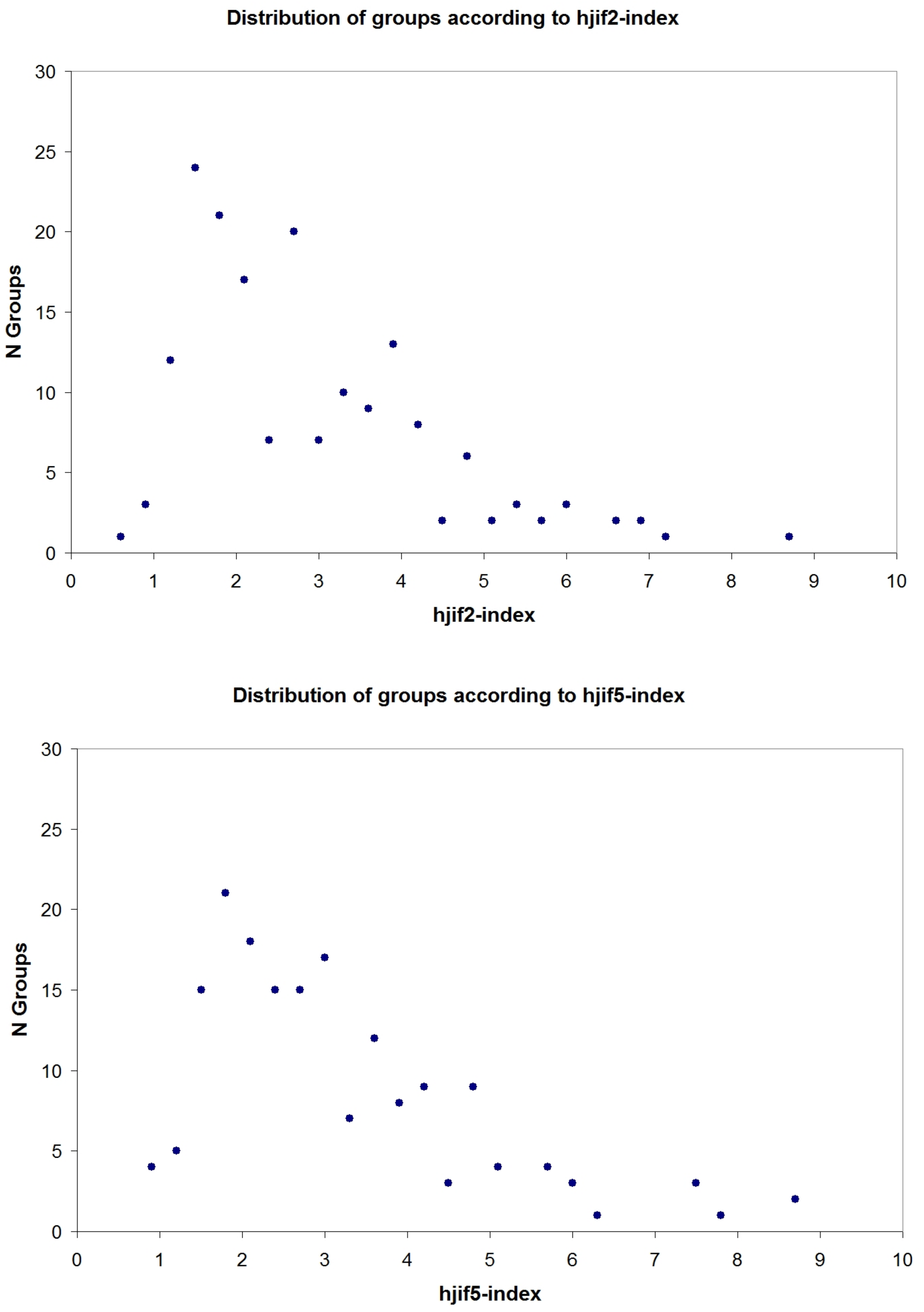
2.2. Distribution of JCR Groups
3. Results and Discussion
3.1. Distribution of JCR Groups According Their Hjif-Index
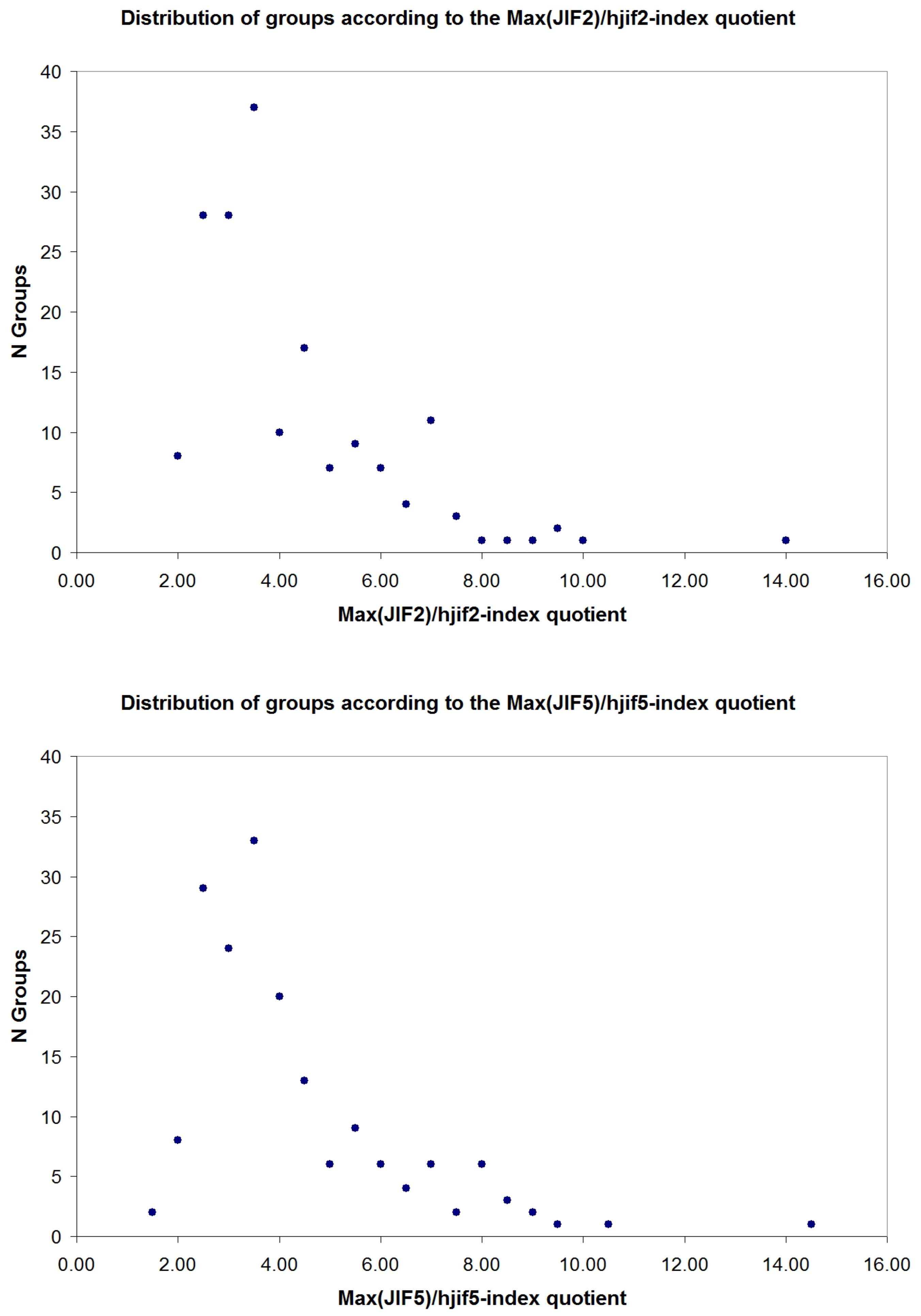
3.2. Quotient Max(JIF)/Hjif-Index
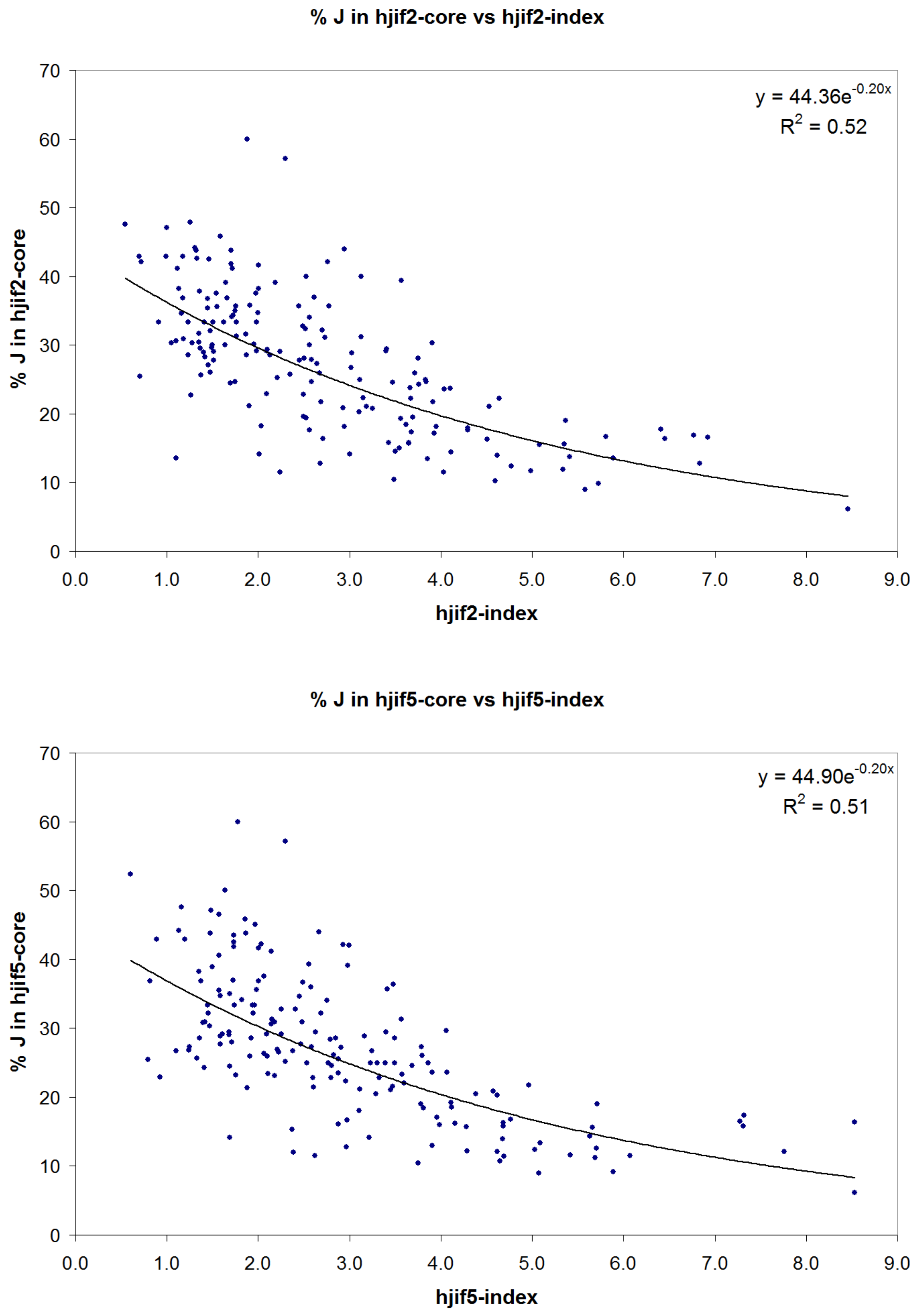
3.3. Relationship between Hjif5-Index and Hjif2-Index
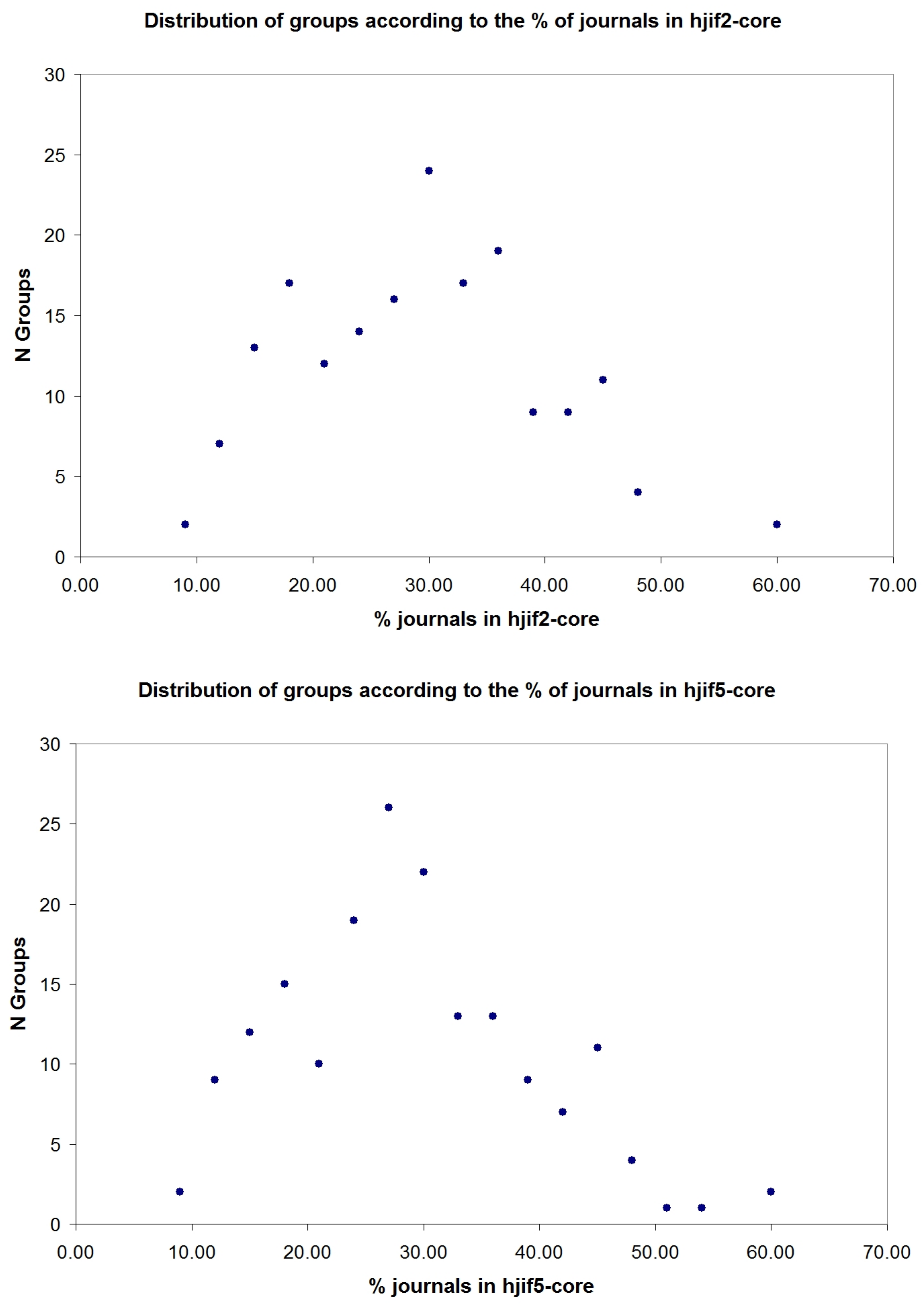
3.4. Distribution of JCR Groups According to the Percentage of Journals in the Hjif-Core
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hirsch, J.E. An Index to quantify an individual’s scientific output. Proc. Natl. Acad. Sci. USA 2005, 102, 16569–16572. [Google Scholar] [CrossRef] [PubMed]
- Braun, T.; Glänzel, W.; Schubert, A. A Hirsch-type index for journals. Scientometrics 2006, 69, 169–173. [Google Scholar] [CrossRef]
- Bar-Ilan, J. The h-index of h-index and of other informetric topics. Scientometrics 2008, 75, 591–605. [Google Scholar] [CrossRef]
- Schubert, A.; Glänzel, W. A systematic analysis of Hirsch-type indices for journals. J. Informetr. 2007, 1, 179–184. [Google Scholar] [CrossRef]
- Bertoli-Barsotti, L.; Lando, T.A. Theoretical model of the relationship between the h-index and other simple citation indicators. Scientometrics 2017, 111, 1415–1448. [Google Scholar] [CrossRef] [PubMed]
- Iglesias, J.E.; Pecharromán, C. Scaling the h-index for different scientific ISI fields. Scientometrics 2007, 73, 303–320. [Google Scholar] [CrossRef]
- Egghe, L. Theory and practice of the g-index. Scientometrics 2006, 69, 131–152. [Google Scholar] [CrossRef]
- Kosmulski, M. A new Hirsch-type index saves time and works equally well as the original h-index. ISSI Newsl. 2006, 2, 4–6. [Google Scholar]
- Franceschini, F.; Galetto, M.; Maisano, D.; Mastrogiacomo, L. The success-index: An alternative approach to the h-index for evaluating an individual's research output. Scientometrics 2011, 92, 621–641. [Google Scholar] [CrossRef]
- Jin, B.H.; Liang, L.M.; Rousseau, R.; Egghe, L. The R- and AR-indices: Complementing the h-index. ISSI Newsl. 2007, 52, 855–863. [Google Scholar] [CrossRef]
- Jin, B.H.; Liang, L.; Rousseau, R.; Egghe, L. The R- and AR-indices: Complementing the h-index. Chin. Sci. Bull. 2007, 52, 855–863. [Google Scholar] [CrossRef]
- Bornmann, L.; Daniel, H.D. The state of h index research. EMBO Rep. 2009, 10, 2–6. [Google Scholar] [CrossRef] [PubMed]
- Alonso, S.; Cabrerizo, F.J.; Herrera-Viedma, E.; Herrera, F. h-Index: A review focused in its variants, computation and standardization for different scientific fields. J. Informetr. 2009, 3, 273–289. [Google Scholar] [CrossRef]
- Panaretos, J.; Malesios, C. Assessing scientific research performance and impact with single indices. Scientometrics 2009, 81, 635–670. [Google Scholar] [CrossRef]
- Egghe, L. The Hirsch index and related impact measures. Annu. Rev. Inf. Sci. Technol. 2010, 44, 65–114. [Google Scholar] [CrossRef]
- Schreiber, M.; Malesios, C.C.; Psarakis, S. Exploratory factor analysis for the Hirsch index, 17 h-type variants, and some traditional bibliometric indicators. J. Informetr. 2012, 6, 347–358. [Google Scholar] [CrossRef]
- Ye, F.; Rousseau, R. Probing the h-core: An investigation of the tail–core ratio for rank distributions. Scientometrics 2009, 84, 431–439. [Google Scholar] [CrossRef]
- Rousseau, R. Simple Models and the Corresponding h- and g-Index. Available online: https://doclib.uhasselt.be/dspace/bitstream/1942/944/1/Rousseau%20Dalian.pdf (accessed on 3 April 2018).
- Mahbuba, D.; Rousseau, R. Year-based h-type indicators. Scientometrics 2013, 96, 785–797. [Google Scholar] [CrossRef]
- Ruane, F.; Tol, R. Rational (successive) h-indices: An application to economics in the Republic of Ireland. Scientometrics 2008, 75, 395–405. [Google Scholar] [CrossRef]
- Guns, R.; Rousseau, R. Real and rational variants of the h-index and the g-index. J. Informetr. 2009, 3, 64–71. [Google Scholar] [CrossRef]
- Glänzel, W.; Moed, H.F. Journal impact measures in bibliometric research. Scientometrics 2002, 53, 171–193. [Google Scholar] [CrossRef]
- Bensman, S.J. Garfield and the impact factor. Annu. Rev. Inf. Sci. Technol. 2007, 41, 93–155. [Google Scholar] [CrossRef]
- Waltman, L. A review of the literature on citation impact indicators. J. Informetr. 2016, 10, 365–391. [Google Scholar] [CrossRef]
- Bornmann, L.; Marx, W. The journal impact factor and alternative metrics. EMBO Rep. 2016, 17, 1094–1097. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.H.; Li, X.; Sun, X.; Wan, J. Detecting impact factor manipulation with data mining techniques. Scientometrics 2016, 109, 1989–2005. [Google Scholar] [CrossRef]
- Archambault, E.; Larivière, V. History of the journal impact factor: Contingencies and consequences. Scientometrics 2009, 79, 635–649. [Google Scholar] [CrossRef]
- Yang, Z.G.; Zhang, C.T. A proposal for a novel impact factor as an alternative to the JCR impact factor. Sci. Rep. 2013, 3. [Google Scholar] [CrossRef] [PubMed]
- Egghe, L.; Liang, L.; Rousseau, R. A relation between h-index and impact factor in the power-law model. J. Am. Soc. Inf. Sci. Technol. 2009, 60, 2362–2365. [Google Scholar] [CrossRef]
- Boell, S.; Wilson, C. Journal impact factors for evaluating scientific performance: Use of h-like indicators. Scientometrics 2010, 82, 613–626. [Google Scholar] [CrossRef][Green Version]
- Van Eck, N.J.; Waltman, L. Generalizing the h-and g-indices. J. Informetr. 2008, 2, 263–271. [Google Scholar] [CrossRef]
- Rousseau, R.; García-Zorita, C.; Sanz-Casado, E. The h-bubble. J. Informetr. 2013, 7, 294–300. [Google Scholar] [CrossRef]
- Barnes, C.S. The construct validity of the h-index. J. Doc. 2016, 72, 878–895. [Google Scholar] [CrossRef]
- Bornmann, L. h-index research in scientometrics: A summary. J. Informetr. 2014, 8, 749–750. [Google Scholar] [CrossRef]
- Campanario, J.M. Empirical study of journal impact factors obtained using the classical two-year citation window versus a five-year citation window. Scientometrics 2011, 87, 189–204. [Google Scholar] [CrossRef]
| 1 | We are indebted to an anonymous referee for this definition. |
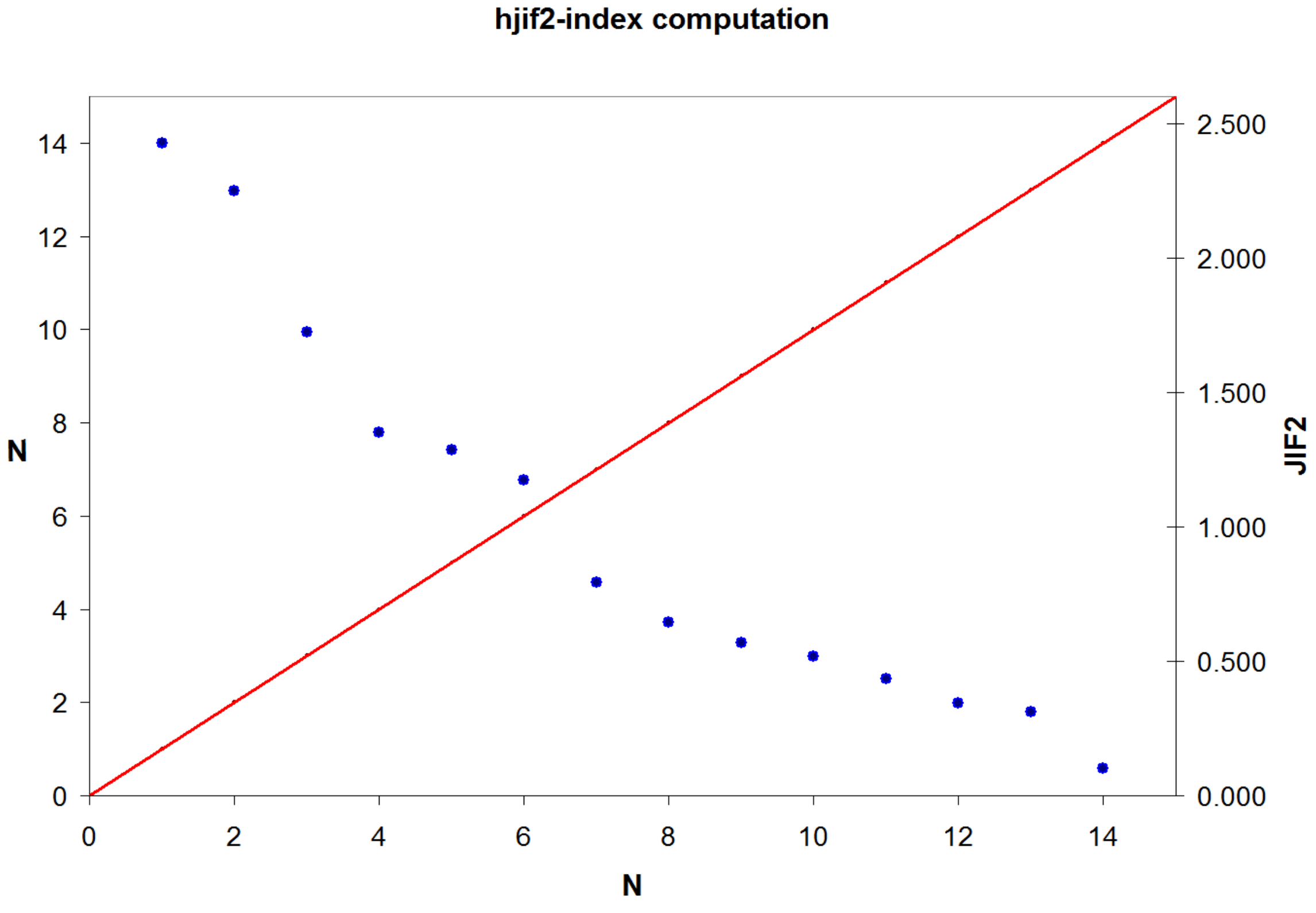
| Journal | JIF | N | Difference from the hjif2-Index | H-Core |
|---|---|---|---|---|
| COAST ENG | 2.428 | 1 | 1.253 | Yes |
| COAST ENG J | 2.250 | 2 | 1.075 | Yes |
| J ATMOS OCEAN TECH | 1.725 | 3 | 0.550 | Yes |
| OCEAN ENG | 1.351 | 4 | 0.176 | Yes |
| APPL OCEAN RES | 1.287 | 5 | 0.112 | Yes |
| IEEE J OCEANIC ENG | 1.175 | 6 | 0.000 | Yes |
| J WATERW PORT COAST | 0.792 | 7 | −0.383 | |
| MAR GEORESOUR GEOTEC | 0.644 | 8 | −0.531 | |
| J OFFSHORE MECH ARCT | 0.570 | 9 | −0.605 | |
| INT J OFFSHORE POLAR | 0.517 | 10 | −0.658 | |
| MAR TECHNOL SOC J | 0.434 | 11 | −0.741 | |
| CHINA OCEAN ENG | 0.344 | 12 | −0.831 | |
| P I CIVIL ENG-MAR EN | 0.312 | 13 | −0.863 | |
| SEA TECHNOL | 0.101 | 14 | −1.074 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cabos, W.; Campanario, J.M. Exploring the Hjif-Index, an Analogue to the H-Like Index for Journal Impact Factors. Publications 2018, 6, 14. https://doi.org/10.3390/publications6020014
Cabos W, Campanario JM. Exploring the Hjif-Index, an Analogue to the H-Like Index for Journal Impact Factors. Publications. 2018; 6(2):14. https://doi.org/10.3390/publications6020014
Chicago/Turabian StyleCabos, William, and Juan Miguel Campanario. 2018. "Exploring the Hjif-Index, an Analogue to the H-Like Index for Journal Impact Factors" Publications 6, no. 2: 14. https://doi.org/10.3390/publications6020014
APA StyleCabos, W., & Campanario, J. M. (2018). Exploring the Hjif-Index, an Analogue to the H-Like Index for Journal Impact Factors. Publications, 6(2), 14. https://doi.org/10.3390/publications6020014






