Measuring Time-Dynamics and Time-Stability of Journal Rankings in Mathematics and Physics by Means of Fractional p-Variations
Abstract
1. Introduction
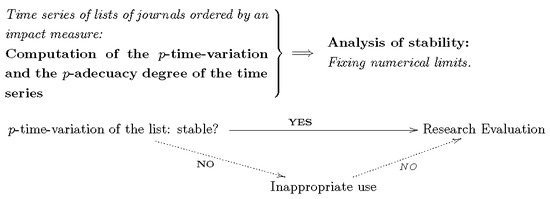
1.1. Measuring Stability of Journal Rankings
1.2. A Specific Model for Ensuring the Plausibility of Journal Rankings
- (1)
- The prestige of a given journal for a scientific community is supposed to be relatively stable. At least, it must change following a long-term pattern.
- (2)
- The position of a journal in a prestige-based list may increase or decrease over a long period, but a great amount of fluctuations in it must be understood as an anomalous behavior.
- (3)
- Consequently, a lot of significant changes in the position of a journal in a list is not a plausible behavior. Such a fact must not be interpreted as a fail in the policy of the journal, but in the measuring tool.
- (4)
- We obtain the following conclusion: an ordered impact list having an excessive rate of fluctuations in the positions of the journals must not be used as a proxy for the prestige of the journals in which the papers are published.
2. Materials and Methods
2.1. p-Variations of Ordered Lists: Definition and Fundamental Properties
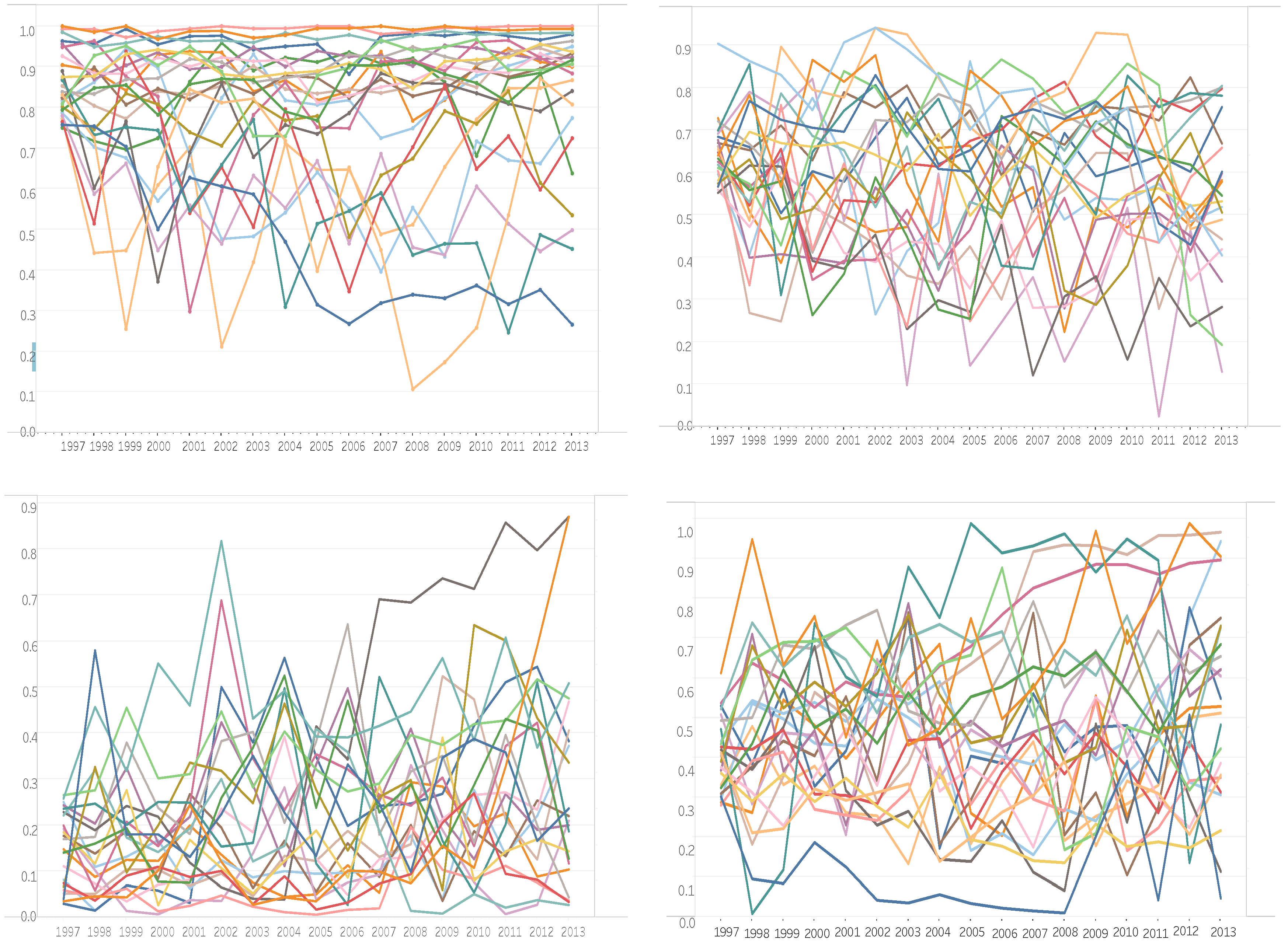
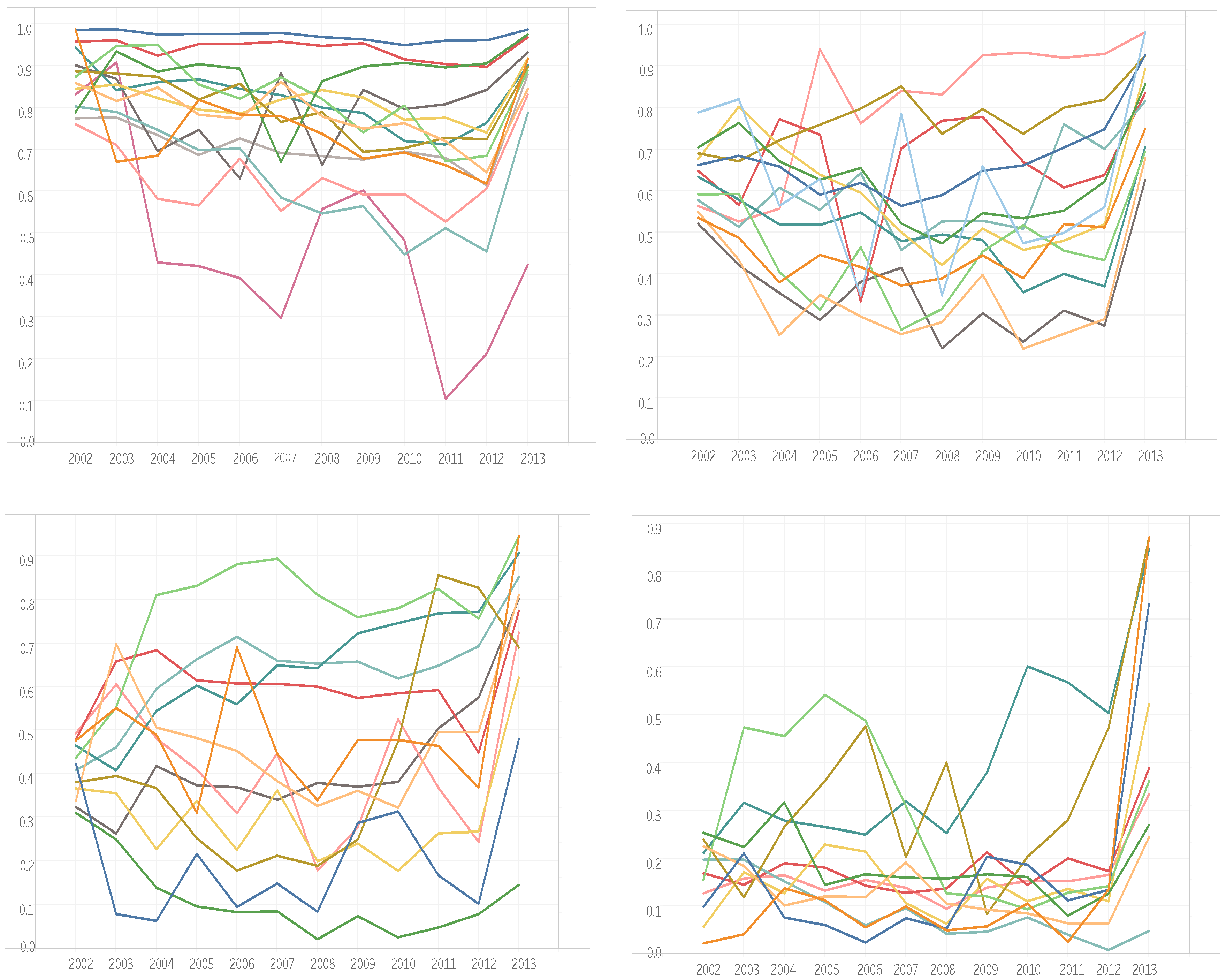
2.2. The Test Example: Eleven-Year Series in Mathematics and Applied Physics
3. Results
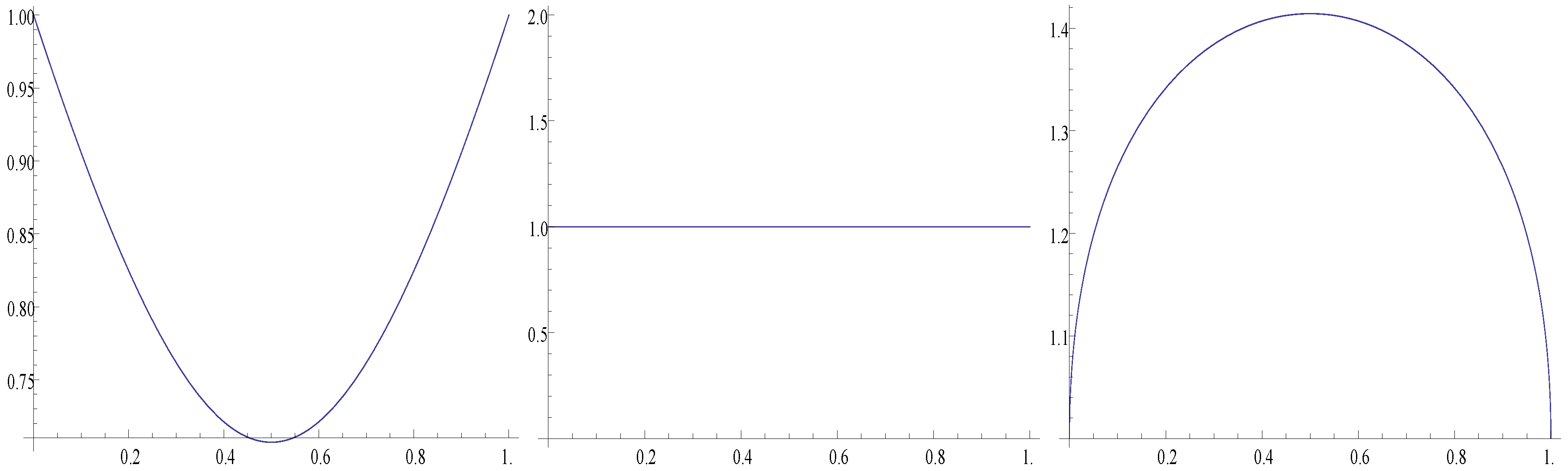
3.1. The p-Fractional p-Variation and the p-Adequacy Degree of a Time Series
- (a)
- Suppose that Candidate 1 has published three papers in journals that are in the first quartile and one in the fourth, and Candidate 2 has published six in the second quartile. The marks that they get are 13 (Candidate 1) and 12 (Candidate 2), and so the institute will contract Candidate 1. However, using the probabilistic interpretation that we give to the index, we know that the lowest value that Candidate 1 should get is , and the upper value for Candidate 2 should be . Consequently, the institute cannot distinguish among both candidates using this system, and must find another procedure.
- (b)
- Consider now a different situation. Suppose that Candidate 1 has published six papers in journals that appear in the fourth quartile. The evaluation system gives . The value of indicates that two of the six papers should be in the third quartile, and so the biggest mark obtained with the evaluation system should be
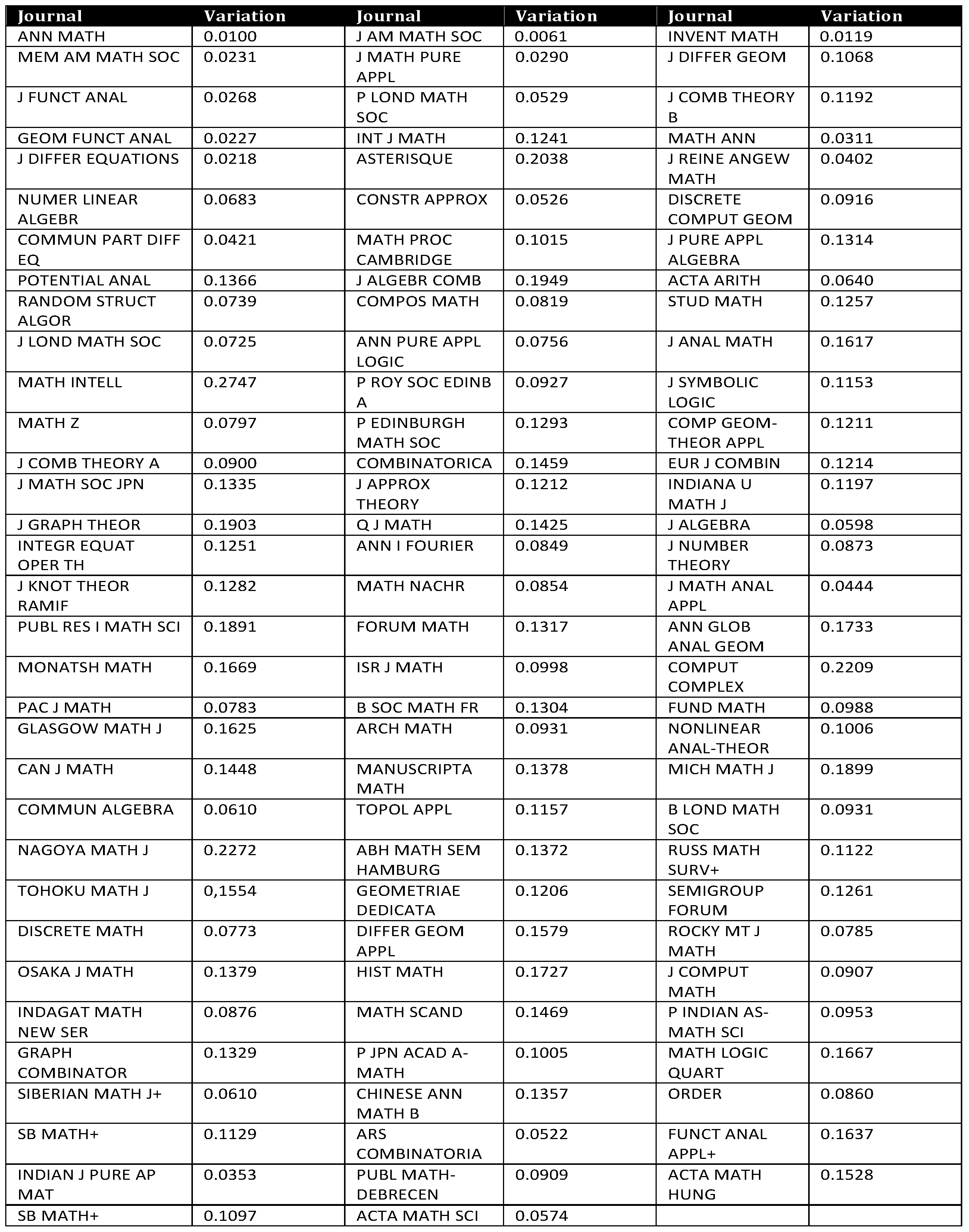
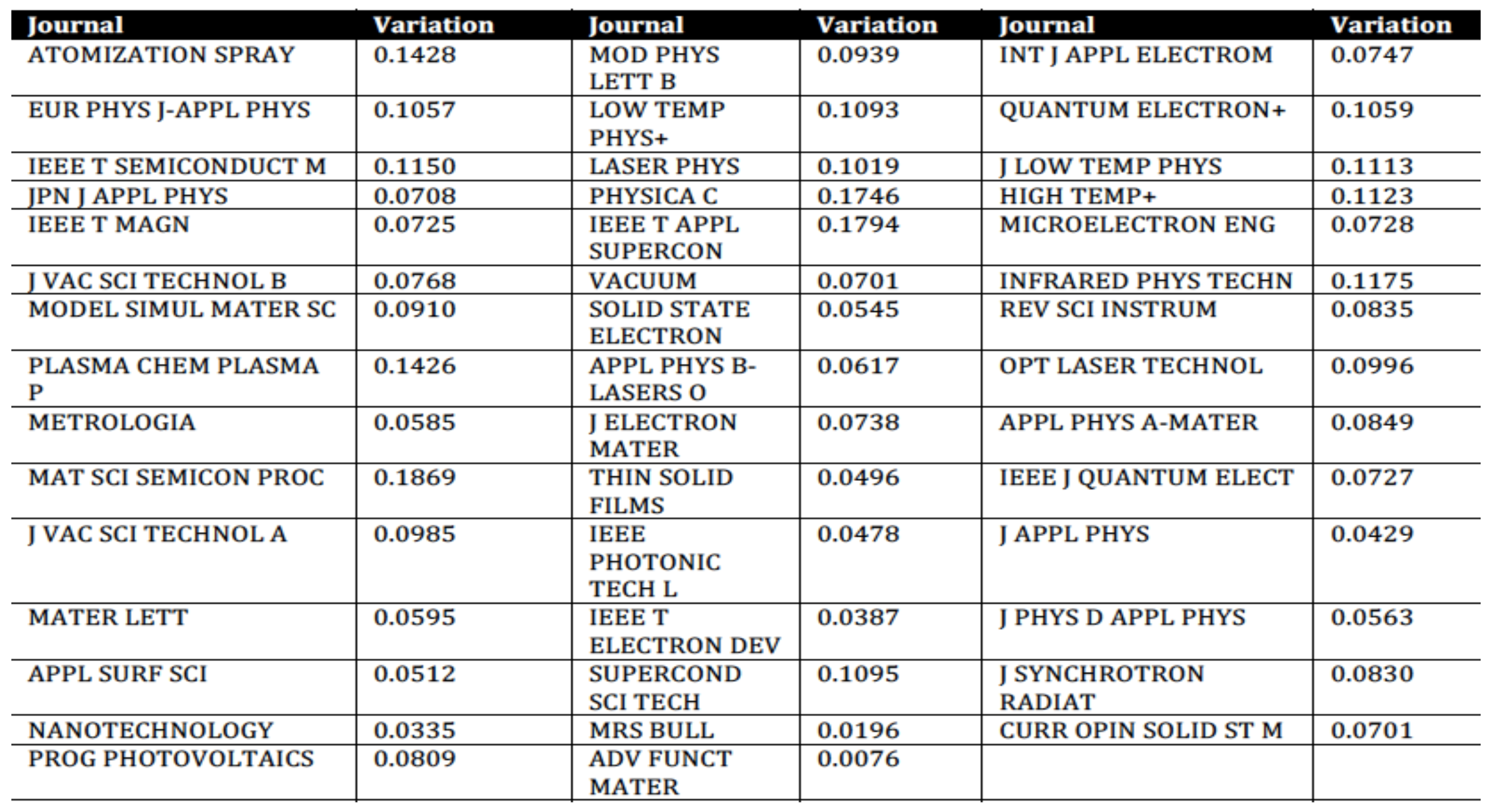
3.2. Time Series of Impact Factor Lists of Mathematics and Applied Physics
4. Discussion
- Using the complete list, we obtain
- If the 20 top journals are removed from the list, we get
- If the 30 top journals are removed, then
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kulczycki, E. Assessing publications through a bibliometric indicator: The case of comprehensive evaluation of scientific units in Poland. Res. Eval. 2017, 26, 41–52. [Google Scholar] [CrossRef]
- Kulczycki, E.; Rozkosz, E.A. Does an expert-based evaluation allow us to go beyond the Impact Factor? Experiences from building a ranking of national journals in Poland. Scientometrics 2017, 111, 417–442. [Google Scholar] [CrossRef] [PubMed]
- Garfield, E. Citation analysis as a tool in journal evaluation. Science 1972, 178, 471–479. [Google Scholar] [CrossRef] [PubMed]
- Garfield, E. The evolution of the Science Citation Index. Int. Microbiol. 2007, 10, 65–69. [Google Scholar] [PubMed]
- King, J. A review of bibliometric and other science indicators and their role in research evaluation. J. Inf. Sci. 1987, 13, 261–276. [Google Scholar] [CrossRef]
- Bordons, M.; Fernández, M.T.; Gómez, I. Advantages and limitations in the use of impact factor measures for the assessment of research performance. Scientometrics 2002, 53, 195–206. [Google Scholar] [CrossRef]
- Moed, H.F. Citation Analysis in Research Evaluation; Springer: Dordrecht, The Netherlands, 2005. [Google Scholar]
- Garfield, E. The History and Meaning of the Journal Impact Factor. J. Am. Med. Assoc. 2006, 293, 90–93. [Google Scholar] [CrossRef] [PubMed]
- Aleixandre-Benavent, R.; Valderrama Zurián, J.C.; González Alcaide, G. Scientific journals impact factor: Limitations and alternative indicators. Prof. Inf. 2007, 16, 4–11. [Google Scholar]
- Archambault, E.; Lariviére, V. History of the journal impact factor: Contingencies and consequences. Scientometrics 2009, 79, 635–649. [Google Scholar] [CrossRef]
- Arnold, D.N.; Fowler, K.K. Nefarious Numbers. Not. AMS 2011, 58, 434–437. [Google Scholar]
- Hecht, F.; Hecht, B.K.; Sandberg, A.A. The journal “impact factor”: A misnamed, misleading, misused measure. Cancer Genet. Cytogenet. 1998, 104, 77–81. [Google Scholar] [CrossRef]
- Rey-Rocha, J.; Martín-Sempere, M.J.; Martínez-Frías, J.; López-Vera, F. Some Misuses of Journal Impact Factor in Research Evaluation. Cortex 2001, 37, 595–597. [Google Scholar] [CrossRef]
- Seglen, P.O. How representative is the journal impact factor. Res. Eval. 1992, 2, 143–149. [Google Scholar] [CrossRef]
- Seglen, P.O. Why the impact factor of journals should not be used for evaluating research. Br. J. Med. 1997, 314, 498–502. [Google Scholar] [CrossRef]
- Van Leeuwen, T.N.; Moed, H.F. Development and application of journal impact measures in the Dutch science system. Scientometrics 2002, 53, 249–266. [Google Scholar] [CrossRef]
- Van Leeuwen, T. Discussing some basic critique on Journal Impact Factors: Revision of earlier comment. Scientometrics 2012, 92, 443–455. [Google Scholar] [CrossRef] [PubMed]
- Ferrer-Sapena, A.; Sánchez-Pérez, E.A.; González, L.M.; Peset, F.; Aleixandre-Benavent, R. The impact factor as a measuring tool of the prestige of the journals in research assessment in mathematics. Res. Eval. 2016, 25, 306–314. [Google Scholar] [CrossRef]
- IMU-Joint Committee on Quantitative Assessment of Research. Citation Statistics: A Report From the International Mathematical Union (IMU) in Cooperation With the International Council of Industrial and Applied Mathematics (ICIAM) and the Institute of Mathematical Statistics (IMS); International Mathematical Union: Berlin, Germany, 2008. [Google Scholar]
- San Francisco Declaration on Research Assessment (DORA). Available online: http://www.ascb.org/dora/ (accessed on 19 September 2017).
- Wilsdon, J.; Allen, L.; Belfiore, E.; Johnson, B. The Metric Tide: Report of the Independent Review of the Role of Metrics in Research Assessment and Management. Tech. Rep. 2015, 111. [Google Scholar] [CrossRef]
- Hicks, D.; Wouters, P.; Waltman, L.; de Rijcke, S.; Rafols, I. The Leiden Manifesto for research metrics. Nature 2015, 520, 429–431. [Google Scholar] [CrossRef] [PubMed]
- Sivertsen, G. Unique, but still best practice? The Research Excellence Framework (REF) from an international perspective. Palgrave Commun. 2017, 3. [Google Scholar] [CrossRef]
- Pajić, D. On the stability of citation-based journal rankings. J. Informetr. 2015, 9, 990–1006. [Google Scholar] [CrossRef]
- Yu, D.; Wang, W.; Zhang, S.; Zhang, W.; Liu, R. A multiple-link, mutually reinforced journal-ranking model to measure the prestige of journals. Scientometrics 2017, 111, 521–542. [Google Scholar] [CrossRef]
- Anderson, D.L.; Tressler, J. Researcher rank stability across alternative output measurement schemes in the context of a time limited research evaluation: The New Zealand case. Appl. Econ. 2017, 1–12. [Google Scholar] [CrossRef]
- Xu, H.; Martin, E.; Mahidadia, A. Contents and time sensitive document ranking of scientific literature. J. Informetr. 2014, 8, 546–561. [Google Scholar] [CrossRef]
- Fiala, D. Time-aware PageRank for bibliographic networks. J. Informetr. 2012, 6, 370–388. [Google Scholar] [CrossRef]
- Pudovkin, A.I.; Garfield, E. Rank-normalized impact factor: Away compare journal performance across subject categories. In Proceedings of the 67th Annual Meeting of the American Society for Information Science and Technology, Providence, RI, USA, 12–17 November 2004; Volume 41, pp. 507–515. [Google Scholar]
- Mansilla, R.; Köppen, E.; Cocho, G.; Miramontes, P. On the behavior of journal impact factor rank-order distribution. J. Informetr. 2007, 1, 155–160. [Google Scholar] [CrossRef]
- Moussa, S.; Touzani, M. Ranking marketing journals using the Google Scholar-based hg-index. J. Informetr. 2010, 4, 107–117. [Google Scholar] [CrossRef]
- Sicilia, M.A.; Sánchez-Alonso, S.; García-Barriocanal, E. Comparing impact factors from two different citation databases: The Case of Computer Science. J. Informetr. 2011, 5, 698–704. [Google Scholar] [CrossRef]
- Ferrer-Sapena, A.; Sánchez-Pérez, E.A.; González, L.M.; Peset, F.; Aleixandre-Benavent, R. Mathematical properties of weighted impact factors based on measures of prestige of the citing journals. Scientometrics 2015, 105, 2089–2108. [Google Scholar] [CrossRef]
- Serenko, A.; Dohan, M. Comparing the expert survey and citation impact journal ranking methods: Example from the field of Artificial Intelligence. J. Informetr. 2011, 5, 629–648. [Google Scholar] [CrossRef]
- Haghdoost, A.; Zare, M.; Bazrafshan, A. How variable are the journal impact measures? Online Inf. Rev. 2014, 38, 723–737. [Google Scholar] [CrossRef]
- Althouse, B.M.; West, J.D.; Bergstrom, C.T.; Bergstrom, T. Differences in impact factor across fields and over time. J. Assoc. Inf. Sci. Technol. 2009, 60, 27–34. [Google Scholar] [CrossRef]
- Aguillo, I. Increasing the between-year stability of the impact factor in the Science Citation Index. Scientometrics 1996, 35, 279–282. [Google Scholar] [CrossRef]
- Nieuwenhuysen, P.; Rousseau, R. A quick and easy method to estimate the random effect on citation measures. Scientometrics 1988, 13, 45–52. [Google Scholar] [CrossRef]
- Black, S. How much do core journals change over a decade? Libr. Resour. Tech. Serv. 2012, 56, 80–93. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferrer-Sapena, A.; Díaz-Novillo, S.; Sánchez-Pérez, E.A. Measuring Time-Dynamics and Time-Stability of Journal Rankings in Mathematics and Physics by Means of Fractional p-Variations. Publications 2017, 5, 21. https://doi.org/10.3390/publications5030021
Ferrer-Sapena A, Díaz-Novillo S, Sánchez-Pérez EA. Measuring Time-Dynamics and Time-Stability of Journal Rankings in Mathematics and Physics by Means of Fractional p-Variations. Publications. 2017; 5(3):21. https://doi.org/10.3390/publications5030021
Chicago/Turabian StyleFerrer-Sapena, Antonia, Susana Díaz-Novillo, and Enrique A. Sánchez-Pérez. 2017. "Measuring Time-Dynamics and Time-Stability of Journal Rankings in Mathematics and Physics by Means of Fractional p-Variations" Publications 5, no. 3: 21. https://doi.org/10.3390/publications5030021
APA StyleFerrer-Sapena, A., Díaz-Novillo, S., & Sánchez-Pérez, E. A. (2017). Measuring Time-Dynamics and Time-Stability of Journal Rankings in Mathematics and Physics by Means of Fractional p-Variations. Publications, 5(3), 21. https://doi.org/10.3390/publications5030021