Coping with the Inequity and Inefficiency of the H-Index: A Cross-Disciplinary Empirical Analysis

Abstract

This paper measures two main inefficiency features (many publications other than articles; many co-authors’ reciprocal citations) and two main inequity features (more co-authors in some disciplines; more citations for authors with more experience). It constructs a representative dataset based on a cross-disciplinary balanced sample (10,000 authors with at least one publication indexed in Scopus from 2006 to 2015). It estimates to what extent four additional improvements of the H-index as top-down regulations (∆H_h = H_h − H_h+1 from H₁ = based on publications to H₅ = net per-capita per-year based on articles) account for inefficiency and inequity across twenty-five disciplines and four subjects. Linear regressions and ANOVA results show that the single improvements of the H-index considerably and decreasingly explain the inefficiency and inequity features but make these vaguely comparable across disciplines and subjects, while the overall improvement of the H-index (H₁–H₅) marginally explains these features but make disciplines and subjects clearly comparable, to a greater extent across subjects than disciplines. Fitting a Gamma distribution to H₅ for each discipline and subject by maximum likelihood shows that the estimated probability densities and the percentages of authors characterised by H₅ ≥ 1 to H₅ ≥ 3 are different across disciplines but similar across subjects.

1. Introduction

To the best of our knowledge, few papers (e.g., [1,2]) suggest an index to evaluate interdisciplinary CVs (i.e., authors applying usual methodologies to unusual topics or vice versa). In particular, Zagonari [1] identifies the interdisciplinary percentage of any CV (i.e., articles in a discipline or subject quoted by articles in different disciplines or subjects) to be applied to the H-index characterising each author, where the H-index is chosen as an easily generated quantitative index. However, this interdisciplinary index requires a homogeneous H-index across disciplines or subjects to avoid gains for some interdisciplinary scientists (e.g., across medicine and computing) and losses for other interdisciplinary scientists (e.g., across art and mathematics) [3].

Within the huge theoretical and empirical literature on variants and extensions of the H-index (e.g., a-index, ar-index, m-quotient, raw h-rate, contemporary h-index, f-index, t-index, wu-index, maxpord index, q²-index within variants, and hw-index, hm-index, hi-index, hc-index, m-quotient, ht-index, fraction count on citation, fraction count on paper, age-based h-index) [4,5,6], some papers suggest some improvements of the H-index to increase homogeneity across disciplines (e.g., [7,8,9,10]). In particular, Zagonari [9] develops an empirically validated theoretical model of a researcher’s publication goal by providing two internal criteria (i.e., efficiency and equity) to evaluate a bibliometric index (i.e., it grounds these concepts on an analytical model representing the researchers’ incentives to maximise their H-index) and by suggesting two standardisations (i.e., calculate publications per author and citations per author per year) and two guidelines (i.e., neglect co-authors’ reciprocal citations and publications other than peer-reviewed articles) to predict which standardisations and guidelines are most likely to succeed in achieving efficiency and equity across disciplines. The following relationships between improvements, criteria, standardisations, and guidelines are identified:

• Inefficiency (i.e., biased incentives to the research activity in terms of scientific achievements) is managed by focusing on articles instead of publications (i.e., publications include non-peer reviewed research) (Inefficiency a, Ifa hereafter) and by using net instead of gross citations (i.e., gross citations include co-authors’ reciprocal citations) (Inefficiency b, Ifb hereafter). In terms of H-index improvements, ∆H₁ = H₁ − H₂ deals with the overvaluation of possibly non-original research such as reviews, proceedings, and editorials, where H₁ = H-index based on publications and H₂ = H-index based on articles; ∆H₂ = H₂ − H₃ deals with the overemphasis put on co-authors’ reciprocal citations as a measure of actual knowledge diffusion, where H₃ = H-index based on net citations for articles.
• Inequity (i.e., biased rankings in favour of some authors and some disciplines) is managed by using a per-capita H-index to account for the different co-authorship practices prevailing in different disciplines (i.e., more co-authors in some disciplines) (Inequity a, Iqa hereafter) and by using a per-year H-index to account for the different citation periods related to authors with more scientific experience (i.e., they can rely on a longer citation period) (Inequity b, Iqb hereafter). In terms of H-index improvements, ∆H₃ = H₃ − H₄ deals with the huge differences in the number of co-authors and thus in the number of articles in favour of some disciplines, where H₄ = net per-capita H-index based on articles; ∆H₄ = H₄ − H₅ deals with the obviously large number of citations received by researchers with more experience and thus the likely worse assessment of the scientific production in disfavour of researchers with less experience, where H₅ = net per-capita per-year H-index based on articles.

Note that all acronyms and variables are described in

Table 1. Description of acronyms and variables.

Acronyms	Description
Ifa	Inefficiency a
Ifb	Inefficiency b
Iqa	Inequity a
Iqb	Inequity b
Variables
Npub	Number of publications
Nart	Number of articles
Ngro	Number of citations including co-author’s citations
Nnet	Number of citations excluding co-author’s citations
Naut	Mean number of co-authors
H1	H-index based on publications
H2	H-index based on articles
H3	H-index based on net citations per article
H4	Net per-capita H-index based on articles
H5	Net per-capita per-year H-index based on articles
∆Hh = Hh − Hh+1	H-index improvement, h = 1, 2, 3, 4, 5
Dj	Dummy variable for discipline j (j = 1,…, 27) (i.e., Dj takes value 1 for a discipline j and 0 for disciplines other than j)
Sk	Dummy variable for subject k (k = 1, 2, 3, 4) (i.e., Sk takes value 1 for a subject k and 0 for subjects other than k)
Aaut	Dummy variable for age (Aaut = 1 if author’s first publication is after 2009, otherwise Aaut = 0)

. Zagonari [9] is focused on the degree of efficiency and equity rather than on the homogeneity across disciplines which can be achieved by the suggested standardisations and guidelines, and a theoretical approach is adopted (although the structural model is validated in terms of means and variances) rather than a statistical approach (where reduced models are tested in terms of residuals and distributions). Note that Ifa favours authors who minimise efforts and risks related to a collaborative and creative scientific activity by relying on the large number of citations to reviews. Ifb favours authors who spend efforts on networking at no risk rather than on a creative scientific activity. Iqa favours authors who reduce efforts and risks (i.e., they misuse the prevailing measurement of scientific activity based on the principle “one article with n co-authors is n articles”), by spending efforts on networking rather than on a creative scientific activity. Iqb favours authors who minimise efforts at no risk (i.e., they misuse the prevailing measurement of scientific activity based on the principle “the overall sum of citations matters”) by spending efforts on networking rather than on a creative scientific activity.

Within the recent empirical literature on indexes for interdisciplinary science (e.g., [11]), the purpose of this paper is to statistically test to what extent the suggested improvements of the H-indexes [9], considered as top-down regulations, account for different publication and citation habits characterising different disciplines and subjects in order to enable suitable comparisons of interdisciplinary scientists [1] across disciplines and subjects. To do so, we suggest some measures of inefficiency and inequity in Section 2. We construct a representative sample in Section 3. We provide results for each single H-index improvement ∆H_h based on linear regressions and analysis of variance (ANOVA) in Section 4.1 as well as results for H₅ based on maximum likelihood fittings and quantile analysis in Section 4.2 by introducing the assumption that the observed H₅ values for both disciplines and subjects are realisations of a gamma distribution. This is followed by a discussion of findings, weaknesses, and strengths in Section 5, before conclusions and final remarks about methodological and practical potentials in Section 6.

Note that the use of H-index improvements suggested by Zagonari [9] instead of other developments will be justified in Section 5. Moreover, our observation unit will be each author (A_i), rather than journals (e.g., [12]) or institutions (e.g., [13]), since our goal is the evaluation of interdisciplinary scientists. Finally, the use of H-index improvements as policies suggested by Zagonari [9] will be justified in Section 6.

In other words, the research questions of the present study can be summarised as follows:

• Does each single H-index improvement ∆H_h properly solve inefficiency and inequity issues?
• Does each single H-index improvement ∆H_h spread inefficiency and inequity issues uniformly across disciplines D_j and subjects S_k?
• Can any discipline D_j and subject S_k be distinguished from other disciplines and subjects, respectively, net of ∆H_h?
• Does the comprehensive H-index improvement H₁–H₅ properly solve inefficiency and inequity issues?
• Does the comprehensive H-index improvement H₁–H₅ spread inefficiency and inequity issues uniformly across disciplines D_j and subjects S_k?
• Can any discipline D_j and subject S_k be distinguished from other disciplines and subjects, respectively, net of H₁–H₅?
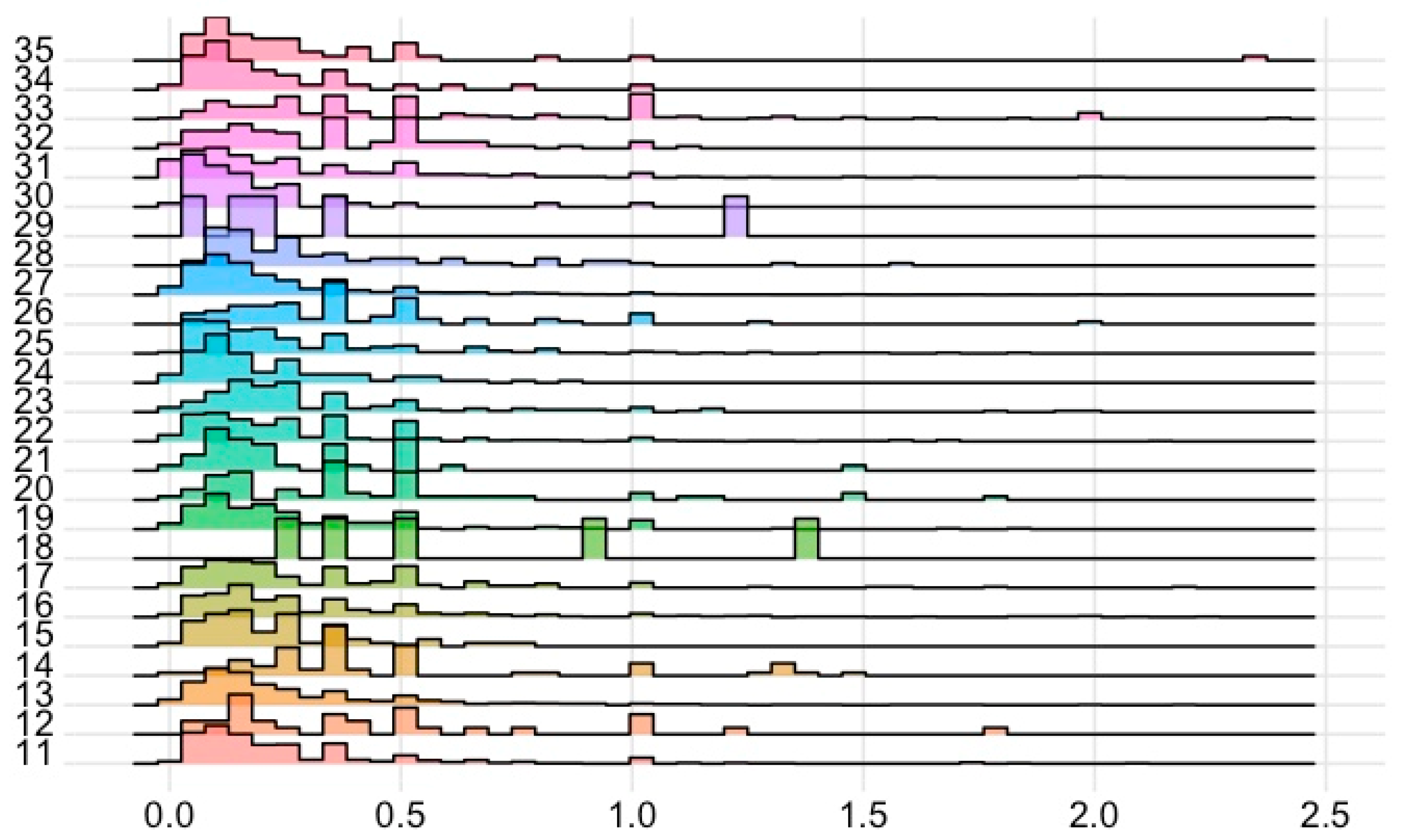
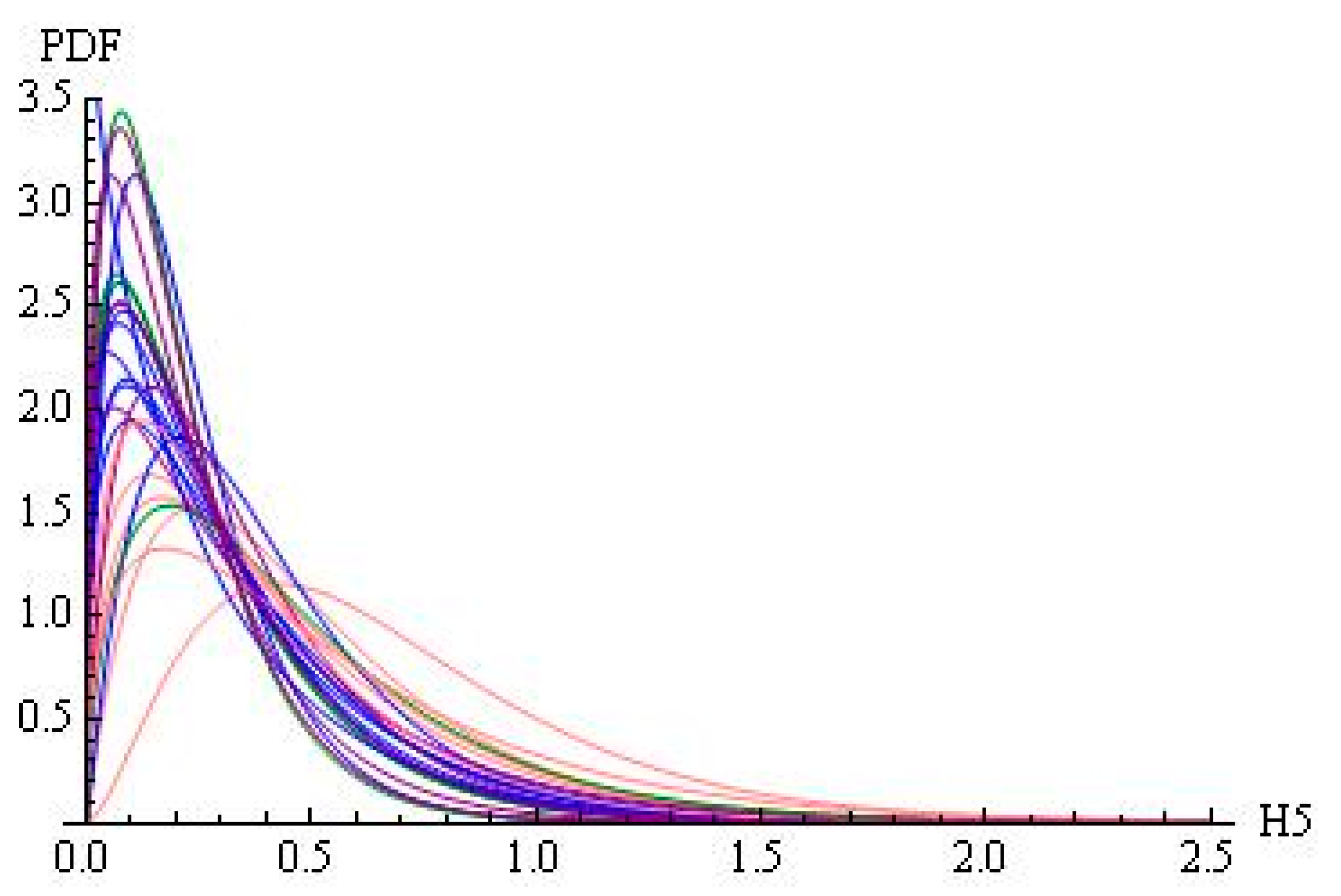
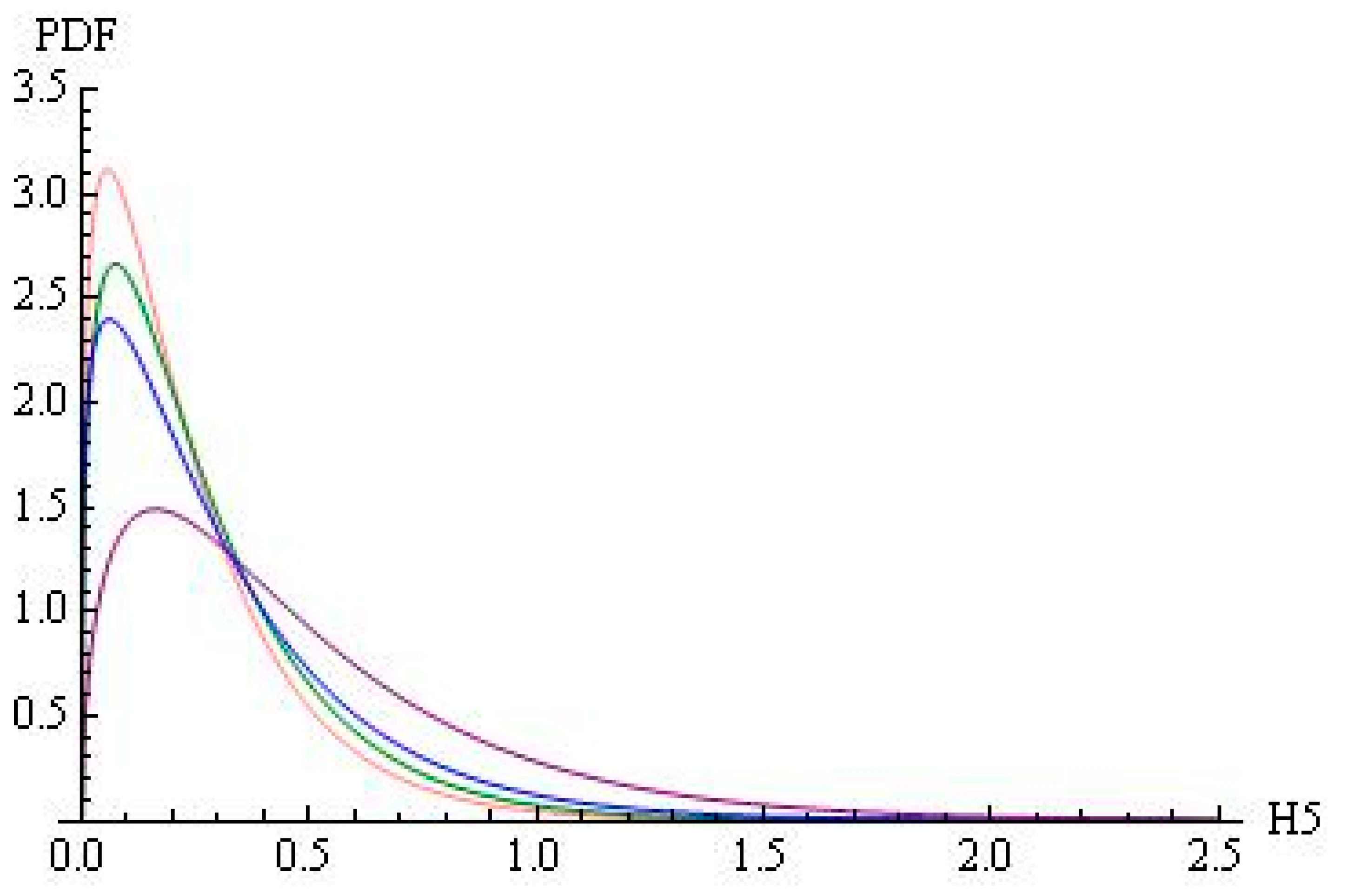
• Are disciplines D_j and subjects S_k characterised by similar parametric distributions for H₅ (i.e., plots have similar shapes) and by similar right tails (i.e., similar percentages of authors with H₅ ≥ 1, H₅ ≥ 1.5, H₅ ≥ 2, H₅ ≥ 2.5, H₅ ≥ 3)?

Note that improvements of H-indexes are taken as policies based on limited information about each single author (e.g., year of the first publication) or discipline and subject (e.g., average number of citations per article). Moreover, the application of the interdisciplinary index to a homogeneous H-index refers to subjects to a greater extent than disciplines (i.e., really powerful interdisciplinary research is across subjects). Statistical analyses of this feature are presented for subjects in the Results and for disciplines in the Appendix A, Appendix B, Appendix C and Appendix D. Finally, as for a classification of studies on bibliometrics in terms of internal vs. external criteria (e.g., [14]) and in terms of theoretical vs. empirical approaches (e.g., [15]), the present paper refers to external theoretical concepts (i.e., efficiency and equity, by adding the concept of homogeneity across disciplines), but it adopts an empirical approach. This feature implies that our results will depend on the used sample: in other words, a theoretical proof based on internal criteria will not be attained, similarly to all other empirical studies. However, we will refer to external criteria of judgment supported by the structural model validated in Zagonari [9] and we will perform a statistical analysis of reduced forms of the same model by referring to the same dataset used in Zagonari [9].

In summary, by focusing on subjects S_k, apart from ∆H₂, neither each single H-index improvement nor the comprehensive H-index improvement solves inefficiency and equity issues (i.e., answer NO to research questions 1 and 4), although the comprehensive H-index improvement makes them confidently uniform across subjects (i.e., answer NO to research question 2 and answer YES to research question 5). Moreover, apart from subject S₁ for Ifa and subject S₄ for Ifb, all subjects are similar in terms of inefficiency and inequity (i.e., answer NO to research question 3 and answer NO to research question 6). Finally, subjects show similar gamma distribution fits and similar right tails (i.e., answer YES to research question 7).

2. Measuring Inefficiency and Inequity by H-Indexes

In order to check if improved H-indexes solve efficiency and equity problems on average and to a greater or smaller extent in each single discipline, efficiency and equity and H improvements described in Section 1 are specified as follows (i.e., Npub = number of publications, Nart = number of articles, Ngro = number of citations including co-author citations, Nnet = number of citations excluding co-author citations, Naut = mean number of co-authors for each author, expert = authors with the first publication before 2011 to include up to 10 years from 2006 to 2015, inexpert = authors with the first publication after 2010 to include up to 5 years from 2006 to 2010):

• Inefficiency a (i.e., many publications other than articles for each author):

$$Npub-Nart~(H_1-H_2)+D_{10}+\cdots +D_j+\cdots +D_{36}$$

(1)

• Inefficiency b (i.e., many co-authors’ reciprocal citations for each author):

$$Ngro-Nnet~(H_2-H_3)+D_{10}+\cdots +D_j+\cdots +D_{36}$$

(2)

• Inequity a (i.e., more co-authors in some disciplines):

$$Nnet-\left(Nnet/Naut\right)~(H_3-H_4)+D_{10}+\cdots +D_j+\cdots +D_{36}$$

(3)

• Inequity b (i.e., more citations for authors with more experience):

$${\left(Nnet/Naut\right)}_{expert}-{\left(Nnet/Naut\right)}_{inexpert}~(H_4-H_5)+D_{10}+\cdots +D_j+\cdots +D_{36}$$

(4)

where issues are depicted on the left-hand side (lhs), policies and disciplines are depicted on the right-hand side (rhs), and “lhs ~ rhs” stands for “lhs depends on the variables on the rhs”. Note that Equations (1)–(4) are reduced analytical forms of the structural theoretical model specified in Zagonari [9]. In particular, each ∆H_h depicts to what extent each bias on the left-hand side is tackled by the improved H-index as a top-down regulation (i.e., ∆H₁ = H₁ − H₂, ∆H₂ = H₂ − H₃, ∆H₃ = H₃ − H₄, ∆H₄ = H₄ − H₅), whereas the dummy variables D_j (i.e., D_j takes value 1 for a discipline j and 0 for disciplines other than j) represent to what extent each discipline is not well represented by each ∆H_h. We will perform similar analyses for subjects S_k. Appendix A provides the list of the 27 disciplines used by Scopus, whereas the 4 subjects can be detailed as follows: 1. health (i.e., medicine, veterinary, nursing, dentistry, health professions), 2. life (i.e., pharmacology and toxicology, biological, neurology, agricultural, immunology), 3. physical (i.e., chemistry, physics and astronomy, mathematics, Earth and planetary, energy, environmental, materials, engineering, computing and information), and 4. social (i.e., psychology, economics and econometrics and finance, arts and humanities, business and management and accounting, decision, sociology).

Note that Npub is likely to be underestimated, since many reviews are published as articles. Moreover, estimations are based on differences if the bias under consideration affects the number of citations only (i.e., Equations (2) and (4)) as well as if the bias affects both the number of authors and the number of citations (i.e., Equations (1) and (3)). Finally, each subsequent bias is additional to the previous one. Thus, in order to test the performances of the comprehensive H-index improvement for addressing the overall bias, we will refer to the following equation:

$${\left(Ngro\right)}_{expert}-{\left(Nnet/Naut\right)}_{inexpert}~(H_1-H_5)+D_{10}+\cdots +D_j+\cdots +D_{36}$$

(5)

where the lhs represents the overall bias, since the focus is on publications for expert authors and on articles for inexpert authors. We will perform similar analyses for subjects by replacing the dummy variables for disciplines D_j with the dummy variables for subjects S_k.

Note that Zagonari [9] does not include H₄ and H₅. Moreover, Zagonari [1] shows that interdisciplinary science requires an additional category, together with orthodox science (i.e., authors publish in a single discipline and in many journals, and the vast majority of the citations are in few disciplines but in many different journals) and heterodox science (i.e., authors publish in a single discipline and in a few journals devoted to that discipline, so that the vast majority of citations are in few disciplines and few journals), to be combined with H₅ to reduce unfair rankings between interdisciplinary scientists (i.e., authors publish in many disciplines and journals, and the vast majority of citations are in many different disciplines and journals) across different disciplines as well as between interdisciplinary scientists and single-discipline scientists collaborating with many authors from different disciplines. Finally, Zagonari [9] does not include quantitative results based on linear regressions or parameter estimations.

3. Constructing the Dataset

In order to obtain a representative dataset for authors, we applied the following stratified sampling. The reference population consists of authors with at least one publication in the Scopus dataset from 2006 to 2015. This population is partitioned by discipline: we used the 27 scientific disciplines suggested by Scopus [16].

By preserving the percentages of authors in each scientific discipline, 10,000 authors are then randomly extracted from the Scopus database. This design required the attribution of each author to a single discipline: we used the attribution suggested by Scopus, where an author is linked to the discipline with the largest percentage of publications.

Table 2. Summary statistics on independent variables for subjects S_k. Notations: mean (SD) is in the first row for each subject, median [min–max] is in the second row for each subject; in columns, Npub = No. publications, Nart = No. articles, Naut = No. co-authors, Ngro = No. gross citations, Nnet = No. net citations.

	Npub	Nart	Naut	Ngro	Nnet
Health	5.112 (14.302)	5.057 (14.032)	12.875 (74.372)	8.091 (24.841)	7.966 (24.302)
	1 [1–444]	1 [1–435]	6.400 [1–2060]	2.333 [0–988]	2.333 [0–965]
Life	5.203 (11.979)	5.171 (11.901)	7.904 (15.337)	9.480 (21.171)	9.289 (20.764)
	2 [1–206]	2 [1–206]	6 [1–461]	3 [0–358]	3 [0–358]
Physical	5.709 (17.865)	5.687 (17.835)	15.874 (135.262)	5.646 (13.910)	5.510 (13.720)
	2 [1–468]	2 [1–468]	4.500 [1–2837.009]	1.667 [0–256]	1.600 [0–256]
Social	2.909 (4.246)	2.906 (4.237)	3.061 (9.622)	4.775 (14.610)	4.737 (14.590)
	1 [1–39]	1 [1–39]	2 [1–228]	1 [0–212]	1 [0–212]

and

Table 3. Summary statistics on all H-indexes for subjects S_k. Notations: mean (SD) is in the first row for each subject, median [min–max] is in the second row for each subject.

	H1	H2	H3	H4	H5
Health	1.916 (3.151)	1.916 (3.151)	1.889 (3.033)	0.329 (0.559)	0.173 (0.249)
	1 [0–43]	1 [0–43]	1 [0–39]	0.167 [0–8.367]	0.111 [0–4.111]
Life	2.188 (3.525)	2.188 (3.525)	2.147 (3.300)	0.423 (0.681)	0.216 (0.291)
	1 [0–72]	1 [0–72]	1 [0–60]	0.200 [0–6.479]	0.143 [0–3.167]
Physical	1.774 (2.913)	1.774 (2.913)	1.728 (2.747)	0.430 (0.705)	0.220 (0.320)
	1 [0–42]	1 [0–42]	1 [0–37]	0.225 [0–12.417]	0.125 [0–5.333]
Social	1.209 (1.606)	1.209 (1.606)	1.198 (1.576)	0.601 (0.839)	0.313 (0.419)
	1 [0–12]	1 [0–12]	1 [0–12]	0.333 [0–6]	0.167 [0–2.667]

provide the summary statistics for subjects S_k, while Appendix B provides the summary statistics for disciplines D_j. Altogether, the dataset includes 1,487,866 co-authors, 507,557 papers, 31,950 journals, and 562,688 citations. The Supplementary Materials provide the histograms of H₁ and H₅ for both disciplines D_j and subjects S_k.

4. Results

4.1. ANOVA and Linear Regressions

In order to check if the improved H-indexes solve efficiency and equity problems on average and to a greater or smaller extent in each discipline, we will perform ANOVA based on linear regressions [17] (see Appendix D for ANOVA based on a quasi-Poisson distribution). In particular, we will translate the theoretical models presented in Section 2 into regression models as follows (i.e., Aaut takes value 1 for authors with the first publication after 2010):

• Inefficiency a (i.e., many publications other than articles for each author):

$$Npub-Nart~(H_1-H_2)+D_{11}+\cdots +D_j+\cdots +D_{35}$$

(6)

• Inefficiency b (i.e., many co-authors’ reciprocal citations for each author):

$$Ngro-Nnet~(H_2-H_3)+D_{11}+\cdots +D_j+\cdots +D_{35}$$

(7)

• Inequity a (i.e., more co-authors in some disciplines):

$$Nnet~Naut+(H_3-H_4)+D_{11}+\cdots +D_j+\cdots +D_{35}$$

(8)

• Inequity b (i.e., more citations for authors with more experience):

$$Nnet~Naut+Aaut+(H_4-H_5)+D_{11}+\cdots +D_j+\cdots +D_{35}$$

(9)

where ~ means that the variable on the lhs is linearly dependent on the variables on the rhs.

Note that we disregarded discipline #10 (multidisciplinary) and discipline #36 (health professions), since few authors are attached to them in our sample (i.e., 2 authors for discipline #10 and 1 author for discipline #36). Moreover, in the model for Iqa (i.e., Equation (8)), Naut is moved to the rhs. Indeed, this inequity is based on the prediction that authors with several co-authors are likely to achieve more citations (i.e., Naut is a stochastic variable). We estimated this relationship before trying to explain the impact of this H-index improvement on rhs and check for residual heterogeneity explained by the discipline dummies. Finally, in the model for Iqb (i.e., Equation (9)), both Naut and Aaut are moved to the rhs. Indeed, this inequity is based on the prediction that expert authors with several co-authors are likely to achieve more citations (i.e., Naut and Aaut are stochastic variables). Again, we estimated these relationships before trying to explain the impact of this H-index improvement on rhs and check for residual heterogeneity explained by the discipline dummies. Thus, the overall bias can be represented by:

$$Ngro~Nnet+Naut+Aaut+(H_1-H_5)+D_{11}+\cdots +D_j+\cdots +D_{35}$$

(10)

where the focus is on articles. We will perform similar analyses for subjects S_k.

Note that we will check firstly for the significance levels of variables and secondly for their coefficient values. Moreover, Equation (10) can be obtained by summing up terms of rhs and lhs in Equations (6)–(9). Finally, we will check for differences between specific disciplines or subjects only if their general explanation of variability is significant.

A methodological remark is worth making here. An ANOVA exercise as a descriptive method (i.e., calculated significance levels) relies on the assumption of normal distributions, although its descriptive statistics (i.e., estimated coefficients and explained variance) allows a simple interpretation of results. Each ANOVA table in Section 4.1 is associated with an analogous table in Appendix D based on a log-linear model involving Poisson and negative-binomial distributions; additional methodological details are provided in Appendix D.

4.1.1. Inefficiency a (Ifa) (Many Publications Other Than Articles)

All authors in our dataset have H₁ = H₂ (i.e., ∆H₁ does not affect Inefficiency a). In other words, publications other than articles do not affect their H-index (e.g., eminent authors are asked to write a review or a book). Consequently, we will apply ANOVA only to disciplines and subjects. In particular,

Table 4. ANOVA on Npub—Nart for disciplines. DF = degree of freedom, ** = significant at 99%. Npub = No. publications, Nart = No. articles.

	DF	Sum Squares	% Tot	Mean Squares	F Value	p-Value	Significance
∆H1 = H1 − H2
Disciplines	24	4.67	0.47	0.194473	1.9541	0.003504	**
Residuals	9972	992.43	99.53	0.099521

shows that the variance explained by disciplines D_j is mildly significant but tiny. In contrast,

Table 5. ANOVA on Npub—Nart for subjects. DF = degree of freedom, *** = significant at 99.9%. Npub = No. publications, Nart = No. articles.

	DF	Sum Squares	% Tot	Mean Squares	F Value	p-Value	Significance
∆H1 = H1 − H2
Subjects	3	2.86	0.29	0.95231	9.5716	2.621 × 10−06	***
Residuals	9993	994.24	99.71	0.09949

shows that the variance explained by subjects S_k is significant but tiny. Note that we will hereafter use slightly significant whenever * applies (i.e., significant at 95%), mildly significant whenever ** applies (i.e., significant at 99%), and significant whenever *** applies (i.e., significant at 99.9%).

Next,

Table A4. Number of publications Npub and of articles Nart in disciplines D_j. Nobs = No. observations.

	Nobs	Npub	Nart	∆	%
Discipline 11	691	3541	3533	8	0.23
Discipline 12	82	153	153	0	0.00
Discipline 13	860	4917	4868	49	1.00
Discipline 14	88	271	271	0	0.00
Discipline 15	91	272	272	0	0.00
Discipline 16	726	4416	4396	20	0.45
Discipline 17	268	1030	1023	7	0.68
Discipline 18	5	24	24	0	0.00
Discipline 19	332	1810	1809	1	0.06
Discipline 20	86	310	310	0	0.00
Discipline 21	57	117	117	0	0.00
Discipline 22	811	3243	3231	12	0.37
Discipline 23	235	1161	1158	3	0.26
Discipline 24	107	374	374	0	0.00
Discipline 25	449	2319	2309	10	0.43
Discipline 26	133	638	638	0	0.00
Discipline 27	3562	18,450	18,254	196	1.06
Discipline 28	96	506	504	2	0.40
Discipline 29	15	28	28	0	0.00
Discipline 30	80	205	204	1	0.49
Discipline 31	631	6305	6277	28	0.44
Discipline 32	115	339	338	1	0.29
Discipline 33	357	1035	1034	1	0.10
Discipline 34	58	170	169	1	0.59
Discipline 35	62	255	250	5	1.96

in Appendix C shows that, apart from D₂₇ and D₃₅, all disciplines D_j are characterised by a percentage of publications other than articles smaller than 1. Similarly,

Table 6. Npub and Nart in subjects S_k. Nobs = No. observations, Npub = No. publications, Nart = No. articles.

	Nobs	Npub	Nart	∆	%
Health	3698	18,904	18,702	202	1.07
Life	1834	9543	9483	60	0.63
Physical	3733	21,311	21,230	81	0.38
Social	733	2132	2130	2	0.09

shows that, apart from S₁, all subjects S_k are characterised by a percentage of publications other than articles smaller than 1.

4.1.2. Inefficiency b (Ifb) (Many Co-Authors’ Reciprocal Citations)

The application of ANOVA to Ifb (i.e., Equation (7)) shows that ∆H₂ explains 26.79% of its variability. In particular,

Table 7. ANOVA on Ngro—Nnet for disciplines. DF = degree of freedom, *** and * = significant at 99.9% and 95%. Ngro = No. gross citations, Nnet = No. net citations.

	DF	Sum Squares	% Tot	Mean Squares	F Value	p-Value	Significance
∆H2 = H2 − H3	1	3140.6	26.79	3140.63	3663.7511	<2 × 10−16	***
Disciplines	24	34.0	0.29	1.42	1.6547	0.02316	*
Residuals	9971	8547.3	72.92	0.86

and

Table 8. ANOVA on Ngro—Nnet for subjects. DF = degree of freedom, *** and * = significant at 99.9% and 95%. Ngro = No. gross citations, Nnet = No. net citations.

	DF	Sum Squares	% Tot	Mean Squares	F Value	p-Value	Significance
∆H2 = H2 − H3	1	3140.6	26.79	3140.63	3659.968	<2 × 10−16	***
Subjects	3	7.2	0.06	2.40	2.792	0.0389	*
Residuals	9992	8574.2	73.15	0.86

show that the residual variances explained by disciplines D_j and subjects S_k are slightly significant and tiny (i.e., ∆H₂ makes D_j and S_k homogeneous with respect to Ifb). In other words, 26.79% of the Ifb variability is explained by ∆H₂. The remaining 73.21% of its variability can be decomposed in variance between disciplines in Table 7 (subjects in Table 8) that accounts for only 0.29% (0.06% in Table 8) and variance within disciplines (subjects) that accounts for the remaining 72.92% (73.15% in Table 8). Thus, even if disciplines and subjects are slightly significant, these factors explain very little of Ifb (i.e., we can safely affirm that, once the Ifb variability explained by ∆H₂ is removed, the remaining variance is within disciplines and subjects to a greater extent than across disciplines and subjects: 72.92% > 0.29%).

Next,

Table A5. Linear regression of Ngro-Nnet on ∆H2 and disciplines Dj. *** = significant at 99.9%. Note that all disciplines apart from D13, D27, and D31 cannot be distinguished statistically from other disciplines.

	Estimate	Std. Error	t Value	Prob(>|t|)	Significance
∆H2 = H2 − H3	1.997354	0.033426	59.755	<2 × 10−16	***
Discipline 11	0.007502	0.035251	0.213	0.831
Discipline 12	0.007289	0.102244	0.071	0.943
Discipline 13	0.201967	0.031618	6.388	1.76 × 10−10	***
Discipline 14	−0.005015	0.098700	−0.051	0.959
Discipline 15	−0.007551	0.097059	−0.078	0.938
Discipline 16	0.015172	0.034374	0.441	0.659
Discipline 17	0.016534	0.056556	0.292	0.770
Discipline 18	0.126019	0.414111	0.304	0.761
Discipline 19	0.049192	0.050915	0.966	0.334
Discipline 20	0.033797	0.099838	0.339	0.735
Discipline 21	0.014254	0.122633	0.116	0.907
Discipline 22	0.010229	0.032514	0.315	0.753
Discipline 23	0.036683	0.060402	0.607	0.544
Discipline 24	0.125332	0.089507	1.400	0.161
Discipline 25	0.014624	0.043702	0.335	0.738
Discipline 26	0.028125	0.080289	0.350	0.726
Discipline 27	0.073994	0.015540	4.762	1.95 × 10−06	***
Discipline 28	0.052234	0.094496	0.553	0.580
Discipline 29	0.000000	0.239056	0.000	1.000
Discipline 30	0.014238	0.103514	0.138	0.891
Discipline 31	0.157578	0.037138	4.243	2.23 × 10−05	***
Discipline 32	0.011230	0.086339	0.130	0.897
Discipline 33	0.019254	0.049002	0.393	0.694
Discipline 34	0.023276	0.121571	0.191	0.848
Discipline 35	−0.009052	0.117595	−0.077	0.939

in Appendix C shows that, apart from D₁₃, D₂₇, and D₃₁, all disciplines D_j are characterised by an insignificant intercept in the linear regression (7) (i.e., ∆H₂ depicts intercepts for those disciplines), where two significant coefficients are positive and large (i.e., larger than 0.1). Similarly,

Table 9. Linear regression of Ngro—Nnet on ∆H₂ and subjects S_k. *** and ** = significant at 99.9% and 99%. Ngro = No. gross citations, Nnet = No. net citations.

	Estimate	Std. Error	t Value	p-Value	Significance
∆H2 = H2 − H3	2.00998	0.03325	60.442	<2 × 10−16	***
Health	0.07116	0.01526	4.663	3.16 × 10−06	***
Life	0.10768	0.02167	4.968	6.88 × 10−07	***
Physical	0.04189	0.01524	2.748	0.006	**
Social	0.01604	0.03422	0.469	0.639

shows that, apart from S₄, all subjects S_k are characterised by a significant and positive intercept in the linear regression (7) (i.e., ∆H₂ depicts intercepts only for that subject), where one significant coefficient is positive and tiny (i.e., larger than 0.1).

Note that we did not detail comparisons between subjects and disciplines, since the variance explained by subjects and disciplines altogether is slightly significant and tiny.

4.1.3. Inequity a (Iqa) (More Co-Authors in Some Disciplines)

The application of ANOVA to Iqa (i.e., Equation (8)) shows that ∆H₃ describes 4.38% of its variability. In particular,

Table 10. ANOVA on Nnet for disciplines. DF = degree of freedom, *** = significant at 99.9%. Nnet = No. net citations, Naut = No. co-authors.

	DF	Sum Squares	% Tot	Mean Squares	F Value	p-Value	Significance
Naut	1	25,395	0.66	25,395	70.0203	<2.2 × 10−16	***
∆H3 = H3 − H4	1	168,777	4.38	168,777	465.3608	<2.2 × 10−16	***
Disciplines	24	46,907	1.22	1954	5.3889	2.728 × 10−16	***
Residuals	9970	3,615,927	93.75	363

shows that the variance explained by disciplines D_j is significant and small (i.e., ∆H₃ does not make Iqa homogeneous across disciplines D_j). In contrast,

Table 11. ANOVA on Nnet for subjects. DF = degree of freedom, *** = significant at 99.9%. Nnet = No. net citations, Naut = No. co-authors.

	DF	Sum Squares	% Tot	Mean Squares	F Value	p-Value	Significance
Naut	1	25,395	0.66	25,395	69.551	<2.2 × 10−16	***
∆H3 = H3 − H4	1	168,777	4.38	168,777	462.241	<2.2 × 10−16	***
Subjects	3	14,837	0.38	4946	13.545	8.129 × 10−09	***
Residuals	9991	3,647,997	94.58	365

shows that the variance explained by subjects S_k is significant and tiny (i.e., ∆H₃ makes Iqa homogeneous across subjects S_k).

Note that

Table 12. Linear regression of Nnet on Naut, ∆H₃ and subjects S_k. *** = significant at 99.9%. Nnet = No. net citations, Naut = No. co-authors.

	Estimate	Std. Error	t Value	p-Value	Significance
Naut	0.009705	0.002054	4.725	2.33 × 10−06	***
∆H3 = H3 − H4	1.680821	0.080859	20.787	<2 × 10−16	***
Health	5.220720	0.337960	15.448	<2 × 10−16	***
Life	6.315327	0.466899	13.526	<2 × 10−16	***
Physical	3.174912	0.329690	9.630	<2 × 10−16	***
Social	3.703891	0.707383	5.236	1.67 × 10−07	***

for subjects and

Table A6. Linear regression of Nnet on Naut, ∆H₃, and disciplines D_j. ***, **, and * = significant at 99.9%, 99%, and 95%. Naut = No. co-authors. Note that disciplines D₁₂, D₁₈, D₂₀, D₂₁, D₂₆, D₂₉, D₃₀, D₃₄, and D₃₅ cannot be distinguished statistically from other disciplines.

	Estimate	Std. Error	t Value	Prob(>|t|)	Significance
Naut	0.01051	0.00207	5.077	3.90 × 10−07	***
∆H3 = H3 − H4	1.61270	0.08130	19.836	<2 × 10−16	***
Discipline 11	2.54715	0.73167	3.481	0.000501	***
Discipline 12	0.85837	2.10310	0.408	0.683176
Discipline 13	9.35233	0.67187	13.920	<2 × 10−16	***
Discipline 14	6.63520	2.03094	3.267	0.001090	**
Discipline 15	4.01396	1.99727	2.010	0.044488	*
Discipline 16	4.61528	0.71962	6.414	1.49 × 10−10	***
Discipline 17	4.35071	1.16601	3.731	0.000192	***
Discipline 18	9.75739	8.51709	1.146	0.251978
Discipline 19	3.84524	1.05085	3.659	0.000254	***
Discipline 20	1.61078	2.05432	0.784	0.433004
Discipline 21	3.41772	2.52302	1.355	0.175571
Discipline 22	1.90671	0.67139	2.840	0.004521	**
Discipline 23	3.95753	1.24667	3.174	0.001506	**
Discipline 24	7.42367	1.84637	4.021	5.85 × 10−05	***
Discipline 25	4.39420	0.90529	4.854	1.23 × 10−06	***
Discipline 26	1.89982	1.65214	1.150	0.250206
Discipline 27	5.40924	0.34334	15.755	<2 × 10−16	***
Discipline 28	10.69129	1.94963	5.484	4.27 × 10−08	***
Discipline 29	2.26224	4.91721	0.460	0.645479
Discipline 30	2.02776	2.13027	0.952	0.341183
Discipline 31	1.70973	0.78243	2.185	0.028901	*
Discipline 32	8.06915	1.77757	4.539	5.71 × 10−06	***
Discipline 33	2.72659	1.00882	2.703	0.006889	**
Discipline 34	2.11780	2.50168	0.847	0.397266
Discipline 35	3.72756	2.42136	1.539	0.123726

in Appendix C for disciplines suggest that adding one co-author to an author significantly affects the number of net citations by around 0.01. In other words, Iqa, although it is statistically significant, it turns out to be a marginal feature for most authors (i.e., to have a substantial effect on the number of citations, an author should publish with several hundreds or thousands of co-authors). However, ∆H₃ contains more information than the number of authors to explain the number of net citations, both for subjects (i.e., 1.68 > 0.0097) and disciplines (i.e., 1.61 > 0.0105).

Next, Table A6 in Appendix C shows that, apart from D₁₂, D₁₈, D₂₀, D₂₁, D₂₆, D₂₉, D₃₀, D₃₄, and D₃₅, all disciplines D_j are characterised by a significant intercept in the linear regression (8) (i.e., ∆H₃ depicts intercepts only for those disciplines), where four significant coefficients are positive and large (i.e., larger than 5). Similarly, Table 12 shows that all subjects S_k are characterised by a significant and positive intercept in the linear regression (7) (i.e., ∆H₃ does not depict intercepts for subjects), where two significant coefficients are positive and large (i.e., larger than 5).

Note that Table 12 and Table A6 in Appendix C show that there is still some heterogeneity not explained by ∆H₃ across disciplines and subjects. In particular, looking at the estimated coefficients and their standard errors, it seems that Subject 1 (health) is similar to Subject 2 (life) and Subject 3 (physical) is similar to Subject 4 (social). The significance levels reported in

Table 13. Differences between subjects S_k (below diagonal) and related p-values (above diagonal).

	Health	Life	Physical	Social
Health	-	0.0450	4.1 × 10−06	0.0508
Life	1.0946	-	9.3 × 10−09	0.0019
Physical	−2.0458	−3.1404	-	0.4944
Social	−1.5168	−2.6114	−0.529	-

sustain the above conjecture: once the effect of ∆H₃ is removed, the residual Iqa is different between Subject 1 (health) and Subject 2 (life) on one side and between Subject 4 (social) and the other subjects on the other side. Similarly, Figure S5 in the Supplementary Materials reports the significance levels of the differences between the dummies for disciplines D_j: there is evidence of residual heterogeneity only for disciplines 13, 27, and 28. This suggests that the set of disciplines could be partitioned into two groups, with disciplines 13, 27, and 28 in the first group, and the other disciplines in the second group.

4.1.4. Inequity b (Iqb) (More Citations for Authors with More Experience)

The application of ANOVA to Iqb (i.e., Equation (9)) shows that ∆H₄ explains 0.46% of its variability. In particular,

Table 14. ANOVA on Nnet for disciplines. DF = degree of freedom, *** = significant at 99.9%. Nnet = No. net citations, Naut = No. co-authors, Aaut = 1 for inexpert authors.

	DF	Sum Squares	% Tot	Mean Squares	F Value	p-Value	Significance
Naut	1	25,395	0.66	25,395	70.9415	<2.2 × 10−16	***
Aaut	1	172,892	4.48	172,892	482.9768	<2.2 × 10−16	***
∆H4 = H4 − H5	1	17,869	0.46	17,869	49.9175	1.711 × 10−12	***
Disciplines	24	72,237	1.87	3010	8.4082	<2.2 × 10−16	***
Residuals	9969	3,568,613	92.52	358

shows that the variance explained by disciplines D_j is significant and small (i.e., ∆H₄ does not make Iqb homogeneous across disciplines Dj). In contrast,

Table 15. ANOVA on Nnet for subjects. DF = degree of freedom, *** = significant at 99.9%. Nnet = No. net citations, Naut = No. co-authors, Aaut = 1 for inexpert authors.

	DF	Sum Squares	% Tot	Mean Squares	F Value	p-Value	Significance
Naut	1	25,395	0.66	25,395	70.158	<2.2 × 10−16	***
Aaut	1	172,892	4.48	172,892	477.644	<2.2 × 10−16	***
∆H4 = H4 − H5	1	17,869	0.46	17,869	49.366	2.262 × 10−12	***
Subjects	3	24,794	0.64	8265	22.833	1.002 × 10−14	***
Residuals	9990	3,616,056	93.75	362

shows that the variance explained by subjects S_k is significant and tiny (i.e., ∆H₄ makes Iqb homogeneous across subjects S_k).

Note that, looking at the estimated coefficients, an expert researcher receives on average 8.84 and 8.86 more net citations per article than an inexpert researcher (

Table 16. Linear regression of Nnet on Naut, Aaut, ∆H₄ and subjects S_k. *** = significant at 99.9%. Nnet = No. net citations, Naut = No. co-authors, Aaut = 1 for inexpert authors.

	Estimate	Std. Error	t Value	p-Value	Significance
Naut	0.017634	0.002015	8.752	<2 × 10−16	***
Aaut	−8.844221	0.408641	−21.643	<2 × 10−16	***
∆H4 = H4 − H5	−0.458533	0.498655	−0.920	0.358
Health	12.266976	0.398495	30.783	<2 × 10−16	***
Life	13.541654	0.512477	26.424	<2 × 10−16	***
Physical	9.790119	0.409115	23.930	<2 × 10−16	***
Social	9.049664	0.757110	11.953	<2 × 10−16	***

for subjects and

Table A7. Linear regression of Nnet on Naut, Aaut, ∆H₄, and disciplines D_j. *** and ** = significant at 100% and 99%. Naut = No. co-authors, Aaut = 1 for inexpert authors. Note that disciplines D₁₈ and D₂₉ cannot be distinguished statistically from other disciplines.

	Estimate	Std. Error	t Value	Prob(>|t|)	Significance
Naut	0.017954	0.002029	8.847	<2 × 10−16	***
Aaut	−8.859996	0.406800	−21.780	<2 × 10−16	***
∆H4 = H4 − H5	−0.450222	0.497463	−0.905	0.365468
Discipline 11	8.897595	0.765770	11.619	<2 × 10−16	***
Discipline 12	5.924150	2.109108	2.809	0.004982	**
Discipline 13	17.224180	0.693190	24.848	<2 × 10−16	***
Discipline 14	12.400369	2.035827	6.091	1.16 × 10−09	***
Discipline 15	10.300187	2.000073	5.150	2.66 × 10−07	***
Discipline 16	11.911298	0.754831	15.780	<2 × 10−16	***
Discipline 17	10.607281	1.186905	8.937	<2 × 10−16	***
Discipline 18	13.276112	8.474326	1.567	0.117234
Discipline 19	10.033894	1.066729	9.406	<2 × 10−16	***
Discipline 20	6.962199	2.061293	3.378	0.000734	***
Discipline 21	9.619067	2.518869	3.819	0.000135	***
Discipline 22	7.704620	0.710005	10.852	<2 × 10−16	***
Discipline 23	10.611399	1.265151	8.387	<2 × 10−16	***
Discipline 24	13.973116	1.841804	7.587	3.58 × 10−14	***
Discipline 25	11.471457	0.932967	12.296	<2 × 10−16	***
Discipline 26	7.228607	1.662872	4.347	1.39 × 10−05	***
Discipline 27	12.389992	0.401181	30.884	<2 × 10−16	***
Discipline 28	17.874425	1.949225	9.170	<2 × 10−16	***
Discipline 29	8.537868	4.894441	1.744	0.081120
Discipline 30	8.369426	2.130282	3.929	8.60 × 10−05	***
Discipline 31	8.540913	0.809086	10.556	<2 × 10−16	***
Discipline 32	13.547450	1.781005	7.607	3.07 × 10−14	***
Discipline 33	7.945013	1.041880	7.626	2.65 × 10−14	***
Discipline 34	7.873618	2.494781	3.156	0.001604	**
Discipline 35	10.362004	2.414967	4.291	1.80 × 10−05	***

in Appendix C for disciplines). However, this relation describes 4.48% of the net citation variability (Table 14 for disciplines and Table 15 for subjects). In other words, Iqb is significantly present in our sample.

Next, Table A7 in Appendix C shows that, apart from D₁₈ and D₂₉, all disciplines D_j are characterised by a significant intercept in the linear regression (9) (i.e., ∆H₄ depicts intercepts only for those disciplines), where ten significant coefficients are positive and large (i.e., larger than 10). Similarly, Table 16 shows that all subjects S_k are characterised by a significant and positive intercept in the linear regression (9) (i.e., ∆H₄ does not depict intercepts for subjects), where two significant coefficients are positive and large (i.e., larger than 10).

Note that

Table 17. Differences between subjects S_k (below diagonal) and related p-values (above diagonal).

	Health	Life	Physical	Social
Health	-	0.0191	2.2 × 10−08	3.1 × 10−05
Life	1.2747	-	5.1 × 10−12	6.9 × 10−08
Physical	−2.4769	−3.7515	-	0.336
Social	−3.2173	−4.4920	−0.7405	-

shows that, once Iqb is explained by ∆H₄, there is still some heterogeneity across subjects, where Subject 1 (health) is similar to Subject 2 (life) on one side and Subject 3 (physical) is similar to Subject 4 (social) on the other side. Similarly, Figure S6 in the Supplementary Materials shows that apart from disciplines 13, 28, 27, and 30, all disciplines are similar.

4.1.5. Overall Bias including All Inefficiency and Inequity

The application of ANOVA to the overall bias (i.e., Equation (10)) shows that ∆H₅ explains 0.04% of its variability. In particular,

Table 18. ANOVA on Ngro for disciplines. DF = degree of freedom, *** = significant at 99.9%. Ngro = No. gross citations, Nnet = No. net citations, Naut = No. co-authors, Aaut = 1 for inexpert authors.

	DF	Sum Squares	% Tot	Mean Squares	F Value	p-Value	Significance
Nnet	1	3,790,911	99.72	3,790,911	3.1661 × 10+06	<2.2 × 10−16	***
Naut	1	302	0.01	302	2.5244 × 10+02	<2.2 × 10−16	***
Aaut	1	19	0.00	19	1.5815 × 10+01	7.053 × 10−05	***
∆H5 = H1 − H5	1	1562	0.04	1562	1.3042 × 10+03	<2.2 × 10−16	***
Disciplines	24	71	0.00	3	2.4638 × 10+00	8.895 × 10−05	***
Residuals	7123	8529	0.22	1

shows that the variance explained by disciplines D_j is significant and null (i.e., ∆H₅ makes D_j homogeneous with respect to the overall bias). In contrast,

Table 19. ANOVA on Ngro for subjects. DF = degree of freedom, *** and * = significant at 99.9% and 95%. Ngro = No. gross citations, Nnet = No. net citations, Naut = No. co-authors, Aaut = 1 for inexpert authors.

	DF	Sum Squares	% Tot	Mean Squares	F Value	p-Value	Significance
Nnet	1	3,790,911	99.72	3,790,911	3.1542 × 10+06	<2.2 × 10−16	***
Naut	1	302	0.01	302	2.5149 × 10+02	<2.2 × 10−16	***
Aaut	1	19	0.00	19	1.5756 × 10+01	7.277 × 10−05	***
∆H5 = H1 − H5	1	1562	0.04	1562	1.2993 × 10+03	<2.2 × 10−16	***
Subjects	3	14	0.00	5	3.7473 × 10+00	0.01053	*
Residuals	7144	8586	0.23	1

shows that the variance explained by subjects S_k is slightly significant and null (i.e., ∆H₅ makes S_k homogeneous with respect to the overall bias).

Next,

Table A8. Linear regression of Ngro on Nnet, Naut, Aaut, ∆H5, and disciplines Dj. ***, **, and * = significant at 99.9%, 99%, and 95%. Nnet = No. net citations, Naut = No. co-authors, Aaut = 1 for inexpert authors. Note that disciplines D12, D18, D26, and D29 cannot be distinguished statistically from other disciplines.

	Estimate	Std. Error	t Value	Prob(>|t|)	Significance
Nnet	1.0156053	0.0005899	1721.619	<2 × 10−16	***
Naut	0.0010315	0.0001243	8.295	<2 × 10−16	***
Aaut	0.1927100	0.0283680	6.793	1.19 × 10−11	***
∆H5 = H1 − H5	0.1597733	0.0044277	36.085	<2 × 10−16	***
Discipline 11	−0.3794002	0.0509842	−7.442	1.11 × 10−13	***
Discipline 12	−0.2588000	0.2001352	−1.293	0.196009
Discipline 13	−0.4355088	0.0471928	−9.228	<2 × 10−16	***
Discipline 14	−0.4084144	0.1377048	−2.966	0.003028	**
Discipline 15	−0.3978104	0.1484945	−2.679	0.007402	**
Discipline 16	−0.5628439	0.0509699	−11.043	<2 × 10−16	***
Discipline 17	−0.4372683	0.0803038	−5.445	5.35 × 10−08	***
Discipline 18	0.0037988	0.4895416	0.008	0.993809
Discipline 19	−0.2416887	0.0723745	−3.339	0.000844	***
Discipline 20	−0.3420827	0.1457847	−2.346	0.018978	*
Discipline 21	−0.3647070	0.1761518	−2.070	0.038450	*
Discipline 22	−0.3409320	0.0521047	−6.543	6.44 × 10−11	***
Discipline 23	−0.4393962	0.0855634	−5.135	2.89 × 10−07	***
Discipline 24	−0.4430399	0.1136581	−3.898	9.79 × 10−05	***
Discipline 25	−0.5087248	0.0650363	−7.822	5.94 × 10−15	***
Discipline 26	−0.2446781	0.1261528	−1.940	0.052475
Discipline 27	−0.4763461	0.0286499	−16.626	<2 × 10−16	***
Discipline 28	−0.6404646	0.1211245	−5.288	1.28 × 10−07	***
Discipline 29	−0.3654419	0.4895745	−0.746	0.455421
Discipline 30	−0.3662411	0.1509943	−2.426	0.015311	*
Discipline 31	−0.1807721	0.0541289	−3.340	0.000843	***
Discipline 32	−0.4443098	0.1151165	−3.860	0.000115	***
Discipline 33	−0.3106706	0.0743621	−4.178	2.98 × 10−05	***
Discipline 34	−0.3491000	0.1713866	−2.037	0.041695	*
Discipline 35	−0.4474059	0.1623079	−2.757	0.005857	**

in Appendix C shows that, apart from D₁₂, D₁₈, D₂₆, and D₂₉, all disciplines D_j are characterised by a significant intercept in the linear regression (10) (i.e., ∆H₅ depicts intercepts only for those disciplines), where one significant coefficient is negative and large (i.e., larger than 0.5). Similarly,

Table 20. Linear regression of Ngro on Nnet, Naut, Aaut, ∆H₅, and subjects S_k. *** = significant at 99.9%. Ngro = No. gross citations, Nnet = No. net citations, Naut = No. co-authors, Aaut = 1 for inexpert authors.

	Estimate	Std. Error	t Value	p-Value	Significance
Nnet	1.0153304	0.0005870	1729.830	<2 × 10−16	***
Naut	0.0011305	0.0001229	9.200	<2 × 10−16	***
Aaut	0.1808438	0.0282857	6.393	1.72 × 10−10	***
∆H5 = H1 − H5	0.1589654	0.0044038	36.097	<2 × 10−16	***
Health	−0.4654963	0.0282006	−16.507	<2 × 10−16	***
Life	−0.4164853	0.0346145	−12.032	<2 × 10−16	***
Physical	−0.3747120	0.0275985	−13.577	<2 × 10−16	***
Social	−0.3403357	0.0523529	−6.501	8.53 × 10−11	***

shows that all subjects S_k are characterised by a significant and negative intercept in the linear regression (10) (i.e., ∆H₅ does not depict intercepts for subjects), where all coefficients are negative and small (i.e., smaller than 0.5). Note that Figure S7 in the Supplementary Materials highlights an overall homogeneity across disciplines, apart from D₃₁ and D₁₆ (i.e., only D₃₁ and D₁₆ are statically different from the other dummies), while we did not detail the differences between subjects, since the variance explained by subjects altogether is slightly significant and tiny. In other words, ∆H₅ explains the overall bias across disciplines, except for those three disciplines.

Therefore, H₅ turns out to be satisfactory in making the overall bias homogeneous across disciplines and subjects. In Section 4.2, we will focus on H₅ to perform additional analyses. Note that the author profile within Scopus enables the calculation of H₁, H₂, and H₃.

4.2. Maximum Likelihood Fittings

Figure 1 shows the histograms of H₅ for the 25 disciplines. Figure 2 presents the maximum likelihood fittings of gamma distributions for the 25 disciplines.

Table A9. Percentages of authors characterised by H₅ larger than 1, 1.5, 2, 2.5, and 3 for disciplines D_j. Normal = middle value, Bold = high value, Italics = low value.

	H5 ≥ 1 (0)	H5 ≥ 1.5 (00)	H5 ≥ 2 (000)	H5 ≥ 2.5 (0000)	H5 ≥ 3 (000000)
Discipline 11	0.0214195000	0.0031949700	0.0004244090	0.0000526374	0.0000006237
Discipline 12	0.1132610000	0.0338257000	0.0089426600	0.0021933800	0.0005108530
Discipline 13	0.0212303000	0.0030915600	0.0003996500	0.0000481475	0.0000005535
Discipline 14	0.1064940000	0.0262324000	0.0055058300	0.0010480800	0.0001867700
Discipline 15	0.0026320400	0.0000941238	0.0000002803	0.0000000075	0.0000000001
Discipline 16	0.0537398000	0.0124615000	0.0025899100	0.0005038630	0.0000937419
Discipline 17	0.0481825000	0.0104430000	0.0020212300	0.0003654780	0.0000631270
Discipline 18	0.2570370000	0.0838338000	0.0223803000	0.0052672800	0.0011368700
Discipline 19	0.0252170000	0.0039244700	0.0005412270	0.0000694763	0.0000008500
Discipline 20	0.0994215000	0.0291084000	0.0075999500	0.0018496200	0.0004288500
Discipline 21	0.0624973000	0.0170231000	0.0042264200	0.0009918090	0.0002238670
Discipline 22	0.0341036000	0.0064675700	0.0010983700	0.0001746360	0.0000265688
Discipline 23	0.0722331000	0.0192680000	0.0046193400	0.0010378100	0.0002230200
Discipline 24	0.0024275000	0.0001010910	0.0000003611	0.0000000118	0.0000000003
Discipline 25	0.0257603000	0.0041443800	0.0005931350	0.0000791911	0.0000100960
Discipline 26	0.0451340000	0.0066194500	0.0008072040	0.0000881770	0.0000008954
Discipline 27	0.0099479400	0.0010265500	0.0000940477	0.0000008035	0.0000000655
Discipline 28	0.0317879000	0.0045656300	0.0005621200	0.0000631578	0.0000006678
Discipline 29	0.0898358000	0.0286542000	0.0083499600	0.0023013000	0.0006097310
Discipline 30	0.0005730750	0.0000106334	0.0000000167	0.0000000002	0.0000000000
Discipline 31	0.0426779000	0.0113684000	0.0028147400	0.0006666810	0.0001531040
Discipline 32	0.0576213000	0.0127117000	0.0024768200	0.0004478000	0.0000769826
Discipline 33	0.2019380000	0.0829548000	0.0307522000	0.0106768000	0.0035321700
Discipline 34	0.0032719200	0.0001645480	0.0000007143	0.0000000284	0.0000000010
Discipline 35	0.0258130000	0.0041717700	0.0006001260	0.0000805640	0.0000103297

in Appendix C shows the percentages of authors characterised by H₅ larger than 1, 1.5, 2, 2.5, and 3 for the 25 disciplines.

Thus, disciplines are characterised by different gamma distributions and different quantiles.

Figure 3 shows the histograms of H₅ for the four subjects. Figure 4 presents the maximum likelihood fittings of gamma distributions for the four subjects.

Table 21. Percentages of authors characterised by H₅ larger than 1, 1.5, 2, 2.5 and 3 for subjects S_k.

	H5 ≥ 1	H5 ≥ 1.5	H5 ≥ 2	H5 ≥ 2.5	H5 ≥ 3
Health	0.01012250	0.00105278	0.00009720	0.00000083	0.00000006
Life	0.01899160	0.00260541	0.00031683	0.00003588	0.00000038
Physical	0.04220660	0.00922697	0.00182136	0.00033814	0.00006023
Social	0.14236600	0.04902840	0.01510380	0.00434077	0.00118783

shows the percentages of authors characterised by H₅ larger than 1, 1.5, 2, 2.5, and 3 for the four subjects.

Thus, subjects are characterised by similar gamma distributions and similar quantiles.

5. Discussion

We applied ANOVA analyses and linear regressions together with maximum likelihood fittings and quantile analyses to answer the seven research questions specified in Section 1.

The main specific insights obtained can be summarised as follows. By focusing on disciplines D_j, apart from ∆H₂, neither each single H-index improvement nor the comprehensive H-index improvement solves inefficiency and equity issues (i.e., answer NO to research questions 1 and 4), although the comprehensive H-index improvement makes them slightly different across disciplines (i.e., answer NO to research question 2 and answer NO to research question 5). Moreover, apart from D₂₇ and D₃₅, all disciplines are characterised by a similar level of Inefficiency a; apart from D₁₃, D₂₇, and D₃₁, all disciplines are characterized by an insignificant level of Inefficiency b; apart from D₁₂, D₁₈, D₂₀, D₂₁, D₂₆, D₂₉, D₃₀, D₃₄, and D₃₅, all disciplines are characterised by a significant level of Inequity a; apart from D₁₈ and D₂₉, all disciplines are characterised by a significant level of Inequity b; apart from D₁₂, D₁₈, D₂₆, and D₂₉, all disciplines are characterised by a significant level of overall bias, and some disciplines are similar but some disciplines are different in terms of inefficiency and inequity (i.e., answer YES to research question 3 and answer YES to research question 6). Finally, disciplines show different gamma distributions and different quantiles (i.e., answer NO to research question 7).

The main general insights obtained can be summarised as follows. By referring to Table 18 for disciplines, the variability of the overall bias amounts to 10,162 (i.e., sum of squares is 1562 + 71 + 8529), where 15.37% (i.e., 1562/10,162) of this bias could have been reduced by using ∆H₅. The remaining bias is within disciplines for 83.93% (i.e., 8529/10,162) and across disciplines for less than 1%. Similarly, by referring to Table 19 for subjects, the variability of the overall bias amounts to 10,162 (i.e., sum of squares is 1562 + 14 + 8586), where 15.37% (i.e., 1562/10,162) of this bias could have been reduced by using ∆H₅. The remaining bias is within subjects for 84.49% (i.e., 8586/10,162) and across subjects for less than 1%.

Note that Inefficiency b (i.e., many co-authors’ reciprocal citations) turning out to be statistically significant for few disciplines (i.e., D₁₃, D₂₇, and D₃₁) could be interpreted as inequity.

Therefore, the present study shows that the net per-capita per-year H-index based on articles can be used to evaluate interdisciplinary scientists. In particular, the empirical approach adopted in the present study highlighted that the suggested improvements of the H-index as policies did not implement efficiency and equity across disciplines and subjects in the dataset under consideration, although all suggested improvements combined produced homogeneity across subjects (i.e., a crucial feature in evaluating interdisciplinary science). Note that a homogeneous H-index across subjects is a necessary condition for a proper assessment of interdisciplinary science, whereas interdisciplinary science does not solve theoretical and empirical problems identified for the H-index. Next, the empirical demonstration that the suggested improvements of the H-index represent a useful tool to evaluate interdisciplinary science does not imply that it will be used whenever comparisons between subjects are required (e.g., in allocating funds in interdisciplinary departments), although it can be easily implemented (e.g., an algorithm is available on Scopus.com to compute the efficiency improvements of the H-index; Zagonari [1] provides software to calculate all suggested improvements of the H-index) [18]. In other words, the adoption of homogeneity as a criterion is a political/academic decision rather than a technical/scientific issue [19].

Nevertheless, two main limits of the present study must be highlighted. First, the applications of ANOVA and linear regressions are justified by the straightforward interpretation of their results, although they provide a statistical description of the sample under consideration based on the assumption of a normal distribution. However, the references to reduced forms (see Equations (1)–(5)) of the structural model developed by Zagonari [9] (i.e., a very plausible model for authors who aim at maximising their H-index) and the consistent results (see Appendix D) obtained by applying a weighted quasi-Poisson distribution (i.e., a very plausible distribution for the stochastic phenomenon of articles’ citations) [20] seem to also support similar insights outside the sample under consideration. Second, the association of each author with a single discipline is justified by the classification of authors adopted by the Scopus dataset, although it might be too simplistic for some authors. However, a continuous classification of authors in terms of percentages to weigh all disciplines in the publication experience of each author would require a similar continuous classification for all journals and all articles.

Some methodological remarks are worth making here.

Improvements of the H-index other than those suggested by Zagonari [9] could have been used. In particular, we disregarded:

• Impact factors [21]. However, this feature is misleading, since a paper poorly cited but published in a high-impact journal should be punished rather than rewarded, since it wasted a popular stage.
• Gender differences [22]. However, this feature is irrelevant in making disciplines and subjects homogeneous.
• Google or WoS indexes [23,24,25]. However, these datasets are shown to be more easily manipulated than the Scopus dataset.
• Negative citations [6]. However, this bias is likely to be negligible, since papers criticising a paper do not need to quote it many times.
• Country differences [26]. However, this feature is irrelevant in making disciplines and subjects homogeneous.
• Co-authorship networks [27]. However, this feature is misleading in focusing on inefficiency and inequity across authors in different disciplines and subjects.

Note that we omitted the editors’ trick of magnifying citations of papers published in a journal as a precondition to publish in it, since some journals are often tightly linked to some topics.

In contrast, we emphasised:

• H-index dynamics. In fact, other papers focused on the same feature [11].
• Linear regressions. However, non-linear estimations require additional assumptions (e.g., a Poisson distribution based on random and over-time independent citations for over-time constant authors) and make interpretations of results more complicated (e.g., impacts of alternative policies ∆H_h and different disciplines D_j or subjects S_k are non-additive) [6].
• Gamma distributions. In fact, other papers used the same distribution [24].

Note that we standardised with respect to each author rather than with respect to disciplines, while possible specific features of disciplines and subjects are caught by dummies D_j and S_k.

In summary, the main strength of the present study is the reference to scientific 27 disciplines and four subjects. For example, Ryan [28] estimates the same variant of the H-index (i.e., H₅), but it refers to 474 observations in five colleges. Next, the main weakness of the present study is its descriptive rather than predictive purpose, by discussing which top-down regulation could have made disciplines and subjects homogeneous in the sample rather than which top-down regulation could make disciplines and subjects homogeneous in the future. For example, Moreira et al. [29] apply the functional form of the distribution of the asymptotic number of citations but to 1283 authors in seven disciplines only (i.e., a similar topic but a smaller sample). Similarly, Kupper [30] applies random forests and gradient boosting machines to 111,156 authors in a single discipline but to predict gender bias (i.e., a similar sample but a narrower topic).

6. Conclusions

The purpose of the present study was to identify an improvement of the H-index, as an easily generated quantitative index based on a readily accessible set of information, in order to enable suitable comparisons of interdisciplinary scientists. We succeeded by considering alternative H-index improvements as top-down regulations (i.e., aware that there is no single bibliometric index accounting for all biases in all disciplines and subjects) and by focusing on both disciplines and subjects (i.e., aware that differences across subjects are more important than differences across disciplines to compare interdisciplinary scientists). Indeed, the net per-capita per-year H-index based on articles does not account for the total variance, although it makes disciplines significant but irrelevant (i.e., research question 1) and subjects insignificant and irrelevant in explaining the total variance (i.e., research questions 2 and 5). Moreover, some disciplines and subjects are highlighted for some H-index improvements (i.e., research questions 3 and 6). Finally, the net per-capita per-year H-index based on articles produces similar gamma distributions and quantiles for subjects but not for disciplines (i.e., research question 7).

In fact, we did much more than identifying an H-index improvement to compare interdisciplinary scientists by suggesting a procedure to empirically evaluate alternative bibliometric indexes. Indeed, it is weak to criticise an index because it does not identify a specific award in a given year (e.g., [4,31,32]) (i.e., critiques from outside but empirical). Moreover, it is not possible to identify a bibliometric index accounting for the many different practices across disciplines (e.g., patents are useful for engineering and chemistry, but inapplicable to arts or economics; the many authors in physics and the many citations in computing cannot be properly compared with the few authors in humanities and the few citations in economics) [33]. Finally, it is weak to criticise an index because it does not account for a specific feature (i.e., critiques from inside but theoretical) [34].

In other words, without any ambition to solve all different (good and bad) practices across disciplines and subjects by relying on general information, we criticised alternative variants of the H-indexes in terms of external and theoretically straightforward criteria (i.e., inefficiency and inequity) by testing the improvements of the H-indexes as policies in achieving an external and empirically straightforward goal such as homogeneity of disciplines and subjects (i.e., theoretical critiques from outside but empirically tested). Note that a possible change in standards in measuring scientific production towards the net per-capita per-year H-index based on articles could foster a potential change in behaviours in publication practices. For example, instead of adding authors as a costless practice, one could organise a network of authors in triplets, where one author appears in each triplet. However, this practice is not costless in terms of coordination efforts and it will favour a smaller number of authors such as the department heads.

The present study could be developed by using a more recent dataset to test the same structural model behind it. However, researchers at Scopus should be engaged to produce a similar sample (i.e., a stratified random sampling requires the complete list of authors). Moreover, the structural model we referred to in our study should be validated again. Finally, in case of adoption of our improved H-indexes within the Scopus framework, everybody could test the present study in any alternative period of time by referring to the same statistics for the whole population of authors.