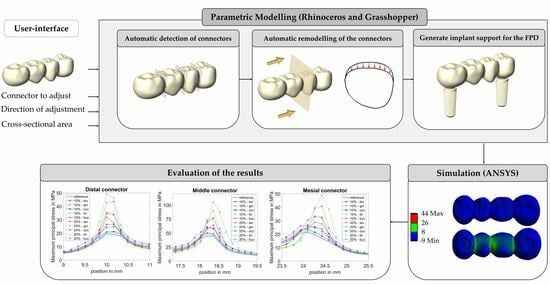
Automated Remodelling of Connectors in Fixed Partial Dentures
Abstract
:1. Introduction
2. Materials and Methods
2.1. CAD-Modelling
2.1.1. Automatic Connector Detection
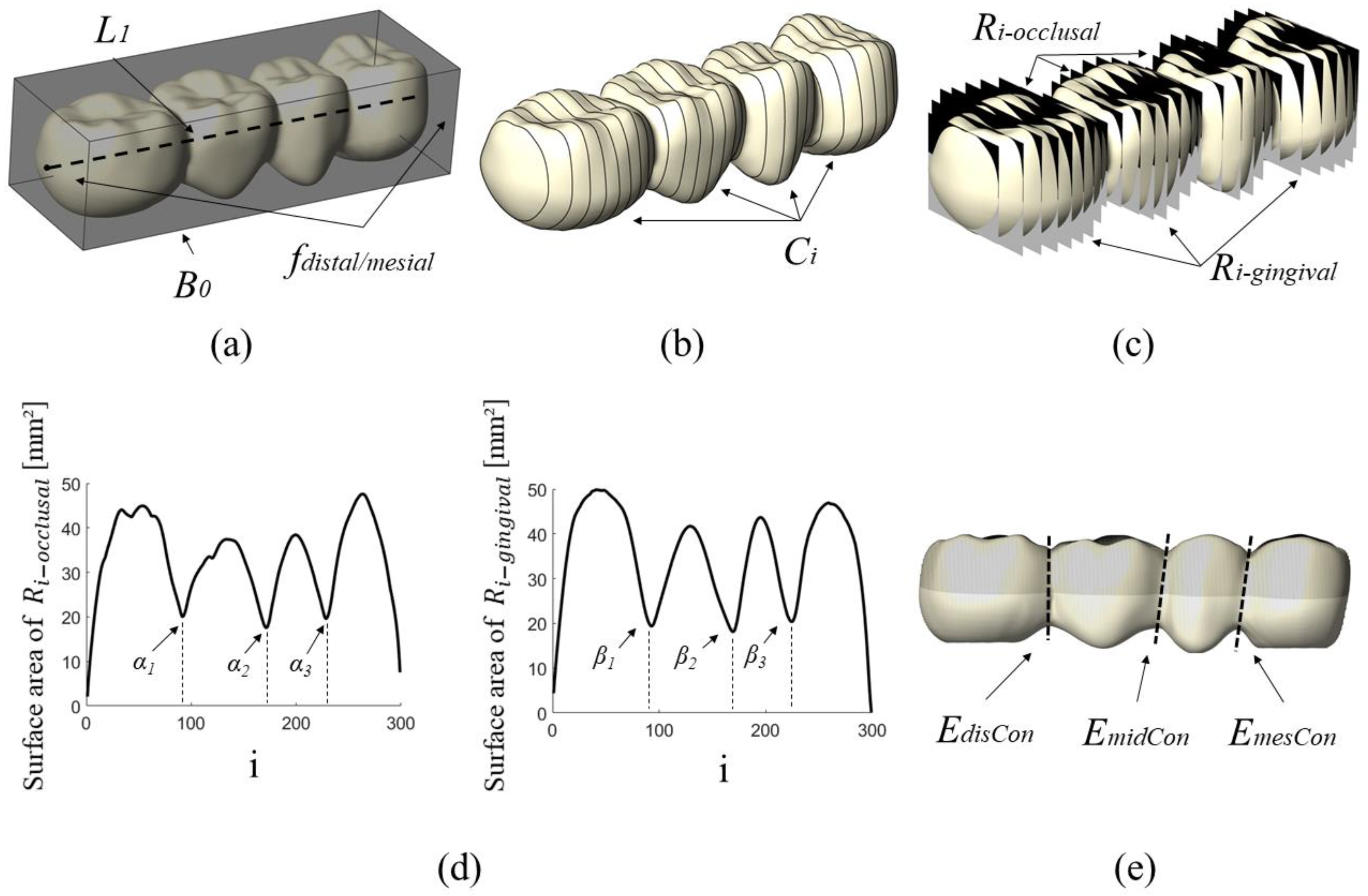
- Find the smallest bounding box B0 (with faces focclusal, fgingival, fmesial, fdistal, flingual and fbuccal) for the FPD mesh geometry MFPD using the bounding box function in Grasshopper. Connect the centre of the smallest faces of B0 (fdistal and fmesial) with the line L1, see Figure 2a.
- Generate 300 equally spaced planes Ei along the line L1 that are perpendicular to L1. Find the intersection curves Ci between the planes Ei and the FPD mesh (MFPD), see Figure 2b.
- Define the plane Emid that lies in the middle between the faces focclusal and fgingival of Box B0. Define the plane Emid2 that lies in the middle between the faces flingual and fbuccal of Box B0.
- Create bounding rectangles Ri for all intersection curves Ci, with the rectangle’s sides parallel to the faces of the box B0, see Figure 2c.
- Divide each bounding rectangle Ri into an occlusal rectangle Ri-occlusal and a gingival rectangle Ri-gingival using Emid, see Figure 2c.
- Compute the surface areas (Ai-occlusal and Ai-gingival) of each bounding rectangle (Ri-occlusal and Ri-gingival). Find the local minima of Ai-occlusal (denoted as αj) and of Ai-gingival (denoted as βj), see Figure 2d. The minima are used to define the position of the connectors. As the connectors may be oblique, the minima for the occlusal and gingival sides are calculated separately.
2.1.2. Connector Adjustment
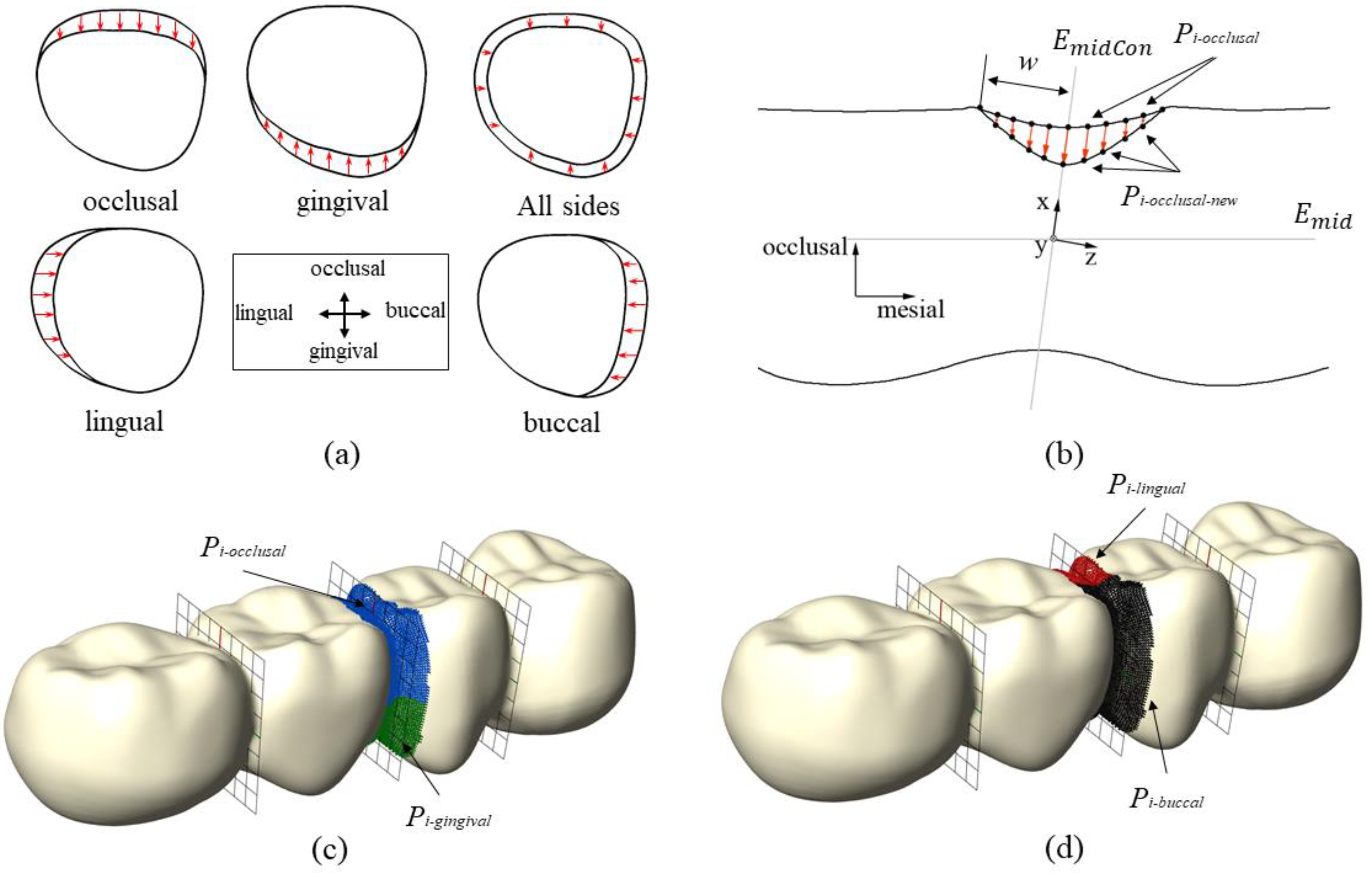
- Define Lo as the upper edge of the previously computed bounding rectangle Ri-occlusal at the position of αj (minimum detected in step 6 in the previous section). Define Lg as the lower edge of Ri-gingival at the position of βj. Define a plane EmidCon that contains Lo and Lg.
- Define a Cartesian coordinate system (xyz), whereas the origin is defined by the point, which lies in Emid, Emid2 (see step 3 in the previous section) and EmidCon. The x-axis points from the origin in the direction of the point that is obtained by Emid2 crossing Lo. The y-axis lies in EmidCon and points to the buccal side (defined by the previously computed bounding Box B0). The z-axis is chosen perpendicular to the x- and y-axis.
- Compute the distances of all points of the FPD mesh to the plane EmidCon and select all points that are closer to the plane than w ( < w), whereas w is a user-defined parameter (w = 1 mm in this study). These selected points are called Pi-C2 and their position is altered in the following steps to adjust the connectors.
- Starting from the point set Pi-C2 select all points with x > 0, which are the points close to the occlusal side, see Figure 3c. These selected points are called Pi-occlusal.
- For each point in Pi-occlusal calculate the distance to the x-y plane (equals EmidCon) and y-z plane. These distances are called and
- Compute a new x-coordinate xnew(i) for each point Pi-occlusal, see Figure 3b. B(t) is a bézier type function, x(i) is the old x-coordinate and k is a parameter chosen in step 7. The equations were:
- Calculate the cross-sectional area A2 of connector C2 and iteratively adjust the value of the parameter k in Equation (1) using Galapagos in Grasshopper until A2 matches the predefined input area value Ainput. The optimization was stopped after an accuracy of ± 0.001 mm2 was achieved.
- Reconstruct the FPD mesh using the updated vertices via the Grasshopper function construct mesh.
2.1.3. Implant Support for the FPD
2.2. Material Properties, Contact Models, Boundary Conditions and Mesh Size
| Component | Material | Young’s Modulus [GPa] | Poisson’s Ratio |
|---|---|---|---|
| Implant 1 | Titanium grade 4 | 104.5 | 0.37 |
| Abutment 1 | Titanium grade 4 | 104.5 | 0.37 |
| Implant screw 1 | Titanium grade 5 | 114.0 | 0.33 |
| Cement layer 2 | Glass ionomer cement | 14.3 | 0.33 |
| FPD 3 | Zirconium dioxide | 210 | 0.27 |
| Cortical bone 4 | - | 13.7 | 0.3 |
| Transition zone | - | 13.7 to 1.37 (graded) | 0.3 |
| Cancellous bone 4 | - | 1.37 | 0.3 |
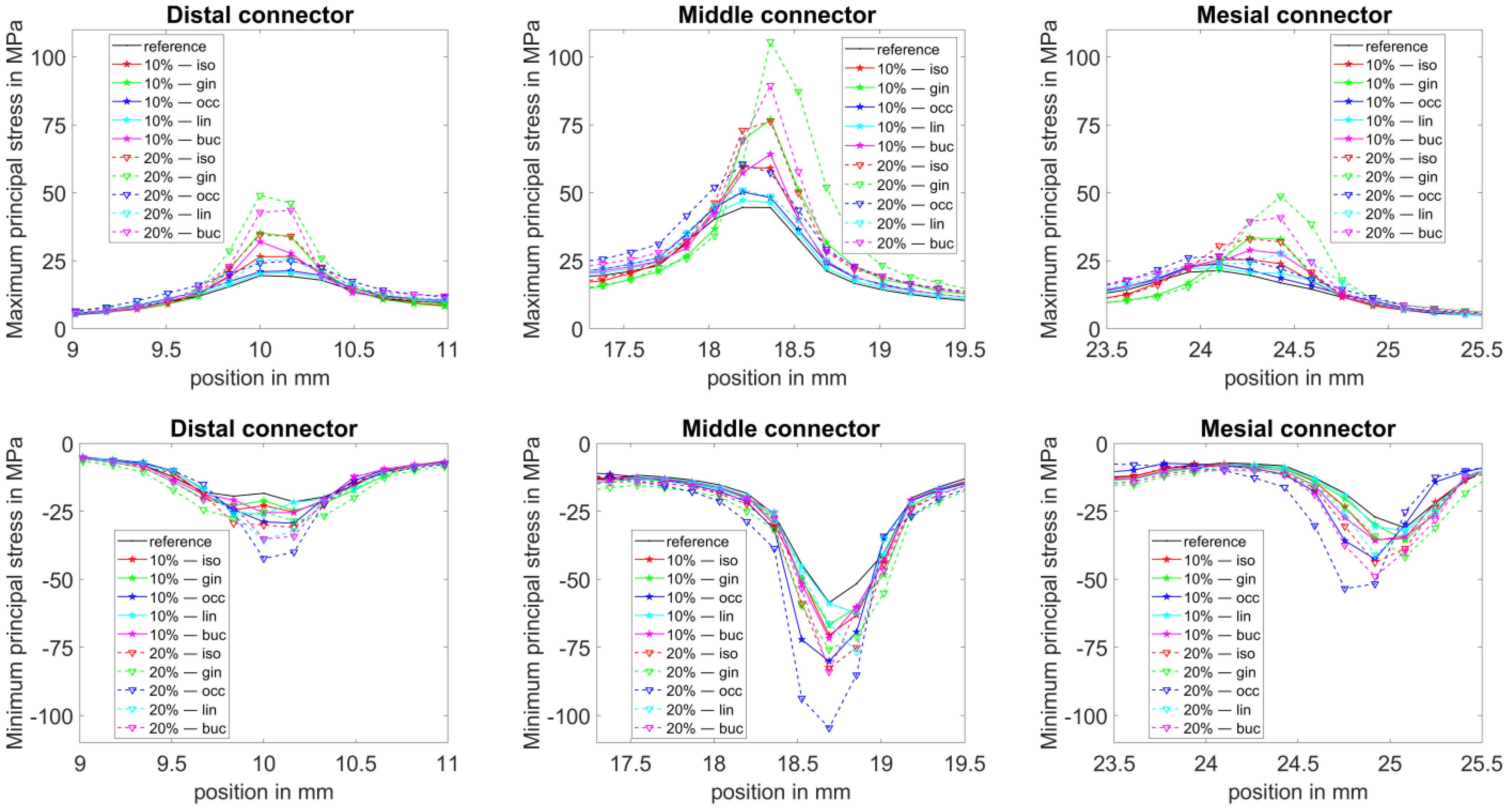
2.3. Evaluation of Results
3. Results
4. Discussion
5. Clinical Relevance
6. Conclusions
- The proposed algorithm enables automatic detection of the connector position and parameterized adjustment of the cross-sectional area of the connectors from various directions.
- Reducing the connector area from the gingival side has a major influence on the tensile stresses, whereas the middle connector in a 4-unit FPD is most vulnerable regarding a cross-sectional area reduction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Stress Increase in %, When Distal Connector Area 10% Reduced | Stress Increase in %, When Distal Connector Area 20% Reduced | |||||
|---|---|---|---|---|---|---|
| Dis. Con | Mid. Con | Mes. Con | Dis. Con | Mid. Con | Mes. Con | |
| Iso | 36 | 0 | 1 | 77 | 0 | 1 |
| Gin | 81 | 1 | −1 | 152 | 1 | 0 |
| Occ | 9 | 0 | 0 | 27 | −1 | −1 |
| Lin | 6 | 1 | 0 | 31 | 1 | 1 |
| Buc | 64 | 0 | 1 | 123 | −1 | 0 |
| Stress Increase in %, When Middle Connector Area 10% Reduced | Stress Increase in %, When Middle Connector Area 20% Reduced | |||||
|---|---|---|---|---|---|---|
| Dis. Con | Mid. Con | Mes. Con | Dis. Con | Mid. Con | Mes. Con | |
| Iso | 0 | 33 | 0 | 3 | 71 | −1 |
| Gin | 0 | 72 | −5 | 1 | 137 | −6 |
| Occ | 1 | 13 | 3 | 4 | 36 | 6 |
| Lin | 0 | 6 | 2 | 1 | 14 | 5 |
| Buc | 1 | 44 | 0 | 2 | 101 | −3 |
| Stress Increase in %, When Mesial Connector Area 10% Reduced | Stress Increase in %, When Mesial Connector Area 20% Reduced | |||||
|---|---|---|---|---|---|---|
| Dis. Con | Mid. Con | Mes. Con | Dis. Con | Mid. Con | Mes. Con | |
| Iso | 1 | −1 | 19 | −1 | 0 | 55 |
| Gin | −1 | −1 | 57 | 0 | −1 | 128 |
| Occ | −1 | 0 | 11 | 0 | 4 | 24 |
| Lin | 0 | 4 | 5 | 0 | 3 | 30 |
| Buc | 0 | 2 | 36 | −1 | −1 | 91 |
References
- Sailer, I.; Pjetursson, B.E.; Zwahlen, M.; Hämmerle, C.H. A systematic review of the survival and complication rates of all-ceramic and metal–ceramic reconstructions after an observation period of at least 3 years. Part II: Fixed dental prostheses. Clin. Oral Implant. Res. 2007, 18, 86–96. [Google Scholar] [CrossRef] [PubMed]
- da Silva, L.H.; de Lima, E.; de Paula Miranda, R.B.; Favero, S.S.; Lohbauer, U.; Cesar, P.F. Dental ceramics: A review of new materials and processing methods. Braz. Oral Res. 2017, 31, 133–146. [Google Scholar] [CrossRef] [PubMed]
- Zarone, F.; Di Mauro, M.I.; Spagnuolo, G.; Gherlone, E.; Sorrentino, R. Fourteen-year evaluation of posterior zirconia-based three-unit fixed dental prostheses. J. Dent. 2020, 101, 103419. [Google Scholar] [CrossRef] [PubMed]
- Laumbacher, H.; Strasser, T.; Knuttel, H.; Rosentritt, M. Long-term clinical performance and complications of zirconia-based tooth-and implant-supported fixed prosthodontic restorations: A summary of systematic reviews. J. Dent. 2021, 111, 103723. [Google Scholar] [CrossRef] [PubMed]
- Kim, W.J.; Li, X.C.; Bidra, A.S. Clinical outcomes of implant-supported monolithic zirconia crowns and fixed partial dentures: A systematic review. J. Prosthodont. Implant Esthet. Reconstr. Dent. 2023, 32, 102–107. [Google Scholar] [CrossRef]
- Oh, W.S.; Anusavice, K.J. Effect of connector design on the fracture resistance of all-ceramic fixed partial dentures. J. Prosthet. Dent. 2002, 87, 536–542. [Google Scholar] [CrossRef]
- Larsson, C.; Holm, L.; Lovgren, N.; Kokubo, Y.; von Steyern, P.V. Fracture strength of four-unit Y-TZP FPD cores designed with varying connector diameter. An in-vitro study. J. Oral Rehabil. 2007, 34, 702–709. [Google Scholar] [CrossRef]
- Bahat, Z.; Mahmood, D.J.H.; von Steyern, P.V. Fracture strength of three-unit fixed partial denture cores (Y-TZP) with different connector dimension and design. Swed. Dent. J. 2009, 33, 149–159. [Google Scholar]
- Wimmer, T.; Ender, A.; Roos, M.; Stawarczyk, B. Fracture load of milled polymeric fixed dental prostheses as a function of connector cross-sectional areas. J. Prosthet. Dent. 2013, 110, 288–295. [Google Scholar] [CrossRef]
- Hamza, T.A.; Attia, M.A.; El-Hossary, M.M.K.; Mosleh, I.E.; Shokry, T.E.; Wee, A.G. Flexural strength of small connector designs of zirconia-based partial fixed dental prostheses. J. Prosthet. Dent. 2016, 115, 224–229. [Google Scholar] [CrossRef]
- de Freitas, B.N.; Tonin, B.S.H.; Zaparolli, D.; Faria, A.C.L.; Toniollo, M.B.; Ribeiro, R.F.; Macedo, A.P. Mechanical comparison of milled fiber-reinforced resin composite and Co–Cr frameworks with different connector cross-sectional geometries: An in vitro study. J. Mech. Behav. Biomed. Mater. 2023, 141, 105759. [Google Scholar] [CrossRef] [PubMed]
- Alberto, L.H.J.; Kalluri, L.; Esquivel-Upshaw, J.F.; Duan, Y. Three-Dimensional Finite Element Analysis of Different Connector Designs for All-Ceramic Implant-Supported Fixed Dental Prostheses. Ceramics 2022, 5, 34–43. [Google Scholar] [CrossRef]
- Almasi, A.; Antoniac, I.; Focsaneanu, S.; Manole, M.; Ciocoiu, R.; Trante, O.; Earar, K.; Saceleanu, A.; Porumb, A.; Ratiu, C. Design Improvement of Y-TZP Three Unit Bridges by Predicted Stress Concentration Using FEA and Experimental Failure Modes after Three Point Bending Test. Rev. Chim. 2019, 70, 336–342. [Google Scholar] [CrossRef]
- Möllers, K.; Pätzold, W.; Parkot, D.; Kirsten, A.; Güth, J.-F.; Edelhoff, D.; Fischer, H. Influence of connector design and material composition and veneering on the stress distribution of all-ceramic fixed dental prostheses: A finite element study. Dent. Mater. 2011, 27, e171–e175. [Google Scholar] [CrossRef]
- Lakshmi, R.D.; Abraham, A.; Sekar, V.; Hariharan, A. Influence of connector dimensions on the stress distribution of monolithic zirconia and lithium-di-silicate inlay retained fixed dental prostheses—A 3D finite element analysis. Tanta Dent. J. 2015, 12, 56–64. [Google Scholar] [CrossRef]
- Demoly, F.; Roth, S. Knowledge-based parametric CAD models of configurable biomechanical structures using geometric skeletons. Comput. Ind. 2017, 92, 104–117. [Google Scholar] [CrossRef]
- Bos, E.; Scholten, T.; Song, Y.; Verlinden, J.; Wolff, J.; Forouzanfar, T.; Helder, M.; Van Zuijlen, P. Developing a parametric ear model for auricular reconstruction: A new step towards patient-specific implants. J. Cranio-Maxillofac. Surg. 2015, 43, 390–395. [Google Scholar] [CrossRef]
- Jemaa, H.; Eisenburger, M.; Greuling, A. Semi-automated generation of bone loss defects around dental implants and its application in finite element analysis. Comput. Methods Biomech. Biomed. Eng. 2023, 1–12. [Google Scholar] [CrossRef]
- Dittmer, M.P.; Borchers, L.; Stiesch, M.; Kohorst, P. Stresses and distortions within zirconia-fixed dental prostheses due to the veneering process. Acta Biomater. 2009, 5, 3231–3239. [Google Scholar] [CrossRef]
- Dittmer, M.P.; Kohorst, P.; Borchers, L.; Schwestka-Polly, R.; Stiesch, M. Stress analysis of an all-ceramic FDP loaded according to different occlusal concepts. J. Oral Rehabil. 2011, 38, 278–285. [Google Scholar] [CrossRef]
- Dittmer, M.P.; Kohorst, P.; Borchers, L.; Stiesch-Scholz, M. Finite element analysis of a four-unit all-ceramic fixed partial denture. J. Prosthodont. 2009, 5, 1349–1355. [Google Scholar] [CrossRef] [PubMed]
- Rand, A.; Kohorst, P.; Greuling, A.; Borchers, L.; Stiesch, M. Stress Distribution in All-Ceramic Posterior 4-Unit Fixed Dental Prostheses Supported in Different Ways: Finite Element Analysis. Implant Dent. 2016, 25, 485–491. [Google Scholar] [CrossRef] [PubMed]
- Sarafidou, K.; Stiesch, M.; Dittmer, M.P.; Borchers, L.; Kohorst, P. Load-bearing capacity of implant-supported, tooth-supported, and combined zirconia-fixed dental prostheses. Implant Dent. 2011, 20, 311–317. [Google Scholar] [CrossRef]
- Sarafidou, K.; Stiesch, M.; Dittmer, M.P.; Jörn, D.; Borchers, L.; Kohorst, P. Load-bearing capacity of artificially aged zirconia fixed dental prostheses with heterogeneous abutment supports. Clin. Oral Investig. 2012, 16, 961–968. [Google Scholar] [CrossRef] [PubMed]
- Guthe, M.; Borodin, P.; Klein, R. Fast and Accurate Hausdorff Distance Calculation between Meshes. J. WSCG 2005, 13, 41–48. [Google Scholar]
- Roffmann, O.; Stiesch, M.; Greuling, A. Preventing stress singularities in peri-implant bone—A finite element analysis using a graded bone. Comput. Methods Biomech. Biomed. Eng. 2023, 1–11. [Google Scholar] [CrossRef]
- de la Rosa Castolo, G.; Guevara Perez, S.V.; Arnoux, P.J.; Badih, L.; Bonnet, F.; Behr, M. Mechanical strength and fracture point of a dental implant under certification conditions: A numerical approach by finite element analysis. J. Prosthet. Dent. 2018, 119, 611–619. [Google Scholar] [CrossRef]
- Denisova, L. The use of acoustic microscopy to study the mechanical properties of glass-ionomer cement. Dent. Mater. 2004, 20, 358–363. [Google Scholar] [CrossRef]
- Piconi, C.; Maccauro, G. Zirconia as a ceramic biomaterial. Biomaterials 1999, 20, 1–25. [Google Scholar] [CrossRef]
- Ko, C.C.; Chu, C.S.; Chung, K.H.; Lee, M.C. Effects of posts on dentin stress distribution in pulpless teeth. J. Prosthet. Dent. 1992, 68, 421–427. [Google Scholar] [CrossRef]
- Osman, M.L.M.; Lim, T.W.; Chang, H.-C.; Ab Ghani, A.R.; Tsoi, J.K.H.; Ab Ghani, S.M. Structural Integrity of Anterior Ceramic Resin-Bonded Fixed Partial Denture: A Finite Element Analysis Study. J. Funct. Biomater. 2023, 14, 108. [Google Scholar] [CrossRef] [PubMed]
- Arinc, H. Effects of Prosthetic Material and Framework Design on Stress Distribution in Dental Implants and Peripheral Bone: A Three-Dimensional Finite Element Analysis. Med. Sci. Monit. 2018, 24, 4279–4287. [Google Scholar] [CrossRef] [PubMed]
- Yamanishi, Y.; Yamaguchi, S.; Imazato, S.; Nakano, T.; Yatani, H. Influences of implant neck design and implant-abutment joint type on peri-implant bone stress and abutment micromovement: Three-dimensional finite element analysis. Dent. Mater. 2012, 28, 26–33. [Google Scholar] [CrossRef]
- Magne, P. Efficient 3D finite element analysis of dental restorative procedures using micro-CT data. Dent. Mater. 2007, 23, 539–548. [Google Scholar] [CrossRef] [PubMed]
- Chun, H.J.; Cheong, S.Y.; Han, J.H.; Heo, S.J.; Chung, J.P.; Rhyu, I.C.; Choi, Y.C.; Baik, H.K.; Ku, Y.; Kim, M.H. Evaluation of design parameters of osseointegrated dental implants using finite element analysis. J. Oral Rehabil. 2002, 29, 565–574. [Google Scholar] [CrossRef] [PubMed]
- Eskitascioglu, G.; Usumez, A.; Sevimay, M.; Soykan, E.; Unsal, E. The influence of occlusal loading location on stresses transferred to implant-supported prostheses and supporting bone: A three-dimensional finite element study. J. Prosthet. Dent. 2004, 91, 144–150. [Google Scholar] [CrossRef]
- Schindler, H.J.; Stengel, E.; Spiess, W.E.L. Feedback control during mastication of solid food textures—A clinical-experimental study. J. Prosthet. Dent. 1998, 80, 330–336. [Google Scholar] [CrossRef]
- Van der Bilt, A. Assessment of mastication with implications for oral rehabilitation: A review. J. Oral Rehabil. 2011, 38, 754–780. [Google Scholar] [CrossRef]
- Geng, J.-P.; Tan, K.B.C.; Liu, G.-R. Application of finite element analysis in implant dentistry: A review of the literature. J. Prosthet. Dent. 2001, 85, 585–598. [Google Scholar] [CrossRef]
- Chang, C.L.; Chen, C.S.; Huang, C.H.; Hsu, M.L. Finite element analysis of the dental implant using a topology optimization method. Med. Eng. Phys. 2012, 34, 999–1008. [Google Scholar] [CrossRef]
- Datte, C.-E.; Nishioka, R.-S.; Bottino, M.-A.; Evangelhista, A.-D.M.; Monteiro, F.M.d.M. Influence of different restorative materials on the stress distribution in dental implants. J. Clin. Exp. Dent. 2018, 10, e439. [Google Scholar] [CrossRef] [PubMed]
- Rand, A.; Stiesch, M.; Eisenburger, M.; Greuling, A. The effect of direct and indirect force transmission on peri-implant bone stress—A contact finite element analysis. Comput. Methods Biomech. Biomed. Eng. 2017, 20, 1132–1139. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jemaa, H.; Eisenburger, M.; Greuling, A. Automated Remodelling of Connectors in Fixed Partial Dentures. Dent. J. 2023, 11, 252. https://doi.org/10.3390/dj11110252
Jemaa H, Eisenburger M, Greuling A. Automated Remodelling of Connectors in Fixed Partial Dentures. Dentistry Journal. 2023; 11(11):252. https://doi.org/10.3390/dj11110252
Chicago/Turabian StyleJemaa, Hassen, Michael Eisenburger, and Andreas Greuling. 2023. "Automated Remodelling of Connectors in Fixed Partial Dentures" Dentistry Journal 11, no. 11: 252. https://doi.org/10.3390/dj11110252
APA StyleJemaa, H., Eisenburger, M., & Greuling, A. (2023). Automated Remodelling of Connectors in Fixed Partial Dentures. Dentistry Journal, 11(11), 252. https://doi.org/10.3390/dj11110252