Non-Covalent Interactions Involving Alkaline-Earth Atoms and Lewis Bases B: An ab Initio Investigation of Beryllium and Magnesium Bonds, B···MR2 (M = Be or Mg, and R = H, F or CH3)
Abstract
1. Introduction
2. Results
2.1. Molecular Geometries
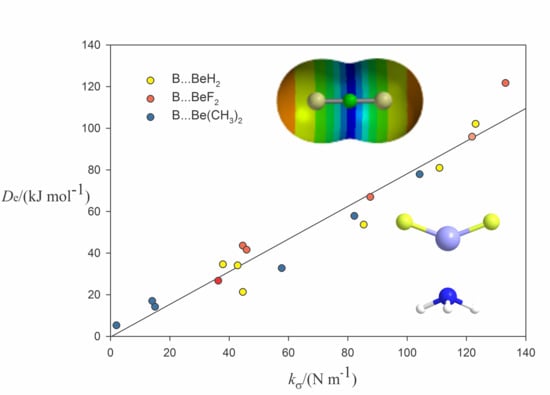
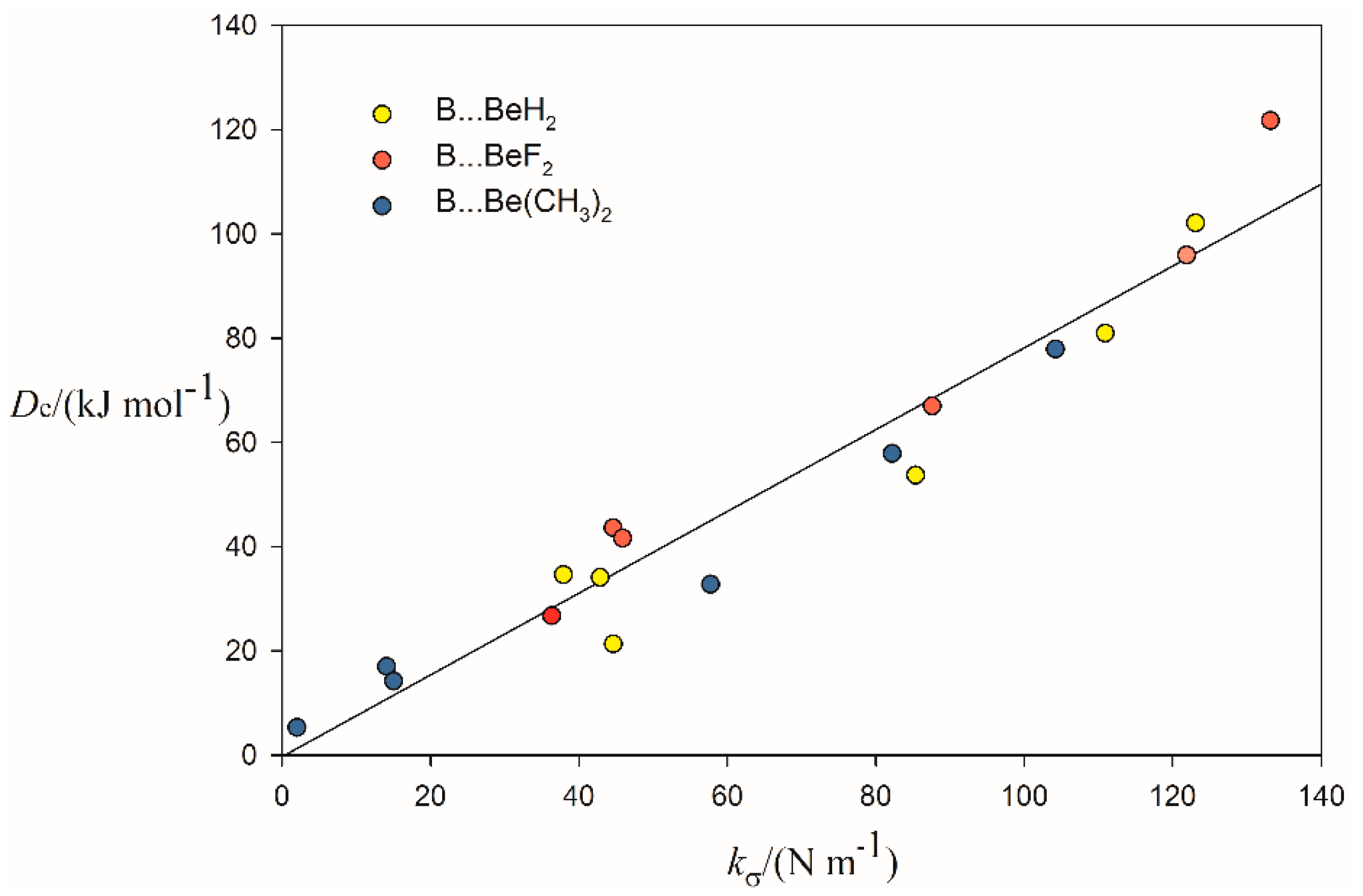
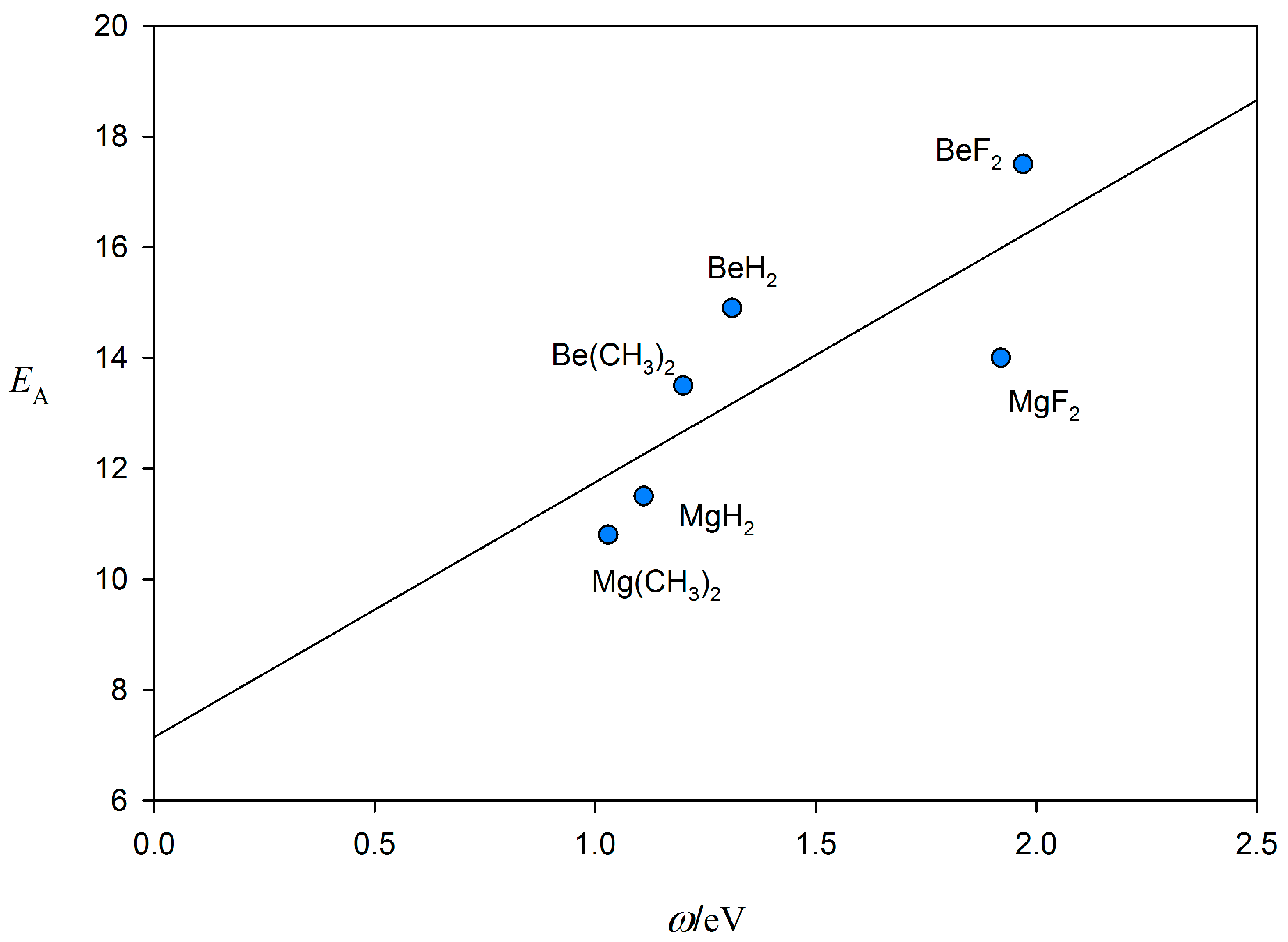
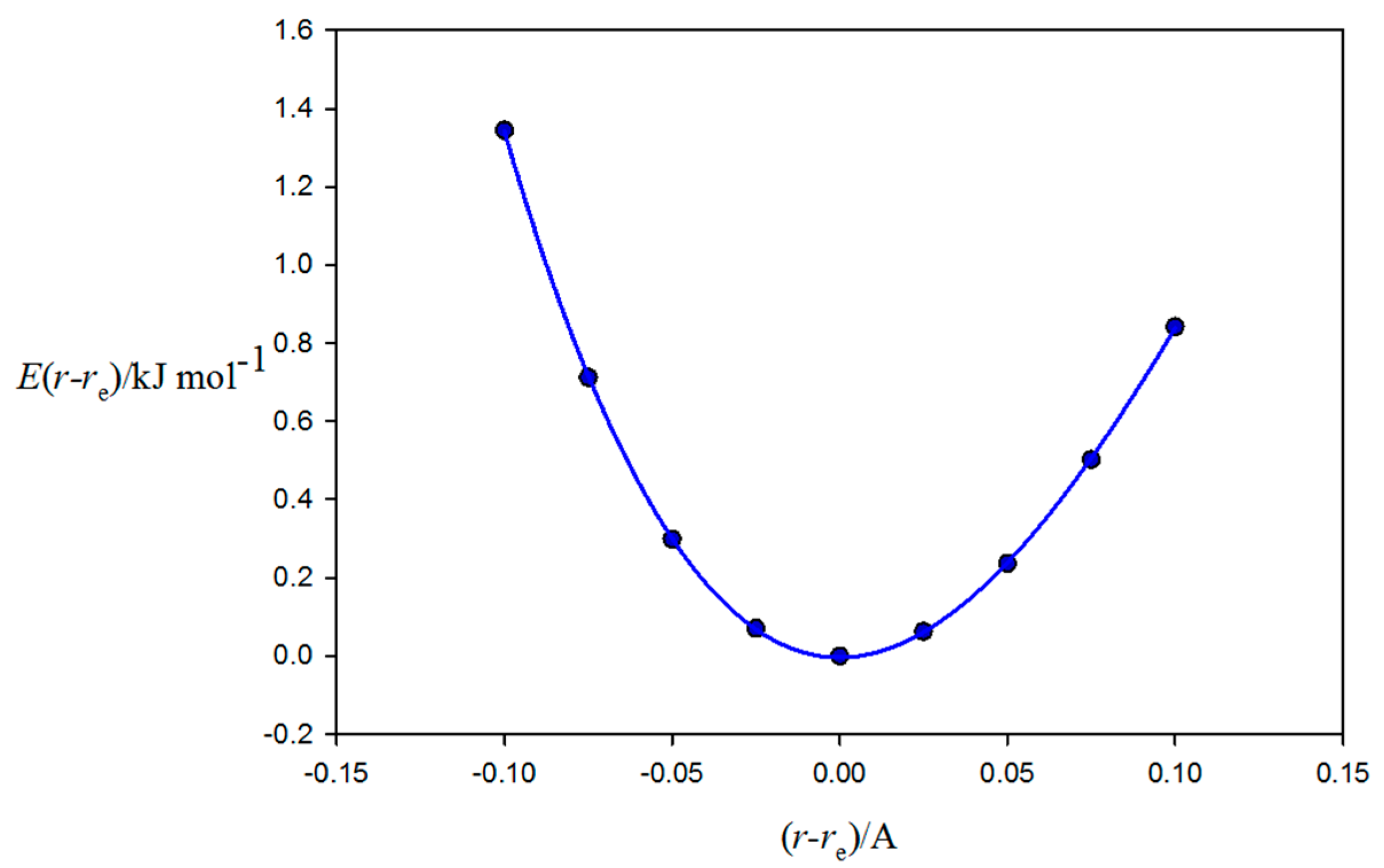
2.2. Relationship between De and kσ
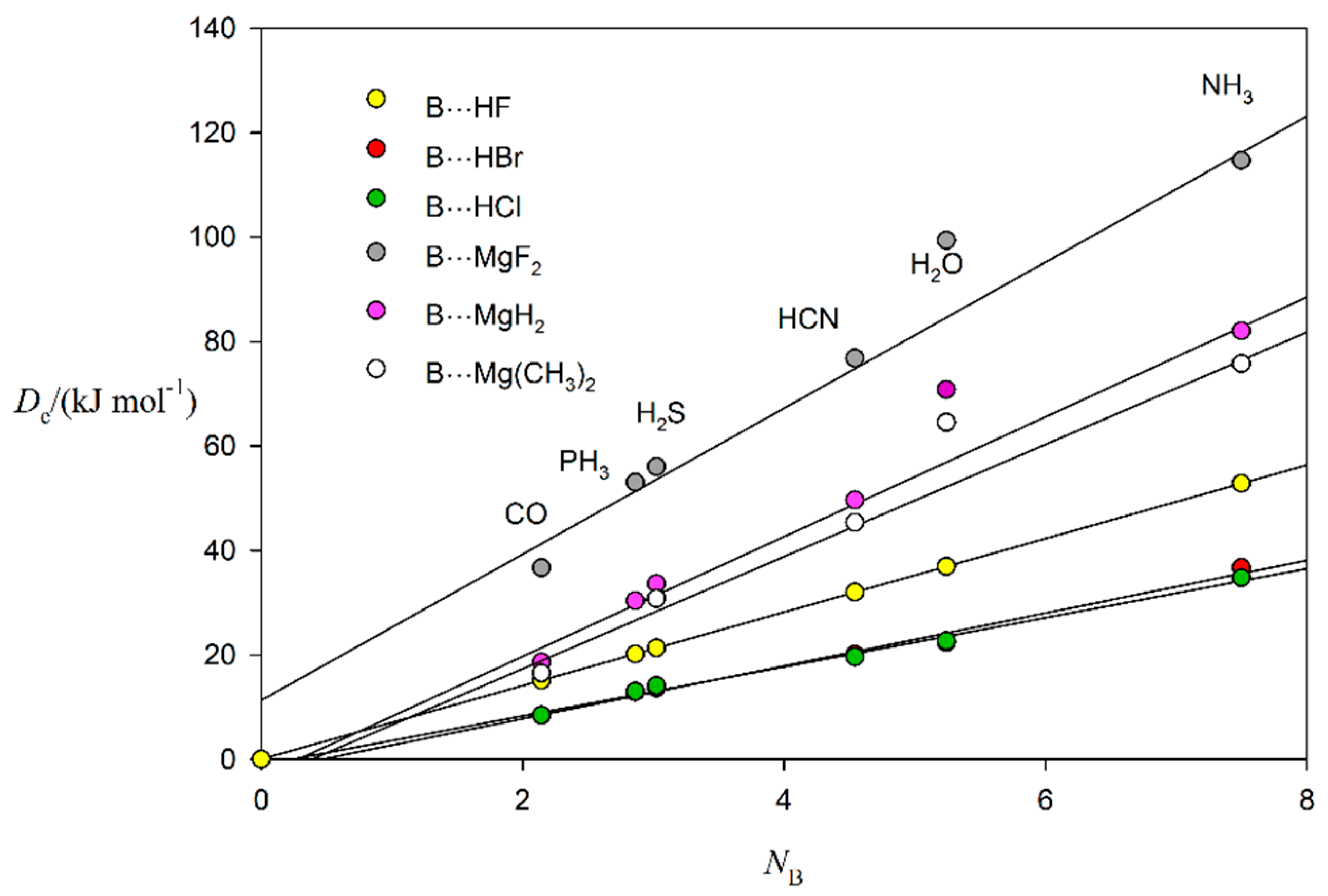
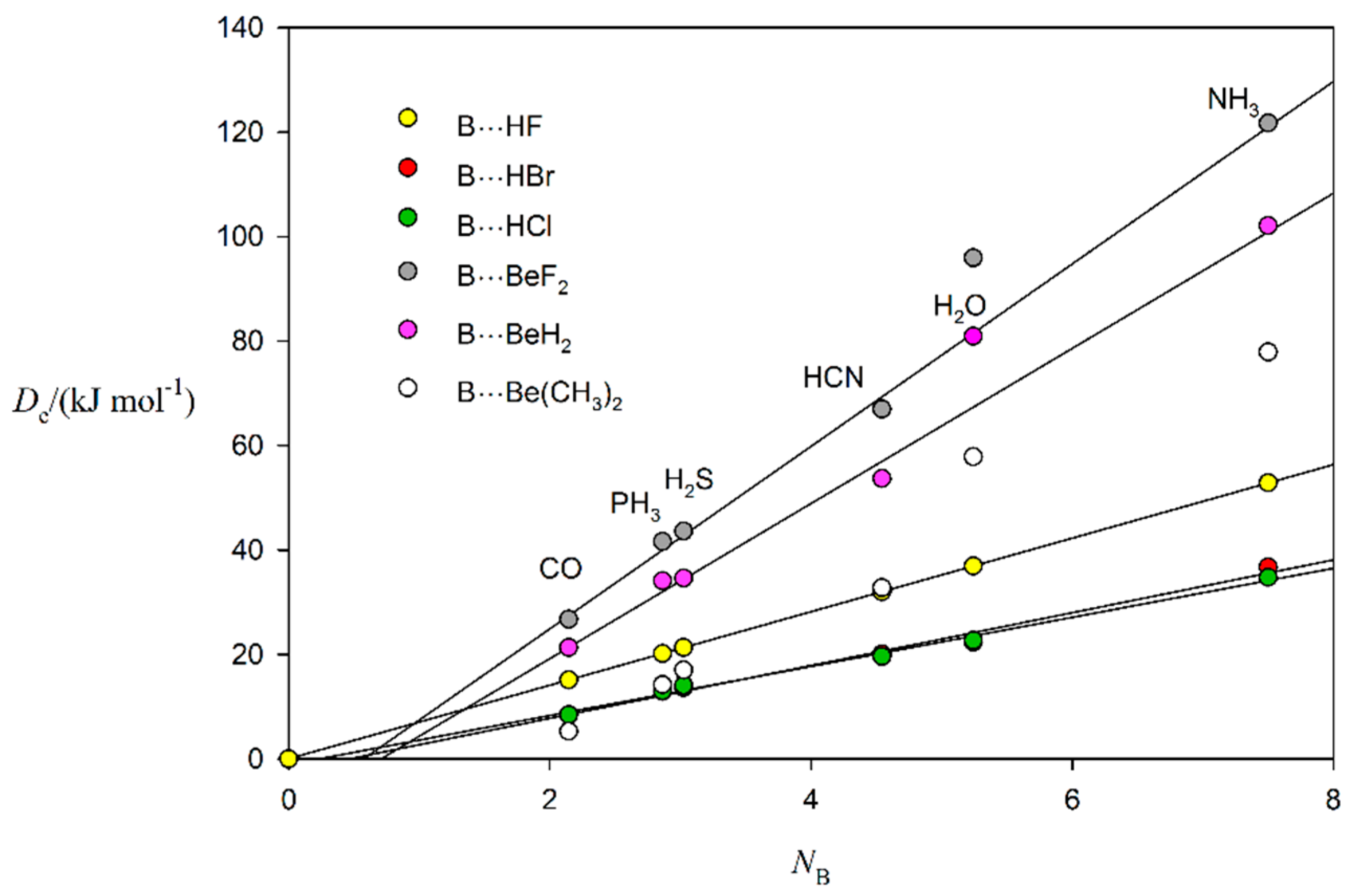
2.3. Nucleophilicities of B and Electrophilicities of BeR2 and MgR2 (R = F, H or CH3)
3. Theoretical Methods
4. Conclusions
The equilibrium geometry of alkaline-earth bonded B···MR2 complexes (M = Be, Mg…) can be predicted by assuming that a radius of the most electrophilic ring around the M atom that is perpendicular to the MR2 line coincides with the axis of a non-bonding electron pair carried by B. Some deviation of MR2 from collinearity could occur.
A alkaline-earth non-covalent bond occurs when there is evidence of a net attractive interaction between an electrophilic region associated with an atom of an element, E{II}, in a molecular entity and a nucleophilic region (e.g., a n-pair or π-pair of electrons) in another, or the same, molecular entity, where E{II} is an element of Group II in the periodic table.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hassel, O.; Rømming, C. Direct structural evidence for weak charge-transfer bonds in solids containing chemically saturated molecules. Quart. Rev. Chem. Soc. 1962, 16, 1–18. [Google Scholar] [CrossRef]
- Legon, A.C. Pre-reactive complexes of dihalogens XY with Lewis bases B in the gas phase: A systematic case for the ‘halogen’ analogue B···XY of the hydrogen bond B···HX. Angew. Chem. Int. Ed. Engl. 1999, 38, 2686–2714. [Google Scholar] [CrossRef]
- Neukirch, H.; Pilati, T.; Resnati, G. Halogen bonding based recognition processes: World parallel to hydrogen bonding. Acc. Chem. Res. 2005, 38, 386–395. [Google Scholar]
- Metrangolo, P.; Resnati, G. (Eds.) Halogen bonding 1, Impact on Materials and Life Sciences. In Topics in Current Chemistry; Springer: Berlin, Germany, 2015; Volume 358, pp. 1–280. [Google Scholar]
- Legon, A.C. The halogen bond: An interim perspective. Phys. Chem. Chem. Phys. 2010, 12, 7736–7747. [Google Scholar] [CrossRef] [PubMed]
- Arunan, E.; Desiraju, G.R.; Klein, R.A.; Sadlej, J.; Scheiner, S.; Alkorta, I.; Clary, D.C.; Crabtree, R.H.; Dannenberg, J.J.; Hobza, P.; et al. Definition of the hydrogen bond (IUPAC Recommendations 2011). Pure Appl. Chem. 2011, 83, 1637–1641. [Google Scholar] [CrossRef]
- Desiraju, G.R.; Ho, P.S.; Kloo, L.; Legon, A.C.; Marquardt, R.; Metrangolo, P.; Politzer, P.A.; Resnati, G.; Rissanen, K. Definition of the halogen bond (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1711–1713. [Google Scholar] [CrossRef]
- Legon, A.C. Tetrel, pnictogen and chalcogen bonds identified in the gas phase before they had names: A systematic look at non-covalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 14884–14896. [Google Scholar] [CrossRef] [PubMed]
- Alcock, N.W. Secondary bonding to non-metallic elements. Adv. Inorg. Chem. Radiochem. 1972, 15, 1–58. [Google Scholar]
- Bauzá, A.; Mooibroek, T.J.; Frontera, A. Tetrel-bonding interaction: Rediscovered supramolecular force? Angew. Chem. Int. Ed. 2013, 52, 12317–12321. [Google Scholar] [CrossRef] [PubMed]
- Zahn, S.; Frank, R.; Hey-Hawkins, E.; Kirchner, B. Pnicogen bonds: A new molecular linker? Chem. Eur. J. 2011, 17, 6034–6038. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Ji, B.; Zhang, Y. Chalcogen bond: A sister noncovalent bond to halogen bond. J. Phys. Chem. A 2009, 113, 8132–8135. [Google Scholar] [CrossRef] [PubMed]
- Categorizing Chalcogen, Pnictogen, and Tetrel Bonds, and Other Interactions Involving Groups 14-16 Elements. Available online: https://iupac.org/projects/project-details/?project_nr=2016-001-2-300 (accessed on 15 January 2019).
- Oliveira, V.; Cremer, D.; Kraka, E. The many facets of chalcogen bonding described by vibrational spectroscopy. J. Phys. Chem. 2017, 121, 6845–6862. [Google Scholar] [CrossRef] [PubMed]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M.; Yamashita, K. Can combined electrostatics and polarization effects alone explain the F···F negative-negative bonding in simple fluoro-substituted benzene derivatives. Computation 2018, 6, 51. [Google Scholar] [CrossRef]
- Wang, C.W.; Fu, Y.Z.; Zhang, L.N.; Danovich, D.; Shaik, S.; Mo, Y. Hydrogen and halogen bonds between ions of like charges: Are they anti-electrostatic in nature? J. Comput. Chem. 2018, 39, 481–487. [Google Scholar] [CrossRef] [PubMed]
- Clark, T. Hydrogen bonds and σ holes. Faraday Discuss. 2017, 203, 9–27. [Google Scholar] [CrossRef] [PubMed]
- Legon, A.C.; Walker, N.R. What’s in a name? “Coinage-metal” non-covalent bonds and their definition. Phys. Chem. Chem. Phys. 2018, 20, 19332–19338. [Google Scholar] [CrossRef] [PubMed]
- Yáñez, M.; Sanz, P.; Mó, O.; Alkorta, I. and Elguero, J. Beryllium bonds, do they exist? J. Chem. Theory Comput. 2009, 5, 2763–2771. [Google Scholar] [CrossRef] [PubMed]
- Alkorta, I.; Legon, A.C. Nucleophilicies of Lewis bases B and electrophilicities of Lewis acids A determined from the dissociation energies of complexes B···A involving hydrogen bonds, tetrel bonds, pnictogen bonds, chalcogen bonds and halogen bonds. Molecules 2017, 22, 1786. [Google Scholar] [CrossRef] [PubMed]
- Alkorta, I.; Legon, A.C. Strengths of non-covalent interactions in hydrogen-bonded complexes B···HX and halogen-bonded complexes B···XY (X, Y = F, Cl): An ab initio investigation. New J. Chem. 2018, 42, 10548–10554. [Google Scholar] [CrossRef]
- Legon, A.C. A reduced radial potential energy function for the halogen bond and the hydrogen bond in complexes B···XY and B···HX, where X and Y are halogen atoms. Phys. Chem. Chem. Phys. 2014, 16, 12415–12421. [Google Scholar] [CrossRef] [PubMed]
- Ingold, C.K. Structure and Mechanism in Organic Chemistry; Cornell University Press: Ithaca, NY, USA, 1953; Chapter 2; pp. 67–72. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Anusiewicz, I.; Skurski, P. An ab initio study on BeX3− superhalogen anions (X = F, Cl, Br). Chem. Phys. Lett. 2002, 358, 426–434. [Google Scholar] [CrossRef]
- Oliveira, V.; Kraka, E.; Cremer, D. Quantitative assessment of halogen bonding utilizing vibrational spectroscopy. Inorg. Chem. 2017, 56, 488–502. [Google Scholar] [CrossRef] [PubMed]
- Legon, A.C.; Millen, D.J. Hydrogen bonding as a probe for electron densities: Limiting gas phase nucleophilicities and electrophilicities of B and HX. J. Am. Chem. Soc. 1987, 109, 356–358. [Google Scholar] [CrossRef]
- Domingo, L.R.; Rios-Gutiérrez, M.; Pérez, P. Applications of the conceptual density functional theory indices to organic chemistry reactivity. Molecules 2016, 21, 748. [Google Scholar] [CrossRef] [PubMed]
- Purvis, G.D., III; Bartlett, R.J. A full coupled-cluster singles and doubles model—The inclusion of disconnected triples. J. Chem. Phys. 1982, 76, 1910–1918. [Google Scholar] [CrossRef]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Feller, D. The use of systematic sequences of wave functions for estimating the complete basis set, full configuration interaction limit in water. J. Chem. Phys. 1993, 98, 7059–7071. [Google Scholar] [CrossRef]
- Halkier, A.; Helgaker, T.; Jorgensen, P.; Klopper, W.; Olsen, J. Basis-set convergence of the energy in molecular Hartree–Fock calculations. Chem. Phys. Lett. 1999, 302, 437–446. [Google Scholar] [CrossRef]
- Werner, H.-J.; Knowles, P.J.; Knizia, G.; Manby, F.R.; Schütz, M.; Celani, P.; Korona, T.; Lindh, R.; Mitrushenkov, A.; Rauhut, G.; et al. MOLPRO, Version 2012.1. Available online: http://www.molpro.net (accessed on 15 January 2019).
- Mayr, H.; Patz, M. Scales of nucleophilicity and electrophilicity: A system of ordering polar organic and organometallic reactions. Angew. Chem. Int. Ed. Engl. 1994, 33, 938–957. [Google Scholar] [CrossRef]

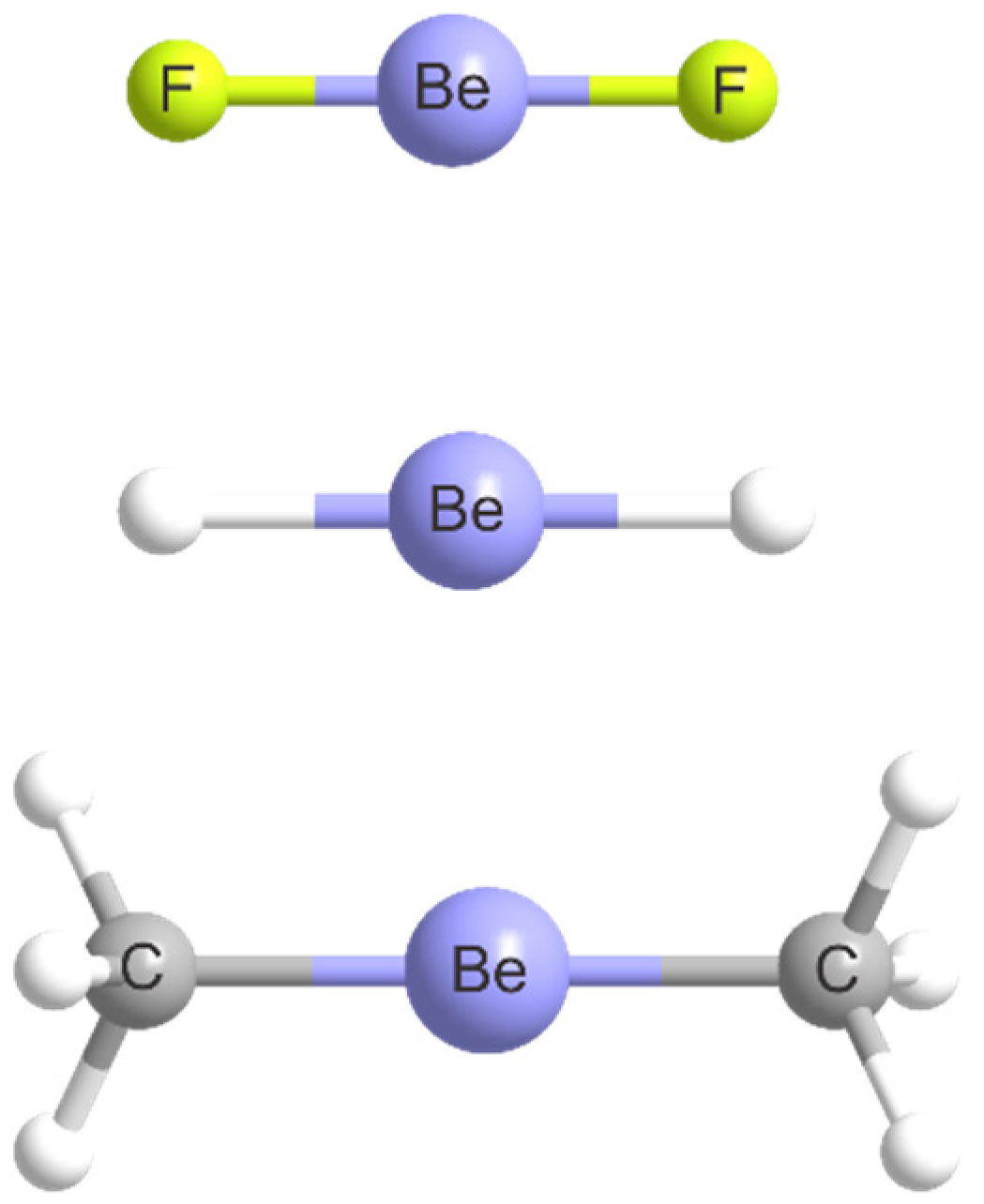
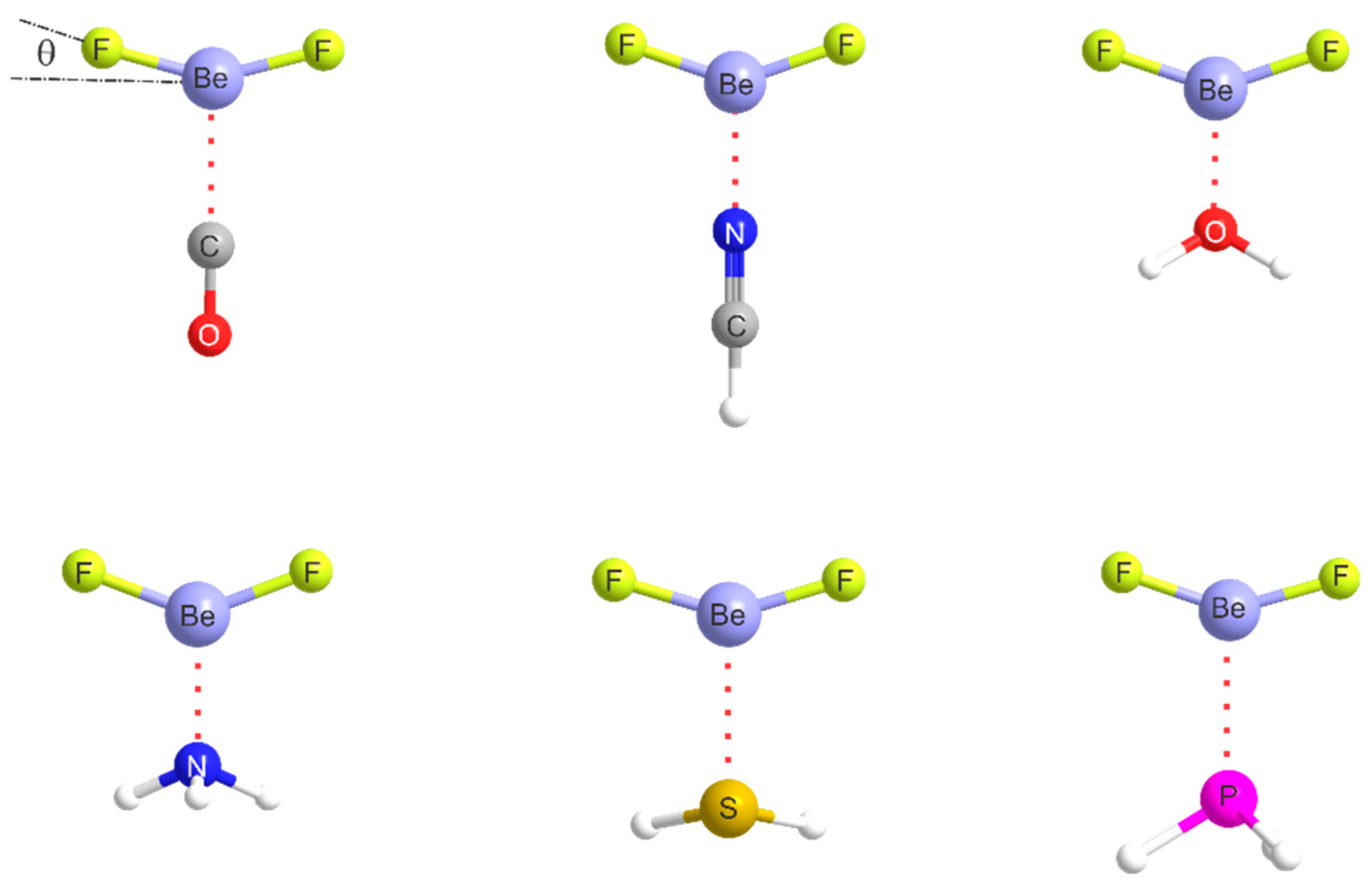
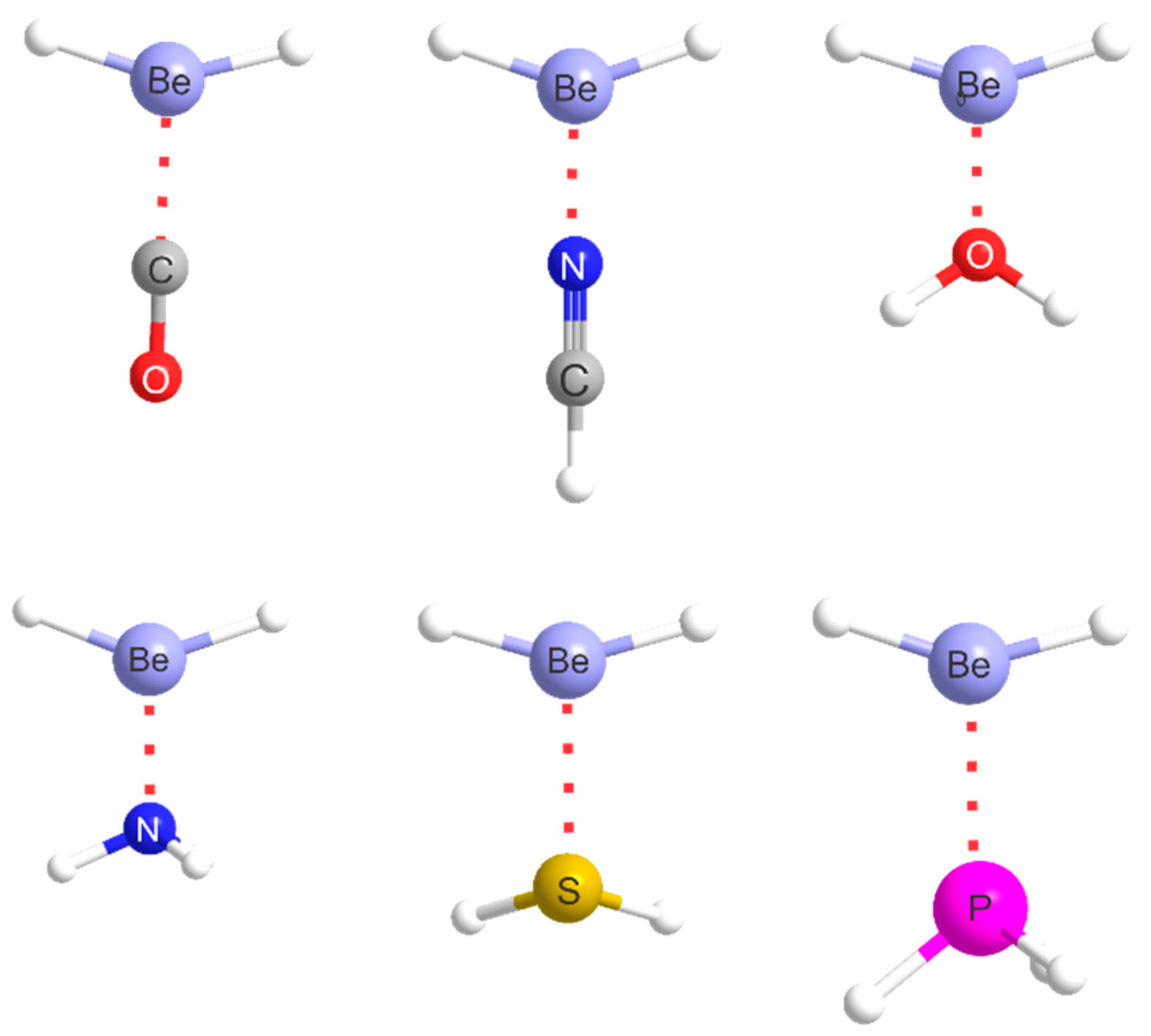
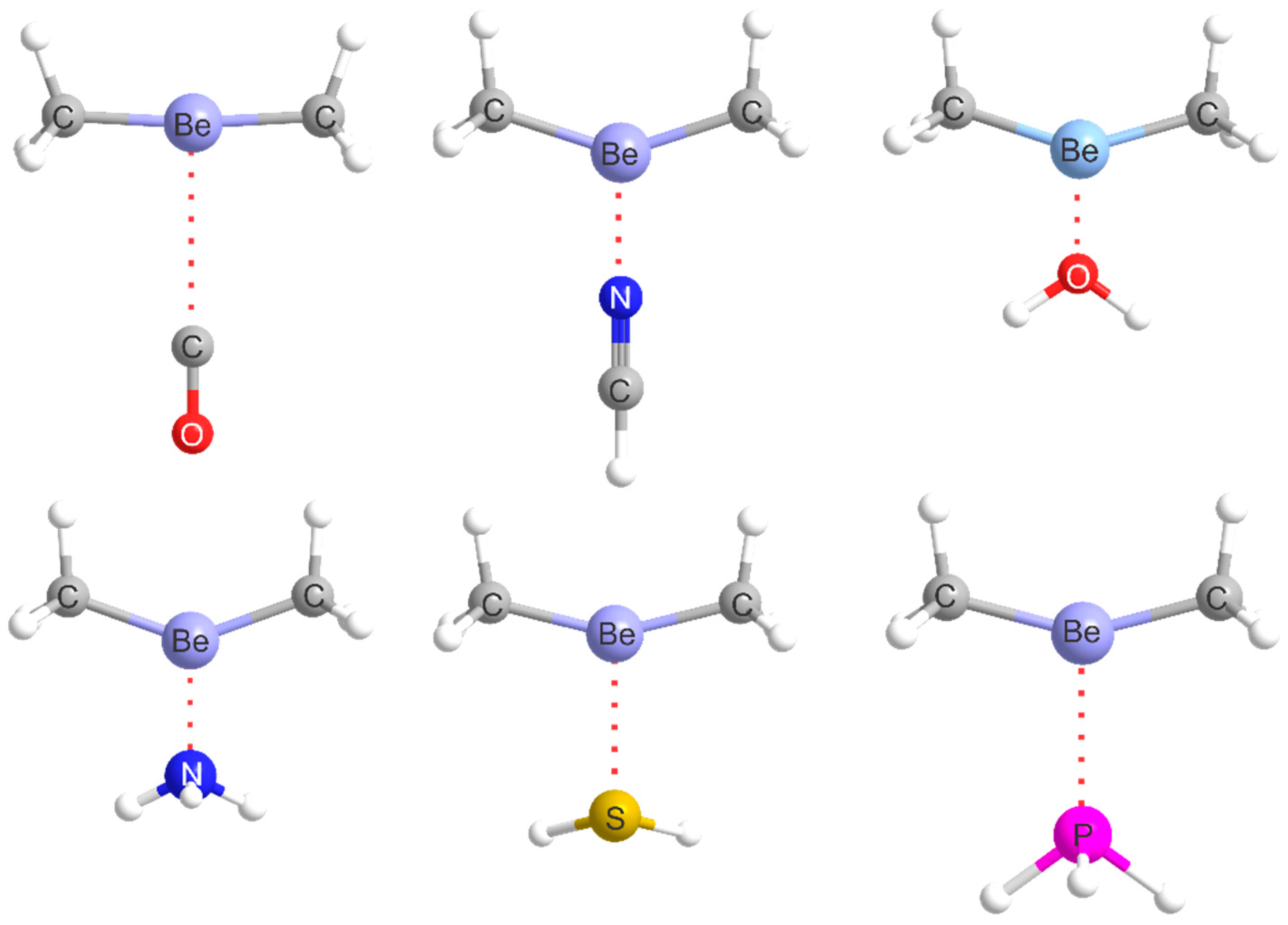

| Complex | Lewis Base B | De/kJ·mol−1 | kσ/N·m−1 | r(Be···A)/Å b | Angle θ/° c | δr(Be–R)/Å d |
|---|---|---|---|---|---|---|
| B⋯BeF2 | CO | 26.72 | 36.33 | 2.040 | 15.0 | 0.024 |
| NCH | 66.98 | 87.59 | 1.818 | 19.2 | 0.035 | |
| H2O | 95.94 | 121.89 | 1.697 | 18.7 | 0.040 | |
| NH3 | 121.73 | 133.19 | 1.777 | 21.1 | 0.045 | |
| H2S | 43.57 | 44.59 | 2.289 | 16.9 | 0.029 | |
| PH3 | 41.59 | 45.87 | 2.337 | 17.7 | 0.035 | |
| B⋯BeH2 | CO | 21.29 | 44.61 | 1.942 | 16.3 | 0.019 |
| NCH | 53.67 | 85.38 | 1.790 | 19.1 | 0.026 | |
| H2O | 80.94 | 110.93 | 1.688 | 18.0 | 0.030 | |
| NH3 | 102.10 | 123.11 | 1.783 | 20.5 | 0.035 | |
| H2S | 34.58 | 37.91 | 2.270 | 16.0 | 0.021 | |
| PH3 | 34.08 | 42.86 | 2.305 | 17.0 | 0.023 | |
| B⋯Be(CH3)2 | CO | 5.28 | 2.00 | 2.922 | 3.2 | 0.004 |
| NCH | 32.75 | 57.73 | 1.844 | 18.1 | 0.035 | |
| H2O | 57.82 | 82.21 | 1.720 | 18.7 | 0.040 | |
| NH3 | 77.89 | 104.24 | 1.809 | 20.0 | 0.046 | |
| H2S | 16.97 | 14.07 | 2.425 | 14.1 | 0.025 | |
| PH3 | 14.19 | 15.02 | 2.456 | 14.8 | 0.027 |
| Complex | Lewis Base B | De/kJ·mol−1 | kσ/N·m−1 | r(Mg⋯A)/Å b | Angle θ/° c | δr(Mg–R)/Åd |
|---|---|---|---|---|---|---|
| B⋯MgF2 | CO | 36.67 | 39.70 | 2.396 | 8.7 | 0.011 |
| NCH | 76.80 | 72.72 | 2.178 | 14.1 | 0.019 | |
| H2O | 99.36 | 97.67 | 2.046 | 11.4 | 0.021 | |
| NH3 | 114.69 | 90.21 | 2.163 | 14.1 | 0.024 | |
| H2S | 56.03 | 44.02 | 2.631 | 10.8 | 0.016 | |
| PH3 | 53.01 | 41.96 | 2.703 | 11.7 | 0.017 | |
| B⋯MgH2 | CO | 18.57 | 16.81 | 2.567 | 7.6 | 0.008 |
| NCH | 49.62 | 45.08 | 2.269 | 13.0 | 0.019 | |
| H2O | 70.81 | 68.88 | 2.111 | 11.3 | 0.023 | |
| NH3 | 82.05 | 64.97 | 2.233 | 14.0 | 0.028 | |
| H2S | 33.59 | 23.74 | 2.777 | 9.7 | 0.015 | |
| PH3 | 30.33 | 21.81 | 2.854 | 9.9 | 0.015 | |
| B⋯Mg(CH3)2 | CO | 16.52 | 13.76 | 2.609 | 6.5 | 0.006 |
| NCH | 45.33 | 41.10 | 2.285 | 12.2 | 0.015 | |
| H2O | 64.50 | 64.03 | 2.124 | 11.1 | 0.019 | |
| NH3 | 75.78 | 61.13 | 2.245 | 13.5 | 0.023 | |
| H2S | 30.79 | 20.72 | 2.808 | 8.5 | 0.011 | |
| PH3 | 27.12 | 18.85 | 2.892 | 8.9 | 0.012 |
| Nucleophilicities | Electrophilicities | ||||
|---|---|---|---|---|---|
| Lewis Base B | NB (This Work) a | NB (From [20]) b | Lewis Acid A | EA (This Work) c | EA (From [20]) b |
| CO | 2.14 | 2.12 | BeF2 | 17.5(4) | - |
| PH3 | 2.86 | 3.12 | BeH2 | 14.9(6) | - |
| H2S | 3.02 | 3.43 | Be(CH3)2 | 13.5(6) | - |
| HCN | 4.54 | 4.27 | MgF2 | 14.0(8) | - |
| H2O | 5.24 | 4.89 | MgH2 | 11.5(5) | - |
| NH3 | 7.50 | 7.52 | Mg(CH3)2 | 10.8(6) | - |
| HF | 7.0 | 6.75 | |||
| HBr | 5.1(3) | 4.59 | |||
| HCl | 4.7(2) | 4.36 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alkorta, I.; Legon, A.C. Non-Covalent Interactions Involving Alkaline-Earth Atoms and Lewis Bases B: An ab Initio Investigation of Beryllium and Magnesium Bonds, B···MR2 (M = Be or Mg, and R = H, F or CH3). Inorganics 2019, 7, 35. https://doi.org/10.3390/inorganics7030035
Alkorta I, Legon AC. Non-Covalent Interactions Involving Alkaline-Earth Atoms and Lewis Bases B: An ab Initio Investigation of Beryllium and Magnesium Bonds, B···MR2 (M = Be or Mg, and R = H, F or CH3). Inorganics. 2019; 7(3):35. https://doi.org/10.3390/inorganics7030035
Chicago/Turabian StyleAlkorta, Ibon, and Anthony C. Legon. 2019. "Non-Covalent Interactions Involving Alkaline-Earth Atoms and Lewis Bases B: An ab Initio Investigation of Beryllium and Magnesium Bonds, B···MR2 (M = Be or Mg, and R = H, F or CH3)" Inorganics 7, no. 3: 35. https://doi.org/10.3390/inorganics7030035
APA StyleAlkorta, I., & Legon, A. C. (2019). Non-Covalent Interactions Involving Alkaline-Earth Atoms and Lewis Bases B: An ab Initio Investigation of Beryllium and Magnesium Bonds, B···MR2 (M = Be or Mg, and R = H, F or CH3). Inorganics, 7(3), 35. https://doi.org/10.3390/inorganics7030035