A Simple Model for Halogen Bond Interaction Energies
Abstract
:1. Introduction
2. Results and Discussion
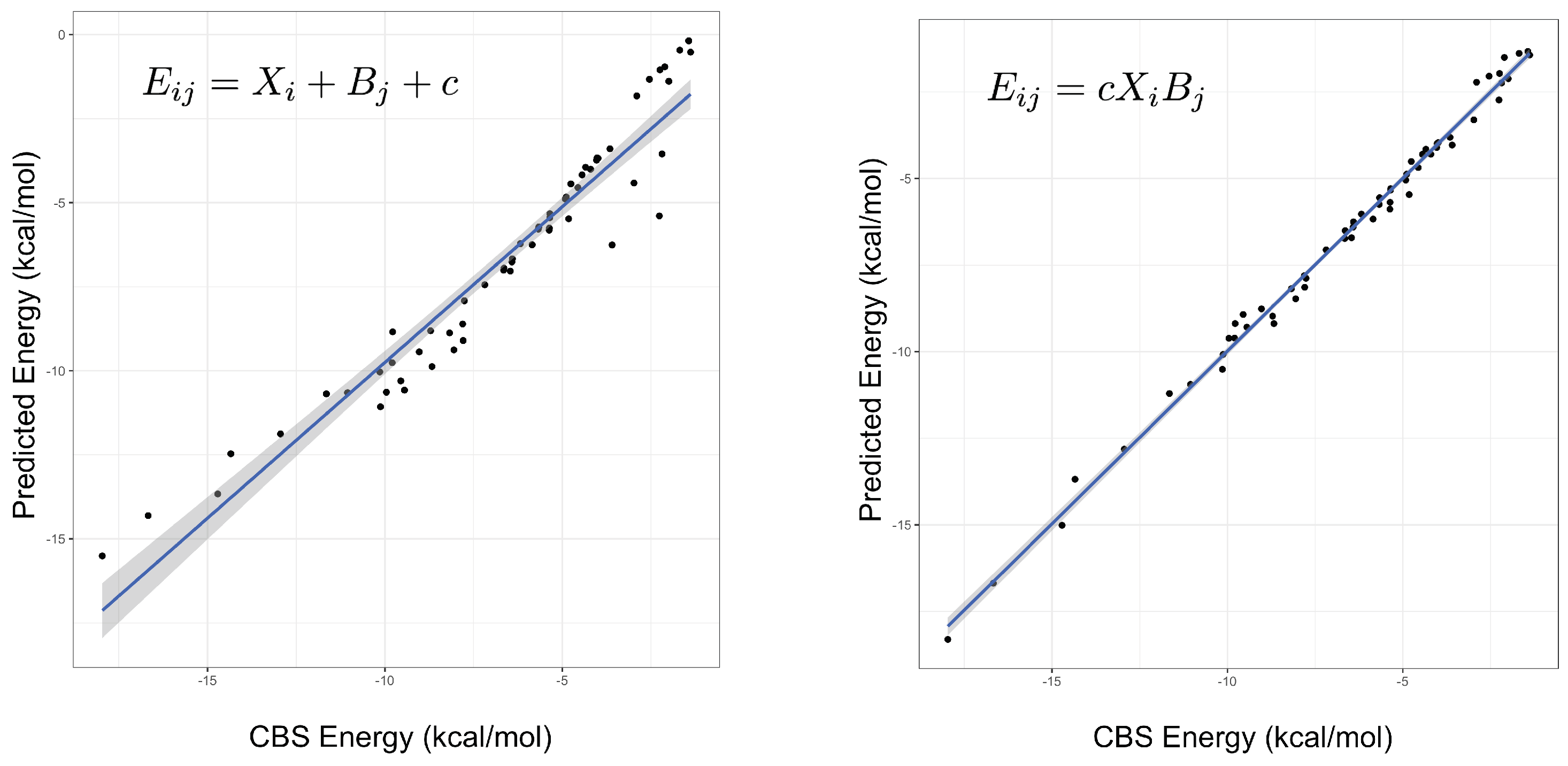
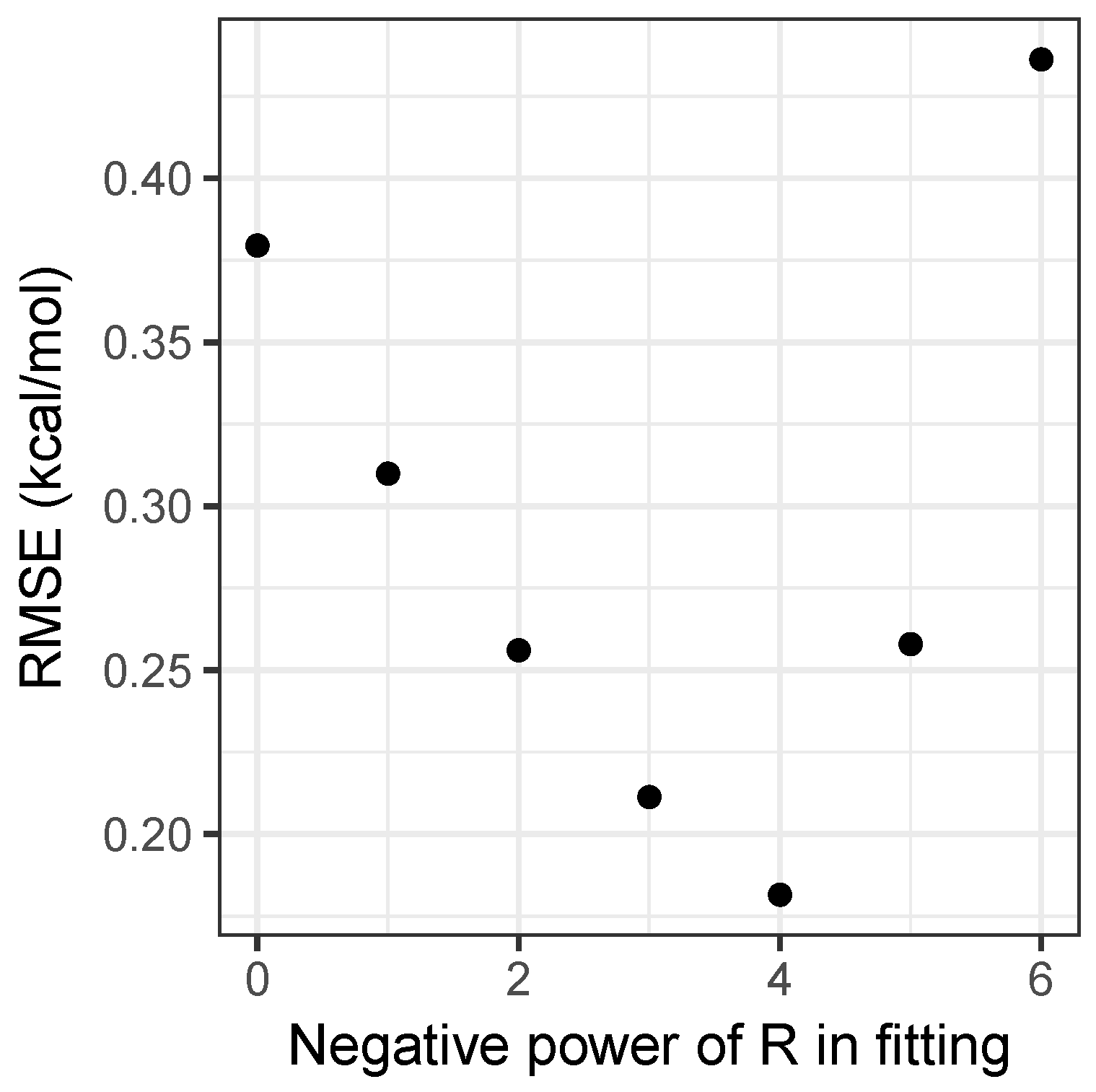
2.1. Model Fitting
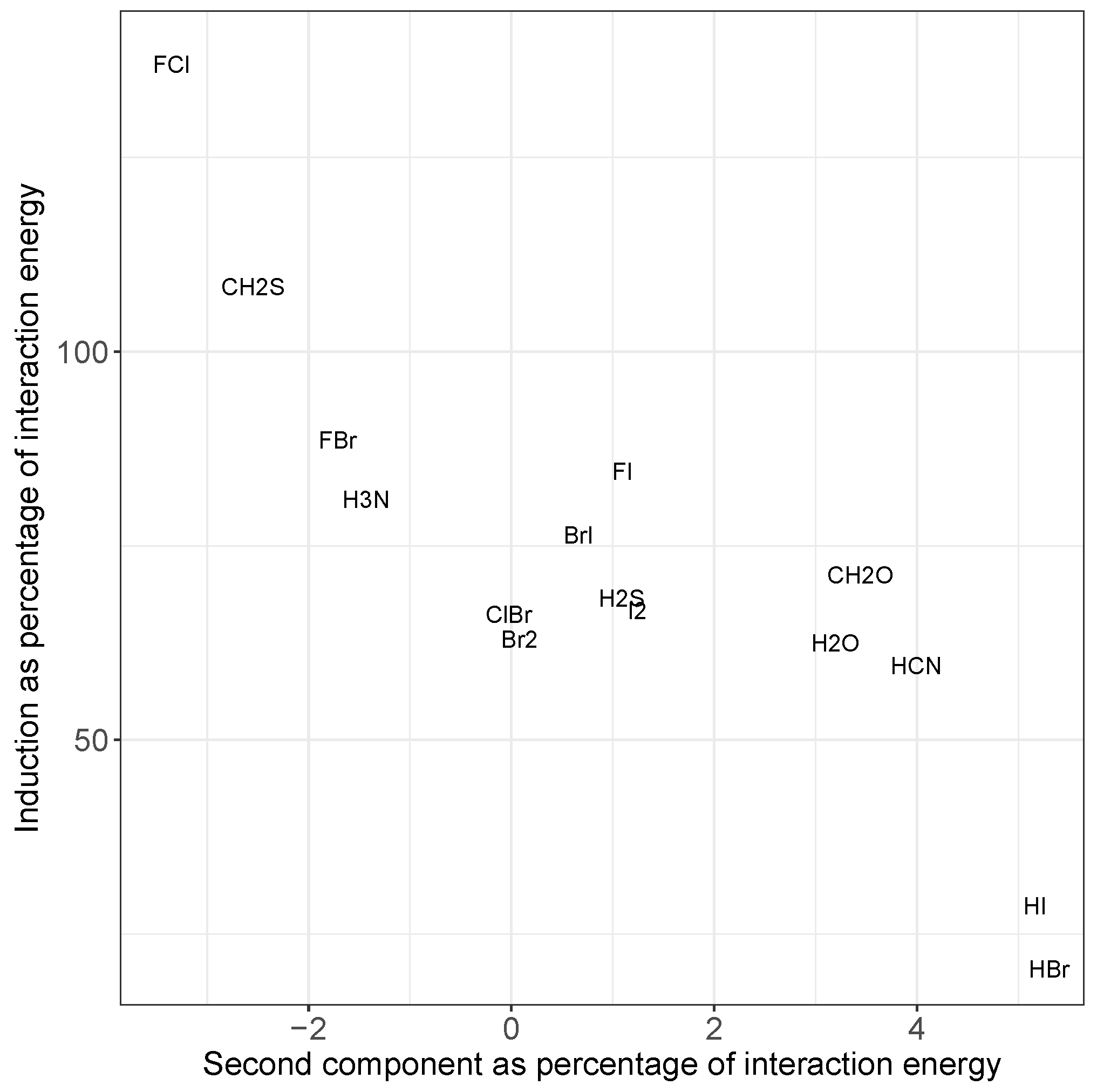
2.2. Principal Component Analysis
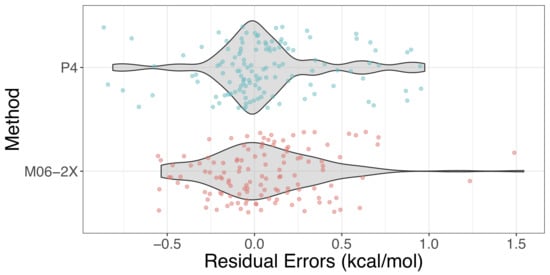
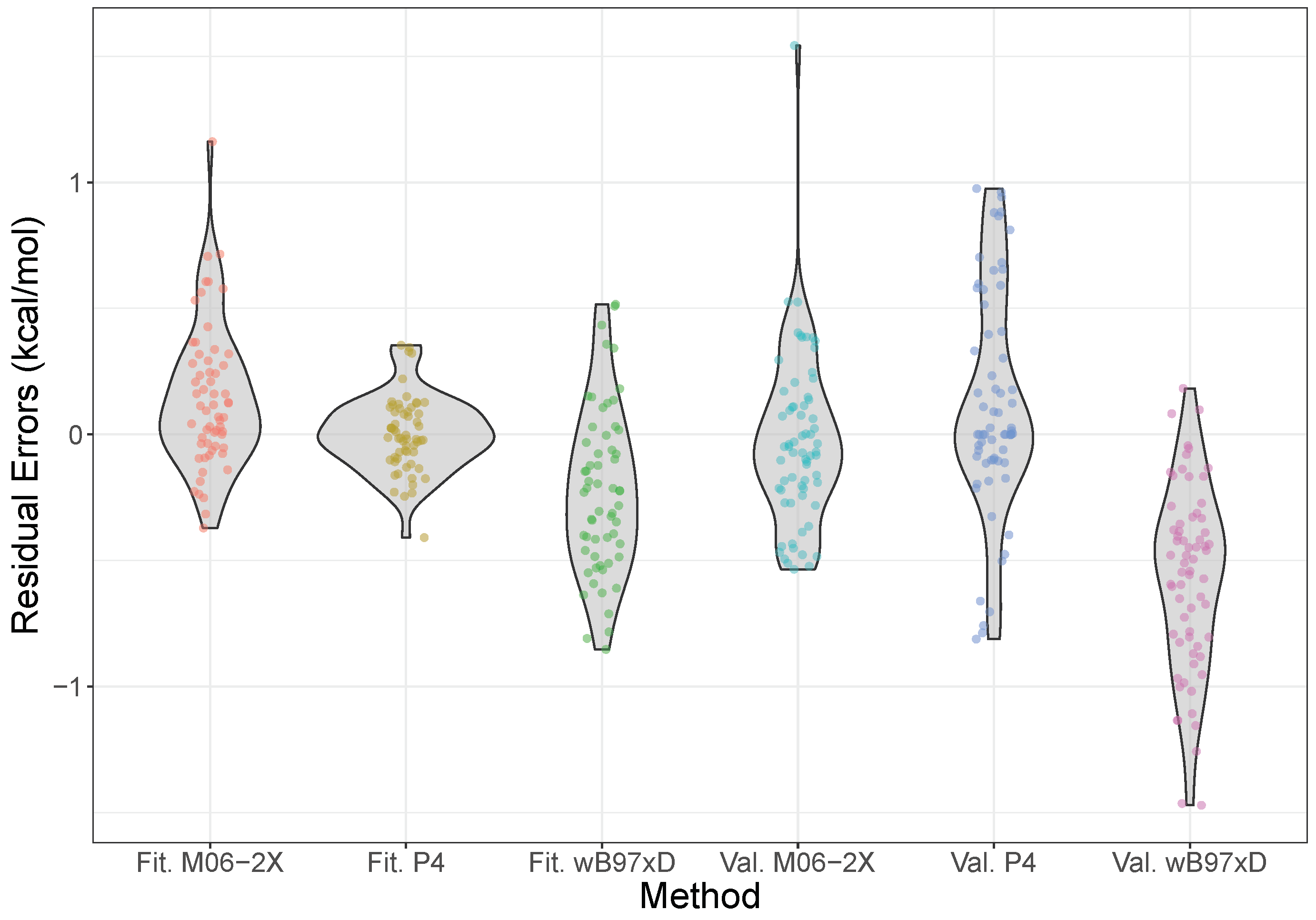
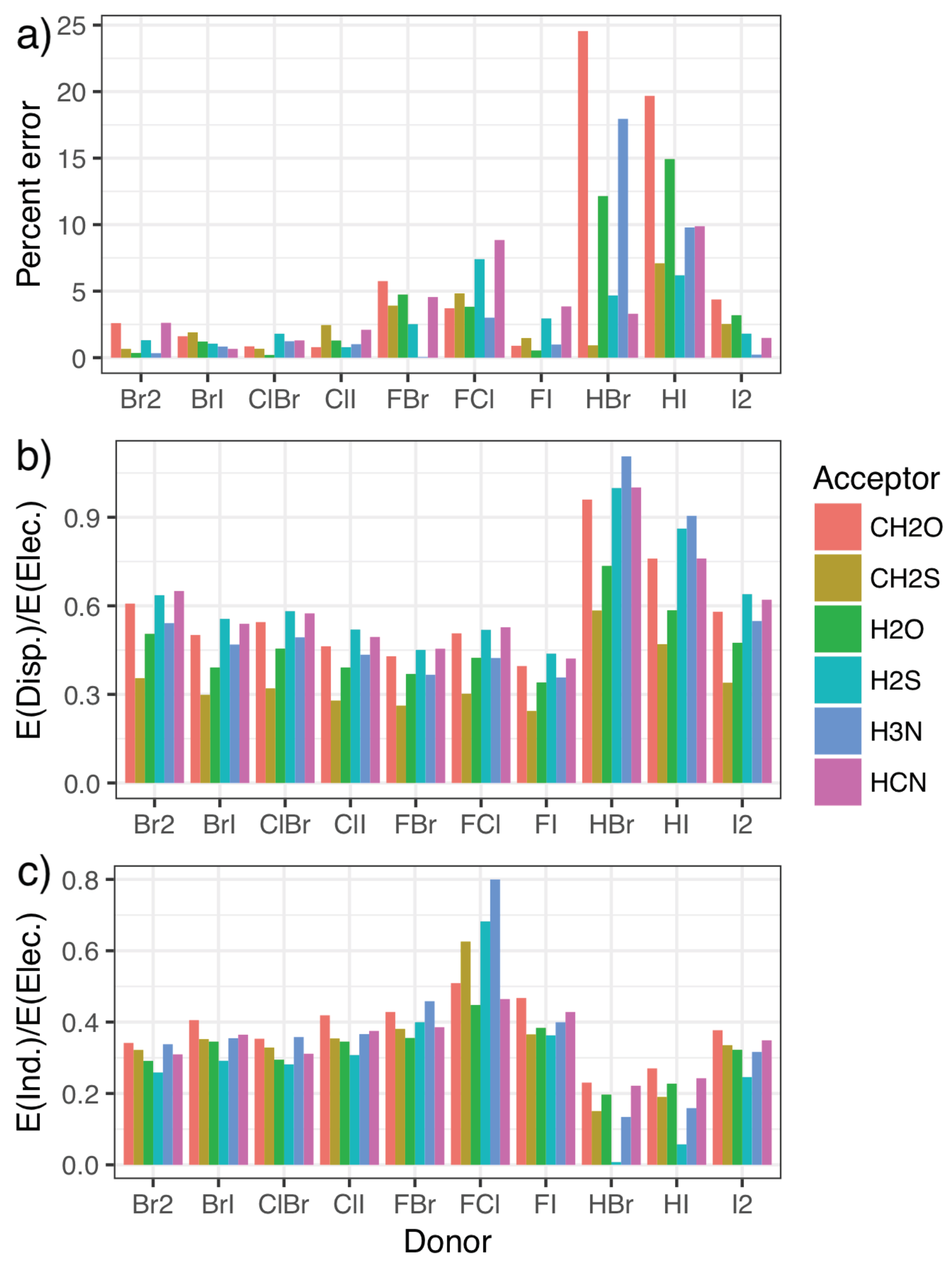
2.3. Validation and Comparison with Other Methods
2.4. The Nature of the Halogen Bond
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Colin, J.J.; Gaultier de Claubry, H. Sur Le Combinaisons De L’iode Avec Les Substances Végétales Et Animales. Ann. Chim. 1814, 90, 87–100. [Google Scholar]
- Colin, J.J. Note Sur Quelques Cominaisons De L’iode. Ann. Chim. 1814, 91, 252–272. [Google Scholar]
- Guthrie, F. On the iodide of iodammonium. J. Chem. Soc. 1863, 16, 239–244. [Google Scholar] [CrossRef]
- Benesi, H.A.; Hildebrand, J.H. A Spectrophotometric Investigation of the Interaction of Iodine with Aromatic Hydrocarbons. J. Am. Chem. Soc. 1949, 71, 2703–2707. [Google Scholar] [CrossRef]
- Hassel, O.; Rømming, C. Direct structural evidence for weak charge-transfer bonds in solids containing chemically saturated molecules. Q. Rev. Chem. Soc. 1962, 16, 1–18. [Google Scholar] [CrossRef]
- Hassel, O. Structural Aspects of Interatomic Charge-Transfer Bonding. Science 1970, 170, 497–502. [Google Scholar] [CrossRef]
- Legon, A.C. Prereactive Complexes of Dihalogens XY with Lewis Bases B in the Gas Phase: A Systematic Case for the Halogen Analogue B⋯XY of the Hydrogen Bond B⋯HX. Angew. Chem. Int. Ed. 1999, 38, 2686–2714. [Google Scholar] [CrossRef]
- Legon, A.C. The halogen bond: An interim perspective. Phys. Chem. Chem. Phys. 2010, 12, 7736–7747. [Google Scholar] [CrossRef]
- Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The Halogen Bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef]
- Beale, T.M.; Chudzinski, M.G.; Sarwar, M.G.; Taylor, M.S. Halogen bonding in solution: Thermodynamics and applications. Chem. Soc. Rev. 2013, 42, 1667–1680. [Google Scholar] [CrossRef]
- Aakeröy, C.B.; Alavi, S.; Beer, P.D.; Beyeh, N.K.; Brammer, L.; Bryce, D.L.; Clark, T.; Cottrell, S.J.; Del Bene, J.E.; Edwards, A.J.; et al. Beyond the halogen bond: General discussion. Faraday Discuss. 2017, 203, 227–244. [Google Scholar] [CrossRef] [PubMed]
- Hill, J.G.; Legon, A.C. On the directionality and non-linearity of halogen and hydrogen bonds. Phys. Chem. Chem. Phys. 2015, 17, 858–867. [Google Scholar] [CrossRef] [PubMed]
- Ouvrard, C.; Le Questel, J.Y.; Berthelot, M.; Laurence, C. Halogen-bond geometry: A crystallographic database investigation of dihalogen complexes. Acta Cryst. B 2003, 59, 512–526. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Lane, P. σ-Hole bonding and hydrogen bonding: Competitive interactions. Int. J. Quantum Chem. 2007, 107, 3046–3052. [Google Scholar] [CrossRef]
- Mukherjee, A.; Tothadi, S.; Desiraju, G.R. Halogen Bonds in Crystal Engineering: Like Hydrogen Bonds yet Different. Acc. Chem. Res. 2014, 47, 2514–2524. [Google Scholar] [CrossRef] [PubMed]
- Brammer, L. Developments in inorganic crystal engineering. Chem. Soc. Rev. 2004, 33, 476–489. [Google Scholar] [CrossRef]
- Robertson, C.C.; Wright, J.S.; Carrington, E.J.; Perutz, R.N.; Hunter, C.A.; Brammer, L. Hydrogen bonding vs. halogen bonding: The solvent decides. Chem. Sci. 2017, 8, 5392–5398. [Google Scholar] [CrossRef]
- Brammer, L. Halogen bonding, chalcogen bonding, pnictogen bonding, tetrel bonding: Origins, current status and discussion. Faraday Discuss. 2017, 203, 485–507. [Google Scholar] [CrossRef]
- Nunes, R.; Vila-Viçosa, D.; Machuqueiro, M.; Costa, P.J. Biomolecular Simulations of Halogen Bonds with a GROMOS Force Field. J. Chem. Theory Comput. 2018, 14, 5383–5392. [Google Scholar] [CrossRef]
- Montaña, Á.M. The σ and π Holes. The Halogen and Tetrel Bondings: Their Nature, Importance and Chemical, Biological and Medicinal Implications. Chem. Sel. 2017, 2, 9094–9112. [Google Scholar] [CrossRef]
- Lu, Y.; Shi, T.; Wang, Y.; Yang, H.; Yan, X.; Luo, X.; Jiang, H.; Zhu, W. Halogen Bonding—A Novel Interaction for Rational Drug Design? J. Med. Chem. 2009, 52, 2854–2862. [Google Scholar] [CrossRef] [PubMed]
- Auffinger, P.; Hays, F.A.; Westhof, E.; Ho, P.S. Halogen bonds in biological molecules. Proc. Natl. Acad. Sci. USA 2004, 101, 16789–16794. [Google Scholar] [CrossRef] [PubMed]
- Sirimulla, S.; Bailey, J.B.; Vegesna, R.; Narayan, M. Halogen Interactions in Protein–Ligand Complexes: Implications of Halogen Bonding for Rational Drug Design. J. Chem. Inf. Model. 2013, 53, 2781–2791. [Google Scholar] [CrossRef] [PubMed]
- Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen bonding: The sigma-hole. Proceedings of “Modeling interactions in biomolecules II”, Prague, September 5th-9th, 2005. J. Mol. Model. 2007, 13, 291–296. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Ji, B.; Zhang, Y. Chalcogen Bond: A Sister Noncovalent Bond to Halogen Bond. J. Phys. Chem. A 2009, 113, 8132–8135. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S. Detailed comparison of the pnicogen bond with chalcogen, halogen, and hydrogen bonds. Int. J. Quantum Chem. 2013, 113, 1609–1620. [Google Scholar] [CrossRef]
- Scheiner, S. The Pnicogen Bond: Its Relation to Hydrogen, Halogen, and Other Noncovalent Bonds. Acc. Chem. Res. 2013, 46, 280–288. [Google Scholar] [CrossRef]
- Legon, A.C. Tetrel, pnictogen and chalcogen bonds identified in the gas phase before they had names: A systematic look at non-covalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 14884–14896. [Google Scholar] [CrossRef]
- Stevens, E.D. Experimental electron density distribution of molecular chlorine. Mol. Phys. 1979, 37, 27–45. [Google Scholar] [CrossRef]
- Stewart, R.F. On the mapping of electrostatic properties from bragg diffraction data. Chem. Phys. Lett. 1979, 65, 335–342. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding: An electrostatically-driven highly directional noncovalent interaction. Phys. Chem. Chem. Phys. 2010, 12, 7748–7757. [Google Scholar] [CrossRef] [PubMed]
- Alkorta, I.; Elguero, J.; Del Bene, J.E. Characterizing Traditional and Chlorine-Shared Halogen Bonds in Complexes of Phosphine Derivatives with ClF and Cl2. J. Phys. Chem. A 2014, 118, 4222–4231. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.S.; Macaveiu, L.; Politzer, P. Factors affecting the strengths of σ-hole electrostatic potentials. J. Comput. Sci. 2014, 5, 590–596. [Google Scholar] [CrossRef]
- Kolár, M.; Hostaš, J.; Hobza, P. The strength and directionality of a halogen bond are co-determined by the magnitude and size of the σ-hole. Phys. Chem. Chem. Phys. 2014, 16, 9987–9996. [Google Scholar] [CrossRef] [PubMed]
- Karpfen, A. Theoretical Characterization of the Trends in Halogen Bonding. In Halogen Bonding: Fundamentals and Applications; Metrangolo, P., Resnati, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 126, pp. 1–15. [Google Scholar] [CrossRef]
- Bundhun, A.; Ramasami, P.; Murray, J.S.; Politzer, P. Trends in σ-hole strengths and interactions of F3MX molecules (M = C, Si, Ge and X = F, Cl, Br, I). J. Mol. Model. 2013, 19, 2739–2746. [Google Scholar] [CrossRef] [PubMed]
- Riley, K.E.; Hobza, P. Investigations into the Nature of Halogen Bonding Including Symmetry Adapted Perturbation Theory Analyses. J. Chem. Theory Comput. 2008, 4, 232–242. [Google Scholar] [CrossRef] [PubMed]
- Wolters, L.P.; Bickelhaupt, F.M. Halogen Bonding versus Hydrogen Bonding: A Molecular Orbital Perspective. Chem. Open 2012, 1, 96–105. [Google Scholar] [CrossRef]
- Wang, C.; Danovich, D.; Mo, Y.; Shaik, S. On The Nature of the Halogen Bond. J. Chem. Theory Comput. 2014, 10, 3726–3737. [Google Scholar] [CrossRef]
- Novák, M.; Foroutan-Nejad, C.; Marek, R. Asymmetric bifurcated halogen bonds. Phys. Chem. Chem. Phys. 2015, 17, 6440–6450. [Google Scholar] [CrossRef]
- Politzer, P.; Riley, K.E.; Bulat, F.A.; Murray, J.S. Perspectives on halogen bonding and other σ-hole interactions: Lex parsimoniae (Occam’s Razor). Comput. Theor. Chem. 2012, 998, 2–8. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding and other σ-hole interactions: A perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S. σ-Hole Interactions: Perspectives and Misconceptions. Crystals 2017, 7, 212. [Google Scholar] [CrossRef]
- Anderson, L.N.; Aquino, F.W.; Raeber, A.E.; Chen, X.; Wong, B.M. Halogen Bonding Interactions: Revised Benchmarks and a New Assessment of Exchange vs Dispersion. J. Chem. Theory Comput. 2018, 14, 180–190. [Google Scholar] [CrossRef] [PubMed]
- Thirman, J.; Engelage, E.; Huber, S.M.; Head-Gordon, M. Characterizing the interplay of Pauli repulsion, electrostatics, dispersion and charge transfer in halogen bonding with energy decomposition analysis. Phys. Chem. Chem. Phys. 2018, 20, 905–915. [Google Scholar] [CrossRef] [PubMed]
- Shaw, R.A.; Hill, J.G.; Legon, A.C. Halogen Bonding with Phosphine: Evidence for Mulliken Inner Complexes and the Importance of Relaxation Energy. J. Phys. Chem. A 2016, 120, 8461–8468. [Google Scholar] [CrossRef] [PubMed]
- Hill, J.G.; Hu, X. Theoretical insights into the nature of halogen bonding in prereactive complexes. Chem. Eur. J. 2013, 19, 3620–3628. [Google Scholar] [CrossRef]
- Stone, A.J. Are halogen bonded structures electrostatically driven? J. Am. Chem. Soc. 2013, 135, 7005–7009. [Google Scholar] [CrossRef]
- Desiraju, G.R.; Ho, P.S.; Kloo, L.; Legon, A.C.; Marquardt, R.; Metrangolo, P.; Politzer, P.; Resnati, G.; Rissanen, K. Definition of the halogen bond (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1711–1713. [Google Scholar] [CrossRef]
- Lommerse, J.P.M.; Stone, A.J.; Taylor, R.; Allen, F.A. The Nature and Geometry of Intermolecular Interactions between Halogens and Oxygen or Nitrogen. J. Am. Chem. Soc. 1996, 118, 3108–3116. [Google Scholar] [CrossRef]
- Riley, K.E.; Murray, J.S.; Fanfrlík, J.; Rezáč, J.; Solá, R.J.; Concha, M.C.; Ramos, F.M.; Politzer, P. Halogen bond tunability II: the varying roles of electrostatic and dispersion contributions to attraction in halogen bonds. J. Mol. Model. 2013, 19, 4651–4659. [Google Scholar] [CrossRef]
- Riley, K.E.; Hobza, P. The relative roles of electrostatics and dispersion in the stabilization of halogen bonds. Phys. Chem. Chem. Phys. 2013, 15, 17742–17751. [Google Scholar] [CrossRef] [PubMed]
- Stone, A.J. Natural Bond Orbitals and the Nature of the Hydrogen Bond. J. Phys. Chem. A 2017, 121, 1531–1534. [Google Scholar] [CrossRef] [PubMed]
- Mulliken, R.S.; Person, W.B. Molecular Complexes: A Lecture and Reprint Volume; Wiley-Interscience: New York, NY, USA, 1969. [Google Scholar]
- Hill, J.G. The halogen bond in thiirane⋯ClF: An example of a Mulliken inner complex. Phys. Chem. Chem. Phys. 2014, 16, 19137–19140. [Google Scholar] [CrossRef] [PubMed]
- Řezáč, J.; de la Lande, A. On the role of charge transfer in halogen bonding. Phys. Chem. Chem. Phys. 2017, 19, 791–803. [Google Scholar] [CrossRef] [PubMed]
- Del Bene, J.; Alkorta, I.; Elguero, J. Halogen Bonding Involving CO and CS with Carbon as the Electron Donor. Molecules 2017, 22, 1955. [Google Scholar] [CrossRef]
- Khanifaev, J.; Peköz, R.; Konuk, M.; Durgun, E. The interaction of halogen atoms and molecules with borophene. Phys. Chem. Chem. Phys. 2017, 19, 28963–28969. [Google Scholar] [CrossRef] [PubMed]
- Rosokha, S.V.; Neretin, I.S.; Rosokha, T.Y.; Hecht, J.; Kochi, J.K. Charge-transfer character of halogen bonding: Molecular structures and electronic spectroscopy of carbon tetrabromide and bromoform complexes with organic σ- and π-donors. Heteroat. Chem. 2006, 17, 449–459. [Google Scholar] [CrossRef]
- Mustoe, C.L.; Gunabalasingam, M.; Yu, D.; Patrick, B.O.; Kennepohl, P. Probing covalency in halogen bonds through donor K-edge X-ray absorption spectroscopy: Polyhalides as coordination complexes. Faraday Discuss. 2017, 203, 79–91. [Google Scholar] [CrossRef]
- Grimme, S. Density functional theory with London dispersion corrections. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 211–228. [Google Scholar] [CrossRef]
- Burns, L.A.; Mayagoitia, A.V.; Sumpter, B.G.; Sherrill, C.D. Density-functional approaches to noncovalent interactions: A comparison of dispersion corrections (DFT-D), exchange-hole dipole moment (XDM) theory, and specialized functionals. J. Chem. Phys. 2011, 134, 084107. [Google Scholar] [CrossRef]
- Riley, K.E.; Pitonak, M.; Jurečka, P.; Hobza, P. Stabilization and Structure Calculations for Noncovalent Interactions in Extended Molecular Systems Based on Wave Function and Density Functional Theories. Chem. Rev. 2010, 110, 5023–5063. [Google Scholar] [CrossRef] [PubMed]
- Riley, K.E.; Hobza, P. Noncovalent interactions in biochemistry. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 3–17. [Google Scholar] [CrossRef]
- Grimme, S.; Hansen, A.; Brandenburg, J.G.; Bannwarth, C. Dispersion-Corrected Mean-Field Electronic Structure Methods. Chem. Rev. 2016, 116, 5105–5154. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Song, S.; Sim, E.; Burke, K. Halogen and Chalcogen Binding Dominated by Density-Driven Errors. J. Phys. Chem. Lett. 2019, 10, 295–301. [Google Scholar] [CrossRef] [PubMed]
- Legon, A.C.; Millen, D.J. Hydrogen bonding as a probe of electron densities: Limiting gas-phase nucleophilicities and electrophilicities of B and HX. J. Am. Chem. Soc. 1987, 109, 356–358. [Google Scholar] [CrossRef]
- Legon, A.C. A reduced radial potential energy function for the halogen bond and the hydrogen bond in complexes B⋯XY and B⋯HX, where X and Y are halogen atoms. Phys. Chem. Chem. Phys. 2014, 16, 12415–12421. [Google Scholar] [CrossRef] [PubMed]
- Alkorta, I.; Legon, A.C. Nucleophilicities of Lewis Bases B and Electrophilicities of Lewis Acids A Determined from the Dissociation Energies of Complexes B⋯A Involving Hydrogen Bonds, Tetrel Bonds, Pnictogen Bonds, Chalcogen Bonds and Halogen Bonds. Molecules 2017, 22, 1786. [Google Scholar] [CrossRef]
- Legon, A.C.; Thumwood, J.M.A.; Waclawik, E.R. Rotational spectroscopy of H3P⋯BrCl and the systematics of intermolecular electron transfer in the series B⋯BrCl, where B = CO, HCN, H2O, C2H2, C2H4, H2S, NH3, and PH3. J. Chem. Phys. 2000, 113, 5278. [Google Scholar] [CrossRef]
- Stephens, S.L.; Walker, N.R.; Legon, A.C. Rotational spectra and properties of complexes B⋯ICF3 (B = Kr or CO) and a comparison of the efficacy of ICl and ICF3 as iodine donors in halogen bond formation. J. Chem. Phys. 2011, 135, 224309. [Google Scholar] [CrossRef]
- Davey, J.B.; Legon, A.C. Rotational spectroscopy of the gas phase complex of water and bromine monochloride in the microwave region: Geometry, binding strength and charge transfer. Phys. Chem. Chem. Phys. 2001, 3, 3006–3011. [Google Scholar] [CrossRef]
- Davey, J.B.; Legon, A.C.; Waclawik, E.R. An investigation of the gas-phase complex of water and iodine monochloride by microwave spectroscopy: Geometry, binding strength and electron redistribution. Phys. Chem. Chem. Phys. 2000, 2, 1659–1665. [Google Scholar] [CrossRef]
- Legon, A.C.; Thumwood, J.M.A. Properties of the halogen-bonded complex H2S⋯Br2 established by rotational spectroscopy and ab initio calculations. Phys. Chem. Chem. Phys. 2001, 3, 2758–2764. [Google Scholar] [CrossRef]
- Kozuch, S.; Martin, J.M.L. Halogen Bonds: Benchmarks and Theoretical Analysis. J. Chem. Theory Comput. 2013, 9, 1918–1931. [Google Scholar] [CrossRef] [PubMed]
- Legon, A.C. The Interaction of Dihalogens and Hydrogen Halides with Lewis Bases in the Gas Phase. Struct Bond. 2008, 126, 17–64. [Google Scholar] [CrossRef]
- Cox, D.R.; Hinkley, D.V. Theoretical Statistics, 1st ed.; Chapman and Hall Press: London, UK, 1979. [Google Scholar]
- Parr, R.G.; Pearson, R.G. Absolute Hardness: Companion Parameter to Absolute Electronegativity. J. Am. Chem. Soc. 1983, 105, 7512–7516. [Google Scholar] [CrossRef]
- Pearson, R.G. Absolute Electronegativity and Hardness: Application to Inorganic Chemistry. Inorg. Chem. 1988, 27, 734–740. [Google Scholar] [CrossRef]
- Stone, A.J.; Misquitta, A.J. Charge-transfer in Symmetry-Adapted Perturbation Theory. Chem. Phys. Lett. 2009, 473, 201–205. [Google Scholar] [CrossRef]
- Shaw, R.A.; Hill, J.G. A Simple Model for Halogen Bonds Jupyter Notebook. Available online: https://github.com/Sheffield-Theoretical-Chemistry/xbond-jupyter (accessed on 1 February 2019).
- Adler, T.B.; Knizia, G.; Werner, H.J. A simple and efficient CCSD(T)-F12 approximation. J. Chem. Phys. 2007, 127, 221106. [Google Scholar] [CrossRef]
- Werner, H.J.; Knowles, P.J.; Knizia, G.; Manby, F.R.; Schütz, M. Molpro: A general-purpose quantum chemistry program package. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 242–253. [Google Scholar] [CrossRef]
- Werner, H.J.; Knowles, P.J.; Knizia, G.; Manby, F.R.; Schütz, M.; Celani, P.; Korona, T.; Lindh, R.; Mitrushenkov, A.; Rauhut, G.; et al. MOLPRO, Version 2012.1, a Package of Ab Initio Programs. Available online: http://www.molpro.net (accessed on 1 February 2019).
- Ten-no, S. Initiation of explicitly correlated Slater-type geminal theory. Chem. Phys. Lett. 2004, 398, 56–61. [Google Scholar] [CrossRef]
- Knizia, G.; Adler, T.B.; Werner, H.J. Simplified CCSD(T)-F12 methods: Theory and benchmarks. J. Chem. Phys. 2009, 130, 054104. [Google Scholar] [CrossRef] [PubMed]
- Peterson, K.A.; Adler, T.B.; Werner, H.J. Systematically convergent basis sets for explicitly correlated wavefunctions: The atoms H, He, B–Ne, and Al–Ar. J. Chem. Phys. 2008, 128, 084102. [Google Scholar] [CrossRef]
- Hill, J.G.; Peterson, K.A. Correlation consistent basis sets for explicitly correlated wavefunctions: Pseudopotential-based basis sets for the post-d main group elements Ga–Rn. J. Chem. Phys. 2014, 141, 094106. [Google Scholar] [CrossRef] [PubMed]
- Peterson, K.A.; Figgen, D.; Goll, E.; Stoll, H.; Dolg, M. Systematically convergent basis sets with relativistic pseudopotentials. II. Small-core pseudopotentials and correlation consistent basis sets for the post-d group 16–18 elements. J. Chem. Phys. 2003, 119, 11113. [Google Scholar] [CrossRef]
- Peterson, K.A.; Shepler, B.C.; Figgen, D.; Stoll, H. On the Spectroscopic and Thermochemical Properties of ClO, BrO, IO, and Their Anions. J. Phys. Chem. A 2006, 110, 13877–13883. [Google Scholar] [CrossRef]
- Hill, J.G.; Peterson, K.A.; Knizia, G.; Werner, H.J. Extrapolating MP2 and CCSD explicitly correlated correlation energies to the complete basis set limit with first and second row correlation consistent basis sets. J. Chem. Phys. 2009, 131, 194105. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F. A fully direct RI-HF algorithm: Implementation, optimised auxiliary basis sets, demonstration of accuracy and efficiency. Phys. Chem. Chem. Phys. 2002, 4, 4285–4291. [Google Scholar] [CrossRef]
- Weigend, F. Hartree-Fock exchange fitting basis sets for H to Rn. J. Comput. Chem. 2008, 29, 167–175. [Google Scholar] [CrossRef]
- Hättig, C. Optimization of auxiliary basis sets for RI-MP2 and RI-CC2 calculations: Core-valence and quintuple-ζ basis sets for H to Ar and QZVPP basis sets for Li to Kr. Phys. Chem. Chem. Phys. 2005, 7, 59–66. [Google Scholar] [CrossRef]
- Valeev, E.F. Improving on the resolution of the identity in linear R12 ab initio theories. Chem. Phys. Lett. 2004, 395, 190–195. [Google Scholar] [CrossRef]
- Knizia, G.; Werner, H.J. Explicitly correlated RMP2 for high-spin open-shell reference states. J. Chem. Phys. 2008, 128, 154103. [Google Scholar] [CrossRef] [PubMed]
- Yousaf, K.E.; Peterson, K.A. Optimized auxiliary basis sets for explicitly correlated methods. J. Chem. Phys. 2008, 129, 184108. [Google Scholar] [CrossRef] [PubMed]
- Shaw, R.A.; Hill, J.G. Approaching the Hartree-Fock Limit through the Complementary Auxiliary Basis Set Singles Correction and Auxiliary Basis Sets. J. Chem. Theory Comput. 2017, 13, 1691–1698. [Google Scholar] [CrossRef] [PubMed]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other function. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Chai, J.D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09 Revision D.01; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Jeziorski, B.; Moszynski, R.; Szalewicz, K. Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of van der Waals Complexes. Chem. Rev. 1994, 94, 1887–1930. [Google Scholar] [CrossRef]
- Szalewicz, K. Symmetry-adapted perturbation theory of intermolecular forces. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 254–272. [Google Scholar] [CrossRef]
- Parker, T.M.; Burns, L.A.; Parrish, R.M.; Ryno, A.G.; Sherrill, C.D. Levels of symmetry adapted perturbation theory (SAPT). I. Efficiency and performance for interaction energies. J. Chem. Phys. 2014, 140, 094106. [Google Scholar] [CrossRef]
- Bukowski, R.; Cencek, W.; Jankowski, P.; Jeziorska, M.; Jeziorski, B.; Kucharski, S.A.; Lotrich, V.F.; Misquitta, A.J.; Moszyński, R.; Patkowski, K.; et al. SAPT2012: An Ab Initio Program for Many-Body Symmetry- Adapted Perturbation Theory Calculations of Intermolecular Interaction Energies; University of Delaware: Newark, DE, USA; University of Warsaw: Warsaw, Poland, 2012. [Google Scholar]
- Hohenstein, E.G.; Sherrill, C.D. Wavefunction methods for noncovalent interactions. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 304–326. [Google Scholar] [CrossRef]
- Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Dunning, T.H.; Peterson, K.A.; Wilson, A.K. Gaussian basis sets for use in correlated molecular calculations. X. The atoms aluminum through argon revisited. J. Chem. Phys. 2001, 114, 9244–9253. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 2951–2959. [Google Scholar]
| Model | RMSE | Max. | MSE | MAE |
|---|---|---|---|---|
| Linear | 1.13 | 3.13 | 0.00 | 0.75 |
| 0.30 | 0.68 | −0.01 | 0.24 | |
| 2.99 | 7.11 | 0.50 | 2.32 | |
| 0.14 | 0.41 | 0.00 | 0.11 |
| Halogen-Bond Donor | Lewis Base | ||
|---|---|---|---|
| F2 | 0.0621 | H2S | |
| FCl | 0.2215 | CH2O | |
| FBr | 0.3306 | H3N | |
| FI | 0.4600 | H2O |
| Lewis Base | C6F5Cl | C6F5Br | C6F5I | |||
|---|---|---|---|---|---|---|
| M06 | Pred. | M06 | Pred. | M06 | Pred. | |
| Sulphox. | ||||||
| Glycine | ||||||
| Valine | ||||||
| Leucine | ||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaw, R.A.; Hill, J.G. A Simple Model for Halogen Bond Interaction Energies. Inorganics 2019, 7, 19. https://doi.org/10.3390/inorganics7020019
Shaw RA, Hill JG. A Simple Model for Halogen Bond Interaction Energies. Inorganics. 2019; 7(2):19. https://doi.org/10.3390/inorganics7020019
Chicago/Turabian StyleShaw, Robert A., and J. Grant Hill. 2019. "A Simple Model for Halogen Bond Interaction Energies" Inorganics 7, no. 2: 19. https://doi.org/10.3390/inorganics7020019
APA StyleShaw, R. A., & Hill, J. G. (2019). A Simple Model for Halogen Bond Interaction Energies. Inorganics, 7(2), 19. https://doi.org/10.3390/inorganics7020019