Pb(II) Extraction with Benzo-18-Crown-6 Ether into Benzene under the Co-Presence of Cd(II) Nitrate in Water
Abstract
1. Introduction
2. Results and Discussion
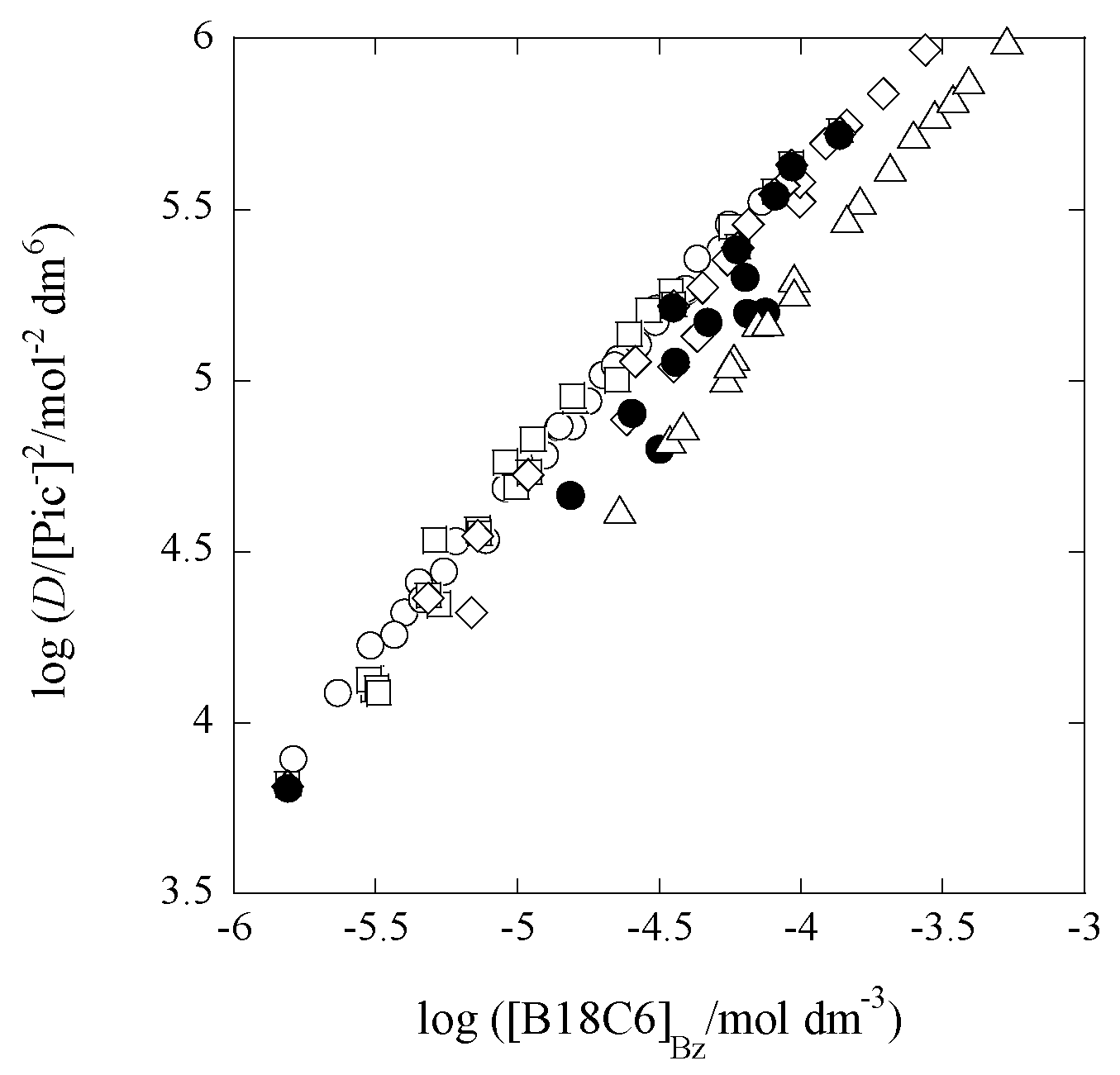
2.1. Determination of Composition of Extracted Species with Pb(II) at Some [Cd]t/[Pb]t Values
2.2. Determination of Kex, Kex±, and KD,Pic
≈ log {Kex + (KD,A/[M2+][L]org[A−])}
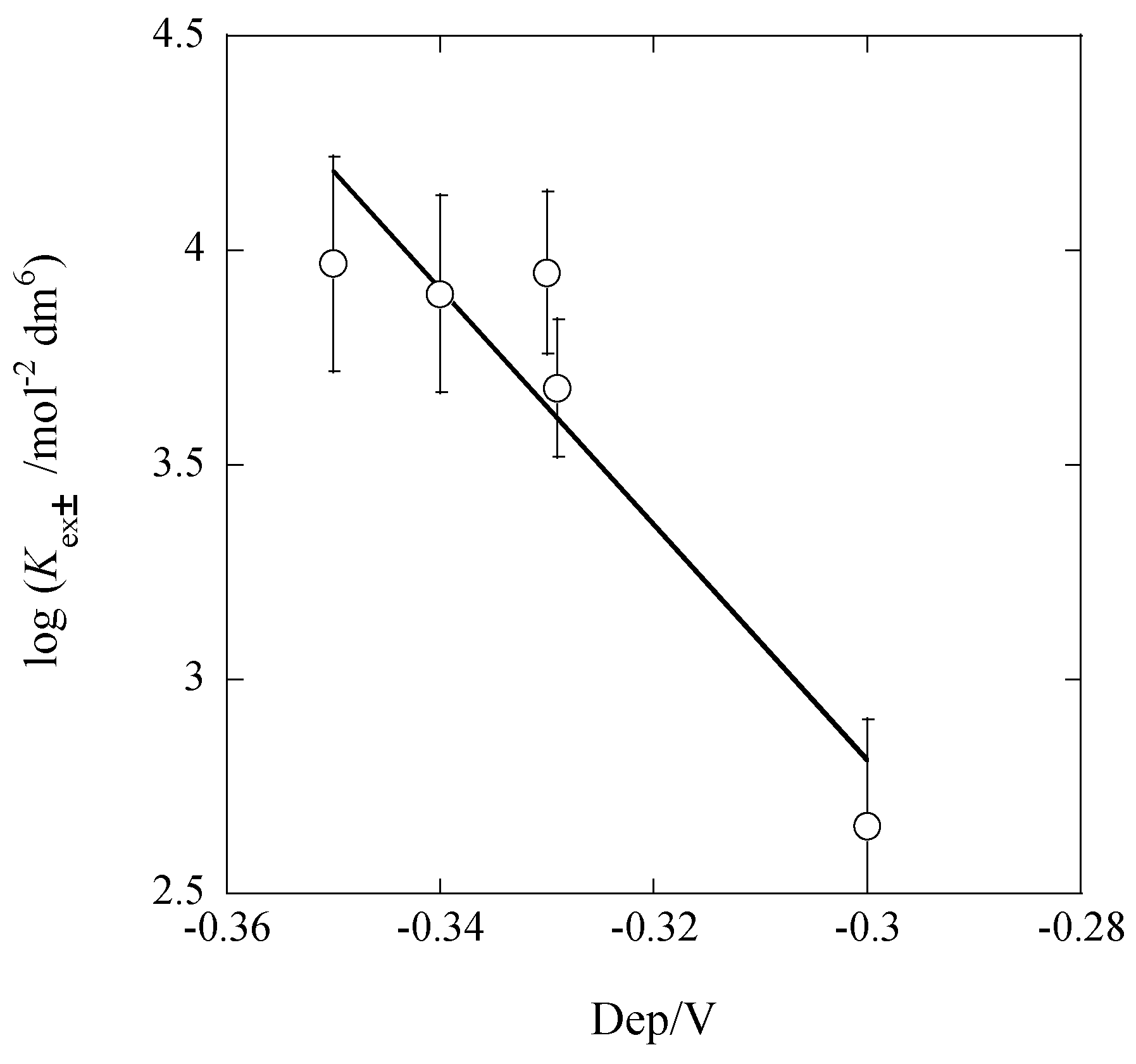
2.3. Dep Determination from KD,Pic
2.4. Determination of KPb/PbL, Kex,ip, K1,Bz, K2,Bz, and KD,PbL
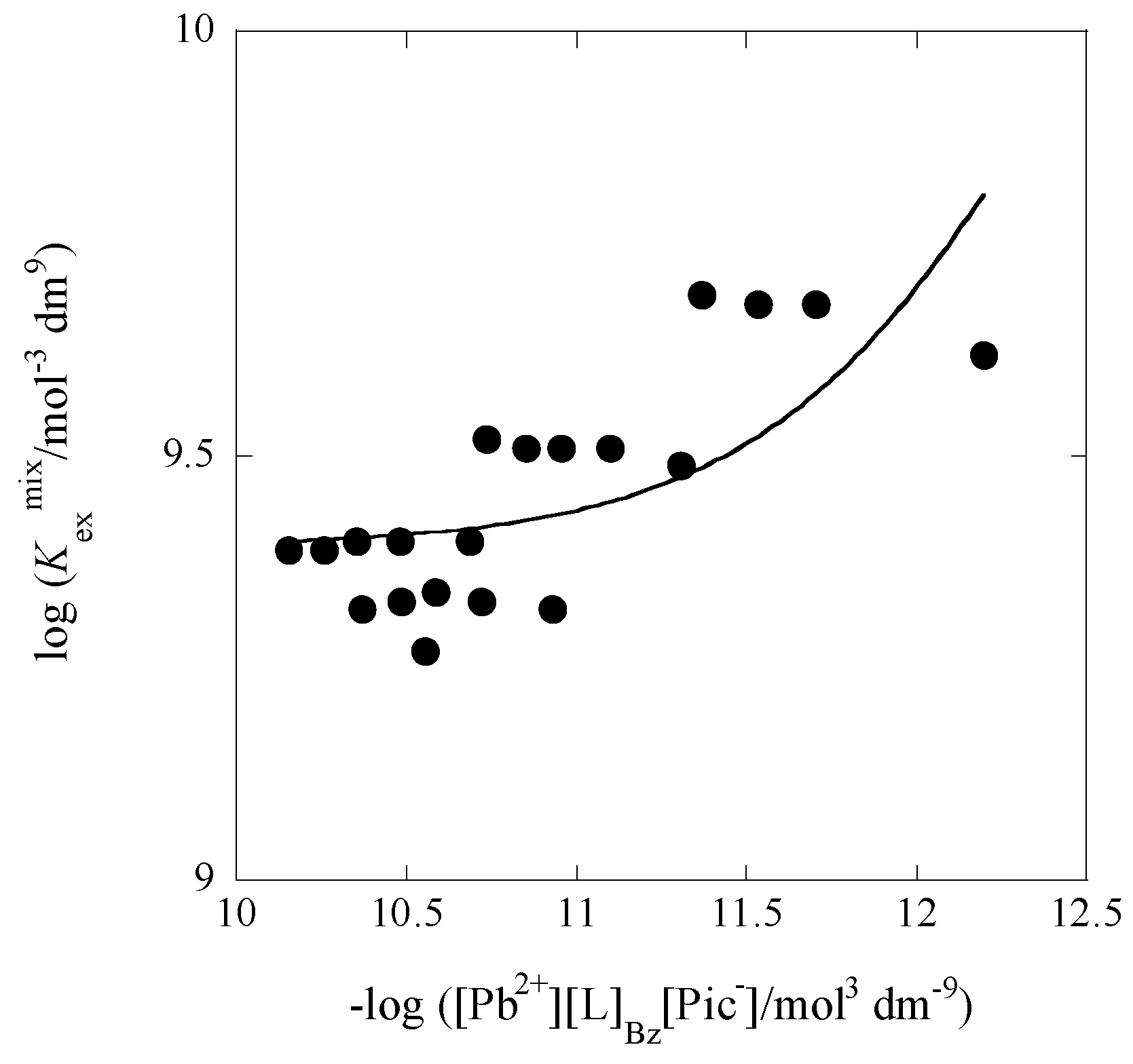
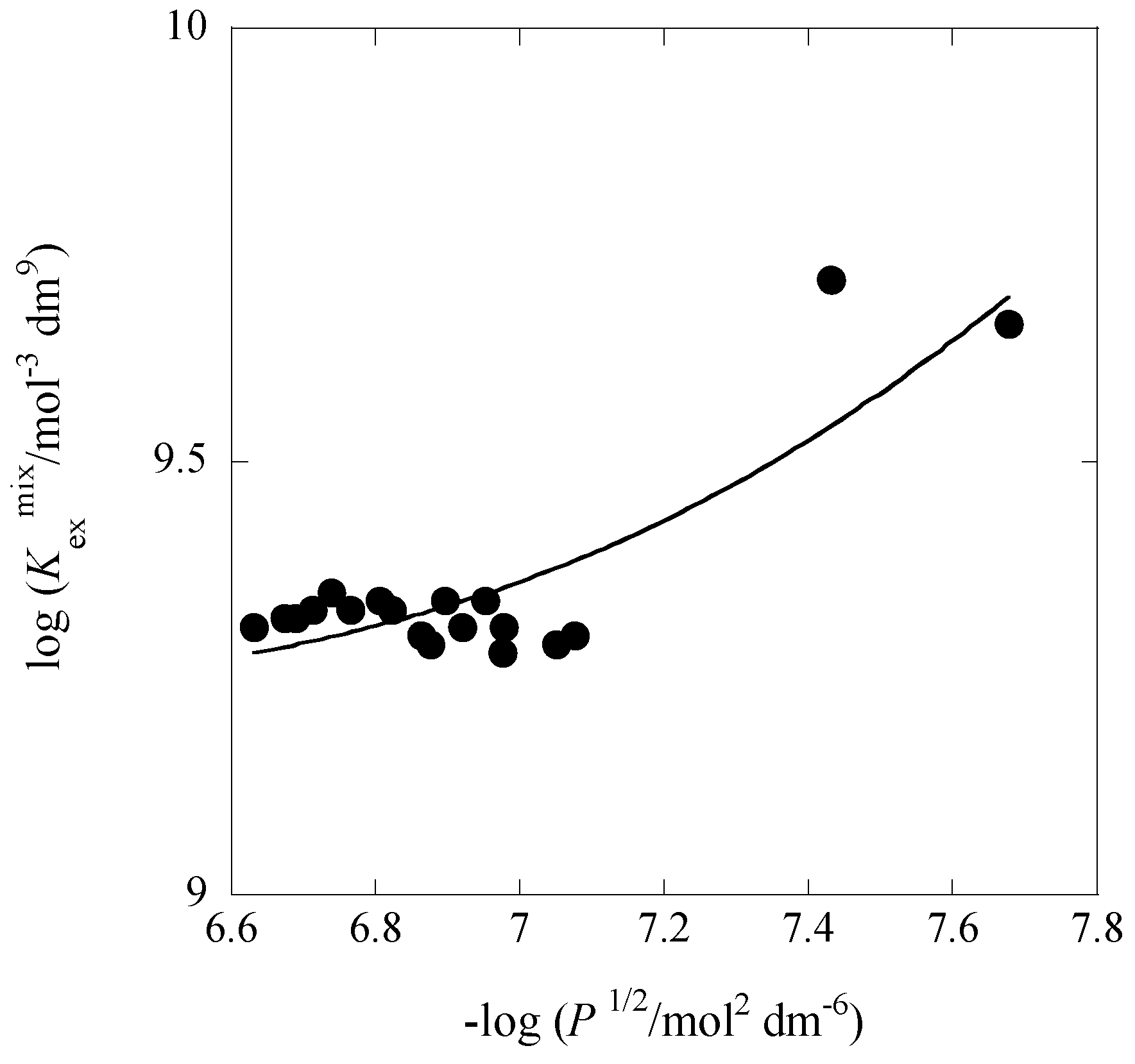
2.5. Correlation between log Kex± and Dep
= 2log KD,PicS − 2(F/2.303RT)Δφeq + log KPb/PbL·K1,Bz
2.6. I Dependences of log Kex and log Kex,ip
2.7. IBz Dependences of log K1,Bz and log K2,Bz
2.8. IBz Dependences of log Kex±0′, log KD,Pic0′, and log KPb/PbL0
2.9. A Try for Estimation of Detailed Separation Factor
2.10. Relative Concentrations of the Three Species Extracted into Bz
3. Materials and Methods
3.1. Materials
3.2. Extraction Procedures
3.3. Extraction Model Employed for the Analysis of the System
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Kex | Extraction constant for MLA2 |
| Kex± | Extraction constant for MLA+ with A− |
| I | Ionic strength for the water phase |
| KD,A | Conditional distribution constant of A− into the org phase |
| KM/ML | Incorporative constant of M2+ with L into the org phase |
| Kex,ip | Ion-pair extraction constant for MLA2 |
| K1,org | Ion-pair formation constant for ML2+ with A− in the org phase |
| D0, D+, D | Distribution ratio for MLA2, that for MLA+, that for mixture |
| Kex+ | Extraction constant for MLA+ |
| Kexmix | Extraction-constant parameter |
| Dep, Δϕeq | Distribution equilibrium potential between the bulk water and org phases |
| KD,PicS | Standard distribution constant of Pic− into the org phase |
| ΔϕPic0′ | Standard formal potential for the Pic− transfer across the water/org interface |
| K2,org | Ion-pair formation constant for MLA+ with A− in the org phase |
| KD,PbL | Conditional distribution constant of PbL2+ into the org phase |
| Kex2± | Extraction constant for ML2+ with 2A− |
| KD,L | Distribution constant of L into the org phase |
| KPbL | Complex formation constant of Pb2+ with L in water |
| Kex0 | Thermodynamic extraction constant of Kex |
| å± | Ion-size parameter, a mean value |
| Kex,ip0 | Thermodynamic ion-pair extraction constant of Kex,ip |
| K1,Bz0 | Thermodynamic ion-pair formation constant for ML2+ with A− in the Bz phase |
| K2,Bz0 | Thermodynamic ion-pair formation constant for MLA+ with A− in the Bz phase |
| Kex±0 | Thermodynamic extraction constant of Kex± |
| KPb/PbL0 | Thermodynamic incorporative constant of Pb2+ with L into the org phase |
| Kex2±0 | Thermodynamic extraction constant of Kex2± |
| D2+,Pb | Distribution ratio for PbL2+ |
References
- Kudo, Y.; Horiuchi, N.; Katsuta, S.; Takeda, Y. Extraction of cadmium bromide and picrate by 18-crown-6 ether into various less-polar diluents: Analysis of overall extraction equilibria based on their component equilibria with formation of their ion pairs in water. J. Mol. Liquids 2013, 177, 257–266. [Google Scholar] [CrossRef]
- Takeda, Y. Extraction of alkali metal picrate with 18-crown-6, benzo-18-crown-6, and dibenzo-18-crown-6 into various organic solvents. Elucidation of fundamental equilibria governing extraction-ability and -selectivity. Bunseki Kagaku 2002, 51, 515–525. (In Japanese) [Google Scholar] [CrossRef]
- Takeda, Y.; Katō, H. The solvent extraction of bivalent metal picrates by 15-crown-5, 18-crown-6, and dibenzo-18-crown-6. Bull. Chem. Soc. Jpn. 1979, 52, 1027–1030. [Google Scholar] [CrossRef]
- Levitskaia, T.G.; Maya, L.; Van Berkel, G.J.; Moyer, B.A. Anion partitioning and ion pairing behavior of anions in the extraction of cesium salts by 4,5″-bis(tert-octylbenzo)dibenzo-24-crown-8 in 1,2-dichloroethane. Inorg. Chem. 2007, 46, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Takeda, Y.; Nishida, M. Solvent extraction of various metal picrates with benzo-18-crown-6 into CHCl3. Bull. Chem. Soc. Jpn. 1989, 62, 1468–1471. [Google Scholar] [CrossRef]
- Takeda, Y.; Kawarabayashi, A.; Takahashi, K.; Kudo, Y. Extraction of alkali metal picrates with benzo-18-crown-6 into various organic solvents. Fundamental equilibria which govern the highest extraction selectivity for K+ among alkali metal ions. Bull. Chem. Soc. Jpn. 1995, 68, 1309–1314. [Google Scholar] [CrossRef]
- Kudo, Y.; Amano, T.; Ikeda, S. Determination of distribution equilibrium-potential differences based on extraction with several crown ethers by nitrobenzene, 1,2-dichloroethane and dichloromethane. Int. J. Chem. 2017, 9, 110–123. [Google Scholar] [CrossRef]
- Kudo, Y.; Tomokata, S. Extraction of cadmium chloride by 18-crown-6 ether into various diluents: A comparative study with bromide and picrate extraction systems. J. Mol. Liquids 2018, 249, 904–911. [Google Scholar] [CrossRef]
- Kudo, Y.; Takahashi, Y.; Numako, C.; Katsuta, S. Extraction of lead picrate by 18-crown-6 ether into various diluents: Examples of sub-analysis of overall extraction equilibrium based on component equilibria. J. Mol. Liquids 2014, 194, 121–129. [Google Scholar] [CrossRef]
- Kolthoff, I.M. Ionic strength effect on extraction of potassium complexed with crown ether 18-crown-6. Preliminary communication. Can. J. Chem. 1981, 59, 1548–1551. [Google Scholar] [CrossRef]
- Kolthoff, I.M.; Chantooni, M.K., Jr. Crown ether complexed alkali metal picrate ion pairs in water saturated dichloromethane as studied by electrolytic conductance and by partitioning into water. Effect of lithium chloride on partitioning. J. Chem. Eng. Data 1997, 42, 49–53. [Google Scholar] [CrossRef]
- Kudo, Y.; Ikeda, S.; Morioka, S.; Tomokata, S. Silver(I) extraction with benzo-18-crown-6 ether from water into 1,2-dichloroethane: Analyses on ionic strength of the phases and their equilibrium potentials. Inorganics 2017, 5, 42. [Google Scholar] [CrossRef]
- Wood, D.J.; Law, J.D.; Tullock, P.A. Extraction of lead and strontium from hazardous waste streams by solvent extraction with 4, 4’,(5’)-di-(t-butyldicyclohexano)-18-crown-6. Solvent Extr. Ion Exch. 1997, 15, 65–78. [Google Scholar] [CrossRef]
- Kazemi, S.Y.; Hamidi, A.S. Competitive removal of lead(II), copper(II), and cadmium(II) ions through a bulk liquid membrane containing macrocyclic crown ethers and oleic acid as ion carriers. J. Chem. Eng. Data 2011, 56, 222–229. [Google Scholar] [CrossRef]
- Bhatluri, K.K.; Manna, M.S.; Saha, P.; Ghoshal, A.K. Supported liquid membrane-based simultaneous separation of cadmium and lead from wastewater. J. Membr. Sci. 2014, 459, 256–263. [Google Scholar] [CrossRef]
- Kudo, Y.; Nakamori, T.; Numako, C. Extraction of sodium picrate by 3m-crown-m ethers and their mono-benzo derivatives (m = 5, 6) into benzene: Estimation of their equilibrium-potential differences at the less-polar diluent/water interface by an extraction method. J. Chem. 2016, 2016, 5175746. [Google Scholar] [CrossRef]
- Panich-Pat, T.; Upatham, S.; Pokethitiyook, P.; Krautrachue, M.; Lanza, G.R. Phytoextraction of metal contaminants by Typha angustifolia: Interaction of lead and cadmium in soil-water microcosms. J. Environ. Prot. 2010, 1, 431–437. [Google Scholar] [CrossRef]
- Katsuta, S.; Tsuchiya, F.; Takeda, Y. Equilibrium studies on complexation in water and solvent extraction of zinc(II) and cadmium(II) with benzo-18-crown-6. Talanta 2000, 51, 637–644. [Google Scholar] [CrossRef]
- Kudo, Y.; Kobayashi, Y.; Katsuta, S.; Takeda, Y. Ion-pair formation of cadmium-18-crown-6 ether complex ions with picrate and chloride ions in water and distribution of its picrate ion-pair complex into benzene. J. Mol. Liquids 2009, 146, 60–65. [Google Scholar] [CrossRef]
- Dernini, S.; Scrugli, A.; Palmas, S.; Polcaro, A.M. Competitive extraction of Pb2+ by dicyclohexano-18-crown-6 from heavy metal aqueous solutions. J. Chem. Eng. Data 1996, 41, 1388–1391. [Google Scholar] [CrossRef]
- Kudo, Y.; Takahashi, Y.; Katsuta, S.; Takeda, Y. Extraction of several divalent metal picrates by 18-crown-6 ether derivatives into benzene: A refinements for analyzing extraction equilibria. Int. J. Chem. 2013, 5, 90–102. [Google Scholar] [CrossRef]
- Kudo, Y.; Katsuta, S.; Ohsawa, Y.; Nozaki, K. Solvent extraction of cadmium picrate by 18-crown-6 ether into several less-polar diluents and nitrobenzene: Re-evaluation of corresponding overall extraction systems. J. Thermodyn. Catal. 2015, 6, 146. [Google Scholar]
- Sanchez Vallejo, L.J.; Ovejero, J.M.; Fernández, R.A.; Dassie, E.A. Single ion transfer at liquid/liquid interface. J. Chem. 2012, 2012, 462197. [Google Scholar]
- Fyles, T.M. Extraction and transport of alkali metal salts by crown ethers and cryptands: Estimation of extraction constants and their relationship to transport flux. Can. J. Chem. 1987, 65, 884–891. [Google Scholar] [CrossRef]
- Abraham, M.H.; Liszi, J. Calculation of ionic solvation—V The calculation of partition coefficients of ions. J. Inorg. Nucl. Chem. 1981, 43, 143–151. [Google Scholar] [CrossRef]
- Kudo, Y.; Takeda, Y.; Matsuda, H. Ion-transfer-polarographic study of distribution equilibrium of metal complex cations with several crown ethers between nitrobenzene and water. Bunseki Kagaku 1991, 40, 779–784. (In Japanese) [Google Scholar] [CrossRef]
- Kudo, Y. An approximation method for determining key extraction constants in the equilibrium-analysis of Cd(II) extraction with 18-crown-6 ether into some diluents. J. Anal. Pharm. Res. 2017, 5, 00144. [Google Scholar] [CrossRef]
- Kudo, Y.; Miyakawa, T.; Takeda, Y.; Matsuda, H. Ion-transfer polarographic study of the distribution of alkali and alkaline-earth metal complexes with 3m-crown-m ether derivatives (m = 5, 6) between water and nitrobenzene phases. J. Incl. Phenom. Mol. Recog. Chem. 1996, 26, 331–341. [Google Scholar] [CrossRef]
- Takeda, Y.; Kohno, R.; Kudo, Y.; Fukada, N. Stabilities in water and transfer activity coefficients from water to nonaqueous solvents of benzo-18-crown-6-metal ion complexes. Bull. Chem. Soc. Jpn. 1989, 62, 999–1003. [Google Scholar] [CrossRef]
- Tamamushi, R. Denki Kagaku (Electrochemistry), 2nd ed.; Tokyo Kagaku Dojin: Tokyo, Japan, 1991; pp. 29–33. [Google Scholar]
- De Levie, R. Aqueous Acid-Base Equilibria and Titrations; Oxford Chemistry Primers; Davies, S.G., Compton, R.G., Evans, J., Gladden, L.F., Eds.; Oxford University Press: Oxford, UK, 1999; pp. 59–63. [Google Scholar]
- Kielland, J. Individual activity coefficients of ions in aqueous solutions. J. Am. Chem. Soc. 1937, 59, 1675–1678. [Google Scholar] [CrossRef]
- Kudo, Y.; Tanaka, Y.; Ichikawa, T.; Katsuta, S. Determination of some component equilibrium-constants by Cd(II) picrate extraction with benzo-18-crown-6 ether into various diluents and their evaluation. J. Anal. Bioanal. Tech. 2017, 8, 391. [Google Scholar] [CrossRef]
- Suljkanoć, M.; Nurković, E.; Suljagić, J. Influence of nonionic surfactants as competitive carriers in bulk liquid membrane transport of metal cations using macrocyclic ligands. J. Chem. Biol. Phys. Sci. Sect. A 2017, 8, 77–89. [Google Scholar]
- Takeda, Y.; Kawarabayashi, A.; Endō, K.; Yahata, T.; Kudo, Y.; Katsuta, S. Solvent extraction of alkali metal (Li–Cs) picrates with 18-crown-6 into various diluents. Elucidation of fundamental equilibria which govern the extraction-ability and -selectivity. Anal. Sci. 1998, 14, 215–223. [Google Scholar] [CrossRef]
- Kudo, Y.; Takahashi, Y.; Katsuta, S. Distribution of picric acid into various diluents. J. Chem. 2013, 2013, 869506. [Google Scholar] [CrossRef]
- Kortüm, G.; Vogel, W.; Andrussow, K. Dissociation Constants of Organic Acids in Aqueous Solution; IUPAC, Section of Analytical Chemistry Commission on Electrochemical Data: Butterworths, London, UK, 1961; p. 454. [Google Scholar]
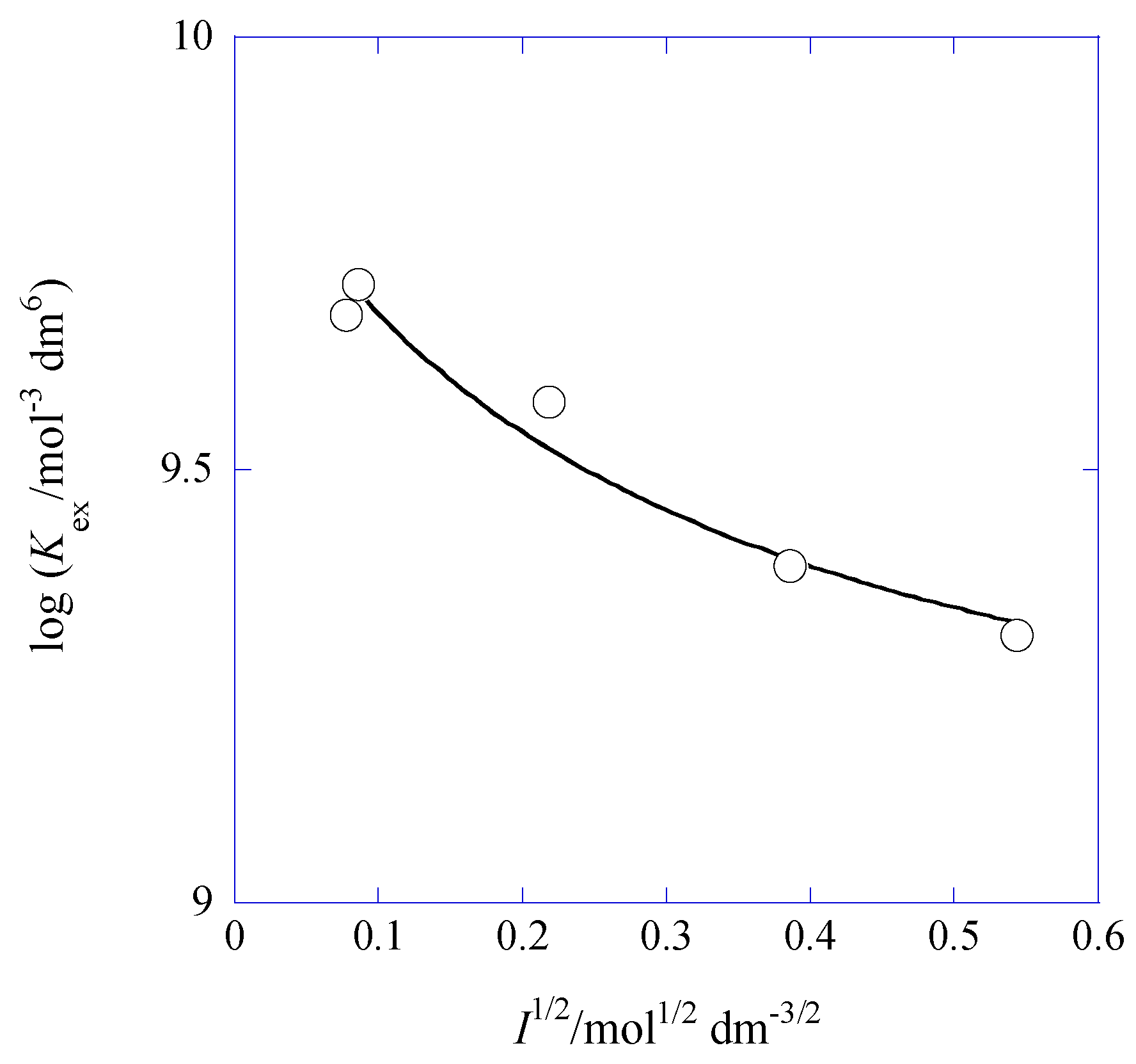
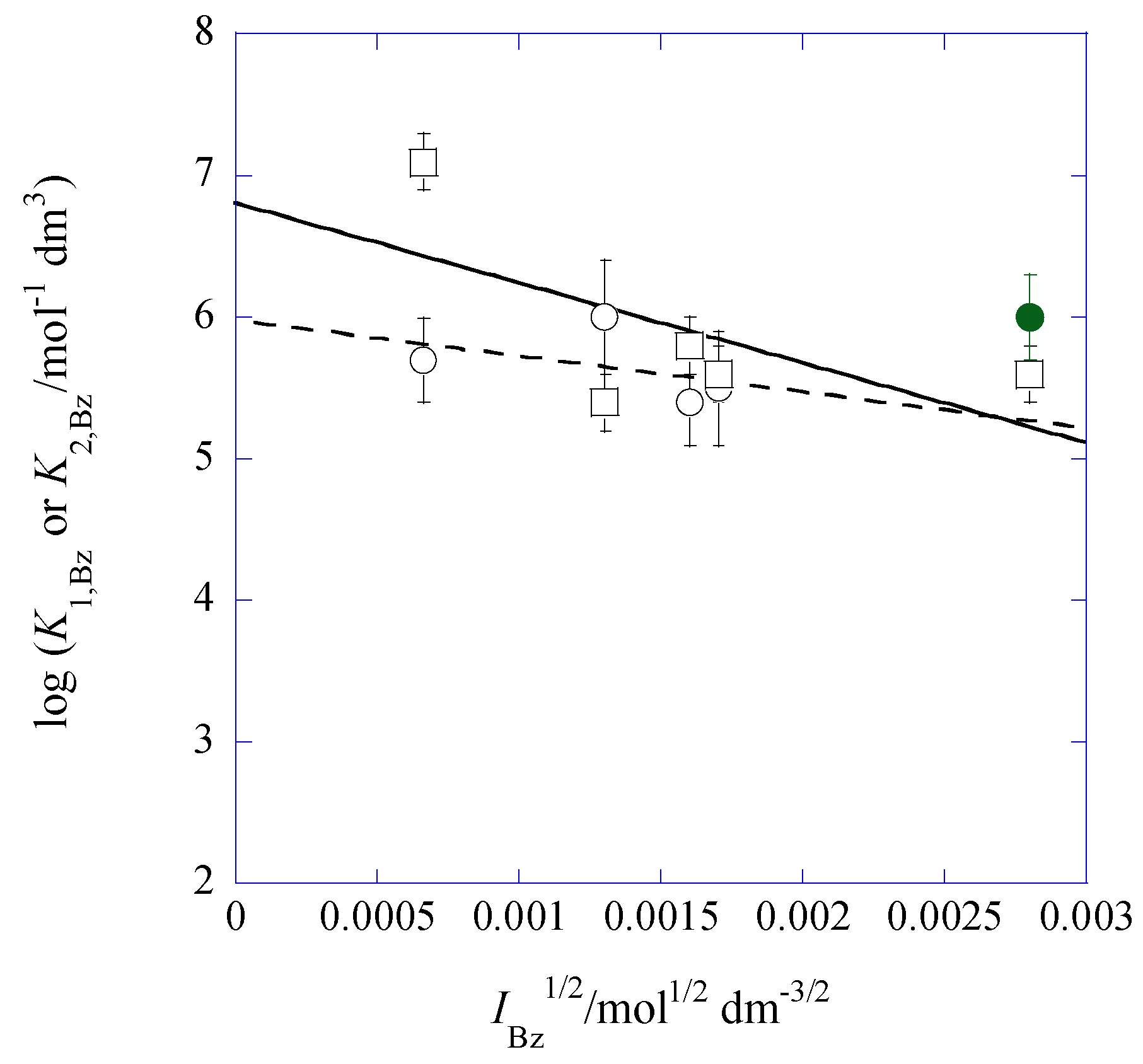
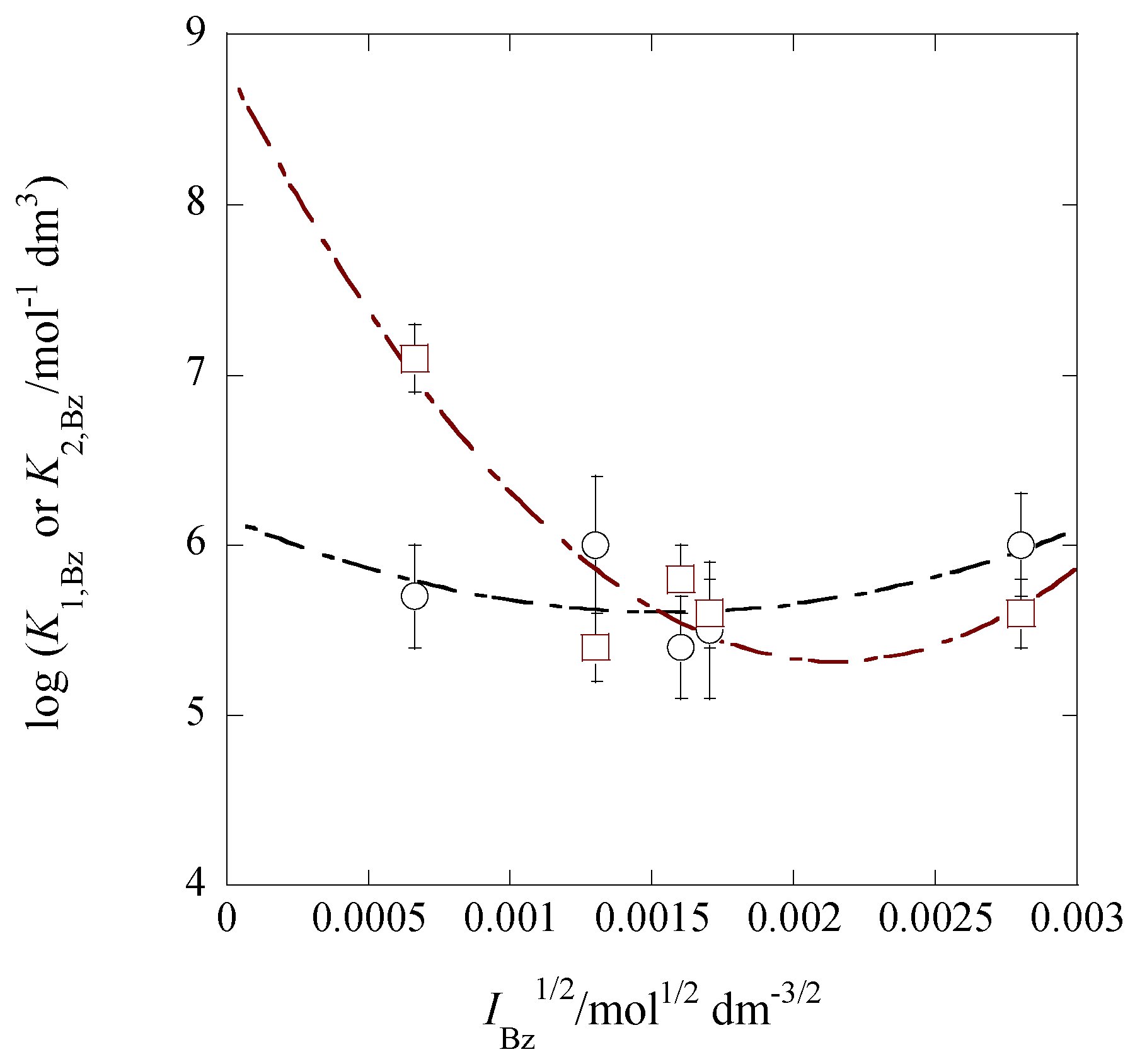
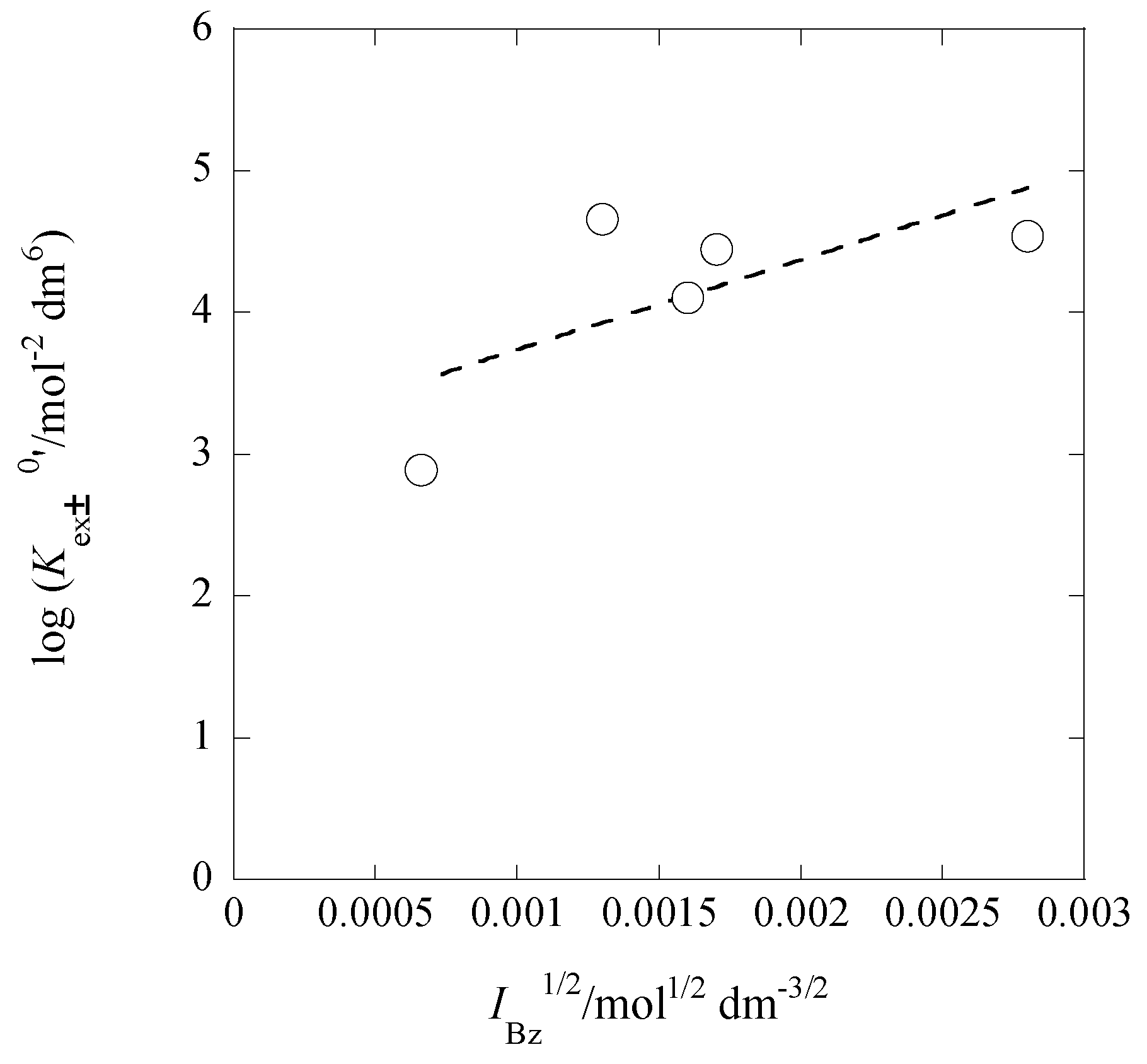
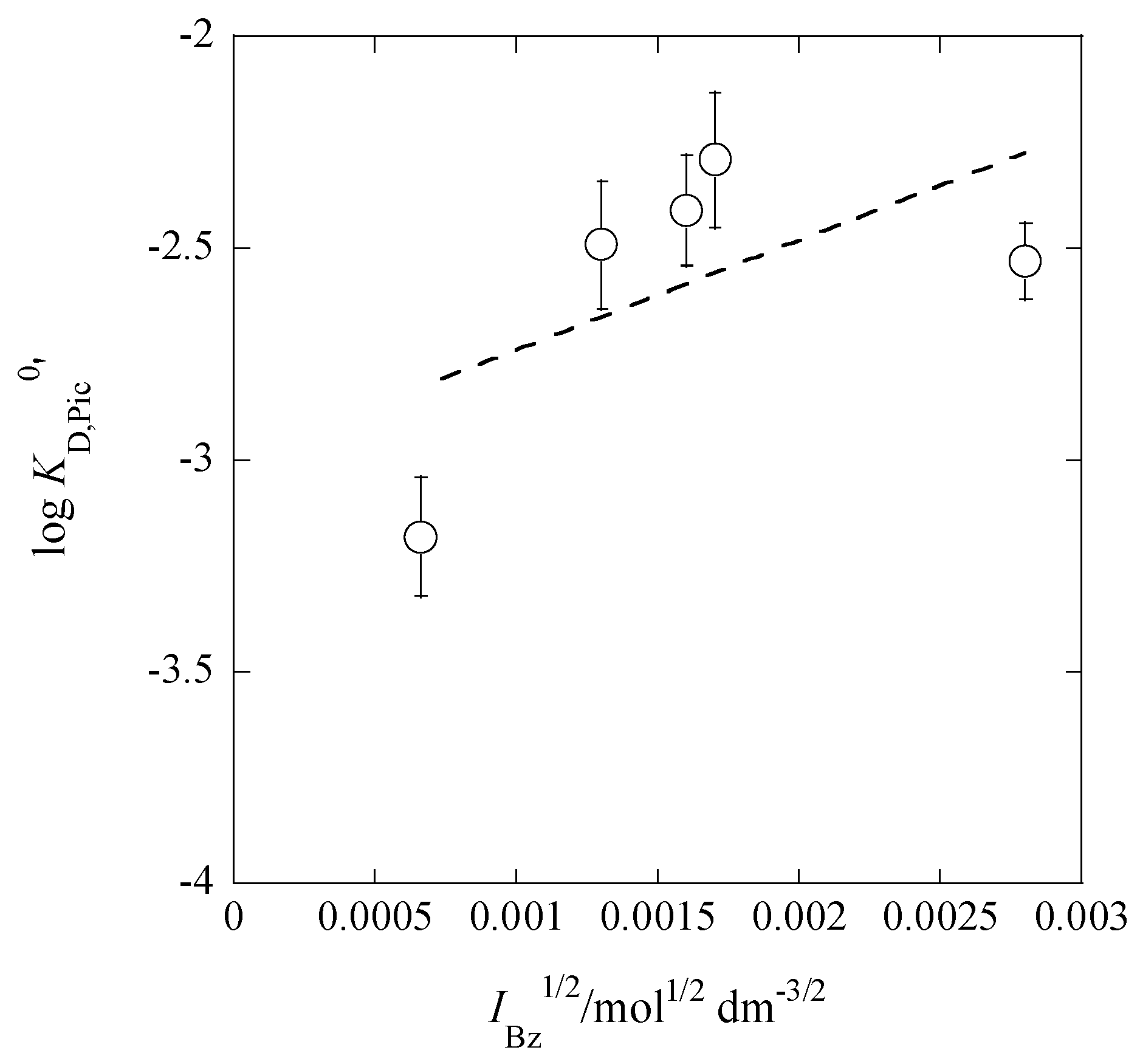
| [Cd]t/[Pb]t 1 | I2/mol dm−3 | log Kex [] 3 | log Kex± 3 (log yPic 4) | log KD,Pic (Δφeq 5/V) |
|---|---|---|---|---|
| 0 | 0.0074 | 9.715 ± 0.006 (9.70 ± 0.01) | 2.66 ± 0.25 (−0.04) | −3.21 ± 0.14 (−0.30) |
| 1.06 | 0.0060 | 9.68 ± 0.02 (9.61 ± 0.04) | 3.90 ± 0.23 (−0.03) | −2.44 ± 0.13 (−0.34) |
| 26.6 | 0.048 | 9.58 ± 0.02 (9.51 ± 0.03) | 3.97 ± 0.25 (−0.07) | −2.37 ± 0.16 (−0.35) |
| 88.5 | 0.15 | 9.39 ± 0.03 (9.24 ± 0.05) | 3.95 ± 0.19 (−0.10) | −2.60 ± 0.15 (−0.33) |
| 178 | 0.29 | 9.31 ± 0.02 (9.21 ± 0.03) | 3.68 ± 0.16 (−0.12) | −2.65 ± 0.09 (−0.33) |
| [Cd]t/[Pb]t | log KPb/PbL (log yPb 1) | log Kex,ip | log K1,Bz (IBz 2/10−6) | log K2,Bz | log KD,PbL |
|---|---|---|---|---|---|
| 0 | 3.42 ± 0.05 (−0.16) | 7.47 | 5.7 ± 0.3 (0.44) | 7.1 ± 0.2 | 1.18 |
| 1.06 | 3.42 ± 0.08 (−0.14) | 7.143 | 5.4 ± 0.3 (2.6) | 5.8 ± 0.2 | 1.17 |
| 26.6 | 3.23 ± 0.12 (−0.34) | 7.34 | 5.5 ± 0.4 (2.7) | 5.6 ± 0.2 | 0.98 |
| 88.5 | 3.13 ± 0.21 (−0.50) | 7.15 | 6.0 ± 0.4 (1.7) | 5.4 ± 0.2 | 0.88 |
| 178 | 2.95 ± 0.28 (−0.62) | 7.06 | 6.0 ± 0.3 (7.8) | 5.6 ± 0.2 | 0.71 |
| [Cd]t/[Pb]t | log K1,Bz | log K2,Bz | ||||||
|---|---|---|---|---|---|---|---|---|
| Equation (14a) | |Dif.| 2 | Equation (14b) | |Dif.| 2 | Equation (15a) | |Dif.| 2 | Equation (15b) | |Dif.| 2 | |
| 0 | 5.81 | 0.2 | 6.16 | 0.2 | 6.44 | 0.6 | 6.98 | 0.1 |
| 1.06 | 5.58 | 0.2 | 5.61 | 0.2 | 5.91 | 0.1 | 5.54 | 0.2 |
| 26.6 | 5.56 | 0.1 | 5.61 | 0.1 | 5.87 | 0.3 | 5.50 | 0.1 |
| 88.5 | 5.66 | 0.4 | 5.62 | 0.4 | 6.08 | 0.6 | 5.87 | 0.4 |
| 178 | 5.28 | 0.8 | 5.96 | 0.1 | 5.24 | 0.4 | 5.62 | 0.0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kudo, Y.; Nakamori, T.; Numako, C. Pb(II) Extraction with Benzo-18-Crown-6 Ether into Benzene under the Co-Presence of Cd(II) Nitrate in Water. Inorganics 2018, 6, 77. https://doi.org/10.3390/inorganics6030077
Kudo Y, Nakamori T, Numako C. Pb(II) Extraction with Benzo-18-Crown-6 Ether into Benzene under the Co-Presence of Cd(II) Nitrate in Water. Inorganics. 2018; 6(3):77. https://doi.org/10.3390/inorganics6030077
Chicago/Turabian StyleKudo, Yoshihiro, Tsubasa Nakamori, and Chiya Numako. 2018. "Pb(II) Extraction with Benzo-18-Crown-6 Ether into Benzene under the Co-Presence of Cd(II) Nitrate in Water" Inorganics 6, no. 3: 77. https://doi.org/10.3390/inorganics6030077
APA StyleKudo, Y., Nakamori, T., & Numako, C. (2018). Pb(II) Extraction with Benzo-18-Crown-6 Ether into Benzene under the Co-Presence of Cd(II) Nitrate in Water. Inorganics, 6(3), 77. https://doi.org/10.3390/inorganics6030077




