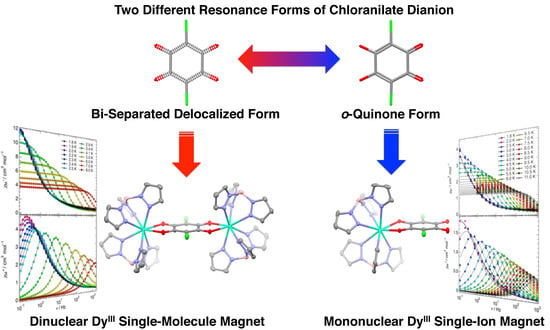
Field-Induced Slow Magnetic Relaxation of Mono- and Dinuclear Dysprosium(III) Complexes Coordinated by a Chloranilate with Different Resonance Forms

Abstract

We synthesized the dinuclear and mononuclear dysprosium(III) complexes [{Dy(Tp)₂}₂(Cl₂An)]·2CH₂Cl₂ (1) and [Co(Cp)₂][Dy(Tp)₂(Cl₂An)] (3), where Cl₂An²⁻ and Tp⁻ are the chloranilate and hydrotris(pyrazolyl)borate ligand, respectively. In addition, the magnitude of the magnetic coupling between the lanthanide centers through the Cl₂An²⁻ bridge has been probed through the synthesis of [{Gd(Tp)₂}₂(Cl₂An)]·2CH₂Cl₂ (2), which is a gadolinium(III) analogue of 1. Complexes 1–3 were characterized by infrared (IR) spectroscopy, elemental analysis, single-crystal X-ray diffraction, and SQUID measurements. IR and single-crystal X-ray structural analyses confirm that the coordination environments of the lanthanide(III) centers in 1 and 3 are similar to each other; i.e., eight-coordinated metal centers, each occupied by an N₆O₂ donor set from two Tp⁻ ligands and one Cl₂An²⁻ ligand. The coordination geometries of the lanthanide(III) centers in 1 and 2 are distorted triangular dodecahedral, while that in the mononuclear complex 3 is square antiprismatic, where the Cl₂An²⁻ ligand takes the bi-separated delocalized form in 1 and 2, and the o-quinone form in 3. Alternating-current (AC) magnetic studies clearly reveal that both 1 and 3 exhibit field-induced slow relaxations of magnetization that occur via Raman and direct processes. Complexes 1 and 3 exhibit different spin relaxation behavior, which reflects the coordination geometry around each Dy^III center and its nuclearity, as well as the molecular packing in the crystal lattice. Although the magnetic analysis of 2 revealed negligible magnetic coupling, Cl₂An²⁻ bridges with small biases may form in the dinuclear complexes, which play roles in the spin relaxation dynamics through dipolar interactions.

1. Introduction

Molecule-based nanomagnets, such as single-molecule magnets (SMMs) [1,2,3,4,5,6,7] and single-ion magnets (SIMs) [8,9,10,11,12], are strictly low-dimensional magnetic systems that exhibit magnetization blocking at low temperatures, quantum tunneling of magnetization (QTM) [13], and quantum coherence [14,15]. Accordingly, SMMs have attracted a great deal of interest as promising candidates for quantum computing [16], high-density information storage [17], and more recently, molecular spintronic materials [18,19,20,21].

Early surveys of SMMs were focused on polynuclear cluster complexes with high nuclearities due to the realization of large ground spin states [2]. However, it is rather difficult to combine a large ground spin state with a large magnetic anisotropy, since the entire molecular symmetry in a polynuclear cluster complex often increases with an increasing nuclearity, leading to a small magnetic anisotropy as a consequence. Therefore, the realization of polynuclear cluster complexes with large spin ground states and large magnetic anisotropies is still a significant challenge.

On the other hand, more recent frontline SMMs studies have tended to focus on enhancing magnetic anisotropy, rather than augmenting ground spin states, which is a much more informative method for increasing the blocking temperature and the activation energy barrier. From these perspectives, studies into SMMs, and more recently, SIMs, based on trivalent lanthanide (Ln^III), ions have proceeded at a rapid pace because of their significant magnetic anisotropies that arise from both spin-orbit coupling and crystal-field splitting, where crystal-field splitting is normally much smaller than spin-orbit coupling in Ln^III ions [22,23]. Hence, it is very important to investigate small changes in ligand-field strength associated with the coordination geometries of Ln^III ions. However, the relationship between the coordination geometry of the Ln^III ion and the slow magnetic relaxation of SMMs or SIMs is still largely unclear, because it is very difficult to systematically control the coordination geometries and the ligand-field strengths of Ln^III ions. We noticed that chloranilate (Cl₂An²⁻) is a promising organic ligand for investigating the above-mentioned Ln^III-based SMMs or SIMs. The dianionic form of Cl₂An²⁻ has a delocalized π system with resonance structures that are represented by p-quinone, o-quinone, tetraquinone, and bi-separated delocalized forms (Scheme 1) [24,25]. The coordination geometry and the ligand-field strength of the central Ln^III ion can be fine-tuned by combining Cl₂An²⁻ with a suitable ancillary ligand, while maintaining a similar coordination environment. Hydrotris(pyrazolyl)borate (Tp⁻) ligands are scorpionate ligands [26] that exhibit hard σ-donating characteristics and have been used to stabilize trivalent Ln^III metal centers. Thus, we chose Tp⁻ as the ancillary ligand.

Based on the above idea, we successfully synthesized mononuclear and dinuclear dysprosium(III) complexes bearing the Cl₂An²⁻ ligand and Tp⁻ as auxiliary ligands, in which the Cl₂An²⁻ ligand adopts the o-quinone and bi-separated delocalized forms, respectively. Comparisons of the spin-relaxation dynamics for the mononuclear and dinuclear complexes will aid in our understanding of dipolar interactions mediated by bridging Cl₂An²⁻ ligands in dinuclear complexes. Herein, we report the syntheses, single-crystal X-ray structures, and detailed magnetic properties of two types of complexes, namely [{Dy(Tp)₂}₂(μ-Cl₂An²⁻)]·2CH₂Cl₂ and [Co(Cp)₂][Dy(Tp)₂(Cl₂An²⁻)], which display slow magnetic relaxations under small static direct-current (DC) magnetic fields.

2. Results and Discussion

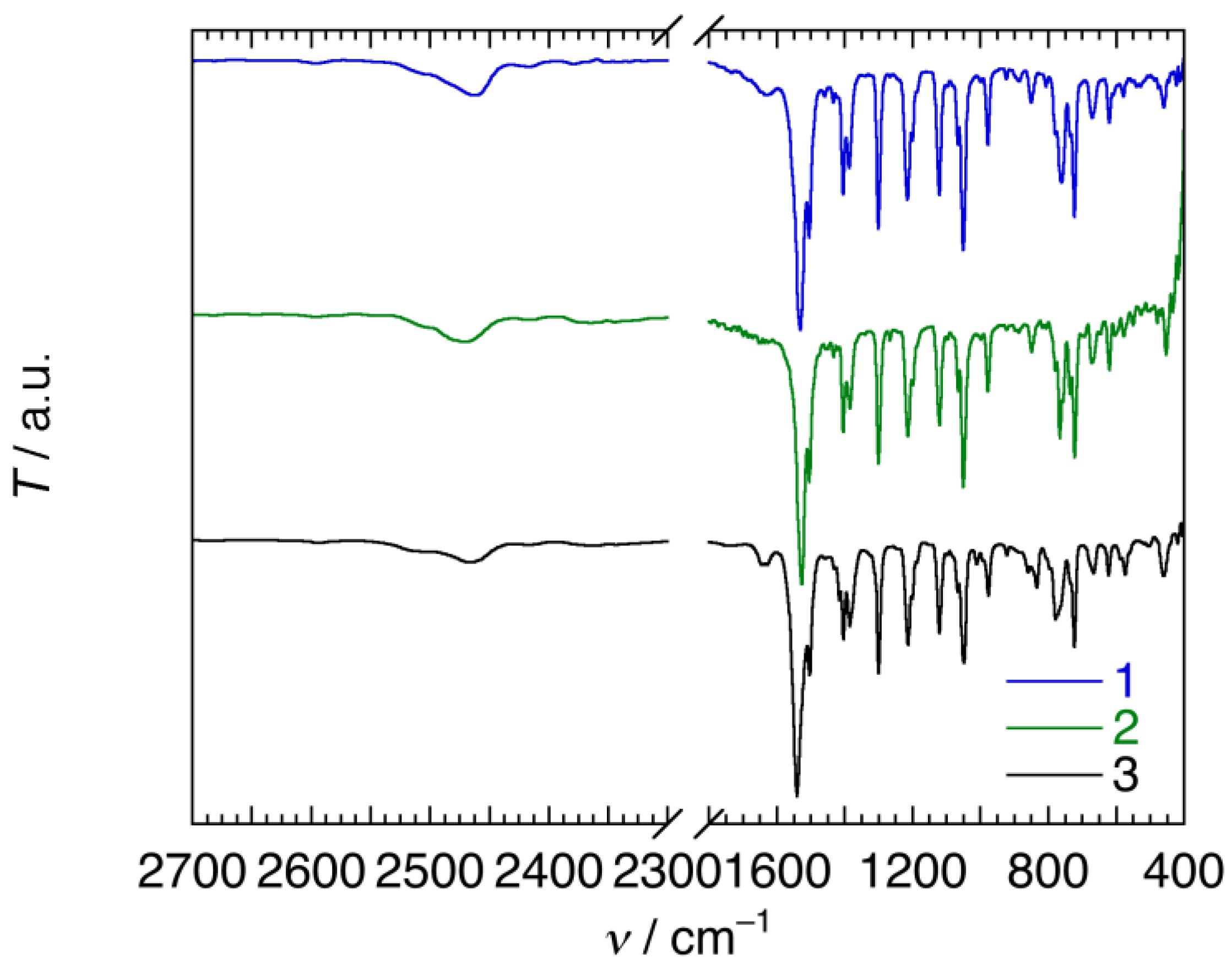
2.1. Syntheses and Characterizations

The [{Ln(Tp)₂}₂(μ-Cl₂An²⁻)] dinuclear complexes (1: Ln = Dy; 2: Ln = Gd) are readily formed by the reaction of 4 equiv. of KTp and 1 equiv. of Na₂Cl₂An with 2 equiv. of the corresponding lanthanide chloride salt in water. The subsequent slow diffusion of hexane into a concentrated CH₂Cl₂ solution of 1 gave purple rod-shaped crystals, with two CH₂Cl₂ solvates per dinuclear unit, suitable for single-crystal X-ray diffraction studies [27]. On the other hand, reaction of 1 with 1 equiv. of cobaltocene (Co(Cp)₂, Cp⁻ = cyclopentadienide) in a N₂-filled glovebox led to the formation of the mononuclear [Co(Cp)₂][Dy(Tp)₂(Cl₂An²⁻)] complex (3); 3 crystallized without any solvent molecules. Therefore, to the best of our knowledge, complexes 1–3 are the first heteroleptic systems containing the Cl₂An²⁻ and Tp⁻ ligands. Infrared (IR) spectroscopy provides complementary information to that obtained by single-crystal X-ray studies with respect to structural features (Figure 1). Complexes 1 and 2 have similar masses (162.5 amu for 1 and 157.25 amu for 2), so large differences in their IR spectra were not observed, although some peaks are shifted. The IR absorptions associated with the bridging Cl₂An²⁻ ligand in both 1 and 2 are typified by predominant C–Cl and C–O vibrations at ~850 and 1528 cm⁻¹, respectively. In contrast, 3 has three characteristic absorption bands centered at 833, 1540, and 1643 cm⁻¹. The first two absorption bands are assigned to C–Cl and C–O vibrations, while the third absorption band is considered to correspond to C=O vibrations. This result is a promising indication that the Cl₂CA²⁻ ligand in 3 is in the o-quinone form [28]. Furthermore, the presence of the ancillary Tp^– ligands in 1–3 is confirmed by characteristic absorptions in their IR spectra at approximately 2470 cm⁻¹ (c.f., KTp⁻, νB–H = ~2440 cm⁻¹) [29].

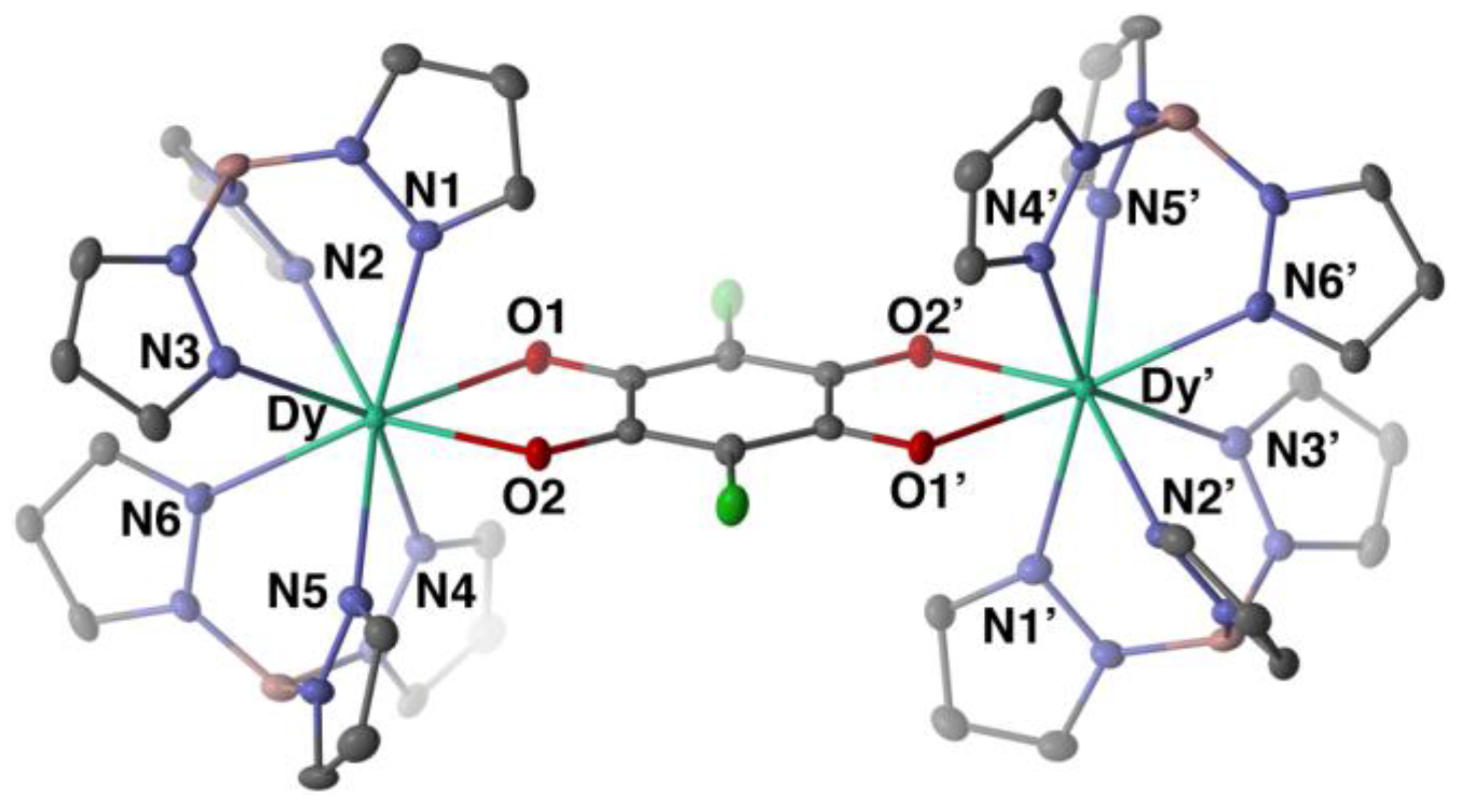
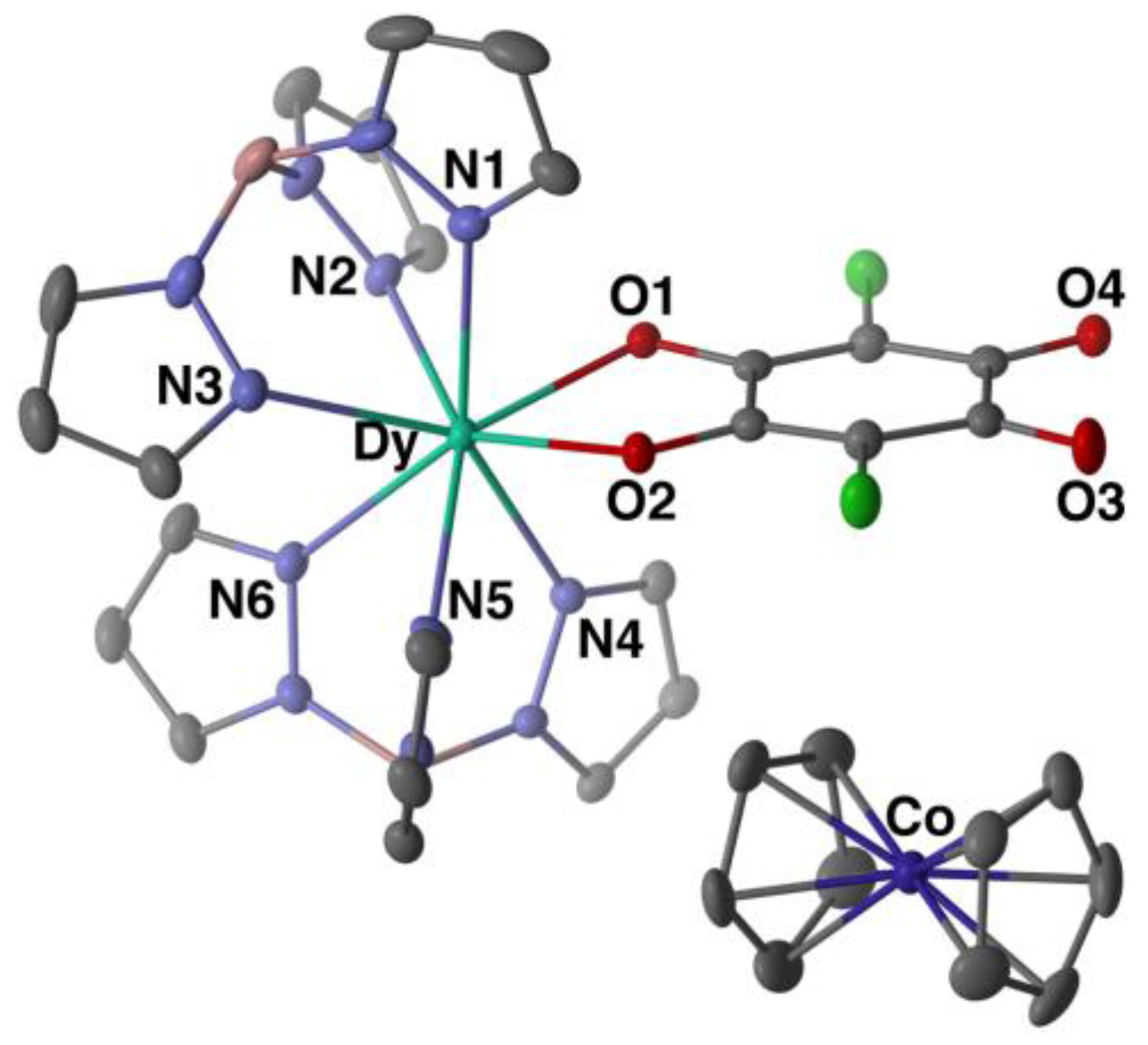
2.2. Molecular Structure Descriptions

The molecular structures of neutral dinuclear complexes 1 and 2 are isostructural and belong to the monoclinic P2₁/n space group (No. 14) (Figure 2). Both 1 and 2 are centrosymmetric complexes with two Ln^III centers bridged by a bis-bidentate Cl₂An²⁻ ligand; consequently, only half of the dimer unit is unique. The coordination environments around the Ln^III centers in 1 and 2 are eight-coordinated with six N atoms from the two Tp⁻ capping ligands, and two O atoms from the Cl₂An²⁻ bridge. The eight-coordinate Ln^III centers adopt slightly distorted triangular dodecahedral geometries based on continuous shape measures (CShMs) [30,31] of 0.785 for 1 and 0.831 for 2.

The bond distances within the rings of quinoidal ligands, such as Cl₂An²⁻, bound to metal ions provide strong information about the electronic structures of the ligands (Scheme 1). The o-quinone form is usually found in mononuclear complexes through terminal bidentate coordination modes, whereas the bi-separated delocalized form is often found in polynuclear complexes and coordination polymers through bis-bidentate coordination modes. The C–O bond distances in the Cl₂An²⁻ ring of 1 are 1.255(2) Å and 1.259(2) Å , while the similar distances in 2 are 1.258(4) Å, and 1.261(4) Å. The C–C bond distances are 1.393(3) Å, 1.396(3) Å, and 1.534(2) Å for 1, and 1.389(5) Å, 1.393(5) Å, and 1.537(4) Å for 2. These values confirm that the Cl₂An²⁻ bridging moieties in complexes 1 and 2 adopt the bi-separated delocalized forms, which also is strongly supported by the IR data. The respective intramolecular Ln^III···Ln^III distances through the Cl₂An²⁻ bridges are 8.6622(5) Å for 1 and 8.7042(5) Å for 2. In addition, the shortest intermolecular Ln···Ln distances of 8.7398(5) Å for 1 and 8.9781(5) Å for 2 are comparable with the intramolecular distances.

The anionic mononuclear complex 3 cocrystallized with [Co(Cp)₂]⁺ in its crystal lattice, and was found to belong to the monoclinic P2₁/c space group (No. 14) (Figure 3). The coordination environment around the Dy^III center of the anionic monomer 3 is structurally similar to those in dimers 1 and 2, differing only slightly in bond distances and angles. The eight-coordinate Dy^III center features a distorted square antiprismatic geometry, according to the CShM value of 1.116, in which the two square faces are defined by N1, N5, N9, and O1, and N3, N7, N11, and O2. The Cl₂An²⁻ moiety of 3 acts as a terminal capping ligand, unlike in dimers 1 and 2. Hence, the resonance structure of Cl₂An²⁻ in the anionic monomer 3 differs significantly from those in 1 and 2 (vide supra). Indeed, the Cl₂An²⁻ C–O ring bond distances in 3 are 1.275(3) Å, 1.275(3) Å, 1.228(3) Å, and 1.234(3) Å, while the C–C bond distances are 1.376(4) Å, 1.382(4) Å, 1.419(4) Å, 1.427(4) Å, 1.519(3) Å, and 1.563(4) Å. These values clearly indicate both single and double-bond character. The Cl₂An²⁻ moiety in complex 3 is therefore in the o-quinone form. Finally, each anionic monomer in 3 is well separated in the crystal lattice, with closest intermolecular Dy^III···Dy^III distances of 9.5145(4) Å.

2.3. Magnetic Properties

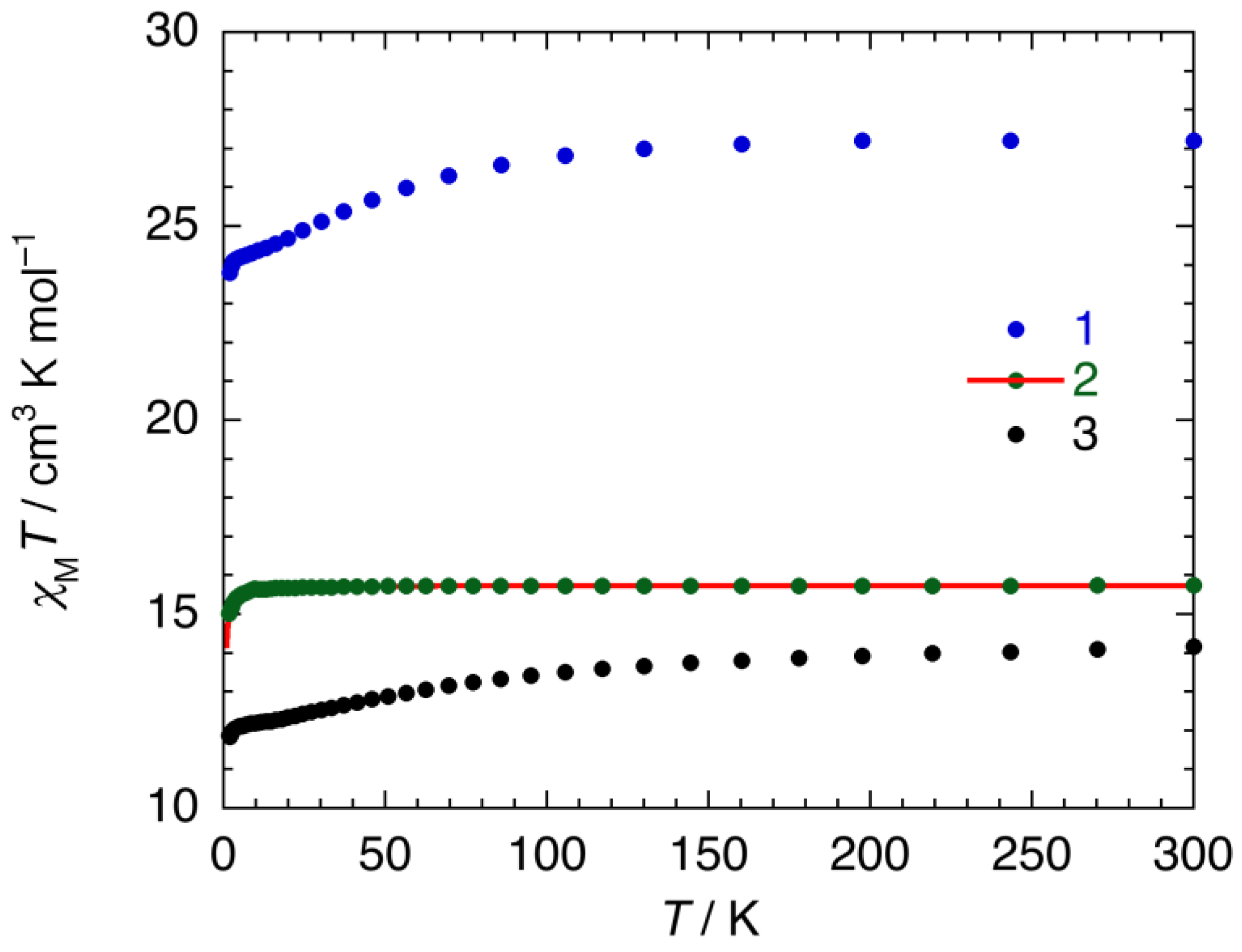
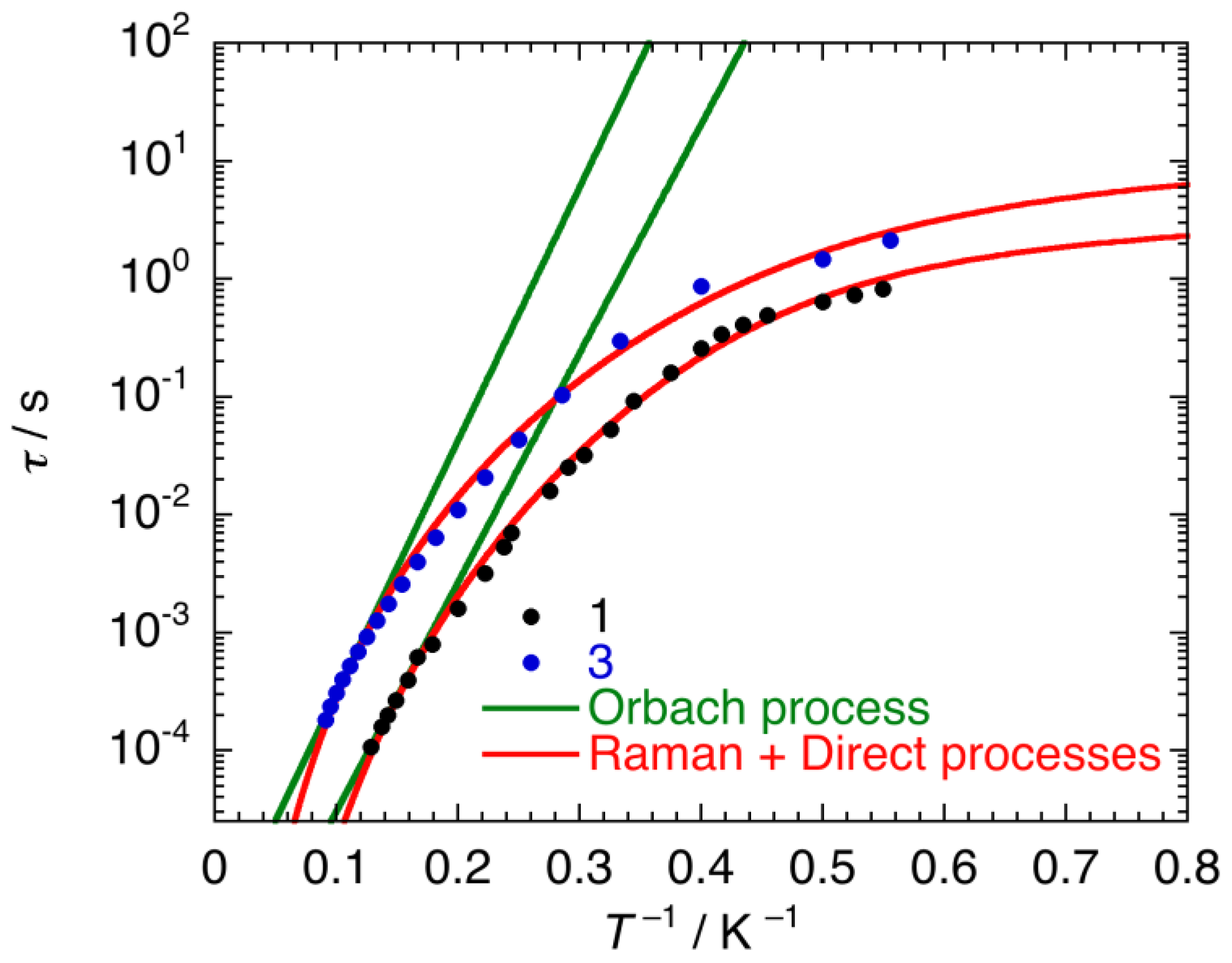
2.3.1. Static Magnetic Properties

DC magnetic susceptibility (χ_M) measurements on 1 were carried out in the 1.8–295 K temperature (T) range in an applied 0.1 T DC field (Figure 4). The value of χ_MT at 295 K for 1 was determined to be 28.29 cm³·K·mol⁻¹, which is in good agreement with the expected value of 28.34 cm³·K·mol⁻¹ for two uncoupled Dy^III ions (⁶H_15/2 with g = 4/3). The χ_MT value remained constant over the 100–300 K T range, below which it decreased smoothly to a value of 23.83 cm³·K·mol⁻¹ at 1.8 K, due to the depopulation of excited Stark sublevels in the crystal-field state. The magnetization (M) of 1 increased rapidly with an increasing magnetic field (H) to 7 T (M = 10.55 μ_B) without saturation at 1.8 K, indicating very strong magnetic anisotropy (Figure S1, Supplementary Materials). Moreover, no hysteresis was observed for 1 above 1.8 K using a conventional SQUID. The detailed determination of the magnetic-exchange coupling constant (J), i.e., magnitude and sign (ferromagnetic or antiferromagnetic), of a polynuclear Ln complex is difficult because of its complicated 4f electronic structure. In contrast, the electronic structure of the Gd^III ion contains a half-filled 4f orbital system, leading to no orbital angular momentum, and can be analyzed as a simple spin-only case (⁸S_7/2 with g = 2). Hence, the qualitative magnitude of J for 1 can be indirectly determined from that of the Gd^III analogue (2). T-dependent χ_MT measurements were performed in the 1.8–300 K T range in an applied DC magnetic field of 0.05 T (Figure 4). The χ_MT value of 2 was determined to be 15.75 cm³·K·mol⁻¹ at 300 K, which corresponds to the spin-only value of two uncoupled Gd^III ions with g = 2.00; the χ_MT value remained constant to 10 K. Further lowering of the temperature to 1.80 K lowered the χ_MT value to 15.02 cm³·K·mol⁻¹. Furthermore, the H-dependent isothermal M data at 1.8 K for 2 show a steady increase with increasing magnetic field, reaching saturation at a value of 14.0 μ_B at 7 T (Figure S1, Supplementary Materials). The magnetic behavior of 2 is the result of the competition between antiferromagnetic exchange between the Gd^III centers via the Cl₂An²⁻ bridge, and single-ion anisotropy arising from the Gd^III ion. To determine whether intermolecular isotropic magnetic exchange or single-ion magnetic anisotropy dominates, plots of χ_MT vs. T, and M vs. H for 2 were constructed using the spin Hamiltonian given by Equation (1):

$$\begin{array}{cc}\hfill \widehat{\mathcal{H}}& ={\widehat{\mathcal{H}}}_{\mathrm{HDVV}}+{\widehat{\mathcal{H}}}_{\mathrm{ZFS}}+{\widehat{\mathcal{H}}}_{\mathrm{Zeeman}}\hfill \\ & =-2J_{\mathrm{Gd}1-\mathrm{Gd}2}{\widehat{S}}_{\mathrm{Gd}1}\cdot {\widehat{S}}_{\mathrm{Gd}2}+2D_{\mathrm{Gd}}\left[{\widehat{S}}_{\mathrm{Gd},z}^2-\frac{S_{\mathrm{Gd}}\left(S_{\mathrm{Gd}}+1\right)}{3}\right]+2E_{\mathrm{Gd}}\left({\widehat{S}}_{\mathrm{Gd},x}^2-{\widehat{S}}_{\mathrm{Gd},y}^2\right)+g{\mu }_{\mathrm{B}}{\widehat{S}}_{\mathrm{T}}\overrightarrow{H}\hfill \end{array}$$

(1)

where S_Gd1 and S_Gd2 are the spin operators for Gd^III ions (S = 7/2), J_Gd1–Gd2 is the isotropic magnetic exchange coupling constant between two Gd^III centers, D_Gd and E_Gd are the axial and rhombic zero-field splitting (ZFS) parameters that are associated with an S = 7/2 Gd^III ion, respectively, g is the isotropic g factor, and μ_B is the Bohr magneton. This model fitted the χ_MT vs. T plot well over the entire 1.8 to 300 K temperature range, and the M vs. H plot at 1.80 K yielded J_Gd1–Gd2/k_B = −0.0066 K, D_Gd/k_B = 0.17 K, and E_Gd/k_B = 1.1 × 10⁻⁵ (≈ 0) K, with g = 2.00 (Figure 4 and Figure S1, Supplementary Materials). The calculated g factor is close to the spin-only value, and a negligible antiferromagnetic interaction between the two Gd^III centers through the Cl₂An²⁻ bridge, and a large ZFS contribution (|D| >> |J|) were found for 2. Except for organic radical bridging ligands, magnetic interactions between paramagnetic Ln^III centers via common organic bridging ligands are well-known to be very weak in general, because 4f orbitals are shielded by outer 6s and 5d orbitals. The two Gd^III centers in 2 are also well-separated by a diamagnetic spacer, namely the Cl₂An²⁻ bridge (vide supra). Therefore, the small calculated J value might be meaningless. As an alternative, we subsequently attempted to fit the magnetic data for 2 by considering only single-ion anisotropy with the mean-field approximation (zJ′), as given by Equation 2:

$$\begin{array}{l}\widehat{\mathcal{H}}={\widehat{\mathcal{H}}}_{\mathrm{ZFS}}+{\widehat{\mathcal{H}}}_{\mathrm{Zeeman}}+{\widehat{\mathcal{H}}}_{\mathrm{MFA}}\\ =2D_{\mathrm{Gd}}\left[{\widehat{S}}_{\mathrm{Gd},z}^2-\frac{S_{\mathrm{Gd}}\left(S_{\mathrm{Gd}}+1\right)}{3}\right]+2E_{\mathrm{Gd}}\left({\widehat{S}}_{\mathrm{Gd},x}^2-{\widehat{S}}_{\mathrm{Gd},y}^2\right)+g{\mu }_{\mathrm{B}}{\widehat{S}}_{\mathrm{T}}\overrightarrow{H}-z{J}^{\prime }\langle {\widehat{S}}_{\mathrm{T}}\rangle {\widehat{S}}_{\mathrm{T}}\end{array}$$

(2)

This model also fitted the χ_MT vs. T plot well over the entire 1.8 to 300 K temperature range, and the M vs. H plot at 1.80 K provided D_Gd/k_B = 0.18 K, E_Gd/k_B = 1.8 × 10⁻⁴ (≈ 0) K, and g = 2.00 with a negligible zJ′/k_B value (~ −10⁻⁵ K). Hence, the χ_MT value for 3 at 300 K is 14.16 cm³·K·mol⁻¹, which is in good agreement with that of the free Dy^III ion (⁶H_15/2 with g = 4/3). The χ_MT product gradually decreased with decreasing T, and finally reached a minimum value of 11.87 cm³·K·mol⁻¹ at 1.8 K. This magnetic behavior is ascribable to the thermal depopulation of the crystal-field state. The M vs. H plot of 3 at 1.8 K displays significant magnetic anisotropy and does not reach saturation up to 7 T (M = 5.10 μ_B).

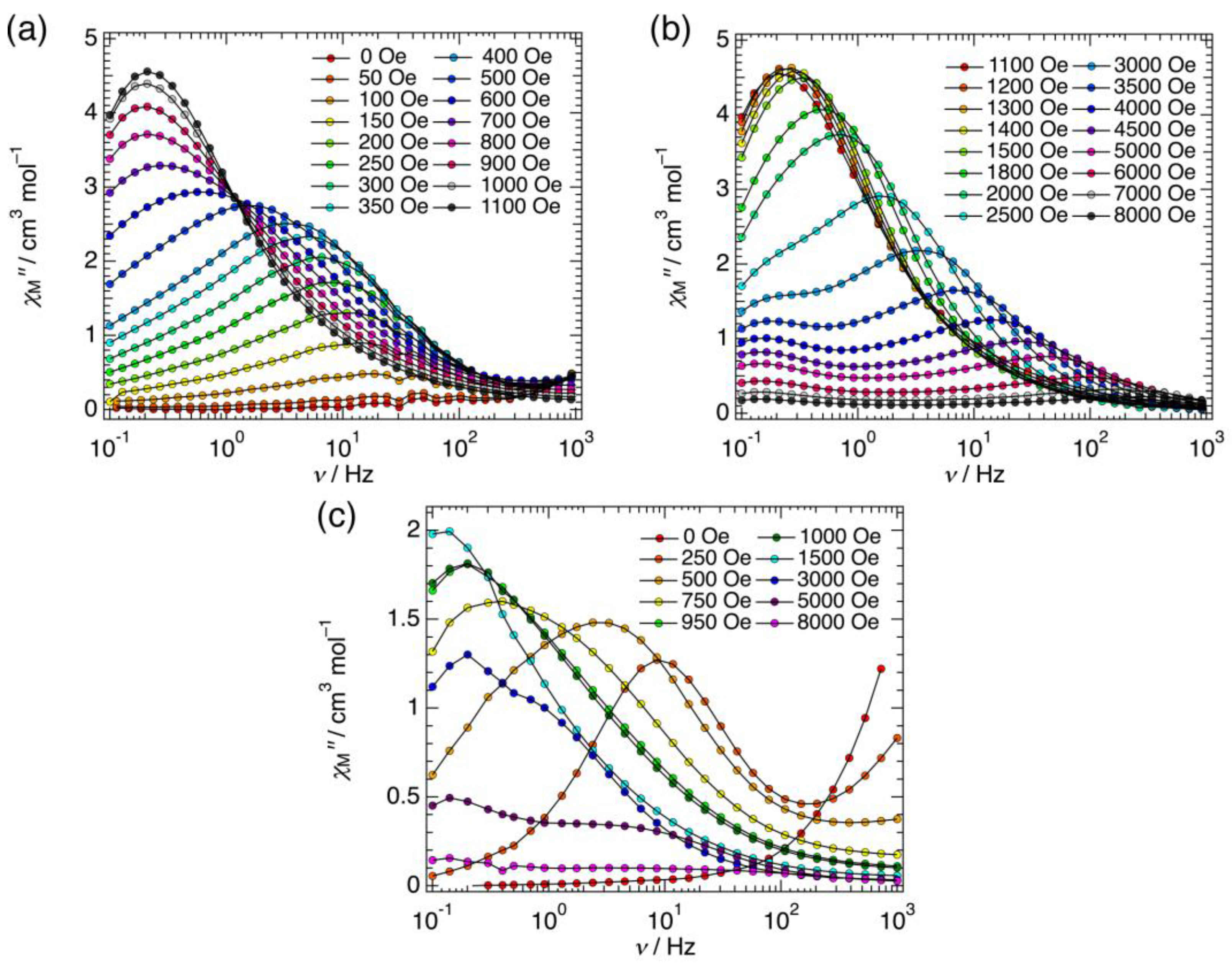
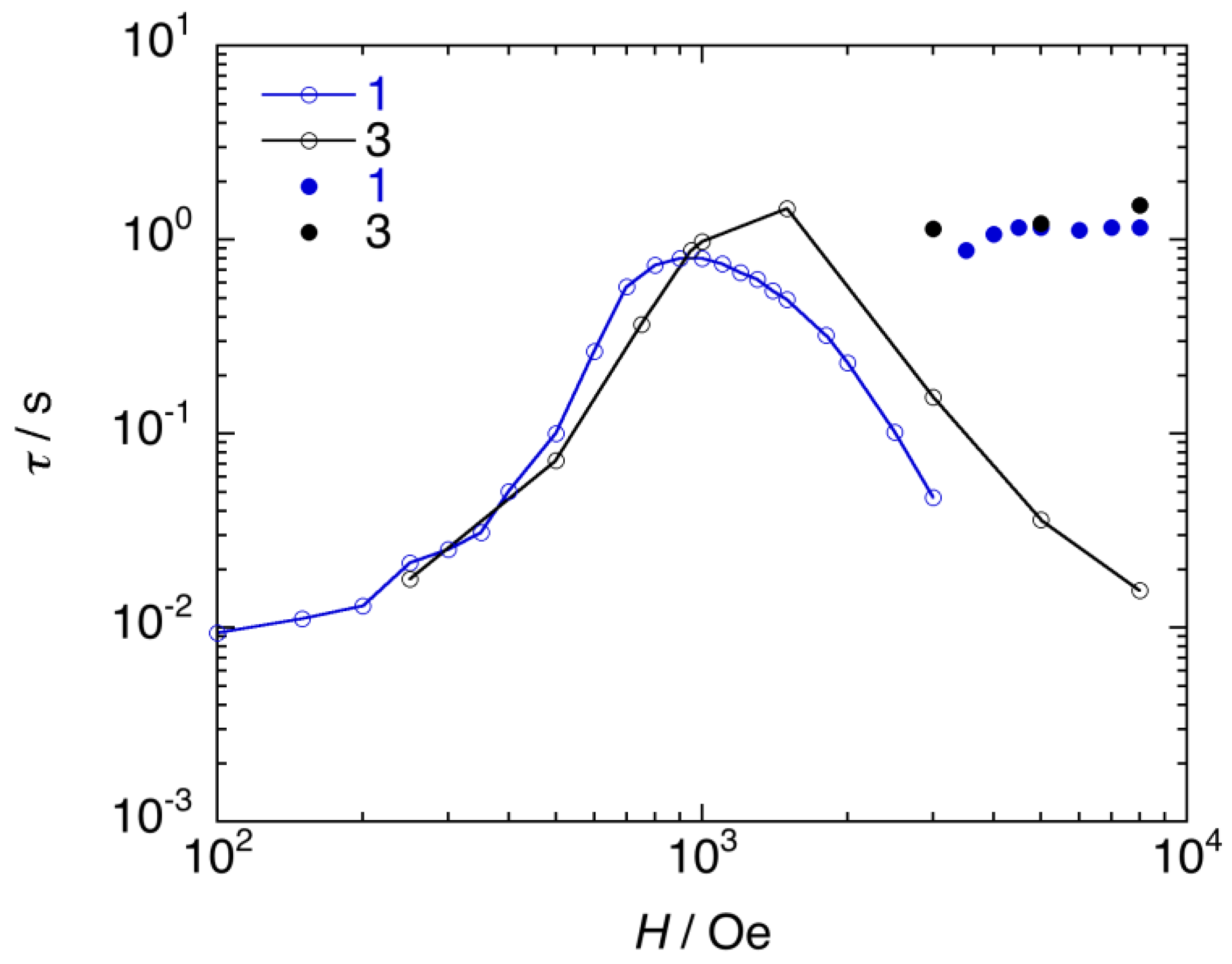
2.3.2. Dynamic Magnetic Properties

To study the slow relaxation of the magnetization of both 1 and 3, alternate-current (AC) susceptibility measurements were performed at a fixed T of 1.8 K with a DC field (H_DC) that varied between 0 and 8000 Oe (Figure 5 and Figure 6). The χ_M″ signals for 1 and 3 in the absence of an applied field increased with increasing frequency (ν), but exhibited only tailing, and no apparent peaks were observed due to blocking in the available ν range. Subsequently, ν-dependent non-zero χ_M″ signals clearly appeared at small static H_DC. This result clearly indicates that zero-field QTM [13] and/or dipolar interactions [32] are suppressed, and/or the non-negligible transverse magnetic anisotropy [33] is broken by the application of H_DC in the ground state. Each χ_M″ peak maximum for 1 shifted to lower ν with an increasing applied H_DC up to ~950 Oe. Further increases in H_DC resulted in the maximum χ_M″ shifting to higher ν. Similarly, the maximum χ_M″ value for 3 shifted to lower ν, reaching a minimum at ~1500 Oe, above which it shifted to higher ν. Therefore, the optimum H_DC values for 1 and 3 were determined to be ~950 Oe for 1 and ~1500 Oe for 3, which was used in the T- and ν-dependent AC susceptibility experiments (Figure 7, Figure 8 and Figure S2, Supplementary Materials).

In addition, the other striking feature for both 1 and 3 is the clear presence of two distinct relaxation processes at higher H_DC fields: the H_DC-dependent component and the H_DC-independent component, which are thermal and QTM relaxation modes, respectively (Figure 6).

Both 1 and 3 show ν-dependent χ_M″ at their respective optimum H_DC. The relaxation time (τ) can be extracted at each blocking temperature using a generalized Debye model (Figure 7). Here, Argand plots [34] (χ_M′ vs. χ_M″ plot) for 1 and 3 were semicircular with small α parameters in the 0.0063–0.31 range for 1 and the 0.035–0.44 range for 3 (Figure 8).

The linear regions at higher T in the semi-logarithmic plots of τ vs. 1/T (Arrhenius plots) for 1 and 3 were used to calculate the thermal energy barrier (Δ_eff) for magnetization reversal, known as Orbach relaxation [35], which provided Δ_eff/k_B = 44.7 K and τ₀ = 3.43 × 10⁻⁷ s for 1, and Δ_eff/k_B = 49.4 K and τ₀ = 2.12 × 10⁻⁶ s for 2 (Figure 9). However, the Arrhenius plots for 1 and 3 deviate from linearity at lower T. Such magnetic relaxation behavior for 1 and 3 suggests the coexistence of thermal relaxation processes and other operative relaxation processes. Hence, τ for 1 and 3 in the given temperature range were analyzed by Equation 3:

$${\tau }^{-1}={\tau }_0^{-1}\exp \left(-\frac{{\Delta }_{\mathrm{eff}}}{k_{\mathrm{B}}T}\right)+C{T}^n+AT+{\tau }_{\mathrm{QTM}}$$

(3)

where the first, second, third, and fourth terms represent Orbach, Raman [35,36,37,38,39], direct [35,36,37,38,39], and QTM processes, respectively. Data for 1 and 3 were analytically reproduced using Equation 3 with appropriate terms for the Raman and direct processes. The best fit was obtained with C = 6.12 × 10⁻³ s⁻¹·K^−7.02 and A = 0.323 s⁻¹·K⁻¹ for 1, while C = 7.22 × 10⁻³ s⁻¹·K^−5.71 and A = 0.106 s⁻¹·K⁻¹ were best for 3 (Figure 9). Generally, the power index (n) of T for a Raman process is 9 because of Kramers ions. The n values of 1 and 3 are lower than the expected value, which might be attributable to the involvement of both optical and acoustic Raman processes during magnetic relaxation [38]. Therefore, both Raman and direct processes dominate the spin dynamics of 1 and 3. Complexes 1 and 3 exhibit different spin-relaxation behavior, which reflect the coordination geometries around their Dy^III centers and their nuclearities, as well as crystal-lattice molecular packing. In addition, although the magnetic analysis of 2 did not reveal any magnetic exchange coupling via the Cl₂An²⁻ ligand, the dinuclear complex 1 might create a small bias that allows for tunneling at zero field.

3. Experimental Section

3.1. Materials and Methods

Co(Cp)₂, DyCl₃·6H₂O, GdCl₃·6H₂O, Na₂Cl₂An·3H₂O, and all of the solvents were purchased from Wako Pure Chemical Industries, Ltd. (Osaka, Japan) KTp was purchased from Tokyo Chemical Industry (TCI) Co., Ltd. (Tokyo, Japan). All of the chemicals were reagent grade and were used as received. Both CH₂Cl₂ and hexane were super dehydrated grade and deoxidized grade. Unless otherwise noted, reactions and subsequent manipulations were performed under aerobic conditions at room temperature, while compound 3 was prepared under an inert N₂ atmosphere using standard glovebox techniques.

3.2. Synthesis of [{Dy(Tp)₂}₂(μ-Cl₂An)]·2CH₂Cl₂ (1)

This complex was prepared from modification of the original method of Kaizaki et al. [26]. An aqueous solution (5 mL) of DyCl₃·6H₂O (75.4 mg, 0.2 mmol) was added dropwise to a stirred aqueous solution (5 mL) of Na₂Cl₂An·3H₂O (30.7 mg, 0.1 mmol) and KTp (100.8 mg, 0.4 mmol), resulting in a fine purple precipitate immediately. After stirring for 10 min, the purple solid was isolated via filtration, washed with a small amount of H₂O (2 × 5 mL) and Et₂O (3 × 5 mL), and dried in vacuo. The purple solid was then dissolved in CH₂Cl₂, and the resultant purple solution was filtered. Diffusion of hexane into the filtrate yielded purple rod-shaped crystals suitable for single-crystal X-ray diffraction analysis within 1 week. Yield: 144.5 mg (52%). Anal. Calcd. for C₄₄H₄₄B₄Cl₆Dy₂N₂₄O₄: C, 34.01; H, 2.85; N, 21.63%. Found: C, 33.98; H, 2.90; N, 21.72%.

3.3. Synthesis of [{Gd(Tp)₂}₂(μ-Cl₂An)]·2CH₂Cl (2)

This complex was prepared according to the same method as that for 1 with GdCl₃·6H₂O instead of DyCl₃·6H₂O. Yield: 48%. C₄₄H₄₄B₄Cl₆Gd₂N₂₄O₄: calcd. C 34.24, H 2.87, N 21.78; found C 34.56, H 2.91, N 21.94.

3.4. Synthesis of [Co(Cp)₂][Dy(Tp)₂(Cl₂An)] (3)

In a N₂-filled glovebox, Co(Cp)₂ dissolved in PhMe (5 mL) was added to a solution of 1 in the same solvent (5 mL). The color of the reaction mixture changed to yellowish green. Upon stirring the mixture, bright yellow microcrystalline solid appeared immediately, which was collected by filtration, washed with a small amount of Et₂O (5 mL), and allowed to dry on the filter for 15 min. The yellowish green solid was then dissolved in MeCN, and the resulting pale yellow solution was filtered. Slow diffusion of Et₂O into the filtrate gave red block-shaped crystals suitable for single-crystal X-ray diffraction analysis for two weeks. Yield: 83%. Anal. Calc. for C₃₄H₃₀B₂Cl₂CoDyN₁₂O₄: C, 41.47; H, 3.07; N, 17.07. Found: C, 41.33; H, 3.14; N, 16.87%.

3.5. Single-crystal X-ray Crystallography Data Collection and Refinement

Single-crystals of 1, 2, and 3 were coated with Nujol and were quickly mounted on MicroLoops (MiTeGen LLC., Ithaca, NY, USA) and immediately cooled in a N₂ cold stream to avoid decomposition. Data collection was performed on a Rigaku R-AXIS RAPID II IP diffractometer (Rigaku Corporation, Tokyo, Japan) with graphite-monochromated Mo Kα radiation (λ = 0.71075 Å) and a low-temperature apparatus. The crystal dimensions for 1, 2, and 3 were 0.60 × 0.15 × 0.10, and 0.50 × 0.10 × 0.10, and 0.60 × 0.20 × 0.10 mm, respectively. Data for 1, 2, and 3 were collected at 163(1), 100(1) and 108(1)K, respectively. Data integration, preliminary data analysis, and absorption corrections were performed using the Rigaku CrystalClear-SM 1.4.0 SP1 [40] and the CrystalStructure 4.1.1 [41] crystallographic software packages. The molecular structures were solved using direct methods included in SIR2011 [42] and refined using the SHELXL program [43]. All nonhydrogen atoms were refined anisotropically. All hydrogen atoms were introduced as fixed contributors. CCDC-1584512, -1584513 and -1584514 for 1, 2, and 3 contain the supplementary crystallographic data for this paper, and can be obtained free of charge from The Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/data_request/cif.

3.6. Physical Measurements

Elemental analyses were performed by the Technical Support Division, Research and Analytical Centre for Giant Molecules, Graduate School of Science, Tohoku University. Fourier transform infrared (FTIR) spectra were acquired as KBr disks at room temperature on a JASCO FT/IR-410 spectrophotometer (JASCO Corporation, Tokyo, Japan). Magnetic data were collected on a Quantum Design MPMS3 or MPMS-5S superconducting quantum interference device (SQUID) magnetometer (Quantum Design Japan, Inc., Tokyo, Japan). All of the magnetic measurements were performed on finely ground microcrystalline powders in a calibrated gelatin capsule. DC susceptibility measurements were performed in the T range of 1.8–300 K in a DC field of 0.05 T or 0.1 T. Field-dependent dc magnetization measurements were performed from −7 to +7 T at 1.8 K. AC susceptibility measurements were performed in the T range of 1.8–20 K in a 3 Oe AC field, oscillating at frequencies of 1 and 997 or 1488 Hz in different applied DC fields. Magnetic susceptibility data were corrected for diamagnetic contributions from the sample holder as well as for the core diamagnetism of each sample estimated using Pascal’s constants [44].

4. Conclusions and Outlook

The dinuclear and mononuclear [{Dy(Tp)₂}₂(μ-Cl₂An)] and [Co(Cp)₂][Dy(Tp)₂(Cl₂An)] eight-coordinate complexes were synthesized. The two complexes have similar N₆O₂ coordination environments that are based on the dianionic Cl₂An²⁻ ligand and Tp⁻ as auxiliary ligands. However, each Cl₂An²⁻ moiety adopts the bi-separated delocalized form in dinuclear [{Dy(Tp)₂}₂(μ-Cl₂An)], and the o-quinone form in mononuclear [Co(Cp)₂][Dy(Tp)₂(Cl₂An)]. Therefore, in this work, both complexes were magnetically characterized to examine how the donor strength affects the slow relaxation of the magnetization. Dynamic magnetic measurements clearly reveal that both of the complexes exhibit temperature-dependent slow relaxations of magnetization facilitated by multiple relaxation pathways. Their spin dynamics are different, reflecting the coordination geometries around the Dy^III centers and their nuclearities, as well as crystal-lattice molecular packing. The redox-active Cl₂An²⁻ ligand is a good candidate for the future construction of redox-switchable SMMs, as anilate derivatives readily undergo redox reactions to form both diamagnetic and paramagnetic species; such redox-switchable SMMs and/or SIMs that may be applied in future technologies, such as molecular spintronics. Furthermore, we are currently constructing dinuclear complexes of all other lanthanides bridged with the Cl₂An²⁻ moiety. This effort will provide valuable insight into the electronic structures, magnetic properties, and trends observed in the series of dinuclear [{Ln(Tp)₂}₂(μ-Cl₂An)] complexes.