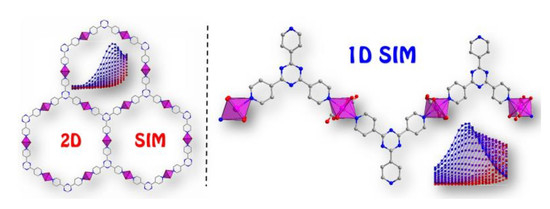
Field-Induced Single-Ion Magnet Behaviour in Two New Cobalt(II) Coordination Polymers with 2,4,6-Tris(4-pyridyl)-1,3,5-triazine

Abstract

We herein reported the syntheses, crystal structures, and magnetic properties of a two-dimensional coordination polymer {[Co^II(TPT)_2/3(H₂O)₄][CH₃COO]₂·(H₂O)₄}_n (1) and a chain compound {[Co^II(TPT)₂(CHOO)₂(H₂O)₂]}_n (2) based on the 2,4,6-Tris(4-pyridyl)-1,3,5-triazine (TPT) ligand. Structure analyses showed that complex 1 had a cationic hexagonal framework structure, while 2 was a neutral zig-zag chain structure with different distorted octahedral coordination environments. Magnetic measurements revealed that both complexes exhibit large easy-plane magnetic anisotropy with the zero-field splitting parameter D = 47.7 and 62.1 cm⁻¹ for 1 and 2, respectively. This magnetic anisotropy leads to the field-induced slow magnetic relaxation behaviour. However, their magnetic dynamics are quite different; while complex 1 experienced a dominating thermally activated Orbach relaxation at the whole measured temperature region, 2 exhibited multiple relaxation pathways involving direct, Raman, and quantum tunneling (QTM) processes at low temperatures and Orbach relaxation at high temperatures. The present complexes enlarge the family of framework-based single-ion magnets (SIMs) and highlight the significance of the structural dimensionality to the final magnetic properties.

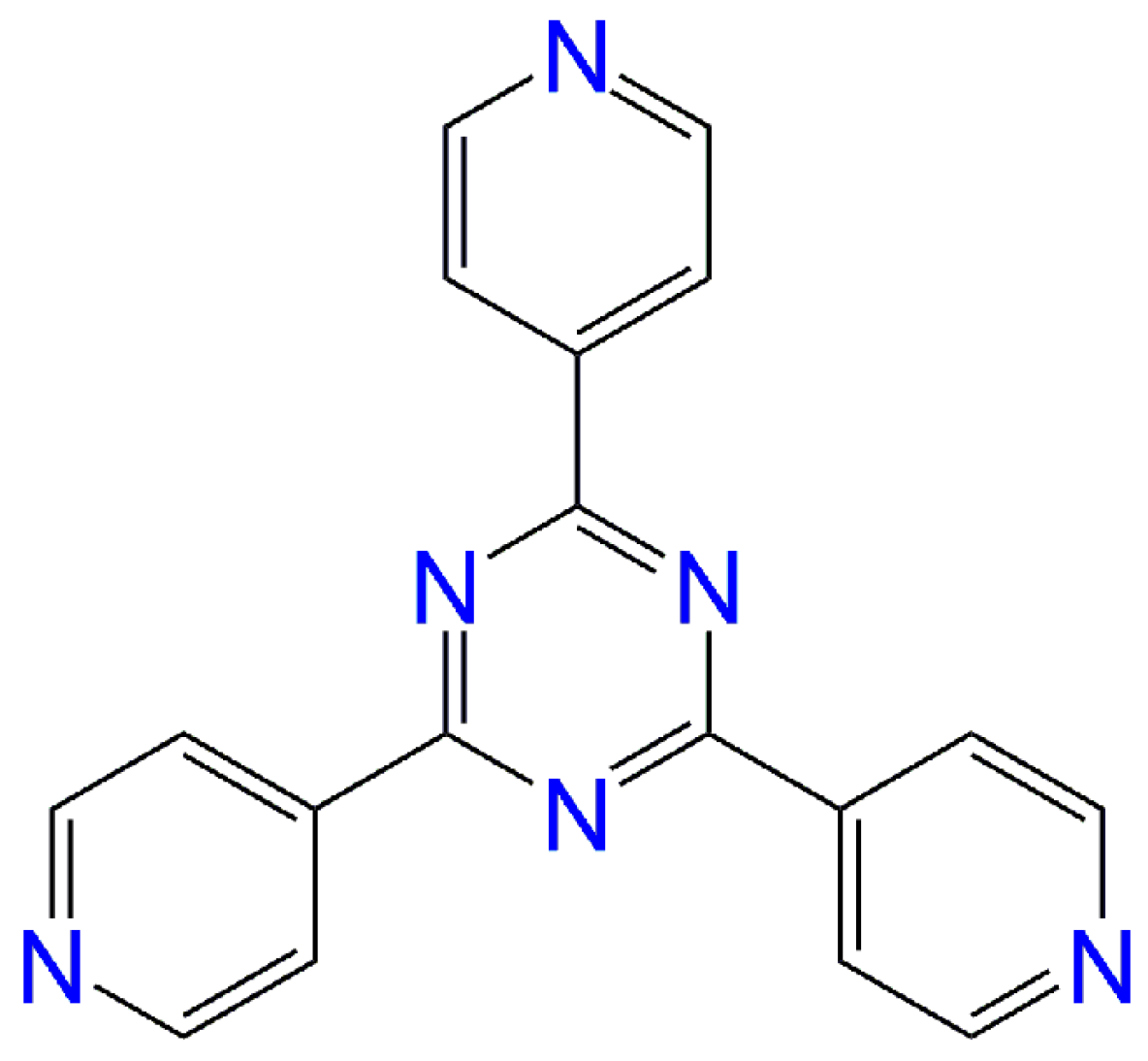
1. Introduction

Single-molecule magnets (SMMs) have attracted continuous interest in the field of molecular magnetism since the discovery of magnetic bistability in Mn₁₂ acetate clusters [1]. These macroscopic compounds have opened a new window to the microscopic world of the quantum and have great potential in high-density information storage and quantum computing [2]. For a long time, metal clusters with high spin states have been highly pursued. However, the magnetisation reversal barriers (U_eff) and blocking temperatures (T_B) have not been effectively enhanced for years. Recent research on mononuclear lanthanide and transition metal based SMMs, also termed as single-ion magnets (SIMs), revealed that high magnetic anisotropy is vitally important to the performance of SMMs [3]. As a result, SIMs have aroused a growing interest in the field of molecular magnetism and numerous related studies have been reported [4].

Since the first report of field-induced slow magnetic relaxation behaviour in a mononuclear Fe^II complex in 2010 by Long and co-workers [5], transition-metal-based SIMs have experienced a fast expansion in the literature, especially for those based on Co(II) ions. Intense efforts have been devoted to the design and synthesis of isolated 3d SIMs with coordination numbers ranging from two to eight in various geometries [6]. Furthermore, the field-induced SIM behaviour has also been explored in some one-dimensional (1D) [7,8], two-dimensional (2D) [9,10,11,12,13,14,15,16], and even three-dimensional (3D) Co^II coordination frameworks [17,18], as long as the magnetic coupling between the spin centres can be ignored. The magnetic anisotropic spin centres in the frameworks can be well isolated by organic linkers or diamagnetic cyanometallates, and thus can be regarded as isolated single-ion magnetic centres. In this sense, the coordination frameworks offer potentially excellent platforms for their structural stability, diversity, and flexibility, and can be used to control the magnetic anisotropy and even the magnetic relaxation processes [19].

Recently, our group has been continuously focused on the single-ion magnetism of Co^II ions with pentagonal bipyramidal (PBP) geometry, and we have reported a series of mononuclear complexes [20,21], as well as 1D and 2D coordination polymers based on the PBP Co^II building blocks [8,9,10]. The influence of axial ligands and magnetic exchange interactions has been carefully studied in these systems. We noticed that PBP mononuclear Co^II complexes are roubst SIM systems with easy-plane magnetic anisotropy, and negligible magnetic interactions can maintain the field-induced SIM behaviour in these frameworks, while weak magnetic interactions suppress the slow magnetic relaxation.

To continue our study, a classic ligand, 2,4,6-Tris(4-pyridyl)-1,3,5-triazine (TPT), which can act as a three-connected node (Figure 1), was assembled with Co^II ions and a rigid macrocyclic pentadentate ligand dibenzo-15-crown-5-ether with the aim of preparing more isolated Co^II SIMs in multi-dimensional frameworks. However, due to unknown reasons, the Co^II centres were not chelated by the macrocyclic ligand in the self-assembly process. Serendipitously, the Co^II ions were bridged by the TPT ligands, forming two new coordination polymers with different structures. Herein, we reported the syntheses, crystal structures, and magnetic properties of a 2D cationic framework compound {[Co^II(TPT)_2/3(H₂O)₄][CH₃COO]₂·(H₂O)₄}_n (1) and a neutral 1D chain compound {[Co^II(TPT)₂(CHOO)₂(H₂O)₂]}_n (2). Magnetic measurements revealed that both complexes exhibit large easy-plane magnetic anisotropy and field-induced slow magnetic relaxation behaviour.

2. Results and Discussion

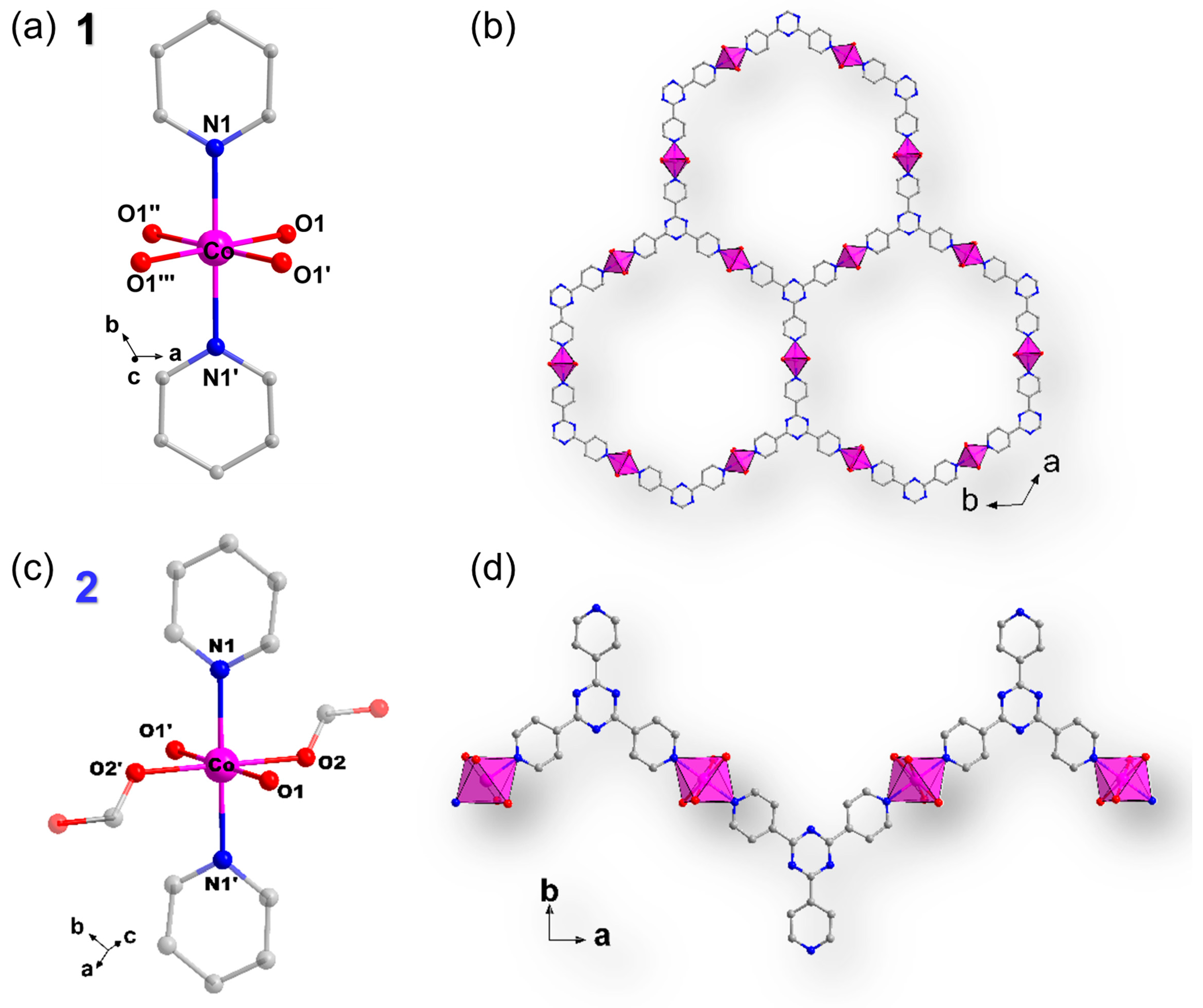
2.1. Crystal Structure Description

Single-crystal X-ray diffraction analyses revealed that complex 1 crystallises in the trigonal space group R $\overline{3}$m and has a 2D hexagonal planar structure (Table S1, Figure 2b). It should be noted that a similar compound [Co(NCS)₂(H₂O)_0.65(MeOH)_0.35(TPT)₂]·2.4(H₂O) (CoNCS) has been structurally studied in detail by Murugesu and co-workers, and it has a Shubnikov hexagonal plane net [17]. The asymmetric unit of 1 contains one lattice water molecule, one acetate anion, and a 25% occupied Co^II ion coordinated by one water molecule and one 50% occupied (TPT)_1/6 ligand (Figure S1). The Co^II centre in 1 resides in a slightly elongated octahedral geometry consisting of four equatorial O atoms from water molecules and two N atoms from bridging TPT ligands in the axial positions (Figure 1a). The average Co–O and Co–N bond lengths are 2.071(2) and 2.144(4) Å, respectively. The continuous shape measure value (CShM) related to the ideal octahedron (O_h symmetry) for the Co^II centre was calculated to be 0.101 using the Shape 2.1 program [22]. As for the ligand TPT, it is on the 3-fold axis and acts as a three-connected node using all three pyridine groups to coordinate three Co^II centres. Bridged by the three-connected bridging ligand, a 2D honeycomb (6, 3) framework was formed. The shortest intralayer Co···Co distance is 13.347 Å. These layers are further packed alternatingly along the c axis in a staggered hcb (Shubnikov hexagonal plane net) mode (Figure S2). Thus, although there is very large opening window in one single layer, there are no significant open channels in the structure of 1. The shortest interlayer Co···Co distance is 8.293 Å. As we can see, the Co^II ions in 1 are well separated by the organic ligands, which will lead to a very weak (if not completely absent) magnetic interaction between these spin centres. This neglible magnetic interaction will not quench the SIM behaviour of 1, as will be discribed later.

As for compound 2, it has a 1D chain structure bridged by two of the three pyridines of the TPT ligand (Figure 2d). Though similar Co^II complexes based on a TPT ligand with a zigzag chain structure have been reported in the literature [23,24], the dynamic magnetic properties of these chains have never been studied. High magnetic anisotropy was revealed in the compound [Co(Piv)₂(TPT)(C₂H₅OH)₂]_n (CoPiv) by Eremenko and co-workers, which showed a spin state switching after desolvation [23]. Complex 2 crystallises in the monoclinic space group C2/c and the Co^II centre is also in a distorted octahedral geometry with a N₂O₄ coordination environment, where the N and O atoms are provided by the TPT ligands, coordinated water molecules, and formate groups, respectively (Figure S3 and Figure 2c). We have to point out that the formate anions should be formed by the hydrolysis of the N,N′-dimethylformamide (DMF) solvent under the hydrothermal condition, which has been reported widely in the literature [25]. The average Co–O and Co–N bond lengths are 2.091(2) and 2.176(1) Å, which are slightly larger than those of compound 1 and close to those of compound CoPiv. The CShM value is calculated to be 0.276, suggesting a more distorted octahedron. Different from that in 1, the TPT ligand in 2 serves as a ditopic bridge, linking the Co(H₂O)₂(CHOO)₂ core to form a neutral 1D chain. The interchain Co···Co distance is 12.913 Å, while the shortest interchain Co···Co distance is of 8.293 Å. As in 1, these long Co···Co distances separate the Co^II ions efficiently and make compound 2 another candidate to be a SIM system with a framework structure (Figure S4).

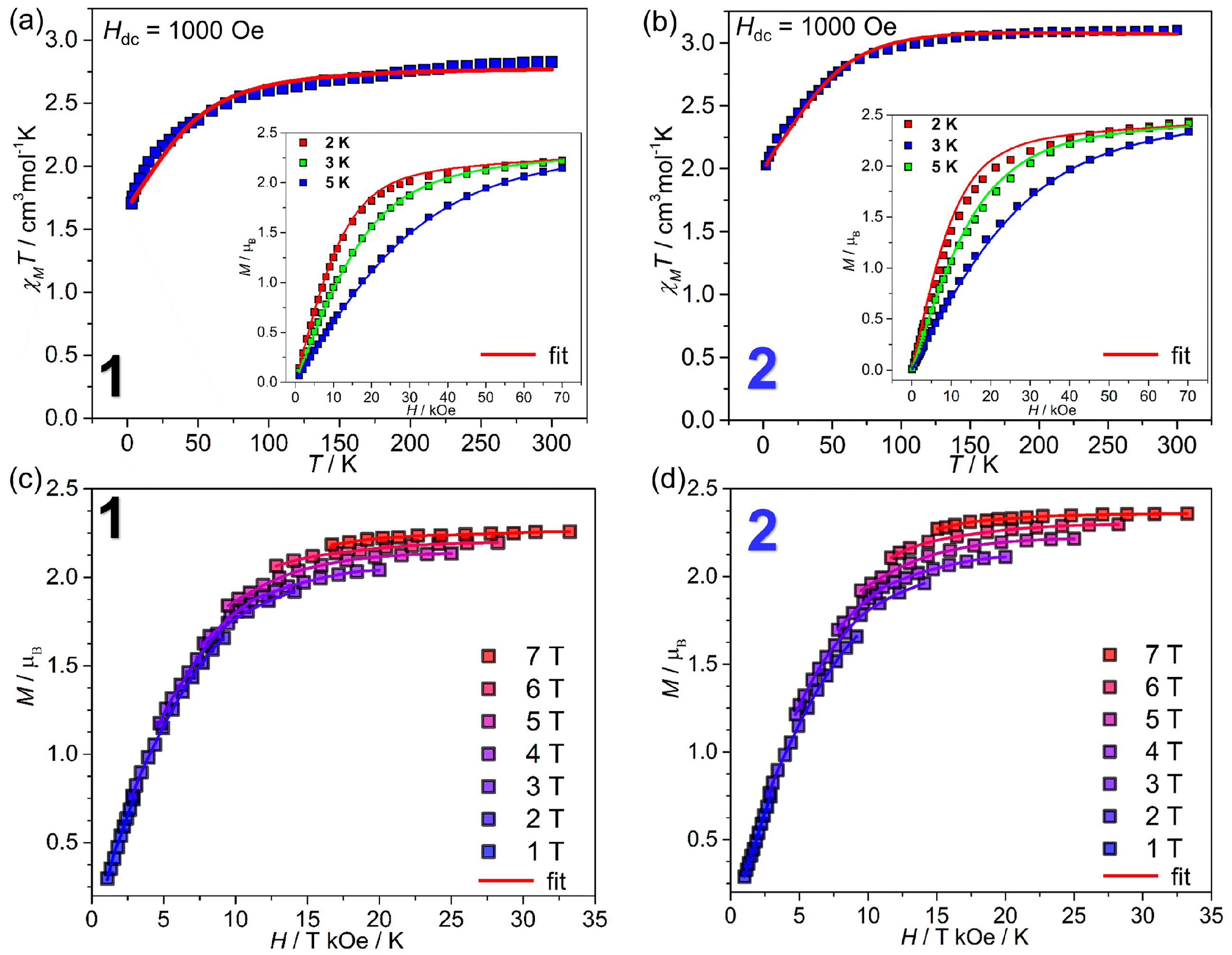
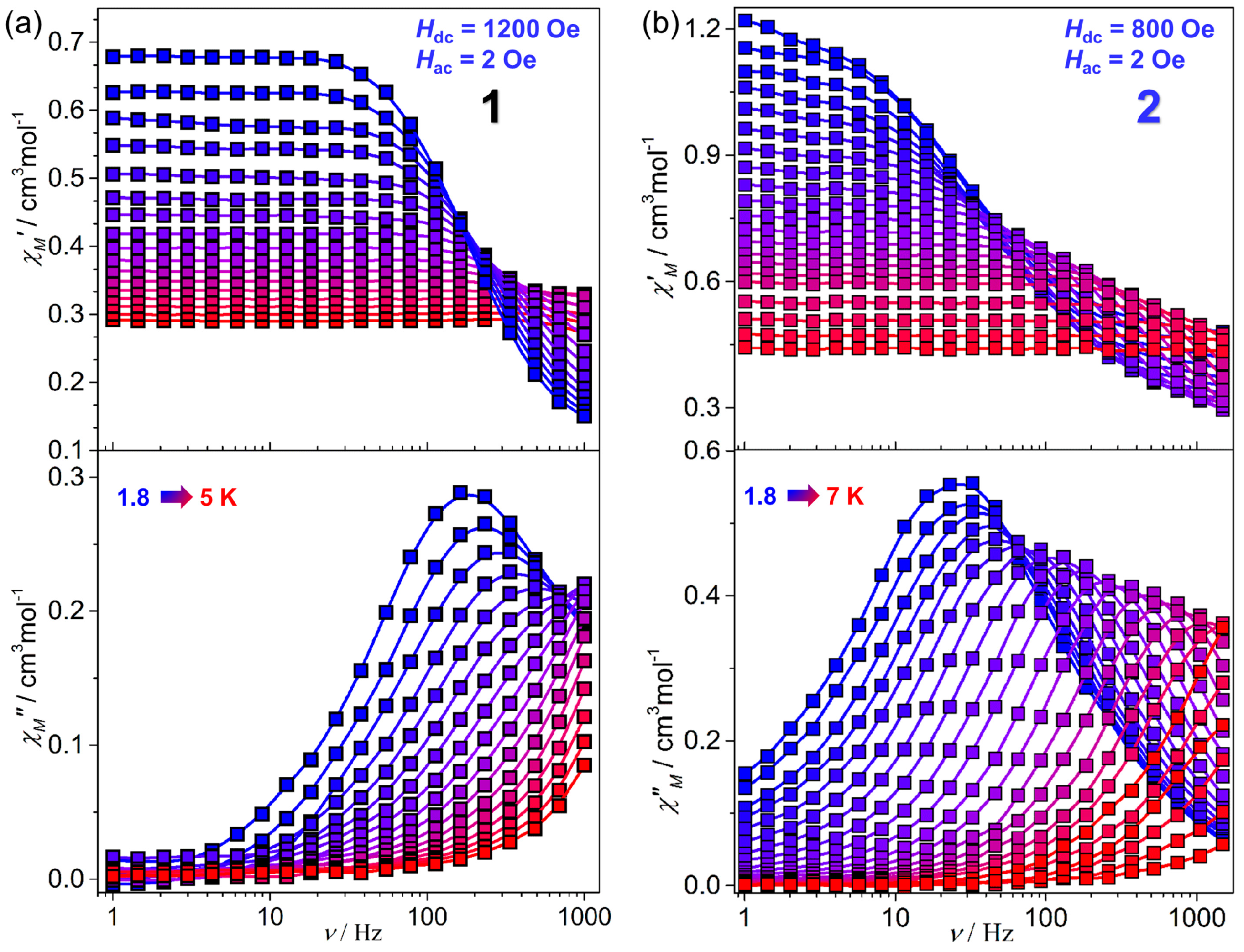
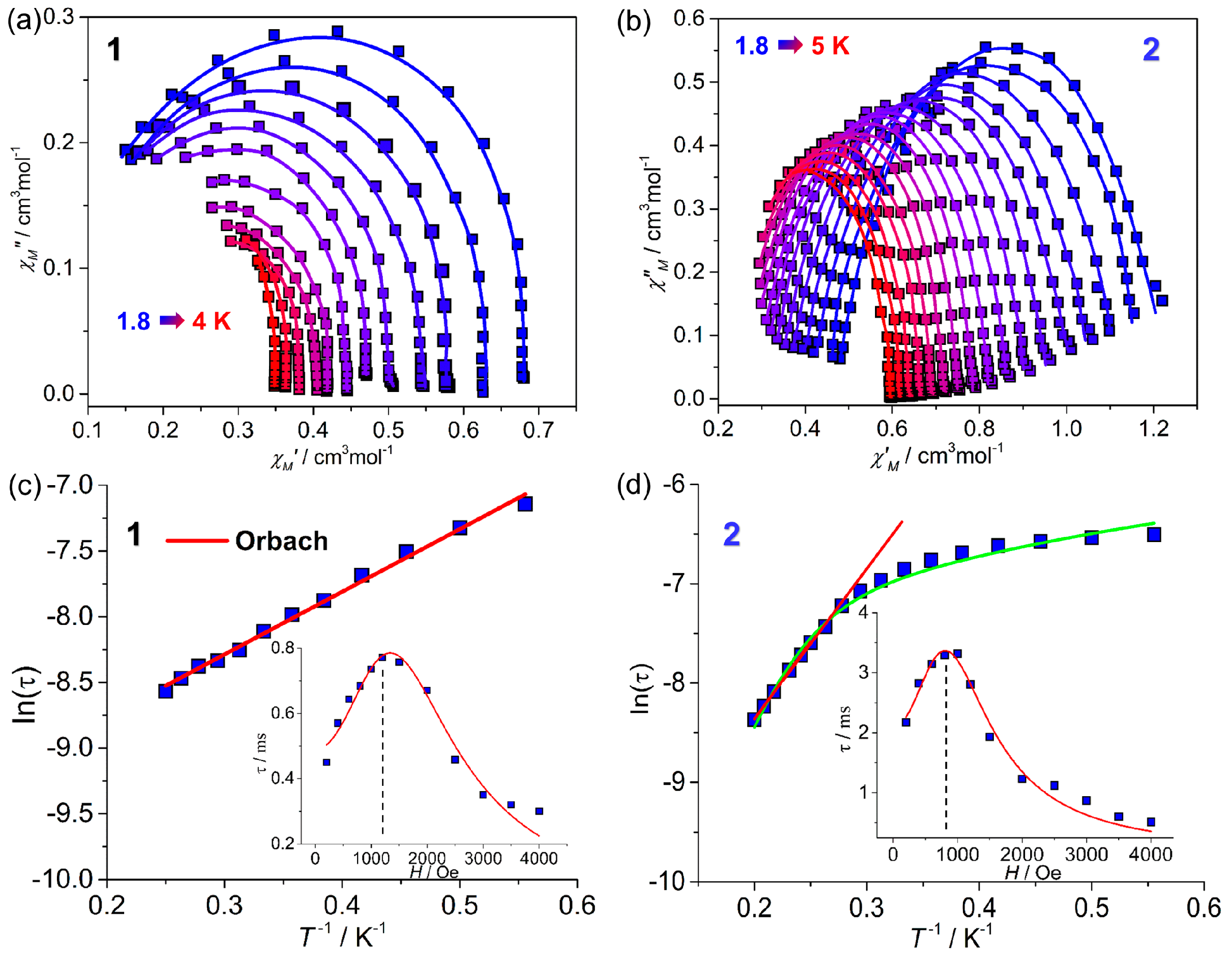
2.2. Magnetic Properties

Variable-temperature magnetic susceptibilities for compounds 1 and 2 in the temperature range of 2–300 K were performed on ground single crystal samples under an external direct current (dc) field of 1000 Oe (Figure 3). At 300 K, the χ_MT values for 1 and 2 are 2.826 and 3.103 cm³·mol⁻¹·K, respectively, which are significantly higher than the spin-only value for a high-spin Co^II ion with g = 2 (1.875 cm³·mol⁻¹·K). These high values can be attributed to the orbit contribution and significant spin-orbit coupling (SOC) and are comparable to the reported values (2.1–3.8 cm³·mol⁻¹·K) for high-spin Co^II centres in the distorted octahedral geometry [11,12,13,14,15,16,17,18]. Upon cooling, the χ_MT curves decrease very slowly down to the vicinity of 50 K and then abruptly decrease to 2 K, which is typical of anisotropic mononuclear Co^II complexes [4]. The χ_MT values of 2 in the high temperature region are obviously larger than those of 1, indicating that 2 might possess a higher magnetic anisotropy. The field-dependent magnetisations for 1 and 2 were also measured at 2, 3, and 5 K with fields up to 70 kOe. The largest magnetisation values at 70 kOe reach 2.22, 2.21, and 2.14 μ_B for 1, and 2.43, 2.42, and 2.33 μ_B for 2 at 2, 3, and 5 K, respectively (Figure 3). The lack of saturation of the magnetisation also suggests the presence of appreciable magnetic anisotropy in these 1D and 2D coordination polymers.

To evaluate the magnetic anisotropy of the Co^II centres in 1 and 2, the magnetic susceptibilities over the whole temperature range and the magnetisation data at 2, 3, and 5 K of 1 and 2 were fitted simultaneously using the PHI [26] program with the following spin Hamiltonian:

H = D[S_z² − S(S + 1)/3] + E(S_x² − S_y²) + μ_B·g·S·B

(1)

where the D, E, S, B, μ_B represent the axial and rhombic zero-field splitting (ZFS) parameters, the spin operator, magnetic field vectors, and the Bohr magneton, respectively. The best fit parameters are D = 47.7 cm⁻¹, E = 0 cm⁻¹, g_z = 2.042, g_x,y = 2.441 for 1, and D = 62.1 cm⁻¹, E = 0.04 cm⁻¹, g_z = 1.989, g_x,y = 2.748 for 2. No acceptable fitting can be achieved with the easy-axial type of initially assigned variables. Thus, these values indicate the easy-plane magnetic anisotropy of the octahedral Co^II ions in 1 and 2, which are consistent with the reported results in CoNCS [18] and Co(AcO)₂(py)₂(H₂O)₂ [27]. Furthermore, the reduced magnetisation data for 1 and 2 collected at different magnetic fields of 1–7 T in the temperature range of 2–10 K (Figure 3) show significant separation between the isofield curves, indicating the large magnetic anisotropy of both complexes. The best fit using Anisofit2.0 [28] gave D = 36.5 cm⁻¹, E = 0.01 cm⁻¹, and g = 2.351 for 1, and D = 56.8 cm⁻¹, E = 0.1 cm⁻¹, and g = 2.34 for 2, which agrees well with the fitting results by PHI. For mononuclear octahedral Co^II SIMs, positive and negative D values were both observed experimentally and confirmed by theoretical calculations [29]. In addition, to gain a clear scope on reported non-isolated Co^II SIMs, the magnetic properties of these systems, including magnetic anisotropy parameters and energy barriers, are compiled in Table S3. From this table, we noticed that the single-ion magnetism in 1D, 2D, and 3D Co^II coordination polymers with local O_h symmetry only exhibit an easy-plane type of magnetic anisotropy [11,12,13,14,15,16,17,18]. The situation in the present compounds further support this phenomenon. The magnitude of the ZFS parameters are influenced by the electronic structures of the ligands, charge of the ligands, crystal field distortions, etc. Thus, the larger magnetic anisotropy of 2 could be attributed to the overall change of coordination environment around the Co^II ions.

To investigate the magnetic dynamics in 1 and 2, alternating current (ac) magnetic susceptibility was measured at 2.0 K under external dc fields of 0–4000 Oe (Figure S3, Supplementary Materials). No out-of-phase signals (χ″) were observed under a zero dc field due to the occurrence of the fast quantum tunneling process (QTM) induced by intermolecular and/or strong hyperfine interactions, which have been observed in most Co^II SIMs [6]. However, after application of dc fields to suppress the QTM effect, both systems showed clear frequency dependence of the in-phase and out-of-phase signals (Figure 4 and Figure 5, Figures S5 and S6, Supplementary Materials), indicating the field-induced SIM behaviour of 1 and 2. From these ac data, Cole-Cole plots of 1 and 2 at various dc fields were constructed (Figure S6, Supplementary Materials) and fitted by the generalised Debye model [30] to give the field-dependent relaxation time τ (insets of Figure 5). The diagrams of τ vs H suggest that the slowest relaxation occurs at around 1200 Oe for 1 but 800 Oe for 2, which were then chosen as the optimum fields for further ac measurements of 1 and 2 (Figure 4 and Figure S7, Supplementary Materials). The Cole-Cole plots of 1 and 2 at different temperatures (1.8–5 K for 1, 1.8–7 K for 1, Figure 5) were used to extract the temperature-dependent relaxation times (τ). The isothermal susceptibility (χ_T), adiabatic susceptibility (χ_S), τ, and α parameters are listed in Tables S3 and S4. The obtained α parameters are in the range of 0–0.1 for 1 and 0–0.23 for 2, suggesting the narrow distribution of the relaxation time. As depicted in Figure 5, the lnτ vs. 1/T plots of 1 and 2 are quite different; it exhibits an almost linear dependence in the temperature range of 1.8–4.0 K for compound 1, while it shows a clear curvature at the range of 1.8–5.0 K for compound 2, implying their different relaxation mechanisms. The linear part of the lnτ vs. 1/T plots can be fitted by the Arrhenius law τ = τ_o exp(U_eff/k_BT) firstly, affording the effective energy barriers (U_eff) of 4.8 cm⁻¹ and 15.5 cm⁻¹ with the pre-exponential factors τ_o being 6 × 10⁻⁶ s and 1 × 10⁻⁶ s for 1 and 2, respectively.

In general, the magnetic relaxation mechanism for a magnetic system is usually quite complex and involves multiple relaxation pathways, such as the Direct, QTM, Raman, and Orbach relaxation processes [31]. These processes can be described by the following equation including the sum of four terms:

$${\tau }^{-1}=A{H}^{2}T+\frac{B_1}{1+B_2{H}^2}+C{T}^n+{{\tau }_0}^{-1}\exp \left(-U_{eff}/k_{B}T\right)$$

(2)

where A, B₁, B₂, C, n are coefficients and H, T, τ₀, U_eff, and k_B have their usual meanings as mentioned before. The first two terms correspond to the field-dependent Direct and QTM processes, while the latter two terms represent the contributions of the two-phonon Raman and thermally activated Orbach mechanisms. Generally, thermally activated behaviour observed in high-temperature region is mainly attributed to the Orbach relaxation process through the excited M_S levels. For 1, the linear variation of the logarithm of relaxation times at the whole temperature region indicates a dominating Orbach relaxation. It is worth noting that such phenomena have also been observed in some other 2D Co^II based SIMs with octahedral local geometry [9,10,11,12,13,14,15,16]. However, multiple relaxation pathways are strongly suggested by the curvature of the Arrhenius plot of 2. Although a dc field of 800 Oe was applied, there is a temperature-independent region in the temperature range of 1.8–2.4 K, which can be attributed to an unquenched QTM process. To avoid over-parameterisation, the τ vs. H data of 2 at 2 K was fitted with the first two terms of Equation (2) to determine the coefficients related to the Direct and QTM relaxation processes (inset of Figure 5d). This gives A = 17.3 s⁻¹·K⁻¹, B₁ = 478 s⁻¹, B₂ = 2.5 kOe⁻². These parameters were then fixed, and the lnτ vs. 1/T plot of 2 was fitted using Equation (2). The obtained values are U_eff = 33.2 cm⁻¹, τ = 4.3 × 10⁻⁶ s, n = 5.8, C = 0.03 s⁻¹·K^−5.8. Normally, n equals 7 and 9 for non-Kramers and Kramers ions [32], respectively. When optical and acoustic phonons are taken into consideration depending on the structure of energy levels, n values between 1 and 6 are also reasonable. Thus, the obtained n value suggests an optical acoustic Raman process involving a virtual state, where both acoustic and optical phonons are considered. From these results, we can see that the effective energy barrier of 2 is much larger than that of 1. A larger easy-plane magnetic anisotropy of 2 might be responsible to this difference. However, the specific reason for the discrepancy of magnetic dynamics of 1 and 2 are currently unknown.

3. Materials and Methods

All reagents were obtained from commercially available sources and used as received unless otherwise noted. 2,4,6-Tris(4-pyridyl)-1,3,5-triazine (TPT) was synthesised according to a previously reported method [33].

3.1. Syntheses of Compounds 1 and 2

{[Co^II(TPT)_2/3(H₂O)₄][CH₃COO]₂·(H₂O)₄}_n (1): 4 mL ethanol solution of cobalt(II) acetate tetrahydrate (50 mg, 0.2 mmol) was added to 6 mL chloroform solution of TPT ligand (62 mg, 0.2 mmol) and dibenzo-15-crown-5-ether (64 mg, 0.2 mmol) ligand. The mixed solution was then stirred for several hours until all materials dissolved. The solution was then filtered and left to stand at room temperature for weeks. Light orange block crystals were formed, which were collected, washed with water, and dried in air. Yield: about 60% based on Co(ac)₂·4H₂O. Elemental analysis (%) for C₁₆H₃₀CoN₄O₁₂: C, 36.30; H, 5.71; N, 10.58. Found: C, 36.12, H, 5.26; N, 10.55. IR (KBr, cm⁻¹): 3277(vs, wide), 2433(s), 1976(w), 1617(s), 1558(vs), 1413(vs), 1375(vs), 1231(w), 1214(s), 1160(w), 1056(s), 1021(s), 869(w), 806(vs), 759(s), 736(s), 668(s), 653(w), 518(s), 482(s).

{[Co^II(TPT)₂(CHOO)₂(H₂O)₂]}_n (2): 4 mL aqueous solution of Co(ClO₄)₂·6H₂O (36 mg, 0.1 mmol) was mixed with 4 mL DMF solution containing TPT (31 mg, 0.1 mmol) and dibenzo-15-crown-5-ether (32 mg, 0.1 mmol) ligands. The solution was sealed in a Teflon-lined stainless steel autoclave and heated at 120 °C for one day. After the autoclave was cooled to room temperature, light orange single crystals of 2 were obtained. Yield: about 50% based on Co(ClO₄)₂·6H₂O. Elemental analysis (%) for C₂₀H₂₁CoN₆O₆: C, 48.00; H, 4.23; N, 16.79. Found: C, 39.83, H, 4.26; N, 16.65. IR (KBr, cm⁻¹): 3399(vs), 3277(vs), 1696(w), 1606(s), 1550(s),1370(s), 1301(vs), 1242(w), 1079(w), 1040(w), 1012(s), 934(w), 848(vs), 762(s), 698(s), 655(w), 642(w), 516(w), 480(s).

Thermal gravimetric analyses (TGA) for the crystal samples of 1 and 2 were performed in the temperature range of 25–700 °C (Figure S8, ESI). The weight loss of 27.6% and 7.3% revealed that the lattice and coordinated water molecules could be removed in the temperature range from 25 to 100 °C, which is consistent with the single crystal data. The purity of the bulk samples of 1 and 2 were confirmed by powder X-ray diffraction (PXRD) spectra and elemental analyses (Figure S9, ESI).

3.2. Physical Measurements

Infrared spectra (IR) data were measured on KBr pellets using a Nexus 870 FT-IR spectrometer (Thermo Fisher Scientific, Waltham, MA, USA) in the range of 4000–400 cm⁻¹. Elemental analyses were performed using an Elementar Vario MICRO analyser (Heraeus, Hanau, Germany). Powder X-ray diffraction data (PXRD) were recorded at 150 K on a Bruker D8 Advanced diffractometer (Bruker, Karlsruhe, Germany) with a Cu Kα X-ray source (λ = 1.54056 Å) operated at 40 kV and 40 mA. Thermal gravimetric analysis (TGA) was conducted in Al₂O₃ crucibles using PerkinElmer Thermal Analysis (PerkinElmer, Wellesley, MA, USA) in the temperature range of 25–700 °C under a nitrogen atmosphere. All magnetic data were collected using a Quantum Design SQUID VSM magnetometer (Quantum Design, San Diego, CA, USA) on the ground single crystal samples from 2 to 300 K at applied dc fields ranging from 0 to 7 T. Alternative current (ac) magnetic susceptibility data were collected in the temperature range of 2–8 K, under an ac field of 2 Oe, oscillating at frequencies in the range of 1–1500 Hz. All magnetic data were corrected for the diamagnetic contributions of the sample holder and of core diamagnetism of the sample using Pascal’s constants.

3.3. X-ray Crystallography

Single crystal X-ray diffraction data were collected on a Bruker APEX Duo diffractometer (Bruker, Karlsruhe, Germany) with a Charge Coupled Device (CCD) area detector (Mo Kα radiation, λ = 0.71073 Å) at 150 K. The APEX II program (Bruker, Karlsruhe, Germany) was used to determine the unit cell parameters and for data collection. The data were integrated and corrected for Lorentz and polarisation effects using SAINT [34]. Absorption corrections were applied with SADABS [35]. The structures were solved by direct methods and refined by the full-matrix least-squares method on F² using the SHELXTL crystallographic software package [36]. All the non-hydrogen atoms were refined anisotropically. Hydrogen atoms of the organic ligands were refined as riding on the corresponding non-hydrogen atoms. Additional details of the data collections and structural refinement parameters are provided in Table S1. Selected bond lengths and angles of 1 and 2 are listed in Table S2 (Supplementary Materials). CCDC 1587443 and 1587444 are the supplementary crystallographic data for this paper. They can be obtained freely from the Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/data_request/cif.

4. Conclusions

In summary, we have synthesised a 2D cationic Co^II framework and a neutral 1D zigzag Co^II chain using a tritopic ligand 2,4,6-Tris(4-pyridyl)-1,3,5-triazine. The Co^II centres are both in a slightly distorted octahedral coordination geometry. The slight discrepancy around Co^II ions caused remarkably distinct magnetic anisotropy and dynamic magnetic properties of these two compounds. The large easy-plane magnetic anisotropy and field-induced slow magnetic relaxation have been verified in these two coordination polymers. The present results enlarge the family of framework-based SIMs and highlight the tuneable single-ion magnetism of metal ions via structural variation. Further efforts along this line to realise switchable single-ion magnet behaviour of Co^II ions by structural transformation are ongoing in our lab.