The Role of Anisotropic Exchange in Single Molecule Magnets: A CASSCF/NEVPT2 Study of the Fe4 SMM Building Block [Fe2(OCH3)2(dbm)4] Dimer
Abstract
:1. Introduction
2. Results and Discussion
2.1. Method Assessment
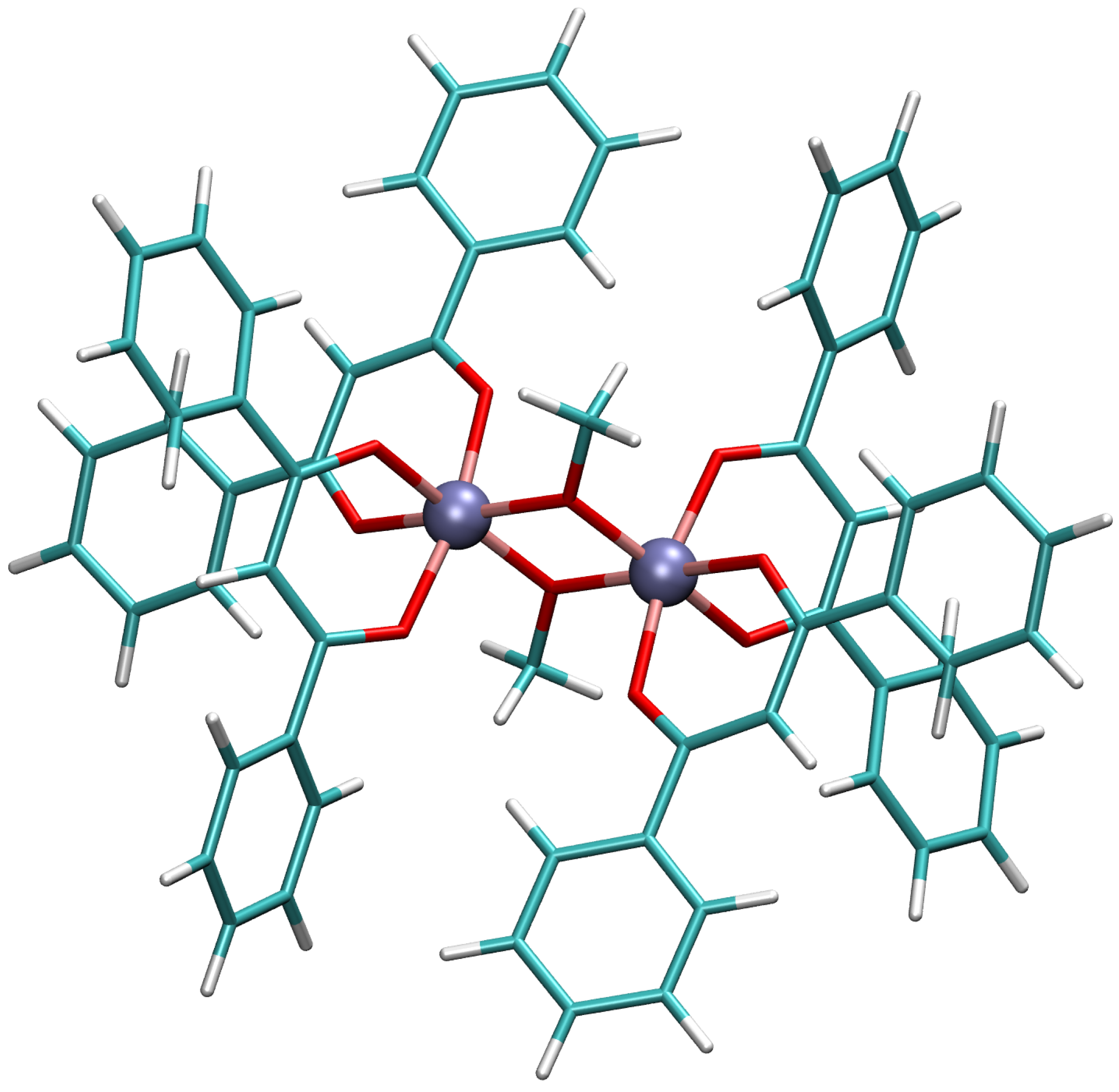
2.1.1. X-ray Structure
2.1.2. Simplified X-ray Structure
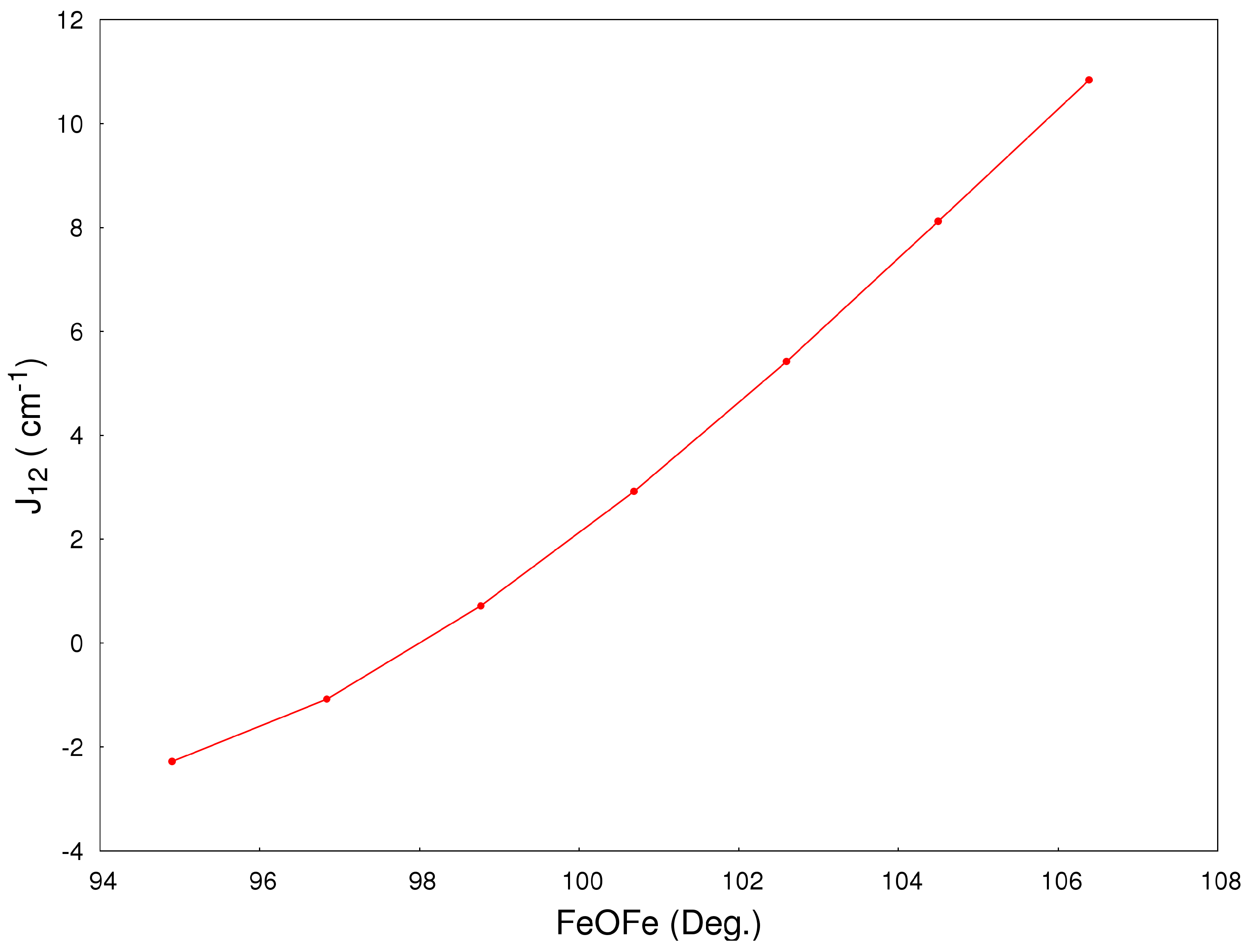
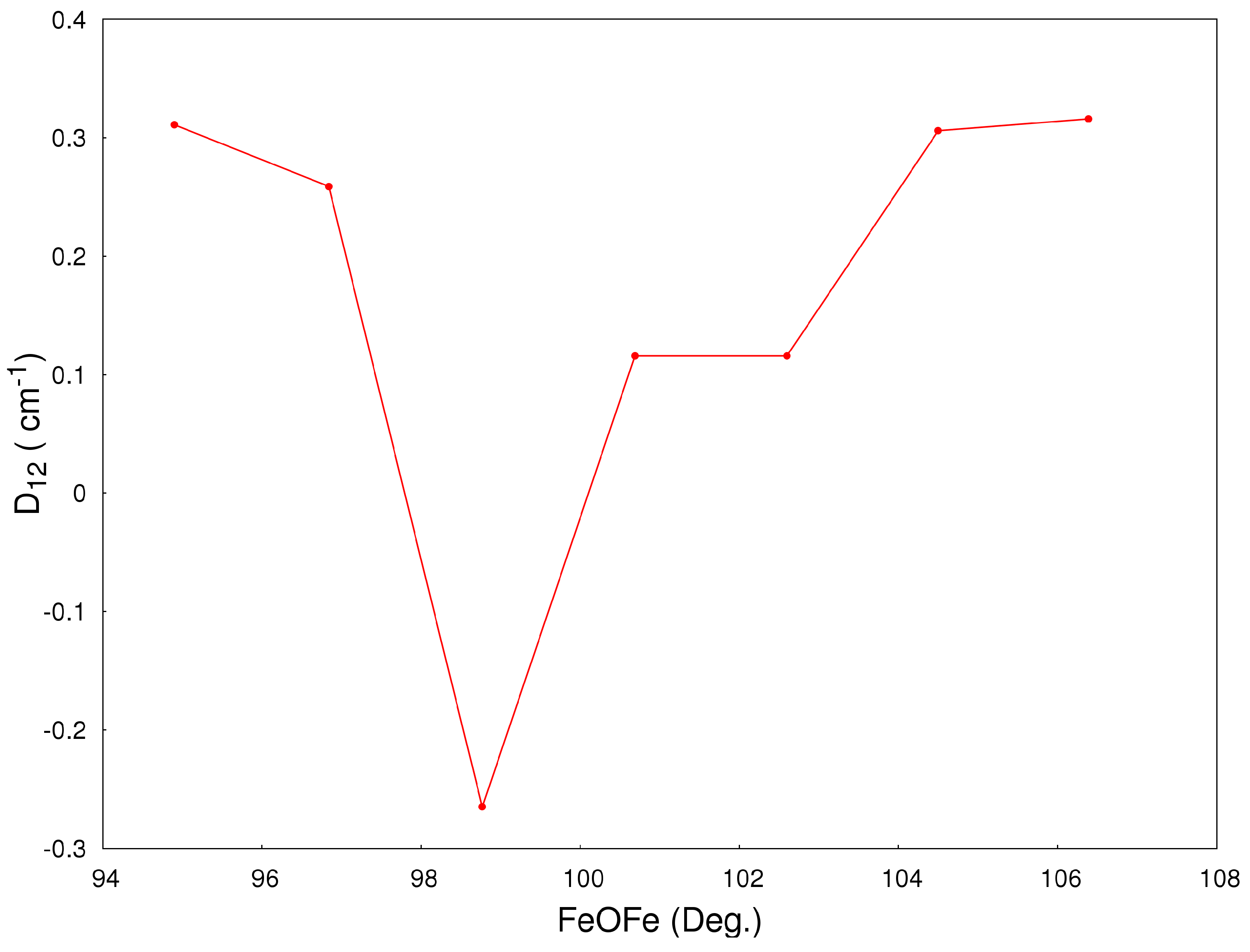
2.2. Magneto-Structural Correlations
3. Theory and Computational Methods
4. Computational Details
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Heisenberg, W. Zur Theorie des Ferromagnetismus. Z. Phys. 1928, 49, 619–636. [Google Scholar] [CrossRef]
- Dirac, P. Quantum Mechanics of Many-Electrons Systems. Proc. R. Soc. 1929, 123, 714–733. [Google Scholar] [CrossRef]
- Van Vleck, J. The Dirac Vector Model in Complex Spectra. Phys. Rev. 1934, 45, 405–419. [Google Scholar] [CrossRef]
- Pederson, M.; Khanna, S. Magnetic anisotropy barrier for spin tunneling in Mn12O12 molecules. Phys. Rev. B 1999, 60, 9566–9572. [Google Scholar] [CrossRef]
- Vahtras, O.; Loboda, O.; Minaev, B.; Ågren, H.; Ruud, K. Ab initio calculations of zero-field splitting parameters. Chem. Phys. 2002, 279, 133–142. [Google Scholar] [CrossRef]
- Calzado, C.J.; Cabrero, J.; Malrieu, J.P.; Caballol, R. Analysis of the magnetic coupling in binuclear complexes. I. Physics of the coupling. J. Chem. Phys. 2002, 116, 2728–2747. [Google Scholar] [CrossRef]
- Ganyushin, D.; Neese, F. First-principles calculations of zero-field splitting parameters. J. Chem. Phys. 2006, 125, 24103. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. Importance of direct spin-spin coupling and spin-flip excitations for the zero-field splittings of transition metal complexes: A case study. J. Am. Chem. Soc. 2006, 128, 10213–10222. [Google Scholar] [CrossRef] [PubMed]
- Maurice, R.; Bastardis, R.; Graaf, C.; Suaud, N.; Mallah, T.; Guihéry, N. Universal theoretical approach to extract anisotropic spin Hamiltonians. J. Chem. Theory Comput. 2009, 5, 2977–2984. [Google Scholar] [CrossRef] [PubMed]
- Bencini, A.; Totti, F.; Daul, C.C.A.; Doclo, K.; Barone, V. Density functional calculations of magnetic exchange interactions in polynuclear transition metal complexes. Inorg. Chem. 1997, 1669, 5022–5030. [Google Scholar] [CrossRef]
- Bencini, A.; Totti, F. A few comments on the application of density functional theory to the calculation of the magnetic structure of oligo-nuclear transition metal clusters. J. Chem. Theory Comput. 2009, 5, 144–154. [Google Scholar] [CrossRef] [PubMed]
- Rocha, A.R.; García-Suárez, V.M.; Bailey, S.W.; Lambert, C.J.; Ferrer, J.; Sanvito, S. Towards molecular spintronics. Nat. Mater. 2005, 4, 335–339. [Google Scholar] [CrossRef] [PubMed]
- Wernsdorfer, W. A long-lasting phase. Nat. Mater. 2007, 6, 174–176. [Google Scholar] [CrossRef] [PubMed]
- Mannini, M.; Pineider, F.; Sainctavit, P.; Danieli, C.; Otero, E.; Sciancalepore, C.; Talarico, A.M.; Arrio, M.A.; Cornia, A.; Gatteschi, D.; et al. Magnetic memory of a single molecule quantum magnet wired to a gold surface. Nat. Mater. 2009, 8, 194–197. [Google Scholar] [CrossRef] [PubMed]
- Urdampilleta, M.; Nguyen, N.V.; Cleuziou, J.P.; Klyatskaya, S.; Ruben, M.; Wernsdorfer, W. Molecular quantum spintronics: Supramolecular spin valves based on single molecule magnets and carbon nanotubes. Int. J. Mol. Sci. 2011, 12, 6656–6667. [Google Scholar] [CrossRef] [PubMed]
- Westrup, K.C.M.; Boulon, M.; Totaro, P.; Nunes, G.G.; Back, D.F.; Barison, A.; Jackson, M.; Paulsen, C.; Gatteschi, D.; Sorace, L.; et al. Adding remnant magnetization and anisotropic exchange to propeller like single molecule magnets through chemical design. Chem. Eur. J. 2014, 20, 13681–13691. [Google Scholar] [CrossRef] [PubMed]
- Lunghi, A.; Totti, F. DFT magnetic characterization of a Fe4 SMMs series: From isotropic exchange interactions to multi-spin zero field splitting. J. Mater. Chem. C 2014, 2, 8333–8343. [Google Scholar] [CrossRef]
- Le Gall, F.; Fabrizi de Biani, F.; Caneschi, A.; Cinelli, P.; Cornia, A.; Fabretti, A.C.; Gatteschi, D. Synthesis, crystal structures and magnetic characterization of four β-diketonate-alkoxide iron (III) dimers. Dependence of the magnetic properties on geometrical and electronic parameters. Inorg. Chim. Acta 1997, 262, 123–132. [Google Scholar] [CrossRef]
- Ter Heerdt, P.; Stefan, M.; Goovaerts, E.; Caneschi, A.; Cornia, A. Single ion and molecular contributions to the zero-field splitting in an iron(III)-oxo dimer studied by single crystal W-band EPR. J. Magn. Reson. 2006, 179, 29–37. [Google Scholar] [CrossRef] [PubMed]
- Bencini, A.; Gatteschi, D. EPR of Exchange Coupled Systems; Springer Science + Business Media: Berlin, Germany, 2012. [Google Scholar]
- Angeli, C.; Cimiraglia, R.; Malrieu, J.P. N-electron valence state perturbation theory: A fast implementation of the strongly contracted variant. Chem. Phys. Lett. 2001, 350, 297–305. [Google Scholar] [CrossRef]
- Atanasov, M.; Aravena, D.; Suturina, E.; Bill, E.; Maganas, D.; Neese, F. First principles approach to the electronic structure, magnetic anisotropy and spin relaxation in mononuclear 3d-transition metal single molecule magnets. Coord. Chem. Rev. 2015, 289–290, 177–214. [Google Scholar] [CrossRef]
- Maurice, R.; Guihéry, N.; Bastardis, R.; Graaf, C.D. Rigorous extraction of the anisotropic multispin Hamiltonian in bimetallic complexes from the exact electronic Hamiltonian. J. Chem. Theory Comput. 2009, 6, 55–65. [Google Scholar] [CrossRef] [PubMed]
- Maurice, R.; de Graaf, C.; Guihéry, N. Magnetic anisotropy in binuclear complexes in the weak-exchange limit: From the multispin to the giant-spin Hamiltonian. Phys. Rev. B 2010, 81, 214427. [Google Scholar] [CrossRef]
- Maurice, R.; Sivalingam, K.; Ganyushin, D.; Guihéry, N.; de Graaf, C.; Neese, F. Theoretical determination of the zero-field splitting in copper acetate monohydrate. Inorg. Chem. 2011, 50, 6229–6236. [Google Scholar] [CrossRef] [PubMed]
- Maurice, R.; Graaf, C.D.; Guihéry, N. Theoretical determination of Spin Hamiltonians with isotropic and anisotropic magnetic interactions in transition metal and lanthanide complexes. Phys. Chem. Chem. Phys. 2013, 15, 18784–18804. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.K.; Rajaraman, G. Probing the origin of magnetic anisotropy in a dinuclear Mn(III)Cu(II) single molecule magnet: The role of exchange anisotropy. Chem. Eur. J. 2014, 20, 5214–5218. [Google Scholar] [CrossRef] [PubMed]
- Tereniak, S.J.; Carlson, R.K.; Clouston, L.J.; Young, V.G.; Bill, E.; Maurice, R.; Chen, Y.S.; Kim, H.J.; Gagliardi, L.; Lu, C.C. Role of the metal in the bonding and properties of bimetallic complexes involving manganese, iron, and cobalt. J. Am. Chem. Soc. 2014, 136, 1842–1855. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R.; Gmbh, F.K. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F. Accurate coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 22, 1057–1065. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.J.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 533–539. [Google Scholar] [CrossRef]
- Garcia, V.M.; Castell, O.; Caballol, R.; Malrieu, J.P. An iterative difference-dedicated configuration interaction. Proposal and test studies. Chem. Phys. Lett. 1995, 238, 222–229. [Google Scholar] [CrossRef]
- Neese, F. A spectroscopy oriented configuration interaction procedure. J. Chem. Phys. 2003, 119, 9428–9443. [Google Scholar] [CrossRef]
- Malrieu, J.P.; Caballol, R.; Calzado, C.J.; de Graaf, C.; Guihéry, N. Magnetic interactions in molecules and highly correlated materials: Physical content, analytical derivation, and rigorous extraction of magnetic hamiltonians. Chem. Rev. 2014, 114, 429–492. [Google Scholar] [CrossRef] [PubMed]
- Retegan, M.; Collomb, M.N.; Neese, F.; Duboc, C. A combined high-field EPR and quantum chemical study on a weakly ferromagnetically coupled dinuclear Mn(III) complex. A complete analysis of the EPR spectrum beyond the strong coupling limit. Phys. Chem. Chem. Phys. 2013, 15, 223–234. [Google Scholar] [CrossRef] [PubMed]
- Gregoli, L.; Danieli, C.; Barra, A.L.; Neugebauer, P.; Pellegrino, G.; Poneti, G.; Sessoli, R.; Cornia, A. Magnetostructural correlations in tetrairon(III) single molecule magnets. Chem. Eur. J. 2009, 15, 6456–6467. [Google Scholar] [CrossRef] [PubMed]
- Lunghi, A.; Iannuzzi, M.; Sessoli, R.; Totti, F. Single molecule magnets grafted on gold: Evolution of magnetic properties from Ab initio molecular dynamics. J. Mater. Chem. C 2015, 3, 7294–7304. [Google Scholar] [CrossRef]
- Fernandez Garcia, G.; Lunghi, A.; Totti, F.; Sessoli, R. Toward mesoscale properties of self-assembled monolayers of SMM on Au(111): An integrated Ad Hoc FF and DFT study. J. Phys. Chem. C 2016, 120, 14774–14781. [Google Scholar] [CrossRef]

| J | D | E/D | D | E/D | |
|---|---|---|---|---|---|
| 1-Ph | 5.32 | 0.329 | 0.113 | −0.108 | 0.321 |
| 1-Me | 5.52 | 0.090 | 0.124 | 0.411 | 0.135 |
| 1-Me | 2.92 | 0.197 | 0.105 | 0.116 | 0.131 |
| Exp. | 15.4 | 0.749 | 0.097 | −0.159 | 0.176 |
| Fe–Fe (Å) | Fe–O (Å) | FeOFe (Deg.) | |
|---|---|---|---|
| 1-Ph | 3.15 | 1.99 | 100.69 |
| 1-Me | 3.12 | 2.03 | 102.69 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lunghi, A.; Totti, F. The Role of Anisotropic Exchange in Single Molecule Magnets: A CASSCF/NEVPT2 Study of the Fe4 SMM Building Block [Fe2(OCH3)2(dbm)4] Dimer. Inorganics 2016, 4, 28. https://doi.org/10.3390/inorganics4040028
Lunghi A, Totti F. The Role of Anisotropic Exchange in Single Molecule Magnets: A CASSCF/NEVPT2 Study of the Fe4 SMM Building Block [Fe2(OCH3)2(dbm)4] Dimer. Inorganics. 2016; 4(4):28. https://doi.org/10.3390/inorganics4040028
Chicago/Turabian StyleLunghi, Alessandro, and Federico Totti. 2016. "The Role of Anisotropic Exchange in Single Molecule Magnets: A CASSCF/NEVPT2 Study of the Fe4 SMM Building Block [Fe2(OCH3)2(dbm)4] Dimer" Inorganics 4, no. 4: 28. https://doi.org/10.3390/inorganics4040028
APA StyleLunghi, A., & Totti, F. (2016). The Role of Anisotropic Exchange in Single Molecule Magnets: A CASSCF/NEVPT2 Study of the Fe4 SMM Building Block [Fe2(OCH3)2(dbm)4] Dimer. Inorganics, 4(4), 28. https://doi.org/10.3390/inorganics4040028