Anion Ordering in Bichalcogenides
Abstract
:1. Introduction
2. Causes and Consequences of Chalcogenide Ordering
2.1. Partial Anionic Substitution
2.2. Structural Dimensionality
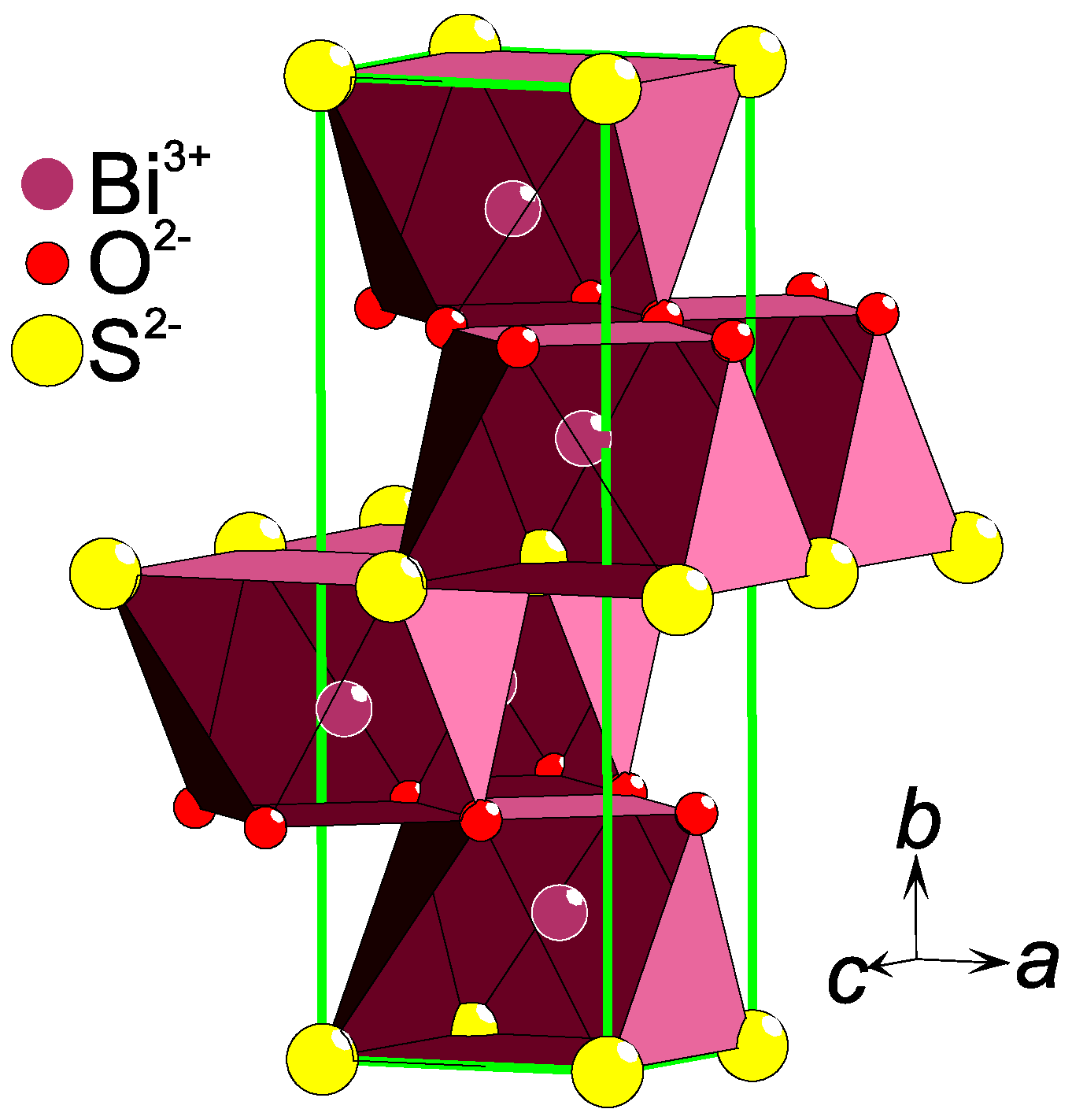
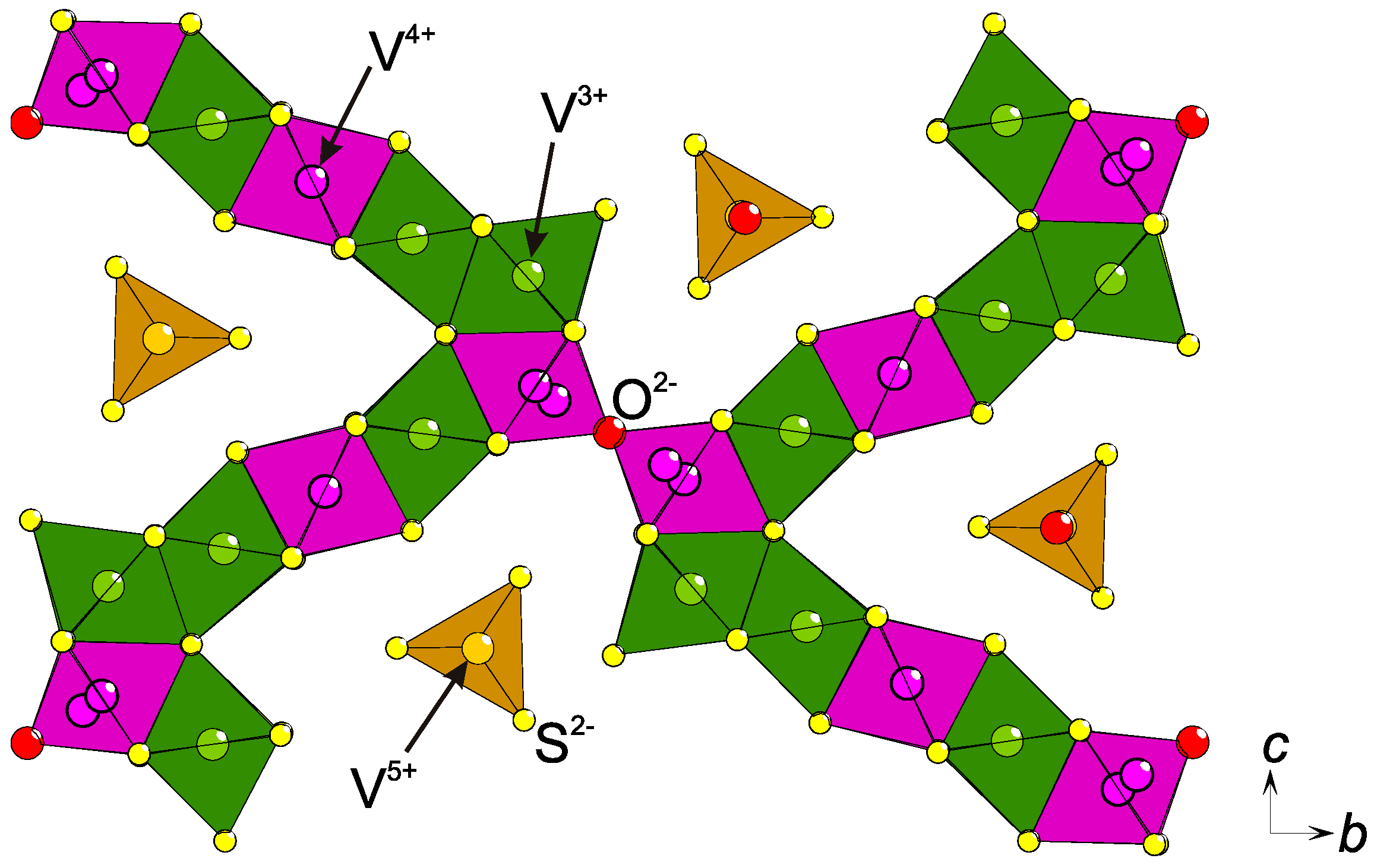
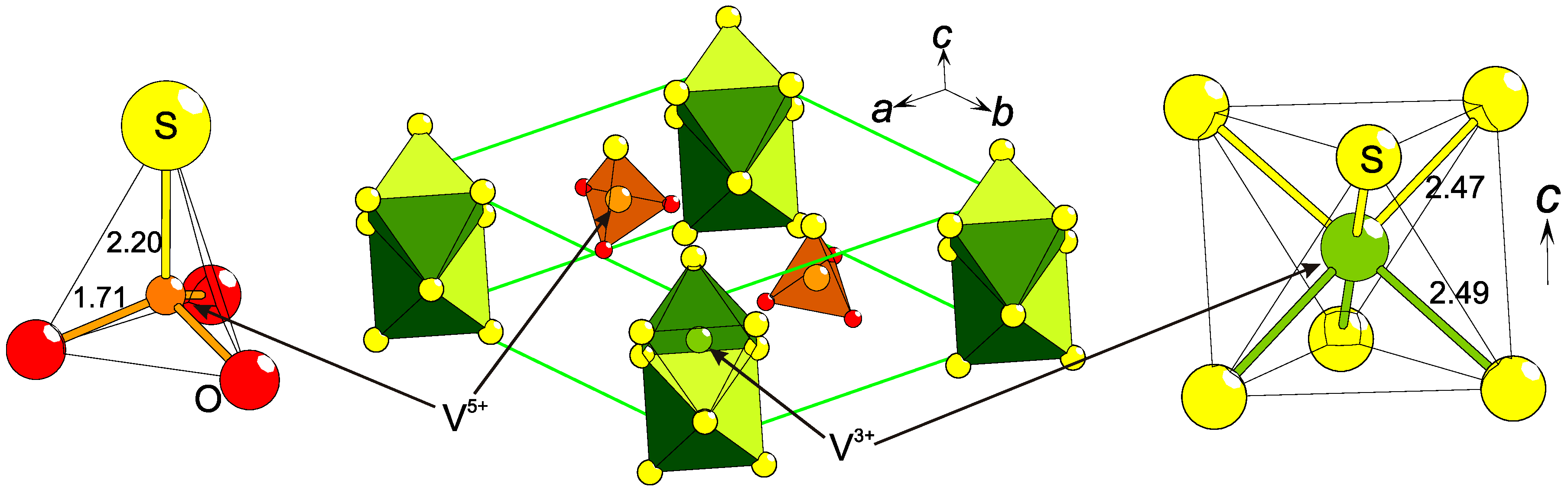
2.3. Charge Ordering
2.4. Low Formal Oxidation States of Cations
2.5. Polar Coordinations
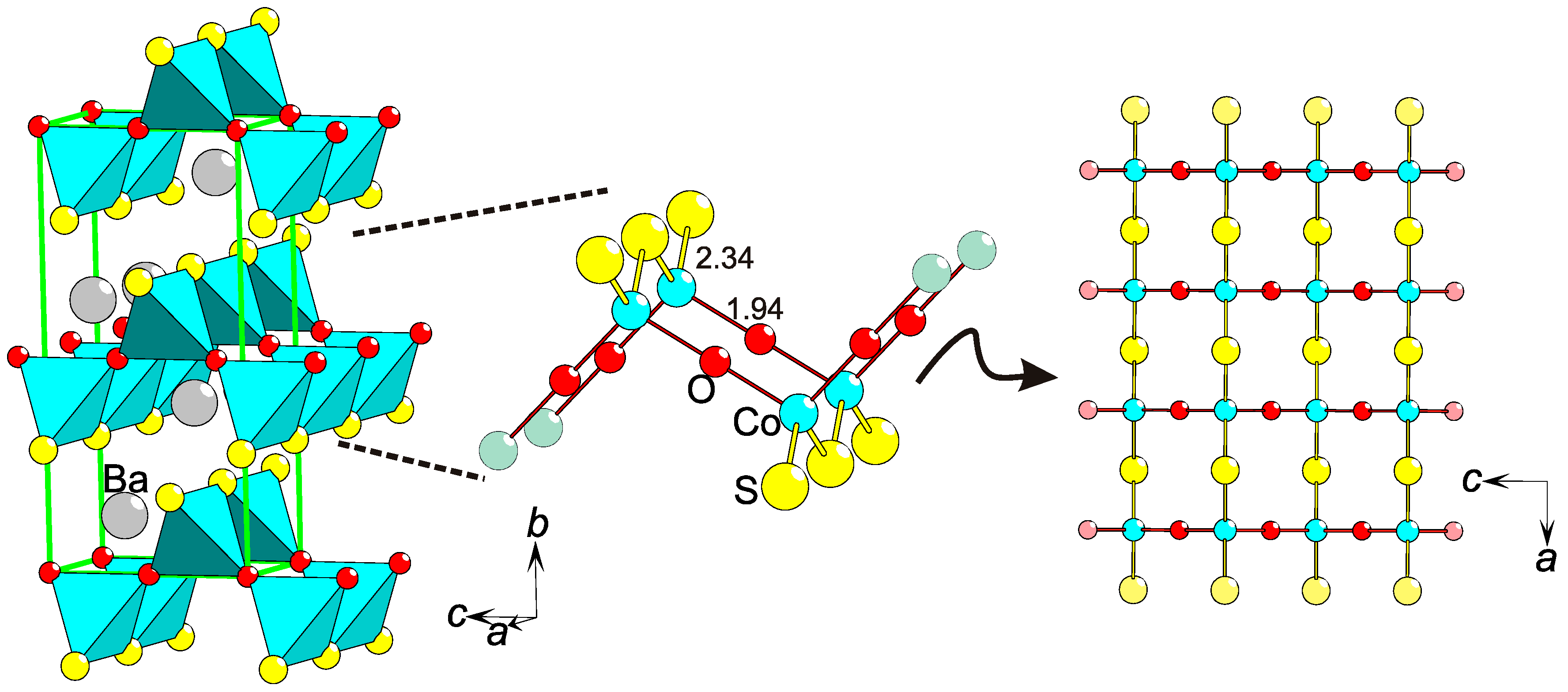
2.6. Structural Polarity
2.7. Coordination Configurations and Crystal Field Effects
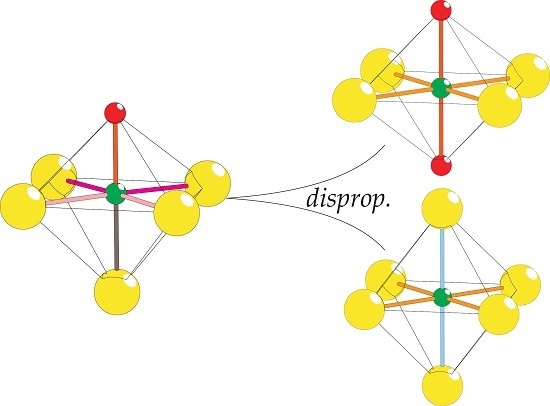
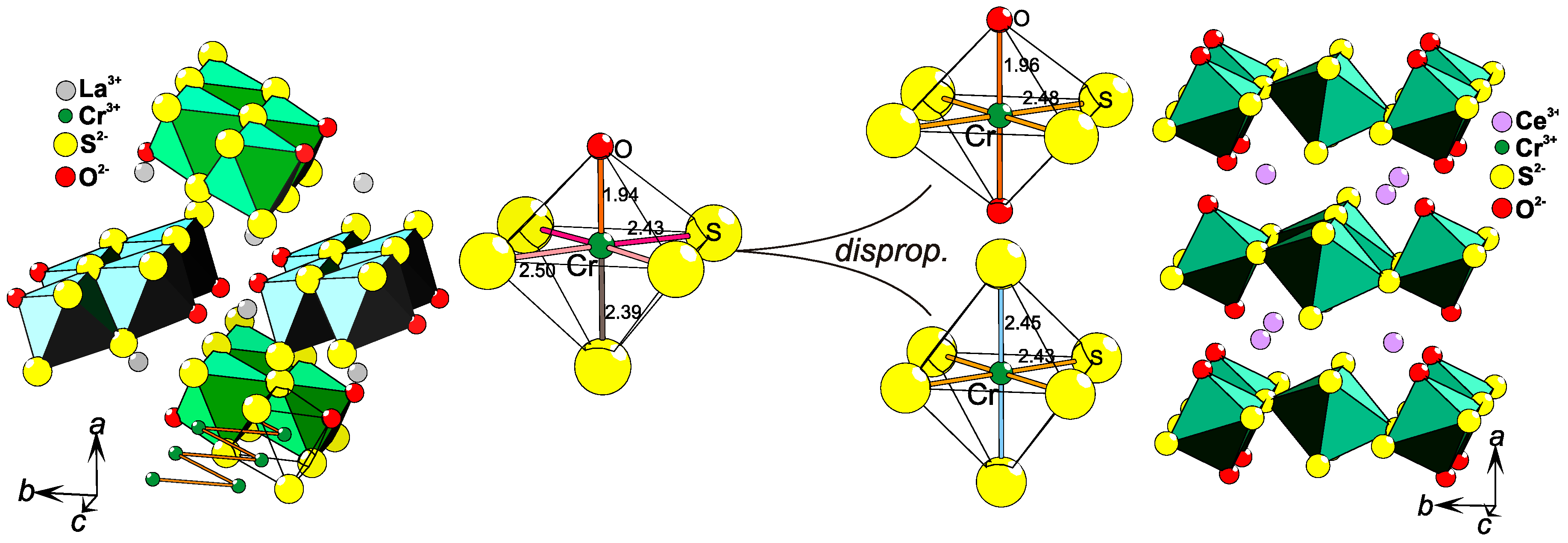
2.8. Coordination Disproportionation
2.9. Magnetic Anisotropy
2.10. Band-Gap Optimization
3. Further Notes
4. Final Words
Acknowledgments
Conflicts of Interest
Abbreviations
| Ch | Chalcogen |
| CN | Coordination Number |
| D | Dimensionality |
| HSAB | Hard–Soft-Acid–Base |
| HS | High Spin |
| LS | Low Spin |
| M | Metal |
| r | radius |
| SHG | Second Harmonic Generation |
| TM | Transition Metal |
References
- Hume-Rothery, W.; Powell, H.M. On the Theory of Super-Lattice Structures in Alloys. Z. Kristallogr. 1935, 91, 23–47. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. 1976, A32, 751–767. [Google Scholar] [CrossRef]
- Zachariasen, W.H. Crystal chemical studies of the 5f-series of elements. I. New structure types. Acta Crystallogr. 1948, 1, 265–268. [Google Scholar] [CrossRef]
- Zachariasen, W.H. Die Kristallstruktur der α-Modifikation von den Sesquioxyden der seltenen Erdmetalle (La2O3, Ce2O3, Pr2O3, Nd2O3). Z. Phys. Chem. 1926, 123, 134–150. [Google Scholar]
- Von Schnering, H.G.; Hoppe, R. Die Kristallstruktur des SrZnO2. Z. Anorg. Allg. Chem. 1961, 312, 87–98. [Google Scholar] [CrossRef]
- Broadley, S.; Gal, Z.A.; Cora, F.; Smura, C.F.; Clarke, S.J. Vertex-Linked ZnO2S2 Tetrahedra in the Oxysulfide BaZnOS: A New Coordination Environment for Zinc in a Condensed Solid. Inorg. Chem. 2005, 44, 9092–9096. [Google Scholar] [CrossRef] [PubMed]
- Guittard, M.; Julien-Pouzol, M. Les composes hexagonaux de type La3CuSiS7. Bull. Soc. Chim. Fr. 1970, 1970, 2467–2469. [Google Scholar]
- De Saint-Giniez, D.; Laruelle, P.; Flahaut, J. Structure cristalline du sulfure double de cerium et d’aluminium Ce6Al3.33S14. Comptes Rendus 1968, 267, 1029–1032. [Google Scholar]
- Calvagna, F.; Zhang, J.-H.; Li, S.-J.; Zheng, C. Synthesis and structural analysis of Ba3V2O3S4. Chem. Mater. 2001, 13, 304–307. [Google Scholar] [CrossRef]
- Hopkins, E.J.; Prots, Y.; Burkhardt, U.; Watier, Y.; Hu, Z.; Kuo, C.-Y.; Chiang, J.-C.; Pi, T.-W.; Tanaka, A.; Tjeng, L.H.; et al. Ba3V2S4O3: A Mott insulating frustrated quasi-one-dimensional S = 1 magnet. Chem. Eur. J. 2015, 21, 7938–7943. [Google Scholar] [CrossRef] [PubMed]
- Meerschaut, A.; Lafond, A.; Palvadeau, P.; Deudon, C.; Cario, L. Synthesis and crystal structure of two new oxychalcogenides: Eu5V3S6O7 and La10Se14O. Mater. Res. Bull. 2002, 37, 1895–1905. [Google Scholar] [CrossRef]
- Mayer, J.M.; Schneemeyer, L.F.; Siegrist, T.; Waszczak, J.V.; van Dover, R.B. Neue Eisenlanthan-Oxidsulfid-und-Oxidselenid-Phasen mit Schichtstruktur: Fe2La2O3E2 (E = S, Se). Angew. Chem. 1992, 104, 1677–1678. [Google Scholar] [CrossRef]
- Koyama, E.; Nakai, I.; Nagashima, K. Crystal chemistry of oxide-chalcogenides. II. Synthesis and crystal structure of the first bismuth oxide-sulfide, Bi2O2S. Acta Crystallogr. 1984, B40, 105–109. [Google Scholar] [CrossRef]
- Free, D.G.; Herkelrath, S.J.C.; Clarke, S.J. Sr2Mn2O4Se: A New Oxychalcogenide with Antiferromagnetic Chains. Z. Anorg. Allg. Chem. 2012, 638, 2532–2537. [Google Scholar] [CrossRef]
- Ijjaali, I.; Bin, D.; Ibers, J.A. Seven new rare-earth transition-metal oxychalcogenides: Syntheses and characterization of Ln4MnOSe6 (Ln = La, Ce, Nd), Ln4FeOSe6 (Ln = La, Ce, Sm), and La4MnOS6. J. Solid State Chem. 2005, 178, 1503–1507. [Google Scholar] [CrossRef]
- Pearson, R.G. Hard and Soft Acids and Bases; Dowden, Hutchinson & Ross: Stroudsburg, PA, USA, 1973. [Google Scholar]
- Litteer, J.B.; Chen, B.-H.; Fettinger, J.C.; Eichhorn, B.W.; Ju, H.L.; Greene, R.L. Synthesis and magnetic and transport properties of Sr6V9S22O2: ”AM2S5” phases revisited. Inorg. Chem. 2000, 39, 458–462. [Google Scholar] [CrossRef] [PubMed]
- Wong, C.J.; Hopkins, E.J.; Prots, Yu.; Hu, Z.; Kuo, C.J.; Pi, T.W.; Valldor, M. Anionic ordering in Ba15V12S34O3, affording three oxidation states of vanadium and a quasi-one-dimensional magnetic lattice. Chem. Mater. 2016, 28, 1621–1624. [Google Scholar] [CrossRef]
- Gueho, C.; Giaquinta, D.; Mansot, J.L.; Ebel, T.; Palvadeau, P. Structure and magnetism of La4Mn5Si4O22 and La4V5Si4O22: Two new rare-earth transition metal sorosilicates. Chem. Mater. 1995, 7, 486–492. [Google Scholar] [CrossRef]
- David, R.; Kabbour, H.; Bordet, P.; Pelloquin, D.; Leynaud, O.; Trentesaux, M.; Mentré, O. Triple CoII, III, IV charge ordering and spin states in modular cobaltites: A systemization through experimental and virtual compounds. J. Mater. Chem. C 2014, 2, 9457–9466. [Google Scholar] [CrossRef]
- Haraldsen, H.; Groenvold, F.; Vihovde, J. Faseforholdene i systemet jern-tellur. Tidsskr. Kjem. Bergves. 1944, 4, 96–98. [Google Scholar]
- Valldor, M.; Merz, P.; Prots, Y.; Schnelle, W. Bad-Metal-Layered Sulfide Oxide CsV2S2O. Eur. J. Inorg. Chem. 2016, 2016, 23–27. [Google Scholar] [CrossRef]
- Tougait, O.; Ibers, J.A. Gd2OSe2. Acta Crystallogr. 2000, C56, 623–624. [Google Scholar]
- Benz, R. Ce2O2Sb and Ce2O2Bi crystal structure. Acta Crystallogr. 1971, B27, 853–854. [Google Scholar] [CrossRef]
- McCullough, J.D.; Brewer, L.; Bromley, L.A. The crystal structure of zirconium oxysulfide, ZrOS. Acta Crystallogr. 1948, 1, 287–289. [Google Scholar] [CrossRef]
- Besara, T.; Ramirez, D.; Sun, J.; Whalen, J.B.; Tokumoto, T.D.; McGill, S.A.; Singh, D.J.; Siegrist, T. Ba2TeO: A new layered oxytelluride. J. Solid State Chem. 2015, 222, 60–65. [Google Scholar] [CrossRef]
- Han, F.; Wan, X.; Shen, B.; Wen, H.-H. BaFe2Se2O as an iron-based Mott insulator with antiferromagnetic order. Phys. Rev. 2012, B86, 014411. [Google Scholar] [CrossRef]
- Lei, H.; Ryu, H.; Ivanovski, V.; Warren, J.B.; Frenkel, A.I.; Cekic, B.; Yin, W.-G.; Petrovic, C. Structure and physical properties of the layered iron oxychalcogenide BaFe2Se2O. Phys Rev. 2012, B86, 195133. [Google Scholar] [CrossRef]
- Valldor, M.; Adler, P.; Prots, Y.; Burkhardt, U.; Tjeng, L.H. S = 2 Spin Ladders in the Sulfide Oxide BaFe2S2O. Eur J. Inorg. Chem. 2014, 36, 6150–6155. [Google Scholar] [CrossRef]
- Huh, S.; Prots, Y.; Adler, P.; Tjeng, L.H.; Valldor, M. Synthesis and Characterization of Frustrated Spin Ladders SrFe2S2O and SrFe2Se2O. Eur. J. Inorg. Chem. 2015, 18, 2982–2988. [Google Scholar] [CrossRef]
- Aminoff, G. Über Lauephotogramme und Struktur von Zinkit. Z. Kristallogr. Cryst. Mater. 1921, 56, 495–505. [Google Scholar] [CrossRef]
- Sambrook, T.; Smura, C.F.; Clarke, S.J. Structure and physical properties of the polar oxysulfide CaZnOS. Inorg. Chem. 2007, 46, 2571–2574. [Google Scholar] [CrossRef] [PubMed]
- Aminoff, G. Untersuchungen über die Kristallstrukturen von Wurtzit und Rotnickelkies. Z. Kristallogr. Cryst. Mater. 1923, 58, 203–219. [Google Scholar] [CrossRef]
- Knop, O.; Brisse, F.; Castelliz, L. Pyrochlores. V. Thermoanalytic, X-ray, neutron, infrared, and dielectric studies of A2Ti2O7 titanates. Can. J. Chem. 1969, 47, 971–990. [Google Scholar] [CrossRef]
- Guittard, M.; Benacerrat, A.; Flahaut, J. Les seleniures L2Se3 et L3Se4 des elements des terres rares. Ann. Chim. 1964, 9, 25–34. [Google Scholar]
- Sasaki, T.; Ukyo, Y.; Kuroda, K.; Arai, S.; Muto, S.; Saka, H. Crystal structure of Ce2Zr2O7 and β-(Ce2Zr2O7.5). J. Ceram. Soc. Jpn. 2004, 112, 440–444. [Google Scholar] [CrossRef]
- Miller, J.F.; Matson, L.K.; Himes, R.C. Studies on the selenides and tellurides of selected rare-earth metals. Proc. Conf. Rare Earth Res. 1962, 1962, 233–248. [Google Scholar]
- Böhm, J. Über das Verglimmen einiger Metalloxyde. Z. Anorg. Allg. Chem. 1925, 149, 217–222. [Google Scholar] [CrossRef]
- Donohue, P.C.; Jeitschko, W. The preparation of Ln2MX5 where Ln = rare earths, M = Zr and Hf, and X = S, Se. Mater. Res. Bull. 1974, 9, 1333–1336. [Google Scholar] [CrossRef]
- Gerlach, W. Die Gitterstruktur der Erdalkalioxyde. Z. Phys. 1922, 9, 184–192. [Google Scholar] [CrossRef]
- Matje, P.; Müller, W.; Schäfer, H. Zur Darstellung und Kristallstruktur von Ba2MnTe3. Z. Naturforsch. 1977, B32, 835–836. [Google Scholar]
- Liu, B.W.; Jiang, X.M.; Wang, G.E.; Zeng, H.Y.; Zhang, M.J.; Li, S.F.; Guo, W.H.; Guo, G.C. Oxochalcogenide BaGeOSe2: Highly distorted mixed-anion building units leading to a large second-harmonic generation response. Chem. Mater. 2015, 27, 8189–8192. [Google Scholar] [CrossRef]
- Jin, S.F.; Huang, Q.; Lin, Z.P.; Li, Z.L.; Wu, X.Z.; Ying, T.P.; Wang, G.; Chen, X.L. Two-dimensional magnetic correlations and partial long-range order in geometrically frustrated CaOFeS with triangle lattice of Fe ions. Phys. Rev. 2015, B91, 094420. [Google Scholar] [CrossRef]
- Bryhan, D.N.; Rakers, R.; Klimaszewski, K.; Patel, N.; Bohac, J.J.; Kremer, R.K.; Mattausch, H.; Zheng, C. La3TWS3O6 (T = Cr, Mn, Fe, Co, Ni): Quinary Rare Earth Transition-Metal Compounds Showing a Nonmagnetic/Magnetic Transition (T = Co)—Synthesis, Structure and Physical Properties. Z. Anorg. Allg. Chem. 2010, 636, 74–78. [Google Scholar] [CrossRef]
- Wu, H. Metal-insulator transition in Sr2−xLaxCoO4 driven by spin-state transition. Phys. Rev. 2012, B86, 075120. [Google Scholar] [CrossRef]
- Valldor, M.; Rößler, U.K.; Prots, Yu.; Kuo, C.-Y.; Chiang, J.-C.; Hu, Z.; Kniep, R.; Tjeng, L.H. Synthesis and Characterization of Ba[CoSO]: Magnetic Complexity in the Presence of Chalcogen Ordering. Chem. Eur. J. 2015, 21, 10821–10828. [Google Scholar] [CrossRef] [PubMed]
- Han, F.; Wang, D.; Malliakas, C.D.; Sturza, M.; Chung, D.Y.; Wan, X.; Kanatzidis, M.G. (CaO)(FeSe): A Layered Wide-Gap Oxychalcogenide Semiconductor. Chem. Mater. 2015, 27, 5695–5701. [Google Scholar] [CrossRef]
- Dugué, P.J.; Vovan, T.; Villers, J. Etude Structurale des Oxysulfures de Chrome(III) et de Terres Rares. I. Structure de I’Oxysulfure LaCrOS2. Acta Crystallogr. 1980, B36, 1291–1294. [Google Scholar] [CrossRef]
- Tougait, O.; Ibers, J.A. Synthesis and crystal structures of the lanthanum titanium oxyselenides La4Ti2O4Se5 and La6Ti3O5Se9. J. Solid State Chem. 2001, 157, 289–295. [Google Scholar] [CrossRef]
- Gardberg, A.S.; Ibers, J.A. Crystal structure of hexapraseodymium dititanium septasulfide hexaoxide, Pr6Ti2S7O6. Z. Kristallogr. 2001, 216, 491–492. [Google Scholar] [CrossRef]
- Cody, J.A.; Ibers, J.A. Synthesis and characterization of the new rare-earth/transition-metal oxysulfides La6Ti2S8O5 and La4Ti3S4O8. J. Solid State Chem. 1995, 114, 406–412. [Google Scholar] [CrossRef]
- Ferro, R. Über einige Selen-und Tellurverbindungen des Urans. Z. Anorg. Allg. Chem. 1954, 275, 320–326. [Google Scholar] [CrossRef]
- Hiramatsu, H.; Yanagi, H.; Kamiya, T.; Ueda, K.; Hirano, M.; Hosono, H. Crystal structures, optoelectronic properties and electronic structures of layered oxychalcogenides MCuOCh (M = Bi, La; Ch = S, Se, Te): Effects of electronic configurations of M3+ ions. Chem. Mater. 2008, 20, 326–334. [Google Scholar] [CrossRef]
- Dugué, P.J.; Vovan, T.; Villers, J. Etude Structurale des Oxysulfures de Chrome(III) et de Terres Rares. II. Structure de I’Oxysulfure CeCrOS2. Acta Crystallogr. 1980, B36, 1294–1297. [Google Scholar] [CrossRef]
- Van, T.V.; Huy Ng, D. Synthese et structure cristalld’une nouvelle famille d’ oxyselenures de chrome III et de lanthanides legers, de formule generale RCrSe2O (R = La, Ce). Comptes Rendus 1981, 293, 933–936. [Google Scholar]
- Zhao, L.-D.; He, J.; Berardan, D.; Lin, Y.; Li, J.-F.; Nanc, C.-W.; Dragoe, N. BiCuSeO oxyselenides: New promising thermoelectric materials. Energy Environ. Sci. 2014, 7, 2900–2924. [Google Scholar] [CrossRef]
- Berardan, D.; Li, J.; Amzallag, E.; Mitra, S.; Sui, J.; Cai, W.; Dragoe, N. Structure and Transport Properties of the BiCuSeO–BiCuSO Solid Solution. Materials 2015, 8, 1043–1058. [Google Scholar] [CrossRef]
- Reuter, B.; Hardel, K. Über die Hochtemperaturmodifikation von Silbersulfidjodid. Naturwiss 1961, 48, 161–162. [Google Scholar] [CrossRef]
- Grossholz, H.; Janka, O.; Schleid, T. Oxide fluoride sulfides of the lanthanoids with the formula M3OF5S (M = Nd, Sm, Gd–Ho). Z. Naturforsch. 2011, B66, 213–220. [Google Scholar] [CrossRef]
- Stolze, K.; Isaeva, A.; Schwarz, U.; Doert, T. UPTe, ThPTe and U2PTe2O: Actinide pnictide chalcogenides with diphosphide anions. Eur. J. Inorg. Chem. 2015, 2015, 778–785. [Google Scholar] [CrossRef]
- Kamihara, Y.; Hiramatsu, H.; Hirano, M.; Kawamura, R.; Yanagi, H.; Kamiya, T.; Hosono, H. Iron-Based Layered Superconductor: LaOFeP. J. Am. Chem. Soc. 2006, 128, 10012–10013. [Google Scholar] [CrossRef] [PubMed]
- Shamoto, S.; Kato, T.; Ono, Y.; Miyazaki, Y.; Ohoyama, K.; Ohashi, M.; Yamaguchi, Y.; Kajitani, T. Structures of β-(ZrNCl) and superconducting Li0.16ZrNCl: Double honeycomb lattice superconductor. Physica C 1998, 306, 7–14. [Google Scholar] [CrossRef]
- Singh, S.K.; Kumar, A.; Gahtori, B.; Shruti, K.; Sharma, G.; Patnaik, S.; Awana, V.P.S. Bulk superconductivity in bismuth oxysulfide Bi4O4S3. J. Am. Chem. Soc. 2012, 134, 16504–16507. [Google Scholar] [CrossRef] [PubMed]
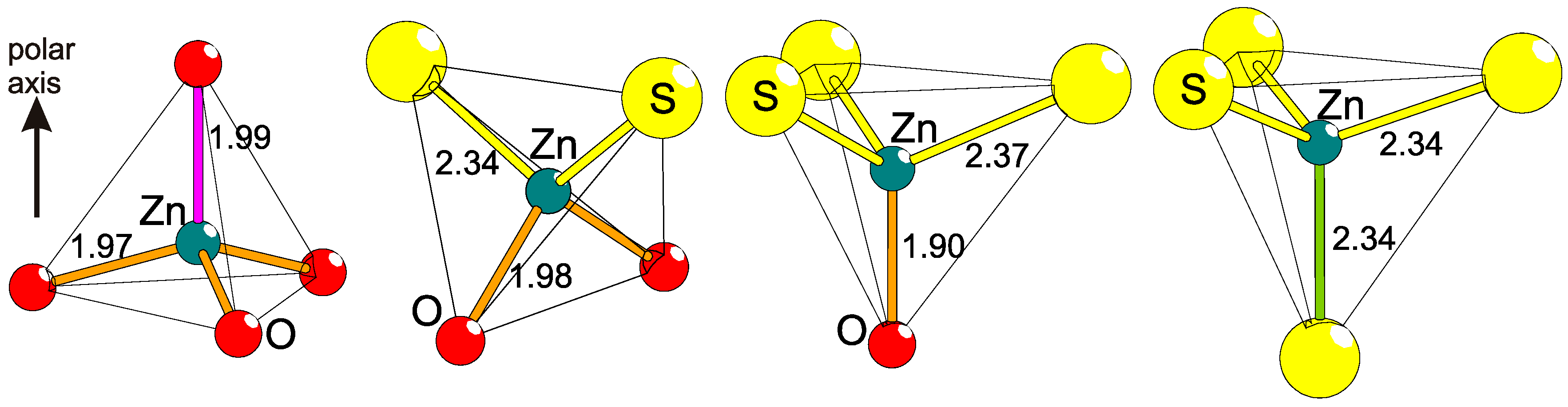

| M−Ch−O | CN 1 × M−O | CN 1 × M−S | CN 1 × M−Se | CN 1 × M−Te |
| Gd2Se2O [23] | 2 × 2.30 | 5 × 2.98 | ||
| Gd2Ti2O7 [34], Gd2Se3 [35] | 8 × 2.46 | 7.5 × 2.98 | ||
| Ce2TeO2 [24] | 4 × 2.37 | 4 × 3.51 | ||
| Ce2Zr2O7 [36], Ce8/3Te4 [37] | 8 × 2.47 | 8 × 3.31 | ||
| ZrSO [25] | 3 × 2.13 | 4 × 2.63 | ||
| ZrO2 [38], Er2ZrS5 [39] | 8 × 2.21 | 7 × 2.59 | ||
| Ba2TeO [26] | 1 × 2.45 | 5 × 3.59 | ||
| BaO [40], Ba2MnTe3 [41] | 6 × 2.76 | 7 × 3.54 |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valldor, M. Anion Ordering in Bichalcogenides. Inorganics 2016, 4, 23. https://doi.org/10.3390/inorganics4030023
Valldor M. Anion Ordering in Bichalcogenides. Inorganics. 2016; 4(3):23. https://doi.org/10.3390/inorganics4030023
Chicago/Turabian StyleValldor, Martin. 2016. "Anion Ordering in Bichalcogenides" Inorganics 4, no. 3: 23. https://doi.org/10.3390/inorganics4030023
APA StyleValldor, M. (2016). Anion Ordering in Bichalcogenides. Inorganics, 4(3), 23. https://doi.org/10.3390/inorganics4030023