Next Article in Journal
Egg White Assisted Synthesis of Fe-Mn Spinel Oxides: Effects of Egg White Ratio, Oxygen Partial Pressure, and Life Cycle Impacts
Previous Article in Journal
Formation and Reversible Cleavage of an Unusual Trisulfide-Bridged Binuclear Pyridine Diimine Iridium Complex
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Inorganics
Volume 14
Issue 1
10.3390/inorganics14010012
inorganics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Extending Hexagon-Based Metal–Organic Frameworks—Mn(II) and Gd(III) MOFs with Hexakis(4-(4-Carboxyphenyl)phenyl)benzene

by
Henrik Björck
1,
William Reinholdsson
1,
Ocean Cheung
2,
Guojon Zhou
3,
Zhehao Huang
3,
Francoise M. Amombo Noa
1,4,* and
Lars Öhrström
1,*
1
Chemistry and Biochemistry, Department of Chemistry and Chemical Engineering, Chalmers University of Technology, 412 96 Gothenburg, Sweden
2
Ångström Laboratory, Department of Materials Science and Engineering, Uppsala University, 751 03 Uppsala, Sweden
3
Department of Chemistry, Stockholm University, 106 91 Stockholm, Sweden
4
Ecole des Sciences de la Santé, Université Catholique D’Afrique Centrale, Yaounde P.O. Box 1110, Cameroon
*
Authors to whom correspondence should be addressed.
Inorganics 2026, 14(1), 12; https://doi.org/10.3390/inorganics14010012 (registering DOI)
Submission received: 7 October 2025 / Revised: 22 December 2025 / Accepted: 23 December 2025 / Published: 27 December 2025
Browse Figures
Versions Notes

Abstract

Hexakis(4-(4-carboxylphenyl)phenyl)benzene, H6cbb, was used to prepare the rod-based metal–organic frameworks (rod-MOFs) [Mn4(cbb)(dmf)2(OAc)2] CTH-50 and [Gd3(cbb)(dmf)2(H2O)(OAc)3] CTH-51 by solvothermal synthesis (dmf = N,N-dimethylformamide) with single crystal diffraction revealing that CTH-50 (by X-ray) and CTH-51 (by electron diffraction) can be described as 5- and 6-connected yav-nets. Gas sorption analysis gave a BET surface area of 787 m2/g for CTH-50 and 187 m2/g for CTH-51, with CTH-50 having an Ideal Adsorbed Solution Theory (IAST) selectivity for SF6 of 35 at 10 kPa, and thermogravimetry indicated the possible stability of CTH-50 to 300 °C and CTH-51 to 400 °C.

1. Introduction

Although Metal–Organic Frameworks [1,2] (MOFs [3]) are increasing in popularity within companies, such as Svante Technologies Inc. building demonstration plants for CO2 capture, and NuMat Technologies Inc., which commercialized the first MOF product in 2016 [4], there is still much fundamental science to be done. In this regard, one such question is: What kind of framework topologies can be built using the toolbox of reticular chemistry? More specifically, how to combine well-known geometrical shapes into 3-periodic networks [5]. This is not a fringe question; it invokes chemistry from its mathematical borders to hands-on synthetic work and the design and understanding of new materials [6,7].
Combinations of many shapes have been reported by Wells [8], Robson [9], and Fischer and Koch [10] (using sphere packings), and a mathematical framework was provided by O’Keeffe and Delgado-Friedrich [11,12,13]. However, of these varied elements (triangles, tetrahedra, etc.), the hexagon is uniquely underrepresented [14].
An emerging MOF application is the capture of SF6, a greenhouse gas some 22,000 times more potent than CO2, used in industrial settings because of its dielectric properties, non-toxicity, and thermal stability [15,16,17,18]. In a previous study, we reported a hexagon Mn-based MOF, CTH-18, with good SF6/N2 selectivity prepared using hexakis(4-carboxyphenyl)benzene, 1 [19].
Non-toxic and inexpensive Mn(II) is an attractive choice for such MOF materials, and is present in most biological systems. It is also a rather less common in MOF chemistry, compared to Zn(II) [20]. To improve SF6 capacity and selectivity, we postulated that shape-matching and pore size could be important [21,22,23]. Thus, we expanded the MOF linker from hexakis(4-carboxyphenyl)benzene, 1 to hexakis(4-(4-carboxyphenyl)phenyl)benzene, 2 (Figure 1). Ideally, if the formed networks are isoreticular, we should then retain the rhombic-shaped channels with corner parts identical to CTH-18, where we think the good primary sorption sites could be reproduced. In addition, we would significantly expand the free volume of the network, increase the overall capacity, and hope that more S-F⋯F-S interactions would also improve the overall performance (Figure 1). We also note that a Mn-based MOF can be used for electro-oxidation processes, although the electrochemical properties of our Mn(II) were not investigated in this study.
Having the rather rare cbb linker 2 in our hands, we also wanted to expand this chemistry to lanthanoids (Ln), as only five MOF structures with cbb can be found in the Cambridge Crystallographic Database, CSD [25]. These are CEFNIN Cu(II) with she topology [26], FAKKEK and FAKKIO Co(II) with kgd-a layered topology [27], IXETEM Zr(IV) with pbz topology [24], and the mixed linker Tb-sph-MOF-3 UFOQOY [28].
In addition to the unique optical, electrical, and magnetic properties of the lanthanoids [29], we wanted to observe whether the typically higher coordination numbers of Ln ions would give any new and unique topologies; for example, any of the missing combinations of the hexagon with other geometric elements, such as the ubiquitous octahedron or tetrahedron. Although it may seem to be a simple mathematical problem, only recently was the combination of perfect hexagons and perfect triangles found (the laf-net) [14], and even more recently the combination of a see-saw geometry with hexagons was described [19].
Furthermore, the tentacle-like appearance of the cbb linker makes crystallography challenging, as we might expect not only the dynamic behaviour of the shorter cpb linker but also less stiffness of the individual tentacles. This is evidenced by the earlier crystallographic studies that all, except for the mixed linker structure UFOQOY [28], yielded rather high r-values of 13.88%, 23.95%, 16.34%, and 8.00%, respectively, and the ellipsoid plots showed signs of dynamic behavior.

2. Results and Discussion

2.1. Synthesis

Solvothermal synthesis in N,N-dimethylformamide (dmf) with hexakis(4-(4-carboxyphenyl)phenyl)benzene, H6cbb, 2, the appropriate metal salts and acetic acid (HOAc) as a modulator was used to produce the metal–organic frameworks in their as-prepared forms, formulated as [Mn4(cbb)(dmf)2(OAc)2]·3dmf·8H2O CTH-50 and [Gd3(cbb)(dmf)2(H2O)(OAc)3]·5dmf·8H2O CTH-51. For both compounds, larger batches were prepared using an ultrasonic bath under similar conditions. The synthesis procedure is detailed in Materials and Methods Section 3.1.

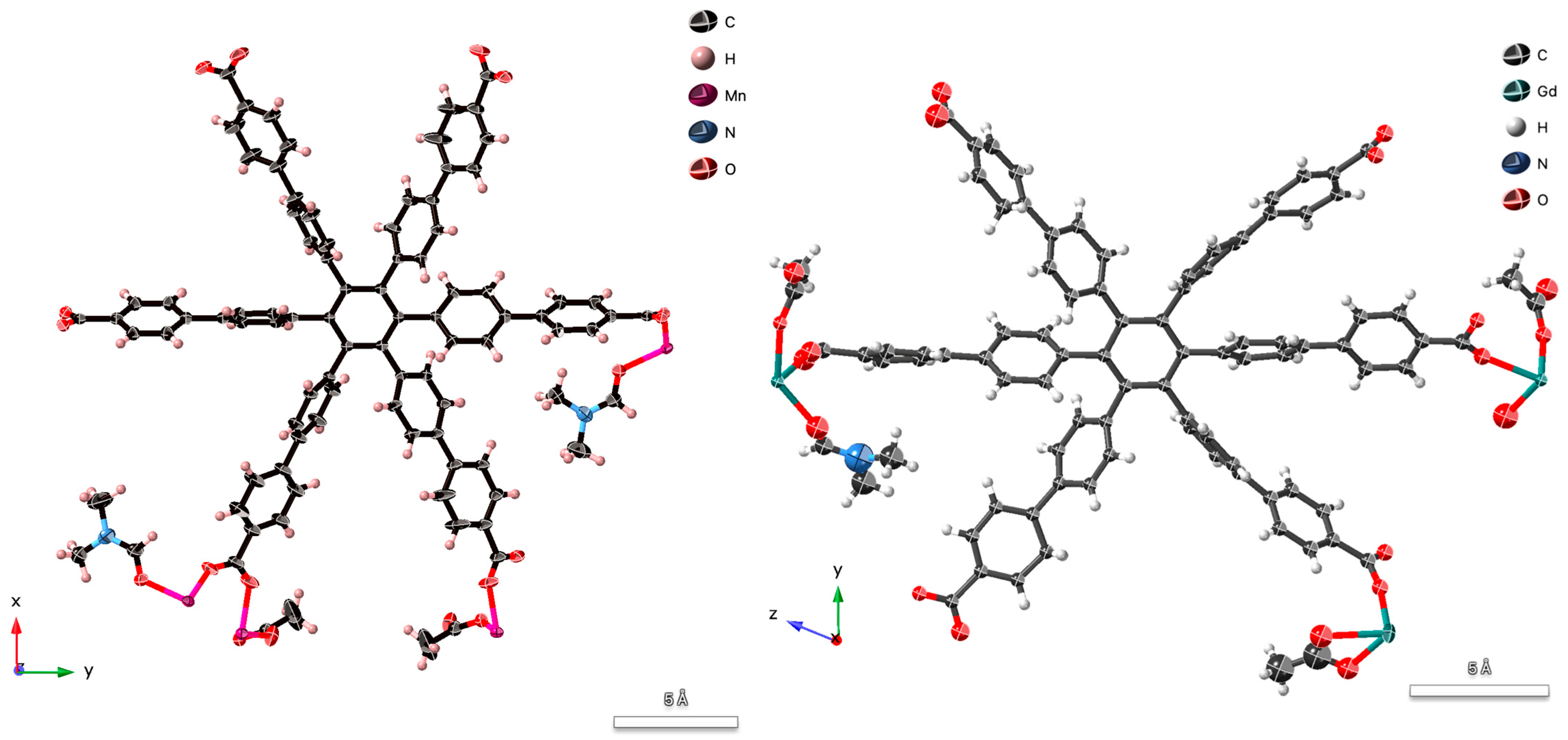
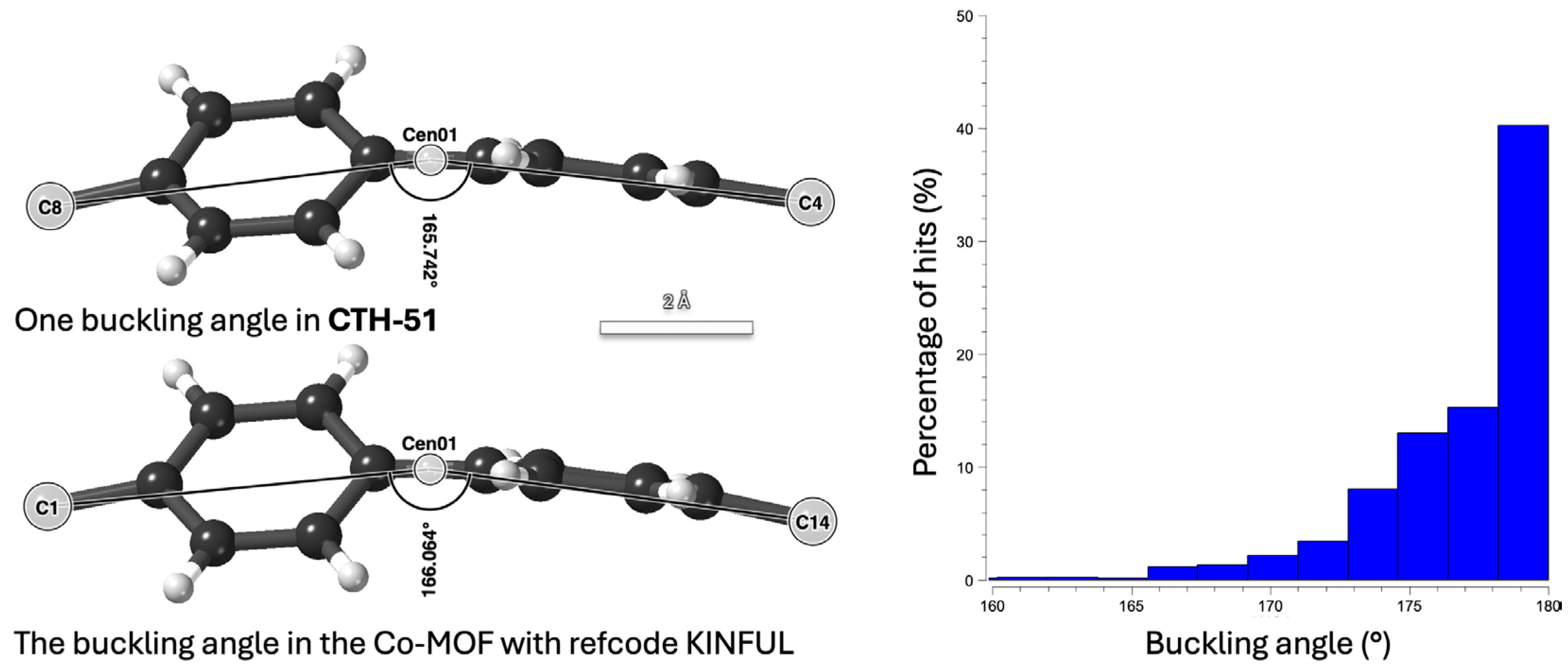
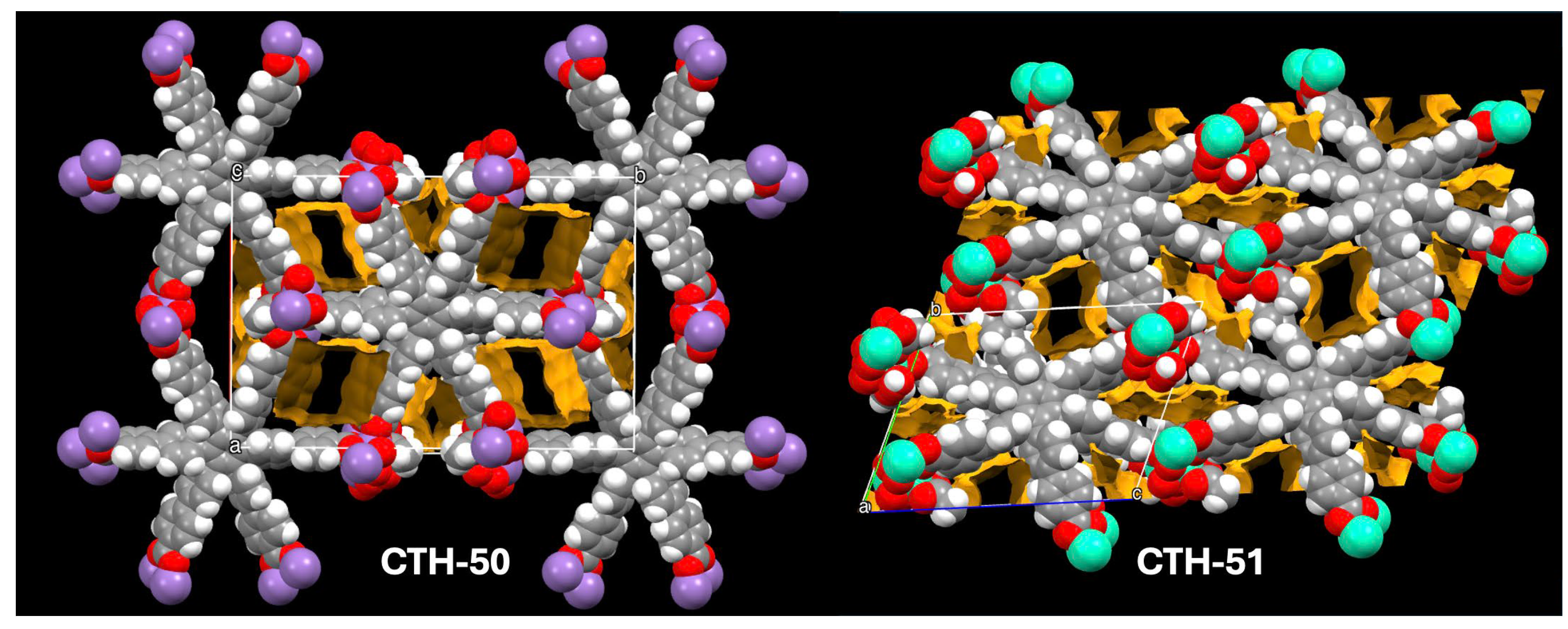
2.2. Single Crystal X-Ray Diffraction

For [Mn4(cbb)(dmf)2(OAc)2] CTH-50, needle-like crystals of CTH-50 were obtained after solvothermal synthesis, and a suitable single crystal was subjected to single crystal X-ray diffraction at 112 K.
The structure of CTH-50 was built by linking Mn(II) cations and ligands (Figure 2, left) to form a 3D network based on hexagons and rod-based Mn(II) secondary building units (SBUs) with acetate ions as additional bridges in the rod. The rods propagated parallel to the z-axis. The network structure is discussed in Section 2.6.
For [Gd3(cbb)(dmf)2(H2O)(OAc)3] CTH-51, very tiny needle-like crystals of CTH-51 were obtained after the solvothermal synthesis, and all attempts at single crystal X-ray diffraction failed to give resolution above 1 Å. Therefore, 3DED, namely continuous rotation electron diffraction (cRED) [30,31], at 293 K, was utilized for the crystal structure analysis. From the reconstructed 3D reciprocal lattice (Figure 2, right), the MOF was crystallized in a triclinic system, and the unit cell parameters could be determined as a = 11.34 Å, b = 19.49 Å, c = 24.44 Å, α = 67.38°, β = 88.01°, and γ = 84.50° (Supplementary Note S2).
The structure of CTH-51 was constructed by linking Gd(III) cations and ligands (Figure 2, right). The structure showed that Gd(III) cations were linked by carboxylate groups forming one-dimensional chains, thus forming a 3D network based on hexagons and rod-based Gd(III) SBUs with acetate ions as additional bridges in the rod. The rods propagated parallel to the x-axis. The network structure is discussed in Section 2.6.
A notable feature of CTH-51 is the considerable buckling [32,33] of the tentacles of the linker. For three of the six tentacles, the angle between the carbonyl carbon, the centroid in the middle of the tentacle, and the central ring carbon atom was below 170° (Figure 3). In contrast, for a fully relaxed tentacle, we would expect this angle to be 180°, which was indeed the case for four out of the six angles in CTH-50, the last two being 174° and 178°, respectively.
The average buckling in CTH-50 was 171.8° compared to 177.3° in CTH-51 (see Supplementary Note S5).
While not unprecedented, only 40% of all Csp2-C6H4-C6H4-Csp2 in the CSD were within 1° from 180° (Figure 3), which was a notable difference and one that narrowed the pores in CTH-51. This was not an artefact of lower crystal quality, as exactly the same buckling was found in a Co-MOF with the CSD code KINFUL [34]. Note that buckling angles as low as 120° appear in cyclic poly paraphenylenes and related compounds, i.e., ref. [6] cycloparaphenylene [35].
Due to the limitations of the cRED technique, which arise from the incomplete reciprocal space coverage caused by the physical constraints of the Transmission Electron Microscope (TEM) goniometer, the completeness of the data directly impacted the accuracy and reliability of the determined structural model, particularly at higher resolutions and when identifying subtle structural details. For this reason, we also performed a low-resolution (1 Å) X-ray structure determination of crystals from the CTH-51 preparation (LRSCXRD) for CTH-51b (see Supplementary Note S4). This analysis revealed the same network and network topology, but with slightly different buckling (average 176.5°) and, consequently, a slightly different unit cell. However, it remained in the same space group, with the following parameters: a = 12.02 Å, b = 21.72 Å, c = 23.73 Å, α = 66.62°, β = 88.43°, and γ = 83.70°. Although the CTH-51b structure was determined at low resolution, the bond parameters of CTH-51 and CTH-51b did not differ significantly; the average Gd-O bond distance for CTH-51 was 2.44 (3) Å and for CTH-51b was 2.45 (4) Å (see Supplementary Note S8).
More importantly, simulating the PXRD from this structural model yielded a more complex pattern, although with the same basic features (see Figure 4). This also illustrated the flexibility of the cbb linker, which was alluded to in the introduction.

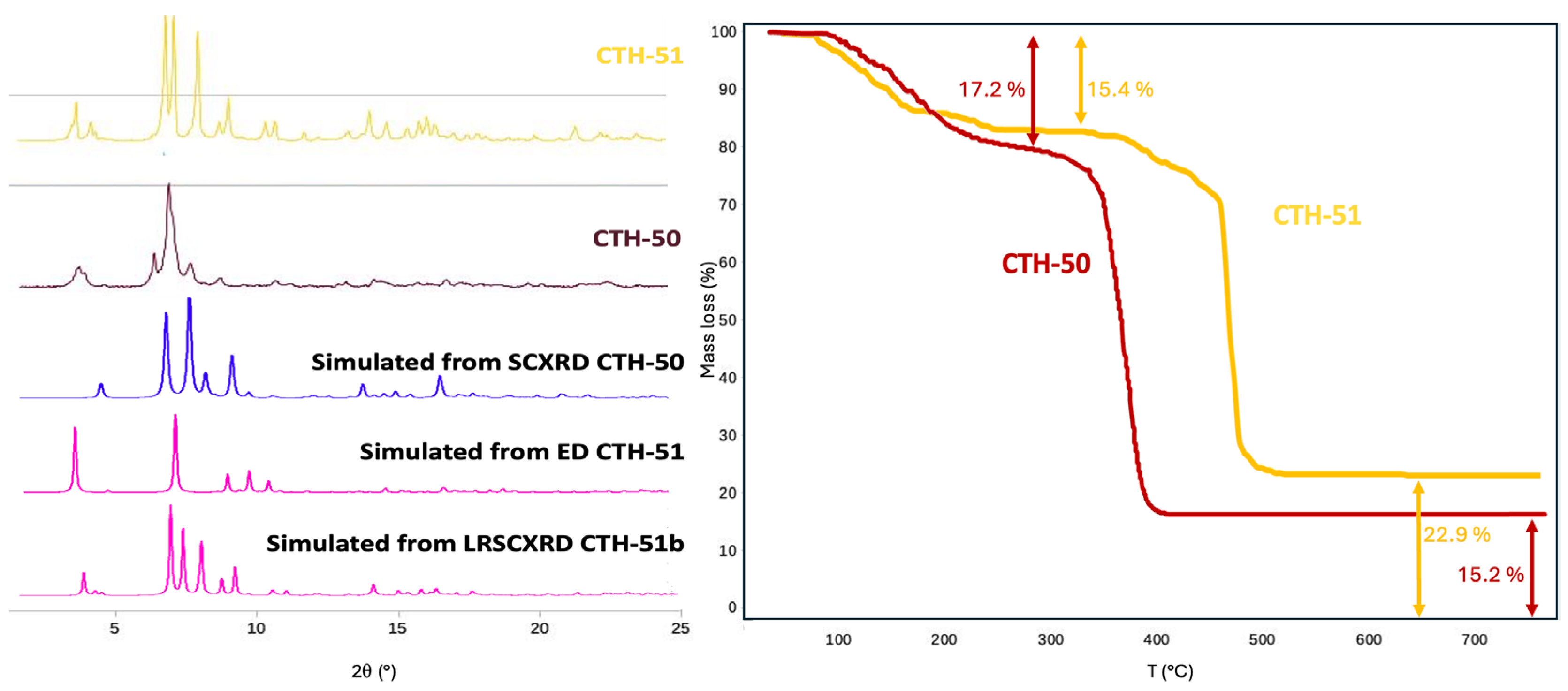
2.3. Powder X-Ray Diffraction

The powder diffraction patterns of CTH-50 and CTH-51 are shown in Figure 4, left, from 2θ 2.5° to 25°, together with the simulated patterns from the single crystal structure determinations as described in the previous section. The small discrepancies could be attributed to the less well-defined content of the pores, typically affecting the peaks around 4–5°, and the less precise electron diffraction structure of CTH-51. Although the single crystal structures indicated the possibility of linker buckling, which could be a dynamic process, there were no indications from the gas sorption experiments that this should be the case (vide infra). The full PXRD patterns of CTH-50 and CTH-51 at 2.5–80° are shown in Supplementary Note S7 and show no significant peaks above 25°.

2.4. Thermogravimetric Analysis

Briefly, 5 mg each of CTH-50 and CTH-51 were used for the thermogravimetric studies in air. The outcome of the TGA results indicated that the gradual solvent was lost from the framework below 300 °C, and the rapid breakdown of the MOF at 300 °C for CTH-50 and 400 °C for CTH-51. For CTH-50, there was a 17.2% mass loss from 100 °C to around 280 °C, corresponding to two dmf and two acetic acid solvents (calculated 15.35%), and a 15.4% mass loss in CTH-51 corresponded to two dmf, one water, and three acetic acid solvents (calculated 16.67%) (see Figure 4). The residual mass at 700 °C was 15.2% for CTH-50 and 22.9% for CTH-51, consistent with the oxide residues expected from the formulas, 16.6% for CTH-50 and 23.3% for CTH-51.

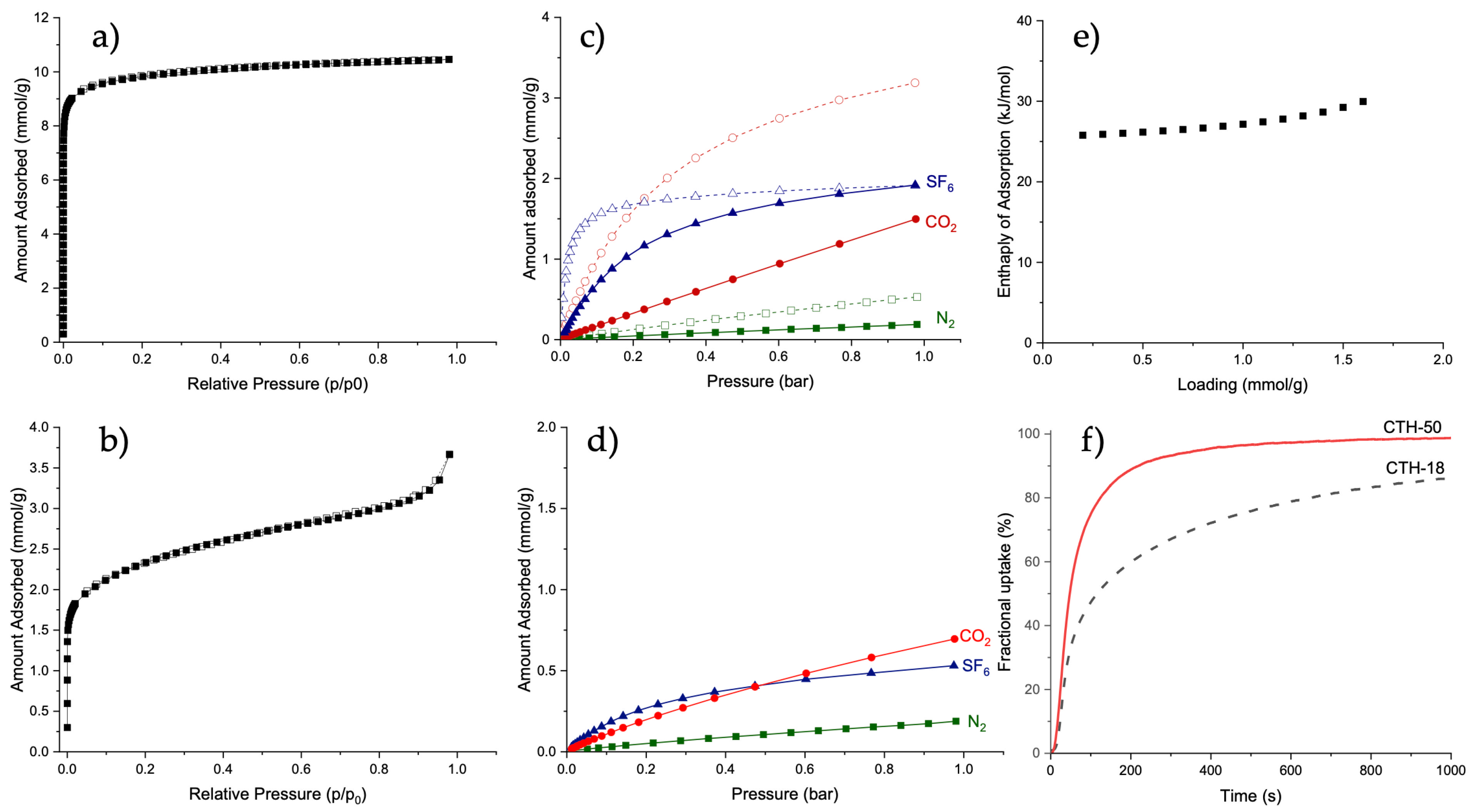
2.5. Gas Sorption Analysis

For the gas sorption analysis of CTH-50, the TGA results were taken into account, and the material was activated in dynamic vacuum at 250 °C prior to gas sorption analysis. The N2 sorption isotherms recorded at 77 K demonstrated the microporous nature of the material, as shown by the steep N2 adsorption isotherm shape at the very low-pressure regime.
The specific BET and Langmuir surface area of CTH-50, estimated using the N2 adsorption isotherm, were 787 and 967 m2/g, respectively. Evoking the routine implementation in the CSD (CSD version 6.00, April 2025) software Mercury(Mercury 2025.2.0 (Build 454209), the solvent accessible surface area of [Mn4(cbb)(dmf)2(OAc)2], CTH-50, with the coordinated dmf molecules removed from the crystallographic information file, was calculated to be 967 m2/g, which is in good agreement with the experimental findings.
The pore size distributions (PSDs) were estimated from the N2 adsorption isotherm using Density Functional Theory (DFT), with the slit pore model. The DFT PSDs of CTH-50 are plotted in the insert of Figure S4 and show two distinct types of pores with estimated diameters of ~6.4 and ~8.3 Å. The estimated pore diameters should not be taken as accurate numbers; however, they were in a comparable range to the crystallographic derived pore sizes of 4.7 × 8.5 Å and 2.5 × 4.5 Å.
These data should be compared with those of the corresponding material, [Mn3(cpb)(dmf)3], CTH-18. Even though we noted in the structure section that they were not isoreticular, they share the same basic rod-MOF structure. The experimentally derived pore sizes of CTH-18 gave estimated diameters of ~4.3 and ~5.1 Å, and the crystallographic pore widths were reported as 4.3 × 6.0 Å and 3.4 × 4.7 Å [19]. Simple geometric estimates from Figure 1 indicated a CTH-50/CTH-18 pore width ratio of 1.5, and the corresponding gas sorption pore width ratios could be calculated as 6.4/4.3 = 1.5 and 8.3/5.1 = 1.6, which were in very reasonable agreement. The 20 °C N2, CH4, SF6, and CO2 adsorption isotherms of CTH-50 were also recorded, and are shown in Figure 5 together with the corresponding measurement for CTH-18 [19].
We postulated that the corner parts of the rhombic channels would be identical to CTH-18, and therefore still provide good sorption properties and SF6/N2 selectivity. This seemed to hold true when using s = (q1/q2)/(p1/p2) as an estimate. The selectivity of CTH-50, 35, was even slightly higher than that of CTH-18, 29 [19].
Second, we postulated that the SF6 molecules sorbed at the corners would create good sorption sites for SF6 in the expanded space created in the middle of the rhombic channels. At 1 bar, the SF6 uptake appeared to be completely saturated for CTH-18, whereas for CTH-50, there was still a bit to go, so we estimated the maximum uptake at higher pressures to be greater for CTH-50. The extended linker should provide a cavity with an increased space for SF6 sorption. On the other hand, the increased pore size could reduce the amount of enhanced VdW interactions between the pore surface and SF6 molecules. This was clearly observed when comparing the sorption kinetics (Figure 5f), where the large pore CTH-50 showed noticeably high SF6 sorption kinetics due to unrestricted diffusion. In addition, the shapes of the SF6 isotherms of CTH-18 and CTH-50 (Figure 5c) also supported this claim; a steep isotherm shape was observed for CTH-18 in the low-pressure region, up to 0.1 bar. Indeed, the enthalpy of SF6 sorption of approximately 25–30 kJ/mol—calculated using the Clausius–Clapeyron equation (Figure 5e) and the total removal of the adsorbed SF6 upon gentle heating at 70 °C (in the cyclic sorption experiment shown in Figure S7, insert)—would suggest that the physisorption interaction was not particularly strong.
Considering the SF6 uptake at 0.1 bar, 0.75 mmol/g, it was less than half of CTH-18, but still comparable to many other MOFs, such as UiO-66-Zr (∼0.75 mmol/g at 298 K) [36] or SU-100 (∼1.08 mmol/g at 298 K) [37]. Notably, all the other gases showed a decreased sorption in CTH-50 of approximately the same magnitude, but clearly also did not reach even close to saturation at 1 bar. Further analysis of the SF6 isotherm of CTH-18 and CTH-50, by fitting them with the single-site Langmuir equation and the Toth isotherm, confirmed that the estimated maximum SF6 capacity of CTH-50 was noticeably higher than that of CTH-18 (see Table 1).
For the gas sorption analysis of CTH-51, considering the TGA results, the material was activated in dynamic vacuum at 250 °C prior to gas sorption analysis. The N2 sorption isotherms recorded at 77 K demonstrated the microporous nature of the material, as shown by the steep N2 adsorption isotherm shape in the very-low-pressure regime.
The specific BET and Langmuir surface area of [Gd3(cbb)(dmf)2(H2O)(OAc)3] CTH-51, estimated using the N2 adsorption isotherm, were 187 and 233 m2/g, respectively. This seemed comparatively low, compared to [La2(cpb)], CTH-17 with a reported SBET of 231 m2/g [38]. Again, structurally similar, with a rod-MOF topology giving rhombic channels, CTH-17 notably lacked all the extra acetate groups in CTH-51. Evoking the routine implementation in the CSD Mercury software [39], the solvent-accessible surface area for [Gd3(cbb)(dmf)2(H2O)(OAc)3] CTH-51-Gd, with the coordinated dmf molecules removed from the crystallographic information file, was calculated to be 311 m2/g, which was in good agreement with the experimental findings. A comparison of the solvent-accessible surfaces of CTH-50 and CTH-51-Gd is shown in Figure 6.
The structural reasons for the difference in surface area between CTH-50 (SBET 787 m2/g) and CTH-51 (SBET 187 m2/g) are shown in Figure 6. It seemed that the three methyl groups of the acetate ions efficiently close some of the expected rhombic channels together with the previously noted tentacle buckling.
The 20 °C N2, SF6, and CO2 adsorption isotherms of CTH-51 were also recorded and are shown in Figure 5d. Again, we observed some preference for SF6 over N2 adsorption at low pressures, but much less than recorded for CTH-50. In contrast, the comparison to [La2(cpb)], CTH-17 was less straight forward as this MOF had a gated CO2 sorption at 0–20 °C, sorbing linearly up to 0.45 mmol/g at 0.4 bar and then abruptly jumping up to 1 mmol/g [38].
However, up to 0.4 bar, the behaviour was somewhat similar, with CTH-51 sorbing 0.4 mmol/g CO2 at 0.4 bar. The gated behaviour in CTH-17 was interpreted as a concerted movement of the La coordination sphere and stacking of the linkers, possibly because of the low coordination number of the lanthanum ion (six). In CTH-51, the coordination number was constantly seven or higher, probably making such movements more difficult in a sterically less forgiving environment.

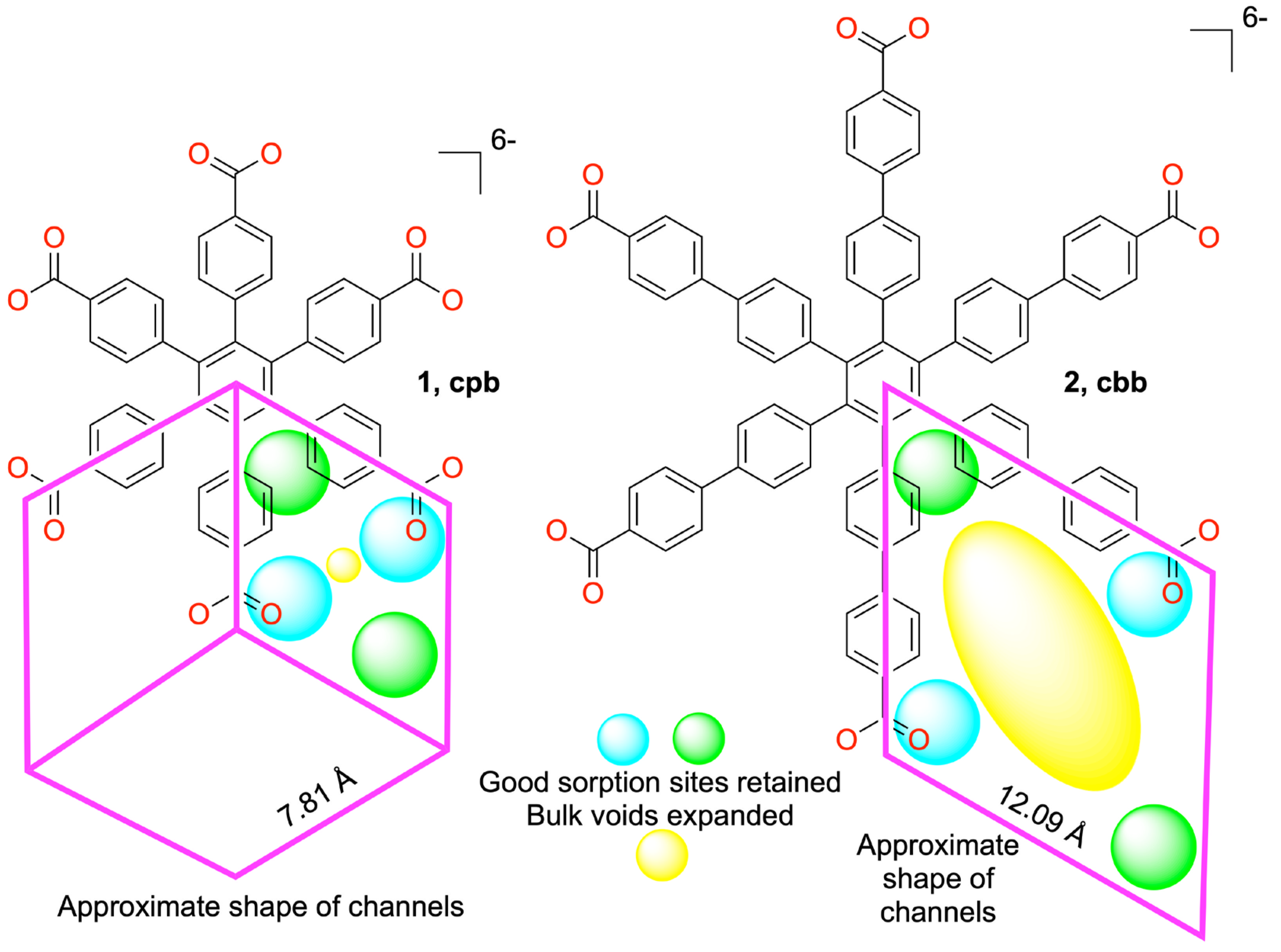
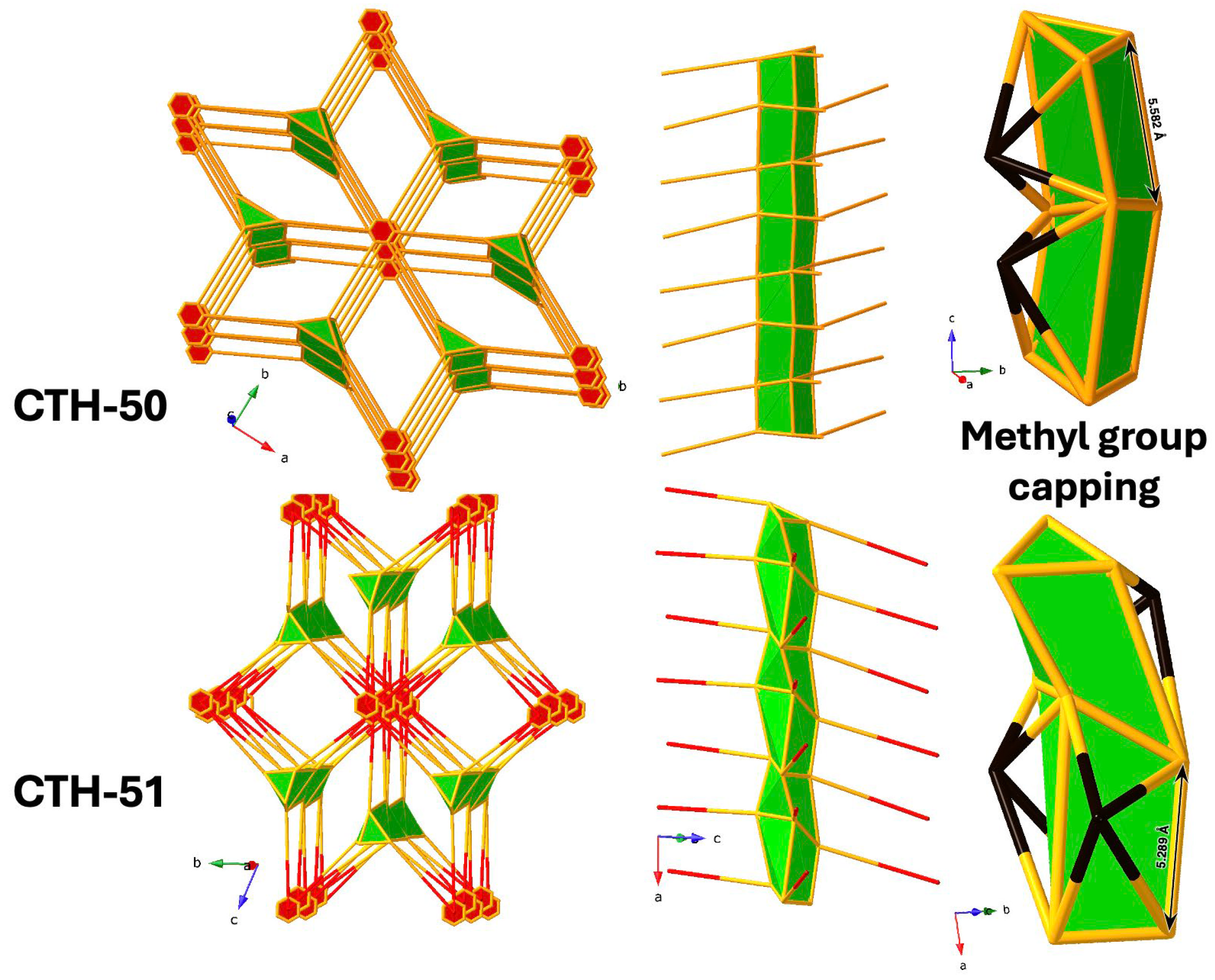
2.6. Network Topology Analysis

Superficially, all the MOFs discussed in this article so far, CTH-50 and CTH-51 with the cbb linker, and CTH-17 and CTH-18 with one benzene ring smaller than the cpb linker, are very similar.
On a first level of topological abstraction, CTH-50, CTH-51, CTH-17, and CTH-18 are all rod-MOFs, meaning that we could not divide the metal secondary building units (metal-SBUs) into discrete entities, such as {Zn4O(CO2)6} for MOF-5; instead, the metal-SBU is formed by a continuous chain of metal–carboxylate coordination entities. For completion, we note that the other variations in metal-SBUs extending in 0D (such as MOF-5), 1D, 2D, and 3D give MOFs that we can name dot-, rod-, sheet-, and frame-MOFs [40,41]).
As there were indications that a higher dimensionality of the metal-SBU was linked to higher stability [42], even this low-level abstraction is practically relevant. For the materials in question, all were stable up to at least 300 °C, judging by TGA, and the variable temperature PXRD of CTH-17 indicated structural stability up to 400 °C.
We also saw great differences between these materials and wonder how much was due to the detailed molecular structure, conformation of the organic linker, coordination number of the metal ion, and other factors, and how much could be explained by a more detailed topology analysis. On a more general level, these network topologies are essential in the communication of MOF structures [8,9,43,44,45], and even before, as blueprints in reticular chemistry synthesis planning [46]. In addition, the resulting properties, such as flexibility and porosity, have been explored using the network topology approach [47]. However, rod-MOFs pose a particular problem as they are commonly analyzed in a different way from dot-MOFs [48,49,50]. We took the two most common approaches to rod-MOF topologies, the STR (straight rod) approach [49,50] and the PoE (points-of-extension) method [48]. The results are presented in Table 2.
In the straight rod approach, we made a straight line of the rod-metal-SBU, and then the linkers at their closest attachment points [49,50]. Frequently, this meant that the nodes were in between two metal ions, as was the case here, where both CTH-50 and CTH-51, though slightly less clear cut for the latter, had three carboxylates bridging two metal ions; thus, the attachment points would fall on the centroid between these metal ions, giving a 5-connected node. We then combined it with the 6-connected cbb6-linker to form the yav-net, a 2-nodal net combining hexagons and trigonal bipyramids, similar to the acetate-bridged CTH-7 and CTH-8, [M4(cpb)(OAc)2(dmf)4] with either Fe(II) or Co(II).
The yav-net is thus a frequent motif with flat hexagonal building blocks and rod-MOFs; however, we note that [Mn3(cpb)(dmf)3], CTH-18 had a different and unique net combining a see-saw geometry of the rod-nodes and hexagons, thus filling an empty space in the reticular chemistry combinatorial table of SBU geometries. The unique topology of CTH-18 is generated by the low coordination number, five, on Mn, and by the partwise connection of the carboxylates to the rod. The absence of coordinated acetate anions also makes the stoichiometry different in CTH-18.
The more elaborate PoE approach connects the carboxylate carbons (the points of extension) to polyhedra, making a three-dimensional model of the rod-SBU. This would enable us to distinguish the different makeup of the rod that the STR approach would miss. In our case of the yav-net, we envisaged consecutive triplets of carboxylate carbons to form either face-sharing trigonal prisms or octahedra. We found a 5,6-c net where trigonal prisms shared triagonal faces, och-nets, in CTH-50, CTH-51, and CTH-17; thus, the three were isoreticular at both levels. The och-nets are illustrated in Figure 7.
However, this abstraction also allowed for the investigation into the importance of the additional acetate groups in an easy way (note that the unit cell of CTH-51 contained 372 atoms). In Figure 7, right, we illustrate how the polyhedral rods in CTH-50 have two faces capped by methyl groups in every pair of trigonal prisms, whereas in the much less porous CTH-51, three of the six sides are capped. Notably, CTH-51 protrudes in all directions, cluttering all the rhombic channels.

3. Materials and Methods

All chemicals utilized for MOF synthesis were purchased from Sigma-Aldrich in Germany, except H6cbb from Extension in China, and were used without further purification. All MOF preparations were repeated, and the yields were generally high. All the studied MOF single crystals were washed and immersed in dmf before conducting single crystal X-ray diffraction analysis to remove any unreacted H6cbb.

3.1. Synthesis

For [Mn4(cbb)(dmf)2(OAc)2]·3dmf·8H2O CTH-50, 6.03 mg H6cbb (0.048 mmol) and 2.85 mg MnCl2·4H2O (0.14 mmol) were used. The two solids were added to separate 10 mL heat-resistant Pyrex glass tubes and dissolved in 3.5 mL dmf and acetic acid (0.5 mL), while heating and stirring at 120 °C. The two solutions were then combined into one of the Pyrex tubes, sealed, and placed in an oven at 120 °C for 3 days. A white crystalline precipitate was formed with a good yield. Elemental analysis (Calc. %) showed the following: C, 59.0; H, 5.05; N, 3.34; Found % C, 58.53; H, 4.59; N, 3.70.
For [Gd3(cbb)(dmf)(OAc)3]·3dmf·8H2O CTH-51, 5.02 mg H6cbb (0.040 mmol) and 5.42 mg Gd(NO3)3·6H2O (0.12 mmol) were used. The two solids were added to separate 10 mL heat-resistant Pyrex glass tubes and dissolved in 3.0 mL dmf and 1.0 mL acetic acid, while heating and stirring at 120 °C. The two solutions were then combined in one of the Pyrex tubes, sealed, and placed in an oven at 120 °C for 3 days. A white crystalline precipitate was formed with a good yield.

3.2. Transmission Electron Microscopic (TEM) Analysis

The samples for TEM analysis were dispersed in isopropanol, and the mixture was dropped onto a copper grid coated with carbon. Observations were conducted using a JEOL JEM2100 microscope (JEOL, Japan) at an acceleration voltage of 200 kV, with a Cs value of 1.0 mm and a point resolution of 0.23 nm. TEM images were captured using a Gatan Orius 833 CCD camera with a resolution of 2048 × 2048 pixels and a pixel size of 7.4 µm. Electron diffraction patterns were recorded using a Timepix pixel detector QTPX-262k with a resolution of 512 × 512 pixels and a pixel size of 55 µm, manufactured by Amsterdam Sci. Instruments, Amsterdam, The Netherlands.

3.3. Continuous-Rotation Electron Diffraction (cRED) Collection

Data acquisition was performed using the Instamatic software (https://sites.google.com/view/xiaodong-zous-group/software/instamatic) [51]. A single-tilt tomography holder was utilized, allowing for the specimen to tilt from −70° to +70° within the TEM. The aperture used for the cRED data collection had a diameter of approximately 0.6 μm. The goniometer tilt speed was set at 0.45° per second, and each frame was exposed for 0.3 s. To minimize beam damage and optimize data quality, each data set was collected within 4 min. Subsequently, the data sets were merged using the XDS packages [52] for structure determination. The dataset had a signal-to-noise ratio within a resolution of 1.0 Å. Owing to the limited goniometer tilting range, the data completeness for a single data set was in the range of 32.8% to 51.3%. To improve overall data completeness [53], eight data sets were merged. With the completeness of the merged data reaching 93.8%, the structure of CTH-51-Gd was solved by ab initio direct methods in the space group P 1 ¯ , with all atoms able to be located directly. The commands SIMU and DELU were used in the structural refinement process. SIMU restrained atoms that were close to each other to have similar anisotropic displacement parameters (ADPs), whereas DELU applied a rigid bond restraint forcing ADPs to be equal in the direction of the bond between them. These two commands were used to stabilize the refinement.

3.4. Single Crystal X-Ray Diffraction

Data were collected using Cu Kα radiation (λ = 1.54184 Å) on a Rigaku XtaLAB Synergy-R diffractometer (Rigaku, Neu-Isenburg, Germany) equipped with a HyPix-6000HE Detector. Diffraction data were acquired and processed with the CrysAlisPro software package (https://rigaku.com/products/crystallography/x-ray-diffraction/crysalispro) [54,55]. Direct or structure expansion methods were used for all structures; the refinements were established by full-matrix least squares with SHELX-2018/3 [56] using the Olex2 (Olex2 version 1.5) [57] software as a graphical interface. The solvent molecules encapsulated in both MOFs were disordered; therefore, the Mask command embedded in the Olex2 software was utilized to estimate the ratio of each solvent by the number of electrons based on the asymmetric unit (ASU). The Rint in CTH-50 was high because of the crystal quality; they were tiny needles and turned opaque once removed from their mother liquid. Details of the structural refinements are provided in the Supporting Information.

3.5. Powder X-Ray Diffraction

Powder X-ray diffraction patterns were recorded using a Bruker D8 Twin diffractometer (Billerica, MA, USA) with Cu-Kα radiation λ = 1.54 Å at room temperature, scanning between 2θ 2.5° and 80°.

3.6. Gas Adsorption Isotherms

Gas adsorption isotherms were recorded on a Micromeritics ASAP2020 surface area analyzer (Atlanta, Georgia, USA) at liquid N2 temperature (−196 °C). The samples (approximately 50–100 mg) were pre-treated up to 250 °C under dynamic vacuum (1 × 10−4 Pa) for 6 h before the analysis. The relative pressure range of 0.05–0.15 was used to estimate the Langmuir and BET surface area of the samples. Additionally, SF6, CO2, and N2 adsorption isotherms were recorded at ambient temperatures (in a temperature-controlled water bath) using the same instrument. The isosteric heat of SF6 sorption was calculated using the Clausius–Clapeyron equation according to procedures detailed in the literature [58]. The heat of SF6 sorption was estimated for SF6 loading at 0.2–1.6 mmol/g using the adsorption isotherms recorded at 10, 20, and 30 °C; the isotherms were fitted with the single-site Langmuir equation.

3.7. Other Tools

Elemental analysis was performed by Mikroanalytisches Labor Kolbe, c/o Fraunhofer Institut, Oberhausen, Germany. For the TGA measurements, we used a Mettler Toledo TGDS/DSC 3+ Star system. CrystalMaker was used for all structural drawings, and Mercury software for porosity calculations. Systre was used for the topology analysis [13].

4. Conclusions

Two new hexagon-based MOFs, CTH-50 and CTH-51, were synthesized using an expanded linker, hexakis(4-(4-carboxylphenyl)phenyl)benzene, H6cbb. CTH-50 showed high SF6 selectivity and uptake owing to its larger pores and faster diffusion. Structural differences, including linker buckling and acetate capping, influenced the porosity. The network topology analysis, however, gave the same results as for the previously obtained La MOF with the shorter linker hexakis(4-carboxyphenyl)benzene CTH-17, but differed in the two Mn MOFs CTH-50 and CTH-18. These findings advance the design of MOFs for gas separation applications.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/inorganics14010012/s1. Crystallographic data, topology input and output files, additional sorption plots and the adsorption information files (AIF).

Author Contributions

Conceptualization, F.M.A.N. and L.Ö.; methodology, H.B., W.R., G.Z., Z.H., F.M.A.N., O.C., and L.Ö.; investigation, H.B., W.R., G.Z., Z.H., F.M.A.N., O.C., and L.Ö.; resources, O.C., F.M.A.N., and L.Ö.; writing—original draft preparation, F.M.A.N., O.C., and L.Ö.; writing—review and editing, H.B., W.R., F.M.A.N., O.C., and L.Ö.; visualization, L.Ö.; project administration, L.Ö.; funding acquisition, F.M.A.N., O.C., and L.Ö. All authors have read and agreed to the published version of the manuscript.

Funding

This work was funded by Chalmers University of Technology through the GENIE project, and we also thank the Chalmers Materials Analysis Laboratory, the Swedish Research Council (Grant No. 2020-04029), and the Olle Engkvist Foundation for funding the single-crystal diffractometer. ZH acknowledges the Swedish Research Council Formas (2020-00831), the Swedish Research Council (VR, 2022-02939), the Wallenberg Initiative Materials Science for Sustainability (WISE) funded by the Knut and Alice Wallenberg Foundation, and the Royal Society of Chemistry (RSC: R21-8610976142) for funding support.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Accession Code CCDC 2491439-2491440 contains supplementary crystallographic data for this study. These data can be obtained free of charge via www.ccdc.cam.ac.uk/data_request/cif (accessed on the 22 September 2025), by emailing data_request@ccdc.cam.ac.uk, or by contacting the Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, UK; Fax: +44-1223-336033. All the other data presented in this study are available in this article.

Acknowledgments

This work was conducted in part at the Chalmers Material Analysis Laboratory, CMAL.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Yaghi, O.M.; Li, G.M.; Li, H.L. Selective Binding and Removal of Guests in a Microporous Metal-Organic Framework. Nature 1995, 378, 703–706. [Google Scholar] [CrossRef]
  2. Li, H.; Eddaoudi, M.; O’Keeffe, M.; Yaghi, O.M. Design and synthesis of an exceptionally stable and highly porous metal-organic framework. Nature 1999, 402, 276–279. [Google Scholar] [CrossRef]
  3. Batten, S.R.; Champness, N.R.; Chen, X.M.; Garcia-Martinez, J.; Kitagawa, S.; Öhrström, L.; O’Keeffe, M.; Suh, M.P.; Reedijk, J. Terminology of metal-organic frameworks and coordination polymers (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1715–1724. [Google Scholar] [CrossRef]
  4. Barsoum, M.L.; Fahy, K.M.; Morris, W.; Dravid, V.P.; Hernandez, B.; Farha, O.K. The Road Ahead for Metal–Organic Frameworks: Current Landscape, Challenges and Future Prospects. ACS Nano 2025, 19, 13–20. [Google Scholar] [CrossRef]
  5. Kalmutzki, M.J.; Hanikel, N.; Yaghi, O.M. Secondary building units as the turning point in the development of the reticular chemistry of MOFs. Sci. Adv. 2018, 4, eaat9180. [Google Scholar] [CrossRef]
  6. Ortín-Rubio, B.; Ghasempour, H.; Guillerm, V.; Morsali, A.; Juanhuix, J.; Imaz, I.; Maspoch, D. Net-Clipping: An Approach to Deduce the Topology of Metal–Organic Frameworks Built with Zigzag Ligands. J. Am. Chem. Soc. 2020, 142, 9135–9140. [Google Scholar] [CrossRef]
  7. Ortín-Rubio, B.; Rostoll-Berenguer, J.; Vila, C.; Proserpio, D.M.; Guillerm, V.; Juanhuix, J.; Imaz, I.; Maspoch, D. Net-clipping as a top-down approach for the prediction of topologies of MOFs built from reduced-symmetry linkers. Chem. Sci. 2023, 14, 12984–12994. [Google Scholar] [CrossRef]
  8. Wells, A.F. Three-Dimensional Nets and Polyhedra; John Wiley & Sons: New York, NY, USA, 1977. [Google Scholar]
  9. Robson, R. A net-based approach to coordination polymers. Dalton Trans. 2000, 21, 3735–3744. [Google Scholar] [CrossRef]
  10. Koch, E.; Fischer, W. Sphere packings with three contacts per sphere and the problem of the least dense sphere packing. Z. Krist. 1995, 210, 407–414. [Google Scholar] [CrossRef]
  11. Delgado-Friedrichs, O.; O’Keeffe, M.; Yaghi, O.M. Three-periodic nets and tilings: Edge-transitive binodal structures. Acta Cryst. A 2006, 62, 350–355. [Google Scholar] [CrossRef]
  12. Delgado-Friedrichs, O.; O’Keeffe, M. Three-periodic tilings and nets: Face-transitive tilings and edge-transitive nets revisited. Acta Cryst. A 2007, 63, 344–347. [Google Scholar] [CrossRef] [PubMed]
  13. Delgado-Friedrichs, O.; O’Keeffe, M. Identification and symmetry computation for crystal nets. Acta Cryst. Sec. A 2003, 59, 351–360. [Google Scholar] [CrossRef] [PubMed]
  14. Amombo Noa, F.M.; Svensson Grape, E.; Brülls, S.M.; Cheung, O.; Malmberg, P.; Inge, A.K.; McKenzie, C.J.; Mårtensson, J.; Öhrström, L. Metal–Organic Frameworks with Hexakis(4-carboxyphenyl)benzene: Extensions to Reticular Chemistry and Introducing Foldable Nets. J. Am. Chem. Soc. 2020, 142, 9471–9481. [Google Scholar] [CrossRef] [PubMed]
  15. Chang, M.; Yan, T.; Wei, Y.; Wang, J.-X.; Liu, D.; Chen, J.-F. Metal–Organic Framework-Based Single-Molecule SF6 Trap for Record SF6 Capture. Chem. Mater. 2022, 34, 9134–9143. [Google Scholar] [CrossRef]
  16. Åhlén, M.; Amombo Noa, F.M.; Öhrström, L.; Hedbom, D.; Strømme, M.; Cheung, O. Pore size effect of 1,3,6,8-tetrakis(4-carboxyphenyl)pyrene-based metal-organic frameworks for enhanced SF6 adsorption with high selectivity. Microporous Mesoporous Mater. 2022, 343, 112161. [Google Scholar] [CrossRef]
  17. Wang, Q.; Hu, Y.; Gu, Y. Molecular Mechanism Behind the Capture of Fluorinated Gases by Metal–Organic Frameworks. Nano-Micro Lett. 2025, 17, 118. [Google Scholar] [CrossRef]
  18. Li, J.; Chen, Y.; Ke, T.; Jin, Y.; Fan, R.; Xu, G.; Yang, L.; Zhang, Z.; Bao, Z.; Ren, Q.; et al. Efficient continuous SF6/N2 separation using low-cost and robust metal-organic frameworks composites. Nat. Commun. 2025, 16, 632. [Google Scholar] [CrossRef]
  19. Amombo Noa, F.M.; Cheung, O.; Åhlén, M.; Ahlberg, E.; Nehla, P.; Salazar-Alvarez, G.; Ershadrad, S.; Sanyal, B.; Öhrström, L. A hexagon based Mn(II) rod metal–organic framework—Structure, SF6 gas sorption, magnetism and electrochemistry. Chem. Commun. 2023, 59, 2106–2109. [Google Scholar] [CrossRef]
  20. Dunning, S.G.; Gupta, N.K.; Reynolds, J.E., III; Sagastuy-Breña, M.; Flores, J.G.; Martínez-Ahumada, E.; Sánchez-González, E.; Lynch, V.M.; Gutiérrez-Alejandre, A.; Aguilar-Pliego, J.; et al. Mn-CUK-1: A Flexible MOF for SO2, H2O, and H2S Capture. Inorg. Chem. 2022, 61, 15037–15044. [Google Scholar] [CrossRef]
  21. Moghadam, P.Z.; Chung, Y.G.; Snurr, R.Q. Progress toward the computational discovery of new metal–organic framework adsorbents for energy applications. Nat. Energy 2024, 9, 121–133. [Google Scholar] [CrossRef]
  22. Wang, J.; Liu, J.; Wang, H.; Zhou, M.; Ke, G.; Zhang, L.; Wu, J.; Gao, Z.; Lu, D. A comprehensive transformer-based approach for high-accuracy gas adsorption predictions in metal-organic frameworks. Nat. Commun. 2024, 15, 1904. [Google Scholar] [CrossRef]
  23. Åhlén, M.; Jaworski, A.; Strømme, M.; Cheung, O. Selective adsorption of CO2 and SF6 on mixed-linker ZIF-7–8s: The effect of linker substitution on uptake capacity and kinetics. Chem. Eng. J. 2021, 422, 130117. [Google Scholar] [CrossRef]
  24. Alezi, D.; Spanopoulos, I.; Tsangarakis, C.; Shkurenko, A.; Adil, K.; Belmabkhout, Y.; O′Keeffe, M.; Eddaoudi, M.; Trikalitis, P.N. Reticular Chemistry at Its Best: Directed Assembly of Hexagonal Building Units into the Awaited Metal-Organic Framework with the Intricate Polybenzene Topology, pbz-MOF. J. Am. Chem. Soc. 2016, 138, 12767–12770. [Google Scholar] [CrossRef]
  25. Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Cryst. B 2016, 72, 171–179. [Google Scholar] [CrossRef] [PubMed]
  26. Gómez-Gualdrón, D.A.; Colón, Y.J.; Zhang, X.; Wang, T.C.; Chen, Y.-S.; Hupp, J.T.; Yildirim, T.; Farha, O.K.; Zhang, J.; Snurr, R.Q. Evaluating topologically diverse metal–organic frameworks for cryo-adsorbed hydrogen storage. Energy. Environ. Sci. 2016, 9, 3279–3289. [Google Scholar] [CrossRef]
  27. Spanopoulos, I.; Tsangarakis, C.; Barnett, S.; Nowell, H.; Klontzas, E.; Froudakis, G.E.; Trikalitis, P.N. Directed assembly of a high surface area 2D metal–organic framework displaying the augmented “kagomé dual” (kgd-a) layered topology with high H2 and CO2 uptake. Inorg. Chem. Front. 2017, 4, 825–832. [Google Scholar] [CrossRef]
  28. Jiang, H.; Jia, J.; Shkurenko, A.; Chen, Z.; Adil, K.; Belmabkhout, Y.; Weselinski, L.J.; Assen, A.H.; Xue, D.-X.; O’Keeffe, M.; et al. Enriching the Reticular Chemistry Repertoire: Merged Nets Approach for the Rational Design of Intricate Mixed-Linker Metal–Organic Framework Platforms. J. Am. Chem. Soc. 2018, 140, 8858–8867. [Google Scholar] [CrossRef]
  29. Su, P.; Song, F.; Cao, J.; Yan, C.-H.; Tang, Y. Rare Earth Complex-Based Functional Materials: From Molecular Design and Performance Regulation to Unique Applications. Acc. Chem. Res. 2025, 58, 218–230. [Google Scholar] [CrossRef]
  30. Huang, Z.; Grape, E.S.; Li, J.; Inge, A.K.; Zou, X. 3D electron diffraction as an important technique for structure elucidation of metal-organic frameworks and covalent organic frameworks. Coord. Chem. Rev. 2021, 427, 213583. [Google Scholar] [CrossRef]
  31. Ge, M.; Wang, Y.; Carraro, F.; Liang, W.; Roostaeinia, M.; Siahrostami, S.; Proserpio, D.M.; Doonan, C.; Falcaro, P.; Zheng, H.; et al. High-Throughput Electron Diffraction Reveals a Hidden Novel Metal–Organic Framework for Electrocatalysis. Angew. Chem. Int. Ed. 2021, 60, 11391–11397. [Google Scholar] [CrossRef]
  32. Geilhufe, R.M. Quantum Buckling in Metal–Organic Framework Materials. Nano Lett. 2021, 21, 10341–10345. [Google Scholar] [CrossRef] [PubMed]
  33. Hahn, N.; Öhrström, L.; Geilhufe, R.M. Collective Buckling in Metal-Organic Framework Materials. arXiv 2025. [Google Scholar] [CrossRef]
  34. Chen, N.-N.; Ni, J.-L.; Wang, J. A new two-dimensional CoII coordination polymer based on bis[4-(2-methyl-1H-imidazol-1-yl)phenyl] ether and biphenyl-4,4′-diyldicarboxylic acid: Synthesis, crystal structure and photocatalytic degradation activity. Acta Cryst. C 2018, 74, 1123–1127. [Google Scholar] [CrossRef] [PubMed]
  35. Lovell, T.C.; Colwell, C.E.; Zakharov, L.N.; Jasti, R. Symmetry breaking and the turn-on fluorescence of small, highly strained carbon nanohoops. Chem. Sci. 2019, 10, 3786–3790. [Google Scholar] [CrossRef]
  36. Kim, M.-B.; Yoon, T.-U.; Hong, D.-Y.; Kim, S.-Y.; Lee, S.-J.; Kim, S.-I.; Lee, S.-K.; Chang, J.-S.; Bae, Y.-S. High SF6/N2 selectivity in a hydrothermally stable zirconium-based metal–organic framework. Chem. Eng. J. 2015, 276, 315–321. [Google Scholar] [CrossRef]
  37. Grape, E.S.; Xu, H.; Cheung, O.; Calmels, M.; Zhao, J.; Dejoie, C.; Proserpio, D.M.; Zou, X.; Inge, A.K. Breathing Metal–Organic Framework Based on Flexible Inorganic Building Units. Cryst. Growth Des. 2020, 20, 320–329. [Google Scholar] [CrossRef]
  38. Amombo Noa, F.M.; Grape, E.S.; Åhlén, M.; Reinholdsson, W.E.; Göb, C.R.; Coudert, F.-X.; Cheung, O.; Inge, A.K.; Öhrström, L. Chiral Lanthanum Metal–Organic Framework with Gated CO2 Sorption and Concerted Framework Flexibility. J. Am. Chem. Soc. 2022, 144, 8725–8733. [Google Scholar] [CrossRef]
  39. Macrae, C.F.; Bruno, I.J.; Chisholm, J.A.; Edgington, P.R.; McCabe, P.; Pidcock, E.; Rodriguez-Monge, L.; Taylor, R.; van de Streek, J.; Wood, P.A. Mercury CSD 2.0—New features for the visualization and investigation of crystal structures. J. Appl. Crystallogr. 2008, 41, 466–470. [Google Scholar] [CrossRef]
  40. Dazem, C.L.F.; Ruser, N.; Grape, E.S.; Inge, A.K.; Proserpio, D.M.; Stock, N.; Öhrström, L.R. How metal ions link in Metal-Organic Frameworks: Dots, rods, sheets, and 3D Secondary Building Units exemplified by a Y(III) 4,4\′92-oxydibenzoate. Dalton Trans. 2025, 54, 5659–5663. [Google Scholar] [CrossRef]
  41. Amombo Noa, F.M.; Abrahamsson, M.; Ahlberg, E.; Cheung, O.; Göb, C.R.; McKenzie, C.J.; Öhrström, L. A unified topology approach to dot-, rod-, and sheet-MOFs. Chem 2021, 7, 2491–2512. [Google Scholar] [CrossRef]
  42. Healy, C.; Patil, K.M.; Wilson, B.H.; Hermanspahn, L.; Harvey-Reid, N.C.; Howard, B.I.; Kleinjan, C.; Kolien, J.; Payet, F.; Telfer, S.G.; et al. The thermal stability of metal-organic frameworks. Coord. Chem. Rev. 2020, 419, 20. [Google Scholar] [CrossRef]
  43. Öhrström, L. Designing, Describing and Disseminating New Materials by using the Network Topology Approach. Chem. Eur. J. 2016, 22, 13758–13763. [Google Scholar] [CrossRef] [PubMed]
  44. Chung, Y.G.; Haldoupis, E.; Bucior, B.J.; Haranczyk, M.; Lee, S.; Zhang, H.; Vogiatzis, K.D.; Milisavljevic, M.; Ling, S.; Camp, J.S.; et al. Advances, Updates, and Analytics for the Computation-Ready, Experimental Metal–Organic Framework Database: CoRE MOF 2019. J. Chem. Eng. Data 2019, 64, 5985–5998. [Google Scholar] [CrossRef]
  45. Alexandrov, E.V.; Blatov, V.A.; Kochetkov, A.V.; Proserpio, D.M. Underlying nets in three-periodic coordination polymers: Topology, taxonomy and prediction from a computer-aided analysis of the Cambridge Structural Database. Crystengcomm 2011, 13, 3947–3958. [Google Scholar] [CrossRef]
  46. Yaghi, O.M.; Kalmutzki, M.J.; Diercks, C.S. Introduction to Reticular Chemistry—Metal-Organic Frameworks and Covalent Organic Frameworks; Wiley-VCH: Weinheim, Germany, 2019. [Google Scholar]
  47. Shevchenko, A.P.; Alexandrov, E.V.; Golov, A.A.; Blatova, O.A.; Duyunova, A.S.; Blatov, V.A. Topology versus porosity: What can reticular chemistry tell about free space in metal-organic frameworks? Chem. Commun. 2020, 56, 9616–9619. [Google Scholar] [CrossRef]
  48. Schoedel, A.; Li, M.; Li, D.; O’Keeffe, M.; Yaghi, O.M. Structures of Metal-Organic Frameworks with Rod Secondary Building Units. Chem. Rev. 2016, 116, 12466–12535. [Google Scholar] [CrossRef]
  49. Xie, L.S.; Alexandrov, E.V.; Skorupskii, G.; Proserpio, D.M.; Dincă, M. Diverse π–π stacking motifs modulate electrical conductivity in tetrathiafulvalene-based metal–organic frameworks. Chem. Sci. 2019, 10, 8558–8565. [Google Scholar] [CrossRef]
  50. Tshuma, P.; Makhubela, B.C.E.; Öhrström, L.; Bourne, S.A.; Chatterjee, N.; Beas, I.N.; Darkwa, J.; Mehlana, G. Cyclometalation of lanthanum(III) based MOF for catalytic hydrogenation of carbon dioxide to formate. RSC Adv. 2020, 10, 3593–3605. [Google Scholar] [CrossRef]
  51. Cichocka, M.O.; Angstrom, J.; Wang, B.; Zou, X.; Smeets, S. High-throughput continuous rotation electron diffraction data acquisition via software automation. J. Appl. Crystallogr. 2018, 51, 1652–1661. [Google Scholar] [CrossRef]
  52. Kabsch, W. XDS. Acta Cryst. D. 2010, 66, 125–132. [Google Scholar] [CrossRef]
  53. Ge, M.; Yang, T.; Wang, Y.; Carraro, F.; Liang, W.; Doonan, C.; Falcaro, P.; Zheng, H.; Zou, X.; Huang, Z. On the completeness of three-dimensional electron diffraction data for structural analysis of metal–organic frameworks. Faraday Discuss. 2021, 231, 66–80. [Google Scholar] [CrossRef]
  54. Crysalis CCD; Oxford Diffraction Ltd.; Abingdon, UK, 2005; Available online: https://rigaku.com/products/crystallography/x-ray-diffraction/crysalispro.
  55. Crysalis RED; Oxford Diffraction Ltd.; Abingdon, UK, 2005; Available online: https://rigaku.com/products/crystallography/x-ray-diffraction/crysalispro.
  56. Sheldrick, G. Crystal structure refinement with SHELXL. Acta Cryst. C 2015, 71, 3–8. [Google Scholar] [CrossRef]
  57. Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
  58. Cheung, O.; Liu, Q.; Bacsik, Z.; Hedin, N. Silicoaluminophosphates as CO2 sorbents. Microporous Mesoporous Mater. 2012, 156, 90–96. [Google Scholar] [CrossRef]
Inorganics 14 00012 g001
Figure 1. The linker hexakis(4-carboxyphenyl) benzene, cpb6−, 1 previously used in CTH-18, and the expanded linker hexakis(4-(4-carboxyphenyl)phenyl)benzene, cbb6−, 2 used previously in pbz-MOF-1 by Trikalitis and co-workers [24] along with a few other MOFs. We postulate that we should retain the rhombic-shaped channels (pink) with the corner parts being identical to the rod-MOF CTH-18 (rod perpendicular to the linker), where we think the good primary sorption sites could be reproduced (blue and green balls), but with the expanded linker now significantly increasing the free volume (yellow) of the network, thus improving the overall capacity.
Figure 1. The linker hexakis(4-carboxyphenyl) benzene, cpb6−, 1 previously used in CTH-18, and the expanded linker hexakis(4-(4-carboxyphenyl)phenyl)benzene, cbb6−, 2 used previously in pbz-MOF-1 by Trikalitis and co-workers [24] along with a few other MOFs. We postulate that we should retain the rhombic-shaped channels (pink) with the corner parts being identical to the rod-MOF CTH-18 (rod perpendicular to the linker), where we think the good primary sorption sites could be reproduced (blue and green balls), but with the expanded linker now significantly increasing the free volume (yellow) of the network, thus improving the overall capacity.
Inorganics 14 00012 g001
Inorganics 14 00012 g002
Figure 2. The molecular part of the single crystal structures of [Mn4(cbb)(dmf)2(OAc)2] (X-ray, XRD) CTH-50 and [Gd3(cbb)(dmf)2(H2O)(OAc)3] CTH-51 (electron, ED). Note the deviation from a hexagonal shape of the cbb linker in CTH-51 caused by the buckling of the linker.
Figure 2. The molecular part of the single crystal structures of [Mn4(cbb)(dmf)2(OAc)2] (X-ray, XRD) CTH-50 and [Gd3(cbb)(dmf)2(H2O)(OAc)3] CTH-51 (electron, ED). Note the deviation from a hexagonal shape of the cbb linker in CTH-51 caused by the buckling of the linker.
Inorganics 14 00012 g002
Inorganics 14 00012 g003
Figure 3. One buckling angle in CTH-51, the buckling angle in the Co-MOF with the CSD code KINFUL [34], and an analysis of the Csp2-C6H4-C6H4-Csp2 angles in the CSD. Buckling angles as low as 120° (outside the graph) appear in cyclic poly para-phenylenes and related compounds.
Figure 3. One buckling angle in CTH-51, the buckling angle in the Co-MOF with the CSD code KINFUL [34], and an analysis of the Csp2-C6H4-C6H4-Csp2 angles in the CSD. Buckling angles as low as 120° (outside the graph) appear in cyclic poly para-phenylenes and related compounds.
Inorganics 14 00012 g003
Inorganics 14 00012 g004
Figure 4. Left—powder diffraction patterns of CTH-50, CTH-51, and the low-resolution CTH-51b together with the simulated patterns from the single crystal structure determinations. Right—thermogravimetric studies under air for CTH-50 and CTH-51.
Figure 4. Left—powder diffraction patterns of CTH-50, CTH-51, and the low-resolution CTH-51b together with the simulated patterns from the single crystal structure determinations. Right—thermogravimetric studies under air for CTH-50 and CTH-51.
Inorganics 14 00012 g004
Inorganics 14 00012 g005
Figure 5. N2 sorption isotherms recorded at 77 K for (a) CTH-50 and (b) CTH-51 (Figures S6 and S7 also show the pore size distribution derived from these data). The 20 °C N2, CH4, SF6, and CO2 adsorption isotherms of (c) CTH-50 (filled data points) together with the corresponding measurement for CTH-18 [19] (dashed lines and open data points), (d) CTH-51, (e) temperature-dependent SF6 adsorption isotherms on CTH-50, and (f) SF6 sorption kinetics of CTH-50 (solid line) and CTH-18 (dash line). Figure S7 shows the cyclic SF6 sorption data on CTH-50, with the adsorption step at 30 °C in pure SF6 and desorption at 70 °C under N2 flow, both at 50 cm3/min.
Figure 5. N2 sorption isotherms recorded at 77 K for (a) CTH-50 and (b) CTH-51 (Figures S6 and S7 also show the pore size distribution derived from these data). The 20 °C N2, CH4, SF6, and CO2 adsorption isotherms of (c) CTH-50 (filled data points) together with the corresponding measurement for CTH-18 [19] (dashed lines and open data points), (d) CTH-51, (e) temperature-dependent SF6 adsorption isotherms on CTH-50, and (f) SF6 sorption kinetics of CTH-50 (solid line) and CTH-18 (dash line). Figure S7 shows the cyclic SF6 sorption data on CTH-50, with the adsorption step at 30 °C in pure SF6 and desorption at 70 °C under N2 flow, both at 50 cm3/min.
Inorganics 14 00012 g005
Inorganics 14 00012 g006
Figure 6. Comparison of the solvent-accessible surfaces (yellow) in CTH-50 (967 m2/g) Mn in purple and CTH-51 (311 m2/g) Gd in greenish-blue (cyan), calculated by Mercury, with both values in agreement with experiment.
Figure 6. Comparison of the solvent-accessible surfaces (yellow) in CTH-50 (967 m2/g) Mn in purple and CTH-51 (311 m2/g) Gd in greenish-blue (cyan), calculated by Mercury, with both values in agreement with experiment.
Inorganics 14 00012 g006
Inorganics 14 00012 g007
Figure 7. Left—the face-connected trigonal prisms connected to hexagons, the och-net, in CTH-50 and CTH-51. Middle—the rods comprising face-sharing trigonal prisms. Right—the polyhedral rods in CTH-50 have two faces capped by methyl groups (schematically illustrated in black) in every pair of trigonal prisms, whereas in the much less porous CTH-51-Gd, three out of six sides are capped. Notably, in CTH-51-Gd, they protrude in all directions.
Figure 7. Left—the face-connected trigonal prisms connected to hexagons, the och-net, in CTH-50 and CTH-51. Middle—the rods comprising face-sharing trigonal prisms. Right—the polyhedral rods in CTH-50 have two faces capped by methyl groups (schematically illustrated in black) in every pair of trigonal prisms, whereas in the much less porous CTH-51-Gd, three out of six sides are capped. Notably, in CTH-51-Gd, they protrude in all directions.
Inorganics 14 00012 g007
Table 1. Estimated maximum SF6 uptake on CTH-18 and CTH-50 using the Langmuir and Toth equations. Note that the Toth equation fitting showed a comparably low R2 on CTH-18. This was likely due to the observed saturation of SF6 on CTH-18 at ambient pressures.
Table 1. Estimated maximum SF6 uptake on CTH-18 and CTH-50 using the Langmuir and Toth equations. Note that the Toth equation fitting showed a comparably low R2 on CTH-18. This was likely due to the observed saturation of SF6 on CTH-18 at ambient pressures.
Qmax (Langmuir)
mmol/g		R2Qmax (Toth)
mmol/g		R2
CTH-181.890.99679(1.69)(0.99885)
CTH-502.410.999682.67(0.99885)
Table 2. Network topology analysis.
Table 2. Network topology analysis.
MOF Mn+LinkSTR Type * STR PoE (p.s. #)
CTH-50Mn(II)cbb 25,6-cyavoch
CTH-51Gd(III)cbb 25,6-cyavoch
CTH-17La(III)cpb 15,6-cyavoch[38]
CTH-18Mn(II)cpb 14,4,6-c{52.63.7}{4.52.62.7}{4.54.66.74} #{36.44.65}{611.74} #[19]
* Connectivity of the nodes. # Instead of a three-letter RCSR code, we give the point symbol.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Björck, H.; Reinholdsson, W.; Cheung, O.; Zhou, G.; Huang, Z.; Amombo Noa, F.M.; Öhrström, L. Extending Hexagon-Based Metal–Organic Frameworks—Mn(II) and Gd(III) MOFs with Hexakis(4-(4-Carboxyphenyl)phenyl)benzene. Inorganics 2026, 14, 12. https://doi.org/10.3390/inorganics14010012

AMA Style

Björck H, Reinholdsson W, Cheung O, Zhou G, Huang Z, Amombo Noa FM, Öhrström L. Extending Hexagon-Based Metal–Organic Frameworks—Mn(II) and Gd(III) MOFs with Hexakis(4-(4-Carboxyphenyl)phenyl)benzene. Inorganics. 2026; 14(1):12. https://doi.org/10.3390/inorganics14010012

Chicago/Turabian Style

Björck, Henrik, William Reinholdsson, Ocean Cheung, Guojon Zhou, Zhehao Huang, Francoise M. Amombo Noa, and Lars Öhrström. 2026. "Extending Hexagon-Based Metal–Organic Frameworks—Mn(II) and Gd(III) MOFs with Hexakis(4-(4-Carboxyphenyl)phenyl)benzene" Inorganics 14, no. 1: 12. https://doi.org/10.3390/inorganics14010012

APA Style

Björck, H., Reinholdsson, W., Cheung, O., Zhou, G., Huang, Z., Amombo Noa, F. M., & Öhrström, L. (2026). Extending Hexagon-Based Metal–Organic Frameworks—Mn(II) and Gd(III) MOFs with Hexakis(4-(4-Carboxyphenyl)phenyl)benzene. Inorganics, 14(1), 12. https://doi.org/10.3390/inorganics14010012

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Article metric data becomes available approximately 24 hours after publication online.
Back to TopTop