Structural Water Accommodation in Co3O4: A Combined Neutron and Synchrotron Radiation Diffraction and DFT Study
Abstract
1. Introduction
2. Results and Discussion
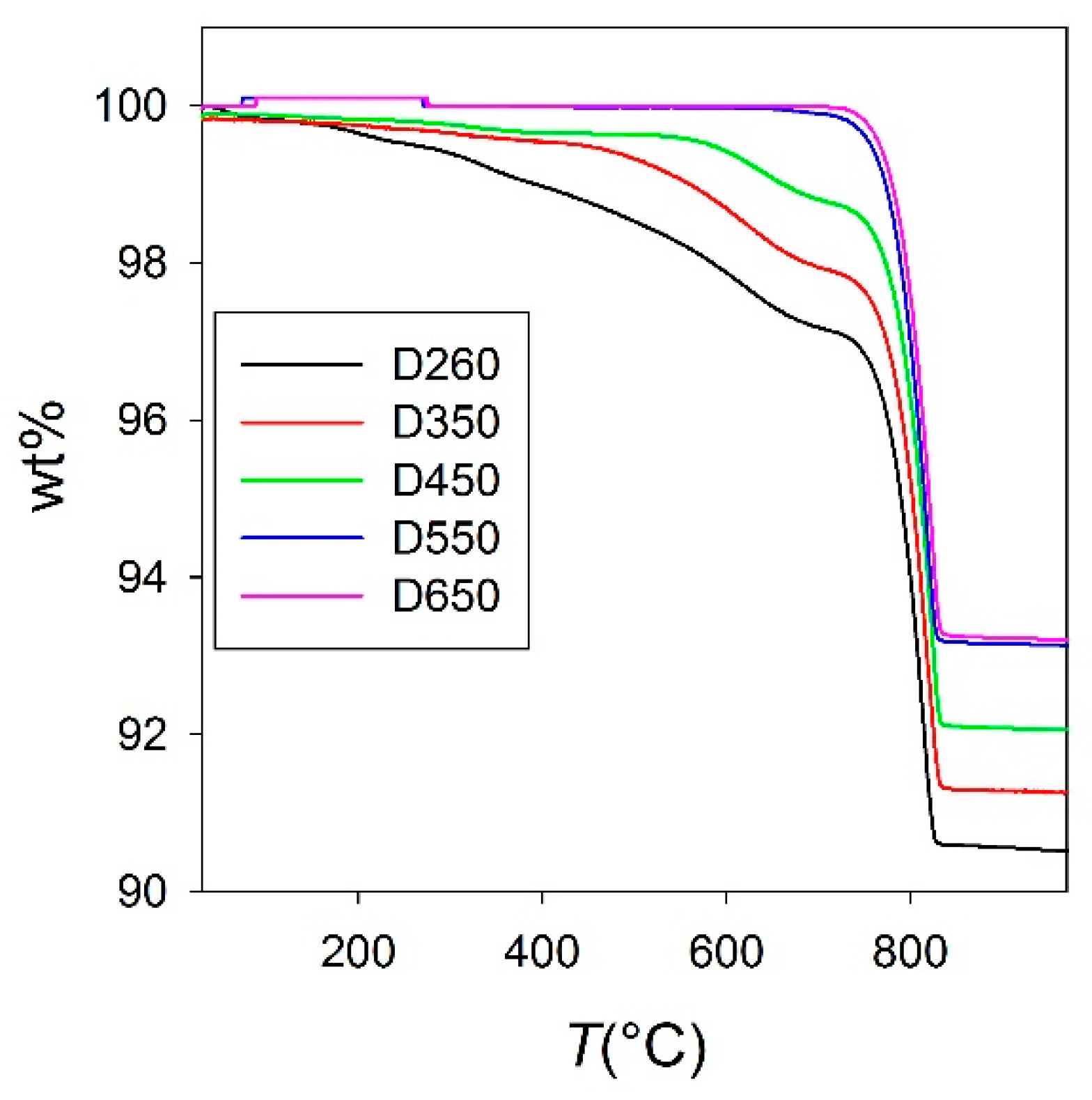
2.1. Thermogravimetric Measurements
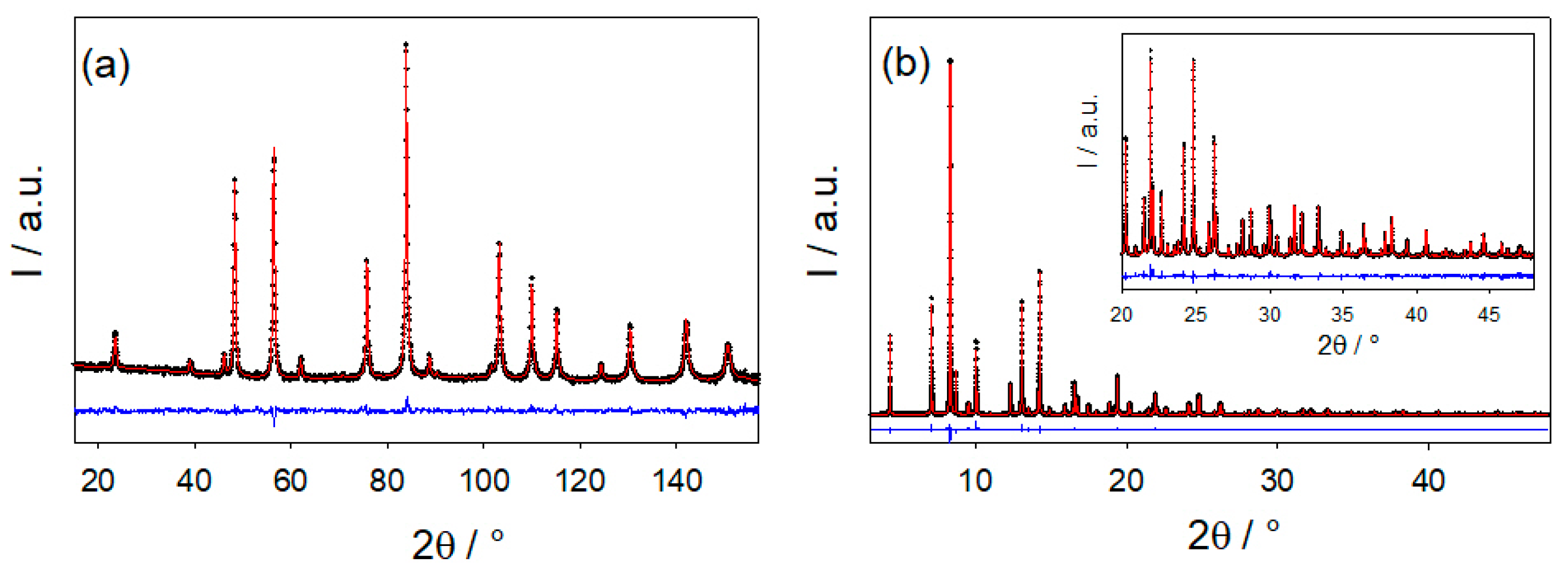
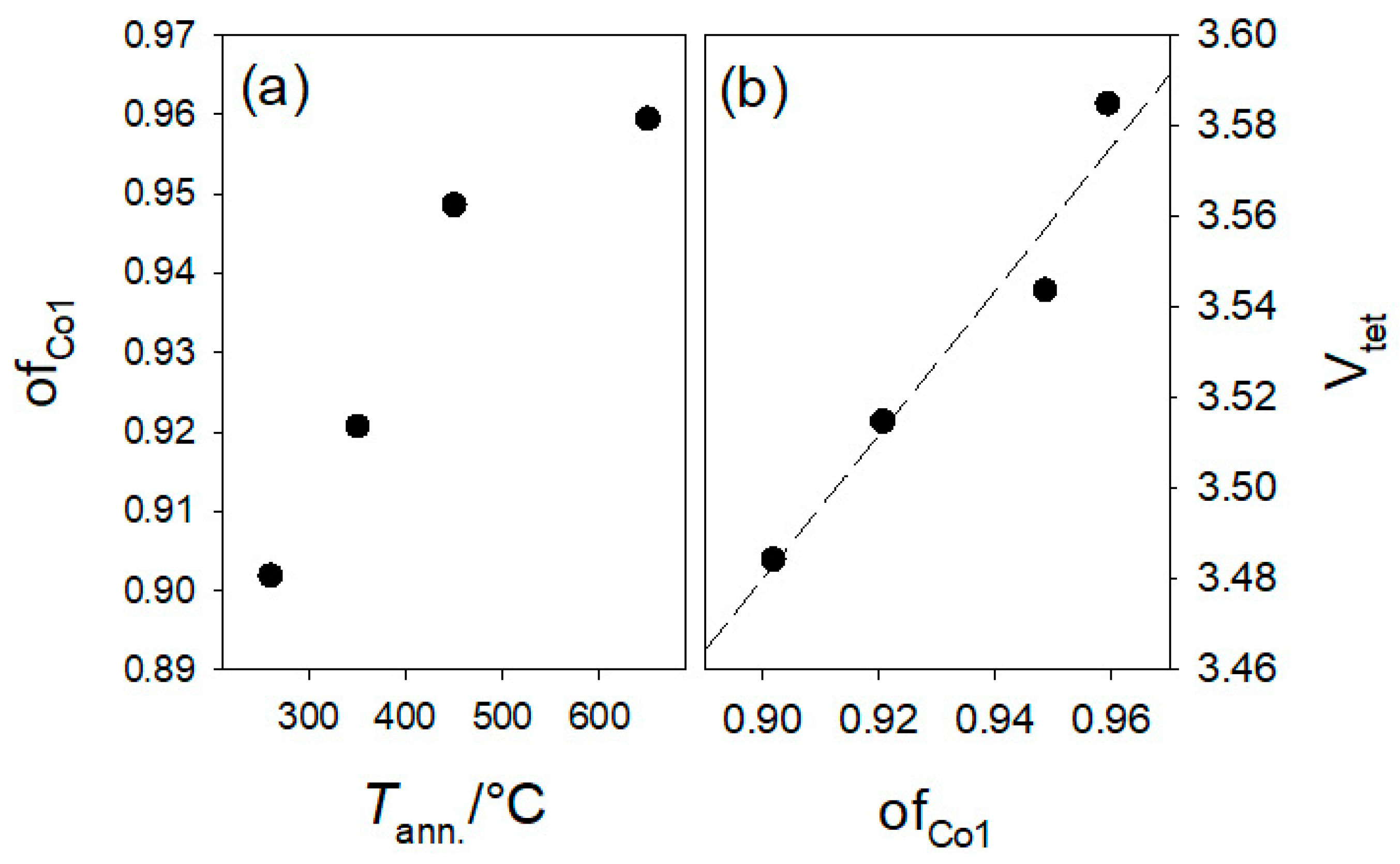
2.2. Average Structure
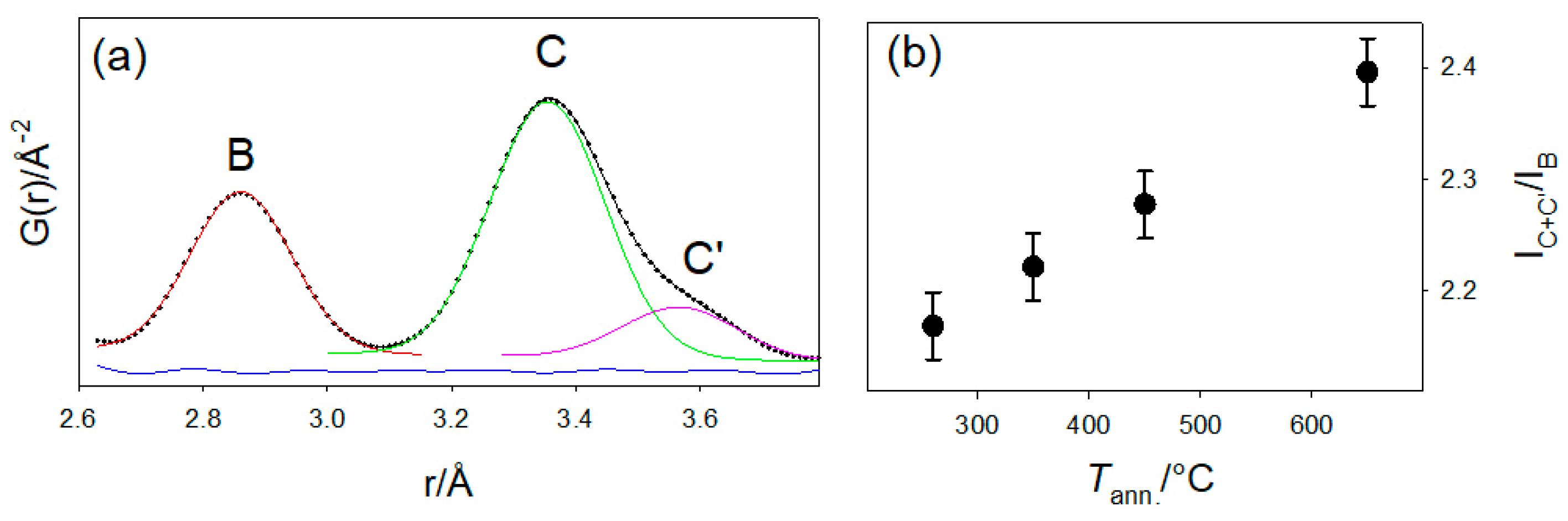
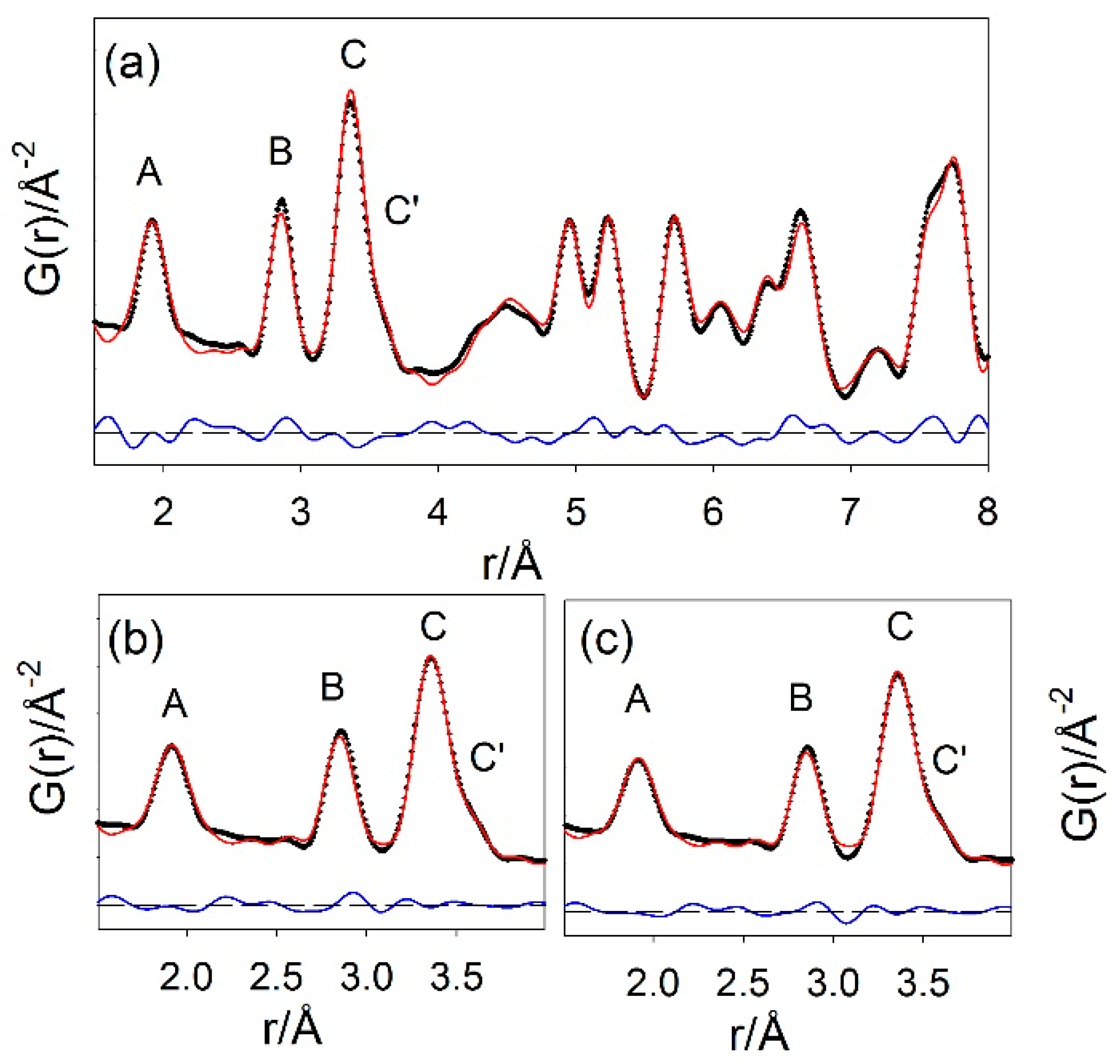
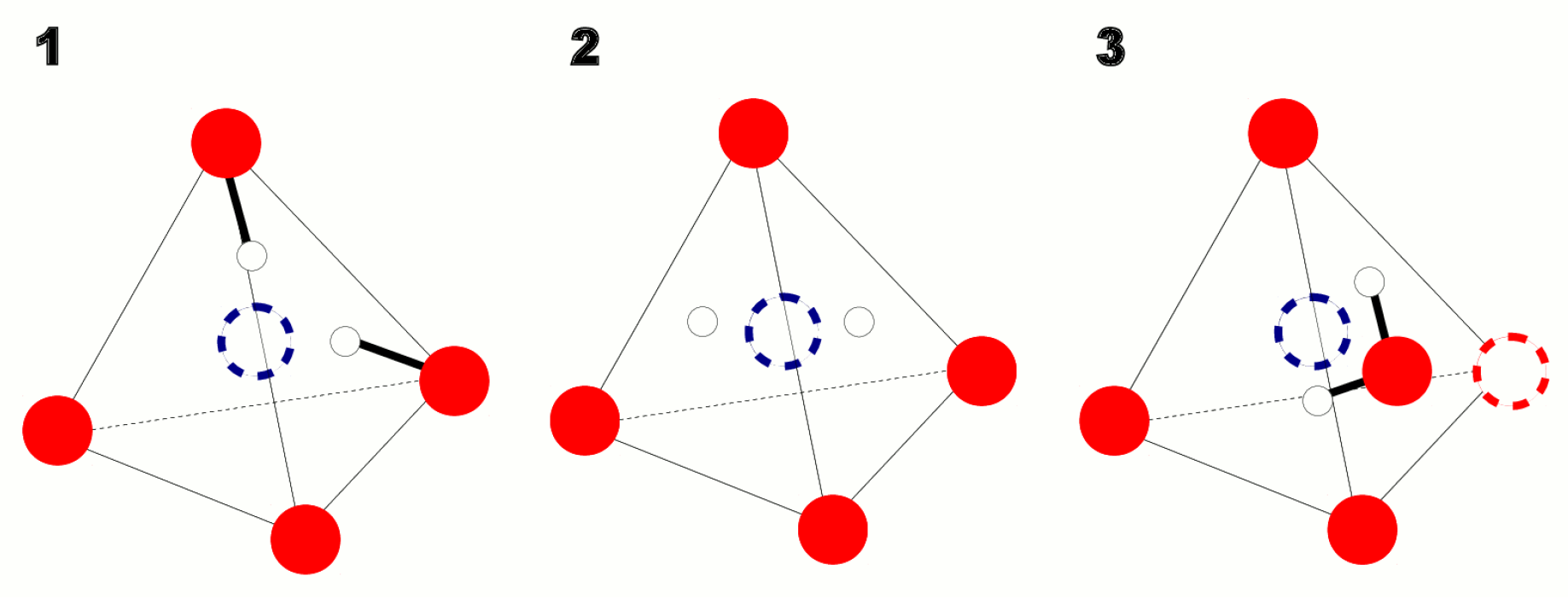
2.3. Local Structure
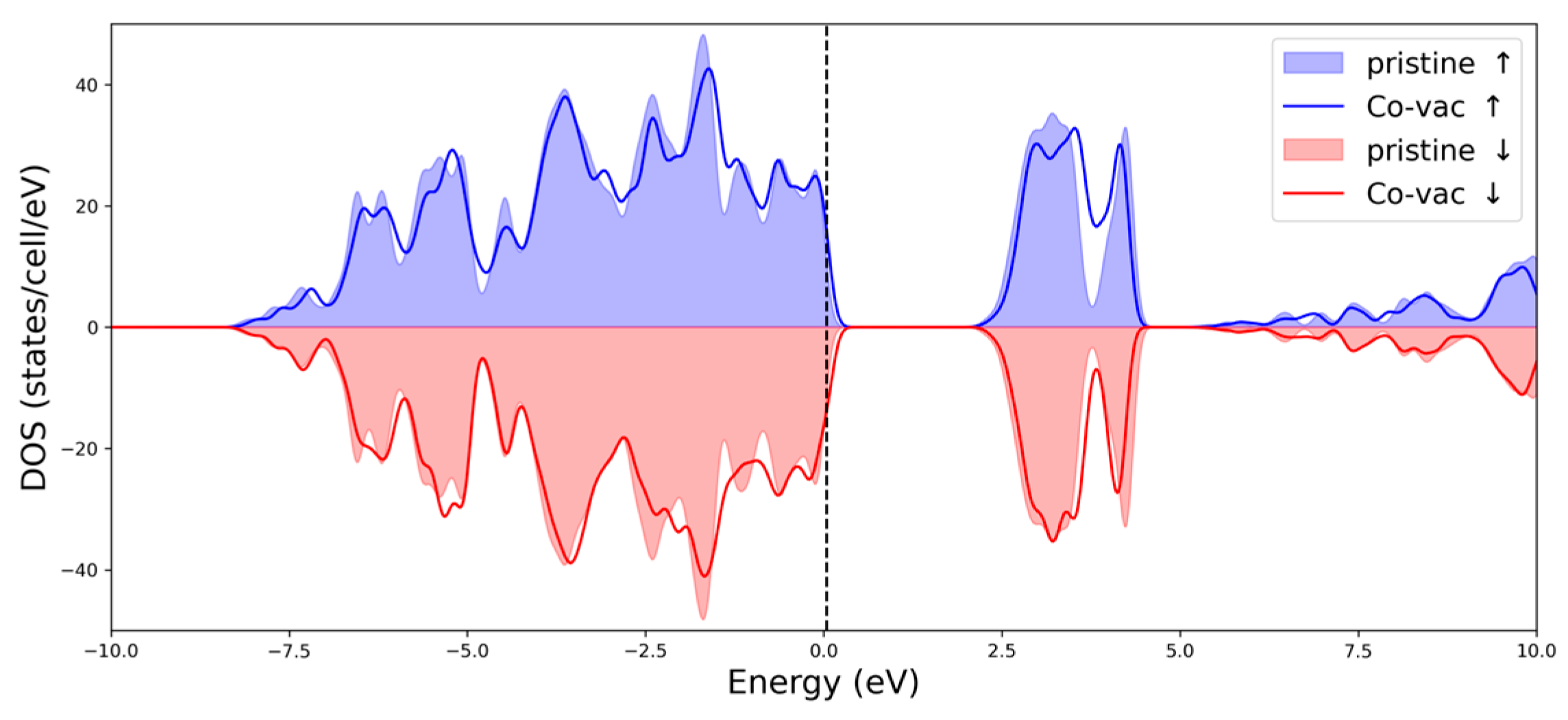
2.4. DFT Calculations
3. Materials and Methods
3.1. Synthesis
3.2. Sample Characterization
3.3. Density-Functional Theory Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bi, F.; Wei, J.; Zhou, Z.; Zhang, Y.; Gao, B.; Liu, N.; Xu, J.; Liu, B.; Huang, Y.; Zhang, X. Insight into the Synergistic Effect of Binary Nonmetallic Codoped Co3O4 Catalysts for Efficient Ethyl Acetate Degradation under Humid Conditions. JACS Au 2025, 5, 363–380. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Wang, X.; Li, C.; Chen, X.; Li, W.; Liu, Z.; Liang, C. Defect Engineering over Co3O4 Catalyst for Surface Lattice Oxygen Activation and Boosted Propane Total Oxidation. J. Catal. 2022, 413, 150–162. [Google Scholar] [CrossRef]
- Bao, L.; Zhu, S.; Chen, Y.; Wang, Y.; Meng, W.; Xu, S.; Lin, Z.; Li, X.; Sun, M.; Guo, L. Anionic Defects Engineering of Co3O4 Catalyst for Toluene Oxidation. Fuel 2022, 314, 122774. [Google Scholar] [CrossRef]
- Yang, J.; Li, W.; Chen, J.; Cheng, N.; Wang, T.; Wang, H.; Xu, D.; Zhang, H.; Wang, J.; Bai, L.; et al. Yolk-Shell Structured Co3O4 Catalyst Modified Ceramic Membrane Synergistically Improved Wastewater Purification and Membrane Fouling Mitigation. Chem. Eng. J. 2024, 501, 157690. [Google Scholar] [CrossRef]
- Xiong, L.; Zhang, L.; Xie, S.; Lian, D.; Hou, X.; Zhang, M.; Chen, L.; Chang, C.-R. Modulating Co–O Covalency in MOF-Derived Co3O4 to Activate Surface Lattice Oxygen for Enhanced Catalytic Ethane Combustion. Chem. Eng. Sci. 2025, 318, 122184. [Google Scholar] [CrossRef]
- Cong, Y.; Wang, Y.; Luo, J.; Fan, L.; Li, X.; Wang, C.; Shen, X.; Xu, Z.; Lv, S.-W. Light-Mediated Enhancement Effect Derived from Carbon Nitrogen Polymer to Regulate Peroxymonosulfate Activation over Co3O4 for Effective Degradation of Fluorinated Pharmaceuticals. Sep. Purif. Technol. 2025, 377, 134254. [Google Scholar] [CrossRef]
- Yilmaz Aydin, D. Thermal and Exergetic Performance Analyses of a Heat Pipe Heat Exchanger Using CMC/Co3O4-Based Non-Newtonian Nanofluids. Appl. Sci. 2025, 15, 7831. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.; Xu, Z.; Qu, C.; Chen, Z.; Hong, D.; Wang, C. Citric Acid Modification of Co3O4/CeO2 Catalysts for Enhanced Oxidation of Low Concentration Methane. Appl. Surf. Sci. 2025, 711, 164061. [Google Scholar] [CrossRef]
- Li, X.; Su, X.; Pei, Y.; Liu, J.; Zheng, X.; Tang, K.; Guan, G.; Hao, X. Generation of Edge Dislocation Defects in Co3O4 Catalysts: An Efficient Tactic to Improve Catalytic Activity for Oxygen Evolution. J. Mater. Chem. A 2019, 7, 10745–10750. [Google Scholar] [CrossRef]
- Zhang, R.; Pan, L.; Guo, B.; Huang, Z.-F.; Chen, Z.; Wang, L.; Zhang, X.; Guo, Z.; Xu, W.; Loh, K.P.; et al. Tracking the Role of Defect Types in Co3O4 Structural Evolution and Active Motifs during Oxygen Evolution Reaction. J. Am. Chem. Soc. 2023, 145, 2271–2281. [Google Scholar] [CrossRef]
- Xu, X.; Jeon, S.; Yu, T. Synthesis of Ru/Co3O4 Nanosheets as a Multifunctional Electrocatalyst for Boosting Urea-Assisted Water Electrolysis. Int. J. Hydrogen Energy 2025, 157, 150472. [Google Scholar] [CrossRef]
- Xie, F.; Kang, X.; Wu, Z.; Zhu, H.; Gu, L.; Duan, X.; Yang, J. Built–in Electric Field Boosted Tandem Catalysis for Rapid Electrochemical Nitrate Reduction to Nitrogen. ACS Nano 2025, 19, 26217–26228. [Google Scholar] [CrossRef]
- Singh, J.; Singh, G.P.; Jain, R.K.; Singh, B.; Singh, K.J.; Singh, R.C. Effect of Calcination Temperature on Structural, Optical and Antibacterial Properties of Ball Mill Synthesized Co3O4 Nanomaterials. J. Mater. Sci. Mater. Electron. 2022, 33, 3250–3266. [Google Scholar] [CrossRef]
- Muradov, M.B.; Mammadyarova, S.J.; Eyvazova, G.M.; Balayeva, O.O.; Hasanova, I.; Aliyeva, G.; Melikova, S.Z.; Abdullayev, M.I. The Effect of Cu Doping on Structural, Optical Properties and Photocatalytic Activity of Co3O4 Nanoparticles Synthesized by Sonochemical Method. Opt. Mater. 2023, 142, 114001. [Google Scholar] [CrossRef]
- Pandey, V.; Adiba, A.; Munjal, S.; Ahmad, T. Optical Bandgap Tuning of Cubic Spinel Co3O4 by Annealing Temperature. Materialia 2022, 26, 101554. [Google Scholar] [CrossRef]
- Ravina; Dalela, S.; Kumar, S.; Choudhary, B.L.; Alvi, P.A. Structural, Optical and Raman Studies of Co3O4 Nano-Particles. Mater. Today Proc. 2023, 79, 165–168. [Google Scholar] [CrossRef]
- Ardeshirfard, H.; Elhamifar, D. An Efficient Method for the Preparation of Magnetic Co3O4 Nanoparticles and the Study of Their Catalytic Application. Front. Catal. 2023, 3, 1194977. [Google Scholar] [CrossRef]
- Jogdand, S.S.; Joshi, S.S. Effect of Polymer Combustion Synthesis on Thermal, Spectroscopic, Structural, and Magnetic Properties of Co3O4 Nanoparticles. Polyhedron 2025, 269, 117419. [Google Scholar] [CrossRef]
- Kumar, G.; Sun, H.-W.; Huang, M.H. Shape-Tunable Co3O4 Nanocrystals Possessing Surface-Dependent Optical and Magnetic Properties. ACS Appl. Nano Mater. 2024, 7, 2155–2163. [Google Scholar] [CrossRef]
- Chauhan, A.; Kumar, R.; Devi, S.; Sonu; Raizada, P.; Singh, P.; Ponnusamy, V.K.; Sudhaik, A.; Mishra, A.K.; Selvasembian, R. Recent Advances on Co3O4-Based Nanostructure Photocatalysis: Structure, Synthesis, Modification Strategies, and Applications. Surf. Interfaces 2024, 54, 105152. [Google Scholar] [CrossRef]
- Dang, V.D.; Hong Nhung, N.T.; Rabani, I.; Tran, N.T.; Thuy, B.T.P.; Truong, H.B. Advances in Co3O4 Nanomaterial-Based Photocatalysts for Water Purification: Mechanisms, Green Synthesis, Activation of Oxidants, Waste-Derived Sources, and Computational Insights. RSC Adv. 2025, 15, 19088–19103. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Gao, J.; Huang, W.; Dai, K.; Zheng, G.; Liu, C.; Shen, C.; Yan, X.; Guo, J.; Guo, Z. Electrically Conductive Strain Sensing Polyurethane Nanocomposites with Synergistic Carbon Nanotubes and Graphene Bifillers. Nanoscale 2016, 8, 12977–12989. [Google Scholar] [CrossRef] [PubMed]
- Sabbar, G.; Mohammed, W.M.; Al-Nafiey, A. Temperature-Dependent Gas Sensing Properties of Cobalt Oxide, Reduced Graphene Oxide, and Composite Thin Films Synthesized by Pulsed Laser Ablation. Arab. J. Sci. Eng. 2025, 1–15. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, C.; Cao, L.; Li, H.; Li, H.; Yang, Z.; Li, J. Versatile 1D-Structured Co3O4–Co/NC@N–Carbon Nanotubes for High-Performance Lithium Storage. Chem. Commun. 2025, 61, 1–10. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, X.; Li, H.; Qian, B.; Zhang, Y.; Wu, Y. Synthesis of Co3O4 Nanospheres for Enhanced Photo-Assisted Supercapacitor. Chem. Eng. J. 2022, 431, 133981. [Google Scholar] [CrossRef]
- Roniboss, A.; Sindhu, S.; Kennedy, L.J.; Arockiasamy, S. Synthesis and Thermal Properties of Two Novel Cobalt (II) Schiff’s Base Complexes as Precursors for Coating Cobalt Oxide (Co3O4) Thin Film by a Plasma Enhanced Metallo-Organic Chemical Vapour Deposition. J. Mol. Struct. 2023, 1272, 134189. [Google Scholar] [CrossRef]
- Bayati-Komitaki, N.; Ganduh, S.H.; Alzaidy, A.H.; Salavati-Niasari, M. A Comprehensive Review of Co3O4Nanostructures in Cancer: Synthesis, Characterization, Reactive Oxygen Species Mechanisms, and Therapeutic Applications. Biomed. Pharmacother. 2024, 180, 117457. [Google Scholar] [CrossRef]
- Trasatti, S. Electrochemistry of Novel Materials; Lipkowski, J., Ross Phil, M.S., Eds.; VCH: Weinheim, Germany, 1994. [Google Scholar]
- Švegl, F.; Orel, B.; Hutchins, M.G.; Kalcher, K. Structural and Spectroelectrochemical Investigations of Sol-Gel Derived Electrochromic Spinel Co3O4 Films. J. Electrochem. Soc. 1996, 143, 1532–1539. [Google Scholar] [CrossRef]
- de Boer, J.H.; Verwey, E.J.W. Semi-Conductors with Partially and with Completely Filled 3d—Lattice Bands. Proc. Phys. Soc. 1937, 49, 59–71. [Google Scholar] [CrossRef]
- Tronel, F.; Guerlou-Demourgues, L.; Ménétrier, M.; Croguennec, L.; Goubault, L.; Bernard, P.; Delmas, C. New Spinel Cobalt Oxides, Potential Conductive Additives for the Positive Electrode of Ni−MH Batteries. Chem. Mater. 2006, 18, 5840–5851. [Google Scholar] [CrossRef]
- Ngamou, P.H.T.; Bahlawane, N. Influence of the Arrangement of the Octahedrally Coordinated Trivalent Cobalt Cations on the Electrical Charge Transport and Surface Reactivity. Chem. Mater. 2010, 22, 4158–4165. [Google Scholar] [CrossRef]
- Antonyraj, C.A.; Srivastava, D.N.; Mane, G.P.; Sankaranarayanan, S.; Vinu, A.; Srinivasan, K. Co3O4 Microcubes with Exceptionally High Conductivity Using a CoAl Layered Double Hydroxide Precursor via Soft Chemically Synthesized Cobalt Carbonate. J. Mater. Chem. A 2014, 2, 6301–6304. [Google Scholar] [CrossRef]
- Belova, I.D.; Roginskaya, Y.E.; Shalaginov, V.V.; Shub, D.M. Effect of Nonstoichiometry on Electrical Properties of Cobalt Oxide (Co3-XO4) Films. Zhurnal Fiz. Khimii 1980, 54, 1789–1793. [Google Scholar]
- Wang, R.-P.; Huang, M.-J.; Hariki, A.; Okamoto, J.; Huang, H.-Y.; Singh, A.; Huang, D.-J.; Nagel, P.; Schuppler, S.; Haarman, T.; et al. Analyzing the Local Electronic Structure of Co3O4 Using 2p3d Resonant Inelastic X-Ray Scattering. J. Phys. Chem. C 2022, 126, 8752–8759. [Google Scholar] [CrossRef] [PubMed]
- Belova, I.D.; Roginskaya, Y.E.; Shifrina, R.R.; Gagarin, S.G.; Plekhanov, Y.V.; Venevtsev, Y.N. Co (III) Ions High-Spin Configuration in Nonstoichiometric Co3O4 Films. Solid State Comm. 1983, 47, 577–584. [Google Scholar] [CrossRef]
- Belova, I.D.; Shalaginov, V.V.; Galyamov, B.S.; Roginskaya, Y.E.; Shub, D.M. Study of the Defect Structure of Nonstoichiometric Cobalt Oxide (Co3O4) Films. Zhurnal Neorg. Khimii 1978, 23, 286–290. [Google Scholar]
- Garavaglia, R.; Mari, C.M.; Trasatti, S. Physicochemical Characterization of Co3O4 Prepared by Thermal Decomposition II: Response to Solution PH. Surf. Technol. 1984, 23, 41–47. [Google Scholar] [CrossRef]
- Surendranath, Y.; Nocera, D.G. Oxygen Evolution Reaction Chemistry of Oxide-Based Electrodes. Prog. Inorg. Chem. 2011, 57, 505–560. [Google Scholar]
- Vittal, R.; Ho, K.-C. Cobalt Oxide Electrodes-Problem and a Solution Through a Novel Approach Using Cetyltrimethylammonium Bromide (CTAB). Catal. Rev. 2015, 57, 145–191. [Google Scholar] [CrossRef]
- Ahmad, W.; Noor, T.; Zeeshan, M. Effect of Synthesis Route on Catalytic Properties and Performance of Co3O4TiO2 for Carbon Monoxide and Hydrocarbon Oxidation under Real Engine Operating Conditions. Catal. Commun. 2017, 89, 19–24. [Google Scholar] [CrossRef]
- Rios, E.; Zelada, G.; Marco, J.F.; Gautier, J.L. Characterization of Bulk and Surface Composition of Polycrystalline Co3O4 Synthesized at 400 °C for Electrocatalysis. Bol. Soc. Chil. Quim. 1998, 43, 447–459. [Google Scholar]
- Longhi, M.; Formaro, L. Water-Dependent Structural and Chemical Relaxation of Bulk Co3O4 from Cobalt Nitrate Decomposition. J. Mater. Chem. 2001, 11, 1228–1232. [Google Scholar] [CrossRef]
- Jahandideh-Roudsari, S.R.; Shourian, M.; Homaei, A. Developing Choline Oxidase Immobilization on Co3O4/RGO Nanohybrid Surface as a High-Performance Biosensor for Diazinon Detection. Bioprocess Biosyst. Eng. 2025, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Coduri, M.; Scavini, M.; Allieta, M.; Brunelli, M.; Ferrero, C. Local Disorder in Yttrium Doped Ceria (Ce1−xY xO2−x/2) Probed by Joint X-Ray and Neutron Powder Diffraction. J. Phys. Conf. Ser. 2012, 340, 012056. [Google Scholar] [CrossRef]
- Sickafus, K.E.; Wills, J.M.; Grimes, N.W. Structure of Spinel. J. Am. Ceram. Soc. 1999, 82, 3279–3292. [Google Scholar] [CrossRef]
- Will, G.; Masciocchi, N.; Parrish, W.; Hart, M. Refinement of Simple Crystal Structures from Synchrotron Radiation Powder Diffraction Data. J. Appl. Crystallogr. 1987, 20, 394–401. [Google Scholar] [CrossRef]
- Casas-Cabanas, M.; Binotto, G.; Larcher, D.; Lecup, A.; Giordani, V.; Tarascon, J.-M. Defect Chemistry and Catalytic Activity of Nanosized Co3O4. Chem. Mater. 2009, 21, 1939–1947. [Google Scholar] [CrossRef]
- Angelov, S.; Zhecheva, E.; Stoyanova, R.; Atanasov, M. Bulk Defects in Co3O4, Pure and Slightly Doped with Lithium, Revealed by EPR of the Tetrahedral Co2+ Ions. J. Phys. Chem. Solids 1990, 51, 1157–1161. [Google Scholar] [CrossRef]
- Kroger, F.A.; Stieltjes, F.H.; Vink, H.J. Thermodynamics and Formulation of Reactions Involving Imperfections in Solids. Philips Res. Rep. 1959, 14, 557–601. [Google Scholar]
- Kaczmarska, A.; Grzesik, Z.; Mrowec, S. On the Defect Structure and Transport Properties of Co3O4 Spinel Oxide. High Temp. Mater. Process. 2012, 31, 371–379. [Google Scholar] [CrossRef]
- Ammundsen, B.; Jones, D.J.; Rozière, J.; Berg, H.; Tellgren, R.; Thomas, J.O. Ion Exchange in Manganese Dioxide Spinel: Proton, Deuteron, and Lithium Sites Determined from Neutron Powder Diffraction Data. Chem. Mater. 1998, 10, 1680–1687. [Google Scholar] [CrossRef]
- Egami, T.; Billinge, S.J.L. Underneath the Bragg Peaks. Mater. Today 2003, 6, 57. [Google Scholar] [CrossRef]
- Roth, W.L. The Magnetic Structure of Co3O4. J. Phys. Chem. Solids 1964, 25, 1–10. [Google Scholar] [CrossRef]
- Chen, J.; Wu, X.; Selloni, A. Electronic Structure and Bonding Properties of Cobalt Oxide in the Spinel Structure. Phys. Rev. B—Condens. Matter Mater. Phys. 2011, 83, 245204. [Google Scholar] [CrossRef]
- Longhi, M.; Formaro, L. An Old Workhorse of Oxide Investigations: New Features of Co3O4. J. Electroanal. Chem. 1999, 464, 149–157. [Google Scholar] [CrossRef]
- Fitch, A.; Dejoie, C.; Covacci, E.; Confalonieri, G.; Grendal, O.; Claustre, L.; Guillou, P.; Kieffer, J.; de Nolf, W.; Petitdemange, S.; et al. ID22—The High-Resolution Powder-Diffraction Beamline at ESRF. J. Synchrotron Radiat. 2023, 30, 1003–1012. [Google Scholar] [CrossRef]
- Dejoie, C.; Coduri, M.; Petitdemange, S.; Giacobbe, C.; Covacci, E.; Grimaldi, O.; Autran, P.-O.; Mogodi, M.W.; Šišak Jung, D.; Fitch, A.N. Combining a Nine-Crystal Multi-Analyser Stage with a Two-Dimensional Detector for High-Resolution Powder X-Ray Diffraction. J. Appl. Crystallogr. 2018, 51, 1721–1733. [Google Scholar] [CrossRef]
- Kieffer, J.; Wright, J.P. PyFAI: A Python Library for High Performance Azimuthal Integration on GPU. Powder Diffr. 2013, 28, S339–S350. [Google Scholar] [CrossRef]
- Juhás, P.; Davis, T.; Farrow, C.L.; Billinge, S.J.L. PDFgetX3: A Rapid and Highly Automatable Program for Processing Powder Diffraction Data into Total Scattering Pair Distribution Functions. J. Appl. Crystallogr. 2013, 46, 560–566. [Google Scholar] [CrossRef]
- Farrow, C.L.; Juhas, P.; Liu, J.W.; Bryndin, D.; Božin, E.S.; Bloch, J.; Proffen, T.; Billinge, S.J.L. PDFfit2 and PDFgui: Computer Programs for Studying Nanostructure in Crystals. J. Phys. Condens. Matter 2007, 19, 335219. [Google Scholar] [CrossRef]
- Coduri, M.; Brunelli, M.; Scavini, M.; Allieta, M.; Masala, P.; Capogna, L.; Fischer, H.E.; Ferrero, C. Rare Earth Doped Ceria: A Combined X-Ray and Neutron Pair Distribution Function Study. Z. Krist. 2012, 227, 272–279. [Google Scholar] [CrossRef]
- Larson, A.C.; von Dreele, R.B. General Structural Analysis System (GSAS). LAUR 86-748; Los Alamos National Laboratory: Los Alamos, NM, USA, 2004. [Google Scholar]
- Toby, B.H. EXPGUI, a Graphical User Interface for GSAS. J. Appl. Crystallogr. 2001, 34, 210–213. [Google Scholar] [CrossRef]
- Qiu, X.; Thompson, J.W.; Billinge, S.J.L. PDFgetX2: A GUI-Driven Program to Obtain the Pair Distribution Function from X-Ray Powder Diffraction Data. J. Appl. Crystallogr. 2004, 37, 678. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Garrity, K.F.; Bennett, J.W.; Rabe, K.M.; Vanderbilt, D. Pseudopotentials for High-Throughput DFT Calculations. Comput. Mater. Sci. 2014, 81, 446–452. [Google Scholar] [CrossRef]




| Sample | D260 | D350 | D450 | D550 | D650 |
|---|---|---|---|---|---|
| Space Group | |||||
| a/Å | 8.0763(2) | 8.0787(1) | 8.0792(2) | 8.0798(3) | 8.0794(3) |
| xO | 0.26352(4) | 0.26356(3) | 0.26358(4) | 0.26364(3) | 0.26364(3) |
| UCo/Å2 | 0.0017(5) | 0.0046(5) | 0.0051(5) | 0.0035(4) | 0.0040(4) |
| UO/Å2 | 0.0021(3) | 0.0046(5) | 0.0049(3) | 0.0040(3) | 0.0046(2) |
| ofCo1 | 0.912(9) | 0.937(8) | 0.957(8) | 0.961(7) | 0.980(6) |
| R(F2) | 0.0213 | 0.0198 | 0.0195 | 0.0218 | 0.0149 |
| Rp | 0.0285 | 0.0306 | 0.0303 | 0.0302 | 0.0292 |
| Sample | H260 | H350 | H450 | H650 |
|---|---|---|---|---|
| Space Group | ||||
| a/Å | 8.0747 | 8.0753 | 8.0761 | 8.0764 |
| xO | 0.3854 | 0.3858 | 0.3861 | 0.3867 |
| UCo/Å2 | 0.0033 | 0.0032 | 0.0032 | 0.0032 |
| UO/Å2 | 0.0151 | 0.0149 | 0.0148 | 0.0156 |
| ofCo1 | 0.90 | 0.92 | 0.95 | 0.96 |
| Rp | 0.095 | 0.090 | 0.094 | 0.097 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Longhi, M.; Coduri, M.; Ghigna, P.; Ceresoli, D.; Scavini, M. Structural Water Accommodation in Co3O4: A Combined Neutron and Synchrotron Radiation Diffraction and DFT Study. Inorganics 2025, 13, 288. https://doi.org/10.3390/inorganics13090288
Longhi M, Coduri M, Ghigna P, Ceresoli D, Scavini M. Structural Water Accommodation in Co3O4: A Combined Neutron and Synchrotron Radiation Diffraction and DFT Study. Inorganics. 2025; 13(9):288. https://doi.org/10.3390/inorganics13090288
Chicago/Turabian StyleLonghi, Mariangela, Mauro Coduri, Paolo Ghigna, Davide Ceresoli, and Marco Scavini. 2025. "Structural Water Accommodation in Co3O4: A Combined Neutron and Synchrotron Radiation Diffraction and DFT Study" Inorganics 13, no. 9: 288. https://doi.org/10.3390/inorganics13090288
APA StyleLonghi, M., Coduri, M., Ghigna, P., Ceresoli, D., & Scavini, M. (2025). Structural Water Accommodation in Co3O4: A Combined Neutron and Synchrotron Radiation Diffraction and DFT Study. Inorganics, 13(9), 288. https://doi.org/10.3390/inorganics13090288










