Glass Transition Temperature and Mean Bond Energy of Chalcogenide Glasses in the As₂Se₃-GeTe-CdTe System

Abstract

Chalcogenide samples from the As₂Se₃-GeTe-CdTe system were synthesized by the melt-quench technique. The surface topography of some of the samples was performed with the help of scanning electron microscopy. Various physical parameters of the chalcogenide glasses were calculated: the degree of cross-linking atom, the average heteropolar bond energy of the glasses, the content of chalcogen in the glass, the mean coordination number, and the average energy of the chemical bonds between the atoms of the metals in the glass. With their help, the components of the overall bond energy were calculated: the mean bond energy of the average cross-linking per atom and the average bond energy per atom of the “remaining matrix”. A linear dependence has been established between the glass transition temperature and the overall mean bond energy and between the glass transition temperature and the mean coordination number. The correlation between microhardness and glass transition temperature of chalcogenide glasses was investigated. The dependance between the composition and physical parameters of the As₂Se₃-GeTe-CdTe glasses was established and discussed.

1. Introduction

The chalcogenide glasses (ChG), unlike the conventional silicate glasses, are characterized by transparency in the IR region of the spectrum, a high refraction coefficient with a non-linear dispersion, and a low glass transition temperature (Tg), close to that of crystallization. A number of physical effects occur in the chalcogenide glasses, such as thermo- and photo-electromotive tension, photo-conductivity and photoluminescence, the Hall effect, etc. In the chalcogenide glasses run convertible photo-structural changes, which are at the base of the photodarkening effect [1,2]. Their comparatively easy production, together with their high chemical and radiation resistance, makes them preferred materials for the manufacture of threshold switches, optical windows in different sectors of the spectrum, active layers of memristive devices, etc. [3]. The ChG are also used as a promising material class for solar absorber material [4], biosensors [5], and a technique for the analysis of conformational or configurational polymorphism of drug molecules [6].

Numerous glass-forming systems are obtained as a result of combinations between different glass formers and the addition of metal chalcogenides.

The addition of crystalline chalcogenides to a typical chalcogenide glass former modifies the glass structure. Even small additions of metal chalcogenides can significantly reduce the viscosity of the melt, which facilitates the crystallization processes. When modifiers are introduced, the tendency to glass formation increases due to the expansion of the possibility of the occurrence of different structural configurations.

Muller proposes that structural units should be considered not as individual atoms, but as groups of atoms together with all possible heterobonds. In covalently constructed chalcogenide glasses, the maximum number of neighbors of a given atom is equal to the valence bonds that it can form. In the glass, the nearest neighbors around a given atom are arranged in almost the same way as in the corresponding crystal, but as one moves away from this atom, the arrangement is disturbed. He suggests that the equal probability of forming structurally equivalent configurations is the reason for the appearance of solids that do not have long-range order. The variety of structurally equivalent configurations is determined by the possibility of changing the valence angles between the bonds of the bridging atoms and of free rotation around them. The angles and lengths of the bonds in the structural units do not change [7].

In glassy chalcogenides, which are made up of several different types of structural units and fragments, the number of possibilities for bonding between them increases. Even if the structural units are of the same type, they can bond both with their vertices and with their edges and sides. The number of ways of bonding increases faster when linear fragments or other types of structural units are included. They occupy different places in the structure of the primary matrix of the glass former by being embedded in the linear chains, closing them, being included in cyclic and spherical structures, breaking chains, etc.

In this sense, the development of new chalcogenide glasses on an As₂Se₃ base with metal chalcogenide, as well as their investigation with the purpose of developing new materials designed, is a promising and interesting task.

The arsenic (III) selenide is a very good glass former and a high-resistance semiconductor. Under normal synthesis conditions and slow cooling of the melt to room temperature, As₂Se₃ is obtained in a glassy state.

GeTe-based glassy materials are characterized by permeability in the range of 2–20 μm. Germanium is known to increase the network connectivity of glass because it forms relatively strong chemical bonds and improves its thermal and mechanical properties [8].

Cadmium telluride exhibits a wide transmission range in the infrared region, ranging from 2 µm to 20 µm. In optics, it is used as a material for making windows in the infrared region, since it is inert to water vapor and has low optical losses. It finds applications in various scientific fields, such as photovoltaic devices, light-emitting diodes, solar cells, X-ray and gamma detectors, as well as biological applications. This wide range of possibilities is mainly due to its optical properties and the value of its band gap, which allows efficient conversion of solar energy into electricity.

Thin CdTe layers as thin as 1 µm have been studied, exhibiting a high absorption coefficient at 104 cm⁻¹, absorbing 92% of visible light. This efficiency is many times higher than that of crystalline silicon, which reaches the same absorption value at a layer thickness of 200 µm.

The structural unit of cadmium telluride has a linear character, CdTe_2/2. The content of dimer structures of CdTe can cause rupture of the glass matrix or densification of its structure if the dimers are embedded in it.

Complicating the matrix by using chalcogenide compounds with different properties, such as CdTe and GeTe in the present work, is expected to have a significant effect on the properties of glasses in the ternary system As₂Se₃-GeTe-CdTe [9].

The properties of the materials are closely connected with their structure, particularly with the parameters that characterize it: the type and energy of the chemical bonds, the angles between them, their length, microhardness, molar volume, etc. Each one of these parameters directly affects the properties of certain material [10].

The glass transition temperature of chalcogenide glasses depends on various parameters such as heating rate, coordination number, thermal history, and aging [11]. Tg is a basic property of the glasses that determines their applicability. The knowledge of the relation between glass transition temperature and any of the structure parameters, e.g., the overall mean bond energy (<E>), provides the possibility to produce material of preset value for the property.

The aim of the present report is to investigate the composition dependence of some physicochemical properties of bulk chalcogenide glasses and the effect of the overall mean bond energy in the chalcogenide glasses of the As₂Se₃-GeTe-CdTe system on (Tg), mean coordination number <Z>, and microhardness (HV).

2. Results and Discussion

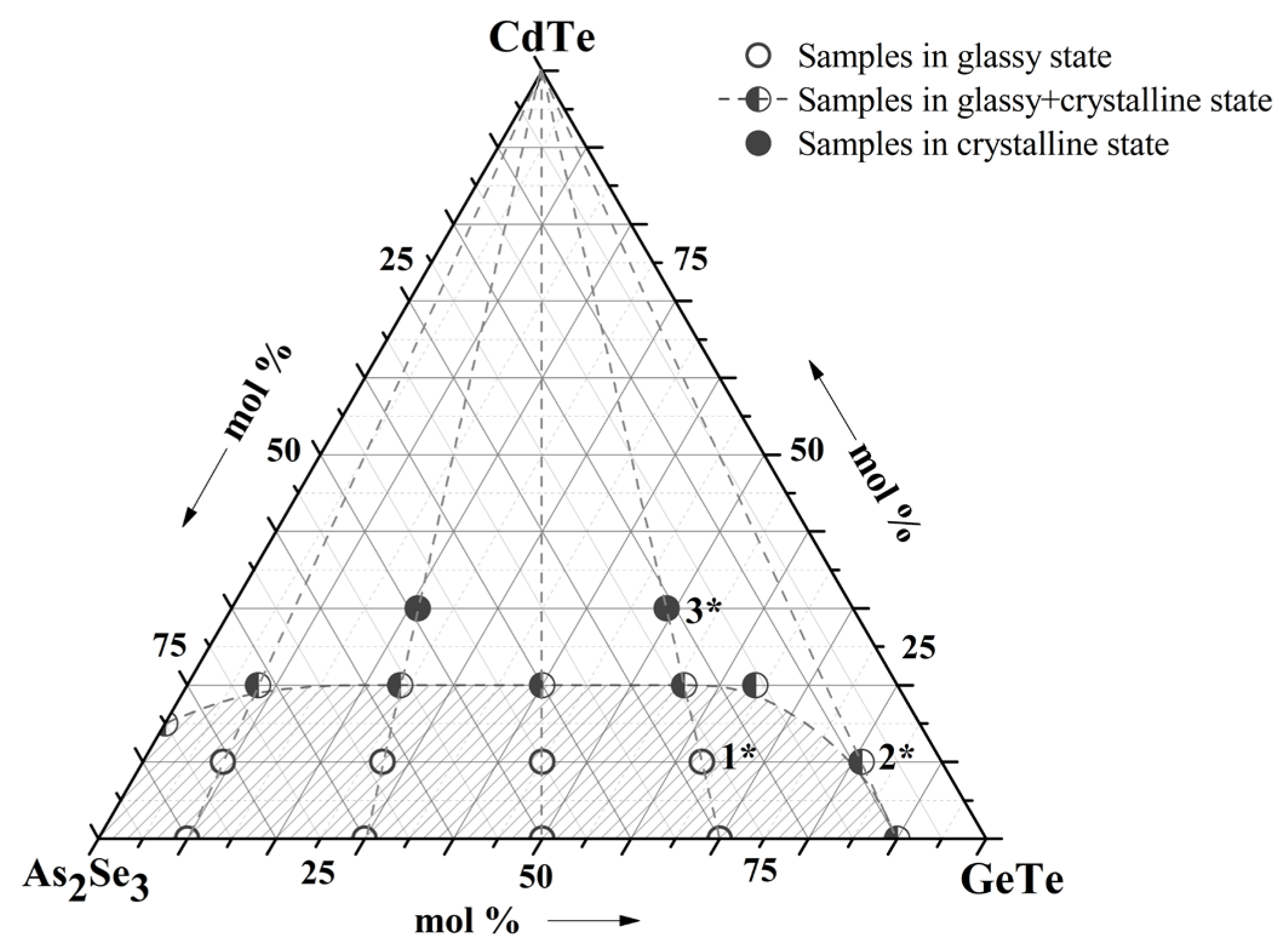
2.1. Chemical Compositions and Scanning Electron Microscopy of the Studied Samples of the System As₂Se₃-GeTe-CdTe

Chemical compositions of studied samples in the system As₂Se₃-GeTe-CdTe are represented in Figure 1. The state of sample compositions—glassy, glassy-crystalline, and crystalline—was established with the help of visual and XRD analysis in our previous work [9]. To investigate the surface topography, a microscopic study of some of the samples was performed—Figure 2. The electronic microscopic observation shows a smooth and homogeneous surface of the sample 1*—(As₂Se₃)₆₃(GeTe)₂₇(CdTe)₁₀ from the glass-forming region, and small crystalline regions are shown on the surface of the sample 2*—(As₂Se₃)₉(GeTe)₈₁(CdTe)₁₀—on the region boundary. The surface of the samples 3*—(As₂Se₃)₄₉(GeTe)₂₁(CdTe)₃₀ is rough, and there are no regions on it belonging to a glassy phase.

On the basis of the performed syntheses and the results obtained from the visual, XRD, and electron microscopic analyses, the region of glass formation within the three-component As₂Se₃-GeTe-CdTe system was outlined.

The glass compositions of the present investigation were chosen from the glass-forming region of the system As₂Se₃-GeTe-CdTe—Figure 1,

Table 1. Glass compositions of the studied samples of the (As₂Se₃)_a(GeTe)_b(CdTe)_c system.

№	Chemical Composition, mol %			m	Chemical Composition, at. Fraction
	As2Se3	GeTe	CdTe		As	Ge	Cd	Se	Te
	a	b	c		x	y	z	m	n
1.	90	10	-	0.1	0.38	0.02	-	0.58	0.02
2.	81	9	10	0.1	0.37	0.02	0.02	0.55	0.04
3.	80	20	-	0.2	0.36	0.05	-	0.55	0.04
4.	70	30	-	0.3	0.34	0.08	-	0.51	0.07
5.	63	27	10	0.3	0.32	0.07	0.03	0.49	0.09
6.	50	50	-	0.5	0.29	0.14	-	0.43	0.14
7.	45	45	10	0.5	0.27	0.13	0.03	0.40	0.16
8.	30	70	-	0.7	0.21	0.24	-	0.31	0.24
9.	27	63	10	0.7	0.19	0.22	0.04	0.29	0.26

.

2.2. Mean Bond Energy and Glass Transition Temperature

Properties of chalcogenide glasses are dependent on their overall mean bond energy. It’s a function of the type of bonds and the bond energy of atoms building the glass network and mean coordination number.

The overall mean bond energy is determined by Equation (1), suggested by Tichy [12]. For complex chalcogenide systems, it has the form:

$$<E>={\overline{E}}_c+{\overline{E}}_{rm}$$

(1)

where:

${\overline{E}}_c$—average energy of cross-linking/atom calculated by Equation (2);

${\overline{E}}_{rm}$—average bond energy for atom of the “remaining matrix”.

The average energy of cross-linking/atom is determined by the dependence:

$${\overline{E}}_c=P_p.E_{hb}$$

(2)

where $P_p$—the degree of cross–linking atom; $E_{hb}$—average energy of the heteropolar bonds for glasses of composition A_xB_yC_zD_mE_n.

The degree of cross-linking atom ($P_p$) is closely connected with the coefficient (R), which determines the chalcogen content in the glass and is calculated by the equation:

$$R={\displaystyle \frac{m{Z}_D+n{Z}_E}{x{Z}_A+y{Z}_B+z{Z}_C}}$$

(3)

When $R>1$, the system is rich in chalcogen and has heteropolar bonds and chalcogen–chalcogen bonds.

When $R=1$, the system has a stechiometric composition because it has heteropolar bonds only.

When $R<1$, the system is deficient in chalcogen and has heteropolar bonds and metal–metal bonds.

In the concrete case, the $R$ values for each composition are less than 1, indicating that the glasses of the examined system are deficient in chalcogen and the system has heteropolar bonds and metal–metal bonds (see Table 2). In such case, it is calculated by means of Equation (4):

$$P_p={\displaystyle \frac{mSe+nTe}{x+y+z+m+n}}$$

(4)

The average energy of the heteropolar bonds $E_{hb}$ in glasses of composition AxByCzDmEn is calculated by means of Equation (5):

$${\mathit{E}}_{\mathit{hb}}={\displaystyle \frac{(\mathit{x}{\mathit{Z}}_{\mathit{A}}{\mathit{E}}_{\mathit{A}\text{-}\mathit{D}}+\mathit{y}{\mathit{Z}}_{\mathit{B}}{\mathit{E}}_{\mathit{B}\text{-}\mathit{D}\mathit{ }}+\mathit{z}{\mathit{Z}}_{\mathit{C}}{\mathit{E}}_{\mathit{C}\text{-}\mathit{D}\mathit{ }}+\mathit{x}{\mathit{Z}}_{\mathit{A}}{\mathit{E}}_{\mathit{A}\text{-}\mathit{E}}+\mathit{y}{\mathit{Z}}_{\mathit{B}}{\mathit{E}}_{\mathit{B}\text{-}\mathit{E}}+\mathit{z}{\mathit{Z}}_{\mathit{C}}{\mathit{E}}_{\mathit{C}\text{-}\mathit{E}})}{(\mathit{x}{\mathit{Z}}_{\mathit{A}\mathit{ }}+\mathit{y}{\mathit{Z}}_{\mathit{B}}+\mathit{z}{\mathit{Z}}_{\mathit{C}})}}$$

(5)

where ${\mathit{E}}_{\mathit{A}\text{-}\mathit{D}}$, ${\mathit{E}}_{\mathit{B}\text{-}\mathit{D}}$, ${\mathit{E}}_{\mathit{C}\text{-}\mathit{D}}$, ${\mathit{E}}_{\mathit{A}\text{-}\mathit{E}}$, ${\mathit{E}}_{\mathit{B}\text{-}\mathit{E}}$, and ${\mathit{E}}_{\mathit{C}\text{-}\mathit{E}}$—energies of the heteropolar bonds; x, y, z, m, n and ${\mathit{Z}}_{\mathit{A}}$, ${\mathit{Z}}_{\mathit{B}}$, ${\mathit{Z}}_{\mathit{C}}$, ${\mathit{Z}}_{\mathit{D}}$, ${\mathit{Z}}_{\mathit{E}}$—the atomic fractions and the coordination numbers of the elements A, B, C, D, and E, respectively.

The values of coordination numbers of constituent elements are 2 for Se and Te, 3 for As, and 4 for Ge and Cd. Values of Z were determined for the glasses with the atomic fraction of chalcogens ≥ 0.55 [12] by the following formula: “8 − N”, where N is the mean number of formal valence electrons per atom in the glass composition. N is equal to the average number of valence electrons per atom in the glass composition. The obtained values are following the literature data [12,13,14,15,16].

The energy of the heteropolar bond is calculated by means of Equation (6), suggested by Pauling [17]:

$$E_{AB}=0.5(E_{AA}+E_{BB})+23({\chi }_A-{\chi }_B{)}^2$$

(6)

where $E_{AA}$, $E_{BB}$ and $X_A$, $X_B$—energy and electric negativity of the homeopolar bonds of A and B atoms, respectively.

The values of the energies of the homeo- and heteropolar bonds that build the glasses of the (As₂Se₃)_a(GeTe)_b(CdTe)_c system are summarized in Table 2, and the values of $P_p$ and $E_{\mathrm{hb}}$—in

Table 3. Values of the subsidiary coefficients of the glasses in the (As₂Se₃)_a(GeTe)_b(CdTe)_c system: the degree of cross-linking atom $\left(P_p\right)$, the content of chalcogen in the glass $\left(R\right)$, the mean coordination number $(<\mathrm{Z}>)$, and an average energy of the heteropolar bonds $\left({\mathrm{E}}_{\mathrm{h}\mathrm{b}}\right)$.

№	$\mathit{R}$	${\mathit{P}}_{\mathit{p}}$	$<\mathit{Z}>$	${\mathit{E}}_{\mathit{h}\mathit{b}},$ $\mathit{e}\mathit{V}$
1.	0.98	1.20	2.42	3.245
2.	0.93	1.18	2.45	3.199
3.	0.92	1.18	2.46	3.316
4.	0.87	1.16	2.50	3.372
5.	0.85	1.16	2.52	3.275
6.	0.76	1.12	2.59	3.476
7.	0.77	1.12	2.57	3.382
8.	0.69	1.10	2.69	3.621
9.	0.68	1.10	2.71	3.496

.

Table 2. Bond energies between atoms build the glasses of the (As₂Se₃)_a(GeTe)_b(CdTe)_c system.

Bond	E, eV	Reference	Bond	E, eV	Reference
As-As	1.38	[12]	Cd-Ge	1.39	[17]
Ge-Ge	1.63	[18]	Se-Te	2.00	[17]
Cd-Cd	0.076	[19]	As-Ge	1.54	[12]
Se-Se	1.90	[12]	As-Se	1.80	[12]
Te-Te	1.48	[20]	As-Te	1.41	[12]
Cd-Se	1.32	[17]	Ge-Se	2.12	[12]
Cd-Te	1.03	[17]	Ge-Te	1.77	[20]

Table 2. Bond energies between atoms build the glasses of the (As₂Se₃)_a(GeTe)_b(CdTe)_c system.

Bond	E, eV	Reference	Bond	E, eV	Reference
As-As	1.38	[12]	Cd-Ge	1.39	[17]
Ge-Ge	1.63	[18]	Se-Te	2.00	[17]
Cd-Cd	0.076	[19]	As-Ge	1.54	[12]
Se-Se	1.90	[12]	As-Se	1.80	[12]
Te-Te	1.48	[20]	As-Te	1.41	[12]
Cd-Se	1.32	[17]	Ge-Se	2.12	[12]
Cd-Te	1.03	[17]	Ge-Te	1.77	[20]

The average bond energy for atom of the “remaining matrix” is determined by means of Equation (7):

$${\overline{E}}_{rm}={\displaystyle \frac{2\left(0.5<\mathit{Z}>-P_p\right)E_{<>}}{<\mathit{Z}>}}$$

(7)

where $<\mathit{Z}>$—the mean coordination number of the glass; $E_{<>}$—average energy of the chemical bonds between the metal atoms (A, B, C).

The values of $<\mathit{Z}>$ and $E_{<>}$ are calculated by Equations (8) and (9), respectively:

$$<\mathit{Z}>=x{\mathit{Z}}_A+y{\mathit{Z}}_B+z{\mathit{Z}}_C+m{\mathit{Z}}_D+n{\mathit{Z}}_E$$

(8)

$$E_{<>}={\displaystyle \frac{E_{A-A}+E_{B-B}+E_{C-C}+E_{A-B}+E_{B-C}+E_{A-C}}{6}}$$

(9)

where the energies of the bonds between the metal atoms are A = As; B = Ge, and C = Cd, i.e., As-As, Ge-Ge, Cd-Cd, As-Ge, Ge-Cd, and As-Cd—Table 2. Table 3 presents the values of $<Z>$, $P_p$, $R$ and $E_{hb}$ and

Table 4. Microhardness, glass transition temperature, overall mean bond energy and its components ${\overline{E}}_c$ and ${\overline{E}}_{rm}$ of samples of the As-Ge-Cd-Se-Te system.

№	HV, kgf mm−2	Tg, K	${\overline{\mathit{E}}}_{\mathit{c}}$, eV	${\overline{\mathit{E}}}_{\mathit{r}\mathit{m}}$, eV	$<\mathit{E}>$, eV
1.	84	475	3.893	0.011	3.905
2.	80	460	3.775	0.049	3.824
3.	90	476	3.913	0.054	3.967
4.	93	478	3.912	0.096	4.008
5.	86	467	3.798	0.106	3.904
6.	129	488	3.894	0.181	4.075
7.	104	479	3.789	0.172	3.961
8.	133	495	3.983	0.244	4.227
9.	109	490	3.846	0.252	4.099

—those of ${\overline{E}}_c$, ${\overline{E}}_{rm}$ and $<E>$, together with $<Z>$, Tg, and HV.

For a description of the bond between Tg and $<E>$, Tanaka [21] suggests an equation analogical to the equation that expresses the dependences between the viscosity (µ) and the temperature T, which is of Arrhenius type:

µ(Tg) = µ_o exp (Eµ/kTg)

(10)

Tanaka assumes that µ(Tg) = 10¹³ Poise; µ_o = 100 ÷ 10⁻⁵ Poise. If we choose µ₀ = 10⁻³ Poise, then for Tg = f (Eµ) the following expression is obtained:

Tg = 314 Eµ

(11)

The experimental values of Tg and $<E>$ are subject to the dependence obtained by regression analysis:

$$\mathrm{Tg}=87.262<E>+129.9$$

(12)

Eµ is determined from Equations (11) and (12):

Eµ = 0.278 <E> + 0.41

(13)

In an analogical manner, using a least-squares method, there are obtained the constants A and B in the dependence:

$$\mathrm{Tg}=\mathrm{A} (0.278<E>+ 0.41)-B$$

(14)

$$\mathrm{Tg}=313.6 (0.278<E>+ 0.41)+1.74$$

(15)

$$\mathrm{Tg}=314.75 (0.278<E>+ 0.41)$$

(16)

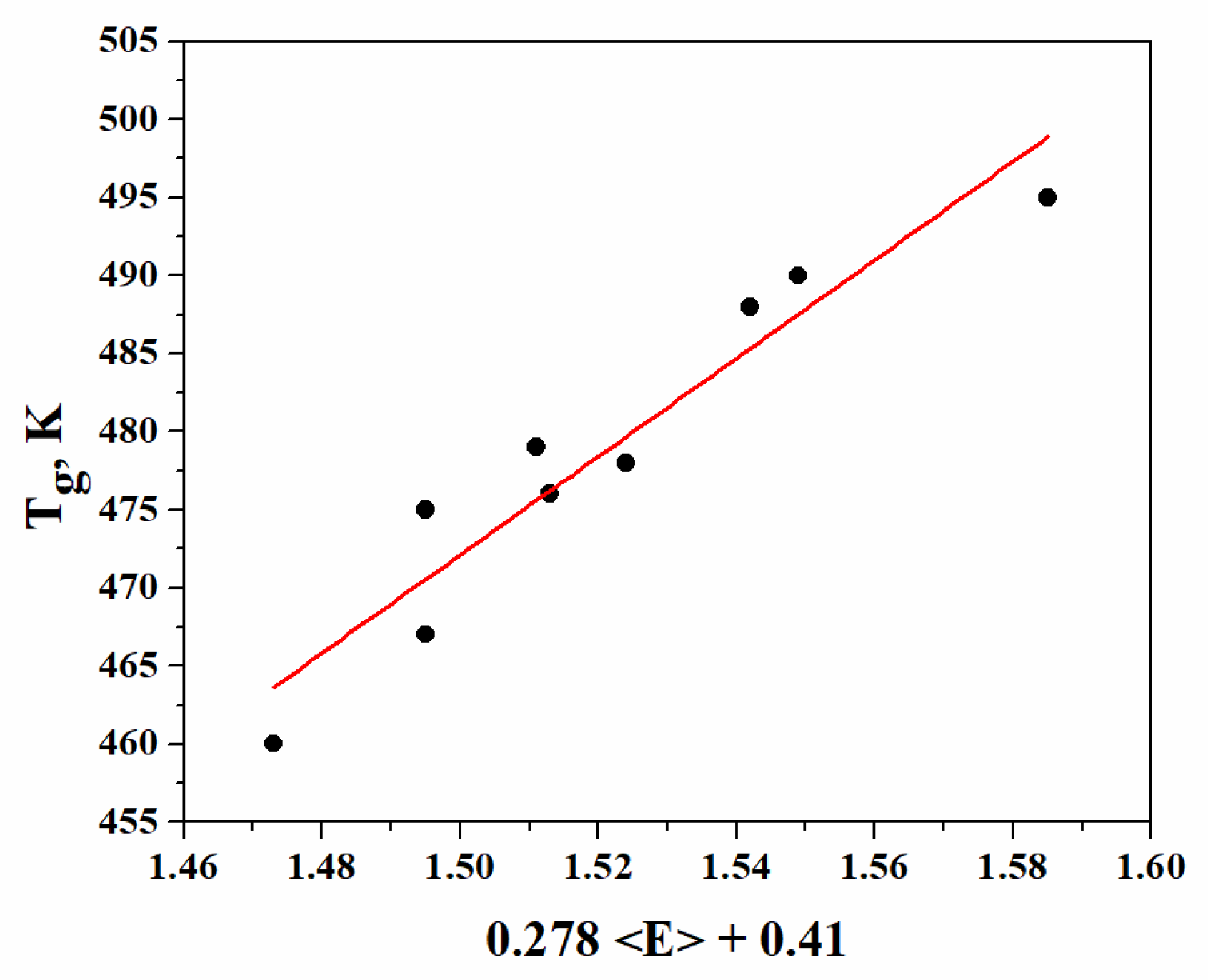
The values of Tg, depending on (0.278 <E> + 0.41) according to Equation (16), are presented in Figure 3.

Good correlation is observed between the glass transition temperature and the overall mean bond energy. The dependence Tg = 314.75 (0.278$<E>$+ 0.41) describes the experimental results with sufficient accuracy. The value of the angular coefficient (314.75 K eV⁻¹), as well as the deviation (ΔT) of the experimental values calculated by this equation, are in good conformity with the theoretically predicted values (314 K eV⁻¹) on the basis of Tanaka’s model.

2.3. Study of the Dependence Composition-Property of Glassy Samples with a Common Composition (As₂Se₃)_a(GeTe)_b(CdTe)_c

To simplify the analysis of the composition-property relationship for chalcogenide glasses with the general composition (As₂Se₃)_a(GeTe)_b(CdTe)_c, the magnitude has been introduced: $m={\displaystyle \frac{\chi GeTe}{(\chi {As}_2{Se}_3+\chi GeTe)}}$, where χGeTe—the molar fraction of GeTe; χAs₂Se₃—the molar fraction of As₂Se₃. The parameter “c” corresponds to the mole percent of the CdTe component, and m takes into account the ratio between the components.

The glass-transition temperature is the important parameter for the characterization of the glassy state and reflects the structure of the glass [22]. The change in the value of the glass transition temperature is associated with a change in the overall mean bond energy.

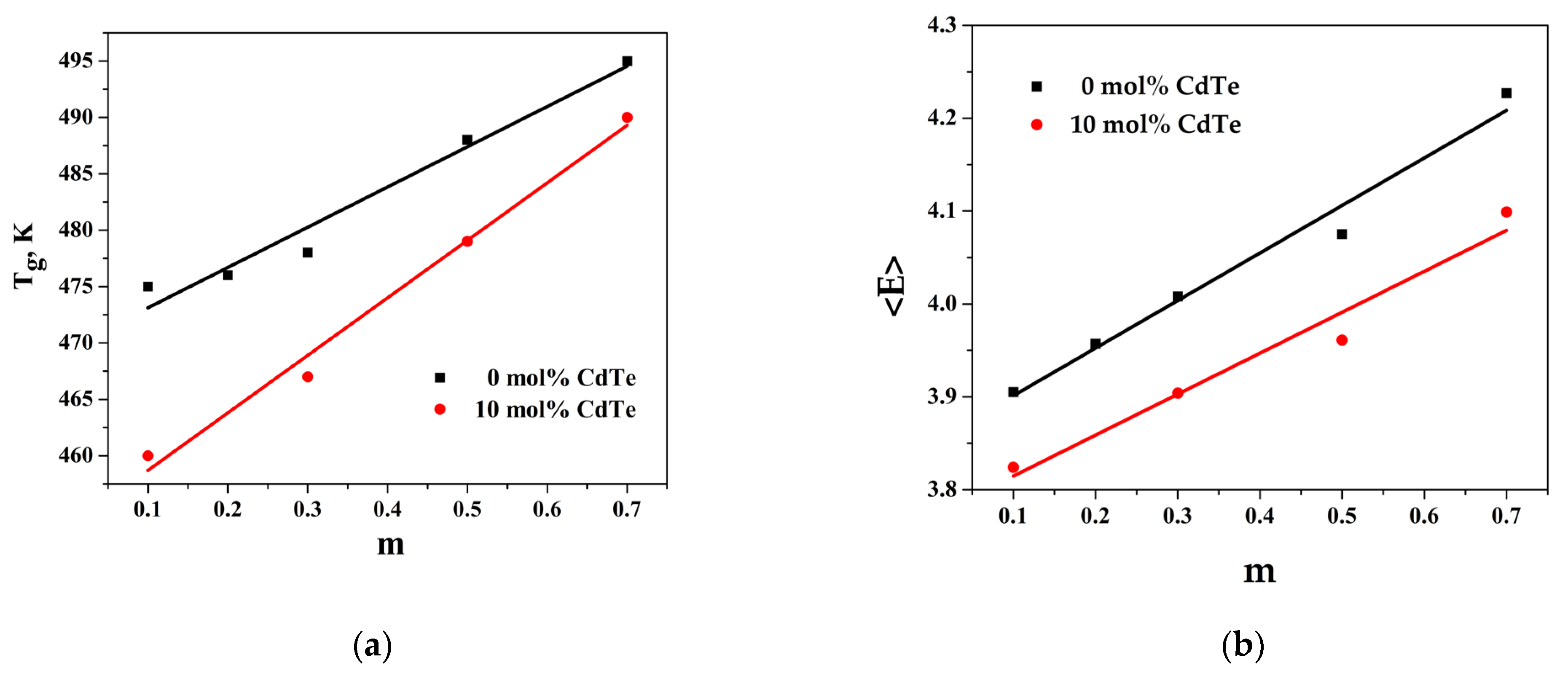
Tg depends on the composition of studied chalcogenide glasses and varies in the range from 460 to 495 K—Table 4. The introduction of CdTe into the system leads to an increase in the metal component of the chemical bond in ChGs. When CdTe content increases (at m = const.), the system mean bond energy decreases linearly, and Tg decreases due to the weakening of average bond strength with increasing CdTe content. On the other hand, with increasing GeTe content (at c = const.), the system mean bond energy increases linearly, and Tg increases, which indicates that the integrity of the structure is enhanced.

The variation in Tg with the composition is represented in Figure 4a, and it can be represented in the following analytic form: for $\chi CdTe=0 \mathrm{m}\mathrm{o}\mathrm{l}\%,$ Tg = 35.7x + 470, R² = 0.968; for $\chi CdTe=10 \mathrm{m}\mathrm{o}\mathrm{l}\%,$ Tg = 51.0x + 454, R² = 0.989.

The dependence of <E> with the composition is represented in Figure 4b: for $\chi CdTe=0 \mathrm{m}\mathrm{o}\mathrm{l}\%,$ <E> = 0.441x + 3.77, R² = 0.978; for $\chi CdTe=10 \mathrm{m}\mathrm{o}\mathrm{l}\%,$ <E> = 0.512x + 3.85, R² = 0.966, where x is the ratio of $m={\displaystyle \frac{\chi GeTe}{(\chi {As}_2{Se}_3+\chi GeTe)}}$ in the glass composition.

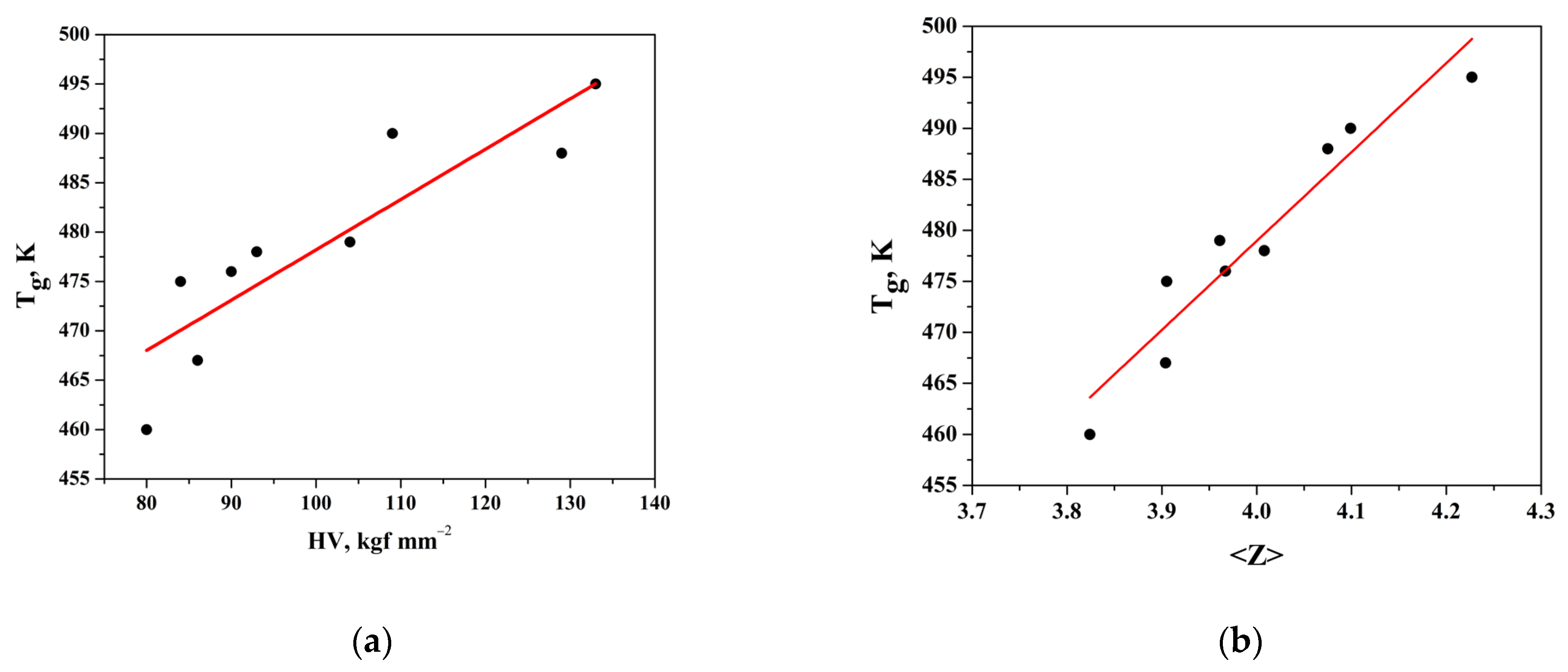
According to Freitas et al. [10], microhardness, from the mechanical point of view, is an accessible physical parameter of cohesive energy. Authors confirm a linear correlation between microhardness (HV) and glass transition temperature (Tg) for 190 binary and ternary chalcogenide glasses.

The measured microhardness values (HV) of the investigated glasses are in the range of 80–133 kg f mm⁻² and depend on the composition—see Table 4.

The dependence HV (m) at c = const. increases, as GeTe is a very good modifier, and added to As₂Se₃, it stabilizes the amorphous nature of samples. The increase in the microhardness (HV) of the glasses from the As₂Se₃-GeTe-CdTe system is associated with a densification of the structure and an increase in connectivity in the glass network, which is expressed as an increase in the value of the glass transition temperature (Tg) and mean bond energy <E>.

On the other hand, the structural unit of cadmium telluride has a linear character of CdTe_2/2. The content of the dimer structure of CdTe causes rupture of the glass matrix, which leads to a decrease in the values of the microhardness (HV).

The variation in Tg and microhardness with the composition is represented in Figure 5a, and it can be represented in the following analytic form: Tg = 0.5097x + 427.25, R² = 0.794.

According to Tichy and Ticha, the value of glass transition temperature should not only be related to the mean bond energy between the atoms of the network but should also be related to the quality of connections of the glass network expressed by the mean coordination number (<Z>)—Figure 5b. The values of the mean coordination number were estimated for the studied system and listed in Table 3. The dependence is of a linear character, and it can be represented in the following analytic form: Tg = 87.186x + 130.2, R² = 0.914. That behavior may be ascribed to an increase in the cross-linking as As₂Se₃ and GeTe get into the system with their pyramidal and tetrahedral structural units. Increasing the cross-linking means an increase in the rigidity of the structure and leads to an increase in the value of (<Z>), Tg, HV, and <E>.

3. Materials and Methods

Chalcogenide glasses (ChG) from the As₂Se₃-GeTe-CdTe system have been synthesized by the procedure described in [9]. For the synthesis of samples (4 g) from the As₂Se₃-GeTe-CdTe system, preliminary synthesized initial components As₂Se₃ and GeTe (arsenic powder, 99,999% Sigma-Aldrich Chemie GmbH, Steinheim, Germany; germanium powder, 99.999%, Thermo Scientific Chemicals, Fisher Scientific, Loughborough, UK; tellurium powder 99.999%, Alfa Aesar, Ward Hill, MA, USA); selenium powder, 99.999%, Thermo Scientific Chemicals, Alfa Aesar Avocado Research Chemicals, Ltd., Ward Hill, MA, USA) and CdTe (Balzers, “coating material”) were used; all these reagents were used without purification. Arsenic powder was heated to 350 °C for 1.5 h under vacuum and was stored in a vacuum desiccator. The starting substances were weighed on an analytical balance with an accuracy of ±0.0002 g in quantities corresponding to the chemical composition of the glass samples, after which they were transferred into quartz ampoules 100 mm long and 10 mm in diameter. The quartz ampoules were pre-treated in order to avoid contamination from the ampoule walls entering the melt. The treatment was carried out in the following order: successive washing with aqua regia at a temperature of 50–60 °C, rinsing with distilled water, and drying in a drying cabinet at 105 °C for 2 h. The ampoules were heated in the flame of an oxygen burner to a “red heat” temperature (850–900 °C) immediately before filling them with the starting substances. The weighing of the starting materials on the analytical balance and the sealing of the ampoules after heating with the flame of the oxygen burner were carried out in an inert atmosphere (nitrogen). The ampoules, evacuated to a residual pressure of 0.133 Pa and soldered on the flame of an oxygen–propane–butane torch, were placed in an electric resistance furnace equipped with a vibrating device. The synthesis was complied with compounds’ physicochemical properties (As₂Se₃, GeTe, and CdTe melting points of 360 °C, 725 °C, and 1041 °C, respectively). The heating rate of the synthesis of the initial compounds was 3–6 °C min⁻¹. For the alloys from the system subjected to investigation, the heating rates between the steps were 3–4 °C min⁻¹ and 2–3 °C min⁻¹. At the maximum synthesis temperature, a continuous stirring of the melt was performed. In the final stage of the alloys’ synthesis, the ampoules were taken out and cooled in the air to 900–950 °C and then rapidly quenched in an ice + water mixture, which provides a cooling rate of 10–15 °C s⁻¹ (depending on the size of the ampoules). The article is a revised and expanded version of a poster presentation entitled “Correlation of the Glass Transition Temperature and Mean Bond Energy in Network of Chalcogenide Glasses”, which was presented at XIV Conference of Chemists, Technologists and Environmentalists of Republic of Srpska, 21–22 October 2022, Banja Luka, Republic of Srpska [23].

The diffractograms of the glassy compositions were obtained under the following conditions: 500 mg of the studied samples was previously ground in an agate mortar and sieved to obtain a powder sample with particle sizes no larger than 63 μm. The thermograms of the vitreous samples were recorded on a derivatograph with a three-channel Y − t recorder by apparatus of the company Kutesz; Type 1040. The accuracy of measuring the temperatures of phase transformations is ±5 °C. Pre-calcined γ-Al₂O₃ served as reference material for this study.

The glass transition temperature of the obtained chalcogenide glasses was determined during non-isothermal heating carried out in the temperature range from room temperature to 1000 °C, at a rate of 10 °C min⁻¹.

Stepanov’s quartz pots are used, vacuumed to a residual pressure of ~0.1 Pa, with sample and reference weights of 300 mg.

Topological studies [24] of some of the synthesized samples were carried out using a microscope, “Zeiss EVO 10” (Jena, Germany).

The microhardness of the bulk glassy alloys was established by the Vickers method using a MIM-7 microscope with a PMT-3 microhardness meter built into it. The load on the pyramid was selected experimentally.

The microhardness values were calculated using the formula:

$$HV={\displaystyle \frac{P}{F}}={\displaystyle \frac{2Psin\alpha /2}{d^2}}={\displaystyle \frac{1854.P}{d^2}}, \mathrm{k}\mathrm{g}\mathrm{f} {\mathrm{m}\mathrm{m}}^{-2}$$

(17)

$$d={\displaystyle \frac{d1+d2}{2N 0.315}}; 1 \mathrm{kgf}=9.81 N$$

(18)

where P—load force, g; d—diagonal of the footprint, μm; 2N—scale division/1 scale division = 0.315 μm; F—surrounding surface from the impression; α—angle at the top of the pyramid −136°.

The microhardness of the samples was calculated based on 20 impressions per sample with a measurement accuracy of ±5% [8].

4. Conclusions

Glasses of the As₂Se₃-GeTe-CdTe system are synthesized. The surface topography of some of the samples was performed with the help of scanning electron microscopy. The overall mean bond energy in the chalcogenide glasses is calculated, and the correlation of the type Tg = 314.75 (0.278 <E> +0.41) is found to conform with Tanaka’s model. The average coordination numbers of the studied glasses were evaluated, and the linear dependence of the type Tg = 87.186x + 130.2 between <Z> and Tg was settled. The dependence between the composition and properties of the glasses was established and discussed. It is found that the introduction of CdTe to the composition of studied glasses linearly decreases the values of Tg, <E>, and HV. It is shown that the glass transition temperature correlates with the microhardness in chalcogenide glasses of the presented system.