Adsorption of CuSO4 on Anatase TiO2 (101) Surface: A DFT Study
Abstract
1. Introduction
2. Results and Discussion
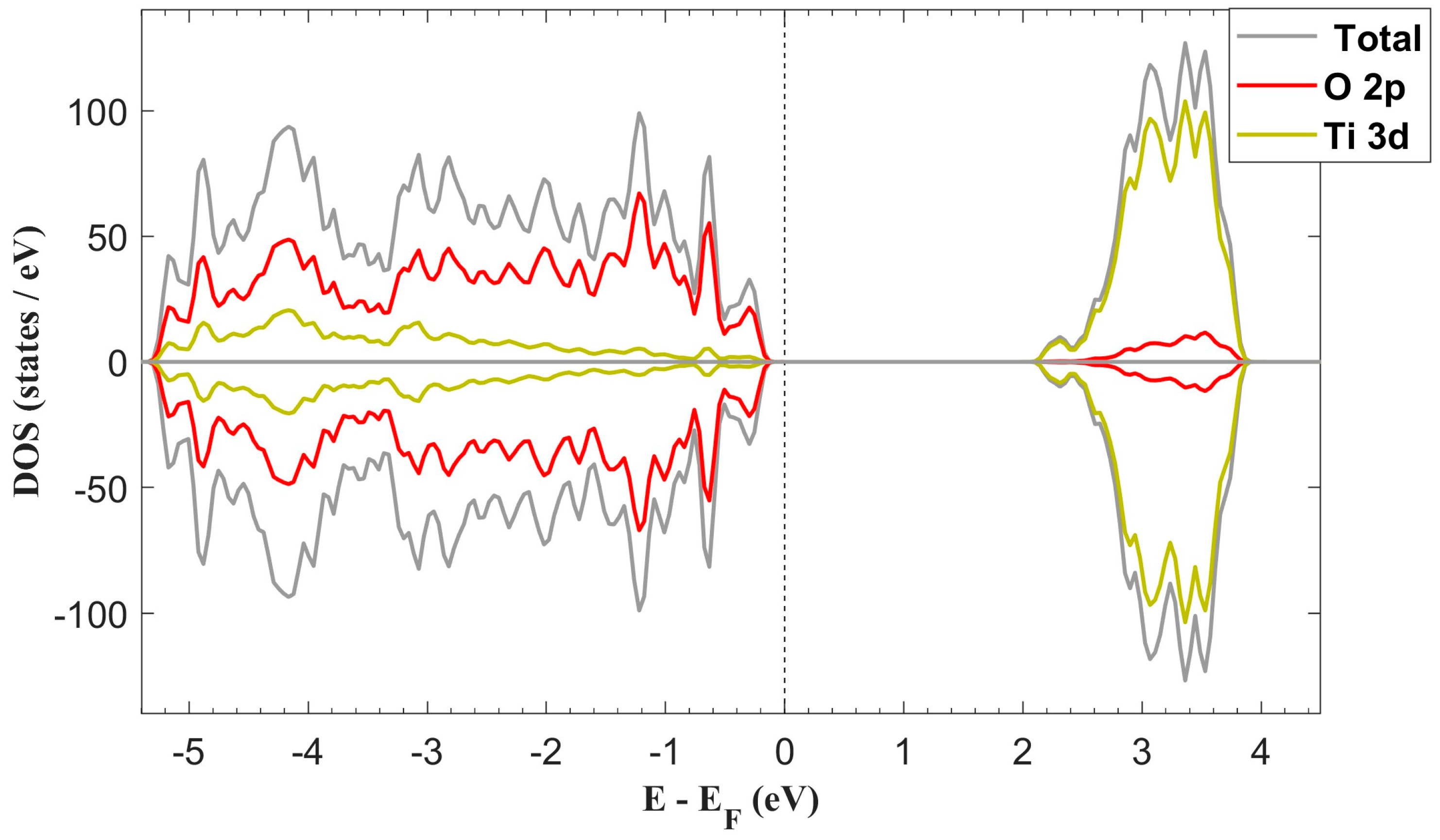
2.1. Pristine Surface
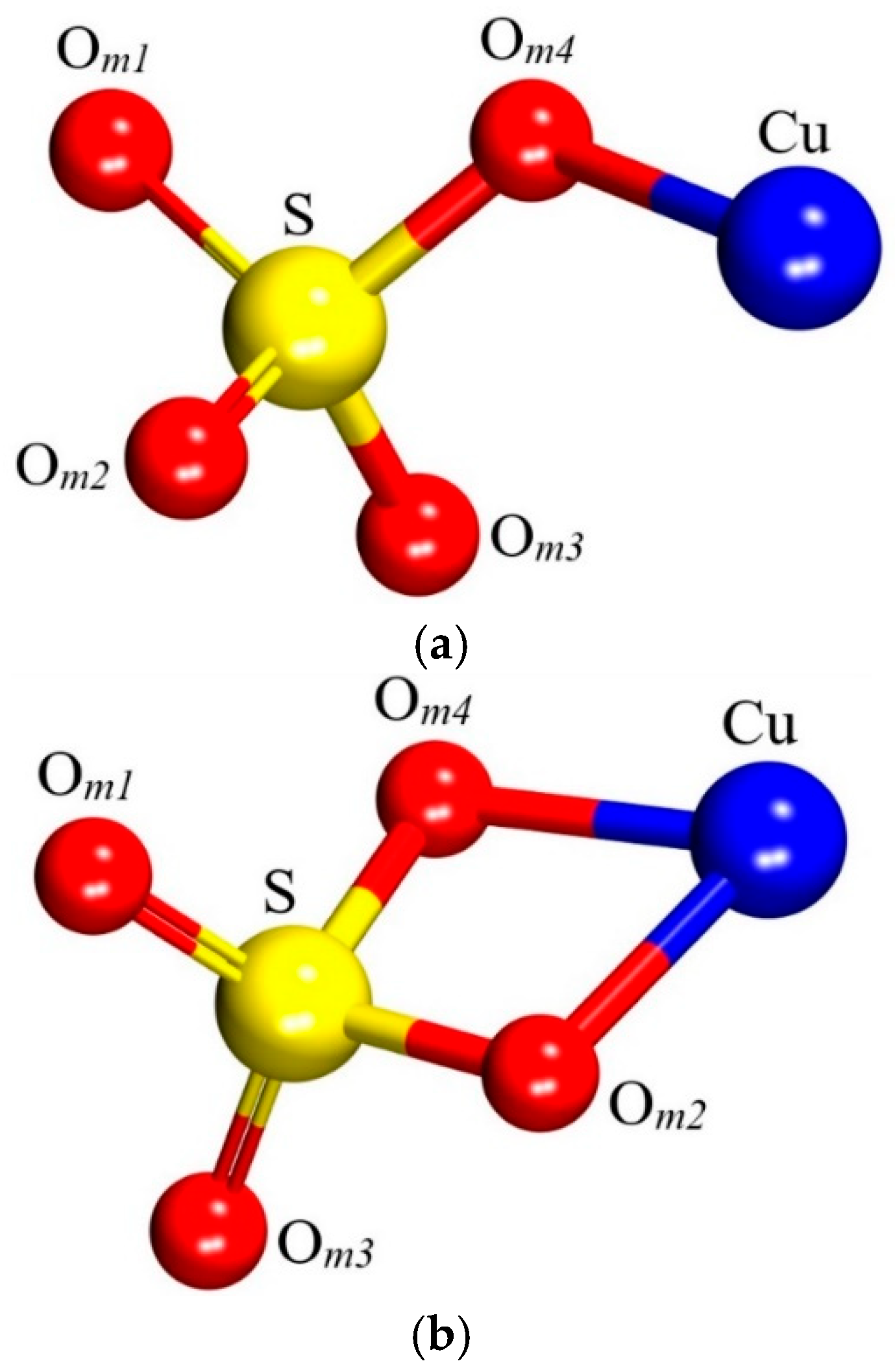
2.2. Free Molecule
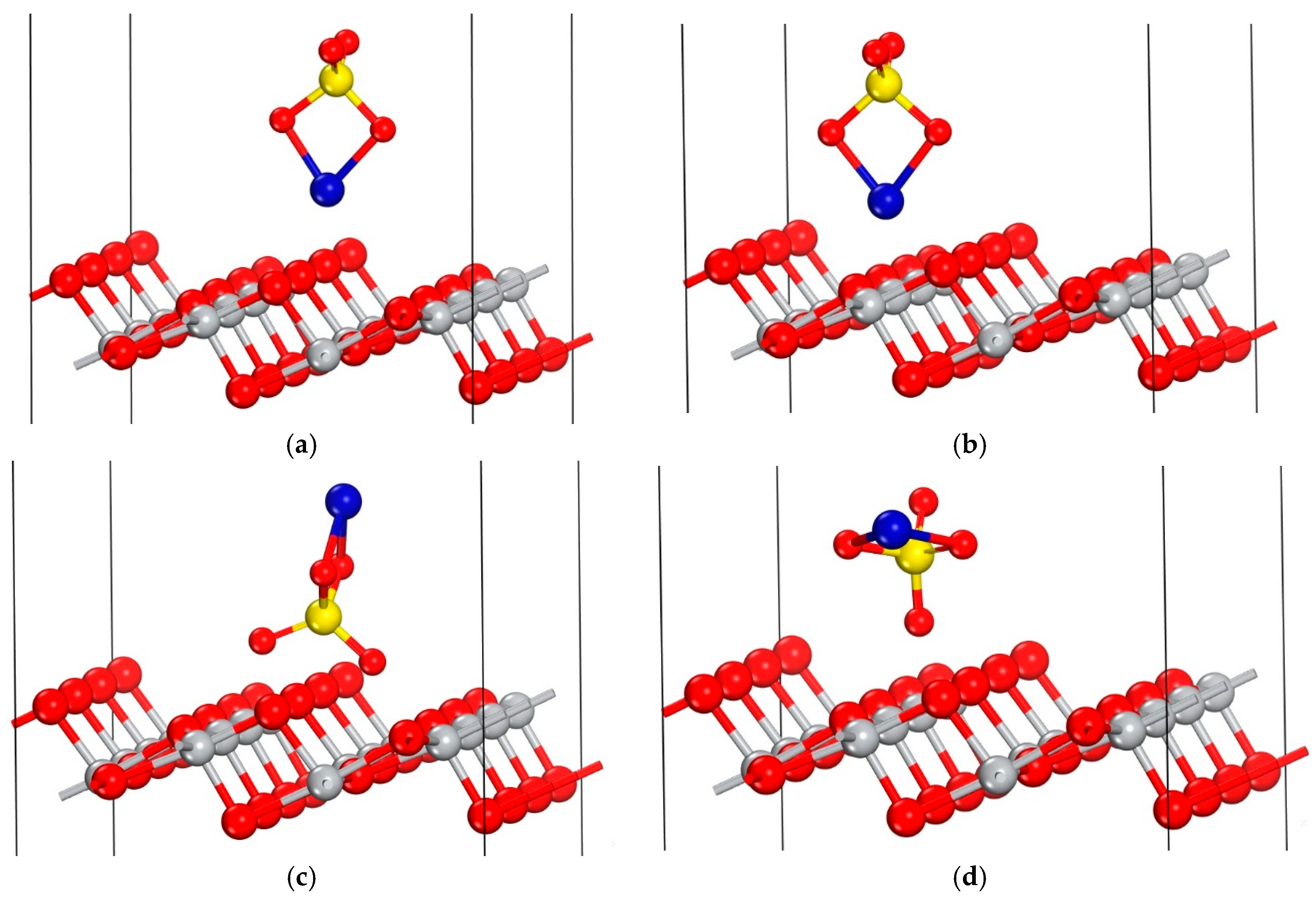
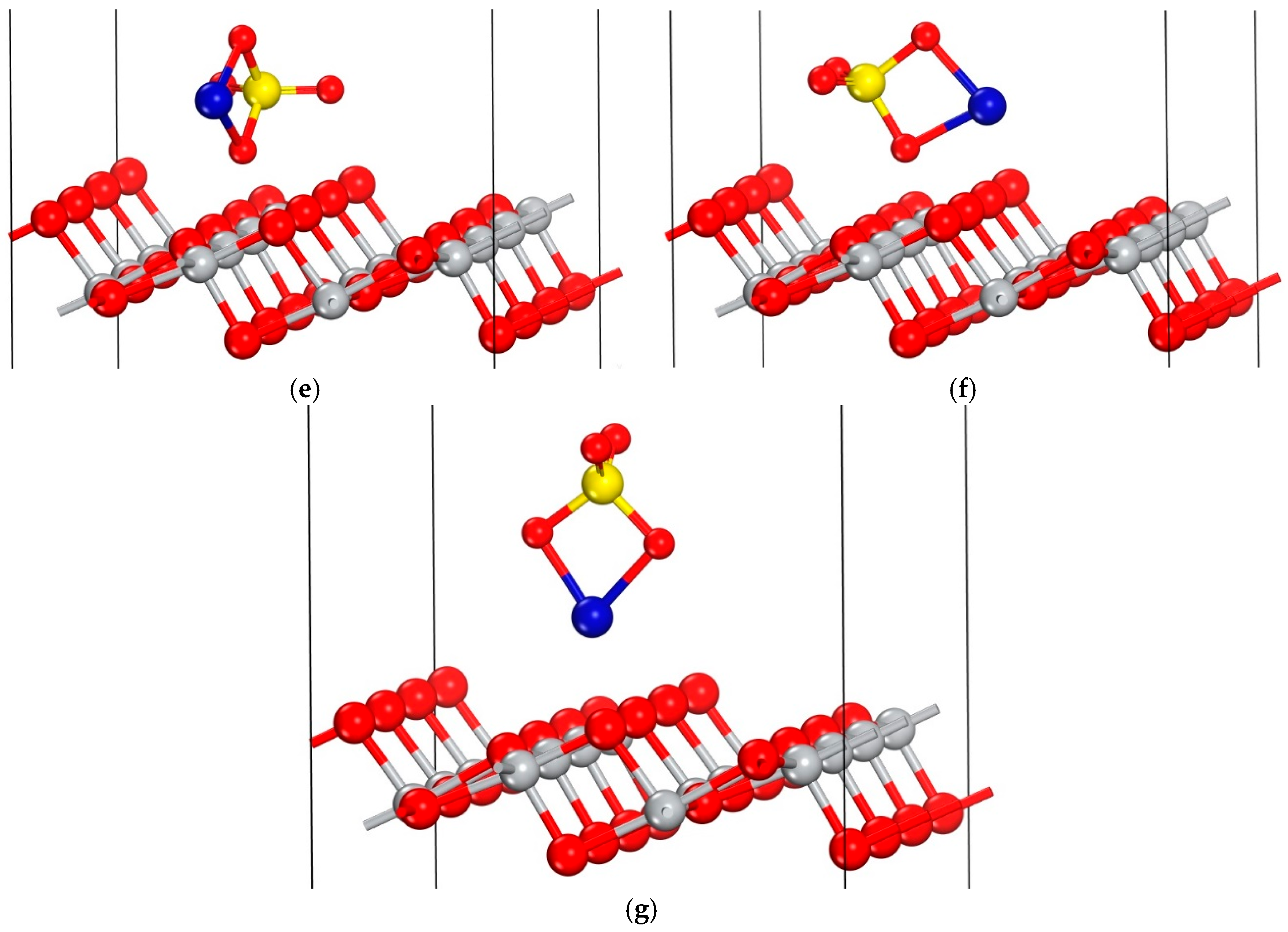
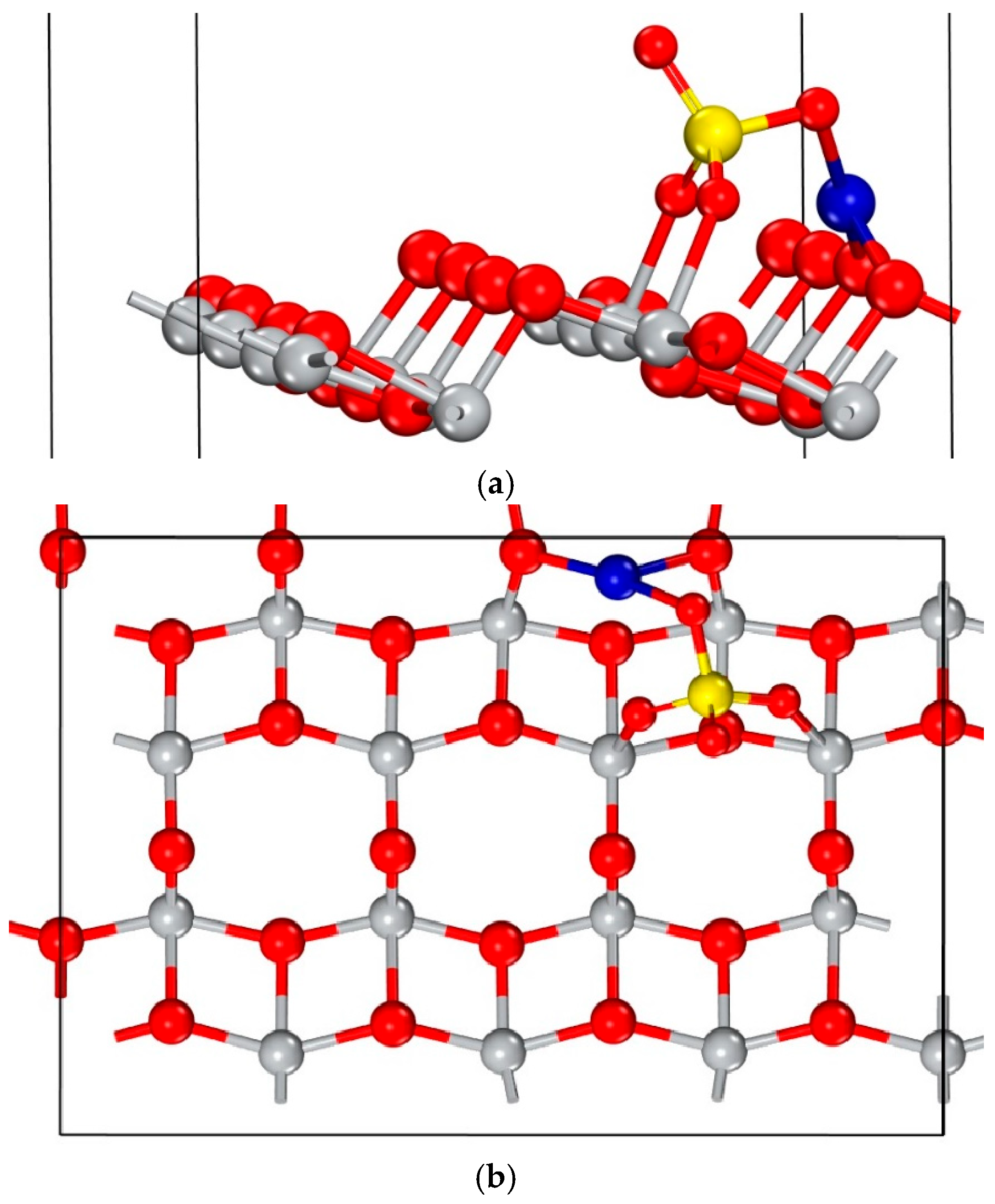
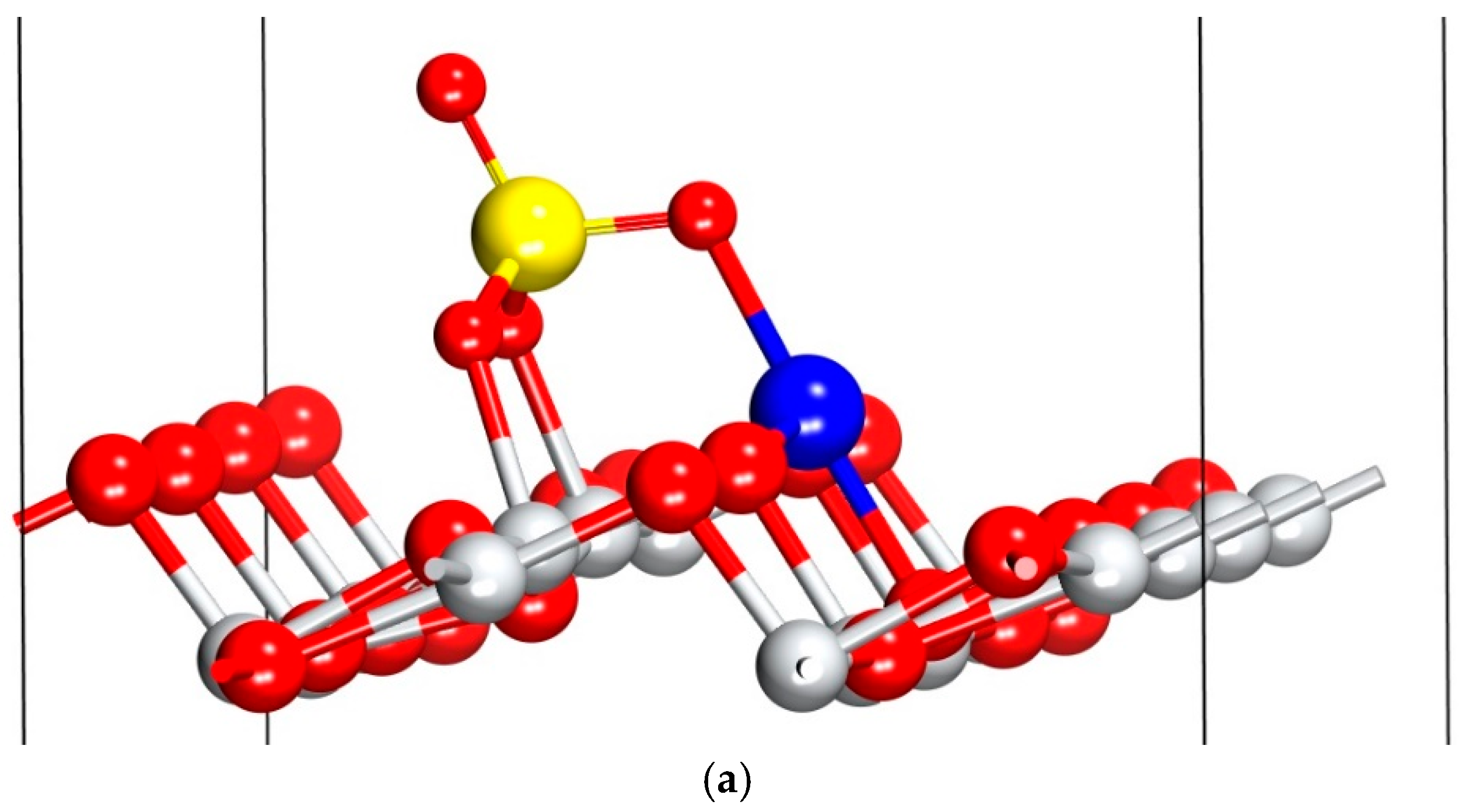
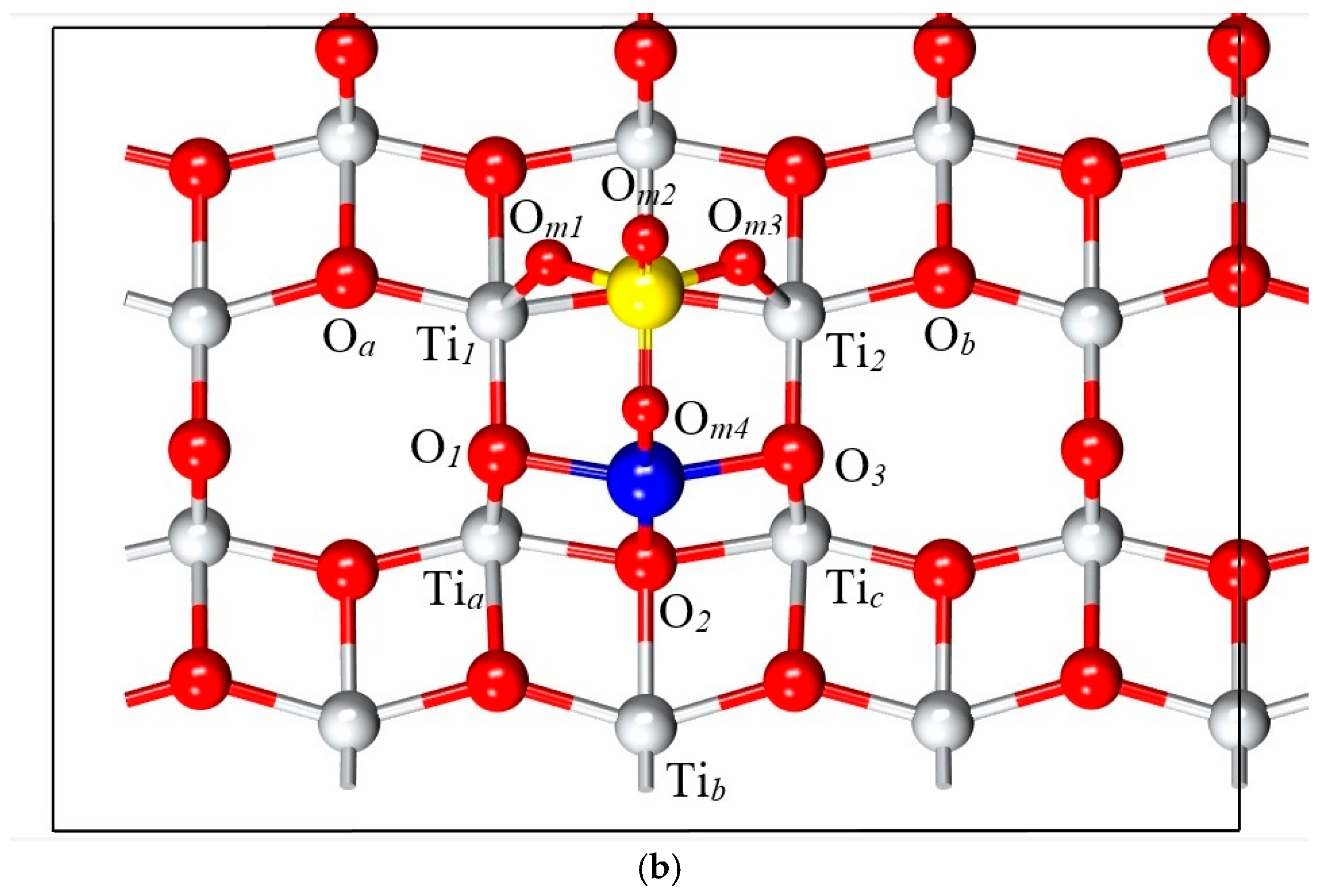
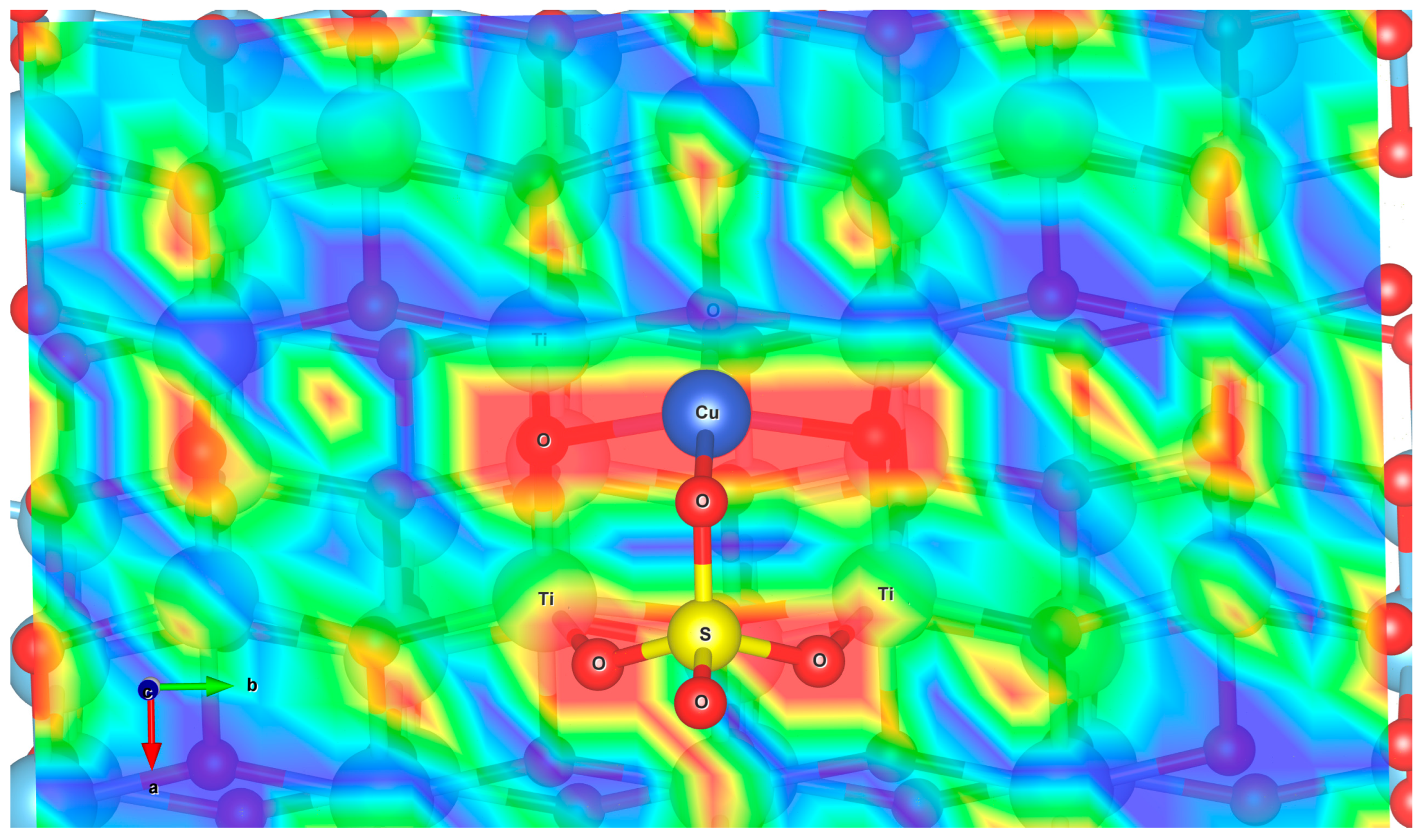
2.3. Adsorption on Anatase TiO2 (101) Surface
3. Computational Details
4. Conclusions
- (1)
- Adsorption Geometry: A preferential adsorption pattern was identified, characterized by the lowest adsorption energy of −4.31 eV. This configuration was consistently obtained regardless of the initial approach of the molecule to the surface, suggesting its prevalence in real samples.
- (2)
- Adsorption Mechanism: The substantial adsorption energy and the formation of new chemical bonds between CuSO4 and the TiO2 surface provide strong evidence for a chemisorption process.
- (3)
- Charge Transfer: Atomic charge analysis reveals a net charge transfer from the TiO2 surface to the CuSO4 molecule. Atoms directly involved in forming new chemical bonds exhibit increased net atomic charges, indicating the ionic nature of these bonds.
- (4)
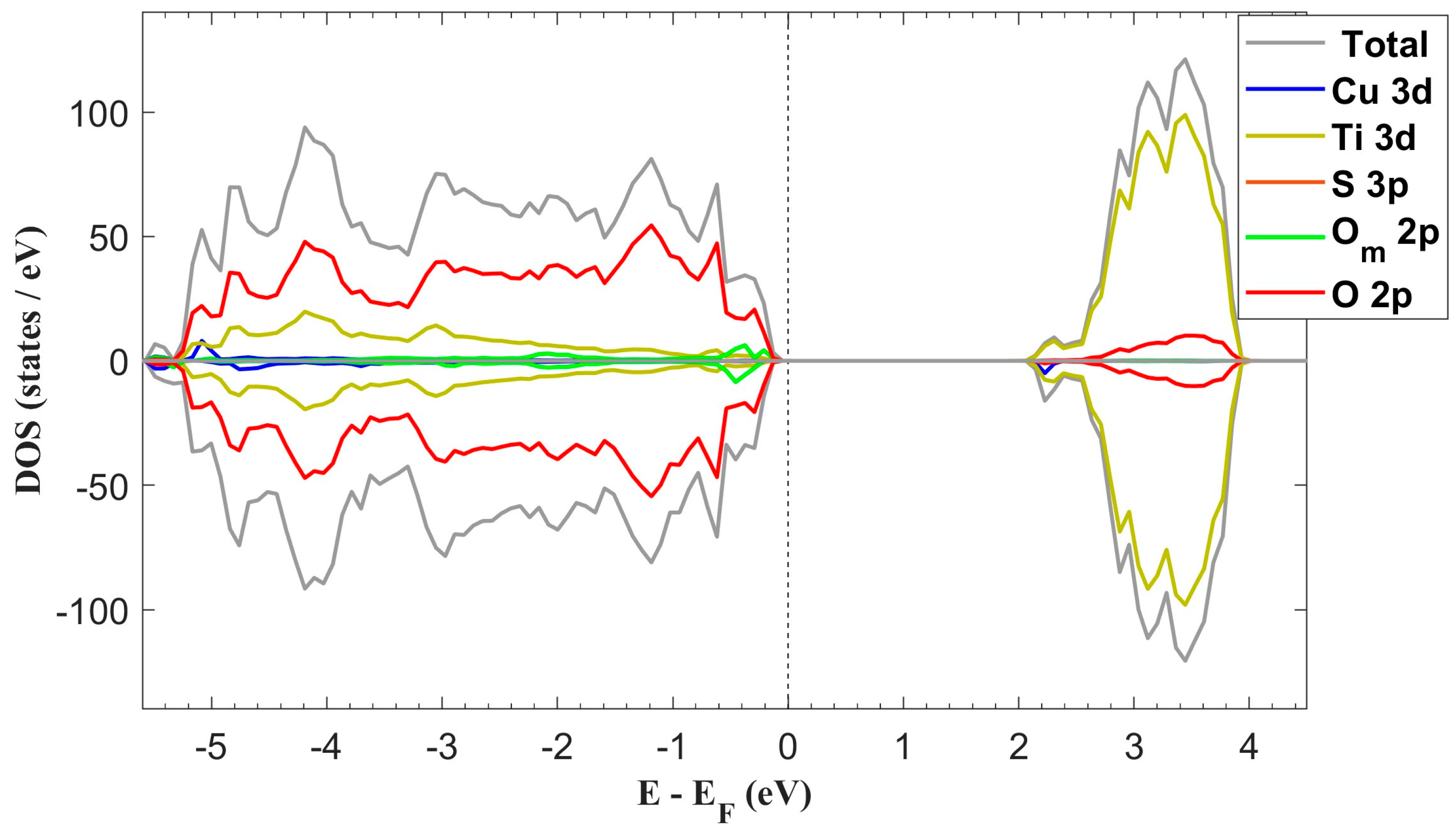
- Electronic Structure Modification: The adsorption process induces a magnetic moment and a slight reduction in the bandwidth. These electronic structure alterations are expected to impact on the electronic and catalytic properties of the material.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pastorino, P.; Prearo, M. High-mountain lakes, indicators of global change: Ecological characterization and environmental pressures. Diversity 2020, 12, 260. [Google Scholar] [CrossRef]
- Wang, X.; Wang, C.; Zhu, T.; Gong, P.; Fu, J.; Cong, Z. Persistent organic pollutants in the polar regions and the Tibetan Plateau: A review of current knowledge and future prospects. Environ. Pollut. 2019, 248, 191–208. [Google Scholar] [CrossRef]
- Vergragt, P.; Akenji, L.; Dewick, P. Sustainable production, consumption, and livelihoods: Global and regional research perspectives. J. Clean. Prod. 2014, 63, 1–12. [Google Scholar] [CrossRef]
- Ren, G.; Han, H.; Wang, Y.; Liu, S.; Zhao, J.; Meng, X.; Li, Z. Recent advances of photocatalytic application in water treatment: A review. Nanomaterials 2021, 11, 1804. [Google Scholar] [CrossRef] [PubMed]
- López, M.C.; Fernández, M.I.; Martínez, C.; Santaballa, J.A. Photochemistry for pollution abatement. Pure Appl. Chem. 2013, 85, 1437–1449. [Google Scholar] [CrossRef]
- Stashans, A.; Marcillo, F.; Castillo, D. Dopamine adsorption configurations on anatase (101) surface. Surf. Rev. Lett. 2015, 22, 1550052. [Google Scholar] [CrossRef]
- Castillo, D.; Ontaneda, J.; Stashans, A. Geometry of dopamine adsorption on rutile (110) surface. Int. J. Mod. Phys. B 2014, 28, 1450071. [Google Scholar] [CrossRef]
- Grätzel, M. Dye-sensitized solar cells. J. Photochem. Photobiol. C Photochem. Rev. 2003, 4, 145–153. [Google Scholar] [CrossRef]
- Yan, L.; Du, J.; Jing, C. How TiO2 facets determine arsenic adsorption and photooxidation: Spectroscopic and DFT studies. Catal. Sci. Technol. 2016, 6, 1526–1538. [Google Scholar] [CrossRef]
- Eddy, D.R.; Permana, M.D.; Sakti, L.K.; Sheha, G.A.N.; Solihudin; Hidayat, S.; Takei, T.; Kumada, N.; Rahayu, I. Heterophase polymorph of TiO2 (Anatase, Rutile, Brookite, TiO2 (B)) for efficient photocatalyst: Fabrication and activity. Nanomaterials 2023, 13, 704. [Google Scholar] [CrossRef]
- Gao, J.; Jia, S.; Liu, J.; Yang, X.; Chen, Z.; Wang, X. Enhanced effect of adsorption and photocatalytics by TiO2 nanoparticles embedded porous PVDF nanofiber scaffolds. J. Mater. Res. 2021, 36, 1538–1548. [Google Scholar]
- Li, Y.; Gao, Y. Interplay between water and TiO2 anatase (101) surface with subsurface oxygen vacancy. Phys. Rev. Lett. 2014, 112, 206101. [Google Scholar] [CrossRef]
- Liu, L.; Li, K.; Chen, X.; Liang, X.; Zheng, Y.; Li, L. Amino acid adsorption on anatase (101) surface at vacuum and aqueous solution: A density functional study. J. Mol. Model. 2018, 24, 107. [Google Scholar]
- Hengerer, R.; Bolliger, B.; Erbudak, M.; Grätzel, M. Structure and stability of the anatase TiO2 (101) and (001) surfaces. Surf. Sci. 2000, 460, 162–169. [Google Scholar] [CrossRef]
- Diebold, U. Structure and properties of TiO2 surfaces: A brief review. Appl. Phys. A 2003, 76, 681–687. [Google Scholar]
- Sakar, M.; Prakash, R.M.; Do, T.-O. Insights into the TiO2-based photocatalytic systems and their mechanisms. Catalysts 2019, 9, 680. [Google Scholar] [CrossRef]
- Irfan, F.; Tanveer, M.U.; Moiz, M.A.; Husain, S.W.; Ramzan, M. TiO2 as an effective photocatalyst mechanisms, applications, and dopants: A review. Eur. Phys. J. B 2022, 95, 184. [Google Scholar]
- Degefu, D.M.; Liao, Z. Photocatalytic degradation of volatile organic compounds using nanocomposite of P-type and N-type transition metal semiconductors. J. Sol-Gel Sci. Technol. 2021, 98, 605–614. [Google Scholar]
- Xing, M.; Wu, Y.; Zhang, J.; Chen, F. Effect of synergy on the visible light activity of B, N and Fe co-doped TiO2 for the degradation of MO. Nanoscale 2010, 2, 1233–1239. [Google Scholar] [CrossRef]
- Liu, M.; Piao, L.; Lu, W.; Ju, S.; Zhao, L.; Zhou, C.; Li, H.; Wang, W. Flower-like TiO2 nanostructures with exposed {001} facets: Facile synthesis and enhanced photocatalysis. Nanoscale 2010, 2, 1115–1117. [Google Scholar]
- Zhang, P.; Shao, C.; Zhang, Z.; Zhang, M.; Mu, J.; Guo, Z.; Liu, Y. TiO2@carbon core/shell nanofibers: Controllable preparation and enhanced visible photocatalytic properties. Nanoscale 2011, 3, 2943–2949. [Google Scholar] [PubMed]
- Luan, Y.; Jing, L.; Xie, Y.; Sun, X.; Feng, Y.; Fu, H. Exceptional photocatalytic activity of 001-facet-exposed TiO2 mainly depending on enhanced adsorbed oxygen by residual hydrogen fluoride. ACS Catal. 2013, 3, 1378–1385. [Google Scholar]
- Jagminas, A.; Ramanavičius, S.; Jasulaitiene, V.; Šimėnas, M. Hydrothermal synthesis and characterization of nanostructured titanium monoxide films. RSC Adv. 2019, 9, 40727–40735. [Google Scholar]
- Domaschke, M.; Zhou, X.; Wergen, L.; Romeis, S.; Miehlich, M.E.; Meyer, K.; Peukert, W.; Schmuki, P. Magnéli-phases in anatase strongly promote cocatalyst free photocatalytic hydrogen evolution. ACS Catal. 2019, 9, 3627–3632. [Google Scholar]
- Yang, F.; Zhang, H.; Wu, Z.H.; Xiang, L.; Yu, Y.X. Formation of Monodispersed Anatase TiO2 Spheres from TiOSO4 for Enhanced Hydrogen Evolution of TiO2/g-C3N4 Photocatalysts. J. Environ. Chem. Eng. 2024, 12, 114888. [Google Scholar]
- Patra, S.G.; Meyerstein, D. On the Mechanism of Heterogeneous Water Oxidation Catalysis: A Theoretical Perspective. Inorganics 2022, 10, 182. [Google Scholar] [CrossRef]
- Yu, Y.; Miao, J.; Wang, J.; He, C.; Chen, J. Facile synthesis of CuSO4/TiO2 catalysts with superior activity and SO2 tolerance for NH3-SCR: Physicochemical properties and reaction mechanism. Catal. Sci. Technol. 2017, 7, 1590–1601. [Google Scholar]
- Luna, M.D.G.; Garcia-Segura, S.; Mercado, C.H.; Lin, Y.-T.; Lu, M.-C. Doping TiO2 with CuSO4 enhances visible light photocatalytic activity for organic pollutant degradation. Environ. Sci. Pollut. Res. 2020, 27, 24604–24613. [Google Scholar]
- Yadav, S.; Arif, T.; Wang, G.; Sodhi, R.N.S.; Cheng, Y.H.; Filleter, T.; Singh, C.V. Interfacial Interactions and Tribological Behavior of Metal-Oxide/2D-Material Contacts. Tribol. Lett. 2021, 69, 91. [Google Scholar]
- Martsinovich, N.; Jones, D.R.; Troisi, A. Electronic Structure of TiO2 Surfaces and Effect of Molecular Adsorbates Using Different DFT Implementations. J. Phys. Chem. C 2010, 114, 22659–22670. [Google Scholar] [CrossRef]
- Treacy, J.P.W.; Hussain, H.; Torrelles, X.; Grinter, D.C.; Cabailh, G.; Bikondoa, O.; Nicklin, C.; Selcuk, S.; Selloni, A.; Lindsay, R.; et al. Geometric Structure of Anatase Ti O2(101). Phys. Rev. B 2017, 95, 075416. [Google Scholar]
- Rafique, M.; Shuai, Y.; Hassan, M. Structural, electronic and optical properties of CO adsorbed on the defective anatase TiO2 (101) surface; A DFT study. J. Mol. Struct. 2017, 1142, 11–17. [Google Scholar]
- Liu, Q.-L.; Zhao, Z.-Y. DFT study on microstructures and electronic structures of Pt mono-/bi-doped anatase TiO2 (101) surface. RSC Adv. 2015, 5, 17984–17992. [Google Scholar] [CrossRef]
- Wildner, M.; Giester, G. Crystal structure refinements of synthetic chalcocyanite (CuSO4) and zincosite (ZnSO4). Miner. Petrol. 1988, 39, 201–209. [Google Scholar]
- Diebold, U. The surface science of titanium dioxide. Surf. Sci. Rep. 2003, 48, 53–229. [Google Scholar]
- Lazzeri, M.; Vittadini, A.; Selloni, A. Structure and energetics of stoichiometric TiO2 anatase surfaces. Phys. Rev. B 2001, 63, 155409. [Google Scholar]
- Marabelli, F.; Parravicini, G.B.; Salghetti-Drioli, F. Optical gap of CuO. Phys. Rev. B 1995, 52, 1433–1436. [Google Scholar]
- Burdett, J.K.; Hughbanks, T.; Miller, G.J.; Richardson, J.W.; Smith, J.V. Structural electronic relationships in inorganic solids: Powder neutron diffraction studies of the rutile and anatase polymorphs of titanium dioxide at 15 and 295 K. J. Am. Chem. Soc. 1987, 109, 3639–3646. [Google Scholar]
- Henkelman, G.; Arnaldsson, A.; Jonsson, H. A Fast and Robust Algorithm for Bader Decomposition of Charge Density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Haynes, W.M. (Ed.) CRC Handbook of Chemistry and Physics, 97th ed.; CRC Press: Boca Raton, FL, USA, 2016; ISBN 978-1-4987-5429-3. [Google Scholar]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Dudarev, S.; Botton, G.; Savrasov, S.; Humphreys, C.; Sutton, A. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505. [Google Scholar] [CrossRef]
- Liechtenstein, A.; Anisimov, V.; Zaanen, J. Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators. Phys. Rev. B 1995, 52, R5467. [Google Scholar] [CrossRef] [PubMed]
- Stashans, A.; Bravo, Y. Large hole polarons in Sc-doped TiO2 crystals. Mod. Phys. Lett. B 2013, 27, 1350113. [Google Scholar] [CrossRef]
- Mishra, A.K.; Roldan, A.; de Leeuw, N.H. CuO Surfaces and CO2 Activation: A Dispersion-Corrected DFT+U Study. J. Phys. Chem. C 2016, 120, 2198–2214. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Neugebauer, J.; Scheffler, M. Adsorbate-substrate and adsorbate-adsorbate interactions of Na and K adlayers on Al (111). Phys. Rev. B 1992, 46, 16067. [Google Scholar] [CrossRef] [PubMed]
- Makov, G.; Payne, M. Periodic boundary conditions in ab initio calculations. Phys. Rev. B 1995, 51, 4014. [Google Scholar] [CrossRef]

| Atom | Atomic Displacements (Å) | ||
|---|---|---|---|
| SXRD | DFT | Present Work | |
| O1 | 0.07 ± 0.01 | 0.14 | 0.08 |
| O2 | 0.15 ± 0.01 | 0.33 | 0.39 |
| O3 | 0.08 ± 0.01 | 0.16 | 0.03 |
| O4 | 0.01 ± 0.01 | 0.07 | 0.04 |
| Ti1 | 0.03 ± 0.01 | 0.01 | 0.03 |
| Ti2 | 0.15 ± 0.01 | 0.28 | 0.15 |
| Distance (Å) | Angle (°) | ||||
|---|---|---|---|---|---|
| Atoms | Exp. | Modeled | Atoms | Exp. | Modeled |
| S–Om1 | 1.46 | 1.44 | S–Om4–Cu | 123.44 | 94.04 |
| S–Om2 | 1.46 | 1.60 | Om1–S–Om3 | 110.52 | 119.39 |
| S–Om3 | 1.46 | 1.44 | |||
| S–Om4 | 1.52 | 1.60 | |||
| Cu–Om4 | 2.04 | 1.85 | |||
| Cu–Om3 | 3.71 | 3.46 | |||
| Cu–Om2 | 3.25 | 1.85 | |||
| Cu–Om1 | 4.33 | 3.51 | |||
| Configuration | Eads (eV) |
|---|---|
| a | –2.06 |
| b | –4.31 |
| c | –1.25 |
| d | –4.31 |
| e | –4.00 |
| f | –4.31 |
| g | –2.67 |
| Bond Length (Å) | Angle (°) | ||||
|---|---|---|---|---|---|
| Atoms | Free Molecule | Adsorbed Molecule | Atoms | Free Molecule | Adsorbed Molecule |
| S–Om1 | 1.45 | 1.53 | Ti1–Om1–S | - | 132.57 |
| S–Om2 | 1.57 | 1.42 | S–Om3–Ti2 | - | 132.62 |
| S–Om3 | 1.45 | 1.53 | S–Om4–Cu | 93.82 | 112.29 |
| S–Om4 | 1.57 | 1.51 | Om1–S–Om3 | 116.04 | 107.58 |
| Cu–Om4 | 1.91 | 1.92 | |||
| Atoms | Pristine Surface | Adsorbed Molecule | Atoms | Pristine Surface | Adsorbed Molecule |
| Om1–Ti1 | - | 2.02 | Oa–Ti1–Om1 | - | 102.16 |
| Om3–Ti2 | - | 2.02 | Om3–Ti2–Ob | - | 102.24 |
| Ti1–Oa | 1.98 | 1.97 | Ti1–O1–Tia | 100.96 | 101.53 |
| Ti2–Ob | 1.98 | 1.97 | Ti2–O3–Tic | 100.96 | 101.52 |
| Cu–O1 | - | 1.94 | Tia–O2–Tic | 155.23 | 152.98 |
| Cu–O2 | - | 2.02 | Cu–O2–Tib | - | 108.19 |
| Cu–O3 | - | 1.94 | |||
| O1–Tia | 1.94 | 1.96 | |||
| O2–Tib | 2.06 | 2.16 | |||
| O3–Tic | 1.94 | 1.96 | |||
| Atomic Charge (e) | ||
|---|---|---|
| Atom | Free Molecule | Adsorbed Molecule |
| Cu | 1.00 | 1.14 |
| S | 3.58 | 3.77 |
| Om1 | –1.27 | –1.26 |
| Om2 | –1.00 | –1.27 |
| Om3 | –1.27 | –1.26 |
| Om4 | –1.04 | –1.23 |
| Atom | Pristine Surface | Adsorbed Molecule |
| Ti1 | 2.26 | 2.32 |
| Ti2 | 2.26 | 2.32 |
| Tia | 2.30 | 2.30 |
| Tib | 2.26 | 2.24 |
| Tic | 2.30 | 2.30 |
| O1 | –1.03 | –1.09 |
| O2 | –1.18 | –1.23 |
| O3 | –1.03 | –1.09 |
| Oa | –1.20 | –1.19 |
| Ob | –1.20 | –1.19 |
| Bond | Covalent Radius (Å) Atom 1 | Covalent Radius (Å) Atom 2 | Expected Covalent Length (Å) | Observed Distance (Å) | Interpretation |
|---|---|---|---|---|---|
| Cu–Osurface | 1.22 (Cu) | 0.64 (O) | 1.86 | 1.94 | Covalent, slightly elongated |
| Om–Ti | 0.64 (O) | 1.48 (Ti) | 2.12 | 2.34 | Partial ionic character |
| S–Om | 1.04 (S) | 0.64 (O) | 1.68 | 1.72 | Very close to covalent |
| Bond | Electronegativity Atom 1 | Electronegativity Atom 2 | Δχ | Predicted Bond Type |
|---|---|---|---|---|
| Cu–Osurface | 1.90 (Cu) | 3.44 (O) | 1.54 | Polar Covalent |
| Om–Ti | 3.44 (O) | 1.54 (Ti) | 1.90 | Ionic-Covalent |
| S–Om | 2.58 (S) | 3.44 (O) | 0.86 | Predominantly Covalent |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maldonado, F.; Castillo, D.; Aguilar, S.; Carrión, J.; Sánchez, A. Adsorption of CuSO4 on Anatase TiO2 (101) Surface: A DFT Study. Inorganics 2025, 13, 114. https://doi.org/10.3390/inorganics13040114
Maldonado F, Castillo D, Aguilar S, Carrión J, Sánchez A. Adsorption of CuSO4 on Anatase TiO2 (101) Surface: A DFT Study. Inorganics. 2025; 13(4):114. https://doi.org/10.3390/inorganics13040114
Chicago/Turabian StyleMaldonado, Frank, Darwin Castillo, Silvio Aguilar, Javier Carrión, and Aramis Sánchez. 2025. "Adsorption of CuSO4 on Anatase TiO2 (101) Surface: A DFT Study" Inorganics 13, no. 4: 114. https://doi.org/10.3390/inorganics13040114
APA StyleMaldonado, F., Castillo, D., Aguilar, S., Carrión, J., & Sánchez, A. (2025). Adsorption of CuSO4 on Anatase TiO2 (101) Surface: A DFT Study. Inorganics, 13(4), 114. https://doi.org/10.3390/inorganics13040114








