Abstract
We completed B3LYP and B3PW computations for AO- and BO2-terminated (001) as well as AO3- and B-terminated (111) surfaces of BSO, BTO, STO, PTO, CTO, BZO, SZO, and CZO perovskites. In particular, we performed the first B3LYP computations for polar BSO (111) surfaces. We observed that most of the upper-layer atoms for AO- and BO2-terminated ABO perovskite (001) surfaces relax inward. In contrast, practically all second-layer atoms relax upward. Lastly, almost all third-layer atoms relax inward. This tendency is less pronounced for atomic relaxation of first, second, and third layer atoms for AO3- and B-terminated ABO perovskite (111) surfaces. For almost all ABO perovskites, their (001) surface rumplings s are considerably larger for AO-terminated compared to BO2-terminated surfaces. On the contrary, the ABO perovskite (001) surface energies, for both AO and BO2-terminations, are essentially equivalent. The ABO perovskite polar (111) surface energies are always substantially larger than their neutral (001) surface energies. In most cases, the surface energies of AO3-terminated ABO perovskite polar (111) surfaces are considerably larger than their B-terminated surface energies. Our computations illustrate a noticeable boost in the B-O bond covalency near the BO2-terminated (001) surface related to the bulk. Our computed ABO perovskite bulk Γ-Γ band gaps are almost always reduced near the AO- and BO2-terminated neutral (001) surfaces as well as in most cases also near the AO3- and B-terminated polar (111) surfaces.
1. Introduction
Crucial role of surface as well as interface phenomena taking place in the ABO3 (in the following called ABO for simplicity) perovskites are very serious issues in today’s condensed matter physics [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]. All BaSnO3 (BSO), BaTiO3 (BTO), SrTiO3 (STO), PbTiO3 (PTO), CaTiO3 (CTO), BaZrO3 (BZO), SrZrO3 (SZO), and CaZrO3 (CZO) perovskites belong to the group of ABO perovskite oxides [26,27,28,29]. In our case, A = Ba, Sr, Pb, or Ca, whereas B = Sn, Ti, or Zr. ABO perovskites have plenty of commercially essential functions. Applications include actuators, capacitors, charge storage apparatus, and countless others [30,31]. For example, BSO may be used as the protonic conductor [32], with application potential for fuel cells [32]. BTO is examined as one of the inexpensive preparation price substitutes for wide band gap semiconductors with application prospects in numerous optoelectric devices [33]. Doped STO is an excellent anode material for solid oxide fuel cells [34] as well as a perfect choice for photocatalytic applications [35]. PTO ferroelectric perovskite is an interesting material for numerous high-temperature as well as high- frequency piezoelectric applications [36]. CTO perovskite oxide has received recognition in the last years due to strong catalytic activity [37]. BZO perovskite is attractive as a thermal barrier coating material, used in gas turbine engines, which work at elevated temperatures [38]. SZO perovskite has been widely used as a catalyst [39], luminescent material [40], and proton conductor [41]. CZO perovskite has numerous technologically important applications, including capacitors and resonators, and also as humidity sensors [42]. For that reason, it is evident that in the last 25 years, ABO perovskite (001) surfaces were massively explored experimentally as well as theoretically [43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82].
In contrast to the ABO perovskite neutral (001) surfaces, their charged, polar, and thereby very complex (111) surfaces are considerably less studied. For example, to the best of our knowledge, BSO (111) surfaces have never been investigated before, neither experimentally nor theoretically. Accordingly, in this paper, we performed the first in the world ab initio calculations, dealing with polar and charged BSO (111) surfaces. BTO perovskite (111) surfaces were analyzed experimentally by Hagendorf et al. [83,84] by means of STM, XPS, and LEED methods. Recently, Chun et al. [8] examined the (111) surface termination of a BTO single crystal employing the combined density functional theory (DFT) as well as X-ray photoelectron spectroscopy (XPS) methods. They computed the (111) surface stability of the BTO stoichiometric Ti and BaO3-terminations applying the DFT + U formalism [8]. Finally, Eglitis [85] performed ab initio hybrid DFT computations for BTO (111) surfaces and demonstrated that the surface energy of the BaO3-terminated (111) surface is considerably larger than for the Ti-terminated (111) surface. Pojani et al. [86] performed semi-empirical Hartree–Fock (HF) calculations and discussed the polarity effects on the STO (111) surfaces. Biswas et al. [87] detected the upper atomic layer of STO (001), (011), and (111) surfaces using the time of flight mass spectroscopy. These authors found [87] that all (001), (011), and (111) surface orientations exhibit the Ti-rich surface [87]. Sekiguchi et al. [88] investigated the changes in STO (111) polar surface structures by AFM, AES, and XPS experimental techniques as a function of the atmosphere [88]. Tanaka et al. [89] observed the clean (111) surfaces of reduced STO crystals by means of STM and RHEED experiments [89]. They observed two different STO (111) surface structures [89]. Namely, the first possible STO (111) surface structure has the SrO3-x outermost layer, whereas the second possible STO (111) surface structure has the Ti outermost layer [89]. Lastly, Eglitis [90] performed ab initio computations of SrO3- and Ti-terminated STO (111) polar surface atomic relaxations, surface rumplings, and energies, as well as charge redistributions and Γ-Γ band gaps [90]. Using the GGA exchange-correlation functional, Pang et al. [91] calculated the structural and electronic properties as well as the stabilities of four different terminations of cubic PTO (111) surfaces. For instance, they computed the directly cleaved Ti- and PbO3-terminated as well as constructed TiO- and PbO2-terminated PTO (111) polar surfaces [91]. Eglitis [85] performed ab initio B3LYP calculations for PbO3 and Ti-terminated PTO (111) surfaces and found that for both terminations, the PTO (111) surface energies are considerably larger than the PTO (001) surface energies [3]. Liu et al. [92] constructed the stoichiometric as well as nonstoichiometric terminations for the CTO (111) surfaces. The LDA computations for the CTO (111) surface and cleavage energies, as well as surface electronic and atomic structure, and surface grand potential, were performed [92]. Eglitis [90,93] performed ab initio computations for the polar CTO (111) surfaces using the B3LYP hybrid exchange-correlation functional. The atomic and electronic structure as well as surface energies and Ti-O chemical bond populations of the Ti and CaO3-terminated polar CTO (111) surfaces were computed [90,93]. The only existing ab initio computations dealing with BaO3- and Zr-terminated polar BaZrO3 (111) surfaces were performed by Eglitis [94,95]. Namely, these authors performed ab initio B3LYP computations for BZO polar (111) surface atomic relaxations and electronic structure as well as energetics for two possible BaO3 and Zr polar (111) surface terminations [94,95]. The only available ab initio computations dealing with polar SrZrO3 (111) surfaces were performed by Eglitis et al. [85,96]. Specifically, Eglitis et al. [85,96] performed ab initio hybrid B3LYP computations for surface relaxations and electronic structure as well as surface energies of Zr- and SrO3-terminated SrZrO3 perovskite polar (111) surfaces. Lastly, the only recent existing and preliminary ab initio B3LYP computations dealing with CZO perovskite polar (111) CaO3- and Zr-terminated surface atomic relaxations and surface energies were performed by Eglitis and Jia [11].
According to the XRD measurement results obtained by Janifer et al. [97], barium stannate (BSO) is a single-phase cubic perovskite [97,98]. Moreover, BSO has a wide optical band gap equal to 3.1 eV [97,98], and the cubic lattice parameter a is identical to 4.119 Å [97,98]. BTO perovskite exhibits three phase transitions [99,100]. At high temperatures, BTO perovskite has a cubic structure with a symmetrical group ) [99]. The BTO perovskite structure changes from this cubic ) to a tetragonal structure (P4mm) at 403 K temperature [99]. Then, at 278 K temperature, the BTO perovskite structure changes to orthorhombic (Amm2) [99]. Lastly, the BTO perovskite structure changes to rhombohedral (R3m) at a temperature of 183 K [99,100]. According to experiments performed by Wemple [101], the BTO room temperature band gaps are 3.38 eV and 3.27 eV, accordingly, for light polarized parallel as well as perpendicular to the ferroelectric c axis [101]. STO perovskite has only one structural phase transition at a temperature of 110 K [102]. This phase transition reduces the STO perovskite symmetry from high symmetry cubic to tetragonal [102]. The experimentally detected STO perovskite direct (Γ-Γ) band gap energy in the room temperature cubic phase is equal to 3.75 eV [103]. PTO perovskite displays the single-phase transition at 763 K temperature from the high-temperature cubic phase to the tetragonal ferroelectric ground state [104]. The PTO perovskite Γ-Γ band gap, measured at room temperature in its tetragonal ferroelectric ground state, is equal to 3.4 eV [105]. Ali et al. [106], using the careful Rietveld analysis of the neutron as well as X-ray powder diffraction data, discovered that the CTO perovskite displays two structural phase transitions [106]. Namely, from a high-temperature cubic CTO structure ) at 1634 ± 13 K temperature to a tetragonal structure (I4/mcm) [106]. Finally, at 1498 ± 25 K temperature, CTO perovskite displays a phase transition to the ground state orthorhombic structure (Pbnm) [106]. The CTO perovskite Γ-Γ band gap, according to the experimental results obtained by Ueda et al. in the orthorhombic phase [107], is approximately 3.5 eV [107]. According to Knight [108], the BZO perovskite is cubic at all measured temperatures within the temperature range from 4.2 K to 450 K [108]. Namely, BZO always has the cubic perovskite structure with the symmetry group ) [108]. Therefore, the experimental BZO Γ-Γ band gap is equal to 5.3 eV [105]. SZO perovskite goes through three structural phase transitions [109]. Initially, below 970 K temperature, SZO perovskite is orthorhombic with the symmetry group Pnma [109]. In the temperature range between 970 K and 1020 K, the SZO perovskite belongs to the other orthorhombic symmetry group Cmcm [109]. At 1020 K temperature, SZO perovskite transfers into the tetragonal structure with the symmetry group I4/mcm [109]. Finally, at a temperature above 1360 K, the SZO perovskite turns into a cubic structure with the symmetry group ) [109]. According to the optical conductivity measurements performed by Lee et al. [110], the SZO Γ-Γ gap within the orthorhombic phase, which is stable at room temperature, is equal to 5.6 eV [110]. CZO perovskite, at low temperatures, has an orthorhombic structure (Pbnm), which is stable up to temperatures of 2173 K ± 100 [111,112]. At higher temperatures, CZO perovskite has a cubic structure with a symmetrical group ) [111,112]. According to Rosa et al. [113], the experimental CZO band gap of the orthorhombic structure at room temperature is equal to 5.7 eV [113].
The intention of our review paper was to execute essential additional computations dealing mostly with BSO neutral (001) and especially polar (111) surfaces that have never been studied before. After completing necessary supplementary first principles computations for ABO perovskite (001) as well as (111) surfaces, we carefully analyzed our results and identified the systematic tendencies frequent for all eight BSO, BTO, STO, PTO, CTO, BZO, SZO, and CZO perovskite neutral (001) [43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,114,115,116,117,118,119,120] and polar (111) [83,84,85,86,87,88,89,90,91,92,93,94,95,96] surfaces. This paper research primarily investigates the surface properties. Concretely, the atomic relaxation, surface energy, chemical bond covalency, as well as electronic band gaps of ABO perovskites (e.g., BSO, BTO, STO, etc.), are established at both neutral (001) and polar (111) surfaces. The study aims to enhance the understanding of how surface characteristics influence the properties of these materials. We want to emphasize that the topic dealing with the theoretical investigation of ABO perovskite surfaces is both original and highly relevant to the field of condensed matter physics and materials science. While ABO perovskites have been extensively studied, the specific examination of polar (111) surfaces in the context of BSO, particularly with B3LYP computations, addresses a notable gap in the literature. Previous research primarily focused on (001) surfaces [1,2,3,4,5,7,8,9,10,11,22,43,45,48,50,56,57,58,59,60,61], making this investigation significant for understanding surface phenomena that impact applications in electronics and catalysis. This study adds considerable depth to the existing literature by providing the first computational analysis of polar (111) surfaces for BSO, and it includes a comprehensive study among various perovskites. The detailed examination of atomic relaxations, surface energies, and bond covalency enhances understanding of how surface properties differ for these ABO perovskite materials compared to bulk behavior, offering insights that can guide future experimental and theoretical investigations.
2. Simulation Approach and Surface Models
In order to carry out the first principles of DFT-B3PW or DFT-B3LYP computations, we employed the CRYSTAL computer program [121]. The CRYSTAL code makes use of Gaussian-type functions (GTFs) localized on all perovskite atoms. They are the basis for the expansion of the crystalline orbitals [122]. The superiority of the CRYSTAL ab initio code [121,122] is its capability to compute confined 2D (001) and (111) ABO perovskite slabs without forced periodicity along the z-axis [121]. In order to make use of the linear combination of atomic orbitals (LCAO-GTF) method [121,122], it is advantageous to utilize the optimized basis sets (BS) [121]. The optimized BS for BTO, STO, and PTO perovskites was developed in Ref. [123]. The BS for Sn was taken from the CRYSTAL computer code [121]. The relevant BS, used for CTO, BZO, SZO, and CZO perovskites and their surfaces, are described in Refs. [2,124,125,126]. All our ABO perovskite bulk as well as (001) and (111) surface computations were performed by means of the B3PW [127,128] or B3LYP [129] hybrid exchange-correlation functionals. Both B3PW and B3LYP functionals give comparable results for ABO perovskites [2,3,4,9,56]. However, it is important to note that the hybrid exchange-correlation functionals, like B3PW or B3LYP, allow us to achieve an excellent agreement with the experiment for the Γ-Γ band gaps of the related complex oxide materials, whereas the GGA-PBE and LDA exchange-correlation functionals, as a rule, underestimate the relevant Γ-Γ band gaps [2,3,4,9,56]. On the other hand, it is well known that the HF approach considerably overestimates the Γ-Γ band gaps [2,3,4,9,56]. We performed the reciprocal space integration by checking out the Brillouin zone for the 5 atom ABO perovskite cubic unit cell, applying the 8 × 8 × 8 times increased Pack Monkhorst mesh [130] for the ABO perovskite bulk [2,3,4,11,124,125,126,131] as well as the 8 × 8 × 1 times increased mesh for their (001) and (111) surfaces [2,3,4,11,85,90,124,125,126,131].
The ABO perovskite (001) surfaces were described using 2D slabs (Figure 1 and Figure 2). These slabs subsist from nine planes located perpendicular to the [001] crystal direction.
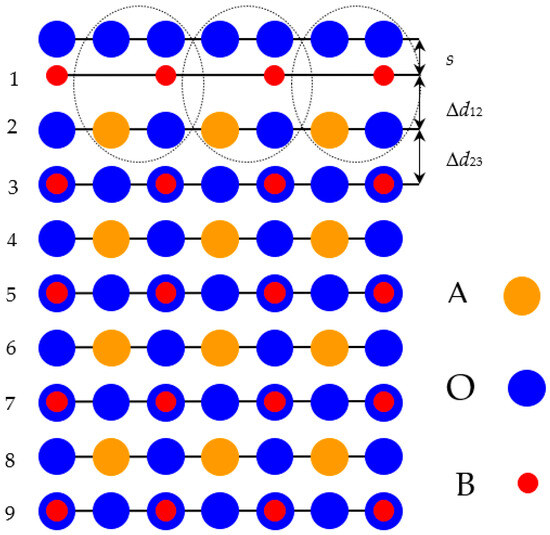
Figure 1.
Outline of the BO2-terminated (001) surface of ABO–type perovskite enclosing nine atomic layers.

Figure 2.
Outline of the AO-terminated (001) surface of ABO–type perovskite enclosing nine atomic layers.
Namely, to compute ABO perovskite (001) surfaces, we considered slabs consisting of nine alternating BO2 and AO layers (Figure 1 and Figure 2). The mirror symmetries of the slabs were retained regarding their central layers (Figure 1 and Figure 2). Our computed 23-atom-containing slab with BO2-terminated surfaces as well as the 22-atom slab with AO-terminated surfaces are depicted in Figure 1 and Figure 2, respectively. Both these slabs are non-stoichiometric. They have unit-cell formulas A4B5O14 and A5B4O13, respectively (Figure 1 and Figure 2). The succession of the ABO-perovskite (001) surface layers as well as the definitions of the interplane separations Δd12, Δd23, and the surface rumpling s are pictured in Figure 1.
In contrast to the ABO perovskite neutral (001) surfaces, the polar (111) surfaces subsist of charged AO3 and B planes, as depicted in Figure 3. The ABO perovskite polar (111) surfaces have been characterized with 2D slabs, subsisting of nine planes perpendicular to the [111] direction in the crystal. In order to compute the ABO perovskite polar (111) surfaces, we employed slabs subsisting of nine alternating B and AO3 layers (Figure 3 and Figure 4). The first slab is terminated by B planes and subsists of a supercell consisting of 21 atoms (B-AO3-B-AO3-B-AO3-B-AO3-B) (Figure 4a). Another slab is terminated by AO3 planes (Figure 4b). The corresponding supercell contains 24 atoms (AO3-B-AO3-B-AO3-B-AO3-B-AO3) (Figure 4b). Both these slabs are non-stoichiometric (Figure 3 and Figure 4). They have unit cell formulas A4B5O12 and A5B4O15, respectively (Figure 4). As we know from earlier ab initio computations, devoted to the polar ABO perovskite (111) surfaces [11,86,92,132,133,134], the powerful electron reallocation takes place for these terminations in order to eliminate the polarity [11,86,92,132,133,134]. Consequently, the AO3- as well as B-terminated ABO-perovskite (111) surfaces maintain their insulating character, and such computations can thereby be realized [11,86,92,132,133,134].
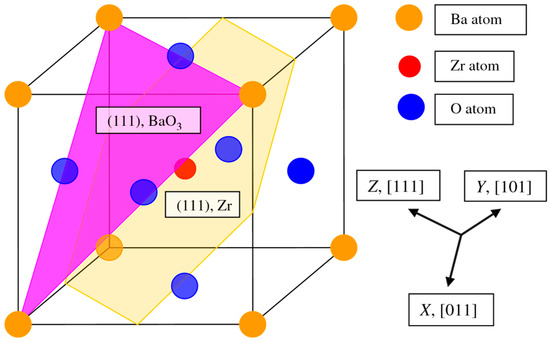
Figure 3.
ABO perovskite structure displaying two (111) surface terminations: AO3 and B.

Figure 4.
Outline of slab constructions used to explore ABO perovskite (111) surfaces. (a) Non-stoichiometric ABO slab consisting of 9 layers with B-terminated (111) surfaces. (b) Non-stoichiometric ABO slab consisting of 9 layers with AO3-terminated (111) surfaces.
The first step for the ABO perovskite (001) and (111) surface energy computations is to calculate the relevant cleavage energies. Our computed cleavage energies are equally shared amid the created surfaces [2,3,4,11,85,94,135]. Namely, the ABO perovskite (001) and (111) surfaces arise as a result of simultaneous (001) as well as (111) cleaved perovskite crystal [2,3,4,11,85,94,135]. In our executed ABO perovskite (001) surface cleavage energy computations, the nine-layer AO- and BO2-terminated slabs together embody 45 atoms corresponding to nine ABO perovskite unit cells:
where Eslabunr(AO) and Eslabunr(BO2) are the unrelaxed AO- and BO2-terminated ABO perovskite nine layer (001) slab total energies. Ebulk denotes the total energy of the ABO perovskite bulk unit cell containing five atoms. The factor equal to ¼ implies that four surfaces were generated due to the ABO perovskite (001) cleavage. In the second step, the AO- and BO2-terminated nine-layer (001) slab relaxation energies, taking into account the relaxation of slabs from both sides, were computed, as follows:
where λ is AO or BO2. Eslabrel(λ) is relaxed from both sides with regard to the AO- or BO2-terminated (001) slab total energy. Eslabunr(λ) is the total energy for unrelaxed AO or BO2-terminated ABO perovskite (001) slab. Lastly, the AO- or BO2-terminated ABO perovskite (001) surface energy should be calculated using the following equation:
Esurfunr(AO + BO2) = ¼ [Eslabunr(AO) + Eslabunr(BO2) − 9Ebulk],
Erel(λ) = ½ [Eslabrel(λ) − Eslabunr(λ)],
Esurf(λ) = Esurfunr(AO + BO2) + Erel(λ).
With this, we computed the ABO perovskite (111) surface as well as cleavage energies. Again, B- and AO3-terminated ABO perovskite (111) surfaces are complementary. For that reason, the cleavage energy is the same for both AO3 and B-terminated ABO perovskite (111) surfaces. Thereby, the cleavage energy for the complementary surface Ecl(AO3 + B) may be computed from the total energies of nine-layer unrelaxed AO3- and B-terminated ABO perovskite (111) slabs, as follows:
where Eslabunr(B) is our computed total energy of unrelaxed 21 atoms containing B-terminated ABO perovskite nine-layer (111) slab. Eslabunr(AO3) is our computed total energy for 24 atoms containing a nine-layer unrelaxed AO3-terminated ABO perovskite (111) slab. The relaxation energies for AO3- and B-terminated ABO perovskite (111) surfaces can be obtained via the following equation:
where β = AO3 or B describes the ABO perovskite (111) surface termination. In the end, the ABO perovskite AO3- or B-terminated (111) surface energy is equal to the sum of the cleavage (4) and relaxation (5) energies, as follows:
Ecl(AO3 + B) = ¼ [Eslabunr(B) + Eslabunr(AO3) − 9Ebulk],
Erel(β) = ½ [Eslabrel(β) − Eslabunr(β)],
Esurf(β) = Ecl(AO3 + B) + Erel(β)
3. Computation Results for ABO Perovskite Bulk as Well as (001) and (111) Surfaces
3.1. ABO Perovskite Bulk Atomic and Electronic Structure
As the starting point of our B3LYP and B3PW computations, we computed the theoretical bulk lattice constants for BSO, BTO, STO, PTO, CTO, BZO, SZO, and CZO perovskites [2,3,4,90,94,123,124,125,126,131] (Table 1). We matched our computation results with the accessible experimental data [106,136,137,138,139,140] (Table 1). For some ABO perovskites, we also performed the theoretical lattice constant computations by means of the ab initio Hartree–Fock (HF) method [121,122,141,142,143]. For our ab initio DFT [144,145] bulk lattice constant computations, we employed the Generalized Gradient approximation [146] suggested by Perdew and Wang (PWGGA) [127,128]. As we can see from Table 1, according to our B3PW computation results, the SZO and BTO perovskite bulk lattice constants (4.155 Å [131] and 4.008 Å [3], respectively) are almost in ultimate agreement with the relevant experimental data (4.154 Å [140] and 4.00 Å [137], respectively). It must be pointed out that for BSO, BTO, STO, PTO, and SZO perovskites, our B3LYP computed bulk lattice constants (4.107 Å, 4.04 Å, 3.94 Å, 3.96 Å, and 4.195 Å, respectively) are larger than the relevant B3PW computed bulk lattice constants (4.087 Å, 4.008 Å, 3.904 Å, 3.936, Å, and 4.155 Å, respectively) (Table 1).

Table 1.
B3LYP-, B3PW-, PWGGA-, and HF-computed bulk lattice constants (in Å) for the BSO, BTO, STO, PTO, CTO, BZO, SZO, and CZO perovskite bulk. The experimental data (in Å) are listed for comparison.
In order to describe the covalency effects, effective atomic charges, and chemical bondings for the ABO perovskites bulk and their (001) as well as (111) surfaces, we employed a classical Mulliken population analysis [147,148,149,150].
Our B3LYP computed effective atomic charges and bond populations for BSO as well as for seven other perovskites are collected in Table 2. As we can see from Table 2, our B3LYP computed effective atomic charges for the BSO bulk are (+1.825e) for the Ba atom, (+2.122e) for the Sn atom, and (−1.316e) for the O atom (Table 2). It is worth noting that our computed Sn atom charge in the BSO perovskite (+2.122e) is the smallest B atom charge among all eight computed ABO perovskites (Table 2). Our B3LYP-computed Sn-O chemical bond population (+0.284e) in BSO perovskite (Table 2) is considerably larger than the respective B-O chemical bond populations for the other seven computed ABO perovskites, ranging from only (+0.084e) for CTO to (+0.108e) for the BZO perovskite.

Table 2.
Our B3LYP or B3PW computed effective atomic charges Q (e) as well as bond populations P (e) in BSO, BTO, STO, PTO, CTO, BZO, SZO, and CZO perovskites.
Our B3LYP- (3.65 eV) or B3PW-computed (3.68 eV) bulk Γ-Γ band gaps for BSO perovskite are in a more acceptable agreement with the experimental result of (3.1 eV) [97,98] than our HF (12.11 eV) or PWGGA (1.71 eV) computation results (Table 3).

Table 3.
Our B3LYP-, B3PW-, PWGGA-, and HF-computed Γ-Γ band gaps (in eV) for ABO perovskite bulk. Experimental ABO perovskite bulk Γ-Γ band gaps are listed for comparison (in eV).
As we can see from Figure 5 and Table 3, our B3PW-computed BTO bulk Γ-Γ band gap is equal to 3.55 eV [123]. It is comparable with our B3LYP-computed BTO bulk Γ-Γ band gap equal to 3.49 eV (Table 3). It is worth noting that our HF-computed BTO bulk Γ-Γ band gap is really huge (11.73 eV), whereas the PWGGA computed band gap is comparatively small, only 1.97 eV (Table 3). There are no experimental data available for the high-temperature cubic BTO bulk Γ-Γ band gap. Nevertheless, Wemple suggested that the BTO room temperature Γ-Γ band gaps are equal to 3.38 and 3.27 eV for parallel and perpendicular, respectively, polarized light to the ferroelectric axis c [101].
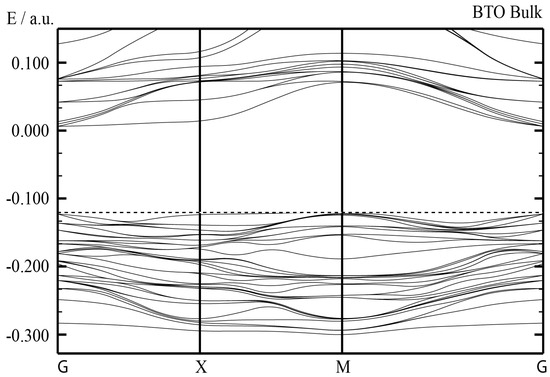
Figure 5.
Our B3PW computed electronic BTO bulk band structure (Table 3). The dashed line correspond to the bulk valence band maximum.
As it is possible to see from Figure 6 and Table 3, our B3PW-computed PTO bulk Γ-Γ band gap is equal to 4.32 eV [123]. It is in the same range as our B3LYP-computed PTO bulk Γ-Γ band gap equal to 4.15 eV [123] (Table 3). It is interesting to notice that our HF-computed PTO bulk Γ-Γ band gap is very large and equal to (12.74 eV) [123]. Just the opposite, the PWGGA computed PTO bulk Γ-Γ band gap is very small, only 2.61 eV (Table 3). To the best of our knowledge, there are no experimental data available for the high-temperature cubic PTO bulk Γ-Γ band gap. As it is possible to see from Table 3, the PWGGA computed STO bulk Γ-Γ band gap is equal to 2.31 eV [123], whereas the HF computed respective band gap is 5.34 times larger and equal to 12.33 eV. It is important to note that STO bulk Γ-Γ band gaps, computed by means of B3LYP (3.89 eV) and B3PW (3.96 eV) hybrid exchange-correlation functionals, almost coincide [123]. They are both in good agreement with the available experimental data for the STO bulk Γ-Γ band gap (3.75 eV) [103].

Figure 6.
Our B3PW computed electronic PTO bulk band structure (Table 3). The dashed line correspond to the bulk valence band maximum.
Our PWGGA-computed BZO bulk Γ-Γ band gap is very small, equal to only 3.24 eV [131] (Table 3). In contrast, our HF computed BZO bulk Γ-Γ band gap is exactly four times larger (12.96 eV) (Table 3) [131]. Again, almost equal and in fair agreement with the experiment (5.3 eV) [105] are our B3LYP- (4.79 eV) [94] as well as B3PW-computed (4.93 eV) (Figure 7) bulk Γ-Γ band gaps.

Figure 7.
Our B3PW-computed electronic band structure for BZO bulk. The dashed line correspond to the bulk valence band maximum.
As we can see from Figure 8 and Table 3, our PWGGA-computed ABO perovskite bulk Γ-Γ band gaps are in the energy range from 1.71 eV (BSO) to 3.53 eV (SZO). The PWGGA-computed ABO perovskite bulk Γ-Γ band gaps (Figure 8) are always considerably smaller than relevant experimental values as well as B3LYP-, B3PW-, and HF-computed respective band gaps (Table 3). As we can see from Figure 8, our B3PW- and B3LYP-computed ABO perovskite bulk Γ-Γ band gaps always are very close and in fair agreement with the available experimental data (Table 3). In contrast, our HF-computed ABO perovskite Γ-Γ bulk band gaps are in the energy range from 11.73 eV (BTO) to 13.54 eV (SZO) and always, to a very great extent, overestimate the relevant experimental data (Table 3 and Figure 8).

Figure 8.
Our computed and experimental bulk Γ-Γ band gaps for seven ABO perovskites derived by different theoretical and experimental methods: (1) PWGGA; (2) Experiment; (3) B3LYP; (4) B3PW; (5) HF.
3.2. ABO Perovskite (001) Surface Atomic and Electronic Structure
Our B3LYP or B3PW computation results for the upper two- or three-layer atomic relaxations of BO2- or AO-terminated ABO perovskite (001) surfaces (Table 4 and Table 5). As we can see from Table 4 and Table 5, in most cases, the ABO perovskite BO2- and AO-terminated (001) surface upper layer atoms relax inward, toward the bulk, the second surface layer atoms relax outward, and third surface layer atoms, again, relax inward. For the AO-terminated ABO perovskite (001) surface upper two layers (Table 5), the metal atom relaxation magnitudes are always considerably larger than the respective oxygen atom relaxation magnitudes. The largest relaxation magnitude between all upper layer atoms exhibits the CaO-terminated CTO (001) surface upper layer Ca atom (−10.01% of a0) (Table 5). Between all second-layer atoms, the largest relaxation magnitude exhibits the TiO2-terminated PTO (001) surface Pb atom (+5.32% of a0) (Table 4).

Table 4.
Our B3LYP- or B3PW-computed atomic relaxation (in % of a0) for BO2-terminated BSO, BTO, STO, PTO, CTO, BZO, SZO, and CZO (001) surfaces.

Table 5.
Our B3LYP- or B3PW-computed atomic relaxation (in % of a0) for AO-terminated BSO, BTO, STO, PTO, CTO, BZO, SZO, and CZO (001) surfaces.
In order to obtain a comparison between experimental results as well as our B3LYP- or B3PW-computed ABO perovskite (001) surface atomic structures, we computed and listed the surface rumpling and the changes in interlayer distances Δd12 and Δd23 in Table 6. We computed the surface rumplings and interlayer distances Δd12 and Δd23 for completely relaxed ABO perovskite (001) surfaces (Table 4 and Table 5). For B3LYP and B3PW computations of interlayer distances, we employed the positions of fully relaxed metal atoms (Table 4 and Table 5).

Table 6.
Our B3LYP- or B3PW-computed and experimentally detected surface rumpling s and relative displacements Δdij (in % of a0) for the three near-surface planes [151,152,153,154].
According to our B3PW computations, the STO surface rumpling s for the SrO-terminated STO (001) surface (5.66% of a0) is 2.67 times larger than the relevant surface rumpling s for the TiO2-terminated STO (001) surface (Table 6). As we can see from Table 6, our B3LYP-computed surface rumpling (1.36% of a0) for the BaO-terminated BSO (001) surface is almost two times larger than for the SnO2-terminated BSO (001) surface (+0.70% of a0). The systematic trend is (Table 6) that for all our computed ABO perovskites, the surface rumpling for AO-terminated (001) surfaces is larger than for BO2-terminated (001) surfaces. The single exception from this systematic trend is our B3PW computed BTO perovskite, where the surface rumpling for the TiO2-terminated BTO (001) surface (2.73% of a0) is approximately two times larger than for the BaO-terminated BTO (001) surface (1.37% of a0) (Table 6). As it is possible to see from Table 6, there is always a contraction between the first and second layer metal atoms (Δd12) for both AO- and BO2-terminated (001) surfaces of all our computed ABO perovskites. The sole exception from this systematic trend is the expansion of the PbO-terminated PTO perovskite (001) surface first and second layer metal atoms by (6.89% of a0) (Table 6). Just the opposite, there is always an expansion between the second- and third-layer metal atoms (Δd23) for both AO- and BO2-terminated (001) surfaces of all our computed ABO perovskites [151,152,153,154] (Table 6). Our B3PW computations for AO- and TiO2-terminated STO (001) surfaces are in fair agreement with previous ab initio LDA computations performed by Meyer et al. [151]. Also, our B3PW computed surface rumpling s amplitudes for SrO- and TiO2-terminated (001) surfaces of STO perovskite are in fair agreement with available LEED [152] and RHEED [153] experiments. It is worth noting that for TiO2-terminated STO (001) surfaces, our B3PW computer surface rumpling s value (2.12% of a0) is in almost perfect agreement with available LEED [152] experimental data (2.1 ± 2% of a0).
As we can see from Table 2 and Table 7 and Figure 9, the B atom charge on BO2-terminated (001) surfaces of BSO (+1.957e), BTO (+2.307e), STO (2.291e), PTO (2.279e), and CTO (2.278e) are smaller than in their bulk (+2.122e, +2.367e, +2.351e, +2.341e, and +2.330e, respectively). On the contrary, for BZO, SZO, and CZO perovskites, the B atom charges on their ZrO2-terminated (001) surfaces (+2.173e, +2.196e, and +2.172e) (Table 7) are larger than in their bulk (+2.134e, +2.174e, and +2.144e, respectively) (Table 2). The largest charge difference is for the Sn atom in the BSO bulk (+2.122e) and on its SnO2-terminated (001) surface (+1.957e) (Figure 9), equal to (+0.165e). As we can see from Figure 10, the absolutely largest chemical bond population is between the Sn and O atoms on the SnO2-terminated BSO perovskite (001) surface (+0.298e) (Table 7). The chemical bond population between the Sn and O atoms is also very large in the BSO bulk (+0.284e) (Table 2). Without doubt, the systematic trend is that for all eight of our ab initio computed ABO perovskites, the B-O atom chemical bond population on their BO2-terminated (001) surface always is larger than in the ABO perovskite bulk (Figure 10).

Table 7.
Our computed magnitudes of atomic displacements are D (in Å), the effective atomic charges Q (in e), and the bond populations P (in e) between the nearest Me-O atoms for the BO2-terminated ABO perovskite (001) surfaces.

Figure 9.
Our ab initio computed BO2-terminated ABO perovskite (001) surface (line 1) upper layer B atom as well as ABO perovskite bulk (line 2) B atom charges (in e).

Figure 10.
Our ab initio computed B-O chemical bond populations P (in e) for the ABO perovskite bulk (1) as well as BO2-terminated (001) surfaces (2).
Our B3LYP computed BSO bulk Γ-Γ band gap (3.65 eV) is reduced near the SnO2-terminated BSO (001) surface (1.90 eV) (Table 8). It is intriguing to observe that our B3LYP-computed BaO-terminated BSO (001) surface Γ-Γ band gap (3.81 eV) is approximately two times larger than the SnO2-terminated (001) band gap (1.90 eV) (Table 8). For STO perovskite, our computed Γ-Γ bulk band gap (3.96 eV) [56] almost coincides with the TiO2-terminated STO (001) surface band gap (3.95 eV) [56]. In general, the ABO perovskite bulk Γ-Γ band gaps, as a rule, are larger than the AO or BO2-terminated (001) surface band gaps (Table 8). The single exception from this general rule is the BSO perovskite, where the AO-terminated (001) surface band gap (3.81 eV) is larger than the bulk Γ-Γ band gap (3.65 eV) (Table 8). Our B3PW-computed BTO (001) surface band structures are depicted in Figure 11. As we can wee from Figure 11a, our B3PW-computed BaO-terminated BTO (001) surface Γ-Γ band gap is equal to 3.49 eV [56]. Even smaller is our B3PW computed Γ-Γ band gap for the TiO2-terminated BTO (001) surface (2.96 eV) (Figure 11b). Figure 12 exhibits our B3PW computed PTO (001) surface band structures [56]. Namely, the Γ-Γ band gap for the PbO-terminated PTO (001) surface (Figure 12a) is equal to 3.58 eV [56], whereas the Γ-Γ band gap for the PTO TiO2-terminated (001) surface is equal to 3.18 eV [56] (Figure 12b). Finally, our B3PW-computed band structures for the BZO (001) surfaces [131] are displayed in Figure 13. Our B3PW-computed Γ-Γ band gap for the BaO-terminated BZO (001) surface is equal to 4.82 eV (Figure 13a), while the ZrO2-terminated BZO (001) surface Γ-Γ band gap is even smaller and equal to 4.48 eV [131] (Figure 13b).

Table 8.
Our B3LYP- or B3PW-computed ABO perovskite bulk as well as AO- and BO2-terminated (001) surface Γ-Γ band gaps (in eV).

Figure 11.
Our B3PW-computed band structures for BaO- and TiO2-terminated BTO (001) surfaces ((a) and (b), respectively). The dashed lines correspond to the bulk valence band maximum.

Figure 12.
Our B3PW-computed band structures for PbO- and TiO2-terminated PTO (001) surfaces ((a) and (b), respectively). The dashed lines correspond to the valence band maximum.

Figure 13.
Our B3PW-omputed band structures for BaO- and ZrO2-terminated BZO (001) surfaces ((a) and (b), respectively). The dashed lines correspond to the valence band maximum.
Our B3LYP- or B3PW-computed eight ABO perovskite bulk as well as AO- and BO2-terminated (001) surface Γ-Γ band gaps are pictured in Figure 14. As we can see from Figure 14, the BSO perovskite SnO2-terminated (001) surface has the absolutely smallest Γ-Γ band gap, equal to 1.90 eV. In contrast, the largest Γ-Γ band gap, between all eight of our computed ABO perovskite BO2-terminated (001) surfaces, is for the ZrO2-terminated CZO (001) surface (5.22 eV) (Table 8 and Figure 14). The smallest Γ-Γ band gap, between all eight of our computed ABO perovskite AO-terminated (001) surfaces (Figure 14), is for the BaO-terminated BTO (001) surface (3.49 eV), whereas the largest is for the SrO-terminated SZO (001) surface (5.04 eV) (Table 8 and Figure 14). As it is possible to see from Table 8 and Figure 14, in 15 cases, that our computed ABO perovskite Γ-Γ band gaps for the AO- and BO2-terminated (001) surfaces are smaller than the respective ABO perovskite bulk Γ-Γ band gaps. The single exception from this systematic trend is our B3LYP computed BSO perovskite BaO-terminated (001) surface Γ-Γ band gap (3.81 eV), which is slightly larger than the BSO perovskite bulk Γ-Γ band gap (3.65 eV).

Figure 14.
Our B3PW- or B3LYP-computed bulk (l) as well as AO- (2) and BO2-terminated (3) eight ABO perovskite (001) surface Γ-Γ band gaps.
Table 9 lists our B3PW- or B3LYP-calculated eight ABO perovskite (001) surface energies. As we can see from Table 9, the absolute largest surface energies, according to our B3LYP computations, are for BSO perovskite BaO (1.38 eV) and SnO2-terminated (1.39 eV) (001) surfaces (Table 9). The energy difference between these two BSO perovskite (001) surface terminations as well as BZO perovskite BaO (1.30 eV) and ZrO2-terminated (1.31 eV) (001) surfaces are extremely small, at only 0.01 eV (Table 9). The absolute smallest ABO perovskite (001) surface energies, according to our B3PW computations, are for PTO AO- (0.83 eV) and TiO2-terminated (0.74 eV) (001) surfaces (Table 9). The unconditionally largest surface energy difference between ABO perovskite AO- and BO2-terminated (001) surfaces is for CZO perovskite CaO- (0.87 eV) and ZrO2-terminated (1.33 eV) (001) surfaces, equal to 0.46 eV.

Table 9.
Our B3LYP- or B3PW-computed (001) surface energies (in eV per surface cell) for BSO, BTO, STO, PTO, CTO, BZO, SZO, and CZO perovskites [2,3,4,124,125,126].
3.3. ABO Perovskite (111) Surface Atomic and Electronic Structure
We performed first in the world ab initio computations for the BSO perovskite (111) surfaces (Table 10 and Table 11). As we can see from the performed B3LYP computations for the Sn-terminated BSO (111) surface (Table 10), the upper layer Sn atom very slightly relaxes inward by (0.50% of a0). Also, both second-layer atoms, Ba and O, relax inward by a rather small relaxation magnitude of (0.51% and 0.30% of a0, respectively). In contrast, the third layer Sn atom moves upward by a slightly larger relaxation magnitude (0.73% of a0) (Table 10). The largest upper layer atom inward relaxation magnitudes are for Ti (11.19% of a0) and Zr (11.07% of a0) atoms on the Ti- and Zr-terminated BTO and CZO (111) surfaces, respectively (Table 10). All eight ABO perovskite (111) surface upper layer B atoms relax inward (Table 10). Also, all eight send layer metal atoms on the B-terminated ABO perovskite (111) surface relax inward. The largest second-layer metal atom inward relaxation magnitude is for the Ti atom (14.02% of a0) on the Ti-terminated CTO (111) surface (Table 10). Contrarily, six of eight second-layer oxygen atoms on the B-terminated ABO perovskite (111) surface relax upward (Table 10). Finally, the metal atom relaxation directions on the third layer of B-terminated ABO perovskite (111) surfaces are rather random. Namely, the BSO, STO, PTO, and SZO perovskite third-layer metal atoms relax upward, whereas the BTO, CTO, BZO, and CZO third-layer atoms relax inward (Table 10).

Table 10.
Our B3LYP-computed relaxation of B-terminated BSO, BTO, STO, PTO, CTO, BZO, SZO, and CZO (111) surface upper three layer atoms (% of a0).

Table 11.
Our B3LYP-computed relaxation of the AO3-terminated BSO, BTO, STO, PTO, CTO, BZO, SZO, and CZO (111) surface upper three layer atoms (% of a0).
As we can see from Table 11, according to our performed B3LYP computations, all eight upper layer O atoms on the AO3-terminated ABO perovskite (111) surfaces always relax inward. Their inward relaxation magnitudes are in the range from 0.03% of a0 for the STO perovskite to 3.98% of a0 for the BTO perovskite (Table 11). In contrast, four upper-layer metal atoms relax upward as well as four metal atoms inward (Table 11). The largest upward relaxation magnitude is for the Ba atom (3.90% of a0) on the BaO3-terminated BSO (111) surface upper layer (Table 11). All second-layer metal atoms on the AO3-terminated ABO perovskite (111) surface relax outward (Table 11). The largest upward relaxation magnitude on the AO3-terminated ABO perovskite (111) surface second layer is for the BTO perovskite Ti atom (2.49% of a0), whereas the smallest upward relaxation magnitude is for the PTO perovskite Ti atom, only (0.02% of a0) (Table 11). On the third layer of the AO3-terminated ABO perovskite (111) surface, most of the metal atoms (five) relax outward, whereas most of the O atoms (seven) relax inward (Table 11). The largest relaxation magnitude, between all third-layer atoms, is for the CTO perovskite Ca atom (2.60% of a0) (Table 11).
As a next step, we computed the Γ-Γ band gaps for seven ABO perovskite B- and AO3-terminated (111) surfaces (Table 12). In most cases, the ABO perovskite bulk Γ-Γ band gaps are reduced near their ABO3- and B-terminated (111) surfaces (Table 12). Namely, for the AO3-terminated ABO perovskite (111) surfaces, only the BaO3-terminated BTO (111) surface Γ-Γ band gap (3.60 eV) is larger than the BTO perovskite Γ-Γ bulk band gap (3.49 eV) (Table 12). The largest reduction in the Γ-Γ band gap on the AO3-terminated (111) surface is for the SrO3-terminated SZO (111) surface, where the surface band gap (4.75 eV) is reduced regarding the SZO bulk Γ-Γ band gap (5.31 eV) by 0.56 eV (Table 12). On the B-terminated ABO3 perovskite (111) surfaces, the bulk Γ-Γ band gaps for STO, PTO, BZO, and SZO perovskites (3.99 eV, 4.15 eV, 4.79, and 5.31 eV, respectively) are reduced near their Ti-, Ti-, Zr-, and Zr-terminated (111) surfaces (3.98 eV, 3.93 eV, 4.47 eV, and 4.57 eV, respectively) (Table 12).

Table 12.
Our B3LYP-computed Γ-Γ band gaps for ABO perovskite bulk as well as their B- and AO3-terminated (111) surfaces (in eV).
Our B3LYP-computed surface energies of polar B (line 3) and AO3-terminated (line 4) ABO perovskite (111) surfaces are presented in Table 13 and plotted in Figure 15, together with ABO perovskite neutral BO2 (line 2) and AO-terminated (line 1) (001) surface energies (Table 9). We computed the ABO perovskite (111) surface energies using Equations (4)–(6). Just opposite to the ABO perovskite (001) surfaces (Table 9), it is possible to see from Table 13 that different polar ABO perovskite (111) surface terminations B and AO3, lead to quite different (111) surface energies (Table 13 and Figure 15). As we can see from Table 13 and Figure 15, the lowest ABO perovskite (111) surface energies are for Ti-terminated CTO (4.18 eV) and STO (4.99 eV) (111) surfaces. At the same time, the largest ABO perovskite (111) surface energies are for the SrO3- and CaO3-terminated SZO and CZO (111) surfaces (9.45 eV and 9.62 eV, respectively) (Table 13). The largest (111) surface energy difference between two different surface terminations for ABO perovskite is for Ti- (6.14 eV) and PbO3-terminated (8.11 eV) PTO perovskite (111) surfaces (1.97 eV) (Table 13 and Figure 15). In contrast, the smallest energy difference is between the Sn- (5.20 eV) and BaO3-terminated (5.13 eV) BSO perovskite (111) surfaces, i.e., only 0.07 eV (Figure 15). It is worth noting that for seven ABO perovskites, their AO3-terminated (111) surface energy is larger than their B-terminated (111) surface energy (Table 13 and Figure 15). The only exception from this systematic trend is the BSO perovskite, where the Sn-terminated (111) surface energy (5.20 eV) is larger than the BaO3-terminated (111) surface energy (5.13 eV).

Table 13.
Our B3LYP-computed surface energies for 8 ABO perovskite B and AO3-terminated (111) surfaces (in eV).

Figure 15.
Our B3LYP-computed ABO perovskite surface energies for neutral AO- (line 1) and BO2-terminated (line 2) (001) surfaces as well polar B- (line 3) and AO3-terminated (line 4) (111) surfaces.
4. Conclusions
As we can see from Figure 8, the hybrid exchange-correlation functionals B3LYP and B3PW allow us to achieve a fair agreement with the experiments for ABO perovskite bulk Γ-Γ band gaps [2,3,4,9,56]. At the same time, the HF method considerably overestimates the bulk Γ-Γ band gaps, whereas the PWGGA method underestimates them [2,3,4,9,56]. This was the key reason why we choose the B3LYP and B3PW hybrid exchange-correlation functionals for our ABO perovskite bulk and surface computations [2,3,4,9,56].
We completed B3LYP and B3PW computations for AO and BO2-terminated (001) as well as AO3- and B-terminated (111) surfaces of BSO, BTO, STO, PTO, CTO, BZO, SZO, and CZO perovskites. We observed that most of the upper-layer atoms for AO- and BO2-terminated ABO perovskite (001) surfaces relax inward. The two exceptions from this systematic trend are the upward relaxation of oxygen atoms on the TiO2-terminated PTO (001) surface by (0.31% of a0) (Table 4) as well as on the SrO-terminated STO (001) surface by (0.84% of a0) (Table 5). In contrast, all second-layer metal atoms relax upward. Also, practically all second-layer oxygen atoms relax upward. Only the oxygen atoms on SnO2- and BaO-terminated BSO as well as SrO-terminated SZO (001) surfaces relax inward by a very small relaxation magnitude of (0.04, 0.07, and 0.05% of a0, respectively) (Table 4 and Table 5). Lastly, almost all third-layer atoms, again, relax inward.
This tendency is less pronounced for atomic relaxation of first-, second-, and third-layer atoms for AO3- and B-terminated ABO perovskite (111) surfaces (Table 10 and Table 11). Namely, 20 from 24, or 83.33%, of ABO perovskite (111) surface upper layer atoms relax inward. Nevertheless, only 14 from 24, or 58.33%, of ABO perovskite (111) surface second layer atoms relax upward. Finally, again, only 58.33% of the third layer (111) surface atoms relax inward. For almost all ABO perovskites, their (001) surface rumplings s are considerably larger for AO-terminated compared to BO2-terminated surfaces. For example, B3PW- or B3LYP-computed surface rumplings s for AO-terminated STO, BSO, and CTO (001) surfaces (5.66, 1.36, and 7.89) are considerably larger than the respective surface rumplings s for BO2-terminated STO, BSO, and CTO (001) surfaces (2.12, 0.70, and 1.61, respectively) (Table 6).
On the contrary, the ABO perovskite (001) surface energies, for both AO- and BO2-terminations, are essentially equivalent. The largest computed ABO perovskite (001) surface energy is for the BO2-terminated BSO (001) surface (1.39 eV), whereas the smallest is for the TiO2-terminated PTO (001) surface (0.74 eV) (Table 9). The ABO perovskite polar (111) surface energies always are substantially larger than their neutral (001) surface energies. Namely, the largest ABO perovskite polar (111) surface energy is for the CaO3-terminated CZO (111) surface (9.62 eV), whereas the smallest is for the Ti-terminated CTO (111) surface (4.18 eV) (Table 13 and Figure 15). In most cases, the surface energies of AO3-terminated ABO perovskite polar (111) surfaces are considerably larger than their B-terminated surface energies. Specifically, for BTO, STO, PTO, CTO, BZO, SZO, and CZO perovskites, their AO3-terminated (111) surface energy is considerably larger than their B-terminated (111) surface energy (Table 13 and Figure 15). The only omission from this systematic trend is BSO perovskite, where the Sn-terminated (111) surface energy (5.20 eV) is 0.07 eV larger than the BaO3-terminated (111) surface energy (5.13 eV).
Our computations illustrate a noticeable boost in the B-O chemical bond covalency near the ABO perovskite BO2-terminated (001) surface related to the bulk. Particularly, for BSO, BTO, STO, PTO, CTO, BZO, SZO, and CZO perovskites, their bulk B-O chemical bond covalency (+0.284e, +0.098e, +0.088e, +0.098e, +0.084e, +0.108e, +0.092e, +0.086e) increases near the BO2-terminated ABO perovskite (001) surface (+0.298e, +0.126e, +0.118e, +0.114e, +0.114e, +0.132e, +0.114e, +0.102e). The absolutely largest B-O chemical bond covalency is near the SnO2-terminated BSO perovskite (001) surface (+0.298e), whereas the smallest B-O chemical bond covalency is between Ti-O atoms (+0.084e) in the CTO perovskite bulk (Table 2 and Table 7). Our computed ABO perovskite bulk Γ-Γ band gaps are almost always reduced near the AO- and BO2-terminated neutral (001) surfaces as well as in most cases also near the AO3- and B-terminated polar (111) surfaces.
We want to stress that our B3LYP and B3PW computations of ABO perovskite neutral (001) as well as polar (111) surface characteristics are very helpful in order to interpret processes, where surfaces exhibit a key role [155,156,157]. For instance, in the chemistry and physics of ABO perovskite surface reactions, (001) and (111) surface as well as interface aspect, and adsorption. Specifically, a wide variety of useful technological applications of ABO perovskites counting electrooptical and piezoelectrical devices as well as fuel cells and microelectrodes have inspired their theoretical research [155,156,157].
Author Contributions
Conceptualization, R.I.E. and J.P.; methodology, R.J.; software, S.P.K.; validation, S.W., R.I.E., and J.P.; formal analysis, R.J.; investigation, S.P.K.; resources, S.W.; data curation, R.I.E., J.P., R.J., S.P.K., and S.W.; writing—original draft preparation, R.I.E.; writing—review and editing, R.I.E., J.P., R.J., S.P.K., and S.W.; visualization, R.J.; supervision, S.W.; project administration, R.I.E.; funding acquisition, J.P. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the Latvian Council of Science Grant Number: LZP-2021/1-464. The Institute of Solid State Physics, University of Latvia (Latvia), as the Centre of Excellence, got funding from the European Union’s Horizon 2020 Framework Program H2020-WIDESPREAD01-2016-2017-Teaming Phase2 under Grant Agreement No. 739508, project CAMART-2. S.P.K. acknowledges support by the National Academy of Science of Ukraine (Funding. No. 0116U002067). S.P.K. thanks the funding from Simons Foundation, under the Contract NUMBER-0121U109816. J.P. acknowledges SWEB project funded by the Horizon Europe programme (Number - GA101087367).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Dawber, M.; Rabe, K.M.; Scott, J.F. Physics of thin-film ferroelectric oxides. Rev. Mod. Phys. 2005, 77, 1083–1130. [Google Scholar]
- Eglitis, R.I.; Vanderbilt, D. Ab initio calculations of the atomic and electronic structure of CaTiO3 (001) and (011) surfaces. Phys. Rev. B 2008, 78, 155420. [Google Scholar] [CrossRef]
- Eglitis, R.I.; Vanderbilt, D. Ab initio calculations of BaTiO3 and PbTiO3 (001) and (011) surface structures. Phys. Rev. B 2007, 76, 155439. [Google Scholar] [CrossRef]
- Eglitis, R.I.; Vanderbilt, D. First-principles calculations of atomic and electronic structure of SrTiO3 (001) and (011) surfaces. Phys. Rev. B 2008, 77, 195408. [Google Scholar] [CrossRef]
- Chun, H.J.; Jeon, J.E.; Park, S.C. Facet-Dependent Ba Dissolution of Tetragonal BaTiO3 Single Crystal Surfaces. J. Phys. Chem. C 2023, 127, 1848–1854. [Google Scholar] [CrossRef]
- Guo, X.W.; Zou, M.J.; Wang, Y.J.; Tang, Y.L.; Zhu, Y.L.; Ma, X.L. Effects of anisotropic misfit strains on equilibrium phases and domain structures in (111)-oriented ferroelectric PbTiO3 films. Acta Mater. 2021, 206, 116639. [Google Scholar] [CrossRef]
- Erdman, N.; Poeppelmeier, K.R.; Asta, M.; Warschkov, O.; Ellis, D.E.; Marks, L.D. The structure and chemistry of the TiO2-rich surface of SrTiO3 (001). Nature 2002, 419, 55–58. [Google Scholar] [CrossRef]
- Chun, H.J.; Lee, Y.; Kim, S.; Yoon, Y.; Kim, Y.; Park, S.C. Surface termination of BaTiO3 (111) single crystal: A combined DFT and XPS study. Appl. Surf. Sci. 2022, 578, 152018. [Google Scholar] [CrossRef]
- Eglitis, R.I.; Kleperis, J.; Purans, J.; Popov, A.I.; Jia, R. Ab initio calculations of CaZrO3 (011) surfaces: Systematic trends in polar (011) surface calculations of ABO3 perovskites. J. Mater. Sci. 2020, 55, 203–217. [Google Scholar] [CrossRef]
- Costa-Amaral, R.; Gohda, Y. First-principles study of the adsorption of 3d transition metals on BaO- and TiO2-terminated cubic-phase BaTiO3 (001) surfaces. J. Chem. Phys. 2020, 152, 204701. [Google Scholar] [CrossRef]
- Eglitis, R.I.; Jia, R. Review of Systematic Tendencies in (001), (011) and (111) Surfaces Using B3PW as Well as B3LYP Computations of BaTiO3, CaTiO3, PbTiO3, SrTiO3, BaZrO3, CaZrO3, PbZrO3 and SrZrO3 Perovskites. Materials 2023, 16, 7623. [Google Scholar] [CrossRef]
- Muff, S.; Fanciulli, M.; Weber, A.P.; Pilet, N.; Ristić, Z.; Wang, Z.; Plumb, N.C.; Radović, M.; Dil, J.H. Observation of a two-dimensional electron gas at CaTiO3 film surfaces. Appl. Surf. Sci. 2018, 432, 41–45. [Google Scholar] [CrossRef]
- Tian, H.; Mao, A.J.; Zhao, H.J.; Cui, Y.; Li, H.; Kuang, X.Y. Large polarization and dielectric response in epitaxial SrZrO3 films. Phys. Chem. Chem. Phys. 2016, 18, 7680–7687. [Google Scholar] [CrossRef]
- Heifets, E.; Kotomin, E.A.; Maier, J. Semi-empirical simulations of surface relaxation for perovskite titanates. Surf. Sci. 2000, 462, 19–35. [Google Scholar] [CrossRef]
- Enterkin, J.A.; Subramanian, A.K.; Russell, B.C.; Castell, M.R.; Poeppelmeier, K.R.; Marks, L.D. A homologous series of structures on the surface of SrTiO3 (110). Nat. Mater. 2010, 9, 245–248. [Google Scholar] [CrossRef] [PubMed]
- Blaess, C.; Matzen, S.; Lin, H.; Magnan, H.; Moussy, J.P.; Rountree, C.L.; Mocuta, C.; Silly, M.G.; Plantevin, O.; Charra, F.; et al. Nitrogen Doping in Epitaxial Self-Oxidized BaTiO3 Ferroelectric Thin Films. J. Phys. Chem. C 2025, 129, 3849–3861. [Google Scholar] [CrossRef]
- Celik, F.A. Electronic structure of two-dimensional-layered PbTiO3 perovskite crystal: An extended tight-binding study based on DFT. Bull. Mater. Sci. 2022, 45, 108. [Google Scholar] [CrossRef]
- Heifets, E.; Ho, J.; Merinov, B. Density functional simulation of the BaZrO3 (011) surface structure. Phys. Rev. B 2007, 75, 155431. [Google Scholar] [CrossRef]
- Wang, Z.; Hao, X.; Gerhold, S.; Schmid, M.; Franchini, C.; Diebold, U. Vacancy clusters at domain boundaries and band bending at the SrTiO3 (110) surface. Phys. Rev. B 2014, 90, 035436. [Google Scholar] [CrossRef]
- Eglitis, R.I.; Kotomin, E.A.; Borstel, G. Quantum chemical modelling of perovskite solid solutions. J. Phys. Condens. Matter 2000, 12, L431. [Google Scholar] [CrossRef]
- Li, W.; Landis, C.M.; Demkov, A. Domain morphology and electro-optic effect in Si-integrated epitaxial BaTiO3 films. Phys. Rev. Mater. 2022, 6, 095203. [Google Scholar] [CrossRef]
- Setvin, M.; Reticcioli, M.; Poelzleitner, F.; Hulva, J.; Schmid, M.; Boatner, L.A.; Franchini, C.; Diebold, U. Polarity compensation mechanisms on the perovskite surface KTaO3 (001). Science 2018, 359, 572–575. [Google Scholar]
- Kruchinin, S.P.; Eglitis, R.I.; Novikov, V.E.; Oleś, A.M.; Wirth, S. Control of Strongly Nonequilibrium Coherently Correlated States and Superconducting Transition Temperature. Symmetry 2023, 15, 1732. [Google Scholar] [CrossRef]
- Ellinger, F.; Shafiq, M.; Ahmad, I.; Reticcioli, M.; Franchini, C. Small polaron formation on the Nb-doped SrTiO3 (001) surface. Phys. Rev. Mater. 2023, 7, 064602. [Google Scholar]
- Eglitis, R.I.; Bocharov, D.; Piskunov, S.; Jia, R. Review of First Principles Simulations of STO/BTO, STO/PTO, and SZO/PZO (001) Heterostructures. Crystals 2023, 13, 799. [Google Scholar] [CrossRef]
- Cohen, R.E. Origin of ferroelectricity in perovskite oxides. Nature 1992, 358, 136–138. [Google Scholar] [CrossRef]
- Krainyukova, N.V.; Hamalii, V.O.; Peschanskii, A.V.; Popov, A.I.; Kotomin, E.A. Low temperature structure transformations on the (001) surface of SrTiO3 single crystals. Low. Temp. Phys. 2020, 46, 740–750. [Google Scholar]
- Bottin, F.; Finocchi, F.; Noguera, C. Stability and electronic structure of the (1 × 1) SrTiO3 (110) polar surfaces by first-principles calculations. Phys. Rev. B 1999, 68, 179–198. [Google Scholar]
- Millers, D.; Grigorjeva, L.; Pankratov, V.; Trepakov, V.A.; Kapphan, S.E. Pulsed electron beam excited transient absorption in SrTiO3. Nucl. Instr. Methods B 2002, 194, 469–473. [Google Scholar] [CrossRef]
- Hwang, H.Y.; Iwasa, Y.; Kawasaki, M.; Keimer, B.; Nagaosa, N.; Tokura, Y. Emergent phenomena at oxide interfaces. Nat. Mater. 2012, 11, 103–113. [Google Scholar]
- Matsuda, T.; Yamanaka, S.; Kurosaki, K.; Kobayashi, S.I. High temperature phase transitions of SrZrO3. J. Alloys Compd. 2003, 351, 43–46. [Google Scholar] [CrossRef]
- Schober, T. Protonic conduction in BaIn0.5Sn0.5O2.75. Solid State Ion. 1998, 109, 1–11. [Google Scholar] [CrossRef]
- Elmahgary, M.G.; Mahran, A.M.; Ganoub, M.; Abdellatif, S.O. Optical investigation and computational modelling of BaTiO3 for optoelectronic devices applications. Sci. Rep. 2023, 13, 4761. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Zhang, C.; Liu, J.; Zhou, J.; Xu, L. A review on the electrical properties of doped SrTiO3 as anode material for solid oxide fuel cells. Mater. Res. Express 2019, 6, 102006. [Google Scholar] [CrossRef]
- Jiang, J.; Kato, K.; Fujimori, H.; Yamakata, A.; Sakata, Y. Investigation on the highly actice SrTiO3 photocatalyst toward overall H2O splitting by doping Na ion. J. Catal. 2020, 390, 81–89. [Google Scholar] [CrossRef]
- Ikegami, S.; Ueda, I.; Nagata, T. Electromechanical properties of PbTiO3 ceramics containing La and Mn. J. Acoust. Soc. Am. 1971, 50, 1060–1966. [Google Scholar] [CrossRef]
- Passi, M.; Pal, B. A review on CaTiO3 photocatalyst: Activity enhancement methods and photocatalytic applications. Powder Technol. 2021, 388, 274–304. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, W.; Wang, B.; Sun, L.; Li, F.; Xue, Z.; Zhou, G.; Liu, B.; Nian, H. Theoretical and experimental investigations on high temperature mechanical and thermal properties of BaZrO3. Ceram. Int. 2018, 44, 16475–16482. [Google Scholar] [CrossRef]
- Nair, J.; Nair, P.; Doesburg, E.B.M.; Ommen, J.G.V.; Ross, J.R.H.; Burggraaf, A.J. Preparation and characterization of lanthanum zirconate. J. Mater. Sci. 1998, 33, 4517–4523. [Google Scholar] [CrossRef]
- Longo, V.M.; Cavalcante, L.S.; Figueiredo, A.T.; Santos, L.P.S.; Longo, E.; Varela, J.A. High intense violet-blue emission at room temperature in structurally disordered SrZrO3 powders. Appl. Phys. Lett. 2007, 90, 091906. [Google Scholar] [CrossRef]
- Higuchi, T.; Tsukamoto, T.; Matsumoto, H.; Shimura, T.; Yashiro, K.; Kawada, T. Electronic structure of protonic conductor SrZrMO (M = Y, Sc) probed by soft-X-ray spectroscopy. Solid State Ion. 2005, 176, 2435–2438. [Google Scholar] [CrossRef]
- Prasanth, C.S.; Kumar, H.P.; Pazhani, R.; Solomon, S.; Thomas, J.K. Synthesis, characterization and microwave dielectric properties of nanocrystalline CaZrO3 ceramics. J. Alloys Compd. 2008, 464, 306–309. [Google Scholar]
- Chang, Y.J.; Phark, S.H. Atomic-scale visualization of initial growth of perovskites on SrTiO3 (001) using scanning tunneling microscope. Curr. Appl. Phys. 2017, 17, 640–656. [Google Scholar]
- Wang, Y.; Zhang, Z.; Wang, Y.; Doan, E.; Yuan, L.; Tang, W.; Yang, K. First-principles investigation of structural, electronic, and energetic properties of BaSnO3 (001) surfaces. Vacuum 2023, 212, 111977. [Google Scholar] [CrossRef]
- Barret, N.; Dionot, J.; Martinotti, D.; Salje, E.K.H.; Mathieu, C. Evidence of surface anomaly during the cubic-tetragonal phase transition in BaTiO3 (001). Appl. Phys. Lett. 2018, 113, 022901. [Google Scholar]
- Chen, P.; Xu, Y.; Wang, N.; Oganov, A.R.; Duan, W. Effects of ferroelectric polarization on surface phase diagram: Evolutionary algorithm study of the BaTiO3 (001) surface. Phys. Rev. B 2015, 92, 085432. [Google Scholar]
- Saghayezhian, M.; Sani, S.M.R.; Zhang, J.; Plummer, E.W. Rumpling and enhanced covalency at the SrTiO3 (001) surface. J. Phys. Chem. C 2019, 123, 8086–8091. [Google Scholar]
- Sambrano, J.R.; Longo, V.M.; Longo, E.; Taft, C.A. Electronic and structural properties of the (001) SrZrO3 surface. J. Mol. Struct. THEOCHEM 2007, 813, 49–56. [Google Scholar] [CrossRef]
- Lee, T.T.; Ekerdt, J.G. Epitaxial growth of high-k BaxSr1-xTiO3 thin films on SrTiO3 (001) substrates by atomic layer deposition. J. Vac. Sci. Technol. A 2020, 38, 032401. [Google Scholar]
- Heifets, E.; Eglitis, R.I.; Kotomin, E.A.; Maier, J.; Borstel, G. Ab initio modeling of surface structure for SrTiO3 perovskite crystals. Phys. Rev. B 2001, 64, 235417. [Google Scholar]
- Zhang, R.; Hwang, G.S. First-principles mechanistic study of the initial growth of SrO by atomic layer deposition on TiO2-terminated SrTiO3 (001). J. Phys. Chem. C 2020, 124, 28116. [Google Scholar] [CrossRef]
- Kasai, M.; Dohi, H. Surface structure and electrochemical properties of platinum films grown on SrTiO3 (100) substrates. Surf. Sci. 2017, 666, 14–22. [Google Scholar] [CrossRef]
- Borstel, G.; Eglitis, R.I.; Kotomin, E.A.; Heifets, E. Modelling of defects and surfaces in perovskite ferroelectrics. Phys. Status Solidi B 2003, 236, 253–264. [Google Scholar] [CrossRef]
- Wang, Y.X. Surface properties of the (001) surface of cubic PbZrO3 and PbTiO3. Phys. Status Solidi B 2007, 244, 602–609. [Google Scholar]
- Zhong, M.; Zeng, W.; Liu, F.S.; Tang, B.; Liu, Q.J. First-principles study of the atomic structures, electronic properties, and surface stability of BaTiO3 (001) and (011) surfaces. Surf. Interface Anal. 2019, 51, 1021–1032. [Google Scholar]
- Piskunov, S.; Kotomin, E.A.; Heifets, E.; Maier, J.; Eglitis, R.I.; Borstel, G. Hybrid DFT calculations of the atomic and electronic structure for ABO3 perovskite (001) surfaces. Surf. Sci. 2005, 575, 75–88. [Google Scholar] [CrossRef]
- Brik, M.G.; Ma, C.G.; Krasnenko, V. First-principles calculations of the structural and electronic properties of the cubic CaZrO3 (001) surfaces. Surf. Sci. 2013, 608, 146–153. [Google Scholar] [CrossRef]
- Eglitis, R.I.; Purans, J.; Popov, A.I.; Bocharov, D.; Chekhovska, A.; Jia, R. Ab initio computations of O and AO as well as ReO2, WO2 and BO2-terminated ReO3, WO3, BaTiO3, SrTiO3 and BaZrO3 (001) surfaces. Symmetry 2022, 14, 1050. [Google Scholar] [CrossRef]
- Alam, N.N.; Malik, N.A.; Samat, M.H.; Hussin, N.H.; Jaafar, N.K.; Radzwan, A.; Mohyedin, M.Z.; Haq, B.U.; Ali, A.M.M.; Hassan, O.H.; et al. Underlaying mechanism of surface (001) cubic ATiO3 (A = Pb,Sn) in enhancing thermoelectric performance of thin-film applications using density functional theory. Surf. Interfaces 2021, 27, 101524. [Google Scholar]
- Zhao, X.; Selloni, A. Structure and stability of NaTaO3 (001) and KTaO3 (001) surfaces. Phys. Rev. Mater. 2019, 3, 015801. [Google Scholar]
- Kolpak, A.M.; Li, D.; Shao, R.; Rappe, A.M.; Bonnell, D.A. Evolution of the surface structure and thermodynamic stability of the BaTiO3 (001) surface. Phys. Rev. Lett. 2008, 101, 036102. [Google Scholar] [CrossRef]
- Rondinelli, J.A.; Spaldin, N.A. Electron-lattice instabilities suppress cuprate-like electronic structures in SrFeO3/SrTiO3 superlattices. Phys. Rev. B 2010, 81, 085109. [Google Scholar] [CrossRef]
- Wang, J.; Neaton, J.B.; Zheng, H.; Nagarjan, V.; Ogale, S.B.; Liu, B.; Viehland, D.; Vaithyanathad, V.; Schlom, D.G.; Vagmare, U.V.; et al. Epitaxial BiFeO3 multiferroic thin film heterostructures. Science 2003, 299, 1719–1722. [Google Scholar] [CrossRef] [PubMed]
- Piskunov, S.; Eglitis, R.I. First principles hybrid DFT calculations of BaTiO3/SrTiO3 (001) interface. Solid State Ion. 2015, 274, 29–33. [Google Scholar] [CrossRef]
- Waldow, S.P.; Souza, R.A.D. Computational study of oxygen diffusion along a [100] dislocations in the perovskite oxide SrTiO3. ACS Appl. Mater. Interfaces 2016, 8, 1224–1256. [Google Scholar] [CrossRef] [PubMed]
- Vivek, M.; Goniakowski, J.; Santander-Syro, A.; Gabay, M. Octahedral rotations and defect-driven metallicity at the (001) surface of CaTiO3. Phys. Rev. B 2023, 107, 045101. [Google Scholar] [CrossRef]
- Wang, Y.X.; Arai, M.; Sasaki, T.; Wang, C.L. First-principles study of the (001) surface of cubic CaTiO3. Phys. Rev. B 2006, 73, 035411. [Google Scholar] [CrossRef]
- Luo, B.; Wang, X.; Tian, E.; Li, G.; Li, L. Structural and electronic properties of cubic KNbO3 (001) surfaces: A first-principles study. Appl. Surf. Sci. 2015, 351, 558–564. [Google Scholar] [CrossRef]
- Krasnenko, V.; Platonenko, A.; Liivand, A.; Rusevich, L.L.; Mastrikov, Y.A.; Zvejnieks, G.; Sokolov, M.; Kotomin, E.A. Modeling of the Lattice Dynamics in Strontium Titanate Films of Various Thicknesses: Raman Scattering Studies. Materials 2023, 16, 6207. [Google Scholar] [CrossRef]
- Iles, N.; Finocchi, F.; Khodja, K.D. A systematic study of ideal and double layer reconstruction of ABO3 (001) surfaces (A = Sr, Ba: B = Ti, Zr) from first principles. J. Phys. Condens. Matter 2010, 22, 305001. [Google Scholar] [CrossRef]
- Heifets, E.; Dorfman, S.; Fuks, D.; Kotomin, E. Atomistic simulation of the [001] surface structure in BaTiO3. Thin Solid Film. 1997, 296, 76–78. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, H.; Zhang, L.; Chen, J.; Xing, X. PbTiO3-based perovskite ferroelectric and multiferroic thin films. Phys. Chem. Chem. Phys. 2017, 19, 17493–17515. [Google Scholar] [CrossRef]
- Kim, J.S.; Yang, J.H.; Kim, B.K.; Kim, Y.C. Proton conduction at BaO-terminated (001) BaZrO3 surface using density functional theory. Solid State Ion. 2015, 275, 19–22. [Google Scholar] [CrossRef]
- Shimada, T.; Wang, J.; Araki, Y.; Mrovec, M.; Elsässer, C.; Kitamura, T. Multiferroic vacancies at ferroelectric PbTiO3 surfaces. Phys. Rev. Lett. 2015, 115, 107202. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, G.P.; Shimada, T.; Wang, J.; Kitamura, T. Disappearance of ferroelectric critical thickness in epitaxial ultrathin BaZrO3 films. Phys. Rev. B 2014, 90, 184107. [Google Scholar] [CrossRef]
- Eglitis, R.I.; Purans, J.; Popov, A.I.; Jia, R. Tendencies in ABO3 Perovskite and SrF2, BaF2 and CaF2 Bulk and Surface F-Center Ab initio Computations at High Symmetry Cubic Structure. Symmetry 2021, 13, 1920. [Google Scholar] [CrossRef]
- Cord, B.; Courths, R. Photoemission study of BaTiO3 (100) surfaces. Surf. Sci. 1985, 152, 1141–1146. [Google Scholar] [CrossRef]
- Eglitis, R.I.; Piskunov, S.; Popov, A.I.; Purans, J.; Bocharov, D.; Jia, R. Systematic Trends in Hybrid-DFT Computations of BaTiO3/SrTiO3, PbTiO3/SrTiO3 and PbZrO3/SrZrO3 (001) Hetero Structures. Condens. Matter 2022, 7, 70. [Google Scholar] [CrossRef]
- Morales, E.H.; Bonnell, D.A. On the relationship between surface reconstructions and step edge stability on BaTiO3. Surf. Sci. 2013, 609, 62–66. [Google Scholar] [CrossRef]
- Eglitis, R.I.; Piskunov, S. First principles calculations of SrZrO3 bulk and ZrO2-terminated (001) surface F centers. Comput. Condens. Matter 2016, 7, 1–6. [Google Scholar] [CrossRef]
- Berlich, A.; Strauss, H.; Langheinrich, C.; Chassé, A.; Morgner, H. Surface termination of BaTiO3 (001) single crystals: A combined electron spectroscopic and theoretical study. Surf. Sci. 2011, 605, 158–165. [Google Scholar]
- Sokolov, M.; Eglitis, R.I.; Piskunov, S.; Zhukovskii, Y.F. Ab initio hybrid DFT calculations of BaTiO3 bulk and BaO-terminated (001) surface F-centers. Int. J. Mod. Phys. B 2017, 31, 1750251. [Google Scholar]
- Hagendorf, C.; Schindler, K.M.; Doege, T.; Neddermeyer, H. An STM, XPS and LEED investigation of the BaTiO3 (111) surface. Surf. Sci. 1998, 402, 581–585. [Google Scholar]
- Hagendorf, C.; Schindler, K.M.; Doege, T.; Neddermeyer, H. A scanning tunneling microscopy, X-ray photoelectron spectroscopy and low-energy electron diffraction investigation of the BaTiO3 (111) surface. Surf. Sci. 1999, 436, 121–130. [Google Scholar] [CrossRef]
- Eglitis, R.I. Ab initio hybrid DFT calculations of BaTiO3, PbTiO3, SrZrO3 and PbZrO3 (111) surfaces. Appl. Surf. Sci. 2015, 358, 556–562. [Google Scholar]
- Pojani, A.; Finocchi, F.; Noguera, C. Polarity on the SrTiO3 (111) and (110) surfaces. Surf. Sci. 1999, 442, 179–198. [Google Scholar]
- Biswas, A.; Rossen, P.B.; Yang, C.H.; Siemons, W.; Jung, M.H.; Yang, I.K.; Ramesh, R.; Jeong, Y.H. Universal Ti-rich termination of atomically flat SrTiO3 (001), (011), and (111) surfaces. Appl. Phys. Lett. 2011, 98, 051904. [Google Scholar] [CrossRef]
- Sekiguchi, S.; Fujimoto, M.; Kang, M.G.; Koizumi, S.; Chao, S.B.; Tanaka, J. Structure Analysis of SrTiO3 (111) Polar Surfaces. Jpn. J. Appl. Phys. 1998, 37, 4140. [Google Scholar]
- Tanaka, H.; Kawai, T. Surface structure of reduced SrTiO3 (111) observed by scanning tunneling microscopy. Surf. Sci. 1996, 365, 437–442. [Google Scholar]
- Eglitis, R.I. Comparative ab initio calculations of SrTiO3 and CaTiO3 polar (111) surfaces. Phys. Status Solidi B 2015, 252, 635–642. [Google Scholar]
- Pang, Q.; Zhang, J.M.; Xu, K.W.; Ji, V. Structural, electronic properties and stability of the (1 × 1) PbTiO3 (111) polar surfaces by first-principles calculations. Appl. Surf. Sci. 2009, 255, 8145–8152. [Google Scholar] [CrossRef]
- Liu, W.; Wang, C.; Cui, J.; Man, Z.Y. Ab initio calculations of the CaTiO3 (111) polar surfaces. Solid State Commun. 2009, 149, 1871–1876. [Google Scholar]
- Eglitis, R.I. Comparative First-Principles Calculations of SrTiO3, BaTiO3, PbTiO3 and CaTiO3 (001), (011) and (111) Surfaces. Ferroelectrics 2015, 483, 53–67. [Google Scholar] [CrossRef]
- Eglitis, R.I. Ab initio calculations of the atomic and electronic structure of BaZrO3 (111) surfaces. Solid State Ion. 2013, 230, 43–47. [Google Scholar]
- Eglitis, R.I. Ab initio calculations of CaZrO3, BaZrO3, PbTiO3 and SrTiO3 (001), (011) and (111) surfaces as well as their (001) interfaces. Integr. Ferroelectr. 2019, 196, 7–15. [Google Scholar]
- Eglitis, R.I.; Kotomin, E.A.; Popov, A.I.; Kruchinin, S.P.; Jia, R. Comparative ab initio calculations of SrTiO3, BaTiO3, PbTiO3 and SrZrO3 (001) and (111) surfaces as well as oxygen vacancies. Low. Temp. Phys. 2022, 48, 80–88. [Google Scholar]
- Janifer, M.A.; Anand, S.; Prabagar, C.J.; Pauline, S. Structural and optical properties of BaSnO3 ceramics by solid state reaction method. Mater. Today Proc. 2021, 47, 2067–2070. [Google Scholar]
- Kim, H.J.; Kim, V.; Kim, T.H.; Kim, J.; Kim, H.M.; Jeon, B.G.; Lee, W.J.; Mun, H.S.; Hong, K.T.; Yu, J.; et al. Physical properties of transparent perovskite oxides (Ba,La)SnO3 with high electrical mobility at room temperature. Phys. Rev. B 2012, 86, 165205. [Google Scholar]
- Evarestov, R.A.; Bandura, A.V. First-principles calculations on the four phases of BaTiO3. J. Comput. Chem. 2012, 33, 1123–1130. [Google Scholar]
- Goudochnikov, P.; Bell, A.J. Correlations between transition temperature, tolerance factor and cohesive energy in 2+:4+ perovskites. J. Phys. Condens. Matter 2007, 19, 176201. [Google Scholar]
- Wemple, S.H. Polarization Fluctuations and the Optical-Absorption Edge in BaTiO3. Phys. Rev. B 1970, 2, 2679–2689. [Google Scholar] [CrossRef]
- Benrekia, A.R.; Benkhettou, N.; Nassour, A.; Driz, M.; Sahnoun, M.; Lebéque, S. Structural, electronic and optical properties of cubic SrTiO3 and KTaO3: Ab initio and GW calculations. Phys. B Condens. Matter 2012, 407, 2632–2636. [Google Scholar] [CrossRef]
- Benthem, K.; Elsässer, C.; French, R.H. Bulk electronic structure of SrTiO3: Experiment and theory. J. Appl. Phys. 2001, 90, 6156–6164. [Google Scholar]
- Waghmare, U.V.; Rabe, K.M. Ab initio statistical mechanics of the ferroelectric phase transition in PbTiO3. Phys. Rev. B 1997, 55, 6161–6173. [Google Scholar] [CrossRef]
- Robertson, J. Band offsets of wide-band-gap oxides and implications for future electronic devices. J. Vacuum. Sci. Technol. 2000, 18, 1785–1791. [Google Scholar] [CrossRef]
- Ali, R.; Yashima, M. Space group and crystal structure of the perovskite CaTiO3 from 296 to 1720K. J. Solid State Chem. 2005, 178, 2867–2872. [Google Scholar]
- Ueda, K.; Yanagi, H.; Noshiro, R.; Hosono, H.; Kawazoe, H. Vacuum ultraviolet reflectance and electron energy loss spectra of CaTiO3. J. Phys. Condens. Matter 1998, 10, 3669–3677. [Google Scholar]
- Knight, K.S. Low-temperature thermophysical and crystallographic properties of BaZrO3 perovskite. J. Mater. Sci. 2020, 55, 6417–6428. [Google Scholar]
- Hasegawa, S.; Sugimoto, T.; Hashimoto, T. Investigation of structural phase transition behavior of SrZrO3 by thermal analysis and high-temperature X-ray diffraction. Solid State Ion. 2010, 181, 1091–1097. [Google Scholar] [CrossRef]
- Lee, Y.S.; Lee, J.S.; Noh, T.W.; Byun, D.Y.; Yoo, K.S.; Yamaura, K.; Takayama-Muromachi, E. Systematic trends in the electronic structure parameters of the 4d transition-metal oxides SrMO3 (M = Zr, Mo, Ru, and Rh). Phys. Rev. B 2003, 67, 113101. [Google Scholar] [CrossRef]
- Koopmans, H.J.A.; Velde, G.M.H.; Gellings, P.J. Powder neutron diffraction study of the perovskites CaTiO3 and CaZrO3. Actra Crystallogr. 1983, C39, 1323–1325. [Google Scholar] [CrossRef]
- Stoch, P.; Szczerba, J.; Lis, J.; Madej, D.; Pedzich, Z. Crystal structure and ab initio calculations of CaZrO3. J. Eur. Ceram. Soc. 2012, 32, 665–670. [Google Scholar] [CrossRef]
- Rosa, I.L.V.; Oliveira, M.C.; Assis, M.; Ferrer, M.; André, R.S.; Longo, E.; Gurgel, M.F.C. A theoretical investigation of the structural and electronic properties of orthorhombic CaZrO3. Ceram. Int. 2015, 41, 3069–3074. [Google Scholar] [CrossRef]
- Eom, K.; Chung, B.; Oh, S.; Zhou, H.; Seo, J.; Oh, S.H.; Jang, J.; Choi, S.Y.; Choi, M.; Seo, I.; et al. Surface triggered stabilization of metastable charge ordered phase in SrTiO3. Nat. Commun. 2024, 15, 1180. [Google Scholar] [CrossRef] [PubMed]
- Kubo, T.; Nozoye, H. Surface structure of SrTiO3. Surf. Sci. 2003, 542, 177–191. [Google Scholar] [CrossRef]
- Maldonado, F.; Rivera, R.; Villamagua, L.; Maldonado, J. DFT modelling of ethanol on BaTiO3 (001) surface. Appl. Surf. Sci. 2018, 456, 276–289. [Google Scholar] [CrossRef]
- Behera, R.K.; Hinojosa, B.B.; Sinott, S.B.; Asthagiri, A.; Philpott, S.R. Coupling of surface relaxation and polarization in PbTiO3 from atomistic simulation. J. Phys. Condens. Matter 2008, 20, 395004. [Google Scholar]
- Si, Y.; Zhang, T.; Liu, C.; Das, S.; Xu, B.; Burkovsky, R.G.; Wei, X.K.; Chen, Z. Antiferroelectric oxide thin-films: Fundamentals, properties and applications. Prog. Mater. Sci. 2024, 142, 101231. [Google Scholar] [CrossRef]
- Porotnikova, N.; Osinkin, D. Segregation and interdiffusion processes in perovskites: A review of recent advances. J. Mater. Chem. A 2024, 12, 2620–2646. [Google Scholar]
- Magagnin, G.; Lubin, C.; Escher, M.; Weber, N.; Tortech, L.; Barrett, N. Ferroelastic Twin Angles at the Surface of CaTiO3 Quantified by Photoemission Electron Microscopy. Phys. Rev. Lett. 2024, 132, 056201. [Google Scholar] [CrossRef]
- Dovesi, R.; Saunders, V.R.; Roetti, C.; Orlando, R.; Zicovich-Wilson, C.M.; Pascale, F.; Civalleri, B.; Doll, K.; Harrison, N.M.; Bush, I.J.; et al. CRYSTAL-2017 User Manual; University of Torino: Torino, Italy, 2017. [Google Scholar]
- Dovesi, R.; Orlando, R.; Roetti, C.; Pisani, C.; Saunders, V.R. The Periodic Hartree-Fock Method and Its Implementation in the Crystal Code. Comput. Simul. Mater. At. Level 2000, 217, 63–88. [Google Scholar]
- Piskunov, S.; Heifets, E.; Eglitis, R.I.; Borstel, G. Bulk properties and electronic structure of SrTiO3, BaTiO3, PbTiO3 perovskites: An ab initio HF/DFT study. Comput. Mater. Sci. 2004, 29, 165–178. [Google Scholar]
- Eglitis, R.I. First-principles calculations of BaZrO3 (001) and (011) surfaces. J. Phys. Condens. Matter 2007, 19, 356004. [Google Scholar] [CrossRef]
- Eglitis, R.I.; Rohlfing, M. First-principles calculations of the atomic and electronic structure of SrZrO3 and PbZrO3 (001) and (011) surfaces. J. Phys. Condens. Matter 2010, 22, 415901. [Google Scholar] [CrossRef] [PubMed]
- Eglitis, R.I. Theoretical Modelling of the Energy Surface (001) and Topology of CaZrO3 Perovskite. Ferroelectrics 2015, 483, 75–85. [Google Scholar]
- Perdew, J.P.; Wang, Y. Accurate and simple density functional for the electronic exchange energy: Generalized gradient approximation. Phys. Rev. B 1986, 33, 8800–8802, Erratum in Phys. Rev. B 1989, 40, 3399. [Google Scholar]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar]
- Monkhorst, H.J. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar]
- Eglitis, R.I.; Popov, A.I. Systematic trends in (001) surface ab initio calculations of ABO3 perovskites. J. Saudi Chem. Soc. 2018, 22, 459–468. [Google Scholar]
- Pojani, A.; Finocchi, F.; Noguera, C. A theoretical study of the unreconstructed polar (111) face of SrTiO3. Appl. Surf. Sci. 1999, 142, 177–181. [Google Scholar] [CrossRef]
- Tasker, P.W. The stability of ionic crystal surfaces. J. Phys. C Solid State Phys. 1979, 12, 4977. [Google Scholar] [CrossRef]
- Noguera, C. Polar oxide surfaces. J. Phys. Condens. Matter 2000, 12, R367. [Google Scholar]
- Eglitis, R.; Purans, J.; Popov, A.I.; Jia, R. Systematic trends in YAlO3, SrTiO3, BaTiO3, BaZrO3 (001) and (111) surface ab initio calculations. Int. J. Mod. Phys. B 2019, 33, 1950390. [Google Scholar] [CrossRef]
- Farfán, J.C.; Rodríguez, J.A.; Fajardo, F.; López, E.V.; Landínez Téllez, D.A.; Roa-Rojas, J. Structural properties, electric response and electronic feature of BaSnO3 perovskite. Phys. B Condens. Matter 2009, 404, 2720–2722. [Google Scholar]
- Hellwege, K.H.; Helwege, A.M. Ferroelectrics and Related Substances. In Landolt-Bornstein, New Series, Group III; Springer: Berlin, Germany, 1969; Volume 3. [Google Scholar]
- Mabud, S.A.; Glazer, A.M. Lattice parameters and birefringence in PbTiO3 single crystals. J. Appl. Cryst. 1979, 12, 49–53. [Google Scholar] [CrossRef]
- Mathews, M.D.; Mirza, E.B.; Momin, A.C. High-temperature X-ray diffractometric studies of CaZrO3, SrZrO3 and BaZrO3. J. Mater. Sci. Lett. 1991, 10, 305–306. [Google Scholar] [CrossRef]
- Kennedy, B.J.; Howard, C.J.; Chakoumakos, B.C. High-temperature phase transitions in SrZrO3. Phys. Rev. B 1999, 59, 4023–4027. [Google Scholar]
- Slater, J.C. A Simplification of the Hartree-Fock Method. Phys. Rev. 1951, 81, 385. [Google Scholar]
- Valatin, J.G. Generalized Hartree-Fock Method. Phys. Rev. 1961, 122, 1012. [Google Scholar] [CrossRef]
- Pisani, C.; Dovesi, R. Exact-exchange Hartree-Fock calculations for periodic systems. I. Illustration of the method. Int. J. Quantum Chem. 1980, 17, 501–516. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Ziesche, P.; Kurth, S.; Perdew, J.P. Density functionals from LDA to GGA. Comput. Mater. Sci. 1998, 11, 122–127. [Google Scholar] [CrossRef]
- Davidson, E.R.; Clark, A.E. A viewpoint on population analyses. Int. J. Quantum Chem. 2022, 122, e26860. [Google Scholar] [CrossRef]
- Zulueta, B.; Tulyani, S.V.; Westmoreland, P.R.; Frisch, M.J.; Petersson, E.J.; Petersson, G.A.; Keith, J.A. A Bond-Energy/Bond-Order and Populations Relationship. J. Chem. Theory Comput. 2022, 18, 4774–4794. [Google Scholar] [CrossRef]
- Kaneko, T.; Sodeyama, K. First-principles molecular dynamics study for S-O bond dissociation of sulfolane on Li-metal negative electrode. Chem. Phys. Lett. 2021, 762, 138199. [Google Scholar] [CrossRef]
- Hu, J.; Jian, X.; Yang, T.; Peng, X. Investigation on the interface characteristic between WC (001) and diamond (111) by first-principles calculation. Diam. Relat. Mater. 2022, 123, 108864. [Google Scholar] [CrossRef]
- Meyer, B.; Padilla, J.; Vanderbilt, D. Theory of PbTiO3, BaTiO3 and SrTiO3 surfaces. Faraday Discuss. 1999, 114, 395–405. [Google Scholar] [CrossRef]
- Bickel, N.; Schmidt, G.; Heinz, K.; Müller, K. Ferroelectric relaxation of the SrTiO3 (100) surface. Phys. Rev. Lett. 1989, 62, 2009–2011. [Google Scholar] [CrossRef]
- Hikita, T.; Hanada, T.; Kudo, M.; Kawai, M. Structure and electronic state of the TiO2 and SrO terminated SrTiO3 (100) surfaces. Surf. Sci. 1993, 287, 377–381. [Google Scholar] [CrossRef]
- Wang, Y.X.; Arai, M. First-principles study of the (001) surface of cubic SrZrO3. Surf. Sci. 2007, 601, 4092–4096. [Google Scholar] [CrossRef]
- Scott, J.F. Ferroelectric Memories; Springer: Berlin, Germany, 2000. [Google Scholar]
- Noguera, C. Physics and Chemistry at Oxide Surfaces; Cambridge University Press: New York, NY, USA, 1996. [Google Scholar]
- Fleig, J. Microelectrodes in solid state ionics. Solid State Ion. 2003, 161, 279–289. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).