The Role of Methyl Substitution in Spin Crossover of Fe(III) Complexes with Pentadentate Schiff Base Ligands
Abstract
1. Introduction
2. Results
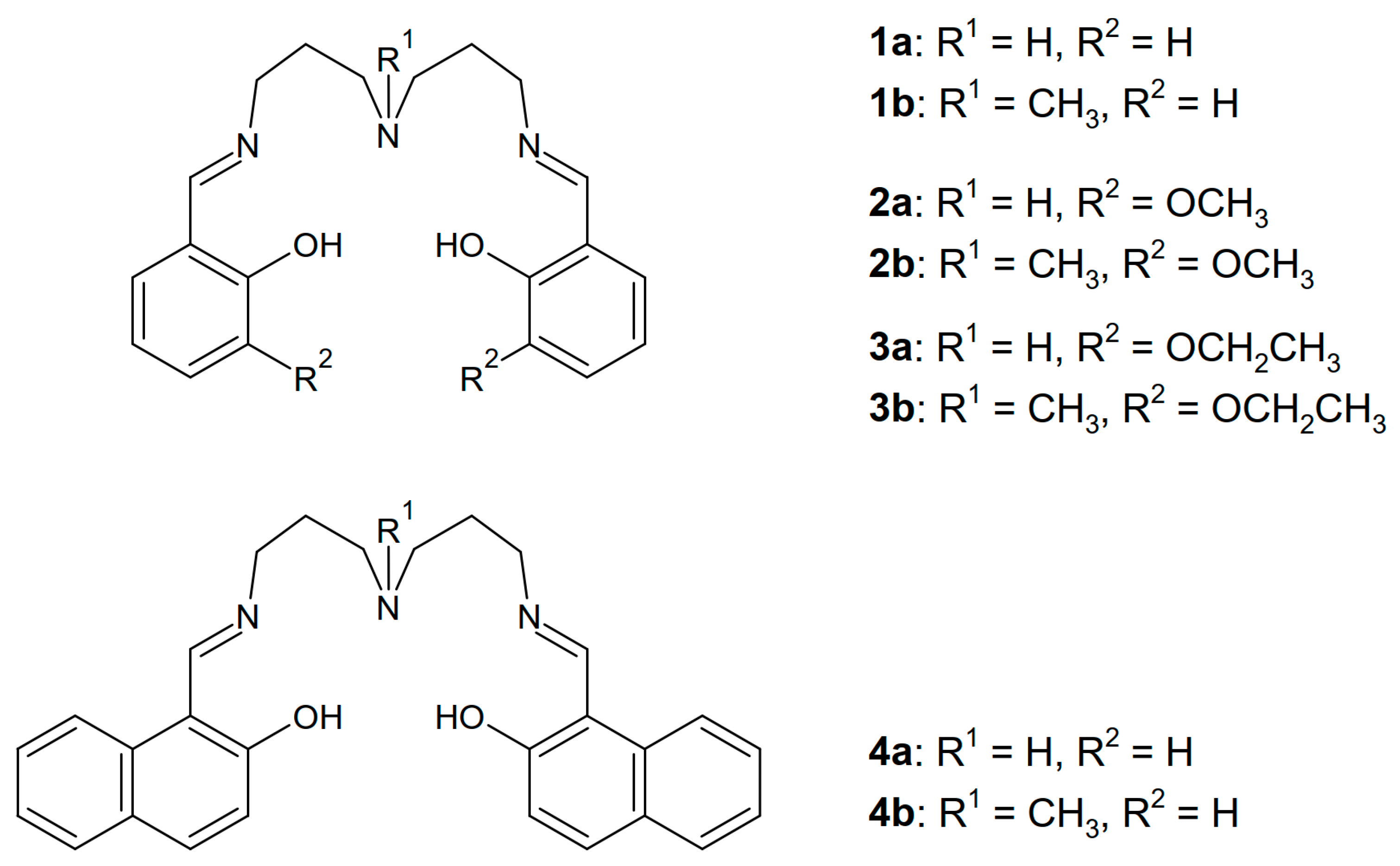
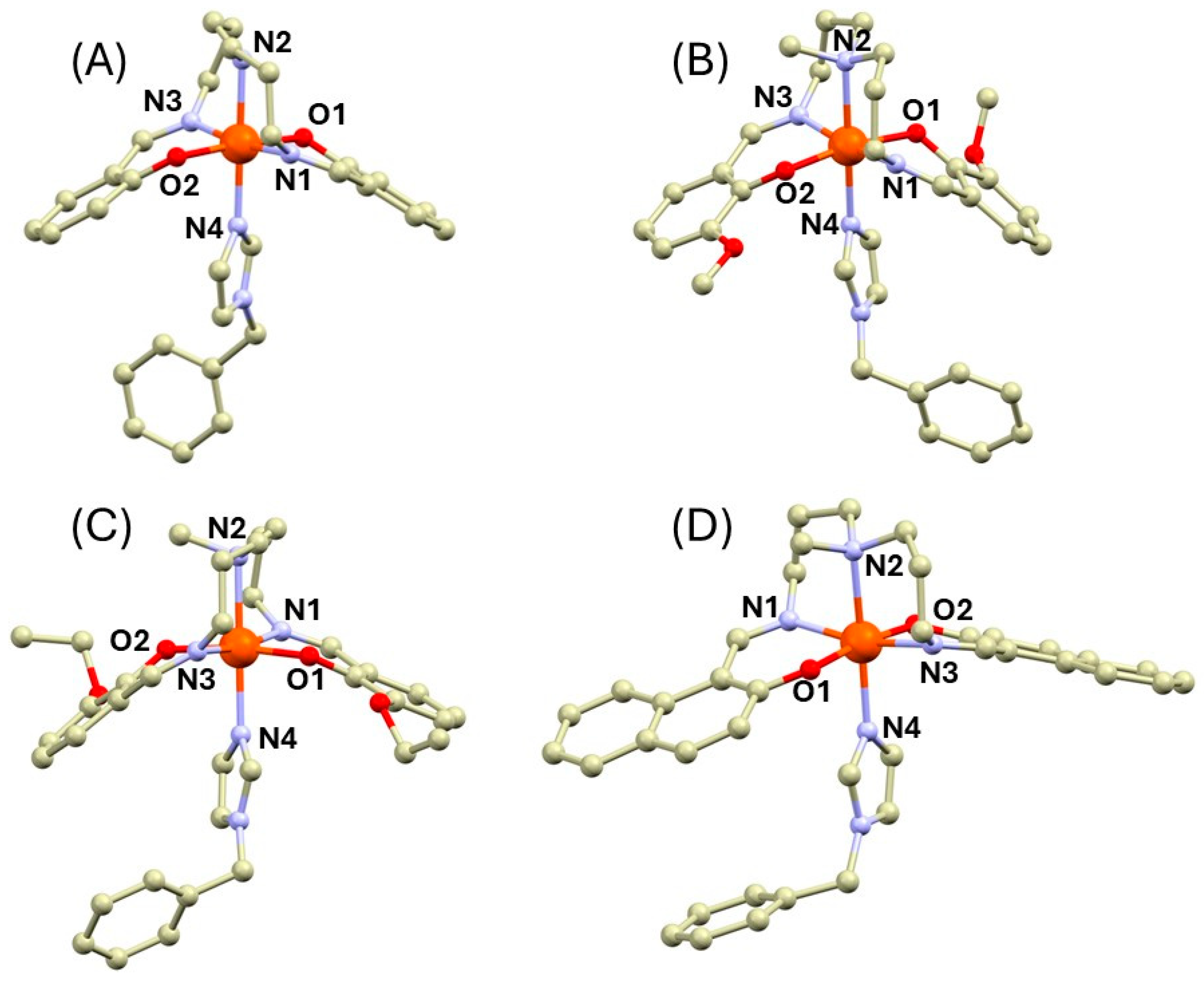
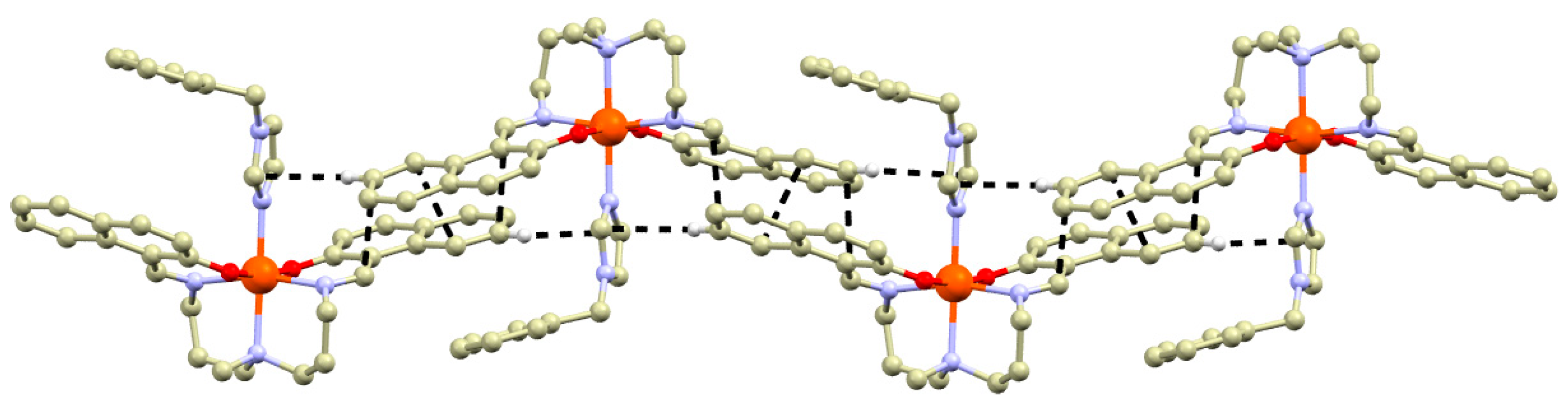
2.1. Synthesis and Crystal Structures
2.2. Magnetic Properties
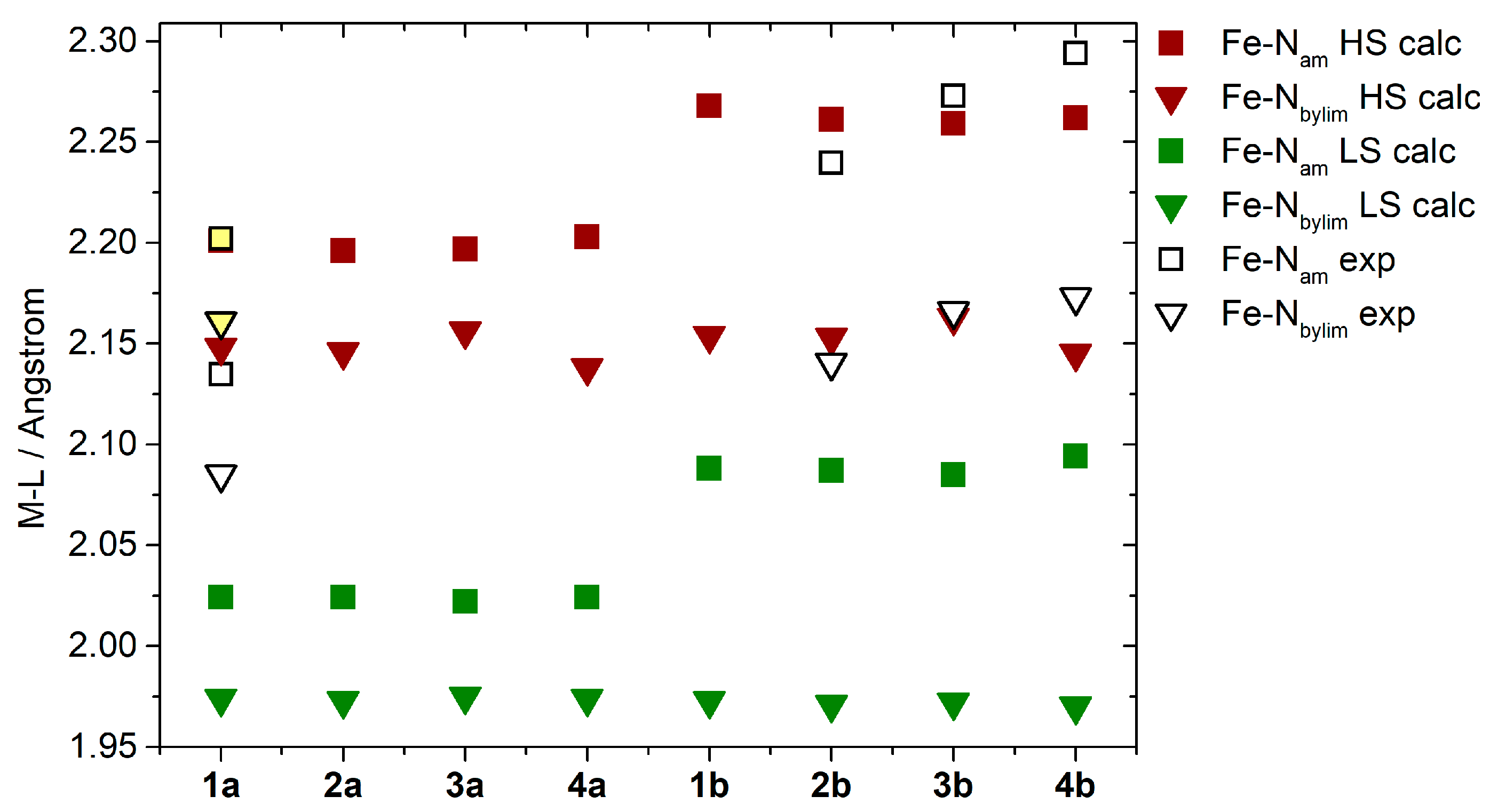
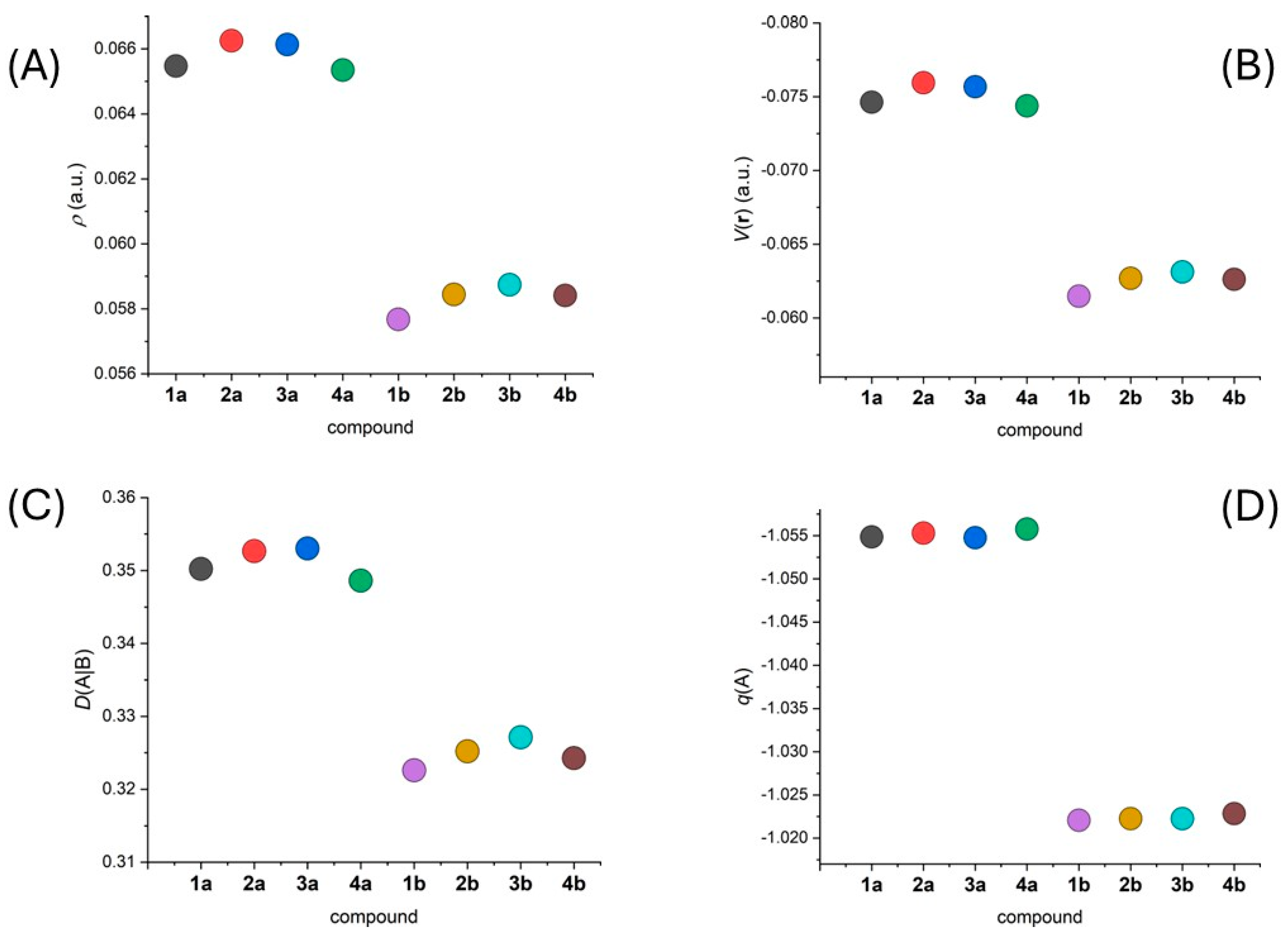
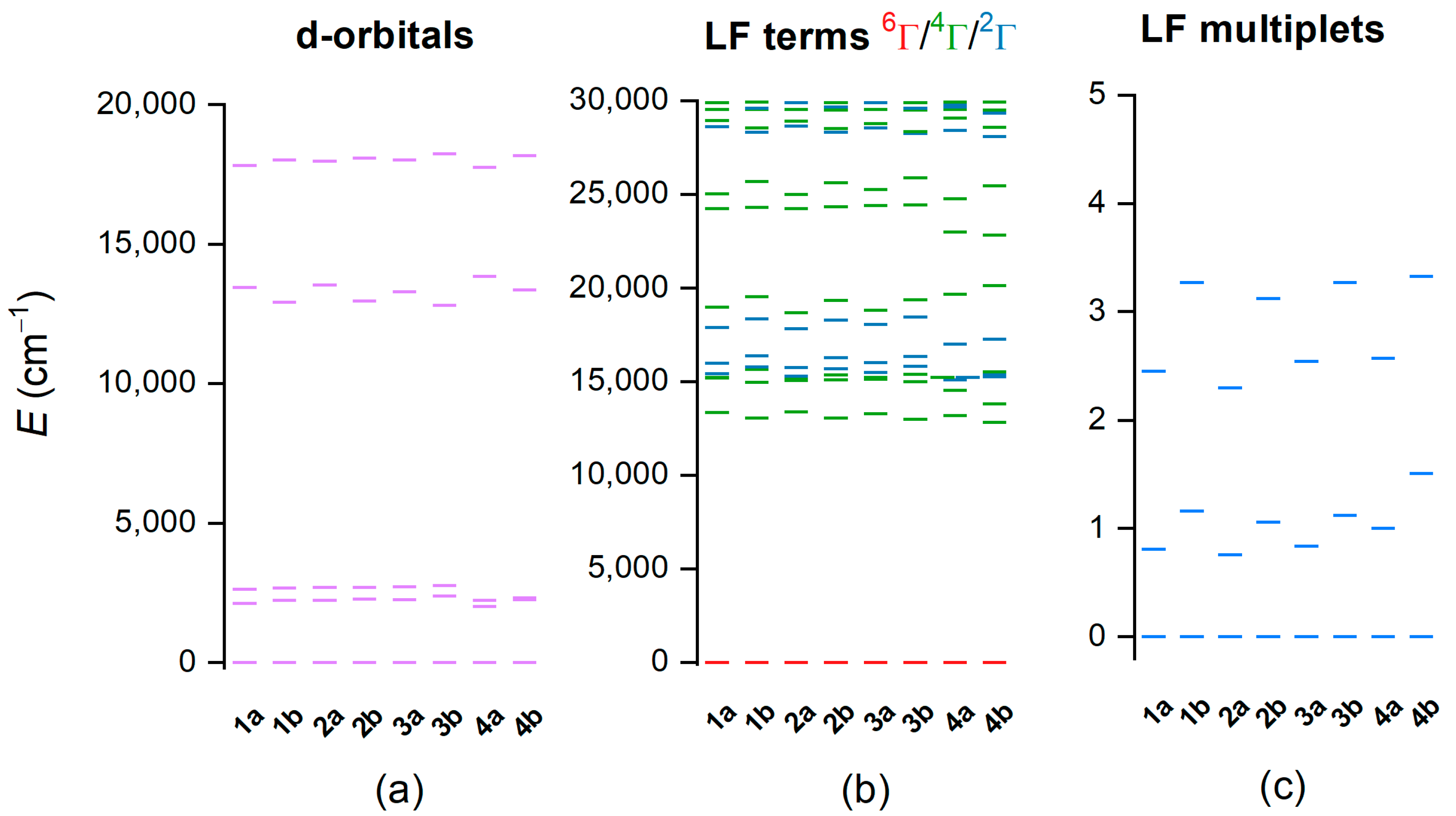
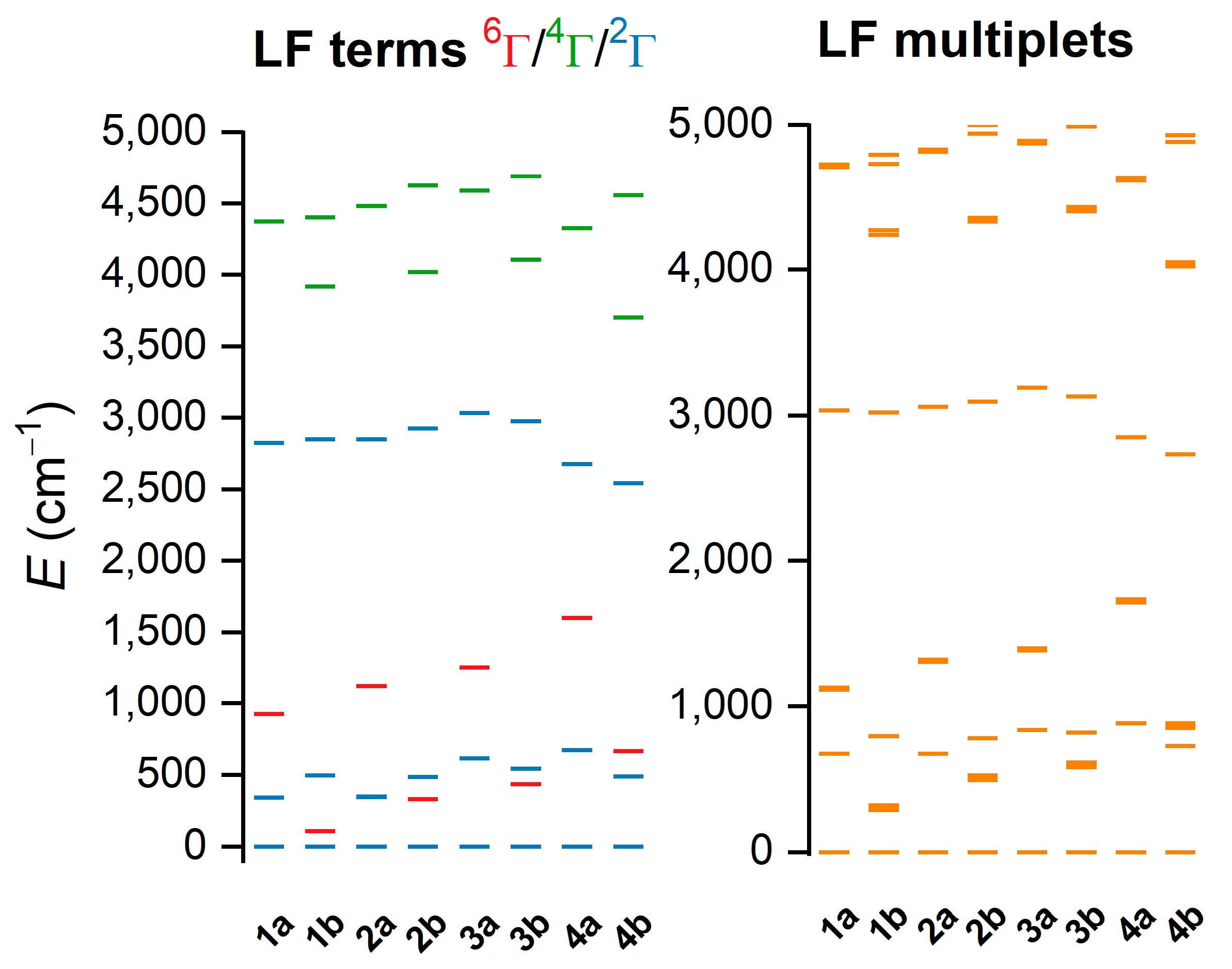
2.3. Theoretical Calculations
3. Materials and Methods
3.1. General Considerations and Instrumentation
3.2. X-Ray Diffraction Analysis
3.3. Synthesis
3.4. Theoretical Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van Koningsbruggen, P.J.; Maeda, Y.; Oshio, H. Iron(III) spin crossover compounds. In Spin Crossover in Transition Metal Compounds I; Gütlich, P., Goodwin, H.A., Eds.; Springer: Berlin, Germany, 2004; pp. 259–324. [Google Scholar]
- Boonprab, T.; Thammasangwan, W.; Chastanet, G.; Gonidec, M.; Harding, P.; Harding, D.J. Halide Anion Effects and Magnetostructural Relationships in Iron(III) Spin Crossover Complexes. Cryst. Growth Des. 2024, 24, 8145–8152. [Google Scholar] [CrossRef]
- Díaz-Torres, R.; Gómez-Coca, S.; Ruiz, E.; Harding, P.; Harding, D.J. Improving spin crossover characteristics in heteroleptic [FeIII(qsal-5-I)(qsal-5-OMe)]A complexes. Dalton Trans. 2023, 52, 18148–18157. [Google Scholar] [CrossRef]
- Harding, D.J.; Harding, P.; Phonsri, W. Spin crossover in iron(III) complexes. Coord. Chem. Rev. 2016, 313, 38–61. [Google Scholar] [CrossRef]
- Matsumoto, N.; Ohta, S.; Yoshimura, C.; Ohyoshi, A.; Kohata, S.; Okawa, H.; Maeda, Y. Studies on spin-equilibrium iron(III) complexes. Part 1. Syntheses and magnetic properties of a new family of spin cross-over iron(III) complexes with a unidentate ligand over a wide range of the spectrochemical series and a quinquedentate ligand derived. J. Chem. Soc. Dalton Trans. 1985, 12, 2575. [Google Scholar] [CrossRef]
- Boča, R.; Fukuda, Y.; Gembický, M.; Herchel, R.; Jaroščiak, R.; Linert, W.; Renz, F.; Yuzurihara, J. Spin crossover in mononuclear and binuclear iron(III) complexes with pentadentate Schiff-base ligands. Chem. Phys. Lett. 2000, 325, 411–419. [Google Scholar] [CrossRef]
- Tanimura, K.; Kitashima, R.; Bréfuel, N.; Nakamura, M.; Matsumoto, N.; Shova, S.; Tuchagues, J.-P. Infinite chain structure and steep spin crossover of a Fe III Complex with a N3O2 pentadentate schiff-base ligand and 4-aminopyridine. Bull. Chem. Soc. Jpn. 2005, 78, 1279–1282. [Google Scholar] [CrossRef]
- Nemec, I.; Svoboda, I.; Herchel, R. Spin Crossover in Three Mononuclear Iron (III) Schiff Base Complexes. Metals 2019, 9, 849. [Google Scholar] [CrossRef]
- Faulmann, C.; Dorbes, S.; De Bonneval, B.G.; Molnár, G.; Bousseksou, A.; Gomez-Garcia, C.J.; Coronado, E.; Valade, L. Towards molecular conductors with a spin-crossover phenomenon: Crystal structures, magnetic properties and Mössbauer spectra of [Fe(salten)mepepy][M(dmit)2] complexes. Eur. J. Inorg. Chem. 2005, 2005, 3261–3270. [Google Scholar] [CrossRef]
- Bannwarth, A.; Schmidt, S.O.; Peters, G.; Sönnichsen, F.D.; Thimm, W.; Herges, R.; Tuczek, F. FeIII spin-crossover complexes with photoisomerizable ligands: Experimental and theoretical studies on the ligand-driven light-induced spin change effect. Eur. J. Inorg. Chem. 2012, 2012, 2776–2783. [Google Scholar] [CrossRef]
- Nemec, I.; Boča, R.; Herchel, R.; Trávníček, Z.; Gembický, M.; Linert, W. Dinuclear Fe(III) complexes with spin crossover. Monatshefte Chem. Chem. Mon. 2009, 140, 815–828. [Google Scholar] [CrossRef]
- Hayami, S.; Hiki, K.; Kawahara, T.; Maeda, Y.; Urakami, D.; Inoue, K.; Ohama, M.; Kawata, S.; Sato, O. Photo-Induced Spin Transition of Iron(III) Compounds with π-π Intermolecular Interactions. Chem.-A Eur. J. 2009, 15, 3497–3508. [Google Scholar] [CrossRef] [PubMed]
- Si-Guo, W.; Najbul, H.M.; Jie-Yu, Z.; Guo-Zhang, H.; Vu, H.A.N.; Liviu, U.; Wei-Xiong, Z.; Zhao-Ping, N.; Ming-Liang, T. Multiresponsive Spin Crossover Driven by Rotation of Tetraphenylborate Anion in an Iron(III) Complex. CCS Chem. 2020, 3, 453–459. [Google Scholar] [CrossRef]
- Pavlik, J.; Masárová, P.; Nemec, I.; Fuhr, O.; Ruben, M.; Šalitroš, I. Heteronuclear Iron(III)-Schiff Base Complexes with the Hexacyanidocobaltate(III) Anion: On the Quest to Understand the Governing Factors of Spin Crossover. Inorg. Chem. 2020, 59, 2747–2757. [Google Scholar] [CrossRef] [PubMed]
- Herchel, R.; Boča, R.; Gembický, M.; Kožísek, J.; Renz, F. Spin Crossover in a Tetranuclear Cr(III)−Fe(III)3 Complex. Inorg. Chem. 2004, 43, 4103–4105. [Google Scholar] [CrossRef]
- Nemec, I.; Herchel, R.; Boča, R.; Trávníček, Z.; Svoboda, I.; Fuess, H.; Linert, W. Tuning of spin crossover behaviour in iron(III) complexes involving pentadentate Schiff bases and pseudohalides. Dalton Trans. 2011, 40, 10090–10099. [Google Scholar] [CrossRef]
- Nemec, I.; Herchel, R.; Trávníček, Z. The relationship between the strength of hydrogen bonding and spin crossover behaviour in a series of iron(iii) Schiff base complexes. Dalton Trans. 2015, 44, 4474–4484. [Google Scholar] [CrossRef]
- Vela, S.; Paulsen, H. Cooperativity in Spin Crossover Systems. An Atomistic Perspective on the Devil’s Staircase. Inorg. Chem. 2018, 57, 9478–9488. [Google Scholar] [CrossRef] [PubMed]
- Nemec, I.; Boča, R.; Gembický, M.; Dlháň, L.; Herchel, R.; Renz, F. High-spin Schiff-base dinuclear iron(III) complexes bridged by N-oxide ligands. Inorg. Chim. Acta 2009, 362, 4754–4759. [Google Scholar] [CrossRef]
- Pogány, L.; Brachňaková, B.; Masárová, P.; Moncol, J.; Pavlik, J.; Gál, M.; Mazúr, M.; Herchel, R.; Nemec, I.; Šalitroš, I. Impact of the Schiff base ligand substituents on the solid state and solution properties of eleven iron(III) complexes. New J. Chem. 2019, 43, 13916–13928. [Google Scholar] [CrossRef]
- Milocco, F.; De Vries, F.; Siebe, H.S.; Engbers, S.; Demeshko, S.; Meyer, F.; Otten, E. Widening the Window of Spin-Crossover Temperatures in Bis(formazanate)iron(II) Complexes via Steric and Noncovalent Interactions. Inorg. Chem. 2021, 60, 2045–2055. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Najibi, A.; Goerigk, L. DFT-D4 counterparts of leading meta-generalized-gradient approximation and hybrid density functionals for energetics and geometries. J. Comput. Chem. 2020, 41, 2562–2572. [Google Scholar] [CrossRef]
- Bursch, M.; Neugebauer, H.; Ehlert, S.; Grimme, S. Dispersion corrected r2SCAN based global hybrid functionals: r2SCANh, r2SCAN0, and r2SCAN50. J. Chem. Phys. 2022, 156, 134105. [Google Scholar] [CrossRef] [PubMed]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes. J. Chem. Phys. 2003, 119, 12129–12137. [Google Scholar] [CrossRef]
- Rajchel, Ł.; Żuchowski, P.S.; Hapka, M.; Modrzejewski, M.; Szczęśniak, M.M.; Chałasiński, G. A density functional theory approach to noncovalent interactions via interacting monomer densities. Phys. Chem. Chem. Phys. 2010, 12, 14686–14692. [Google Scholar] [CrossRef]
- Friede, M.; Ehlert, S.; Grimme, S.; Mewes, J.-M. Do Optimally Tuned Range-Separated Hybrid Functionals Require a Reparametrization of the Dispersion Correction? It Depends. J. Chem. Theory Comput. 2023, 19, 8097–8107. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Calculate Root-Mean-Square Deviation (RMSD) of Two Molecules Using Rotation, GitHub. Version rmsd-1.5.1. Available online: https://github.com/charnley/rmsd (accessed on 11 November 2024).
- Li, W.; Li, X.; Robeyns, K.; Wolff, M.; Kfoury, J.; Oláh, J.; Herchel, R.; Demeshko, S.; Meyer, F.; Garcia, Y. Spin-state versatility in FeII4L6 supramolecular cages with a pyridyl-hydrazone ligand scaffold modulated by solvents and counter anions. Dalton Trans. 2024, 53, 1449–1459. [Google Scholar] [CrossRef]
- Figgis, B.N.; Hitchman, M.A. Ligand Field Theory and Its Applications; Wiley: New York, NY, USA, 1999; ISBN 978-0-471-31776-0. [Google Scholar]
- Bader, R. Atoms in Molecules: A Quantum Theory; Oxford University Press: New York, NY, USA, 1994; ISBN 978-0-19-855865-1. [Google Scholar]
- Atanasov, M.; Ganyushin, D.; Sivalingam, K.; Neese, F. A Modern First-Principles View on Ligand Field Theory Through the Eyes of Correlated Multireference Wavefunctions; Springer: Berlin/Heidelberg, Germany, 2011; pp. 149–220. ISBN 978-3-642-27378-0. [Google Scholar]
- Singh, S.K.; Eng, J.; Atanasov, M.; Neese, F. Covalency and chemical bonding in transition metal complexes: An ab initio based ligand field perspective. Coord. Chem. Rev. 2017, 344, 2–25. [Google Scholar] [CrossRef]
- CrysAlisPro, Version 1.171.40.82a, Rigaku Oxford Diffraction: Oxford, UK, 2020.
- Bruker AXS Inc. APEX2, SMART-Plus and SADABS; Bruker AXS Inc.: Madison, WI, USA, 2004. [Google Scholar]
- Sheldrick, G.M. SHELXT–Integrated space-group and crystal-structure determination. Acta Crystallogr. A 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Shedrick, G.M. A short history of SHELX. Acta Crystallogr. 2008, A64, 112–122. [Google Scholar] [CrossRef] [PubMed]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system—Version 5.0. WIREs Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
- Neese, F. A perspective on the future of quantum chemical software: The example of the ORCA program package. Faraday Discuss. 2024, 254, 295–314. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Hansen, A.; Becker, U. Efficient, approximate and parallel Hartree-Fock and hybrid DFT calculations. A “chain-of-spheres” algorithm for the Hartree-Fock exchange. Chem. Phys. 2009, 356, 98–109. [Google Scholar] [CrossRef]
- Izsák, R.; Neese, F. An overlap fitted chain of spheres exchange method. J. Chem. Phys. 2011, 135, 144105. [Google Scholar] [CrossRef] [PubMed]
- Helmich-Paris, B.; de Souza, B.; Neese, F.; Izsák, R. An improved chain of spheres for exchange algorithm. J. Chem. Phys. 2021, 155, 104109. [Google Scholar] [CrossRef] [PubMed]
- Caldeweyher, E.; Ehlert, S.; Hansen, A.; Neugebauer, H.; Spicher, S.; Bannwarth, C.; Grimme, S. A generally applicable atomic-charge dependent London dispersion correction. J. Chem. Phys. 2019, 150, 154122. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Ratés, M.; Neese, F. Effect of the Solute Cavity on the Solvation Energy and its Derivatives within the Framework of the Gaussian Charge Scheme. J. Comput. Chem. 2020, 41, 922–939. [Google Scholar] [CrossRef]
- AIMAll (Version 19.10.12), Todd A. Keith, TK Gristmill Software: Overland Park, KS, USA, 2019. Available online: https://aim.tkgristmill.com (accessed on 16 March 2023).
- Malmqvist, P.-Å.; Roos, B.O. The CASSCF state interaction method. Chem. Phys. Lett. 1989, 155, 189–194. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Malrieu, J.-P. N-electron valence state perturbation theory: A fast implementation of the strongly contracted variant. Chem. Phys. Lett. 2001, 350, 297–305. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J.-P. Introduction of n -electron valence states for multireference perturbation theory. J. Chem. Phys. 2001, 114, 10252–10264. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nemec, I.; Herchel, R. The Role of Methyl Substitution in Spin Crossover of Fe(III) Complexes with Pentadentate Schiff Base Ligands. Inorganics 2025, 13, 57. https://doi.org/10.3390/inorganics13020057
Nemec I, Herchel R. The Role of Methyl Substitution in Spin Crossover of Fe(III) Complexes with Pentadentate Schiff Base Ligands. Inorganics. 2025; 13(2):57. https://doi.org/10.3390/inorganics13020057
Chicago/Turabian StyleNemec, Ivan, and Radovan Herchel. 2025. "The Role of Methyl Substitution in Spin Crossover of Fe(III) Complexes with Pentadentate Schiff Base Ligands" Inorganics 13, no. 2: 57. https://doi.org/10.3390/inorganics13020057
APA StyleNemec, I., & Herchel, R. (2025). The Role of Methyl Substitution in Spin Crossover of Fe(III) Complexes with Pentadentate Schiff Base Ligands. Inorganics, 13(2), 57. https://doi.org/10.3390/inorganics13020057






