Reactive Crystallization of Lithium Carbonate from LiCl and Na2CO3: Effect of Polyacrylic Acid Monitored by Focused Reflectance Measurement
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Solution Preparation and Precipitation Tests
2.3. Data Analysis
2.4. Characterization
3. Results
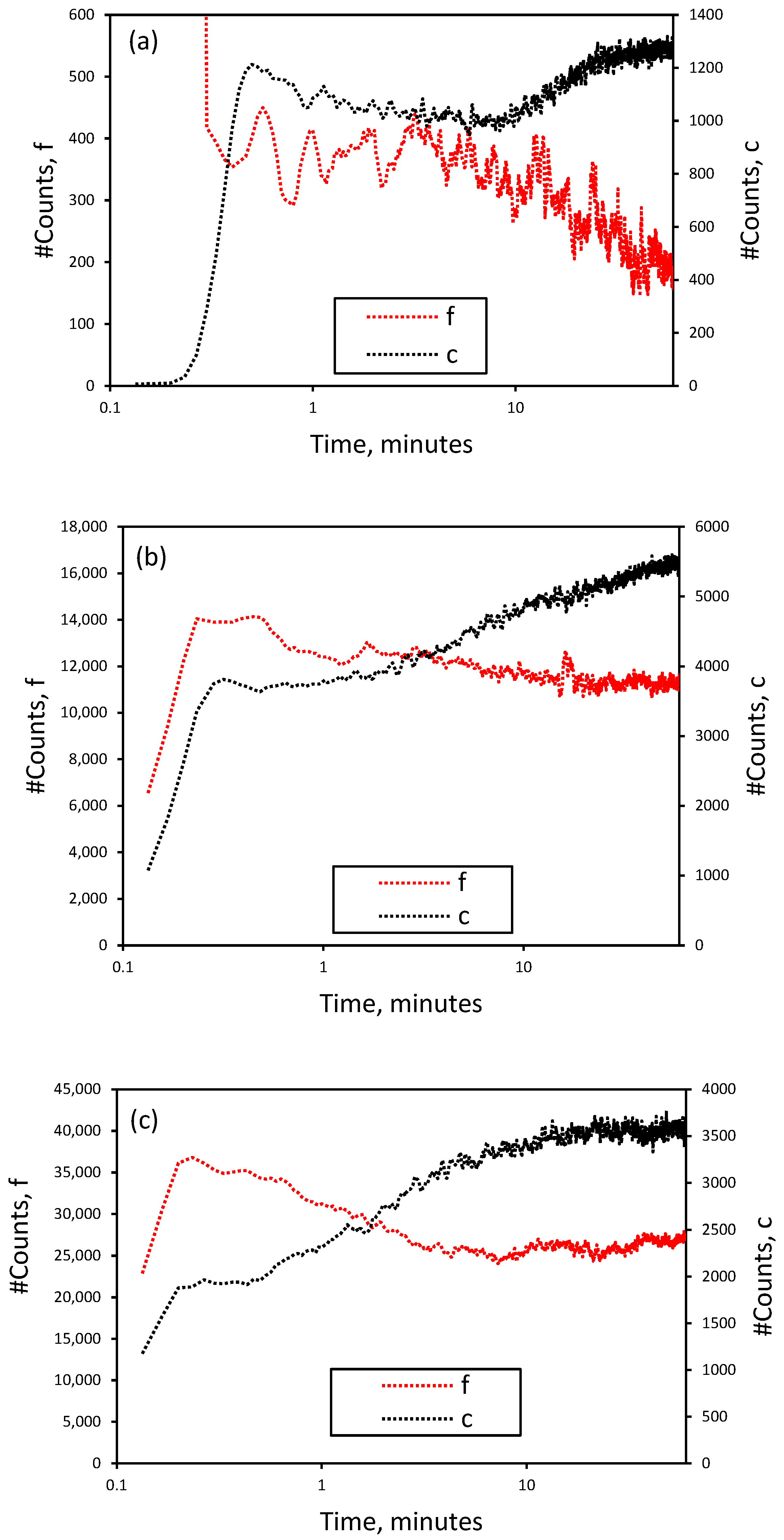
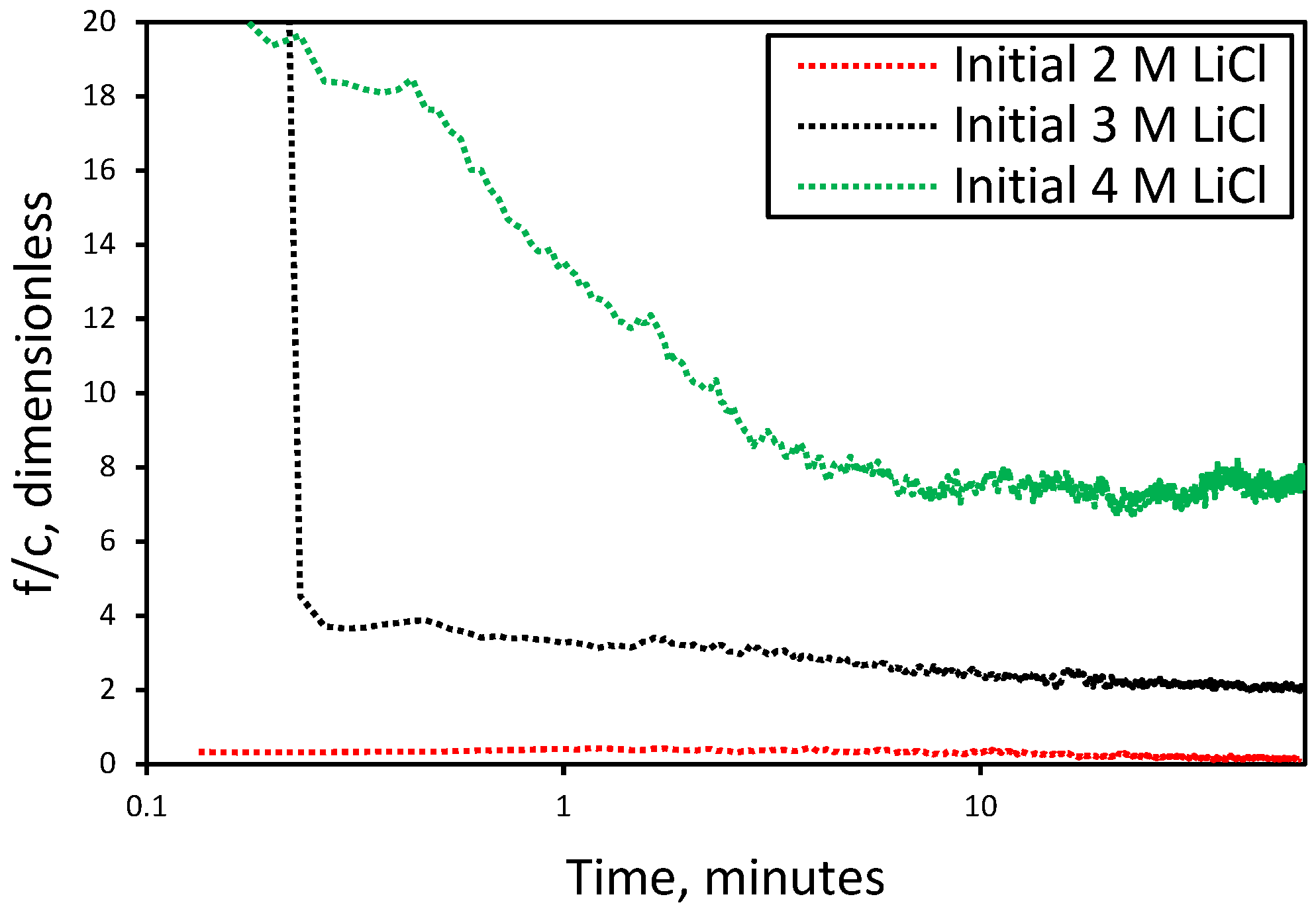
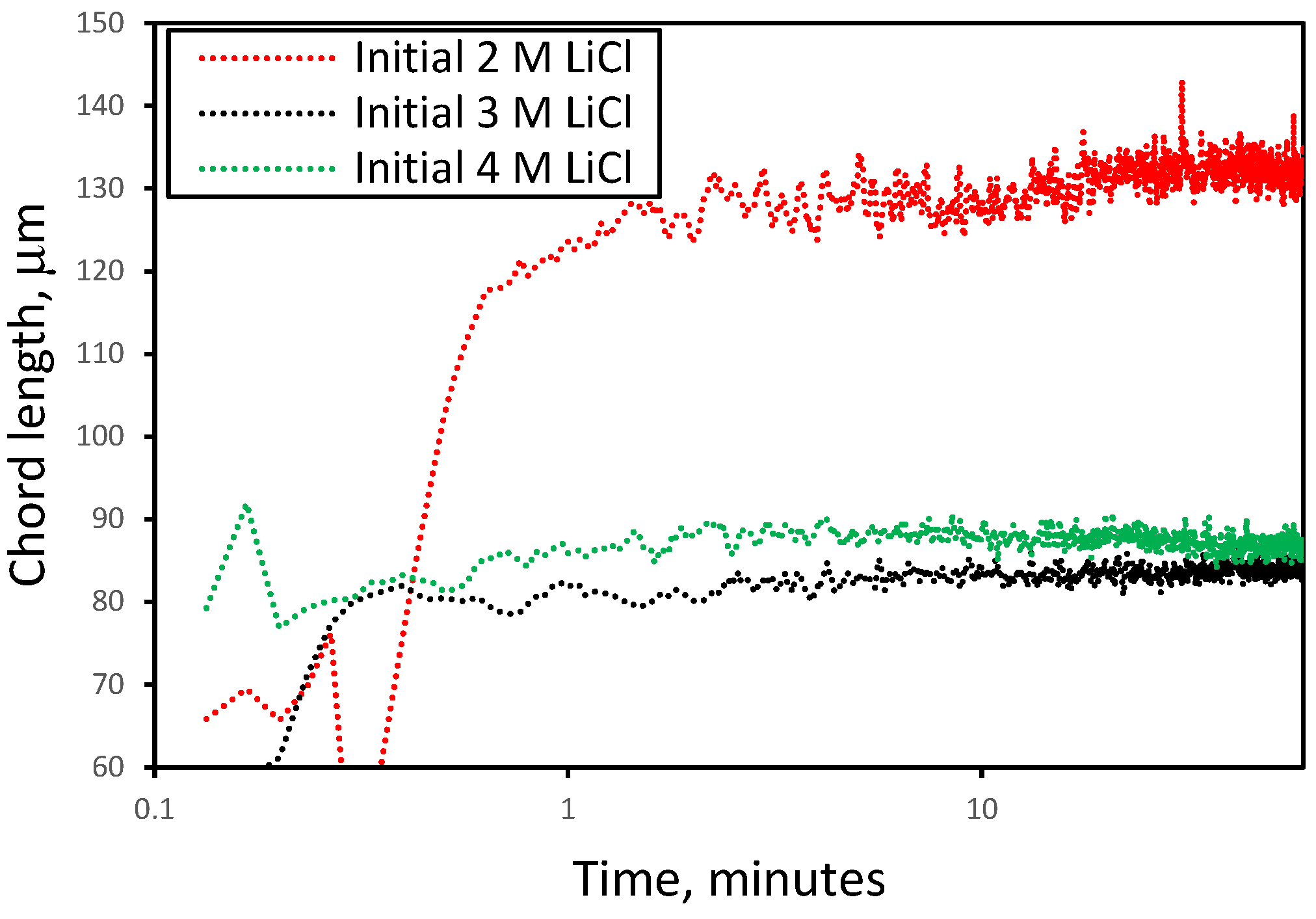
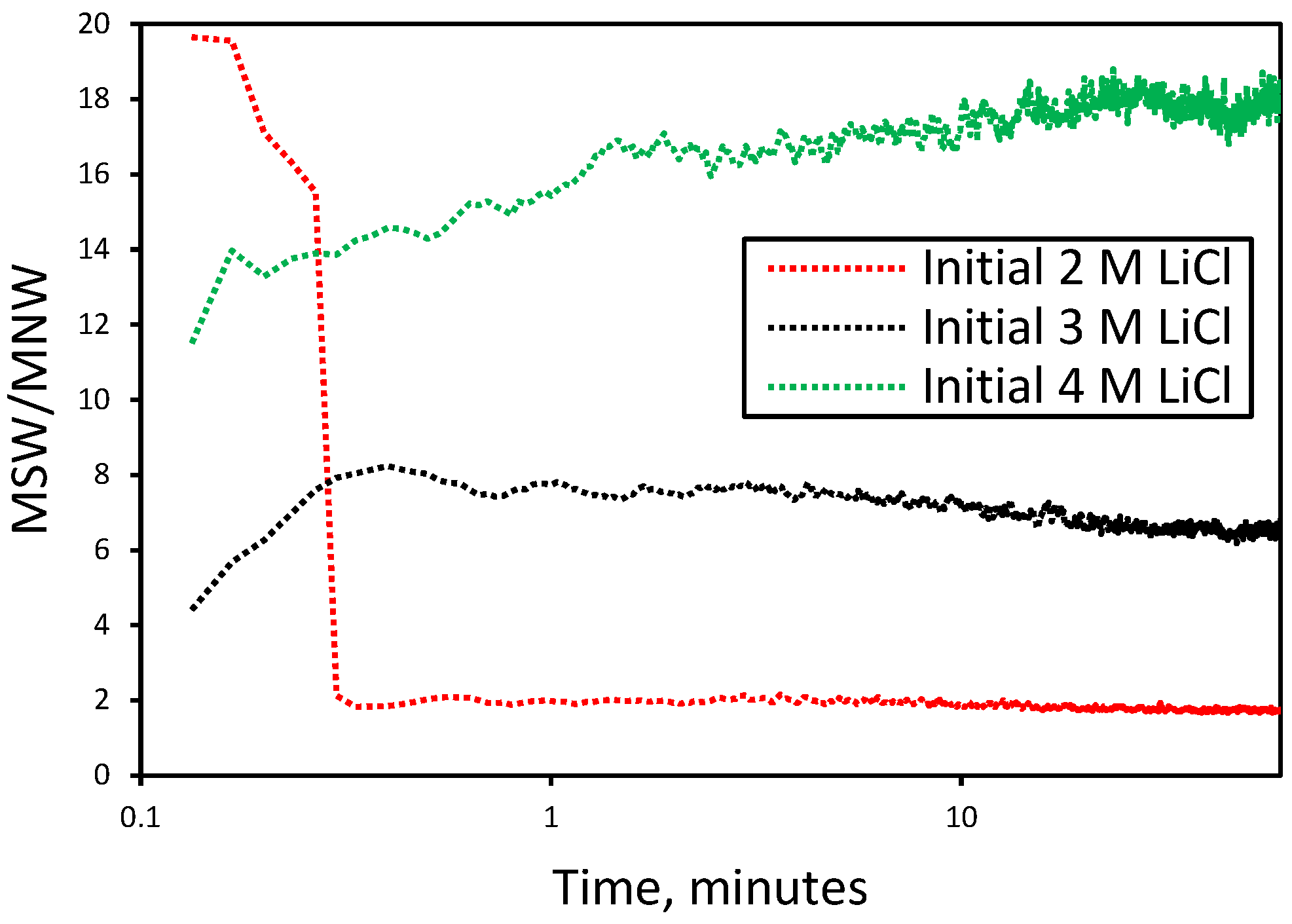
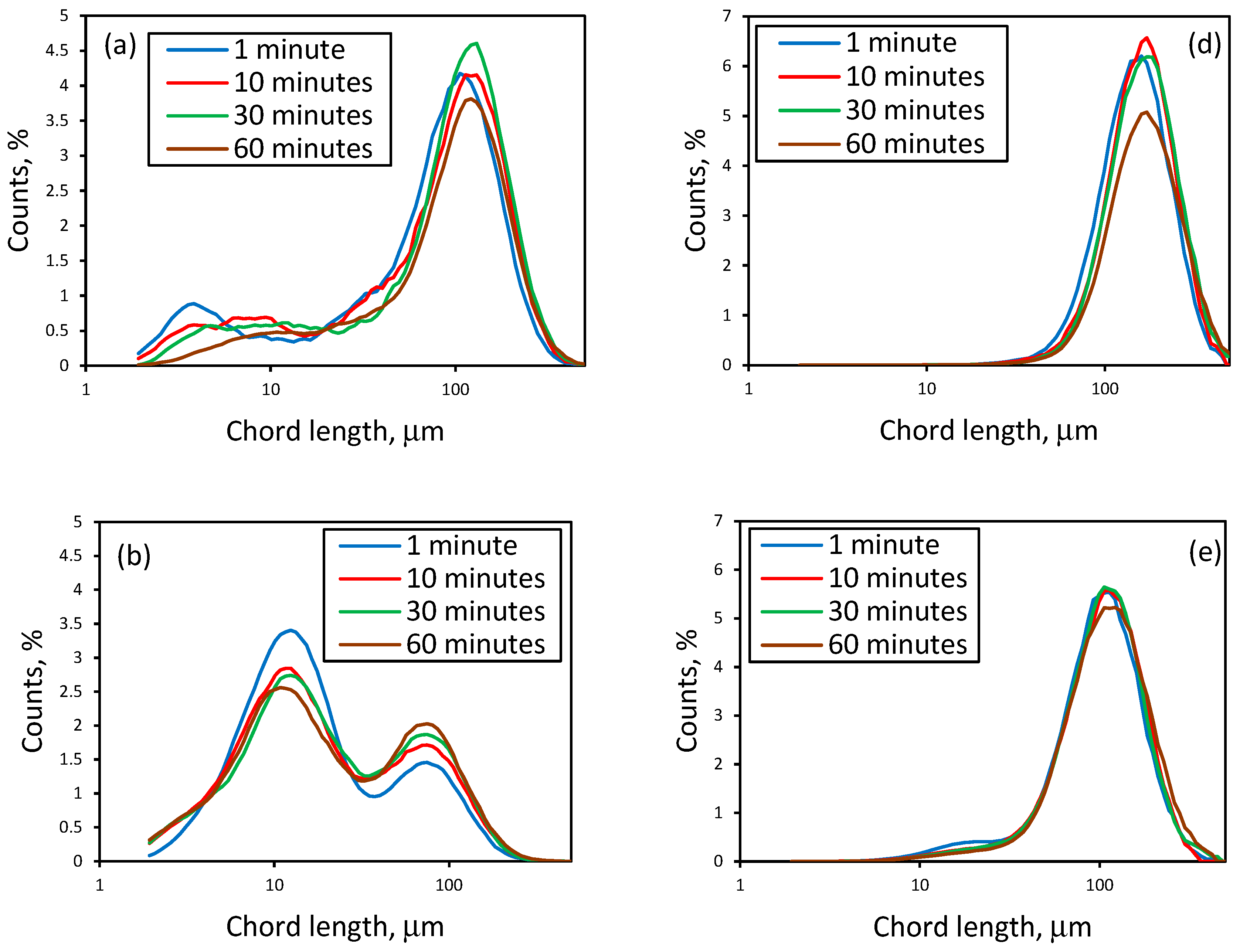
3.1. Effect of Initial LiCl Concentration on Crystal Shape and Size in the Absence of Additives
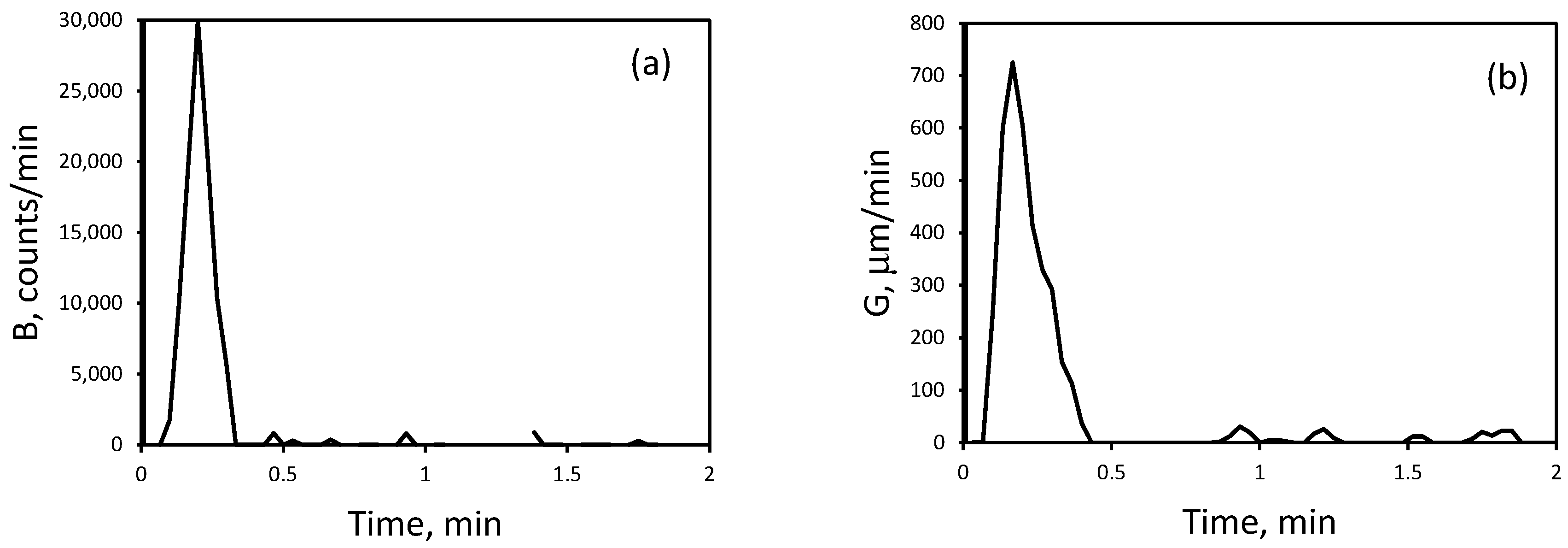
3.2. Nucleation and Crystallization Growth Rates of Lithium Carbonate
- (i)
- Mechanically induced secondary nucleation, resulting from collisions between particles, the impeller, or the reactor walls, which generate microscopic fragments capable of acting as new nuclei [50].
- (ii)
- Localized dissolution of very small or unstable crystals, followed by recrystallization on lower-energy surfaces, temporarily increases the particle count.
- (iii)
- External perturbations, such as variations in stirring speed, impurities, or thermal fluctuations, transiently alter the supersaturation and trigger additional nucleation or breakage events.
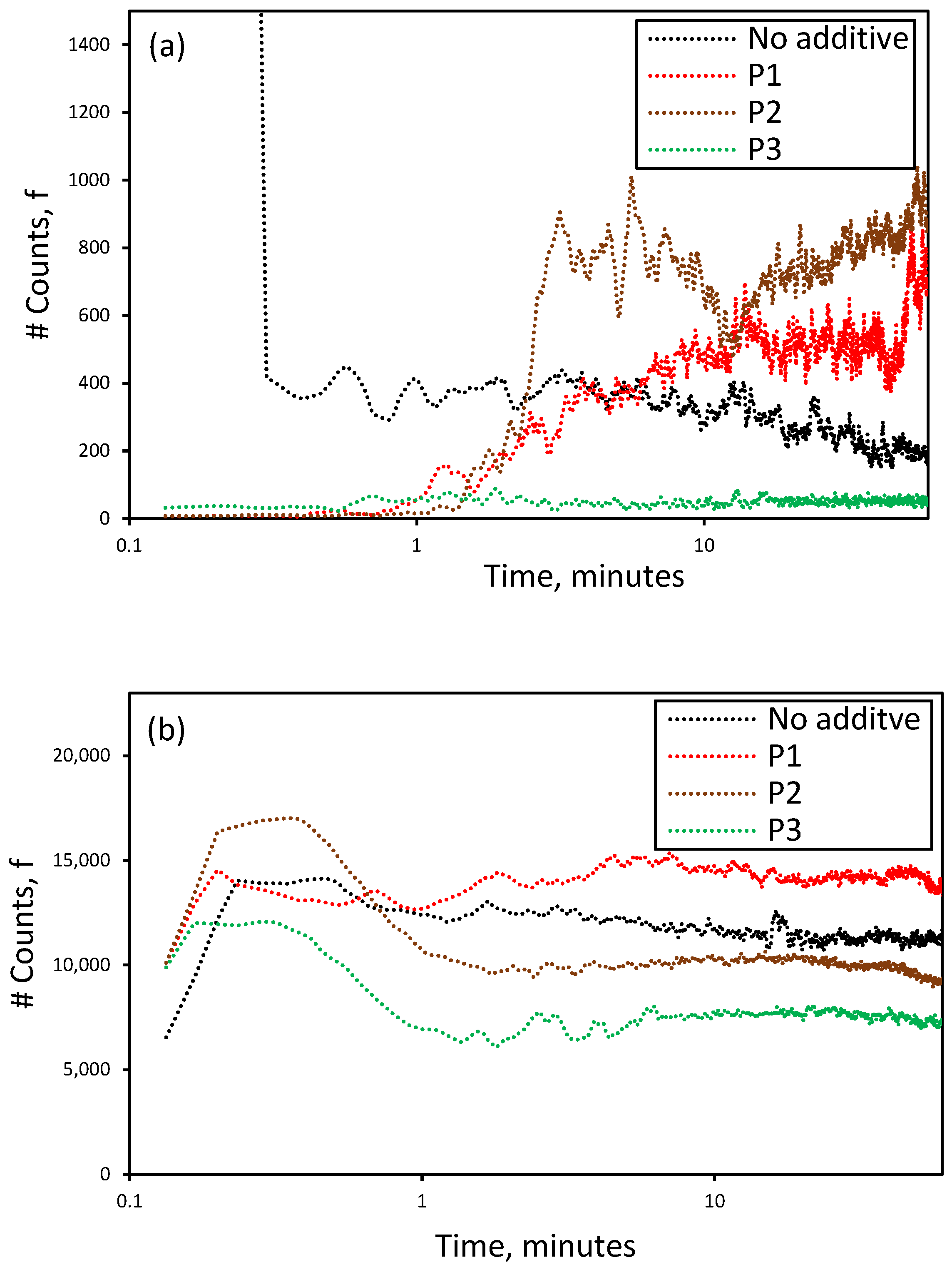
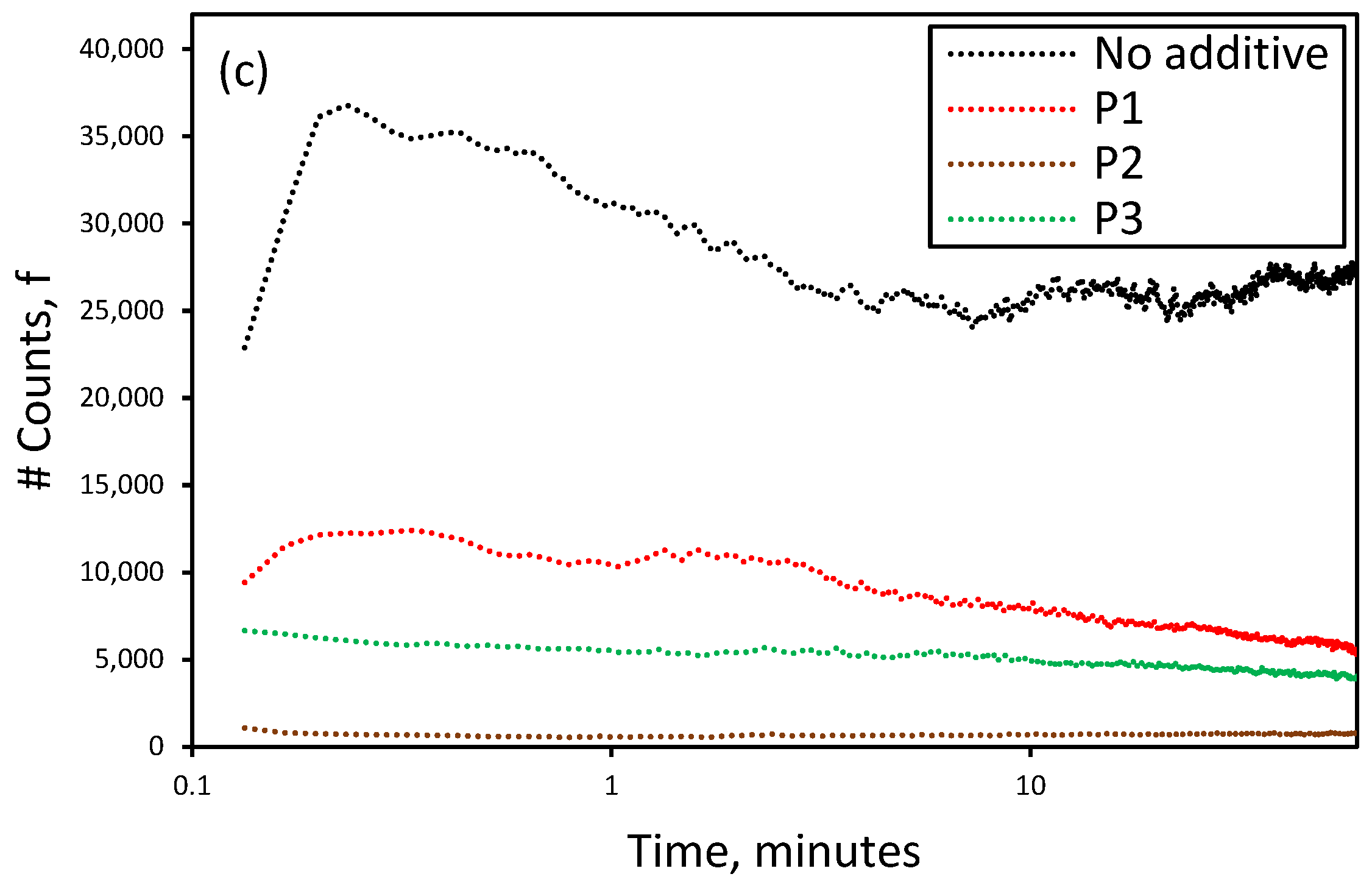
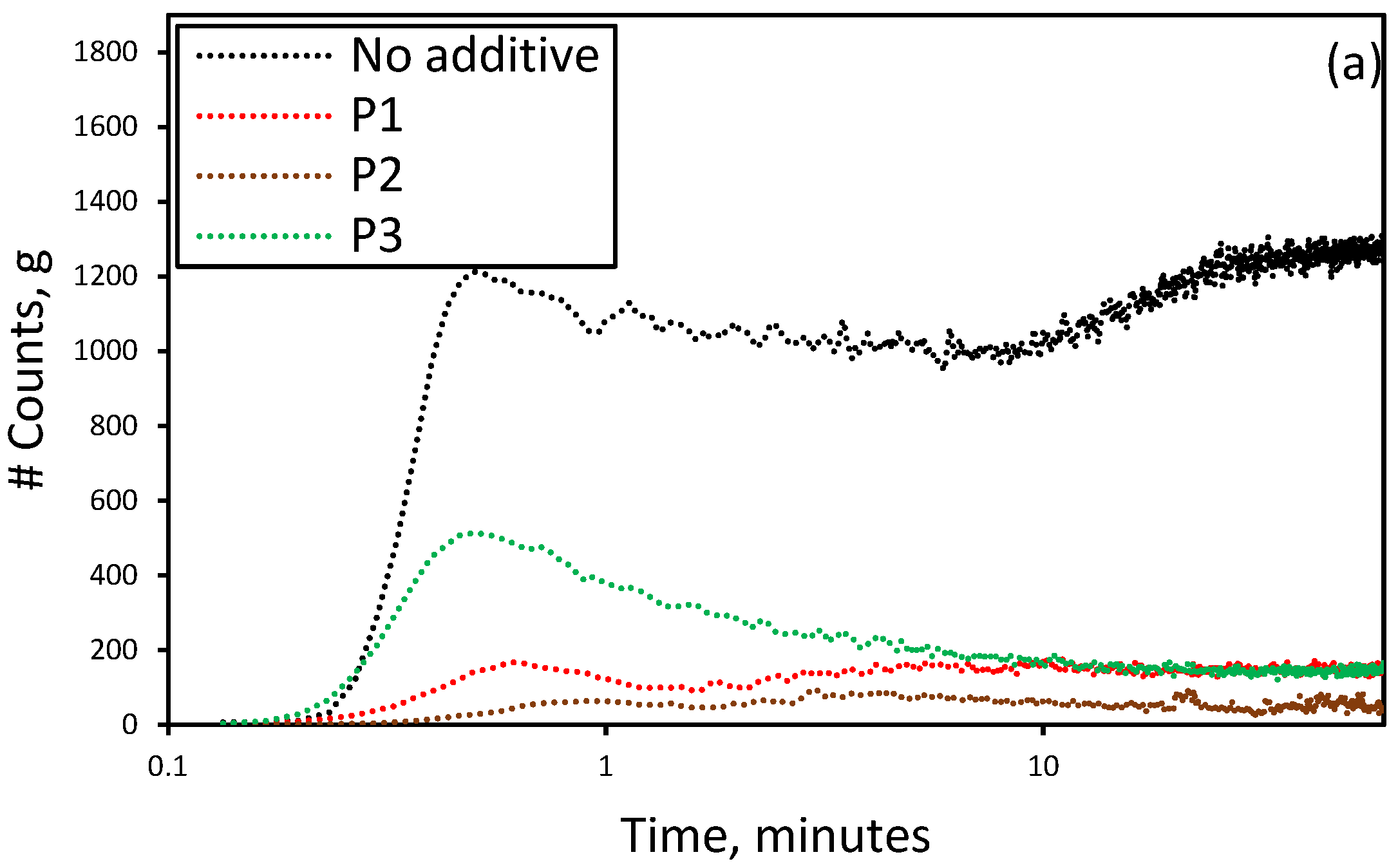
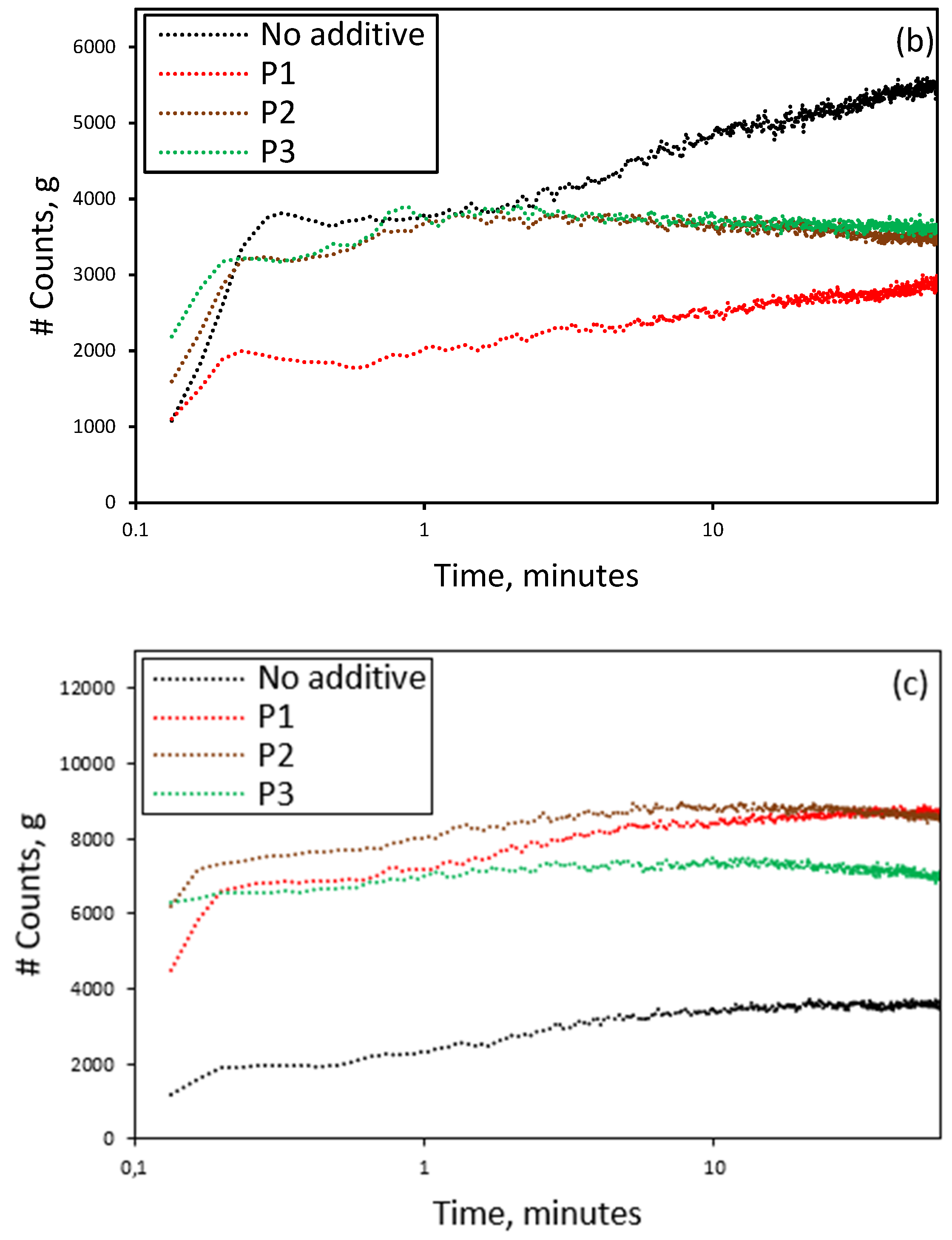
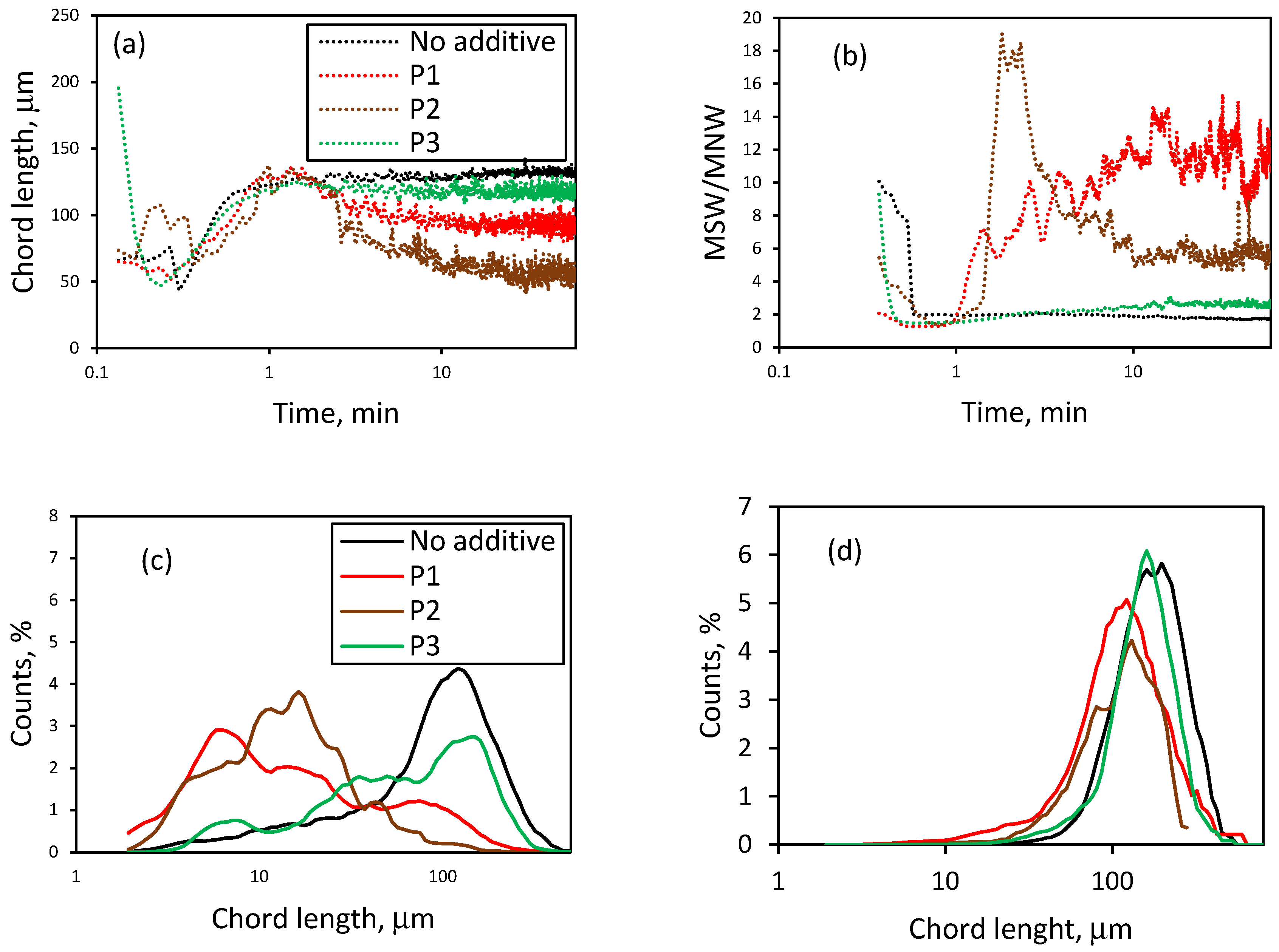
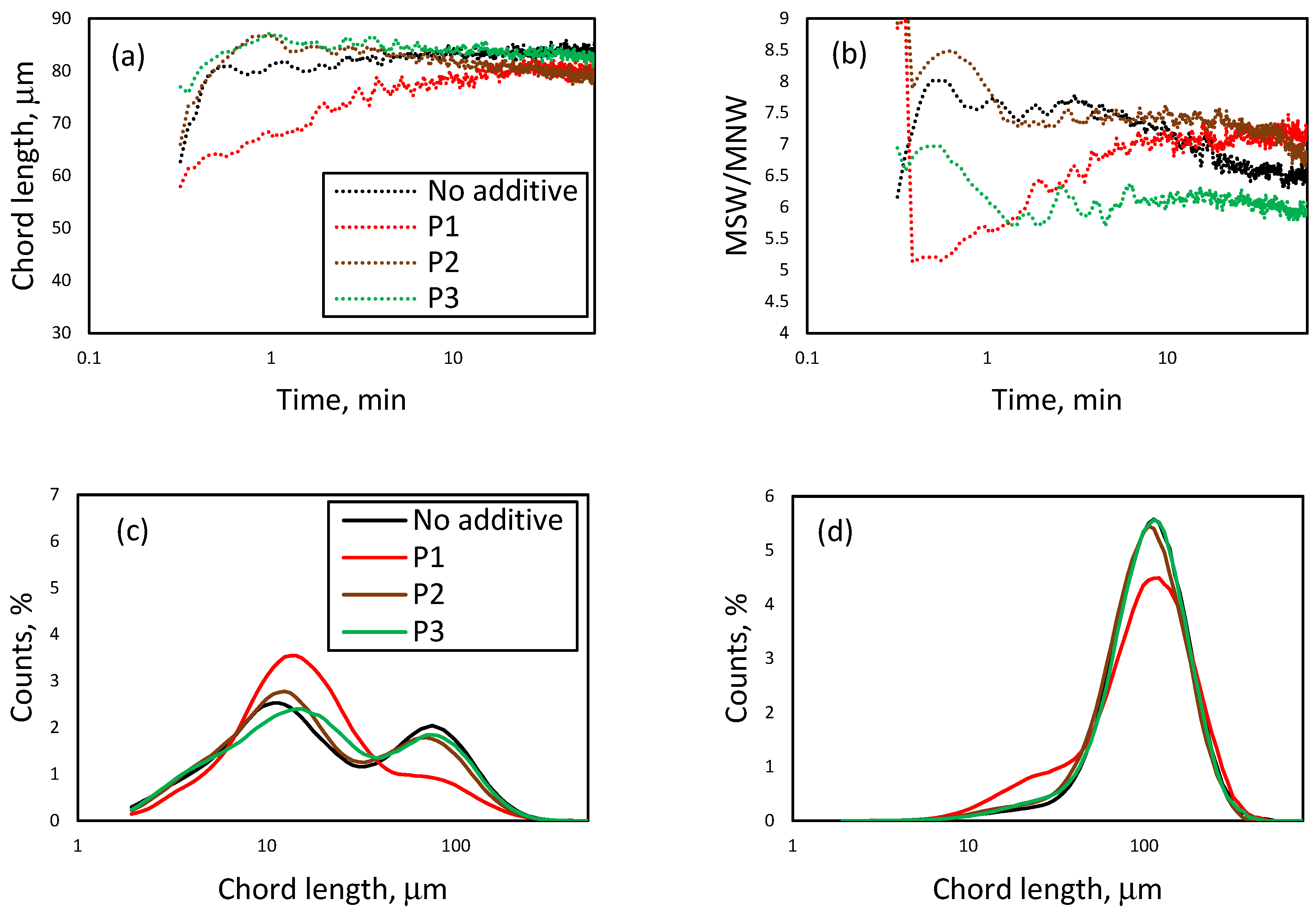
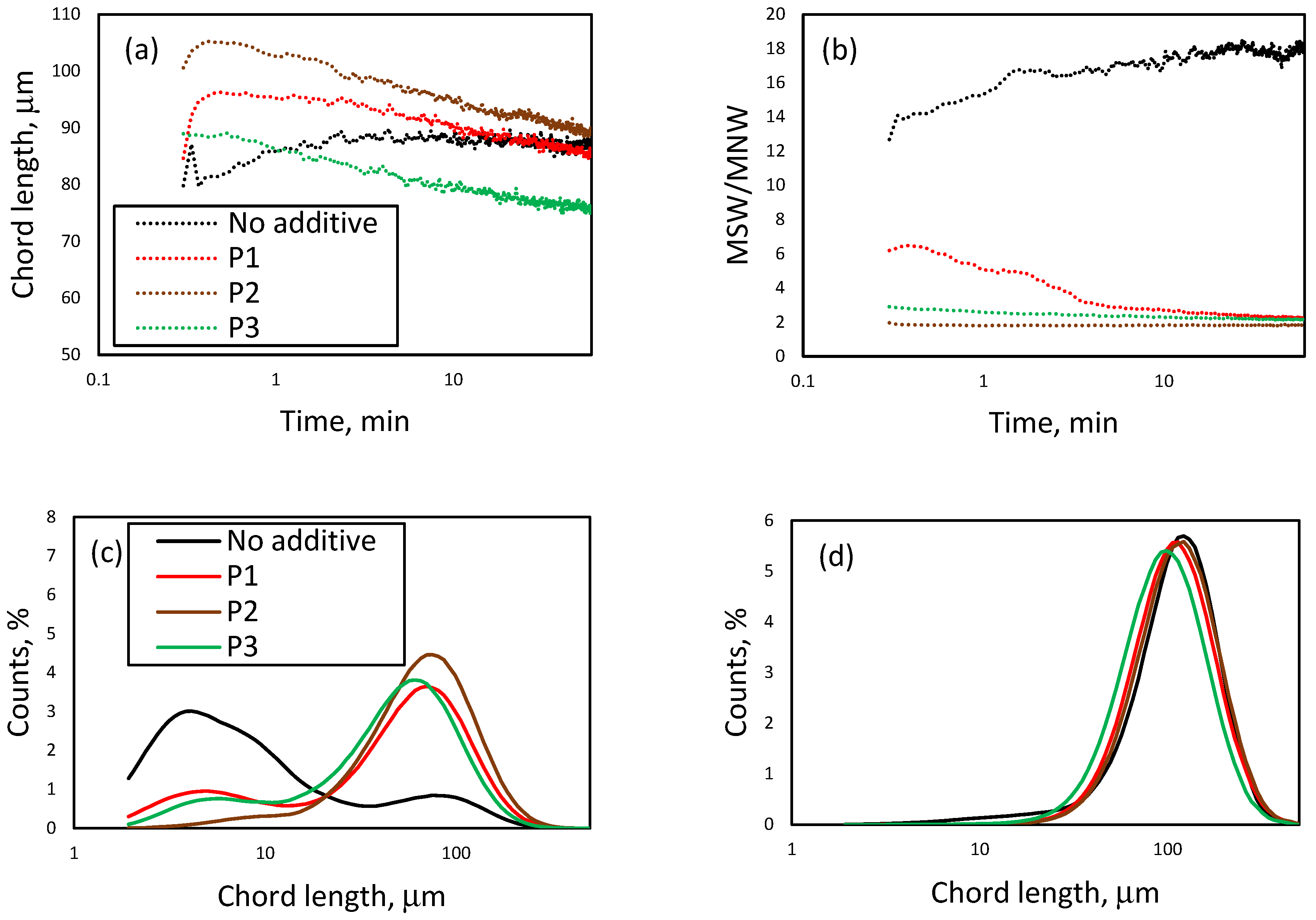
3.3. Effect of the Presence of Additives on the Reactive Crystallization of Lithium Carbonate
3.4. Effect of Additives on Size and Size Distribution
- (i)
- (ii)
- Stabilization of amorphous nuclei: Long-chain PAA can stabilize amorphous phases, such as calcium carbonate nanoparticles, either within hydrogels [56] or in oriented aggregation of nanoclusters instead of ion-to-ion growth [57]. In Li2CO3, this implies the presence of polymer-bound amorphous precursors requiring more time or specific conditions to crystallize, explaining the longer induction times [24,25,58,59].
- (iii)
- Increase in heterogeneous or secondary nuclei: Although dissolved, long-chain PAA can form microaggregates that serve as nucleation surfaces. In CaCO3, high-molecular-weight PAA increases nucleation sites for amorphous phases [60], consistent with the rise in fines observed for P2 at 2 M LiCl, where numerous small amorphous nuclei crystallize nearly simultaneously [24,25,27,28,53].
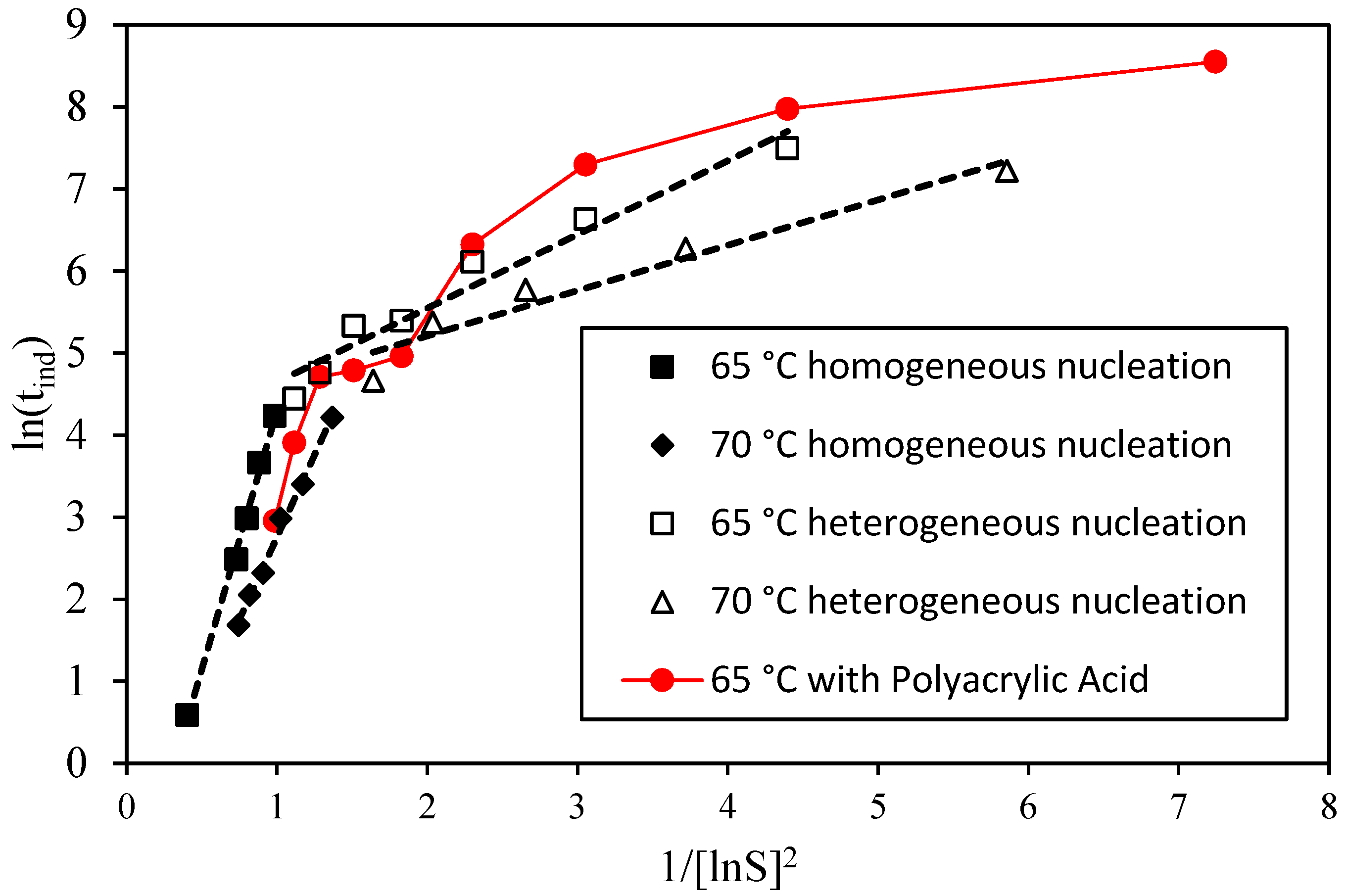
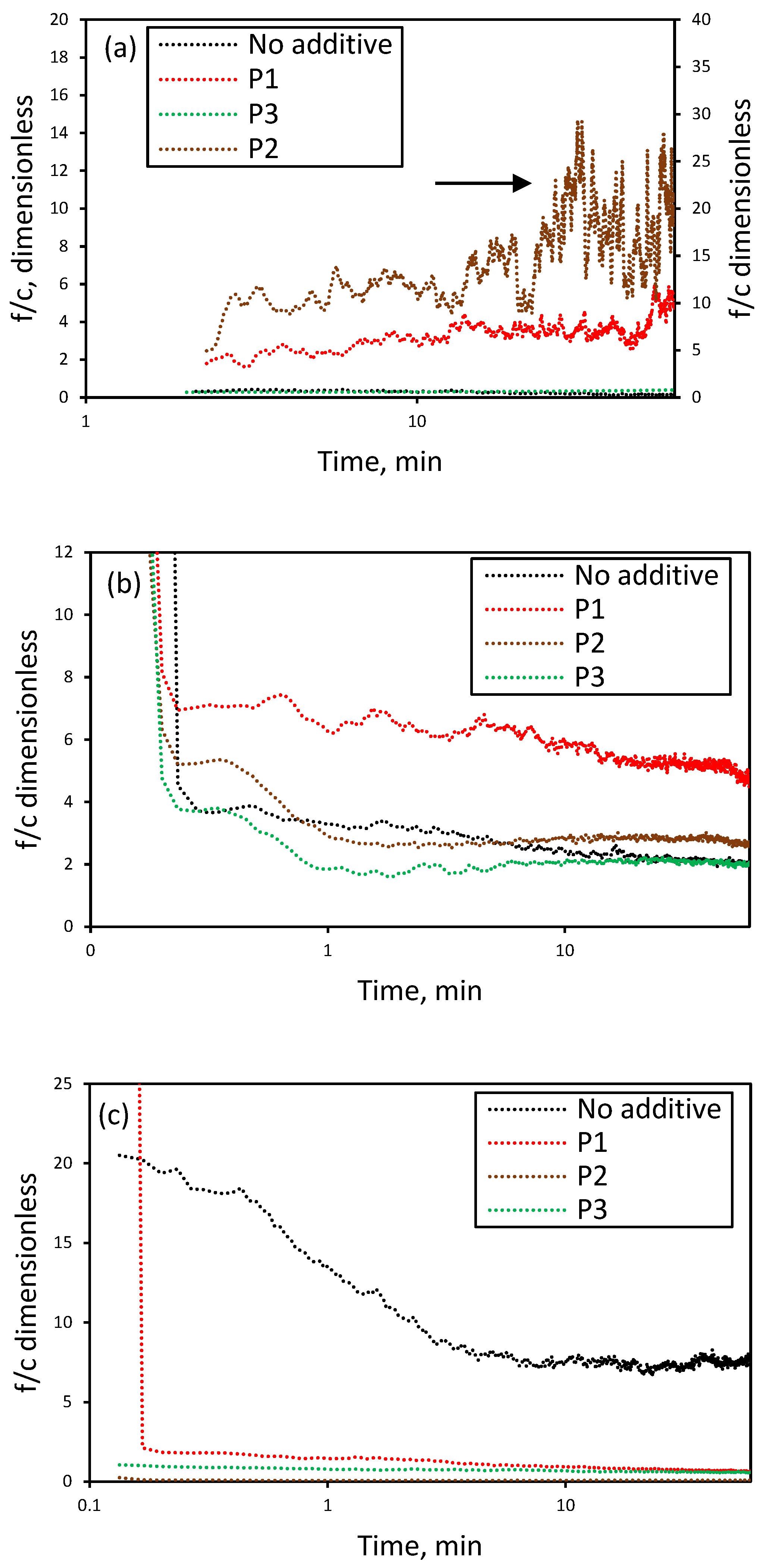
3.5. Effect of Additives on the Nucleation and Crystallization Growth Rates of Lithium Carbonate
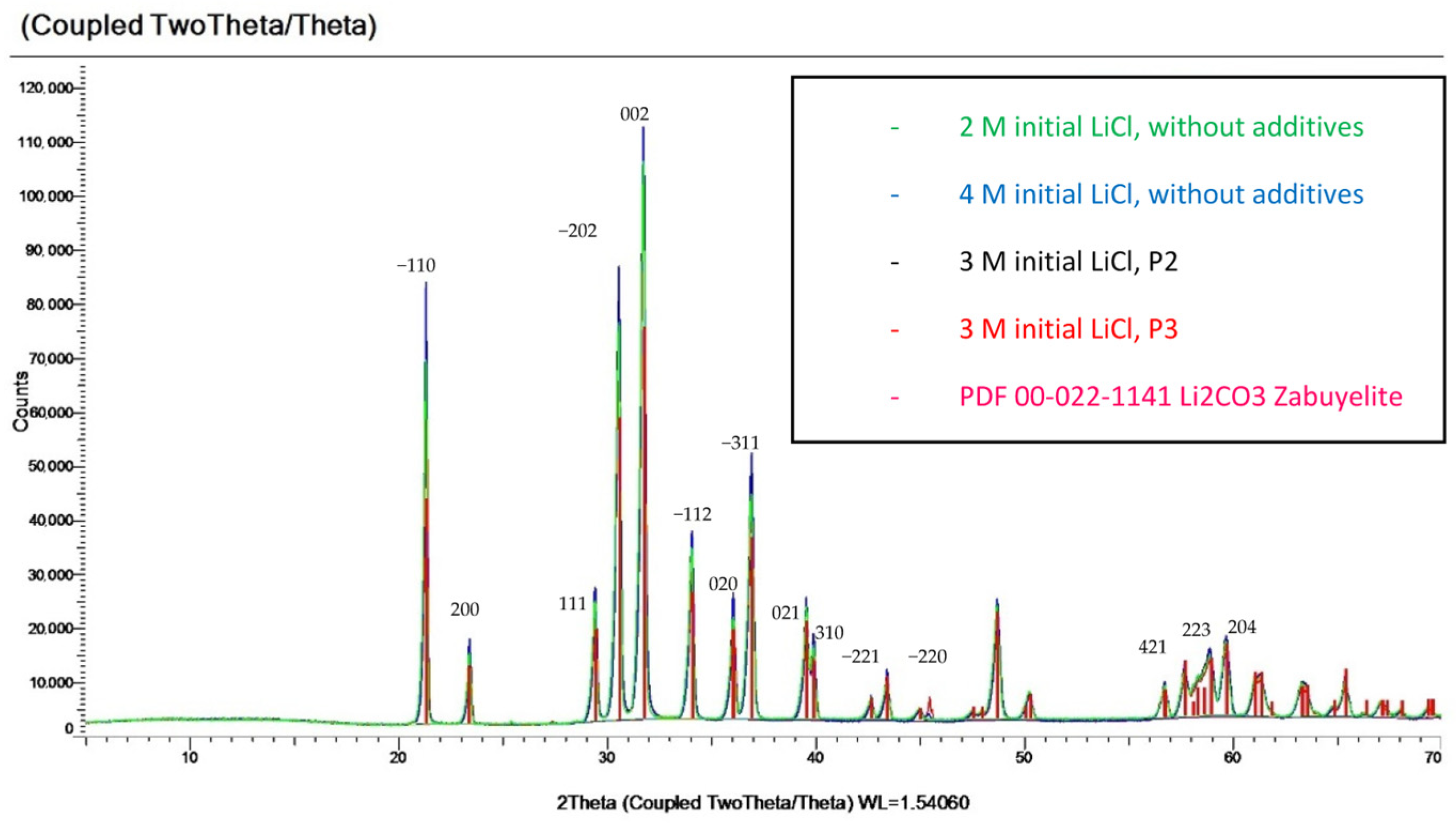
3.6. SEM Images and X-Ray Diffraction
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Swain, B. Recovery and recycling of lithium: A review. Sep. Purif. Technol. 2017, 172, 388–403. [Google Scholar] [CrossRef]
- Tan, J.; Wang, Q.; Lin, Y.; Xiang, X. Direct preparation of battery-grade lithium carbonate via a nucleation–crystallization isolating process intensified by a micro-liquid film reactor. Can. J. Chem. Eng. 2022, 101, 870–882. [Google Scholar] [CrossRef]
- Ulrichsen, A.; Hampsey, E.; Taylor, R.H.; Gadelrab, R.; Strawbridge, R.; Young, A.H. Comparing measurements of lithium treatment efficacy in people with bipolar disorder: Systematic review and meta-analysis. BJPsych Open 2023, 9, e98. [Google Scholar] [CrossRef]
- Gao, Z.-W.; Lan, T.; Yin, H.; Liu, Y. Development and Commercial Application of Lithium-Ion Batteries in Electric Vehicles: A Review. Processes 2025, 13, 756. [Google Scholar] [CrossRef]
- Baudino, L.; Santos, C.; Pirri, C.F.; La Mantia, F.; Lamberti, A. Recent Advances in the Lithium Recovery from Water Resources: From Passive to Electrochemical Methods. Adv. Sci. 2022, 9, e2201380. [Google Scholar] [CrossRef]
- Szlugaj, J.; Radwanek-Bąk, B. Lithium sources and their current use. Gospod. Surowcami Miner.-Miner. Resour. Manag. 2022, 38, 61–88. [Google Scholar] [CrossRef]
- Ma, X.; Meng, Z.; Bellonia, M.V.; Spangenberger, J.; Harper, G.; Gratz, E.; Olivetti, E.; Arsenault, R.; Wang, Y. The evolution of lithium-ion battery recycling. Nat. Rev. Clean Technol. 2025, 1, 75–94. [Google Scholar] [CrossRef]
- Saleem, U.; Wilhelms, A.; Sottmann, J.; Knuutila, H.K.; Bandyopadhyay, S. Direct lithium extraction (DLE) methods and their potential in Li-ion battery recycling. Sep. Purif. Technol. 2025, 361, 131315. [Google Scholar] [CrossRef]
- Yuan, X.; Jiang, T.; Duan, C.; He, Y.; Wang, H.; Zhang, G. Multiple components synergistic separation and high-efficiency lithium extraction from spent lithium ion battery. Process. Saf. Environ. Prot. 2025, 197. [Google Scholar] [CrossRef]
- Kavanagh, L.; Keohane, J.; Garcia Cabellos, G.; Lloyd, A.; Cleary, J. Global Lithium Sources—Industrial Use and Future in the Electric Vehicle Industry: A Review. Resources 2018, 7, 57. [Google Scholar] [CrossRef]
- Cabello, J. Reservas, recursos y exploración de litio en salares del norte de Chile. Andean Geol. 2022, 49, 297–306. [Google Scholar] [CrossRef]
- Boryta, D.A.; Kullberg, T.F.; Thurston, A.M. Production of Lithium Compounds Directly from Lithium Containing Brines. U.S. Patent 7449161B2, 28 June 2007. [Google Scholar]
- Aguilar, P.G.; Graber, T.A. Determination of the Reaction Kinetic Parameters for Li2CO3 Crystallization from Li2SO4 and Na2CO3 Solutions Using Calorimetric Measurements. Ind. Eng. Chem. Res. 2018, 57, 4815–4823. [Google Scholar] [CrossRef]
- Liu, H.; Azimi, G. Process analysis and study of factors affecting the lithium carbonate crystallization from sulfate media during lithium extraction. Hydrometallurgy 2021, 199, 105532. [Google Scholar] [CrossRef]
- Sun, Y.; Song, X.; Wang, J.; Luo, Y.; Yu, J. Unseeded Supersolubility of Lithium Carbonate: Experimental Measurement and Simulation with Mathematical Models. J. Cryst. Growth 2009, 311, 4714–4719. [Google Scholar] [CrossRef]
- Sun, Y.; Song, X.; Wang, J.; Luo, Y.; Yu, J. Determination of seeded supersolubility of lithium carbonate using FBRM. J. Cryst. Growth 2010, 312, 294–300. [Google Scholar] [CrossRef]
- Zhao, S.; Gao, J.; Ma, S.; Li, C.; Ma, Y.; He, Y.; Gong, J.; Zhou, F.; Zhang, B.; Tang, W. Mechanism and Modelling of Reactive Crystallization Process of Lithium Carbonate. Processes 2019, 7, 248. [Google Scholar] [CrossRef]
- Chen, P.-C.; Jhuang, J.-H.; Tseng, C.-E.; Lin, Z.-Y. Crystallization Kinetics of Lithium Carbonate in a Continuous Stirred-Tank Crystallizer. Crystals 2024, 14, 1021. [Google Scholar] [CrossRef]
- Graber, T.A.; Taboada, M.E.; Cortés, L.; Piceros, E.; Meruane, G.; Aguilar, P. Reactive Crystallization Process of Li2CO3 from LiCl and Na2CO3 Mechanism and Modeling. Ind. Eng. Chem. Res. 2024, 63, 10299–10308. [Google Scholar] [CrossRef]
- Sun, Y.; Song, X.; Wang, J.; Yu, J. Preparation of Li2CO3 by gas-liquid reactive crystallization of LiOH and CO2. Cryst. Res. Technol. 2012, 47, 437–442. [Google Scholar] [CrossRef]
- Sun, Y.-Z.; Song, X.-F.; Jin, M.-M.; Jin, W.; Yu, J.-G. Gas–Liquid Reactive Crystallization of Lithium Carbonate by a Falling Film Column. Ind. Eng. Chem. Res. 2013, 52, 17598–17606. [Google Scholar] [CrossRef]
- Lovette, M.A.; Browning, A.R.; Griffin, D.W.; Sizemore, J.P.; Snyder, R.C.; Doherty, M.F. Crystal Shape Engineering. Ind. Eng. Chem. Res. 2008, 47, 9812–9833. [Google Scholar] [CrossRef]
- Matahwa, H.; Ramiah, V.; Sanderson, R. Calcium carbonate crystallization in the presence of modified polysaccharides and linear polymeric additives. J. Cryst. Growth 2008, 310, 4561–4569. [Google Scholar] [CrossRef]
- Gebauer, D.; Cölfen, H.; Verch, A.; Antonietti, M. The Multiple Roles of Additives in CaCO3Crystallization: A Quantitative Case Study. Adv. Mater. 2009, 21, 435–439. [Google Scholar] [CrossRef]
- Nicoleau, L.; Van Driessche, A.E.; Kellermeier, M. A kinetic analysis of the role of polymers in mineral nucleation: The example of gypsum. Cem. Concr. Res. 2019, 124, 105837. [Google Scholar] [CrossRef]
- Lemanowicz, M.; Mielańczyk, A.; Walica, T.; Kotek, M.; Gierczycki, A. Application of Polymers as a Tool in Crystallization—A Review. Polymers 2021, 13, 2695. [Google Scholar] [CrossRef]
- Watamura, H.; Sonobe, Y.; Hirasawa, I. Polyacrylic Acid-Assisted Crystallization Phenomena of Carbonate Crystals. Chem. Eng. Technol. 2014, 37, 1422–1426. [Google Scholar] [CrossRef]
- Watamura, H.; Marukawa, H.; Hirasawa, I. Polyelectrolyte effects on the crystallization phenomena of the lithium carbonate. J. Cryst. Growth 2013, 373, 111–117. [Google Scholar] [CrossRef]
- Taborga, P.; Brito, I.; Graber, T. Effect of additives on size and shape of lithium carbonate crystals. J. Cryst. Growth 2017, 460, 5–12. [Google Scholar] [CrossRef]
- Yang, W.; Zhou, L.; Dai, J.; Zhou, L.; Zhang, M.; Xie, C.; Hao, H.; Hou, B.; Bao, Y.; Yin, Q. Crystallization of Lithium Carbonate from Aqueous Solution: New Insights into Crystal Agglomeration. Ind. Eng. Chem. Res. 2019, 58, 18448–18455. [Google Scholar] [CrossRef]
- Wang, Y.; Du, S.; Wang, X.; Sun, M.; Yang, Y.; Gong, J. Spherulitic growth and morphology control of lithium carbonate: The stepwise evolution of core-shell structures. Powder Technol. 2019, 355, 617–628. [Google Scholar] [CrossRef]
- Li, X.; Xu, D.; Yang, J.; Yan, Z.; Luo, T.; Li, X.; Zhang, Z.; Wang, X. Utilization of FBRM and PVM to analyze the effects of different additives on the crystallization of ammonium dihydrogen phosphate. J. Cryst. Growth 2021, 576, 126378. [Google Scholar] [CrossRef]
- Albis, A.; Jiménez, Y.P.; Graber, T.A.; Lorenz, H. Reactive Crystallization Kinetics of K2SO4 from Picromerite-Based MgSO4 and KCl. Crystals 2021, 11, 1558. [Google Scholar] [CrossRef]
- Al Nasser, W.N.; Al Salhi, F.H. Kinetics determination of calcium carbonate precipitation behavior by inline techniques. Powder Technol. 2015, 270, 548–560. [Google Scholar] [CrossRef]
- Tadayyon, A.; Rohani, S. Control of fines suspension density in the fines loop of a continuous KCl crystallizer using transmittance measurement and an FBRM® probe. Can. J. Chem. Eng. 2000, 78, 663–673. [Google Scholar] [CrossRef]
- Kougoulos, E.; Jones, A.; Jennings, K.; Wood-Kaczmar, M. Use of focused beam reflectance measurement (FBRM) and process video imaging (PVI) in a modified mixed suspension mixed product removal (MSMPR) cooling crystallizer. J. Cryst. Growth 2005, 273, 529–534. [Google Scholar] [CrossRef]
- Martos, C.; Coto, B.; Peña, J.; Rodríguez, R.; Merino-Garcia, D.; Pastor, G. Effect of precipitation procedure and detection technique on particle size distribution of CaCO3. J. Cryst. Growth 2010, 312, 2756–2763. [Google Scholar] [CrossRef]
- Leyssens, T.; Baudry, C.; Hernandez, M.L.E. Optimization of a Crystallization by Online FBRM Analysis of Needle-Shaped Crystals. Org. Process. Res. Dev. 2011, 15, 413–426. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, L.; Xu, S.; Du, S.; Dong, W.; Gong, J. Optimization of cooling strategy and seeding by FBRM analysis of batch crystallization. J. Cryst. Growth 2018, 486, 1–9. [Google Scholar] [CrossRef]
- Al Nasser, W.N.; Al Salhi, F.H. Scaling and aggregation kinetics determination of calcium carbonate using inline technique. Chem. Eng. Sci. 2013, 86, 70–77. [Google Scholar] [CrossRef]
- Xue, J.; Liu, C.; Luo, M.; Lin, M.; Jiang, Y.; Li, P.; Yu, J.; Rohani, S. Secondary nucleation and growth kinetics of aluminum hydroxide crystallization from potassium aluminate solution. J. Cryst. Growth 2019, 507, 232–240. [Google Scholar] [CrossRef]
- Serpa, F.S.; Silva, G.M.; Freitas, L.F.; Filho, E.B.M.; Nascimento, J.F.; Pereira, L.S.; Salazar-Banda, G.R.; Borges, G.R.; Dariva, C.; Franceschi, E. An experimental study of calcium carbonate precipitation with hydrate inhibitor in MEG recovery unit. Upstream Oil Gas Technol. 2022, 8, 100061. [Google Scholar] [CrossRef]
- Rasteiro, M.G.; Koponen, A. Monitoring Aggregation Processes in Multiphase Systems: A Review. Powders 2024, 3, 77–110. [Google Scholar] [CrossRef]
- Heath, A.R.; Fawell, P.D.; Bahri, P.A.; Swift, J.D. Estimating Average Particle Size by Focused Beam Reflectance Measurement (FBRM). Part. Part. Syst. Charact. 2002, 19, 84. [Google Scholar] [CrossRef]
- Trifkovic, M.; Sheikhzadeh, M.; Rohani, S. Kinetics Estimation and Single and Multi-Objective Optimization of a Seeded, Anti-Solvent, Isothermal Batch Crystallizer. Ind. Eng. Chem. Res. 2008, 47, 1586–1595. [Google Scholar] [CrossRef]
- Tavare, N.S.; Gaikar, V.G. Precipitation of salicyclic acid: Hydrotropy and reaction. Ind. Eng. Chem. Res. 1991, 30, 722–728. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, M.; Huang, X.; Park, J.; Hoffman, M.E.; Feng, Y.; An, A.K.; Li, Q.; Hoek, E.M.V.; Jassby, D. Mitigating CaCO3 crystal nucleation and growth through continuous ion displacement via alternating electric fields. Nat. Commun. 2025, 16, 35. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.; Li, H.; Li, S.; Hou, X.; Xu, D.; Lin, R.; Tang, Q. Crystallization behavior and kinetics of calcium carbonate in highly alkaline and supersaturated system. J. Cryst. Growth 2015, 428, 16–23. [Google Scholar] [CrossRef]
- Han, B.; Haq, R.A.U.; Louhi-Kultanen, M. Lithium carbonate precipitation by homogeneous and heterogeneous reactive crystallization. Hydrometallurgy 2020, 195, 105386. [Google Scholar] [CrossRef]
- Ahn, B.; Bosetti, L.; Mazzotti, M. Secondary Nucleation by Interparticle Energies. III. Nucleation Rate Model. Cryst. Growth Des. 2022, 22, 3625–3636. [Google Scholar] [CrossRef]
- Söhnel, O.; Mullin, J.W. Interpretation of crystallization induction periods. J. Colloid Interface Sci. 1988, 123, 43–50. [Google Scholar] [CrossRef]
- McDonald, M.A.; Salami, H.; Harris, P.R.; Lagerman, C.E.; Yang, X.; Bommarius, A.S.; Grover, M.A.; Rousseau, R.W. Reactive crystallization: A review. React. Chem. Eng. 2021, 6, 364–400. [Google Scholar] [CrossRef]
- Gebauer, D. How Can Additives Control the Early Stages of Mineralisation? Minerals 2018, 8, 179. [Google Scholar] [CrossRef]
- Teychené, S.; Rodríguez-Ruiz, I.; Ramamoorthy, R.K. Reactive crystallization: From mixing to control of kinetics by additives. Curr. Opin. Colloid Interface Sci. 2020, 46, 1–19. [Google Scholar] [CrossRef]
- Huang, S.-C.; Naka, K.; Chujo, Y. Effect of Molecular Weights of Poly (acrylic acid) on Crystallization of Calcium Carbonate by the Delayed Addition Method. Polym. J. 2008, 40, 154–162. [Google Scholar] [CrossRef]
- Sun, S.; Mao, L.; Lei, Z.; Yu, S.; Cölfen, H. Hydrogels from Amorphous Calcium Carbonate and Polyacrylic Acid: Bio-Inspired Materials for “Mineral Plastics”. Angew. Chem. Int. Ed. Engl. 2016, 55, 11765–11769. [Google Scholar] [CrossRef]
- Donnet, M.; Aimable, A.; Lemaître, J.; Bowen, P. Contribution of Aggregation to the Growth Mechanism of Seeded Calcium Carbonate Precipitation in the Presence of Polyacrylic Acid. J. Phys. Chem. B 2010, 114, 12058–12067. [Google Scholar] [CrossRef] [PubMed]
- Anwar, J.; Boateng, P.K.; Tamaki, R.; Odedra, S. Mode of Action and Design Rules for Additives That Modulate Crystal Nucleation. Angew. Chem. 2009, 121, 1624–1628. [Google Scholar] [CrossRef]
- Jehannin, M.; Rao, A.; Cölfen, H. New Horizons of Nonclassical Crystallization. J. Am. Chem. Soc. 2019, 141, 10120–10136. [Google Scholar] [CrossRef] [PubMed]
- Tang, Q.; Nie, J.; Fang, W.; Xie, H.; Wang, W.; Wang, H.; Ping, H.; Li, B.; Fu, Z. Effects of Polyacrylic Acid with Different Molecular Weights on Stress Generation through Regulating the Growth of Calcium Carbonate within Collagen. ACS Appl. Bio Mater. 2025, 8, 2386–2396. [Google Scholar] [CrossRef] [PubMed]





| [LiCl]0 (mol/L) | [Na2CO3]0 (mol/L) | No Additive | PAA (Mw 1800) | PAA (Mw 230,000) | PAA (Mw 450,000) |
|---|---|---|---|---|---|
| 2.0 | 1.0 | Test 1 | Test 4 | Test 7 | Test 10 |
| 3.0 | 1.5 | Test 2 | Test 5 | Test 8 | Test 11 |
| 4.0 | 2.0 | Test 3 | Test 6 | Test 9 | Test 12 |
| Experiment | Bmax, [Counts/min] | Gmax, [μm/min] |
|---|---|---|
| Initial LiCl concentration of 2 M | 3.00 × 104 | 7.50 × 102 |
| Initial LiCl concentration of 3 M | 6.73 × 105 | 2.97 × 105 |
| Initial LiCl concentration of 4 M | 9.67 × 105 | 1.36 × 106 |
| 2 M Initial LiCl | 3 M Initial LiCl | 4 M Initial LiCl | ||||
|---|---|---|---|---|---|---|
| Bmax | Gmax | Bmax | Gmax | Bmax | Gmax | |
| No additive | ||||||
| P1 | ||||||
| P2 | ||||||
| P3 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piceros, E.; Jeldres, R.I.; Robles, P.; Graber, T.A. Reactive Crystallization of Lithium Carbonate from LiCl and Na2CO3: Effect of Polyacrylic Acid Monitored by Focused Reflectance Measurement. Inorganics 2025, 13, 377. https://doi.org/10.3390/inorganics13110377
Piceros E, Jeldres RI, Robles P, Graber TA. Reactive Crystallization of Lithium Carbonate from LiCl and Na2CO3: Effect of Polyacrylic Acid Monitored by Focused Reflectance Measurement. Inorganics. 2025; 13(11):377. https://doi.org/10.3390/inorganics13110377
Chicago/Turabian StylePiceros, Eder, Ricardo I. Jeldres, Pedro Robles, and Teófilo A. Graber. 2025. "Reactive Crystallization of Lithium Carbonate from LiCl and Na2CO3: Effect of Polyacrylic Acid Monitored by Focused Reflectance Measurement" Inorganics 13, no. 11: 377. https://doi.org/10.3390/inorganics13110377
APA StylePiceros, E., Jeldres, R. I., Robles, P., & Graber, T. A. (2025). Reactive Crystallization of Lithium Carbonate from LiCl and Na2CO3: Effect of Polyacrylic Acid Monitored by Focused Reflectance Measurement. Inorganics, 13(11), 377. https://doi.org/10.3390/inorganics13110377







