Theoretical Study on the Ortho–Para Reactivity Difference in Ru-Catalyzed Amination of Aminopyridines via η⁶-Coordination: Role of Meisenheimer Intermediate Coordination Ability

Abstract

η⁶-Coordination catalysis has emerged as an effective strategy for activating electron-rich (hetero)arenes toward nucleophilic substitution. Recent experimental studies on Ru(II)-catalyzed amination of aminopyridines revealed a striking ortho–para reactivity difference, with ortho-substituted substrates undergoing efficient amination while para analogs are unreactive under identical conditions. Herein, we present a density functional theory investigation to elucidate the origin of this divergence. Computed free-energy profiles show that both substitution patterns follow a similar stepwise mechanism involving Ru-bound Meisenheimer intermediates and a proton-transfer relay, with C–N bond cleavage/rearomatization as the rate-determining step. However, the para pathway suffers from a substantially higher overall barrier, originating from the intrinsically less stable Meisenheimer intermediates. Energy decomposition analysis indicates that the decisive factor is weaker orbital interaction between the CpRu(II) fragment and the para-substituted Meisenheimer intermediate, whereas electrostatics and dispersion play negligible roles. These findings highlight the key role of metal–substrate orbital interactions in stabilizing dearomatized intermediates, offering mechanistic insights for rational design of η⁶-coordination catalysis with enhanced reactivity and selectivity.

1. Introduction

π-Coordination has become a powerful and widely applicable strategy for the activation of inert (hetero)aromatic compounds [1]. In this mode of activation, aromatic substrates form reversible η⁶-complexes with transition-metal centers through π-electron donation, resulting in perturbation of the electronic structure and reactivity of the arene ring [2]. While the concept of arene π-complexation was first explored decades ago [3], its catalytic potential has seen rapid expansion in recent years [4,5,6,7,8,9,10,11,12,13,14,15,16], enabling a range of transformations that are inaccessible to the corresponding uncoordinated arenes. This activation approach is particularly attractive for electron-rich systems, where conventional strategies like nucleophilic aromatic substitution are typically challenging to provide efficient reactivity.

In recent years, a series of powerful catalytic substitution reactions have been developed based on this π-coordination strategy by Shi and co-workers [17]. Particularly, recent developments have demonstrated that arenophilic metal complexes—most notably low-valent Ru(II) and Rh(III) species—can promote distinctive redox-neutral η⁶-coordination catalysis to achieve efficient activation and functionalization of otherwise robust C–F, C–OH, and C–NH₂ bonds on electron-rich (hetero)arenes [17]. Central to these advances is the use of η⁶-binding to transiently reverse the polarity of the arene, creating electrophilic character at positions that are otherwise nucleophilic in nature. These reactions proceed under mild conditions, often without additives or oxidants, and tolerate a broad scope of nucleophiles and substitution patterns, establishing a versatile platform for aromatic substitution chemistry.

This new activation paradigm also raises important mechanistic questions. The reactivity patterns observed under η⁶-coordination catalysis often diverge from those expected in classical aromatic substitution reactions. A striking example appears in a recent report on Ru-catalyzed amination of aminopyridines from the Shi group [18], in which pyridines bearing an amino group at the ortho position undergo efficient C–N bond formation with primary amines, whereas their para-substituted counterparts exhibit no reactivity under otherwise identical conditions (Scheme 1). This observation is particularly noteworthy, as both ortho and para substitution patterns typically exhibit comparable reactivity in conventional aromatic substitution reactions. The unexpected reactivity difference suggests that η⁶-coordination catalysis may introduce additional factors influencing substrate activation, beyond the classical substituent effects of aromatic substitution described in textbooks. However, Shi’s previous synthetic study [18] did not fully provide an explanation for this reactivity divergence, underscoring the need for further mechanistic investigation.

To understand the origins of this ortho–para reactivity difference, we conducted a mechanistic investigation using density functional theory (DFT) calculations. Based on the free energy profile analysis of the reaction pathways and electronic structure characterization of key intermediates, we herein report that the observed reactivity pattern is linked to the distinct coordination ability of the Meisenheimer-type intermediates to the Ru(II) center. The enhanced metal binding in the ortho-substituted substrate stabilizes key transient intermediates in the catalytic cycle, whereas the weak coordination in the para-substituted case leads to unfavorable overall barrier. These findings elucidate a fundamental connection between intermediate coordination and catalytic efficiency, providing new design principles for η⁶-coordination catalysis.

2. Results and Discussion

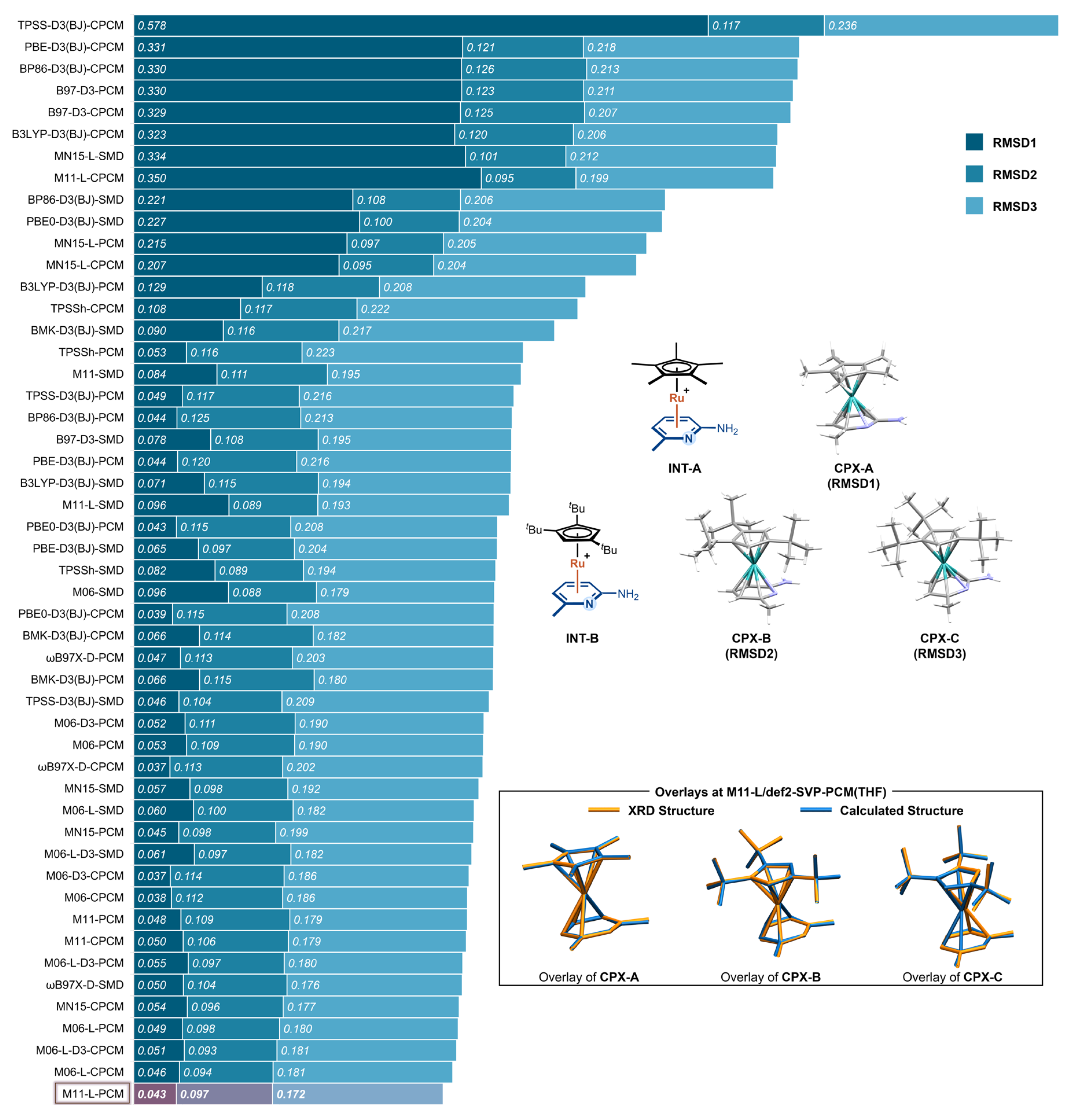
2.1. Benchmarking Computational Methods for Ru(II)–Aminopyridine π-Complexes

To identify a reliable level of theory for calculating the Ru(II) π-activation complexes, we first performed a comprehensive benchmarking study across a series of commonly used DFT functionals and solvation models. Three crystallographically characterized Ru(II)–6-methylpyridin-2-amine complexes from Shi’s study [18] were selected as reference structures (Figure 1): CPX-A corresponds to the π-complex INT-A featuring a Cp* ligand; CPX-B and CPX-C correspond to two distinct conformers of the π-complex INT-B, which bears a tBu-substituted Cp ligand coordinated to the same aminopyridine substrate. These complexes provide representative models for evaluating the structural accuracy of optimized π-coordinated Ru(II) intermediates.

A total of 17 DFT functionals were evaluated: BP86 [19]-D3 [20] (BJ) [21], B3LYP [22]-D3(BJ), PBE [23]-D3(BJ), PBE0 [24]-D3(BJ), B97 [25]-D3, M06 [26], M06-D3, M06-L [27], M06-L-D3, MN15 [28], MN15-L [29], M11 [30], M11-L [31], BMK [32]-D3(BJ), TPSS [33]-D3(BJ), TPSSh [34], and ωB97X-D [35]. Each was tested in combination with three implicit solvation models—PCM, CPCM, and SMD—yielding 51 method combinations. All geometry optimizations were performed using the def2-SVP basis set with THF as the solvent, and basis set variation was not considered in this benchmark. For each structure, the root-mean-square deviation (RMSD) of non-hydrogen atoms was computed relative to the corresponding crystal structure. The three values—RMSD1 (for CPX-A), RMSD2 (for CPX-B), and RMSD3 (for CPX-C)—were used to quantify the agreement between computed and experimental geometries.

The benchmarking results are summarized in Figure 1. The computed RMSD values span a broad range from 0.037 Å to 0.578 Å, reflecting significant differences in structural accuracy across the method combinations. Among the three complexes, CPX-A exhibits the greatest sensitivity to the computational method, with RMSD values ranging from 0.037 Å (M06-D3–CPCM) to 0.578 Å (TPSS-D3(BJ)–CPCM). In contrast, CPX-B is the least sensitive, with all methods yielding RMSD values between 0.093 Å (M06-L-D3-CPCM) and 0.126 Å (BP86-D3(BJ)–CPCM). CPX-C shows moderate sensitivity, with RMSD values from 0.172 Å (M11-L–PCM) to 0.236 Å (TPSS-D3(BJ)–CPCM). These results underscore the varying degrees of geometric responsiveness to methodological choices and highlight the importance of method selection in modeling π-coordinated Ru(II) complexes.

The data also reveal notable synergistic effects between the DFT functional and solvation model. In some cases, the combination of a suboptimal functional and an unfavorable solvent model leads to drastic over-relaxation. A striking example is TPSS-D3(BJ) combined with CPCM, which gives the highest deviation observed—an RMSD of 0.578 Å for CPX-A. By contrast, the same functional with PCM or SMD yields much lower RMSD values (0.049 Å and 0.046 Å, respectively), illustrating the pronounced impact of solvation treatment when coupled with sensitive functionals.

Despite such cases, the choice of functional has a more dominant influence than the solvation model. Once a reliable functional is selected—such as members of the Minnesota family (M06, M06-L, MN15, MN15-L) or ωB97X-D—the differences among PCM, CPCM, and SMD become relatively minor. These functionals deliver consistently low RMSD values across all three complexes, making them broadly applicable regardless of the solvent model. Still, a few extreme functional–solvent combinations, such as MN15–L–SMD and M11–L–PCM, yield significantly higher RMSD values for CPX-A (0.334 Å and 0.350 Å, respectively).

Among all tested combinations, M11–L/def2-SVP-PCM(THF) delivers the best overall performance, with RMSD values of 0.043 Å for CPX-A, 0.097 Å for CPX-B, and 0.172 Å for CPX-C. The method reliably reproduces key structural parameters and overall coordination geometries, as illustrated by the structural overlays in Figure 1. Based on its consistently high accuracy across different ligand environments, M11–L/def2-SVP-PCM(THF) was selected as the level of theory for all subsequent geometry optimizations and mechanistic studies.

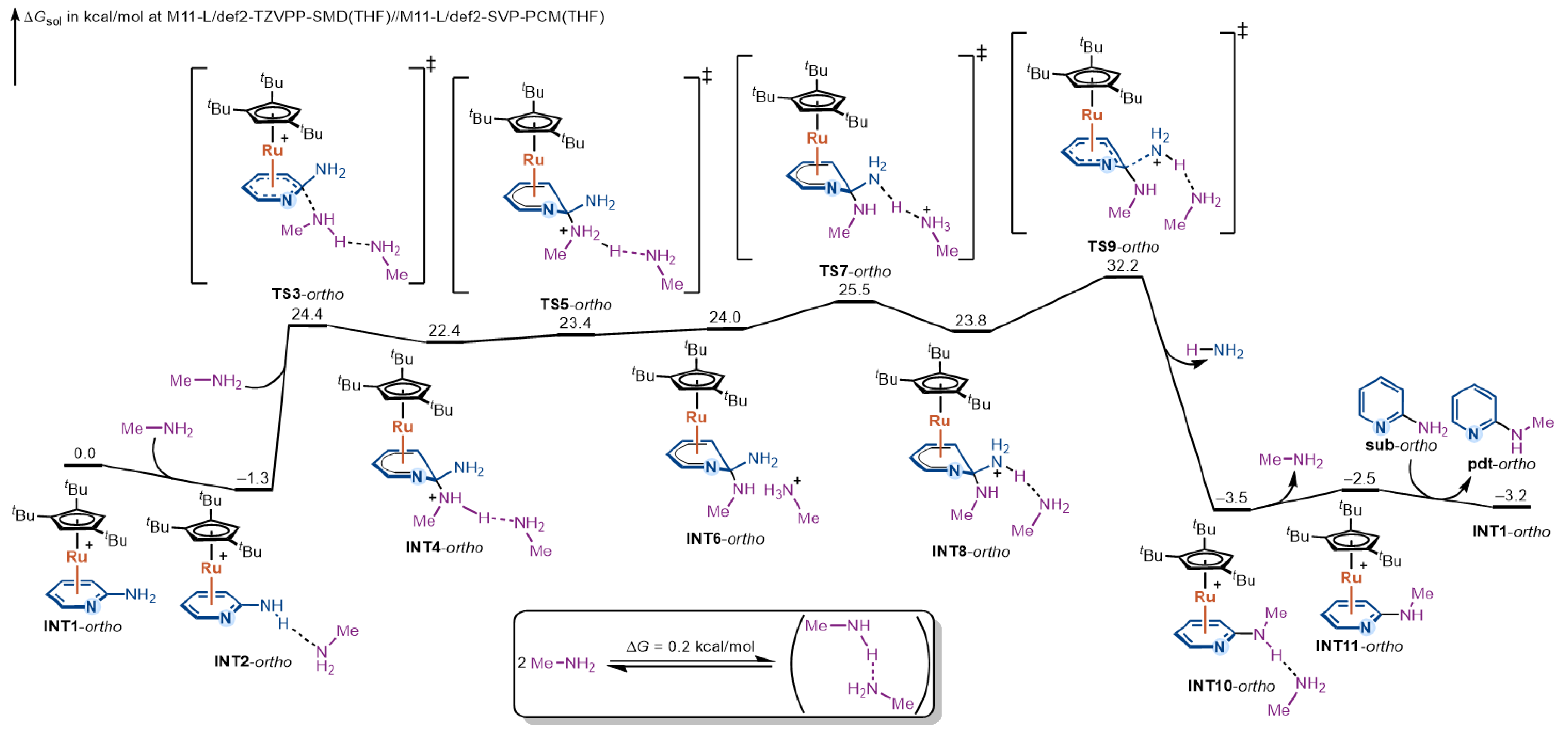
2.2. DFT-Computed Mechanistic Profile for the Ortho-Substitution Pathway

We first examined the reaction mechanism for ortho-aminopyridine; the complete free-energy profile is shown in Figure 2. The catalytic cycle is initiated by η⁶-coordination of the substrate to Ru(II), furnishing the π-complex INT1-ortho. Approach of methylamine gives the more stable, hydrogen-bonded adduct INT2-ortho, from which nucleophilic addition occurs via TS3-ortho to form the Meisenheimer intermediate INT4-ortho. The barrier from INT2-ortho to TS3-ortho is 25.7 kcal/mol, representing the first significant ascent along the pathway.

From INT4-ortho, a stepwise proton-transfer relay enhances the leaving-group ability. The proton on the ammonium moiety (purple-labeled in Figure 2) is first transferred to the hydrogen-bonded methylamine to give INT6-ortho; the newly formed methanaminium then delivers a proton to the departing amino group (blue-labeled in Figure 2), affording INT8-ortho. Because the basicities of the relevant amines are similar, the three Meisenheimer intermediates (INT4-ortho, INT6-ortho, INT8-ortho) are comparable in stability, and each protonation step proceeds with a very small intrinsic barrier within 2 kcal/mol. Therefore, the kinetics of these proton transfer steps do not contribute to rate determination.

After proton transfer, INT8-ortho undergoes C–N bond cleavage at the leaving-group site with rearomatization of the pyridine ring via TS9-ortho. The intrinsic barrier from INT8-ortho to TS9-ortho is 8.4 kcal/mol. Although modest intrinsically, the overall rate-determining step arises here because the dearomatized Meisenheimer manifold is itself high in free energy: measured from the on-cycle resting state INT2-ortho, the overall free-energy barrier is 33.5 kcal/mol via TS9-ortho. The height of this barrier reflects the balance between stabilization provided by Ru-bound Meisenheimer intermediate and the energetic cost of C–N bond cleavage. This C–N cleavage step yields a highly stabilized product-coordinated complex INT10-ortho. Subsequent facile arene exchange releases the product and regenerates the active intermediate INT1-ortho for the next catalytic cycle.

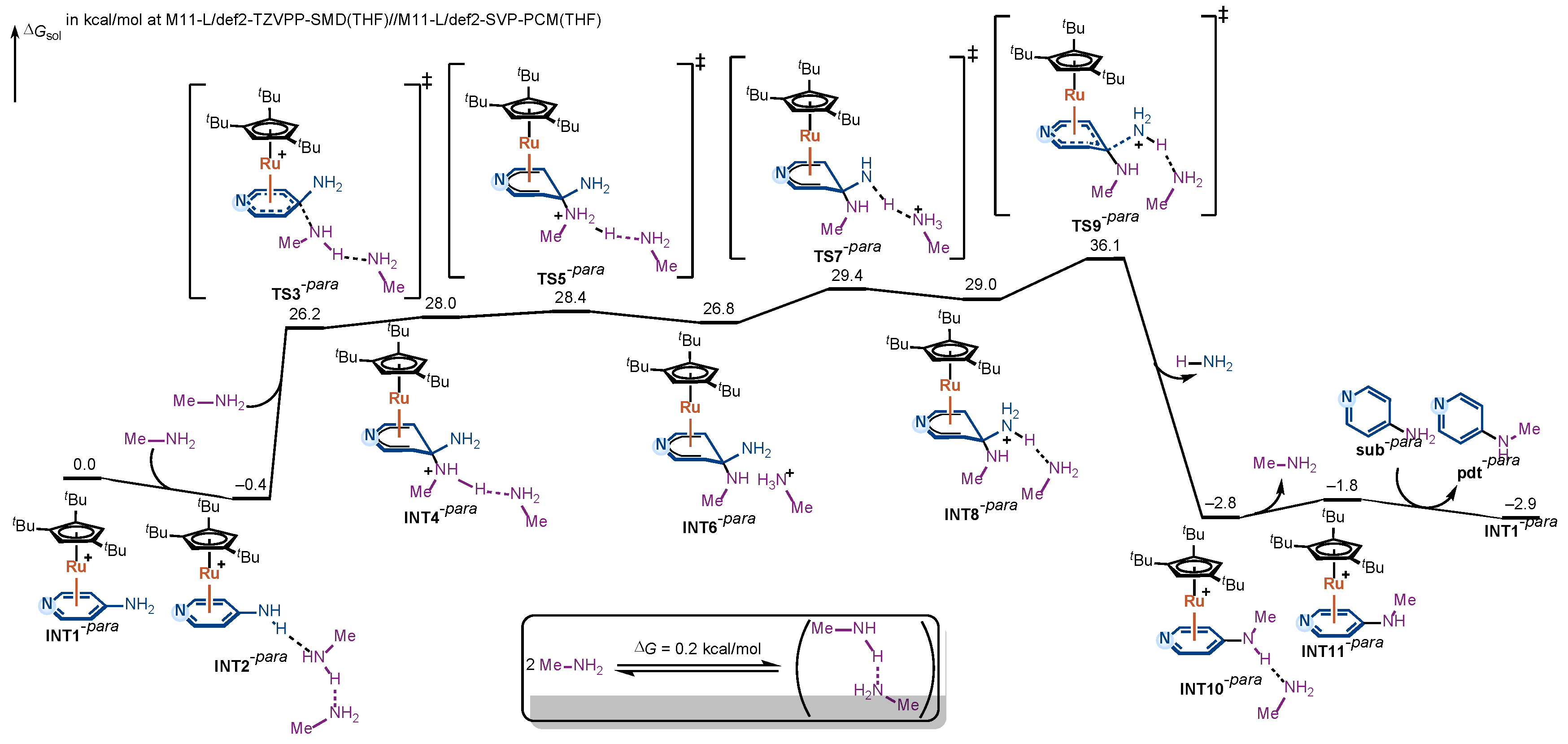
2.3. DFT-Computed Mechanistic Profile for the Para-Substitution Pathway

The computed free-energy profile for the para-aminopyridine amination pathway is shown in Figure 3. As in the ortho case, the reaction begins with η⁶-coordination of the substrate to the Ru(II) catalyst, forming the π-complex INT1-para. Coordination of methylamine affords the hydrogen-bonded adduct INT2-para, from which nucleophilic attack proceeds via TS3-para to give the Meisenheimer intermediate INT4-para. The barrier from INT2-para to TS3-para is calculated to be 26.6 kcal/mol, comparable to that of the ortho pathway.

From INT4-para, the same stepwise proton-transfer sequence is observed. The proton from the ammonium moiety (purple-labeled in Figure 3) is first delivered to the hydrogen-bonded methylamine, yielding INT6-para; the resulting methanaminium then transfers its proton to the departing amino group (blue-labeled in Figure 3), affording INT8-para. As in the ortho case, these Meisenheimer intermediates (INT4-para, INT6-para, INT8-para) are similar in relative stability, and each proton-transfer step has a small intrinsic barrier, making no significant contribution to the overall rate.

After protonation of the leaving group, INT8-para undergoes C–N bond cleavage with rearomatization through TS9-para. The intrinsic barrier from INT8-para to TS9-para is 7.1 kcal/mol, even lower than in the ortho pathway. However, due to the intrinsically reduced stability of the Meisenheimer intermediates in the para pathway, INT4-para, INT6-para, and INT8-para all lie substantially higher in energy than their ortho counterparts. In particular, INT8-para is calculated to be 29.0 kcal/mol above the on-cycle resting state INT2-para. Consequently, the overall free-energy barrier, measured from INT2-para to TS9-para, reaches 36.5 kcal/mol, which is 3.0 kcal/mol higher than in the ortho pathway. Based on the Eyring equation, this 3.0 kcal/mol free-energy difference would translate into a remarkable difference in the reaction rate constants, further confirming the consistency between our computational results and the experimental observations.

The above comparison reveals that, in the para pathway, the rate-determining step is again the C–N bond cleavage/rearomatization from a high-energy Meisenheimer intermediate. It is the elevated energy of the Meisenheimer intermediate directly translates into the higher overall barrier, accounting for the experimentally observed lack of reactivity of para-substituted aminopyridines.

2.4. Energy Decomposition Analysis of Meisenheimer Intermediate Stability

To further elucidate the origins of the stability difference between the Meisenheimer intermediates in the ortho and para pathways, we performed a quantitative energy decomposition analysis (EDA) using the sobEDA approach developed by Lu and co-workers [36]. In this analysis, the interaction between the CpRu(II) fragment and the substrate fragment was decomposed into electrostatic, exchange-repulsion, Coulomb correlation, and orbital interaction terms. The calculations were carried out for the substrate–Ru π-complex (INT1) and the corresponding protonated Meisenheimer intermediate (INT8) in each pathway, and the results are summarized in Figure 4.

For each pathway, the change in the interaction energy terms from INT1 to INT8 (Δ-ortho and Δ-para) reflects the energetic contributions of the CpRu(II)–substrate interaction to the stabilization/destabilization of the Meisenheimer intermediate relative to the resting π-complex. Comparing these Δ values between the ortho and para cases yields the ΔΔpara–ortho values, which capture the subtle influence of the substitution pattern on each interaction component and, ultimately, on the stability of the Meisenheimer intermediate.

As shown in Figure 4, the differences in electrostatic, exchange-repulsion, and Coulomb correlation contributions between the two pathways largely cancel each other out (4.62, −13.54, and 7.30 kcal/mol, respectively), indicating that nuclear–nuclear and electrostatic effects are not the decisive factors in the stability difference. Instead, the key distinction lies in the orbital interaction term: the para pathway exhibits orbital interactions that are 8.30 kcal/mol less favorable than in the ortho pathway. This reduced orbital stabilization directly accounts for the less favorable total interaction energy in the para case, with a 6.68 kcal/mol energy difference. Therefore, the weaker orbital stabilization of the para Meisenheimer intermediate—rather than electrostatics or dispersion—accounts for its reduced stability and the higher overall barrier.

To clarify the influence of steric effects on reactivity, we also analyzed the structure of the Meisenheimer intermediate INT8. For both the ortho and para cases, steric congestion between the tert-butyl group of the ligand and the departing amino group is limited, with only one H–H contact of 2.21 Å observed in INT8-ortho. Therefore, the impact of steric effects on the reaction reactivity is limited.

3. Materials and Methods

All density functional theory (DFT) calculation results are obtained with Gaussian 16 program [37]. Default G16 SCF convergence criteria (scf = tight), optimization convergence criteria and integral grid parameters (int = (ultrafine, acc2e = 12)) for Gaussian 16 are applied unless otherwise stated. Geometry optimizations are conducted with M11-L functional, and def2-SVP basis set was used for all atoms, with solvent effects at THF evaluated. Single-point energies and solvent effects at THF are also evaluated with the same functional and def2-TZVPP basis set for all atoms. The solvation energies are calculated with a self-consistent reaction field (SCRF) using the PCM implicit solvent model for geometry optimizations and SMD implicit solvent model for single-point energies. Frequency analysis is also performed at the same level of theory as geometry optimization using harmonic oscillator model to confirm whether optimized stationary points are either local minimum or transition state, as well as to evaluate zero-point vibrational energies and thermal corrections for enthalpies and free energies at 298.15 K.

Energy decomposition analysis (EDA) was conducted with sobEDA [36] and Multiwfn [38] software. The 3D diagrams of optimized structures shown in this Supplementary Information for computations are generated with CYLview software [39].

4. Conclusions

In summary, our DFT study reveals that the pronounced ortho–para reactivity difference in Ru(II)-catalyzed amination of aminopyridines arises from distinct stabilities of the Ru-bound Meisenheimer intermediates. While both substitution patterns proceed through comparable stepwise pathways, the ortho intermediates benefit from stronger CpRu–substrate orbital interactions, leading to lower free-energy barriers for the C–N bond cleavage/rearomatization step. In contrast, the para intermediates exhibit significantly reduced orbital stabilization, rendering them energetically higher and raising the overall barrier beyond the experimentally accessible range. Energy decomposition analysis pinpoints the reduced orbital interaction in the para case as the primary contributor to its lower stability, with electrostatic, exchange-repulsion, and correlation terms largely canceling out. These mechanistic insights underscore the importance of metal–substrate orbital overlap in η⁶-coordination catalysis and suggest that strategic incorporation of proximal donor groups to enhance such interactions could be a general approach for improving catalytic performance in arene substitution reactions. Building on this mechanistic study, we will further investigate the reactivity differences in various substituted 2-aminopyridine derivatives and employ physical organic parameter-based linear regression [40,41] to establish more broadly applicable theoretical models that can guide the design and development of such reactions.