Abstract
Given the increase in current density in the constituent materials of electrical systems, improving the electrical conductivity of these materials, particularly copper (Cu), is crucial. This would also help to mitigate the heat generated by Joule heating. The incorporation of graphene (Gr) into a composite material (Cu/Gr) is a viable solution. However, to ensure the proper transfer of properties between the reinforcement and the matrix, several elements must be considered, including the orientation of the reinforcement. As a 2D material, controlling graphene’s orientation within the structure is essential but often overlooked. To address this issue, hot rolling was implemented to improve the alignment of the reinforcement. The inclusion of graphene led to a 12 HV increase in the material’s hardness, demonstrating a positive composite effect. Simultaneously, rolling increased the material’s hardness from 67.6 to 75.1 HV by introducing more dislocations into the material. To characterize the graphene’s alignment, polarized Raman spectroscopy was used. This technique highlighted the improved alignment of the reinforcement in the rolling direction, a change that was visible and confirmed by scanning electron microscopy micrographs.
1. Introduction
Graphene, the latest allotropic form of carbon, was first described theoretically in 1947 by physician Phillipe R. Wallace [1]. However, it was not until 2004 that K. Novoselov et al. [2] and A. Geim et al. [3] isolated it for the first time. Since then, graphene has become particularly popular because of its extraordinary physical properties. The main properties of graphene are (1) the ballistic behavior of its charge carriers with the very high mobility of its electrons at room temperature (140,000 V/(cm2·s) [4] and 170,000 V/(cm2·s) [5]), (2) an excellent thermal conductivity ranging from 1000 to 3000 W/mK [6,7], and (3) the high transparency of the material, where only 2.7% of visible light is absorbed [8]. All of these remarkable properties arise from the unique structure of graphene. Indeed, the sp2 hybridization of its carbon atoms induces the purely 2D morphology of the material as well as the delocalization of the electrons of the pz orbitals of the carbon atoms. This peculiar structure allows the free movement of outer-shell electrons (π electrons), leading to a higher electrical conduction than metals such as silver (Ag) with or copper (Cu) with [9]. Indeed, experimental values of have been obtained at room temperature [10,11,12]. Graphene alone is not always the most studied form. Research is progressing, and we are starting to uncover applications for materials with ‘graphene-like’ properties. These include fluoro-graphene for sensors [13] and sulfur–graphene for recharging lithium batteries [14]. However, as a 2D material, its electrical conductivity properties are anisotropic and are primarily relevant in the in-plane direction. Therefore, during the fabrication of organic or inorganic composite materials, the orientations of graphene reinforcements inside organic or inorganic matrices must be taken into account [15,16] and, specifically, when electrical and/or thermal properties are the main desired properties [17,18,19,20]. Simulation studies have shown that the effect of the reinforcement becomes negligible when the average disorientation of the graphene reinforcement exceeds 15° relative to the measurement direction [21]. Other elements, such as the purity, defect rate, dimensions, number of graphene sheets, and matrix–reinforcement interfacial properties, can also influence the properties of the graphene and the global composite properties.
To control the orientation of the reinforcement inside metallic matrices, various fabrication methods and post-processing techniques are available. For example, the use of the 2D plate-like morphology of Cu powder [18] aids in aligning graphene in its preferred direction, thereby mimicking the natural structure of mother-of-pearl. In addition, fabrication processes such as uniaxial hot pressing tend to induce the preferential orientation of the reinforcements in a plane perpendicular to the direction of pressing. Post-processing treatments, such as hot or cold rolling and extrusion [22], are also needed to optimize the orientation of the reinforcement. Moreover, post-treatments can induce the delamination of the graphene/graphite flakes and, therefore, create longer conduction paths [23,24].
These post-treatments can also deform the original grain shapes of the metallic matrix and induce the deformation of the grains in the direction of the hot rolling (HR) or extrusion. This microstructure enhances the electrical or thermal properties by reducing the diffusion of electrons at the grain boundaries. However, the stresses applied to the material can also induce the recrystallization of the metallic grains, which may alter the microstructures [25] and negatively impact the electrical properties of the material. As has been observed in the work by Miao Wang et al. [23], rolling at high temperatures leads to a spherical morphology of the particles induced by recrystallization.
To control the alignment of a reinforcement, several methods exist. The most common one (i.e., image analysis carried out with scanning electron micrographs) cannot be used because of the nanometric size of graphene reinforcements. To accurately measure the orientation and flatness of graphene, polarized Raman spectroscopy is a reliable technique. It has been shown that the G-band of graphene is dependent on the polarization of the incident laser beam [26,27,28]. This technique is used to determine the flatness of a graphene mono-sheet as well as the structure at its edge [29]. This analytical method has also been used to characterize the alignment of graphene in organic matrix composite materials [14]. However, very few works (e.g., K. Chu et al.’s [30]) using this technique can be found for composite materials with a metal matrix such as Cu. However, the main difficulties are based on (1) the absorption of the beam by the metal, (2) the complexity of obtaining a Raman signal from the nanometric reinforcement, and (3) the need to cryofracture the material, which is not trivial in a ductile material.
In our work, we propose a post-processing treatment to improve the alignment of graphene in a composite material with a Cu matrix. The evolution of the alignment of the graphene (Gr) reinforcement was monitored after several rolling passes using polarized Raman spectroscopy. The effect of the graphene addition on the hardness of the Cu/Gr composite materials was analyzed. The microstructure of the composite materials, analyzed using X-ray diffraction (XRD), scanning electron microscopy (SEM), and electron backscattered diffraction (EBSD), was correlated with the graphene alignment and the hardness of the Cu/Gr composite.
2. Experimental Section
2.1. Type of Cu Powder and Graphene
Dendritic copper (named Cu-D) powders, with an average length of 50 µm and a diameter of 10 µm (cf. Figure 1a), were purchased from ECKART a division of Altana (Hartenstein, Germany). The powders were used as received, without any treatment. The multilayer graphene (MLG) powder, with an average thickness of 2.5 ± 0.5 nm (approximately 3–9 atomic layers; see Figure 1b) and a lateral size of 7.5 ± 2.5 µm (see Figure 1c), was purchased from KNANO (Xiamen, China). XPS analysis showed that the percentage of oxygen on the surface of the KNG-5 powder was close to 1.5 atm.% (0.4% for the C=O group, 0.8% for the C-O group, and 0.4% for the OH group). Raman spectroscopy analysis revealed an ID/IG ratio close to 0.12, an ID/I2D ratio close to 0.55, and a crystalline size (La) close to 330 nm (according to Equation (1)). The ID/ID’ was also calculated to be close to 6.7, suggesting (as shown by A. Eckmann et al. [31]) that the defects were primarily lacunae present in the graphene (Gr) crystallographic network. The crystalline size of the graphene used was calculated using the following equation (from L.G. Cançado et al.’s study [32]):
where El is the energy of the incident beam (1.96 eV for the 633 nm wavelength laser used), and is the wavelength of the incident laser beam (633 nm).
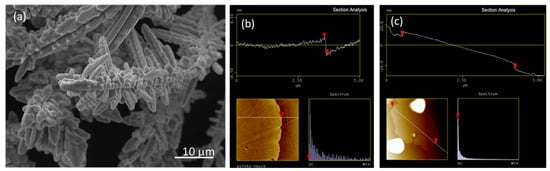
Figure 1.
(a) Typical SEM micrograph of the dendritic Cu powder, and typical atomic force microscopy (AFM) image showing (b) the thickness and (c) the diameter of the KNANO graphene used in this study (both thickness and diameter are measured at the position of the read arrows).
For a perfect graphene sheet (without any surface contamination), the hardness in the plane is close to the hardness of a pure diamond [29].
2.2. Fabrication of the Composite Material and Post-Treatment
2.2.1. Fabrication of the Composite Materials
After the surface treatment and functionalization of the graphene materials (i.e., per [33,34]) the treated Gr materials were first homogenously dispersed inside an ethanol medium at a concentration of 0.1 g/L using an acoustic mixer (LABRAM II, Resodyn, Butte, MT, USA) operating at 60 Hz for 6 min with an acceleration of 80 g. Subsequently, the Gr suspension was sprayed onto the surface of the Gr powders using the same apparatus working in the spray mode. More details of the apparatus can be found in [35]. After drying in an oven (at 70 °C), the Cu + Gr composite powders were then deoxidized at 400 °C for 60 min in an Ar (5% H2) atmosphere. The concentration of Gr was tuned to 0.1 vol.%, which was close to the percolation thresholds discovered by various authors [36]. The densification of the material was carried out using a Thermolab® press, equipped with an inductive heating system, at a temperature of 650 °C for 45 min under a pressure of 60 MPa. The temperature was monitored via a K-type thermocouple (Prosensor, Amanvillers, France) located inside the mold and close to the composite powders. The temperature reduction was managed according to the thermal inertia of the enclosure. The relative densities of the parts were greater than 99.4%, as measured by the Archimedes method.
2.2.2. HR Post-Treatment
The HR materials (Cu/Gr composite materials (x = 40 mm, y = 10 mm, and z = 5 mm)) were placed in an oven (Beijing JinYeHong Metallurgical Mechanical Equipment Corp Ltd., Beijing, China), under a neutral atmosphere, for 30 min at 500 °C (above the recrystallization temperature of Cu (326 °C), according to Y. Dong et al. [31]), and then immediately hot-rolled (Cavallin 130 mm Rolling Mill (Beijing JinYeHong Metallurgical Mechanical Equipment Corp. Ltd., Beijing, China)) at a speed close to 10−2 m/s. The temperature of the roller was close to 100 °C, as measured by a thermocouple (Prosensor, Amanvillers, France) prior to hot rolling.
After each HR pass, the composite materials were annealed at 500 °C for 60 min in an Ar/5% H2 atmosphere (HR + A). Each pass resulted in a 10% reduction in thickness. Table 1 illustrates how the percentage reduction in the thickness of the composite materials changed with the number of passes, relative to the initial thickness of the materials (5 mm). Finally, each material that had undergone 15 HR passes (a 10% reduction during each HR pass) underwent 15 pre-heating (at 500 °C for 30 min) and 15 post-heating (annealing) (at 500 °C for 100 min) treatments.

Table 1.
Reduction in the thickness of the composite materials with the number of HR passes (accuracy close to 1%).
It is important to note that all analyses (Raman spectroscopy, X-ray diffraction, EBSD, and hardness testing) were conducted in the (x, y) plane of all the tested materials.
2.2.3. Polarized Raman Spectroscopy
In the case of Gr, polarized Raman spectroscopy is often used to determine the flatness of edges or full sheets [13,15]. This technique exploits the dependence of the intensity of the G-band of Gr (~1580 cm−1) on the polarization of the incident laser beam [27,28,29,30]. When the incident laser beam is oriented parallel to the basal plane of graphene, the intensity of the G-band is maximized at a polarization angle of 0° or 180° (relative to the basal plane). Conversely, the intensity of the G-band decreases as the polarization angle increases from 0° to 90°. Note that this is only true in the case of a perfectly aligned sheet; otherwise, the intensities obtained of the G-band tend to even out. In this study, once the G-band intensity values were obtained, normalization and refinement through the use of the minimum and maximum intensities were performed using Equation (2) [27].
where IG is the intensity of the G-band, with min for the minimum and max for the maximum, and θin is the angle of polarization of the incident laser beam. The intensity obtained after this normalization was used to determine the alignment of the Gr in the matrix. During the measurements, the polarization of the incident laser was tuned using a half-wave plate at the output exit of the laser.
However, to ensure that the results obtained were representative of the material, proper sample preparation was essential. First, it was not advisable to determine the orientation of the reinforcement at the edges of the sample, as the graphene may have been deformed there. A central analysis was necessary for accurate results. The composite materials were broken in liquid nitrogen. Therefore, polarized Raman spectroscopy was performed on fractured cross-sections of the composite materials, subjected to various numbers of passes. An excitation wavelength of 532 nm was used with a maximum power of 1 mW to minimize laser heating. The measurements were conducted with a spectral resolution of 0.1 cm−1 using a high-resolution Jobin Yvon Horiba LabRam HR micro-Raman spectrometer (Houston, TX, USA), which was equipped with a charge-coupled device detector. Raman spectra were obtained in the backscattering micro-configuration. The incoming and backscattered lights were focused using a 10× objective. The polarizations of the incoming and scattered light were aligned parallel to each other. The angle between the polarization direction and the sample normal was rotated with a λ/2 waveplate.
2.3. Hardness and Microstructural Characterization
Hardness measurements are performed using a Vickers micro-indenter with a square-based pyramid-shaped diamond tip (WILSON Hardness, Vickers 452 SVD, London, UK). The measurements were carried out parallel to the direction of compression with a force of 196 N to obtain the largest possible footprint. Each sample was indented ten times on both sides to ensure higher accuracy.
The density of the composite materials was measured using the Archimedes method (Sartorius Analitic® balance (d = 0.1 mg)). A scanning electron microscope (Tescan VEGA®, Brno, Czech republic) was used to characterize the morphology of the composite powders and high-resolution transmission electron microscopy (HRTEM) (JEOL®-2100 microscope Tokyo, Japan) for the nano CuO(Cu) dots on the surface of the Gr. Microstructural characterization was carried out by electron backscattered diffraction (EBSD, EDAX®, Billerika, MA, USA, with a probe size of 330 nm and a step of 0.1 µm). To improve the EBSD lattice quality and sharpen the diffraction bands, the samples were polished by metallographic and ion milling. The final mechanical polishing was performed with a ¼ µm diamond suspension followed by ion milling using a Fischione polisher SEM MILL MODEL 1061 Milling (Vuko Place Warriewood NSW 2102 Australia) with an angle of 5° at 5 kV for 10 min. EBSD maps were obtained via an SEM JEOL JSM-7800F LV, Tokyo, Japan, operated at 20 kV equipped with an EBSD Symmetry camera from the Oxford Society. The EBSD data were processed with the AztecCrystal software package (Copyright © 2020 Oxford Instruments plc, Tubney Woods, Abingdon, Oxon OX13 5QX, UK). X-ray diffraction (XRD) was carried out using a Philips PANalytical X’Pert Pro, Madison, WI, USA, equipped with a copper source (λKα1 = 0.15405 nm and λKα2 = 0.15443 nm) between 2θ = 10 and 80°, with a 0.02° (2θ) step and a 2.022° (2θ) active width in the detector.
3. Results and Discussion
3.1. Cu/Gr Composite Materials and HR Post-Treatment
Raman spectroscopy was employed to determine the evolution of the defect rate in the graphene (Gr) induced by the various processes, including the surface treatment of the Gr, the densification of the Cu-Gr powders, and the subsequent HR post-treatment. An example of the Raman spectra of our material is presented in Figure 2, with the evolution of the ID/IG ratio of the Gr shown in Figure 3. With an initial ID/IG ratio of 0.12, neither the surface treatments (ID/IG = 0.1) nor the heat reduction treatment (ID/IG = 0.08) induced any defects in the Gr. However, after the last step, i.e., the densification of the material, the ID/IG ratio sharply increased to a value of 0.64. The various post-rolling steps did not appear to introduce any additional defects in the material. This was likely due to the low reduction rate (10%) applied, as well as the annealing step after each HR pass, which tends to alleviate the stresses induced by the rolling process. During the densification step, uniaxial pressure (50 MPa), at 600 °C, was applied to the Cu + Gr mixture. This pressure, to any metal matrix, tends to orient the reinforcement in a plane perpendicular to the pressure direction [35]. Therefore, during the densification steps, the Gr materials, initially randomly dispersed, tended to align perpendicularly to the pressure direction. Even if at 600 °C, while the mechanical properties of the Cu matrix were low (for example, for Young’s modulus (E), Ecu (20 °C)~115 GPa and Ecu (600 °C)~40 GPa), the orientation of the Gr may have created structural defects (i.e., point defects, 1D defects, defects between the Gr layers, 3D defects induced by the curvature of the Gr, etc.), which lowered the properties of the Gr and increased the ID/IG ratio [37].
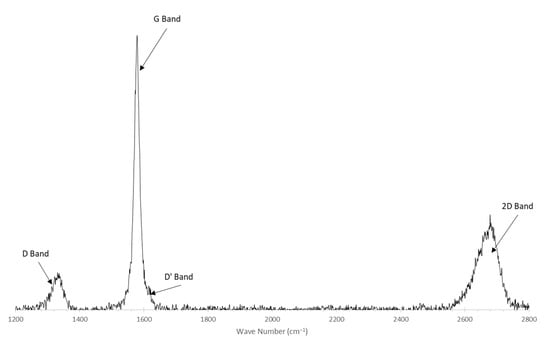
Figure 2.
Typical Raman spectrum of KNG-5 graphene.
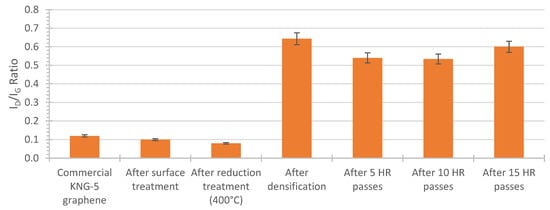
Figure 3.
Evolution of the ID/IG ratio of the Gr induced by the fabrication process of the Cu/Gr composite materials.
Even though this specific spectroscopy can reveal the degree of degradation of the Gr during the material fabrication steps, it does not indicate the potential orientation of the Gr induced by HR. This aspect is critical, given the anisotropic properties of Gr.
3.2. Polarized Raman Spectroscopy: Effect on HR of Gr Alignment
Polarized Raman spectroscopy was performed to correlate the HR process with the Gr orientation. Figure 4 illustrates the evolution of the G-band intensity with the polarization angle of the incident laser beam, considering the effects of the HR post-treatment and the number of passes.
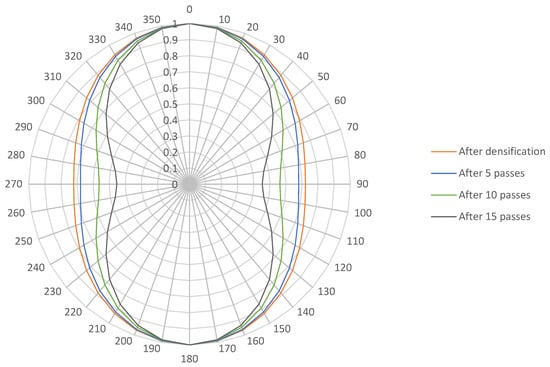
Figure 4.
G-mode intensity for Cu/Gr composite materials as a function of the angle between the polarization of the incoming light and the composite in-plane axis.
For the interpretation of this graph, it is crucial to concentrate on the changes in the minimum intensity of the G-band at 90° and 270°. In the initial state (without rolling), the minimum intensity was not equal to 1, indicating that, as described previously, the uniaxial hot-pressing step had already caused some alignment of the graphene (Gr) in a plane perpendicular to the pressing direction. Experiments were also carried out directing the Raman laser perpendicular to the basal plane of the graphene, and a G-band value of 0.95 was obtained. This clearly demonstrated a preferential orientation of the graphene after densification. As the rolling passes progressed, the minimum intensity of the G-band tended to decrease from 0.72 before HR to 0.68, 0.56, and 0.45 after 5, 10, and 15 HR passes, respectively. These decreases show that the HR treatments improved the alignment of the Gr in a plane perpendicular to the pressing direction and, thus. parallel to the rolling direction. It must be noted that the intensity of the G-band did not generally go down to zero, even when the laser polarization was at 90° to the Gr plane, due to the misalignment or waviness of the Gr. It is also important to note that this experiment did not provide an accurate measurement of the average disorientation of the graphene sheets. In fact, this technique only allowed us to obtain a qualitative change in the orientation.
SEM analyses were carried out to visualize the alignment of the graphene. A sample containing 1 vol.% of graphene was prepared and laminated under the same conditions. Due to agglomeration, the graphene sheets became visible by SEM (Figure 5). Before lamination, the graphene sheets showed a preferential orientation, but this remained imperfect, with the presence of folds on the reinforcement. After 15 HR passes, a better orientation of the sheets was obtained, as well as improved flatness. Polarized Raman spectroscopy was proven to be a reliable and effective technique for characterizing the alignment of graphene in the structures of composite materials.

Figure 5.
SEM analysis of Gr orientation before (a) and after (b) hot rolling.
3.3. Microstructural Analysis and Hardness Measurements
3.3.1. XRD Analysis
Figure 6 shows the XRD patterns of the pure Cu materials and the Cu/Gr composite materials before and after 15 HR passes. For the Cu/Gr composite materials, the presence of the Gr (200) peak was observed at 26.7°.
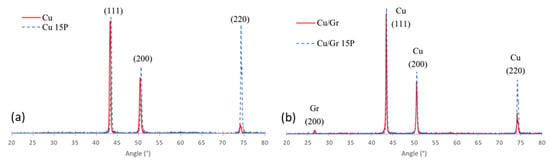
Figure 6.
XRD analysis of (a) pure Cu materials and (b) Cu/Gr composite materials before HR and after 15 passes of HR and annealing.
The areas of all Cu peaks were determined using the EVA software (https://www.bruker.com/fr/products-and-solutions/diffractometers-and-x-ray-microscopes/x-ray-diffractometers/diffrac-suite-software/diffrac-eva.html, accessed on 27 March 2024) after subtracting both the background and the contribution of Kα2 radiation. The changes in the area ratios of both (200)/(111) and (220)/(111) are shown in Table 2. For both the Cu and Cu/Gr materials, the (111)/(200) ratio remained relatively stable before and after hot rolling (HR). However, there was a significant decrease in the (111)/(220) ratio observed in the Cu materials after HR, with a more moderate decrease noted in the Cu/Gr composite. This was mainly due to an increase in the (220) peak intensity. Also, as shown in Figure 6 and Table 2, the incorporation of Gr inside Cu slightly enhanced the (220) preferred orientation of the composite material before the HR step. However, after HR, this tendency was weaker compared with pure Cu.

Table 2.
Evolution of the area ratios (200)/(111) and (220)/(111) for the Cu and Cu/Gr materials before and after 15 HR passes.
T. Leffers et al. [35] showed that the HR of face-centered cubic metals induces two types of rolling textures: the “copper-type texture” and the “brass-type texture”. The “copper-type texture” ({123} <121>) is favored by a low strain rate and a high staking fault energy (SFE) (γSFE > 30 mJ/m2) and the “brass-type texture”, which is described by a combination of “brass orientation - {110} <112>” and ”Goss orientation - ({110} <001>”, is favored by a low SFE and a high strain rate. {hkl} <uvw> means that the crystallographic ({hkl} plane is parallel to the rolling plane, and the crystallographic <uvw> direction is parallel to the rolling direction. It must be mentioned that the stacking fault energy (SFE) of copper, approximately 45 mJ/m2, categorizes it as a medium–high SFE material. Taking into account the results of T. Leffers et al. [38], the hot-rolling (HR) conditions for both pure copper and the Cu/Gr composite materials tended to induce a “brass-type texture,” with this effect being more pronounced in the Cu/Gr composite compared with pure copper. The graphene reinforcement, which can act as a crystallographic default and nucleation site for grain growth, tended to enhance the (220) orientation before HR compared with pure Cu. This behavior decreased after HR. The exact role of Gr is not fully understood yet.
3.3.2. EBSD Analysis
Table 3 shows the evolution of the grain size, as measured from the inverse-pole figure in the z-direction (perpendicular to the plane of the materials and the extrusion direction) (IPF(z)), for both pure Cu and the Cu/Gr composite materials before and after the hot-rolling (HR) and annealing treatments (see Figure 7).

Table 3.
Evolution of the grain size for Cu and Cu/Gr materials in the post-treatment conditions.

Figure 7.
IPF(z) orientation color map of the Cu and Cu/Gr materials before and after hot rolling (15 passes (15HR)). The color code is linked to the grain orientation in the crystal lattice.
For pure Cu, the HR and annealing treatments reduced the surface grain size of the densified materials from 13 μm2 before HR to 9 μm2 after 15 HR passes. This increase was more pronounced with the number of treatments: 5 μm after 1 HR pass and 9 μm after 15 HR passes. The increase in grain size should be attributed to the pre- and post- heat-rolling treatment for each HR pass and the recrystallization of the Cu grains. Recrystallization mechanisms are influenced by several factors, including the energy stored in the grains during deformation, the temperature, the extent of deformation, and the presence of a second phase. For materials with low-energy stacking faults like Cu, the twinning induced by annealing is often a complementary recrystallization mechanism. For two-phase materials (Cu + Gr), there is also another mechanism, particle-stimulated nucleation (PSN), which is linked to the formation of nuclei around precipitates.
The tendency was different for the Cu/Gr composite materials. Indeed, an increase in the surface grain size (going from 15 to 19 μm2) was measured after HR. The presence of Gr inside Cu played an important role in the Cu grain size. This tendency was unusual due to the fact that most metal matrix composite materials, reinforced with nanomaterials, show a decrease in grain size compared with non-reinforced materials.
The color code in the IPF(z) orientation maps (i.e., Figure 7) represents the position of a sample direction in the crystal lattice. For Cu after HR, an increase in the (101) orientation can be observed in the IPF(z) maps (i.e., Figure 7). This tendency should be correlated with the XRD analysis, showing that mostly for Cu, the HR process enhanced the (220) orientation. This tendency was no longer visible for the Cu/Gr composite.
Figure 8 shows the coincident site lattice (CSL) maps of the (111) twins (Σ3) for a disorientation ranging from 58° to 64°. The twins are colored in blue in the four maps of Figure 8, and Table 3 shows the surface fractions of the (111) twins for the Cu and Cu/Gr materials before and after the 15 HR passes.

Figure 8.
CSL maps of (111) twins for Cu and Cu/Gr materials before and after hot rolling (15 passes (15HR)). The blue color represents the (111) twins (Σ3) for disorientation ranging from 58° to 64°.
3.3.3. Hardness Measurements
The mechanical performances of the composites reinforced with nanosized particles were evaluated for hardness. The mechanical properties of composite materials mainly depend on the type of reinforcement, shape, quantity of reinforcement, distribution, size, etc. [39]. Generally, the mechanical properties (i.e., a 0.2% yield strength, ultimate tensile strength, and hardness) of nanocomposites are improved by increasing the volume fraction of the nanosized reinforcement [40,41]. The hardness of the material was measured after 1, 2, 3, 4, 5, 10, and 15 HR + annealing steps (i.e., Figure 9). Without the presence of the reinforcement, it was observed that the hardness of the material gradually increased during the first three rolling passes to reach an asymptote after five passes, reaching a value of 64.1 HV. For the composite, the presence of Gr increased the hardness by more than 20% in comparison with the initial material (67.6 HV vs. 55.8 HV). This increase in the hardness was consistent with previous works that showed an increase in the hardness of metals reinforced with nanoscale materials. The hardness of the material increased from 67.6 to 72.1 HV after the first pass and then reached a maximum of 75.1 HV after five passes. This value remained constant after further passes. This experiment was also carried out on a material that had not undergone annealing: a hardness of 87.4 HV was reached, clearly showing the benefit of the annealing steps. The increase in hardness observed between the two materials was likely due to the reinforcement. The difference in the hardness between the initial state and after 15 passes remained consistent, suggesting that the reinforcement significantly contributed to the observed hardness improvement. These results indicate that the increase in the hardness of the composite material (Cu/Gr) during the hardening process was not caused by improved alignment. Instead, they suggest that the observed change in the hardness was more likely due to alterations in the microstructure.
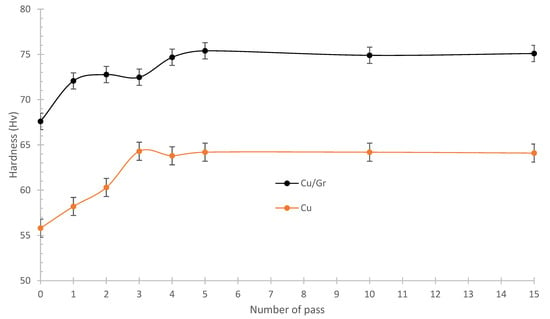
Figure 9.
Evolution of the hardness (HV) of Cu and Cu/Gr materials with the number of HR passes and annealing.
Several parameters can play a role in the increase in the hardness of non-reinforced and reinforced metals. In nanocomposites, nanoparticles act as a barrier against the movement of dislocations, known as Orowan strengthening [42]. As indicated by Hall–Petch relationship, finer grains result in stronger yield strength [43]. In the Orowan strengthening mechanism, nanoparticles pin down the dislocation lines and generate Orowan loops around the particles, and the induced stress resistance can be expressed as:
where G is the shear modulus of the material, b is Burger’s vector, and r is the average radius of the nanoparticles, assuming a spherical shape. The distance λ between the particles can be calculated by:
where f is the volume fraction of the particles. The reduction in the distance between the nanoparticles results in an increase in the required stress τ0 for forcing dislocations to move among the reinforcement particles; thus, the overall strength of the material increases:
It is evident that smaller particles contribute more significantly to strengthening through the Orowan process. However, the effectiveness of Orowan strengthening significantly degrades when particle agglomeration or clusters are present.
Also, the effect of twins on hardness is well known. Indeed, J. Gates et al. have shown that a high density of twins is important to strengthen micro-hardness [44]. Finally, the increase in strength can also be attributed to the mismatch in the coefficient of thermal expansion (CTE) values of the matrix and reinforcement. The metal matrix has higher CTE values than those of carbon. During the cooling stage, thermal stress resulting from the difference in the CTEs can be released by generating dislocations in the vicinity of the interfaces. These dislocations contribute to the hardening of the materials [36].
For Cu, the microstructural analysis of the different samples showed a decrease in the surface grain size and an increase in the surface fraction of twins. Therefore, the increase in the hardness with the number of HR passes can be attributed to (1) the decrease in the grain size (Hall–Petch), which is common for metals, (2) the increase in dislocation density induced by HR, and (3) the increase in the surface fraction of twins.
For the Cu/Gr materials, the microstructural analysis of the different samples showed an increase in both the surface grain size and the surface fraction of twins. Therefore, the increase in the hardness with the number of HR passes can be attributed to (1) the intrinsic properties of Gr (which is much harder than Cu), (2) the increase in the dislocation density induced by HR and the CTE difference between Cu and Gr, and (3) the increase in the surface fraction of twins.
The increase in the hardness of the composite materials compared with the non-reinforced ones (see Figure 9) was not due to an indirect effect related to the matrix grain size. Instead, it was attributed to a direct effect, where the mechanical properties of the graphene (Gr) reinforcement and effective property transfer between the matrix and the reinforcement lead to enhanced mechanical properties in the composites.
4. Conclusions
The aim of this work was to improve and quantify the alignment of graphene within a metal matrix composite. Polarized Raman spectroscopy showed that the uniaxial pressing of the material resulted in a preferential orientation of the graphene reinforcement in a plane perpendicular to the pressing direction. The intensity of the G-band showed a significant decrease between polarization angles of 0 and 90°. To further improve the orientation and flatness of the graphene sheets in the direction of stress, hot-rolling processes were carried out. The polarized Raman spectroscopy results show a decrease in the G-band at a polarization angle of 90° (270°), demonstrating the improved alignment of the reinforcement in the direction of stress. Regarding the microstructural deformations induced in the matrix, the EBSD analyses showed that the incorporation of the graphene did not result in a significant modification in the grain size (15 µm2 for the composite and 13 µm2 for pure Cu), which was unusual. The post-treatments resulted in a preferential orientation of the Cu grains in the (220) plane, as demonstrated by the XRD analysis. This was consistent with the EBSD results. After Cu HR, an increase in the (101) orientation was observed in the IPF(z) maps. The Cu/Gr composites showed a higher hardness than pure Cu (67.6 HV vs. 55.8 HV), which was attributed to a composite effect, as with the high hardness of the graphene sheet. This increase was also visible after the rolling passes for pure Cu and the composite (64.1 and 75.1 HV, respectively), induced by the increase in the number of dislocations despite the relaxation heat treatments. The EBSD analyses showed a slight increase in the copper grain size with the incorporation of the graphene reinforcement, which was contradictory to the Orowan reinforcement. This trend was also observed after hot rolling (15 µm2, initially, vs. 19 µm2 after HR), which, again, contradicted the hardness measurements. Conversely, the results for pure Cu showed a more consistent trend: the grain size decreased after hot rolling (from 35 µm2, initially, to 9 µm2 after HR). However, there remained some ambiguity regarding the structural modifications of the matrix. Nevertheless, we successfully improved the orientation of graphene in the direction of stress application through a lamination post-treatment and demonstrated this qualitatively. This advancement is crucial for the development of 2D-reinforced composite materials, as orientation is a key and often underestimated factor in enhancing physical properties.
Author Contributions
This work was completed through the contributions of all authors. The individual contributions were supervision and conceptualization: J.-F.S. and F.D.; manuscript writing: J.-F.S., Y.L. and A.B.; material elaboration, characterization, and post-treatment: A.B.; SEM and EBSD characterization: A.A., G.J. and A.V.; XRD analysis: J.-L.B.; Raman characterization: J.-L.G.-P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All the data required to evaluate the conclusions presented in this paper are included within this paper. The datasets generated during the current study are available from the corresponding author upon reasonable request.
Acknowledgments
The Institute of Condensed Matter Chemistry of Bordeaux (ICMCB) and Schneider Electric SAS are acknowledged for their provision of equipment and scientific support.
Conflicts of Interest
Authors Antoine Bident and Florence Delange were employed by the company Schneider Electric SAS. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Wallace, P.R. The Band Theory of Graphite. Phys. Rev. 1947, 71, 622. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 660–669. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. The rise of Graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Dean, C.R.; Yong, A.F.; Meric, I.; Wang, L.; Sorgenfrei, S.; Watanabe, K.; Taniguchi, T.; Kim, P.; Shepard, K.L.; Hone, J. Boron nitride substrates for high-quality graphene electronics. Nat. Nanotechnol. 2010, 5, 722–726. [Google Scholar] [CrossRef] [PubMed]
- Hirai, H.; Tsuchiya, H.; Kamakura, Y.; Mori, N.; Ogawa, M. Electron mobility calculation for graphene on substrates. J. Appl. Phys. 2014, 116, 08703. [Google Scholar] [CrossRef]
- Loh, G.C.; Teo EH, T.; Tay, B.K. Thermal transport around tears in graphene. J. Appl. Phys. 2011, 109, 043508. [Google Scholar] [CrossRef]
- Du, X.M.; Zheng, K.F.; Chen, R.Q.; Liu, F.G. First-principle study of the interaction between graphene and metals. Dig. J. Nanomater. Biostructures 2017, 12, 463–471. [Google Scholar]
- Nair, R.R.; Blake, P.; Grigorenko, N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres NM, R.; Giem, K. Fine Structure Constant Defines Visual Transparency of Graphene. Science 2008, 320, 1308. [Google Scholar] [CrossRef]
- Du, X.; Skachko, I.; Barker, A.; Andrei, E.Y. Approaching ballistic transport in suspended graphene. Nat. Nanotechnol. 2008, 3, 491–495. [Google Scholar] [CrossRef]
- Wu, Q.; Xu, Y.; Yao, Z.; Liu, A.; Shi, G. Supercapacitors based on flexible graphene/polyaniline nanofiber composite films. ACS Nano 2010, 4, 1963–1970. [Google Scholar] [CrossRef]
- Stankovich, S.; Dikin, D.A.; Dommett GH, B.; Kohlhaas, K.M.; Zimney, E.J.; Stach, E.A.; Piner, R.D.; Nguyen, S.T.; Ruoff, R.S. Graphene-based composite materials. Nature 2006, 442, 282–286. [Google Scholar] [CrossRef]
- Nirmalraj, P.N.; Lutz, T.; Kumar, S.; Duesberg, G.S.; Boland, J.J. Nanoscale Mapping of Electrical Resistivity and Connectivity in Graphene Strips and Networks. Nano Lett. 2011, 11, 16–22. [Google Scholar] [CrossRef]
- Wei, C.-K.; Peng, H.-Y.; Tsai, Y.-C.; Chen, T.-C.; Yang, C.-M. Fluorographene sensing membrane in a light-addressable potentiometric sensor. Ceram. Int. 2019, 45, 9074–9081. [Google Scholar] [CrossRef]
- Wang, J.-Z.; Lu, L.; Choucair, M.; Stride, J.A.; Xun, X.; Liu, H.-K. Sulfur-graphene composite for rechargeable lithium batteries. J. Power Sources 2011, 196, 7030–7034. [Google Scholar] [CrossRef]
- Jagannadham, K. Orientation dependence of thermal conductivity in copper-graphene composites. J. Appl. Phys. 2011, 110, 074901. [Google Scholar] [CrossRef]
- Boden, A.; Boerner, B.; Kusch, P.; Firkowska, I.; Reich, S. Nanoplatelet Size to Control the Alignment and Thermal Conductivity in Copper−Graphite Composites. Nano Lett. 2014, 14, 3640–3644. [Google Scholar] [CrossRef]
- Wu, S.; Ladani, R.B.; Zhang, J.; Bafekrpour, E.; Ghorbani, K.; Mouritz, A.P.; Kinloch, A.J.; Wang, C.H. Aligning multilayer graphene flakes with an external electric field to improve multifunctional properties of epoxy nanocomposites. Carbon 2015, 94, 607–618. [Google Scholar] [CrossRef]
- Cao, M.; Xiong, D.-B.; Tan, Z.; Ji, G. Aligning graphene in bulk copper: Nacre-inspired nanolaminated architecture coupled with in-situ processing for enhanced mechanical properties and high electrical conductivity. Carbon 2017, 117, 65–74. [Google Scholar] [CrossRef]
- Embrey, L. Three-Dimensional Graphene Foam Reinforced Epoxy Composites. Master’s Thesis, Florida International University, Miami, FL, USA, 2017. [Google Scholar] [CrossRef]
- Saheb, N.; Qadir, N.U.I.; Siddiqui, M.U.; Arif, A.F.M. Characterization of Nanoreinforcement Dispersion in Inorganic Nanocomposites: A Review. Materials 2014, 7, 4148–4181. [Google Scholar] [CrossRef]
- Li, W.; Liu, Y.; Wu, G. Preparation of graphite flakes/Al with preferred orientation and high thermal conductivity by squeeze casting. Carbon 2015, 95, 945–951. [Google Scholar] [CrossRef]
- Montmitonnet, P. Laminage à chaud-Théorie du laminage, Technique de l’Ingénieur M7840 v1. 1991. Available online: https://www.techniques-ingenieur.fr/base-documentaire/materiaux-th11/elaboration-des-metaux-ferreux-42367210/laminage-a-chaud-m7840/ (accessed on 27 December 2023).
- Wang, M.; Sheng, J.; Wang, L.-D.; Yang, Z.-Y.; Shi, Z.-D.; Wang, X.-J.; Fei, W.-D. Hot rolling behavior of graphene/Cu composites. J. Alloys Compd. 2020, 816, 153204. [Google Scholar] [CrossRef]
- Cassinese, A. Conductive Composites, Wiley Online Library 2011. Available online: https://onlinelibrary.wiley.com/doi/abs/10.1002/9781118097298.weoc054 (accessed on 27 December 2023).
- Lin, J.; Balint, D.; Pietrzyk, M. (Eds.) Microstructure Evolution in Metal Forming Processes; A volume in Woodhead Publishing Series in Metals and Surface Engineering; Woodhead Publishing: Cambridge, UK, 2012. [Google Scholar]
- Li, Z.; Young, R.J.; Kinloch, I.A.; Wilson, N.R.; Marsden, A.J.; Raju, A.P.A. Quantitative determination of the spatial orientation of graphene by polarized Raman spectroscopy. Carbon 2015, 88, 215–224. [Google Scholar] [CrossRef]
- Casiraghi, C.; Hartschuh, A.; Qian, H.; Piscanec, S.; Georgi, C.; Fasoli, A.; Novoselov, K.S.; Basko, D.M.; Ferrari, A.C. Raman Spectroscopy of Graphene Edges. Nano Lett. 2009, 9, 1433–1441. [Google Scholar] [CrossRef] [PubMed]
- Sahoo, S.; Palai, R.; Katiyar, R.S. Polarized Raman scattering in monolayer, bilayer, and suspended bilayer graphene. J. Appl. Phys. 2011, 110, 044320. [Google Scholar] [CrossRef]
- Cong, C.; Yu, T.; Wang, H. Raman Study on the G Mode of Graphene for Determination of Edge Orientation. ACS Nano 2010, 4, 3175–3180. [Google Scholar] [CrossRef] [PubMed]
- Chu, K.; Wang, F.; Huang, D.-J. Anisotropic mechanical properties of graphene/copper composites with aligned graphene. Mater. Sci. Eng. A 2018, 713, 269–277. [Google Scholar] [CrossRef]
- Eckmann, A.; Felten, A.; Mishchenko, A.; Britnell, L.; Krupke, R.; Noveselov, K.S.; Casiraghi, C. Probing the nature in graphene by Raman spectroscopy. Nano Lett. 2012, 12, 3925–3930. [Google Scholar] [CrossRef]
- Cançado, L.G.; Takai, K.; Enoki, T. General equation of the determination of the crystallite size of nanographite by Raman Spectroscopy. Appl. Phys. Lett. 2006, 88, 163106. [Google Scholar] [CrossRef]
- Bident, A. Elaboration de Matériaux Composites Cuivre/Graphene à Propriétés Physiques Améliorées par Métallurgie des Poudres. Ph.D. Thesis, University of Bordeaux, Bordeaux, France, 2022. [Google Scholar]
- Bident, A.; Delange, F.; Labrugere, C.; Debiemme-Chouvy, C.; Lu, Y.; Silvain, J.-F. Fabrication and characterization of copper and copper alloy reinforced by graphene. J. Compos. Mater. 2024, 58, 109–117. [Google Scholar] [CrossRef]
- Silvain, J.-F.; Heintz, J.-M.; Veillere, A.; Constantin, L.; Lu, Y.F. A review of processing of Cu/C base plate composites for interfacial control and improved properties. Int. J. Extrem. Manuf. 2020, 2, 012002. [Google Scholar] [CrossRef]
- Alemour, B.; Yaacob, M.H.; Hassan, M.R. Review of Electrical Properties of Graphene Conductive Composites. Int. J. Nanoelectron. Mater. 2018, 11, 371–398. [Google Scholar]
- Banhart, F.; Kotakoski, J.; Krasheninnikov, A.V. Structural defects in graphene. ACS Nano 2011, 5, 26–41. [Google Scholar] [CrossRef] [PubMed]
- Leffers, T.; Ray, R.K. The brass-type texture and its deviation from the copper-type texture. Prog. Mater. Sci. 2009, 54, 351–396. [Google Scholar] [CrossRef]
- Prasad Reddy, A.; Vamsi Krishna, P.; Narasimha Rao, R.; Murthy, N.V. Silicon carbide reinforced aluminium metal matrix nano composite—A review. Mater. Today Proc. 2017, 4, 3959–3971. [Google Scholar] [CrossRef]
- Carreño-Gallardo, C.; Estrada-Guel, I.; López-Meléndez, C.; Martínez-Sánchez, R. Dispersion of silicon carbide nanoparticles in a AA2024 aluminium alloy by a high-energy ball mill. J. Alloys Comp. 2014, 586, S68–S72. [Google Scholar] [CrossRef]
- Tayeh, T.; Douin, J.; Jouannigot, S.; Zakhour, M.; Nakhl, M.; Silvain, J.-F.; Bobet, J.-L. Hardness and Young’s modulus behavior of Al composites reinforced by nanometric TiB2 elaborated by mechanosynthesis. Mater. Sci. Eng. A 2014, 591, 1–8. [Google Scholar] [CrossRef]
- Orowan, E. Symposium on Internal Stresses in Metals; Institute of Metals: London, UK, 1948; p. 451. [Google Scholar]
- Kumar, N.; Gautam, G.; Gautam, R.K.; Mohan, A.; Mohan, S. Synthesis and characterization of TiB2 reinforced aluminum matrix composites: A review. J. Inst. Eng. India Ser. D 2015, 97, 233–253. [Google Scholar] [CrossRef]
- Gates, J.; Atrens, A.; Smith, I. Microstructure of as-quenched 3.5 NiCrMoV rotor steel; Part I, General structure and retain ausenite. Mater. Werkst 1987, 18, 165–170. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).