Abstract
The interfacial perpendicular magnetic anisotropy (PMA) observed at ferromagnet/oxide interfaces presents great promise for energy-efficient spintronic technologies. The epitaxial strain induced by the lattice mismatch between films and substrates serves as an effective strategy for the tuning of the material properties. However, the current understanding of the strain effects on interfacial PMA remains insufficient. Here, we present an extensive study of the biaxial strain effects on the interfacial magnetism and interfacial magnetic anisotropy constant () in a slab-based Fe/MgO heterostructure using first-principles density functional theory calculations. Our results reveal a strong correlation between the spin moment of interfacial Fe atoms and the Fe-O bond length in both unstrained and strained systems. The overall , which includes contributions from both the Fe/MgO interface and the Fe surface, increases as the compressive strain increases. This is consistent with recent experimental findings that show that the PMA energy increases when the in-plane lattice constant of Fe decreases. In contrast, the overall initially decreases with a small tensile strain of less than 0.4% and shows an increasing trend as the tensile strain increases from 0.4% to 2%. However, beyond 2%, the overall decreases again. These changes in can be explained by the strain-induced variations of Fe 3d orbitals near the Fermi energy. This study provides a comprehensive understanding of the strain effects on magnetic anisotropy in Fe-based heterostructures, offering insights for the further optimization of interfacial magnetic properties.
1. Introduction
Magnetic tunnel junctions (MTJs) with interfacial perpendicular magnetic anisotropy (PMA) have attracted great interest due to their potential applications in high-density magnetic data memory devices [1,2,3,4,5,6,7]. This is primarily because MTJs with perpendicular magnetization have lower switching currents compared to those with in-plane magnetization [1]. A large interfacial magnetic anisotropy constant () is essential for high thermal stability, ensuring long data retention times for nonvolatile magnetic memories, particularly in small-scale devices [8,9,10].
In 2010, Ohno et al. reported a significant of 1.3 mJ/ in CoFeB/MgO-based MTJs, showing high thermal stability at dimensions as small as a 40 nm diameter, along with a low switching current of 49 μA and a high tunnel magnetoresistance ratio [2]. This was considered a significant breakthrough in terms of advancing magnetic random access memory technology [11]. Since then, a series of fundamental experimental [12] and theoretical [13,14] studies have been conducted to explore the atomic origin of the substantial at the Fe/MgO interface and the possible factors influencing , such as the thickness [15,16] and surface states [17] of Fe films, disorder effects and the insertion of heavy atoms at the Fe/MgO interface [7,18,19], and electrical field control [20,21].
In addition to the above-mentioned factors, the epitaxial strain caused by lattice mismatch serves as an effective strategy for the tuning of material properties, ranging from microstructures to electronic and magnetic characteristics [19,22,23,24,25,26,27,28,29,30]. A recent experimental study showed that Fe/Cr/Fe multilayers grown on MgO and MgO/SrTi substrates exhibited different film structures, including variations in epitaxy, residual strain, and dislocation [31]. Similarly, a strain-induced microstructural transformation was observed in an epitaxial Fe/MgO heterostructure grown on an As substrate [32]. A prior ab-initio computational study of the O-rich MgO/FeO/Fe (001) interface shows that a 5.8% tensile strain leads to a transition at the interface from ferromagnetic to half-metallic electronic states [33]. An early experimental study demonstrates that epitaxially grown on SrTi and MgO substrates not only show different microstructures but also different degrees of magnetic anisotropy. The compressive strain on films grown on SrTi significantly enhances the out-of-plane magnetization, while tensile-strained films on MgO show weak magnetic anisotropy [30]. Ab initio electronic structure calculations on Ta/FeCo/MgO heterostructures reveal that tensile strain between 2% and 4% results in a change in the magnetic easy axis from a perpendicular to an in-plane orientation [29]. First-principles calculations reveal that the tensile strain has a substantial impact on the PMA of Co/graphene and Co/BN interfaces, enhancing the PMA by 48.5% and 80.8%, respectively, with respect to the unstrained systems [34]. This contrasts with the trend observed in the above-mentioned MgO-based heterostructures [29,30].
Despite these intriguing studies, a comprehensive examination of the impact of epitaxial strain on the PMA of Fe/MgO heterostructures remains lacking. Recently, an experimental study revealed that the PMA energy increases when the in-plane lattice constant of the epitaxial Fe film decreases [35]. This suggests that compressive strain on the Fe thin film can enhance the out-of-plane magnetic anisotropy. However, a comprehensive theoretical and computational study on this topic is still lacking. Therefore, a detailed and systematic investigation of PMA in pure Fe/MgO heterostructures as a function of the epitaxial strain is essential.
In this work, we conducted an extensive computational and theoretical study of the biaxial strain effects on the interfacial magnetism and magnetic anisotropy in Fe/MgO heterostructures. We first studied the effects of various Fe film thicknesses on the interfacial magnetism and in the unstrained / heterostructures with varying n values from 1 to 11, and we determined the microscopic origin of . Next, we investigated how biaxial compressive and tensile strain influence the interfacial magnetism and . Our findings offer a comprehensive understanding of the strain effects on the interfacial magnetic properties of Fe/MgO heterostructures.
2. Results and Discussion
2.1. Structural Models
To study the relationship between interfacial magnetic anisotropy and the thickness of the Fe thin film, a heterostructure-based slab model was used, as shown in Figure 1a, in which the bcc-Fe films are placed along the [001] direction of the MgO substrate. For convenience, the first, second, third, fourth, fifth, sixth, and seventh layers from the interface are labeled as IF-I, IF-II, IF-III, IF-IV, IF-V, IF-VI, and IF-VII, respectively. To exclude the surface effects of the Fe thin film on the magnetic anisotropy, we also built a Fe slab model that shared the same thickness as the Fe film in the Fe/MgO heterostructure, as shown in Figure 1b. A vacuum layer of about 20 Å is added along the [001] direction on the Fe surface layer to eliminate the interaction between the periodic images in the two slab models. To provide a clear representation of the structural models, the bulk bcc-Fe and cubic MgO structures are also displayed in Figure 1c,b, respectively. The experimental lattice constants are 2.867 Å for bcc-Fe [36] and 4.213 Å for cubic MgO [37]. To align with the lattice constant of bulk bcc-Fe, the MgO is rotated by 45 relative to the Fe, resulting in a reasonable lattice mismatch of 3.76% between the Fe and MgO. To model the deposition of thin Fe layers on MgO substrate [2,38], the in-plane lattice parameter of the MgO substrate was fixed in our calculations, which led to a tensile strain in the Fe film.
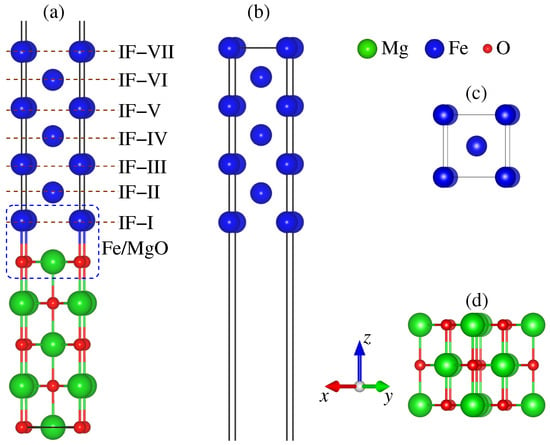
Figure 1.
(Color online) Schematic representations of (a) / and (b) /vacuum thin film structures. IF-I, IF-II, IF-III, IF-IV, IF-V, IF-VI, and IF-VII represent the first, second, third, fourth, fifth, sixth, and seventh (surface) Fe layers from the interface, respectively. (c,d) represent the bulk bcc-Fe and MgO structures, respectively.
In this work, both unstrained and strained Fe/MgO heterostructures are studied. The unstrained model refers to the Fe/MgO heterostructure where the in-plane lattice parameter equals the MgO lattice constant, denoting 0% strain. Note that, in this unstrained model, the Fe thin film still experiences intrinsic tensile strain from the MgO substrate due to lattice mismatch. The strained models are created by further adjusting the in-plane lattice parameters of the Fe/MgO heterostructures from −4% to +4%, using the MgO lattice constant as a reference. The interfacial PMA energy density, also known as the interfacial magnetic anisotropy constant, was calculated as = ()/A, where and represent the total energies of the system with magnetization oriented along the in-plane [100] and out-of-plane [001] directions, respectively. A denotes the interfacial area. Consequently, a positive value of indicates an easy magnetization axis perpendicular to the plane, while a negative value indicates an easy magnetization axis parallel to the plane. It is important to note that for the slab-based Fe/MgO heterostructure model, the calculated overall includes contributions from both the Fe/MgO interface and the Fe surface. For the strained models, the overall also contains a contribution from the uniaxial magnetocrystalline anisotropy. To exclude the uniaxial magnetocrystalline anisotropy, we built corresponding Fe slab models with the same number of Fe layers as the Fe/MgO heterostructures. The interfacial was then determined by calculating the difference in between the Fe/MgO slab model and the Fe slab model, thereby canceling out the uniaxial magnetocrystalline anisotropy.
2.2. Unstrained Fe/MgO Interface
First, we investigated the effects of the Fe film thickness on the interfacial magnetic moment and in the unstrained Fe/MgO system. The calculated interfacial Fe-O bond length () and magnetic moment of interfacial Fe atoms () as a function of the number of Fe layers in the / (n = 1–11) heterostructures are shown in Figure 2a,b, in which the subscripts n and 5 refer to the numbers of Fe layers and MgO layers, respectively. It clearly shows a strong correlation between and and that a short Fe-O bond length leads to a small magnetic moment in the interfacial Fe atom. This is because a smaller leads to the stronger orbital hybridization of Fe 3d and O 2p orbitals, which causes more unoccupied spin-up states and more occupied spin-down states. This further weakens the spin polarization of interfacial Fe atoms, which can be confirmed from the analysis of the partial density of states for the interfacial Fe atoms and corresponding charge states. This finding is also consistent with our theoretical analysis of the magnetism in 2p-light-element doped II-VI semiconductors [39], in which the spin magnetic moment was reduced with a decrease in the C-Zn bond length.
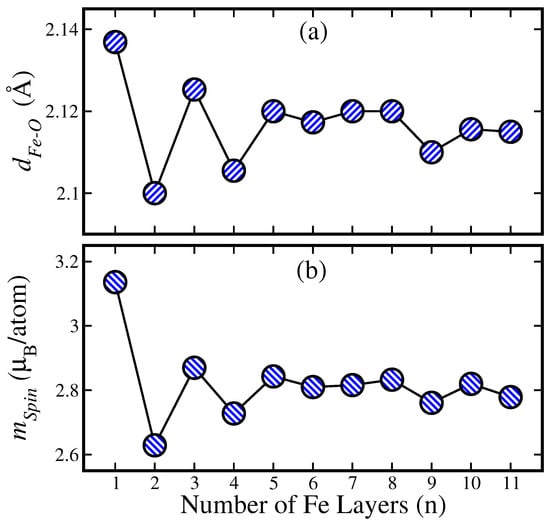
Figure 2.
(Color online) Calculated interfacial (a) Fe-O bond length () and (b) Fe spin moment () as function of number of Fe layers (n) in / heterostructure, in which n = 1–11.
The calculated and the anisotropy of the orbital magnetic moment () as a function of the number of Fe layers are shown in Figure 3a,a′, respectively. Here, the orbital magnetic moment anisotropy is defined as = , where and are the orbital magnetic moments of the interfacial Fe atom along the out-of-plane [001] and in-plane [100] directions, respectively. Figure 3 clearly shows that is strongly correlated with , following Brouno’s relation ( ) [40]. Both and show oscillatory behavior for the /MgO with n = 1–3 and become saturated at n > 3. A maximum value (3.3 mJ/) of is obtained for the /MgO model, i.e., one Fe monolayer deposited on the MgO substrate. The calculated total of /MgO ranges from 2 to 3 mJ/ at n > 3, which includes the contribution from the surface Fe layer and hence is larger than that of the superlattice model [7,41].
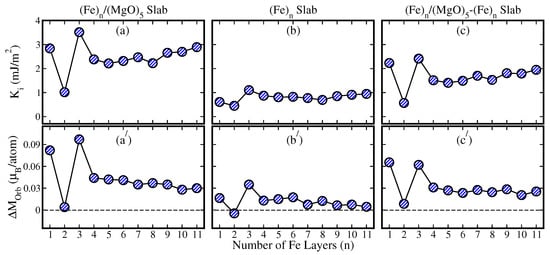
Figure 3.
(Color online) Calculated and for (a,a′) Slab-based / heterostructure, (b,b′)) slab (without MgO substrate), and (c,c′) [/] − [] (differences in and with and without MgO substrate in each case) as a function of the number of Fe layers (n), where n = 1–11.
To analyze the contribution of the Fe surface layers, we also plotted and as a function of the number (n) of Fe layers in the Fe slab model , as shown in Figure 3b,b′, respectively. At n > 3, the is nearly constant, at ∼0.77 mJ/, which is close to the previously reported value of 0.87 mJ/ [14]. As a result, to analyze the contribution to the exclusively from the Fe/MgO interface, we calculated the difference in and between the Fe/MgO slab model and Fe slab model, respectively; see Figure 3c,c′. A reasonable saturated value of about 1.51 mJ/ of is obtained at 4 ≤ n ≤ 8, which is comparable to the experimental value of 1.48 mJ/ [12] and the theoretical values of 1.40 and 1.28 mJ/ [7,41].
2.3. Strained Fe/MgO Interface
Next, taking the /MgO heterostructure as an example model, we studied the effects of in-plane biaxial strain on the magnetic moment and magnetic anisotropy at the interface. The biaxial strain is modeled by changing the lattice parameter of the Fe/MgO heterostructure from −4% to +4%. The “−” and “+” signs denote compressive and tensile strain, respectively. The calculated interfacial Fe-O bond length () and magnetic moments of the interfacial Fe atoms () as a function of the biaxial strain are shown in Figure 4. It shows that as the Fe/MgO heterostructure undergoes strain from −4% to +4%, i.e., from compressive strain to tensile strain, decreases almost linearly and also decreases, suggesting a strong correlation between and , as found in Figure 2.
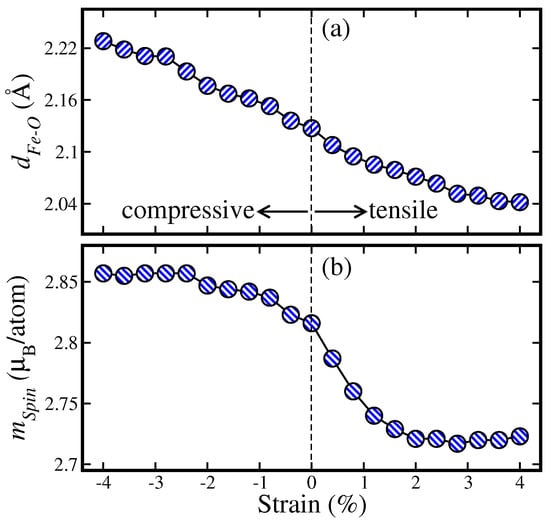
Figure 4.
(Color online) Calculated interfacial (a) Fe-O bond length () and (b) Fe spin moment () as a function of biaxial strain from −4% to +4% for the slab-based / heterostructure model. The “−” and “+” signs represent the compressive and tensile strain, respectively, in this and subsequent figures.
The calculated overall magnetic anisotropy (), including contributions from both the Fe/MgO interface and Fe surface, and for the /MgO slab model as a function of the strain are plotted in Figure 5a,a′, respectively. It shows that generally increases as the compressive strain increases. This is similar to the case of the Ta/Fe/MgO slab model, where a % compressive strain enhances [42]. Our calculations are also in good agreement with recent experimental findings in which the increased steadily as the in-plane lattice constant of Fe decreased [35]. When tensile strain was applied on the /MgO slab model, the initially decreased with a small tensile strain of less than 0.4% and then increased as the strain changed from +0.4% to +2%. However, beyond 2%, decreases as the strain changes from +2% to +4%; see Figure 5a. Interestingly, these results are also consistent with recent experimental findings that show that the interfacial first increases slightly and then decreases as the in-plane lattice constant of the Fe film increases (reflected by the thickness of the V layer, shown in Figure 4a in Ref. [35]).
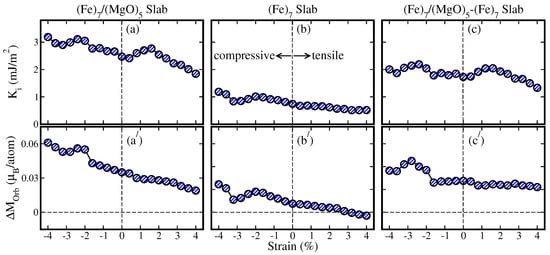
Figure 5.
(Color online) Calculated and for (a,a′)) the slab-based / heterostructure, (b,b′) slab (without MgO substrate), and (c,c′) [/] − [] (differences in and with and without MgO substrate in each case) thin film structure as a function of biaxial strain along the [110]-direction on the MgO substrate ranging from −4% to +4%.
To exclude the surface effects of the Fe thin film on the magnetic anisotropy at the Fe/MgO interface, we calculated the and for the Fe slab model as a function of the strain, as shown in Figure 5b,b′, respectively. As the strain changes from −2% to +4%, both and show a slightly decreasing trend. To show clearly the variation in that is purely contributed by the Fe/MgO interface as strain, we calculated the difference in () between the Fe/MgO slab model and Fe slab model; see Figure 5c,c′. Surprisingly, the contributed by the Fe/MgO interface is nearly unchanged when compressive strain in the range of −2% to 0 is applied, while firstly increases and then decreases slightly as tensile strain is applied, as shown in Figure 5c. This indicates that the interfacial at the Fe/MgO interface is mostly unaffected by epitaxial compressive strain within the range of −2% to 0. Instead, the modulation of the overall in this strain range is largely due to the strain applied to the Fe slab model. Interestingly, these computational findings align with the experimental conclusions, which also indicate that the interfacial PMA at the Fe/MgO interface remains largely unchanged by epitaxial strain. Instead, the modulation of the overall PMA energy primarily stems from the Fe surfaces, corresponding to the Fe slab model in this work [35]. Nevertheless, a peak value of reaching approximately 2.19 mJ/ is observed under the compressive strain of −2.4%, representing a notable 45% increase compared to the unstrained system. Notably, the peak of also corresponds to a peak within nearly the same range as for the compressive strain. Additionally, it is worth noting that Shiga et al.’s experimental measurements indicate a maximum interfacial anisotropy energy of approximately 1.9 mJ/ for annealed Fe/MgO samples with the minimum thickness of the V layer (corresponding to the maximum reduction in the in-plane lattice constant of the Fe thin film grown on V and MgO) [35], which is close to our calculated value of 2.19 mJ/ for the Fe/MgO model under compressive strain in the range of −2% to −3%.
To elucidate the microscopic origin of , we plotted the layer-resolved and of the /MgO model with −4%, 0%, and % biaxial strain, as shown in Figure 6a,b, respectively. It shows that the two layers at the interface (IF-I and IF-II) and surface (IF-VII) Fe layers both contribute to the PMA, while the interfacial Fe atom at the IF-I layer plays the largest role for both the strained and unstrained systems. A correlation between and is clearly shown. As compared to the unstrained system, compressive (−4%) strain leads to a higher and , while tensile (−4%) strain leads to a smaller and .
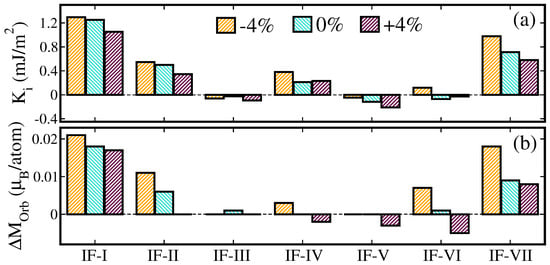
Figure 6.
(Color online) Calculated layer-resolved (a) and (b) in / thin film structure for −4%, 0%, and +4% biaxial tensile strain along the [110]-direction on the MgO substrate. IF-I, IF-II, IF-III, IF-IV, IF-V, IF-VI, and IF-VII represent the first, second, third, fourth, fifth, sixth, and seventh Fe layers from the interface, respectively, as shown in Figure 1a.
To gain atomistic insights, we calculated the orbital-resolved from the interfacial Fe atom for the /MgO model with −4%, 0%, and % biaxial strain, as shown in Figure 7a–c, respectively. It shows that the major positive contribution to the is associated with the hybridization between the and orbitals for the three systems, about +0.55, +0.61, and +0.46 mJ/, respectively. In the system with −4% biaxial strain, there is also a substantial contribution of +0.21 mJ/ from and orbital hybridization and +0.22 mJ/ from and orbital hybridization. In contrast, a relatively small contribution of +0.13 mJ/ and +0.14 mJ/ to from the and orbital hybridization occurs in the unstrained and strained (+4%) systems, respectively.
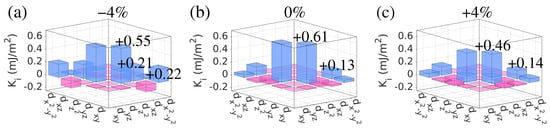
Figure 7.
(Color online) Calculated 3d-resolved contributions from various orbital hybridizations of the interfacial (IF-I) Fe atoms for (a) −4%, (b) 0%, and (c) % biaxial strain along the [110]-direction on the MgO substrate in the / thin film structure. Blue and red colors indicate the positive (out-of-plane) and negative (in-plane) contributions to , respectively.
To further understand the underlying mechanism governing the variation in , we calculated the spin-polarized partial density of states (PDOS) projected on the interfacial Fe 3d orbitals for the /MgO system with −4%, 0%, and +4% biaxial strain, as shown in Figure 8a–c, respectively. It is known that large magnetic anisotropy can occur when there are many occupied and unoccupied states near the Fermi level, as the energy difference between the unoccupied states and occupied states plays a critical role in determining [18]. As shown in the Figure 8, the spin-down states near the Fermi level decrease and also move away from the Fermi level from compressive strain (−4%) to tensile strain (+4%), implying a decrease in . In the case of −4% compressive strain, Figure 8a clearly shows that the Fermi level crosses all five spin-down d orbitals, and the orbital coupling between the and , and , and and is responsible for the of 0.21, 0.22, and 0.55 mJ/, respectively, as shown in Figure 7a. In the case of the unstrained model, all five spin-down d orbitals move away from the Fermi level to higher energy, indicating relatively weak orbital coupling, as shown in Figure 8b, thus leading to a relatively small . In the case of +4% compressive strain, the unoccupied spin-down states move even further away from the Fermi level, which generally leads to a decrease in the total , as shown in Figure 8c.
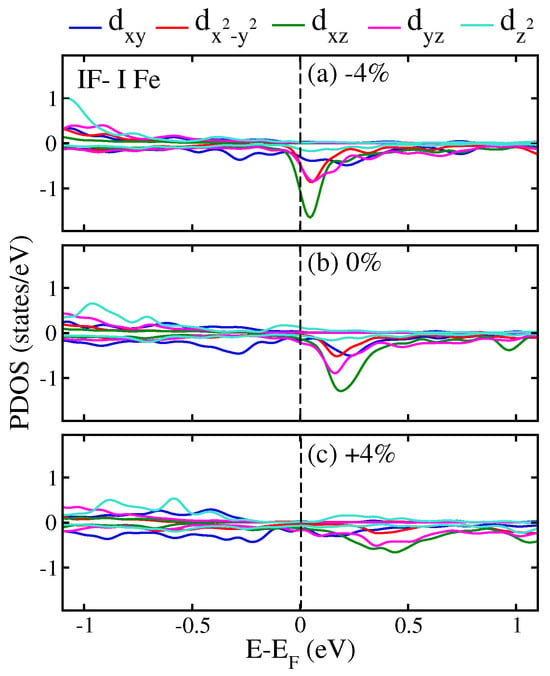
Figure 8.
(Color online) Calculated spin-polarized partial density of states (PDOS) projected on IF-I Fe 3d orbitals for (a) −4%, (b) 0%, and (c) +4% biaxial tensile strain along the [110]-direction on the MgO substrate in the / thin film structure.
3. Materials and Methods
The Vienna Ab Initio Simulation Package (VASP) was used in our first-principles calculations [43,44]. The projector augmented wave (PAW) method was utilized for electron–ion interactions [44], and the exchange-correlation functional was treated using the generalized gradient approximation (GGA) parameterized by Perdew–Burke–Ernzerhof (PBE) [45]. A cutoff energy of 450 eV was set for the plane wave basis set, with a k-point mesh. Self-consistency was achieved with a total energy convergence criterion of less than eV. All structures were optimized along the c-direction while maintaining the ab-plane fixed, until the atomic forces were minimized to within 5 meV/Å.
4. Conclusions
In conclusion, first-principles calculations were conducted to explore the biaxial strain effects on the interfacial magnetic properties of Fe/MgO heterostructures. The spin moments of interfacial Fe atoms are found to be strongly correlated to the interfacial Fe-O bond length in both the strained and unstrained systems. The overall , consisting of contributions from both the Fe/MgO interface and the Fe surface, increases notably with the compressive strain. In contrast, the overall initially decreases with a small tensile strain of less than 0.4%. As the tensile strain increases from 0.4% to 2%, trends upward. However, beyond 2%, decreases again. These variations in can be attributed to the strain-induced changes in the Fe 3d orbitals near the Fermi energy. Our computational findings offer a comprehensive understanding of the strain effects on magnetic anisotropy in Fe-based heterostructures, providing insights for the further optimization of the interfacial magnetic properties.
Author Contributions
Conceptualization, S.N. and K.Y.; Investigation, S.N., S.J. and K.Y.; Resources, K.Y.; Writing—original draft preparation, S.N.; Writing—review and editing, K.Y.; Supervision, K.Y.; Project administration, K.Y.; Funding acquisition, K.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Academic Senate General Campus Research Grant Committee at the University of California San Diego. K.Y. gratefully acknowledges the partial support from the American Chemical Society Petroleum Research Fund under award number 65212-ND10.
Data Availability Statement
Data are contained within the article.
Acknowledgments
This work used the Expanse cluster at the San Diego Supercomputer Center through allocation DMR160045 from the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) program, which was supported by the National Science Foundation.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PMA | Perpendicular magnetic anisotropy |
| MTJ | Magnetic tunnel junction |
| VASP | Vienna Ab Initio Simulation Package |
| PAW | Projector augmented wave |
| GGA | Generalized gradient approximation |
| PBE | Perdew–Burke–Ernzerhof |
References
- Nakayama, M.; Kai, T.; Shimomura, N.; Amano, M.; Kitagawa, E.; Nagase, T.; Yoshikawa, M.; Kishi, T.; Ikegawa, S.; Yoda, H. Spin Transfer Switching in TbCoFe/CoFeB/MgO/CoFeB/TbCoFe Magnetic Tunnel Junctions with Perpendicular Magnetic Anisotropy. J. Appl. Phys. 2008, 103, 07A710. [Google Scholar] [CrossRef]
- Ikeda, S.; Miura, K.; Yamamoto, H.; Mizunuma, K.; Gan, H.D.; Endo, M.; Kanai, S.; Hayakawa, J.; Matsukura, F.; Ohno, H. A Perpendicular-Anisotropy CoFeB-MgO Magnetic Tunnel Junction. Nat. Mater. 2010, 9, 721–724. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Yang, K. Engineering Mn3Ga/GaAs Interfaces: A First-Principles Study on Energetic Stability and Magnetic Anisotropy. J. Phys. D Appl. Phys. 2024, 57, 255006. [Google Scholar] [CrossRef]
- Jiang, S.; Yang, K. High-Throughput Design of Perpendicular Magnetic Anisotropy at Quaternary Heusler and MgO Interfaces. Npj Comput. Mater. 2023, 9, 123. [Google Scholar] [CrossRef]
- Jiang, S.; Nazir, S.; Yang, K. High-Throughput Design of Interfacial Perpendicular Magnetic Anisotropy at Heusler/MgO Heterostructures. ACS Appl. Mater. Interfaces 2022, 14, 9734–9743. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.; Nazir, S.; Yang, K. Origin of the Large Interfacial Perpendicular Magnetic Anisotropy in MgO/Co2FeAl. Phys. Rev. B 2020, 101, 134405. [Google Scholar] [CrossRef]
- Nazir, S.; Jiang, S.; Cheng, J.; Yang, K. Enhanced Interfacial Perpendicular Magnetic Anisotropy in Fe/MgO Heterostructure Via Interfacial Engineering. Appl. Phys. Lett. 2019, 114, 072407. [Google Scholar] [CrossRef]
- Dieny, B.; Chshiev, M. Perpendicular Magnetic Anisotropy at Transition Metal/Oxide Interfaces and Applications. Rev. Mod. Phys. 2017, 89, 025008. [Google Scholar] [CrossRef]
- Tsunegi, S.; Kubota, H.; Tamaru, S.; Yakushiji, K.; Konoto, M.; Fukushima, A.; Taniguchi, T.; Arai, H.; Imamura, H.; Yuasa, S. Damping Parameter and Interfacial Perpendicular Magnetic Anisotropy of FeB Nanopillar Sandwiched Between MgO Barrier and Cap Layers in Magnetic Tunnel Junctions. Appl. Phys. Express 2014, 7, 033004. [Google Scholar] [CrossRef]
- Xiang, Q.; Mandal, R.; Sukegawa, H.; Takahashi, Y.K.; Mitani, S. Large Perpendicular Magnetic Anisotropy in Epitaxial Fe/MgAl2O4 (001) Heterostructures. Appl. Phys. Express 2018, 11, 063008. [Google Scholar] [CrossRef]
- Kent, A.D. Perpendicular All the Way. Nat. Mater. 2010, 9, 699. [Google Scholar] [CrossRef] [PubMed]
- Okabayashi, J.; Koo, J.W.; Sukegawa, H.; Mitani, S.; Takagi, Y.; Yokoyama, T. Perpendicular Magnetic Anisotropy at the Interface Between Ultrathin Fe Film and MgO Studied by Angular-Dependent X-Ray Magnetic Circular Dichroism. Appl. Phys. Lett. 2014, 105, 122408. [Google Scholar] [CrossRef]
- Yang, H.X.; Chshiev, M.; Dieny, B.; Lee, J.H.; Manchon, A.; Shin, K.H. First-Principles Investigation of the Very Large Perpendicular Magnetic Anisotropy at Fe/MgO and Co/MgO Interfaces. Phys. Rev. B 2011, 84, 054401. [Google Scholar] [CrossRef]
- Hallal, A.; Yang, H.X.; Dieny, B.; Chshiev, M. Anatomy of Perpendicular Magnetic Anisotropy in Fe/MgO Magnetic Tunnel Junctions: First-Principles Insight. Phys. Rev. B 2013, 88, 184423. [Google Scholar] [CrossRef]
- Lambert, C.H.; Rajanikanth, A.; Hauet, T.; Mangin, S.; Fullerton, E.E.; Andrieu, S. Quantifying Perpendicular Magnetic Anisotropy at the Fe-MgO(001) Interface. Appl. Phys. Lett. 2013, 102, 122410. [Google Scholar] [CrossRef]
- Kozioł-Rachwat, A.; Skowronski, W.; Slezak, T.; Wilgocka-Slezak, D.; Przewoznik, J.; Stobiecki, T.; Qin, Q.H.; van Dijken, S.; Korecki, J. Room-Temperature Perpendicular Magnetic Anisotropy of MgO/Fe/MgO Ultrathin Films. J. Appl. Phys. 2013, 114, 224307. [Google Scholar] [CrossRef]
- Koo, J.W.; Mitani, S.; Sasaki, T.T.; Sukegawa, H.; Wen, Z.C.; Ohkubo, T.; Niizeki, T.; Inomata, K.; Hono, K. Large Perpendicular Magnetic Anisotropy at Fe/MgO Interface. Appl. Phys. Lett. 2013, 103, 192401. [Google Scholar] [CrossRef]
- Nazir, S.; Yang, K. Elucidate Interfacial Disorder Effects on the Perpendicular Magnetic Anisotropy at Fe/MgO Heterostructure from First-Principles Calculations. J. Phys. Condens. Matter 2022, 34, 214009. [Google Scholar] [CrossRef]
- Hu, Y.; Yan, S.; Jin, D.; Qiao, W.; Bai, R.; Zhou, T. Giant and Strain-Tunable Interfacial Magnetic Anisotropy in MgO-Based Magnetic Heterostructures with Heavy Atoms Insertion. Phys. Scr. 2022, 98, 015022. [Google Scholar] [CrossRef]
- Niranjan, M.K.; Duan, C.G.; Jaswal, S.S.; Tsymbal, E.Y. Electric Field Effect on Magnetization at the Fe/MgO(001) Interface. Appl. Phys. Lett. 2010, 96, 222504. [Google Scholar] [CrossRef]
- Nakamura, K.; Akiyama, T.; Ito, T.; Weinert, M.; Freeman, A.J. Role of an Interfacial FeO Layer in the Electric-Field-Driven Switching of Magnetocrystalline Anisotropy at the Fe/MgO Interface. Phys. Rev. B 2010, 81, 220409. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y.; Wen, H.; Dong, C. Strain and Ferroelectric Polarization Influence on Perpendicular Magnetic Anisotropy of CoFe3N/BaTiO3 Heterostructure. Results Phys. 2024, 57, 107388. [Google Scholar] [CrossRef]
- Rodewald, J.; Thien, J.; Ruwisch, K.; Pohlmann, T.; Hoppe, M.; Schmalhorst, J.; Küpper, K.; Wollschläger, J. Structure-Related Electronic and Magnetic Properties in Ultrathin Epitaxial NixFe3−xO4 Films on MgO(001). Nanomaterials 2024, 14, 694. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Behtash, M.; Wong, J.; Yang, K. Enhancing Ferroelectric Dipole Ordering in Organic–Inorganic Hybrid Perovskite CH3NH3PbI3: Strain and Doping Engineering. J. Phys. Chem. C 2018, 122, 177–184. [Google Scholar] [CrossRef]
- Chen, Y.; Lei, Y.; Li, Y.; Yu, Y.; Cai, J.; Chiu, M.H.; Rao, R.; Gu, Y.; Wang, C.; Choi, W.; et al. Strain Engineering and Epitaxial Stabilization of Halide Perovskites. Nature 2020, 577, 209. [Google Scholar] [CrossRef] [PubMed]
- Nazir, S.; Behtash, M.; Yang, K. Enhancing Interfacial Conductivity and Spatial Charge Confinement of LaAlO3/SrTiO3 Heterostructures Via Strain Engineering. Appl. Phys. Lett. 2014, 105, 141602. [Google Scholar] [CrossRef]
- Nazir, S.; Behtash, M.; Yang, K. The Role of Uniaxial Strain in Tailoring the Interfacial Properties of LaAlO3/SrTiO3(001) Heterostructure. RSC Adv. 2015, 5, 15682–15689. [Google Scholar] [CrossRef]
- Nazir, S.; Yang, K. First-Principles Characterization of the Critical Thickness for Forming Metallic States in Strained LaAlO3/SrTiO3(001) Heterostructure. ACS Appl. Mater. Interfaces 2014, 6, 22351–22358. [Google Scholar] [CrossRef]
- Ong, P.V.; Kioussis, N.; Amiri, P.K.; Wang, K.L.; Carman, G.P. Strain Control Magnetocrystalline Anisotropy of Ta/FeCo/MgO Heterostructures. J. Appl. Phys. 2015, 117, 17B518. [Google Scholar] [CrossRef]
- Huang, W.; Zhu, J.; Zeng, H.; Wei, X.; Zhang, Y.; Li, Y. Strain Induced Magnetic Anisotropy in Highly Epitaxial CoFe2O4 Thin Films. Appl. Phys. Lett. 2006, 89, 262506. [Google Scholar] [CrossRef]
- Magnifouet, G.; Vallet, M.; Meslin, E.; Walls, M.; Bouillet, C.; Arabski, J.; Pierron-Bohnes, V. Strains in Fe/Cr/Fe Trilayers and (Fe/Cr)5/Fe Multilayers Epitaxied on MgO and MgO/SrTiO3. Thin Solid Films 2023, 780, 139949. [Google Scholar] [CrossRef]
- Kim, K.h.; Kim, H.j.; Kim, G.H.; Chang, J.; Han, S.h. Strain-Induced Microstructural Evolution in Epitaxial Fe/MgO Layers Grown on InxGa1−xAs(001) Substrates. Appl. Phys. Lett. 2009, 95, 164103. [Google Scholar] [CrossRef]
- Park, J.; Yu, B.D. Epitaxial Strain and Interfacial Electronic Topological Transition in O-rich MgO/FeO/Fe(001) Interfaces. Phys. Rev. B 2011, 83, 144431. [Google Scholar] [CrossRef]
- Han, X.; Cui, H.; Liu, B.; Tian, C.; Wang, J.; Chen, H.; Yuan, H. Effects of Overlayer Capping and Lattice Strain on Perpendicular Magnetic Anisotropy of TM/FePt/MgO Heterostructures. Sci. Rep. 2018, 8, 9429. [Google Scholar] [CrossRef] [PubMed]
- Shiga, M.; Sakamoto, S.; Tsujikawa, T.; Ando, R.; Amemiya, K.; Miwa, S. Influence of Epitaxial Strain on the Perpendicular Magnetic Anisotropy of Fe/MgO Systems. Phys. Rev. B 2021, 104, L140406. [Google Scholar] [CrossRef]
- Subagyo, A.; Oka, H.; Eilers, G.; Sueoka, K.; Mukasa, K. Scanning Tunneling Microscopy Observation of Epitaxial Bcc-Fe(001) Surface. Jpn. J. Appl. Phys. 2000, 39, 3777. [Google Scholar] [CrossRef]
- Dugerjav, O.; Kim, H.; Seo, J.M. Growth of a Crystalline and Ultrathin MgO Film on Fe(001). AIP Adv. 2011, 1, 032156. [Google Scholar] [CrossRef]
- Baumann, S.; Donati, F.; Stepanow, S.; Rusponi, S.; Paul, W.; Gangopadhyay, S.; Rau, I.G.; Pacchioni, G.E.; Gragnaniello, L.; Pivetta, M.; et al. Origin of Perpendicular Magnetic Anisotropy and Large Orbital Moment in Fe Atoms on MgO. Phys. Rev. Lett. 2015, 115, 237202. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Wu, R.; Shen, L.; Feng, Y.P.; Dai, Y.; Huang, B. Origin of d0 Magnetism in II-VI and III-V Semiconductors by Substitutional Doping at Anion Site. Phys. Rev. B 2010, 81, 125211. [Google Scholar] [CrossRef]
- Bruno, P. Tight-Binding Approach to the Orbital Magnetic Moment and Magnetocrystalline Anisotropy of Transition-Metal Monolayers. Phys. Rev. B 1989, 39, 865–868. [Google Scholar] [CrossRef]
- Masuda, K.; Kasai, S.; Miura, Y.; Hono, K. Giant Interfacial Perpendicular Magnetic Anisotropy in Fe/CuIn1−xGaxSe2 Beyond Fe/MgO. Phys. Rev. B 2017, 96, 174401. [Google Scholar] [CrossRef]
- Odkhuu, D. Giant Strain Control of Magnetoelectric Effect in Ta/Fe/MgO. Sci. Rep. 2016, 6, 32742–32750. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmuller, J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient Iterative Schemes for Ab-Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).